Similar presentations:
Комплексный чертёж плоскости и поверхности
1. Лекция 3
Комплексный чертёжплоскости и поверхности
2. Задание плоскости на комплексном чертеже
• Плоскость является частным случаемповерхности - это двумерная
геометрическая фигура, она имеет
только длину и ширину, и не имеет
толщины. Обозначается прописными
буквами греческого алфавита.
Плоскость - это множество точек, но
определяется она тремя точками
(напомним, что прямую линию
определяют две точки).
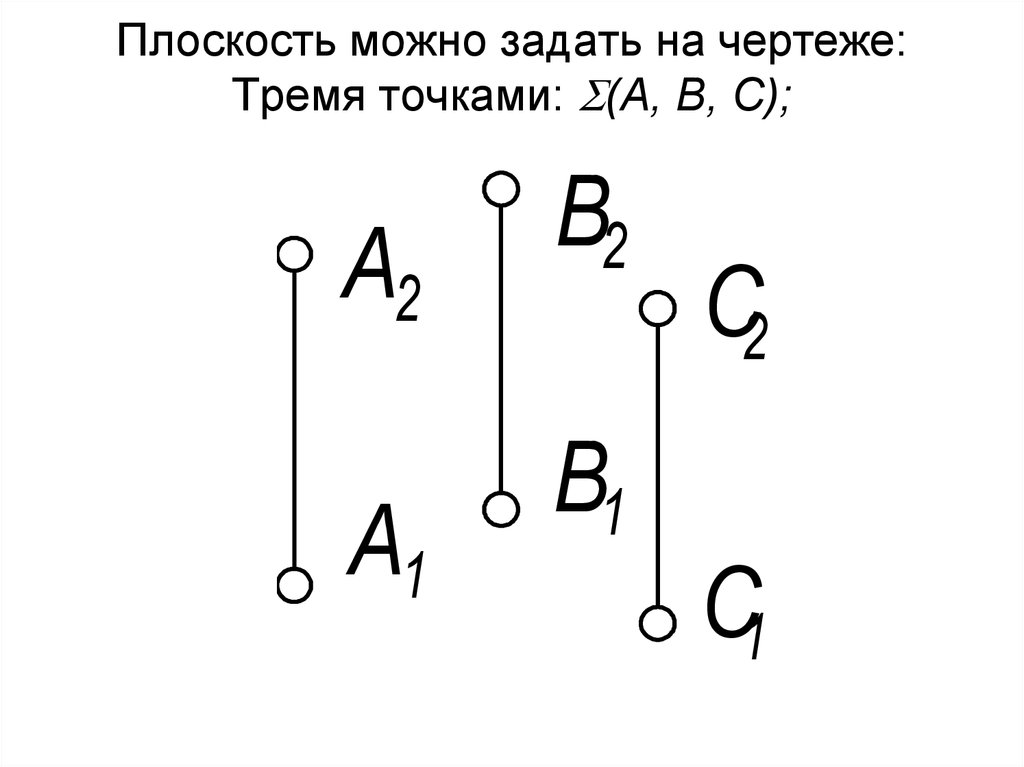
3. Плоскость можно задать на чертеже: Тремя точками: (А, В, С);
Плоскость можно задать на чертеже:Тремя точками: (А, В, С);
А2
А1
В2
В1
С2
С1
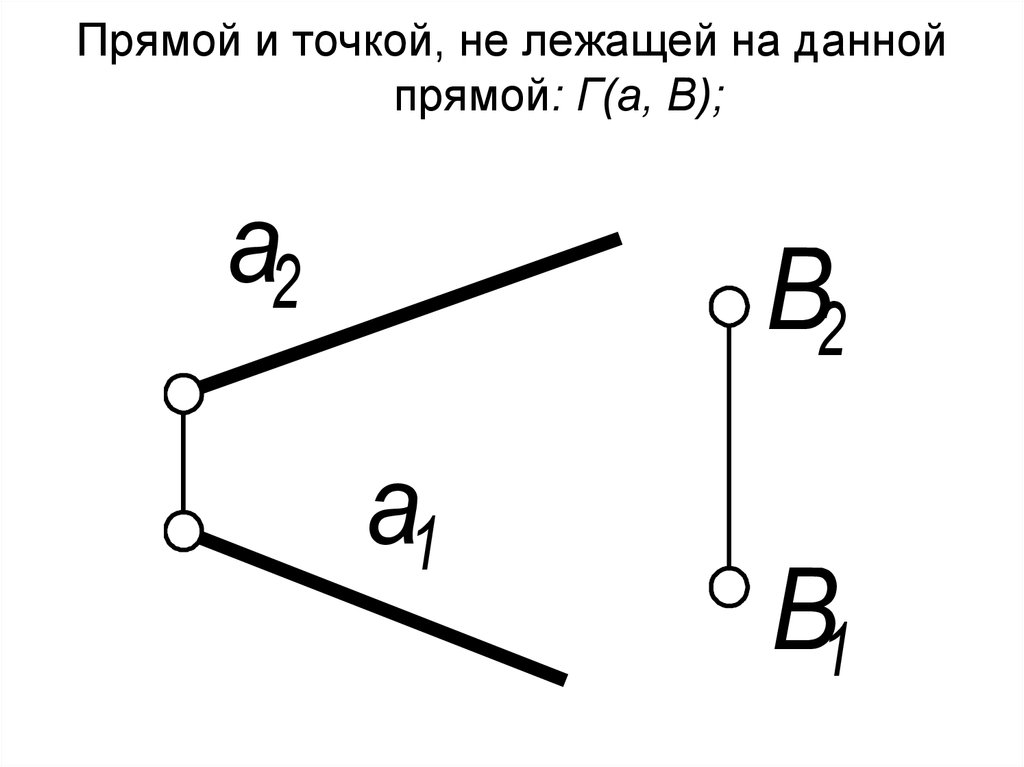
4. Прямой и точкой, не лежащей на данной прямой: Г(а, В);
а2В2
а1
В1
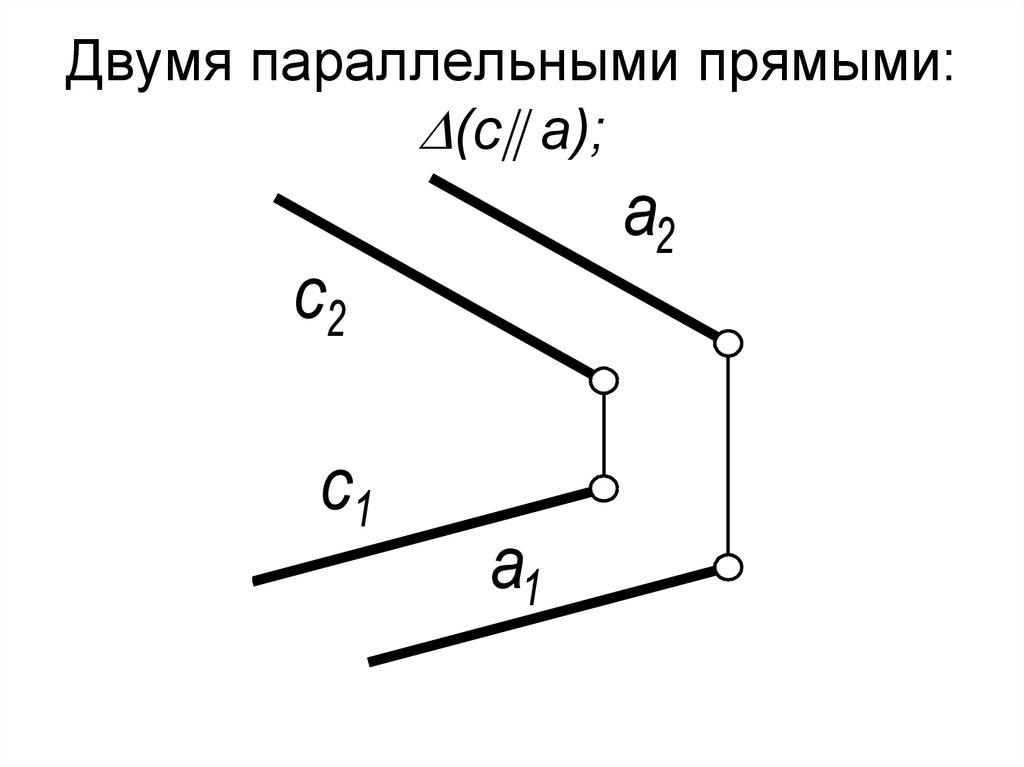
5. Двумя параллельными прямыми: (с а);
Двумя параллельными прямыми:(с а);
а2
с2
с1
а1
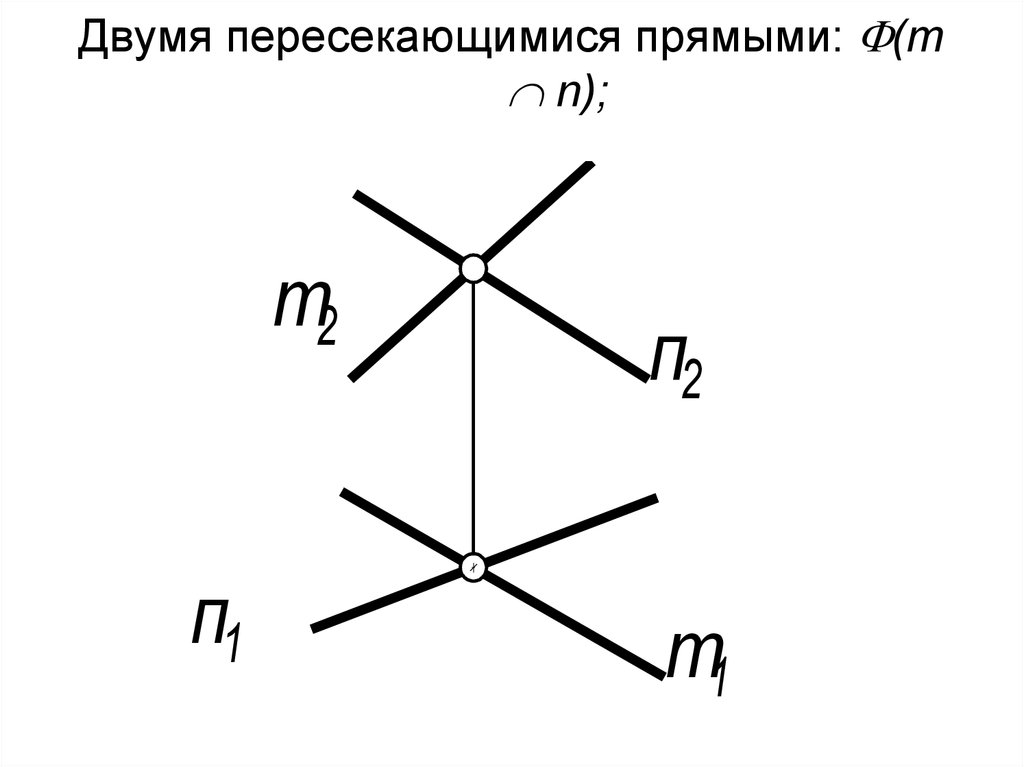
6. Двумя пересекающимися прямыми: (m n);
Двумя пересекающимися прямыми: (mn);
т2
п1
п2
т1
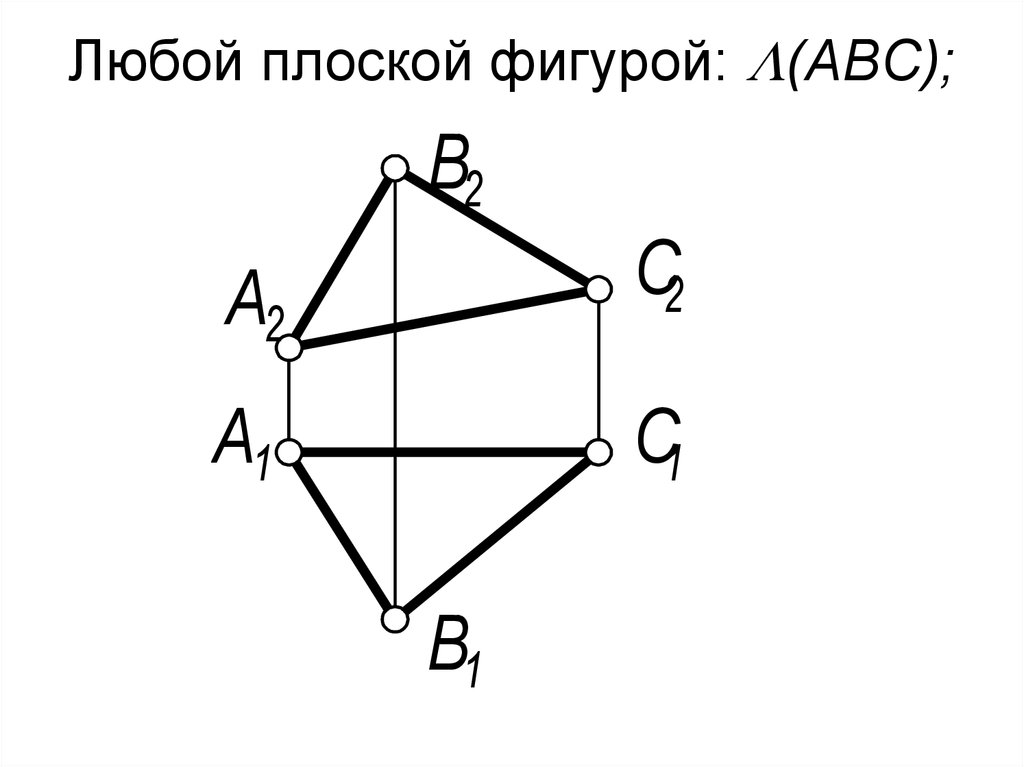
7. Любой плоской фигурой: (АВС);
Любой плоской фигурой: (АВС);В2
А2
С2
А1
С1
В1
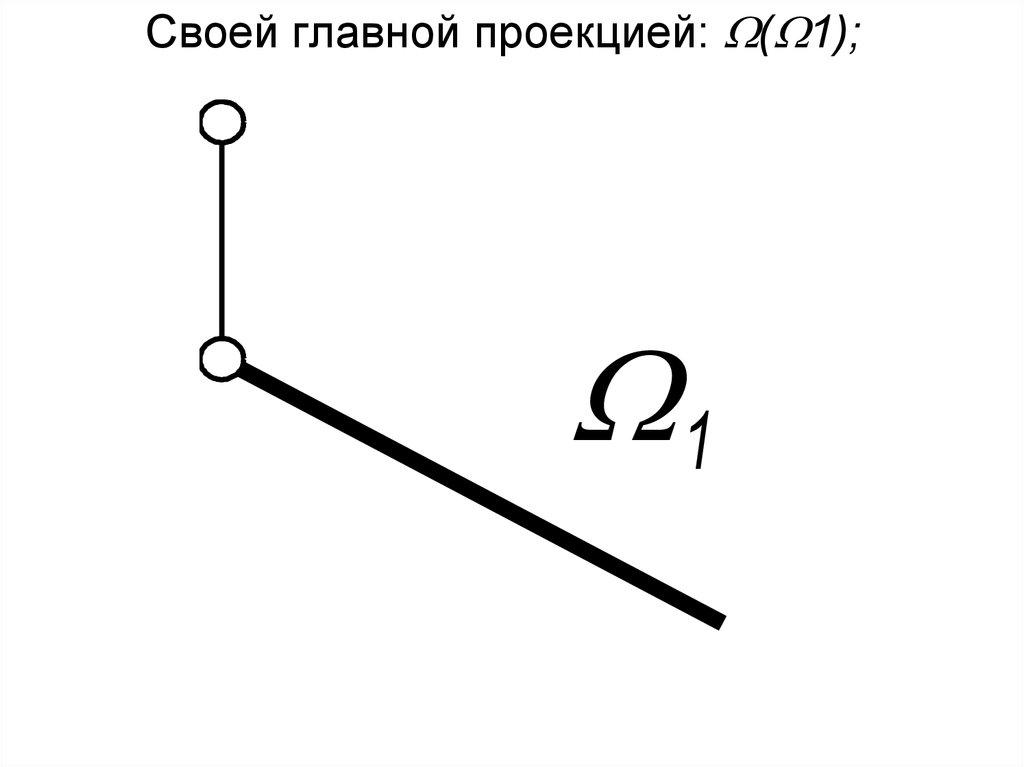
8. Своей главной проекцией: (1);
Своей главной проекцией: ( 1);1
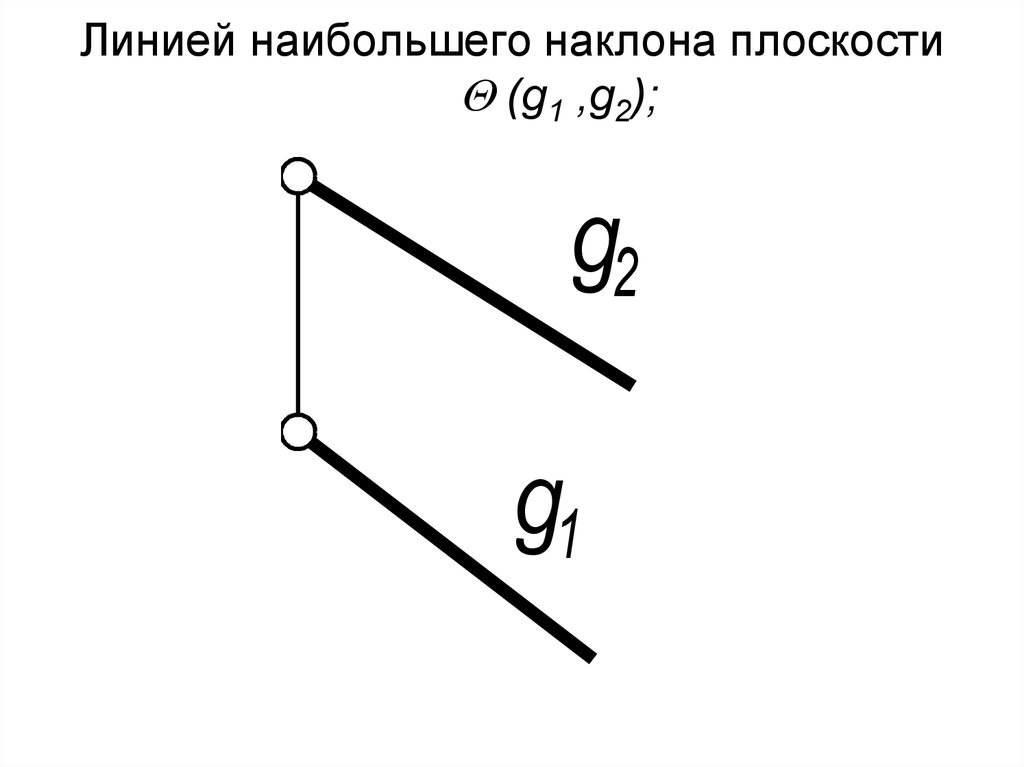
9. Линией наибольшего наклона плоскости (g1 ,g2);
Линией наибольшего наклона плоскости(g1 ,g2);
g2
g1
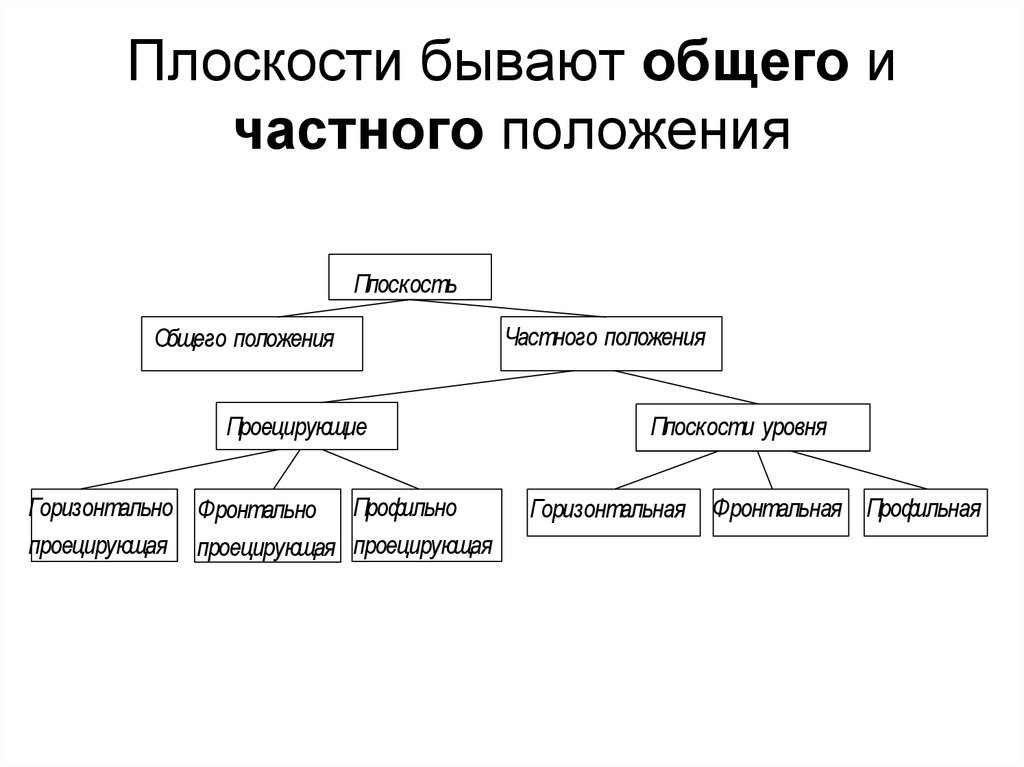
10. Плоскости бывают общего и частного положения
ПлоскостьОбщего положения
Проецирующие
Горизонтально Фронтально Профильно
проецирующая проецирующая проецирующая
Частного положения
Плоскости уровня
Горизонтальная
Фронтальная Профильная
11. Взаимная принадлежность точки, прямой и плоскости
• Точка принадлежит плоскости, еслиона принадлежит какой-нибудь
прямой, лежащей в этой плоскости.
• Построение точки в плоскости сводится
к двум операциям: построению в
плоскости вспомогательной прямой и
построению точки на этой прямой.
12. Задача: Плоскость задана пересекающимися прямыми а и b . Точка М(М2 ) принадлежит плоскости. Найти М1. Краткая запись условия
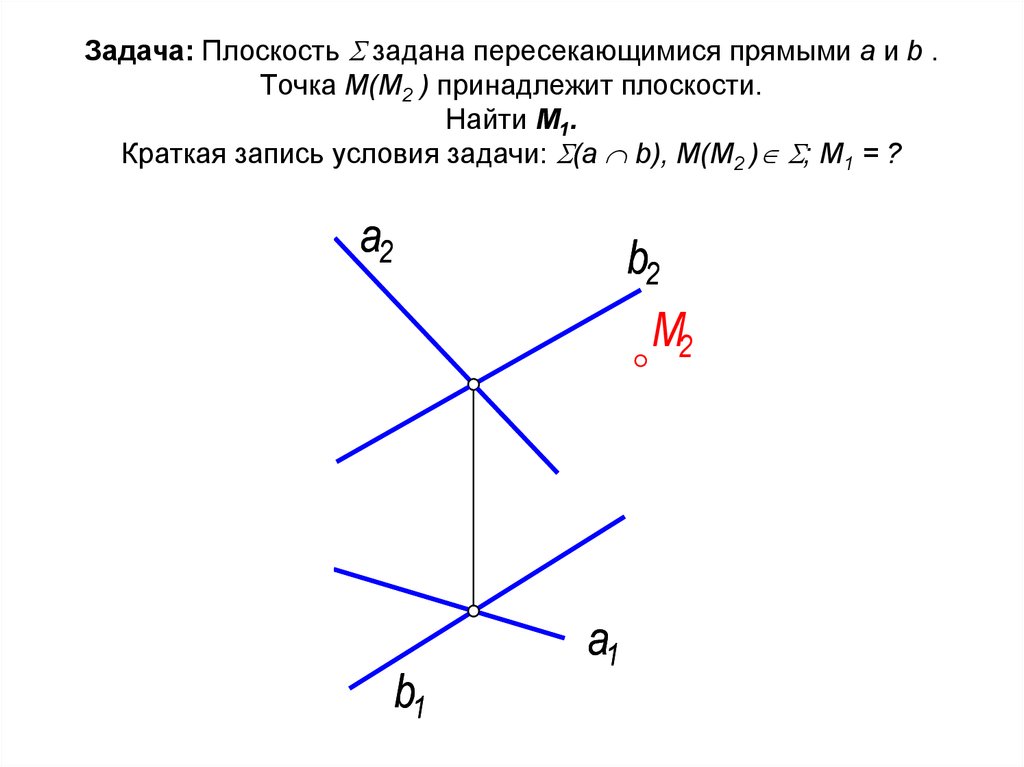
Задача: Плоскость задана пересекающимися прямыми а и b .Точка М(М2 ) принадлежит плоскости.
Найти М1.
Краткая запись условия задачи: (а b), М(М2 ) ; М1 = ?
а2
b2
M2
a1
b1
13. Решение: Через точку М2 проводим вспомогательную прямую k : k2 a2 =12; k2 b2 =22; затем находим горизонтальные проекции
Решение: Через точку М2 проводим вспомогательную прямуюk : k2 a2 =12; k2 b2 =22; затем находим горизонтальные
проекции точек 1 и 2 по условию принадлежности прямым а и b
соответственно; через две точки 11 и 21 проводим прямую k1 и на
ней, с помощью линии связи, находим точку М1. И таких прямых
можно провести сколько угодно, то есть, вариантов решения
бесчисленное множество.
а2
12
k2 2
2
k1
21
a1
11
b1
b2
M2
M1
14. Прямая принадлежит плоскости, если она:
1. Проходит через две точкиплоскости;
2. Проходит через одну точку
плоскости и параллельна какойнибудь прямой, лежащей в этой
плоскости.
15. Задача: Плоскость Г задана АВС. Точка М(М1) принадлежит Г. Найти М2. М(М1) Г(АВС). М2 = ?
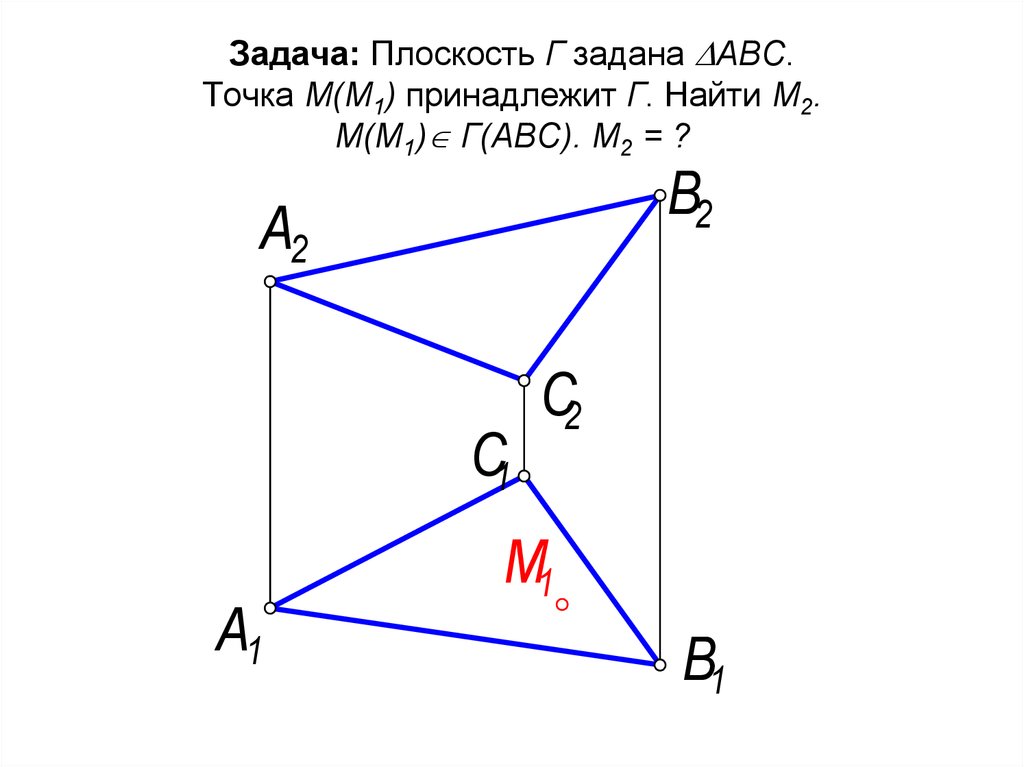
Задача: Плоскость Г задана АВС.Точка М(М1) принадлежит Г. Найти М2.
М(М1) Г(АВС). М2 = ?
В2
А2
С1
А1
С2
М1
В1
16. Решение: Через точку М1 проведём прямую k, параллельную стороне треугольника АВ. Она пересечёт сторону АС в точке 1: k1 A1
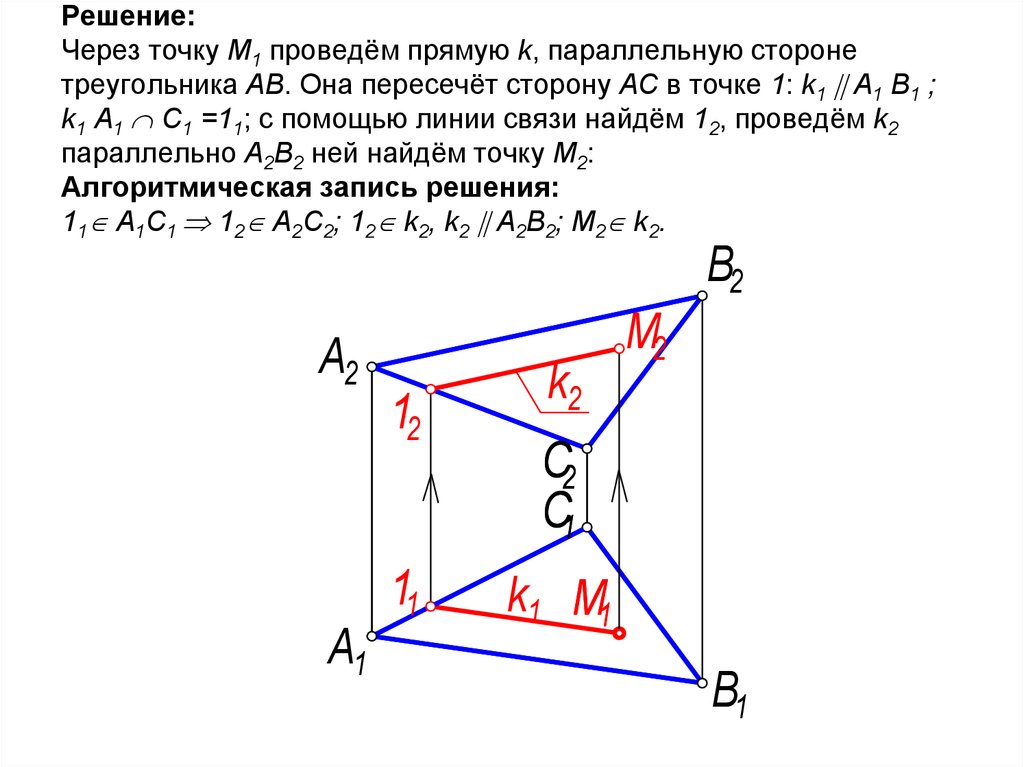
Решение:Через точку М1 проведём прямую k, параллельную стороне
треугольника АВ. Она пересечёт сторону АС в точке 1: k1 A1 B1 ;
k1 A1 C1 =11; с помощью линии связи найдём 12, проведём k2
параллельно А2В2 ней найдём точку М2:
Алгоритмическая запись решения:
11 A1C1 12 A2C2; 12 k2, k2 A2B2; M2 k2.
В2
А2
12
А1
11
k2
М2
С2
С1
k1 М1
В1
17. Плоскости частного положения Плоскости, параллельные или перпендикулярные одной из плоскостей проекций, называются плоскостями
частногоположения.
Имеется две группы таких плоскостей:
• Проецирующие плоскости
• Плоскости уровня
18. Проецирующие плоскости
• Если плоскость перпендикулярнатолько одной плоскости проекций, то
она называется проецирующей.
• Одна из её проекций вырождается в
прямую линию, называемую главной
проекцией и обладающую
собирательными свойствами.
19. Горизонтально проецирующая плоскость
Это плоскость, перпендикулярная горизонтальнойплоскости проекций: Г П1.
Графический признак:
Горизонтальная проекция Г1 горизонтально
проецирующей плоскости прямая линия, не
параллельная и не перпендикулярная линиям
связи. Это главная проекция.
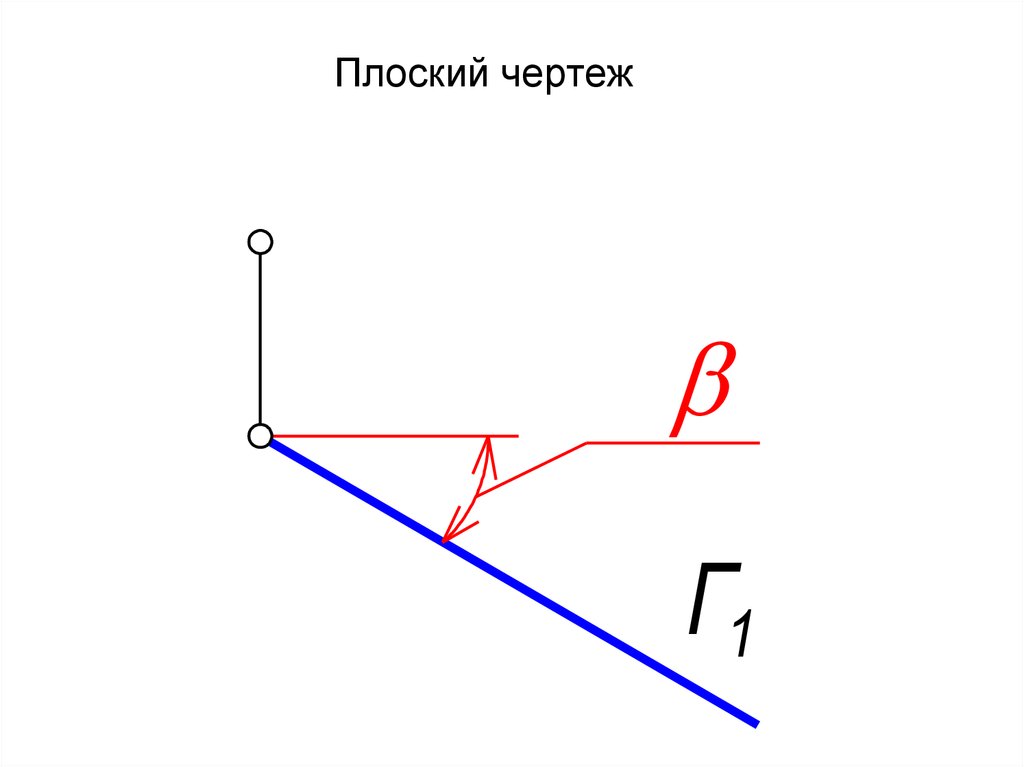
Например:
Г П1 - горизонтально проецирующая плоскость.
Г П1 Г1 - прямая линия, главная проекция.
• - угол наклона плоскости Г к П2.
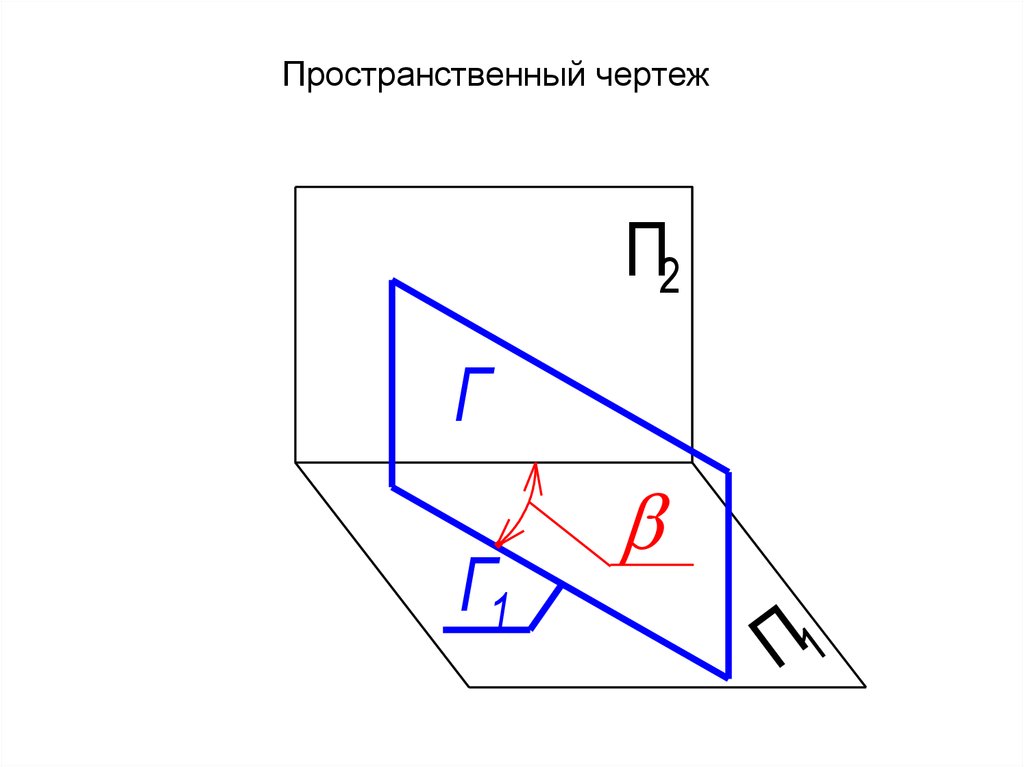
20. Пространственный чертеж
П2Г
Г1
П1
21. Плоский чертеж
Г122. Фронтально проецирующая плоскость
Это плоскость, перпендикулярнаяфронтальной плоскости проекций:
П2
Графический признак:
Фронтальная проекция 2 фронтально
проецирующей плоскости - прямая
линия, не параллельная и не
перпендикулярная линиям связи. Это
главная проекция.
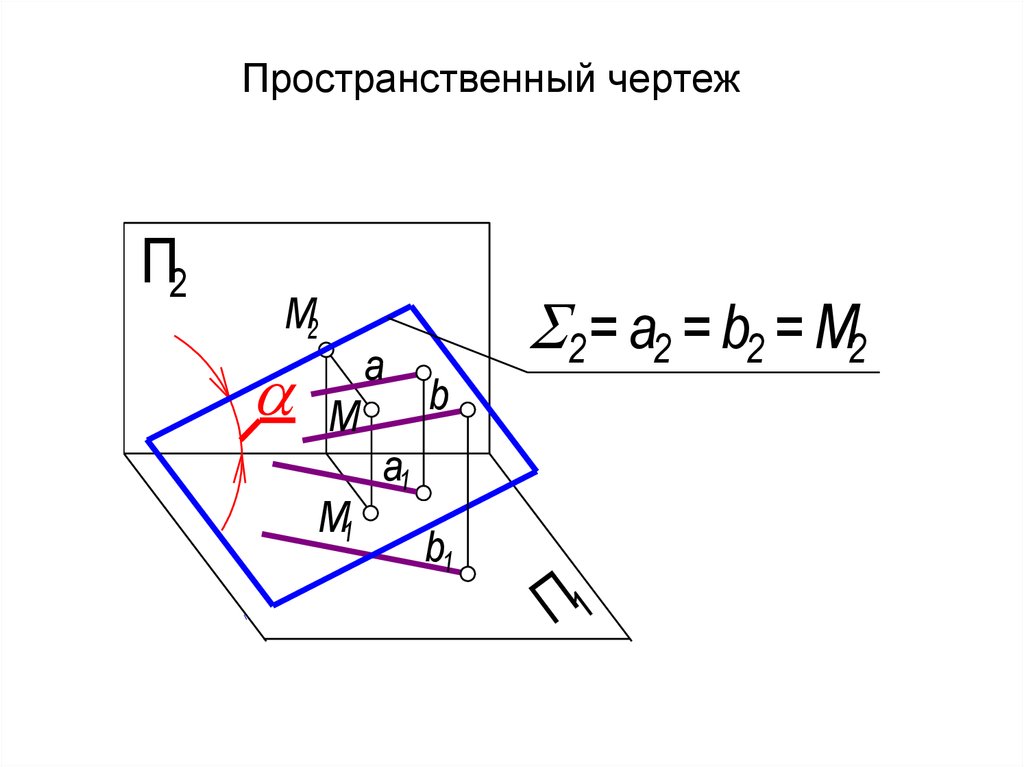
23. Пространственный чертеж
П2M2
М
а
2= а2 = b2 = M2
b
a1
M1
b1
П1
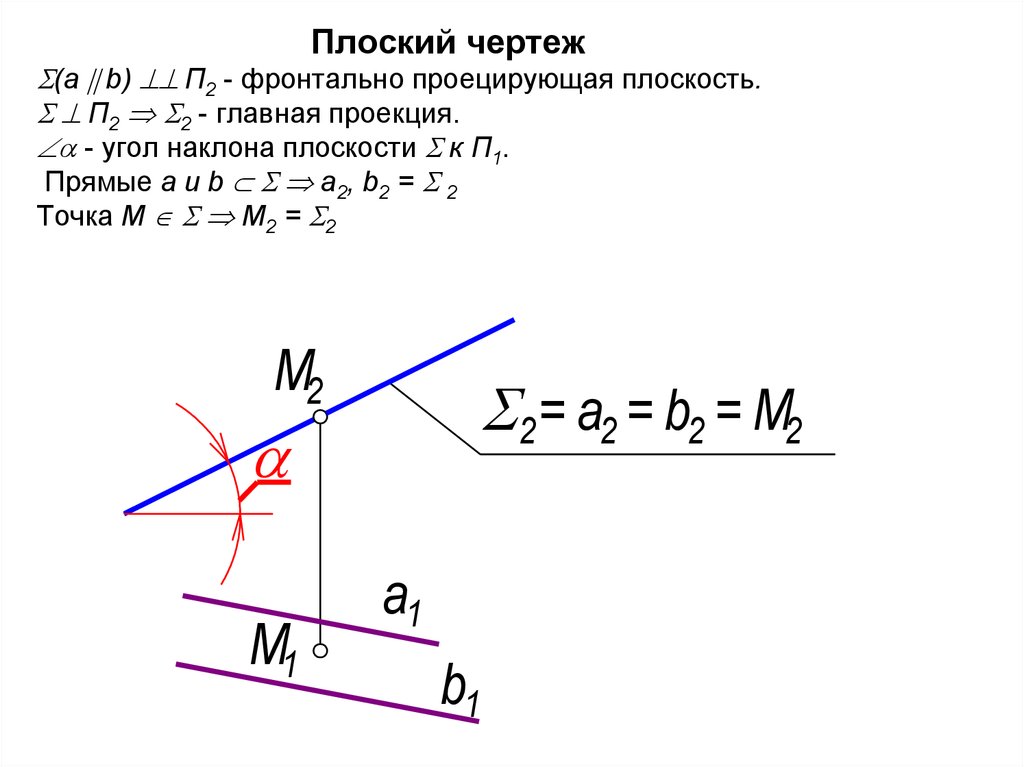
24. Плоский чертеж (а b) П2 - фронтально проецирующая плоскость. П2 2 - главная проекция. - угол наклона плоскости
Плоский чертеж(а b) П2 - фронтально проецирующая плоскость.
П2 2 - главная проекция.
- угол наклона плоскости к П1.
Прямые а и b а2, b2 = 2
Точка М М2 = 2
M2
2= а2 = b2 = M2
M1
a1
b1
25. Плоскости уровня (дважды проецирующие)
• Если плоскость перпендикулярнаодновременно двум плоскостям
проекций, а, следовательно,
параллельна третьей, то она
называется плоскостью уровня.
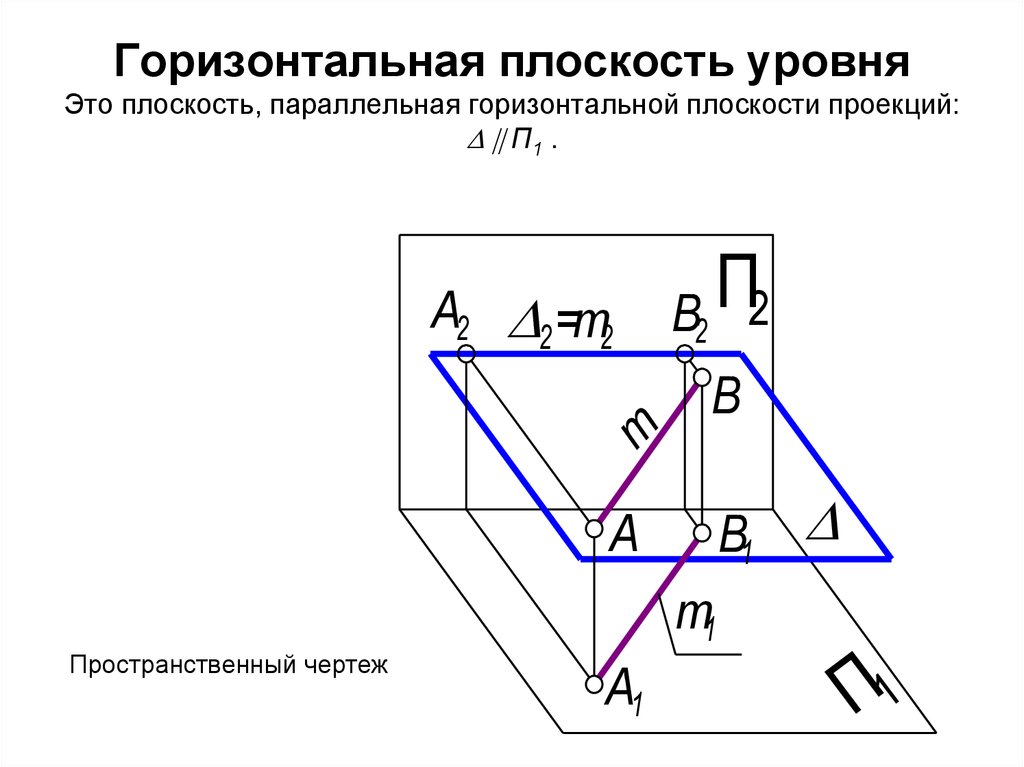
26. Горизонтальная плоскость уровня Это плоскость, параллельная горизонтальной плоскости проекций: П1 .
Горизонтальная плоскость уровняЭто плоскость, параллельная горизонтальной плоскости проекций:
П1 .
А2
2 =т2
П
В2 2
т
В
В1
А
т1
Пространственный чертеж
А1
П1
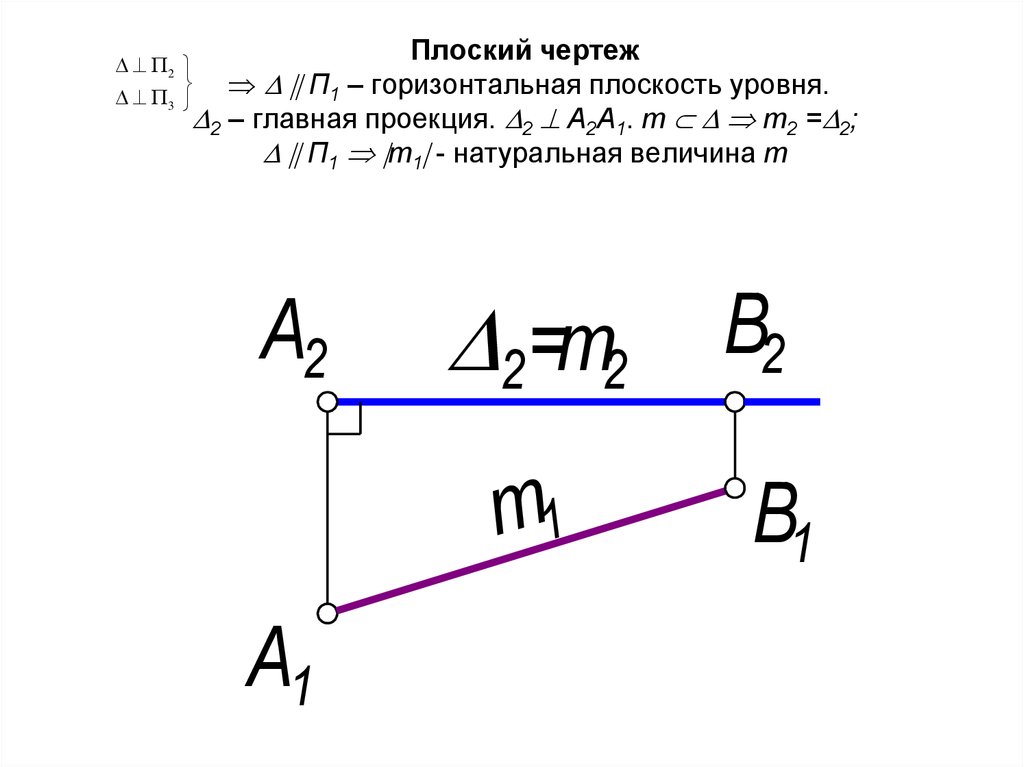
27. Плоский чертеж П1 – горизонтальная плоскость уровня. 2 – главная проекция. 2 А2А1. m m2 =2; П1 m1 -
Плоский чертежП1 – горизонтальная плоскость уровня.
2 – главная проекция. 2 А2А1. m m2 = 2;
П1 m1 - натуральная величина m
2
3
А2
2=т2
т1
А1
В2
В1
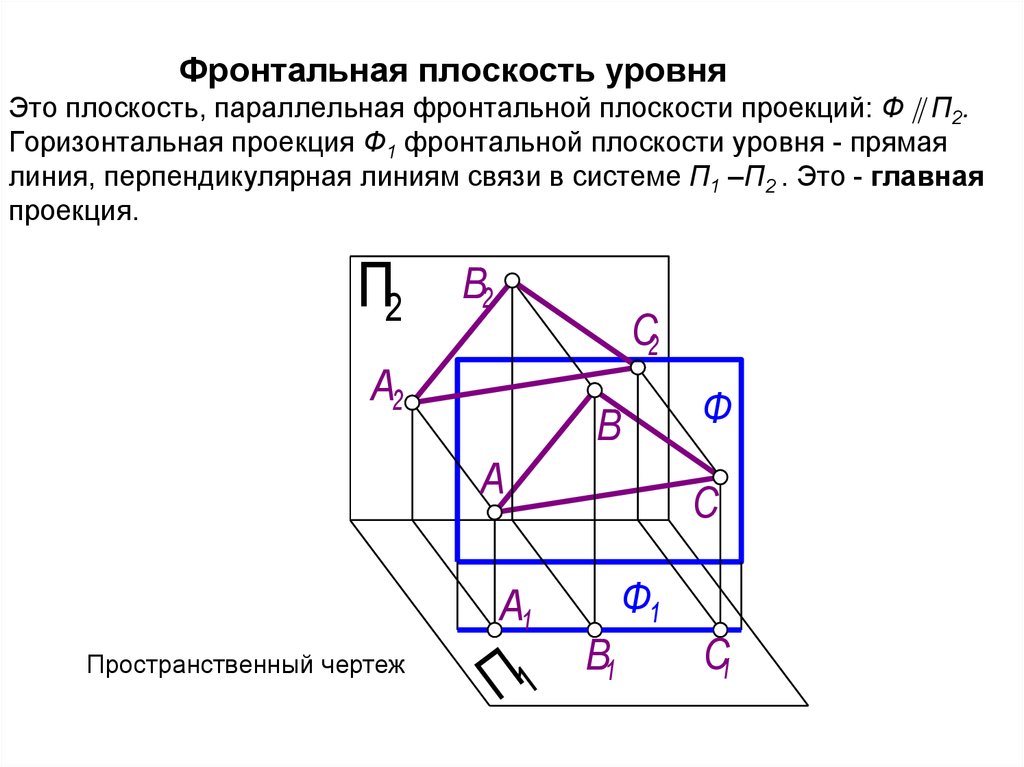
28. Фронтальная плоскость уровня Это плоскость, параллельная фронтальной плоскости проекций: Ф П2. Горизонтальная проекция Ф1
Фронтальная плоскость уровняЭто плоскость, параллельная фронтальной плоскости проекций: Ф П2.
Горизонтальная проекция Ф1 фронтальной плоскости уровня - прямая
линия, перпендикулярная линиям связи в системе П1 –П2 . Это - главная
проекция.
П2
В2
С2
А2
В
А
А1
Пространственный чертеж
П1
Ф
С
Ф1
В1
С1
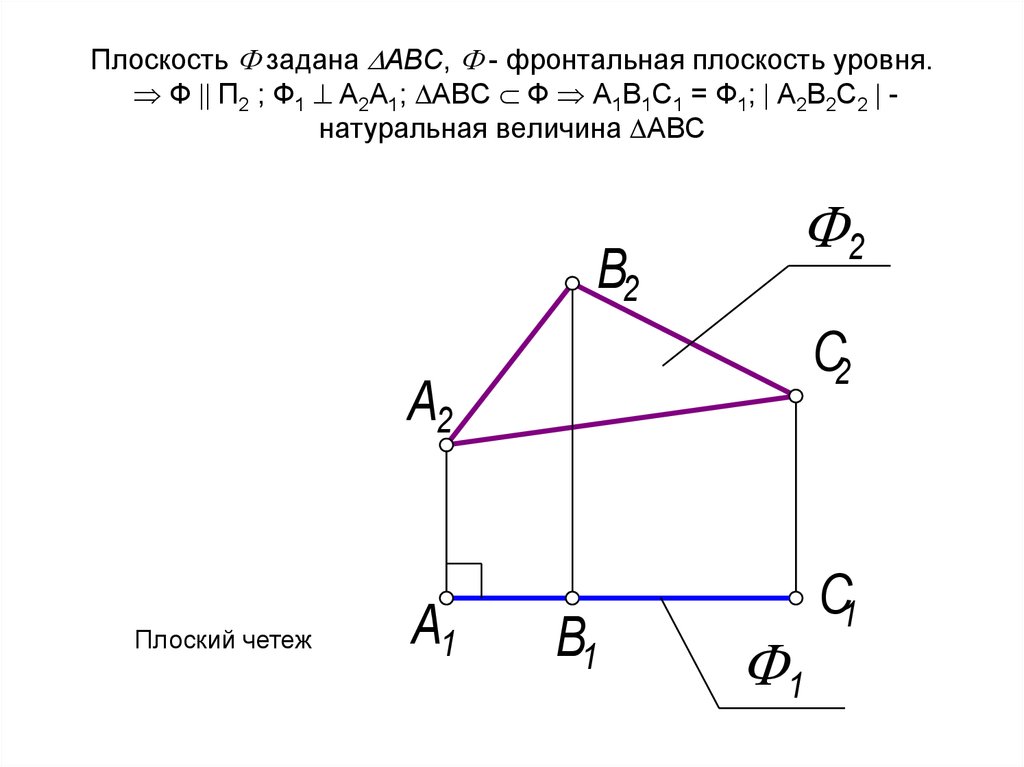
29. Плоскость задана АВС, - фронтальная плоскость уровня. Ф П2 ; Ф1 А2А1; АВС Ф А1В1С1 = Ф1; A2B2C2
Плоскость задана АВС, - фронтальная плоскость уровня.Ф П2 ; Ф1 А2А1; АВС Ф А1В1С1 = Ф1; A2B2C2 натуральная величина АВС
В2
С2
А2
Плоский четеж
А1
2
В1
С1
1
30. Особые линии плоскости
• Если прямая принадлежит плоскости изанимает в ней какое-то особое
положение, то она называется особой
линией плоскости. К ним относятся
линии уровня плоскости: горизонталь,
фронталь и профильная прямая, а
также линии наибольшего наклона
плоскости.
31. Горизонталь плоскости Это прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций Г (a b)
Горизонталь плоскостиЭто прямая, принадлежащая плоскости, и параллельная
горизонтальной плоскости проекций
Г (a b) Построить: h Г; h П1
1. Проводим h2 перпендикулярно линиям связи.
а2
12 h2
11
b2
22
21
a1
b1
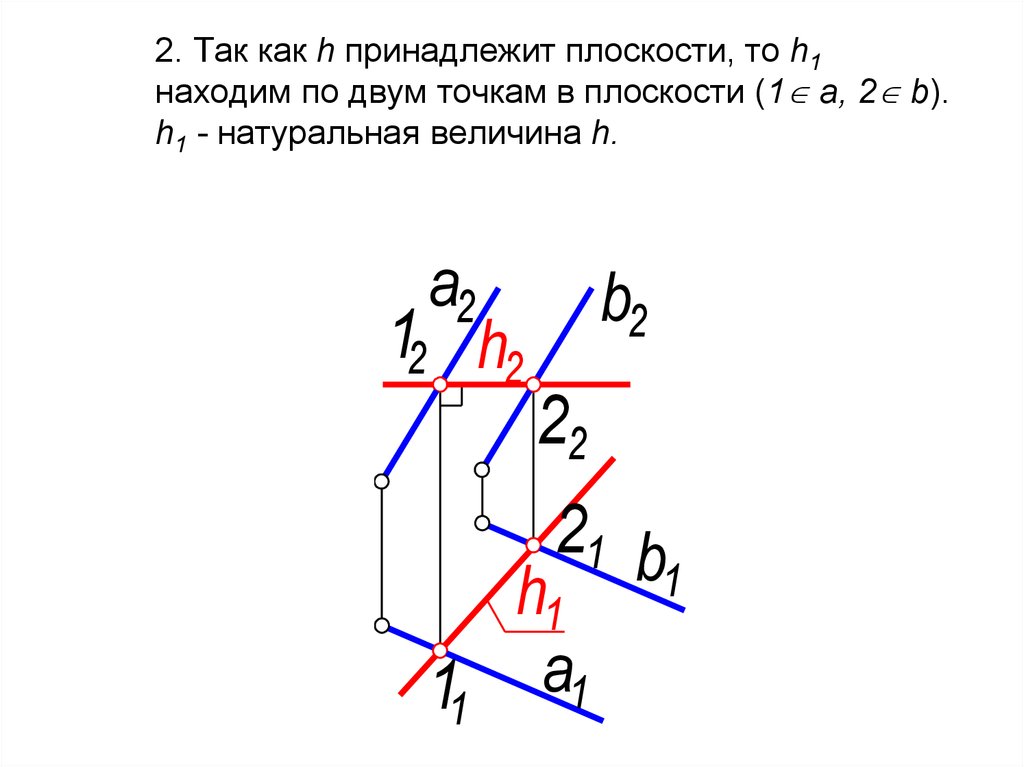
32. 2. Так как h принадлежит плоскости, то h1 находим по двум точкам в плоскости (1 а, 2 b). h1 - натуральная величина h.
2. Так как h принадлежит плоскости, то h1находим по двум точкам в плоскости (1 а, 2 b).
h1 - натуральная величина h.
а2
b2
12 h2
22
21 b
1
h
1
11
a1
33.
• Построение горизонтали вплоскости начинают с
фронтальной проекции h2: она
всегда перпендикулярна
линиям связи в системе П2 –П1.
h1 находят по принадлежности
плоскости и она является
натуральной длиной
горизонтали.
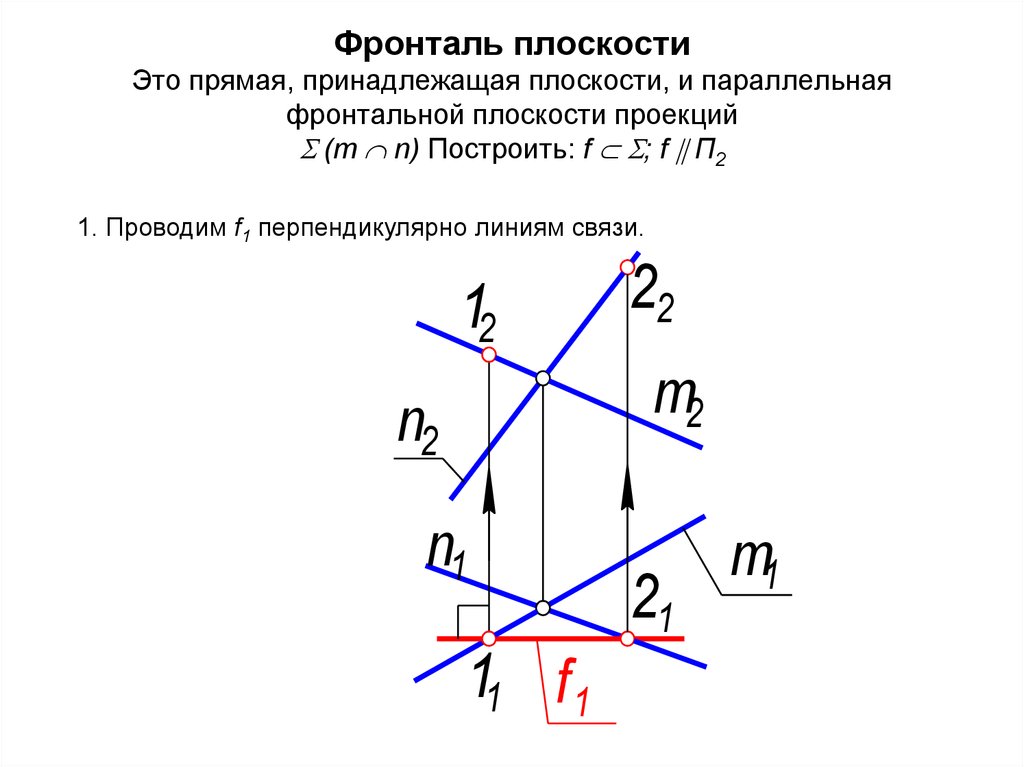
34. Фронталь плоскости Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций (m n) Построить: f
Фронталь плоскостиЭто прямая, принадлежащая плоскости, и параллельная
фронтальной плоскости проекций
(m n) Построить: f ; f П2
1. Проводим f1 перпендикулярно линиям связи.
12
22
m2
n2
n1
11 f 1
21
m1
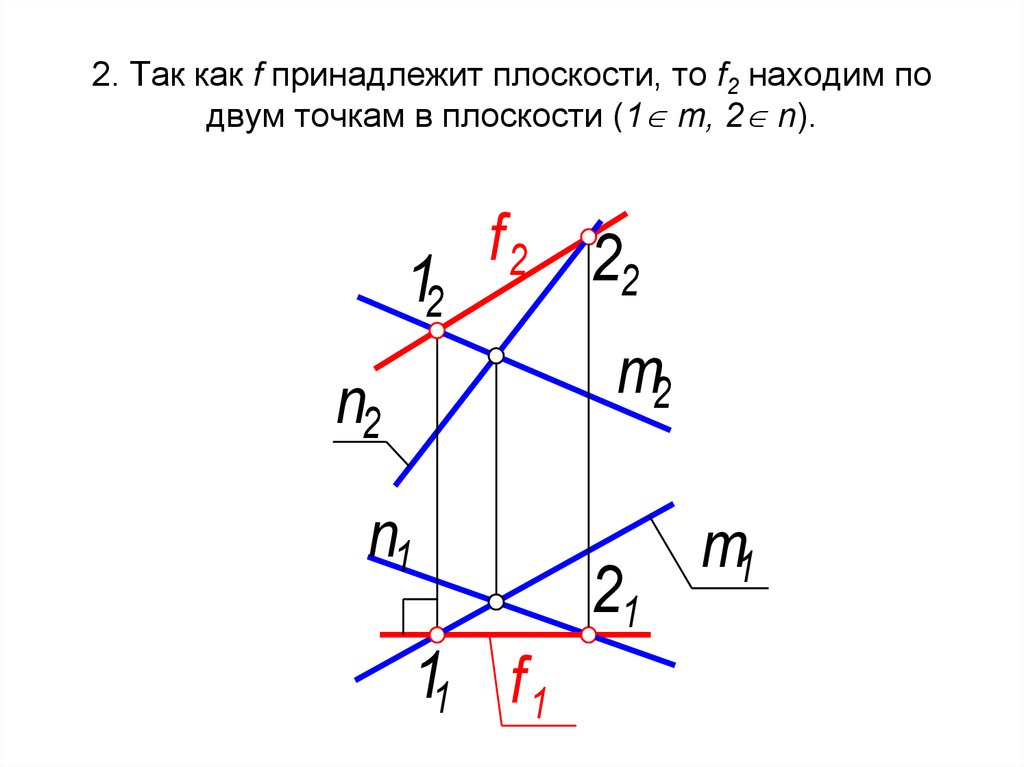
35. 2. Так как f принадлежит плоскости, то f2 находим по двум точкам в плоскости (1 m, 2 n).
2. Так как f принадлежит плоскости, то f2 находим подвум точкам в плоскости (1 m, 2 n).
f2 2
2
12
m
2
n2
n1
11 f 1
21
m1
36.
• Построение фронтали вплоскости начинают с
горизонтальной проекции f1 :
она всегда перпендикулярна
линиям связи в системе П2 –П1.
f2 находят по принадлежности
плоскости.Это - натуральная
величина f.
37. Линия наибольшего наклона плоскости
• Это прямая, принадлежащая плоскости иперпендикулярная одной из линий
уровня плоскости. С её помощью
определяют угол наклона заданной
плоскости к одной из плоскостей
проекций. Условимся линию
наибольшего наклона плоскости к П1
обозначать буквой g , к П2 - буквой е.
• Линия наибольшего наклона плоскости к
горизонтальной плоскости проекций
называется линией ската
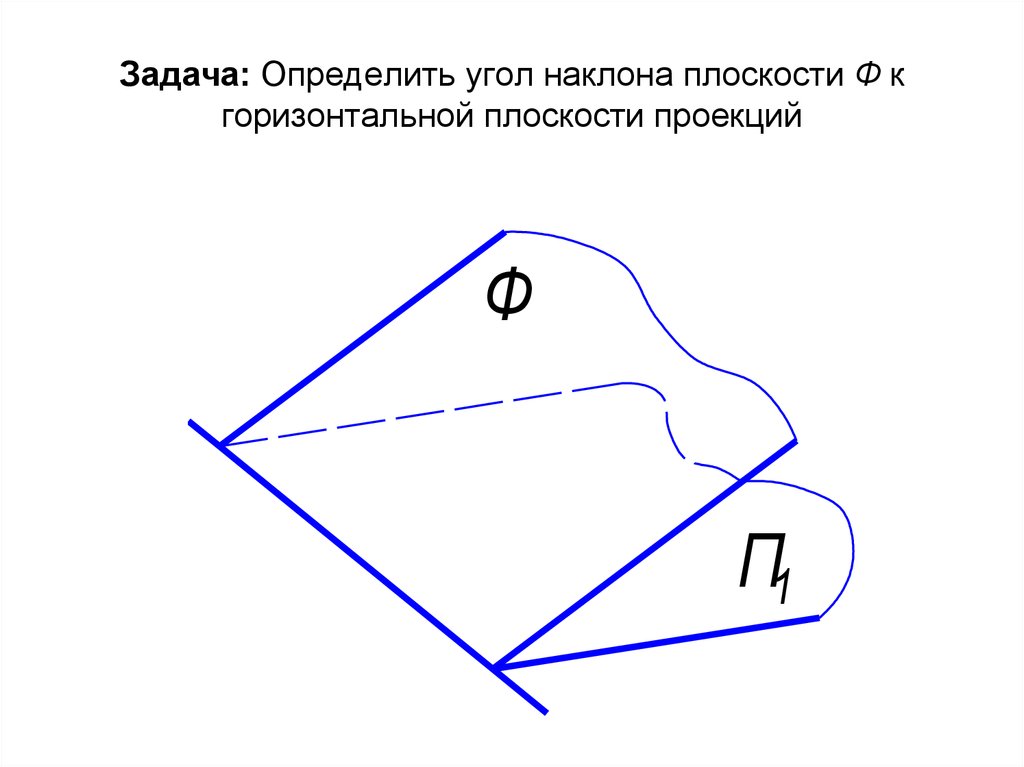
38. Задача: Определить угол наклона плоскости Ф к горизонтальной плоскости проекций
ФП1
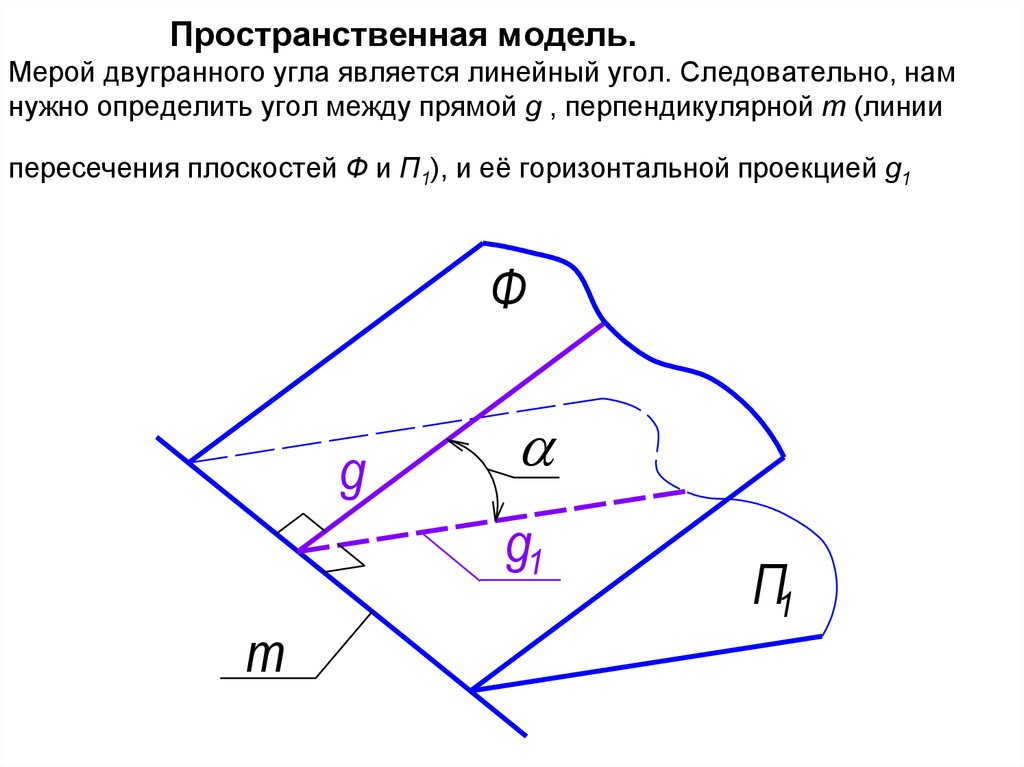
39. Пространственная модель. Мерой двугранного угла является линейный угол. Следовательно, нам нужно определить угол между прямой g
, перпендикулярной m (линиипересечения плоскостей Ф и П1), и её горизонтальной проекцией g1
Ф
g
g1
m
П1
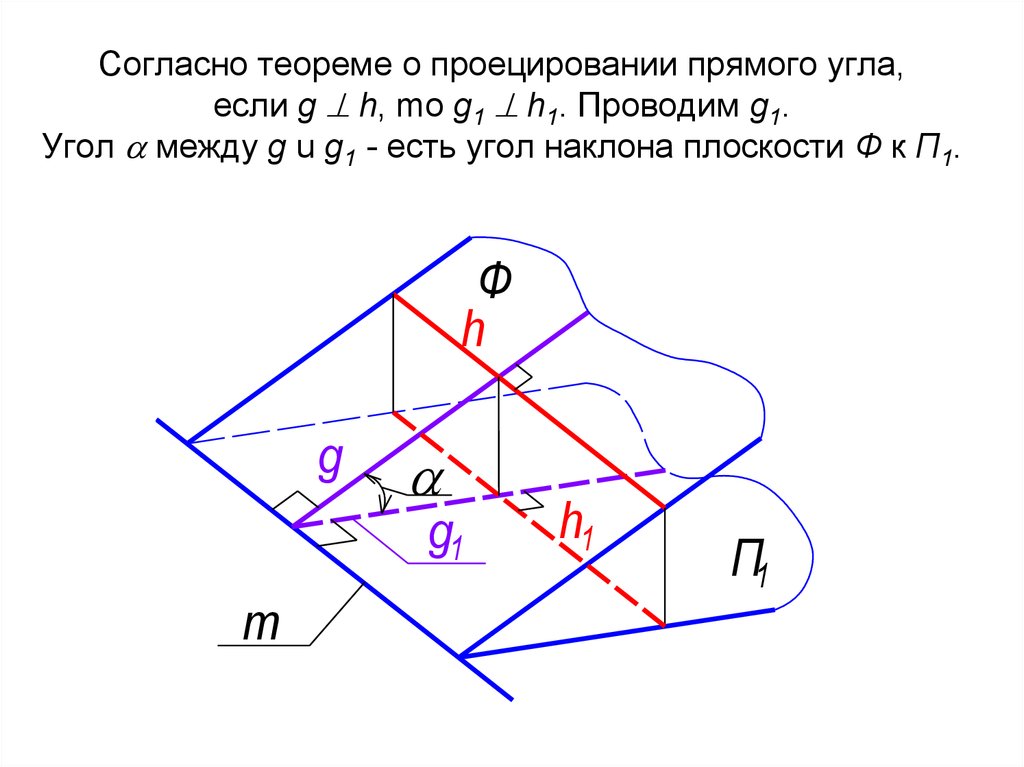
40. Согласно теореме о проецировании прямого угла, если g h, mo g1 h1. Проводим g1. Угол между g u g1 - есть угол наклона
Согласно теореме о проецировании прямого угла,если g h, mo g1 h1. Проводим g1.
Угол между g u g1 - есть угол наклона плоскости Ф к П1.
Ф
h
g
g1
m
h1
П1
41. Таким образом, угол наклона плоскости к горизонтальной плоскости проекций - это угол между горизонтальной проекцией линии ската
этой плоскостии её натуральной величиной.
Выполним алгоритмическую
запись вышеизложенного:
Ф П1 = g g1; g h g1 h1.
42. Плоский чертёж. Зададим плоскость Ф треугольником АВС
• Алгоритм решения задачи:• 1. Проводим в плоскости Ф(АВС) горизонталь
h(h1,h2).
• 2. Проводим g1(B1K1) h1. Находим
g2(B2K2) по принадлежности плоскости.
• 3. Находим натуральную величину g методом
прямоугольного треугольника (рис. 2-21).
• 4. Угол между g1 u g - есть угол наклона
плоскости Ф(АВС) к П1.
43.
В2В2
h2
12
h2
12
С2
А2
В2
А2
h1
А1
К1
С1
g1
А1
11
В1
К2
К1
С1
h1
g1
А1
11
11
В1
С2
g2
А2
h1
h2
12
С2
В1
С1
44.
В2С2
g2
А2
К2
С1
К1
А1
g1
В1
н. в. g
К
1
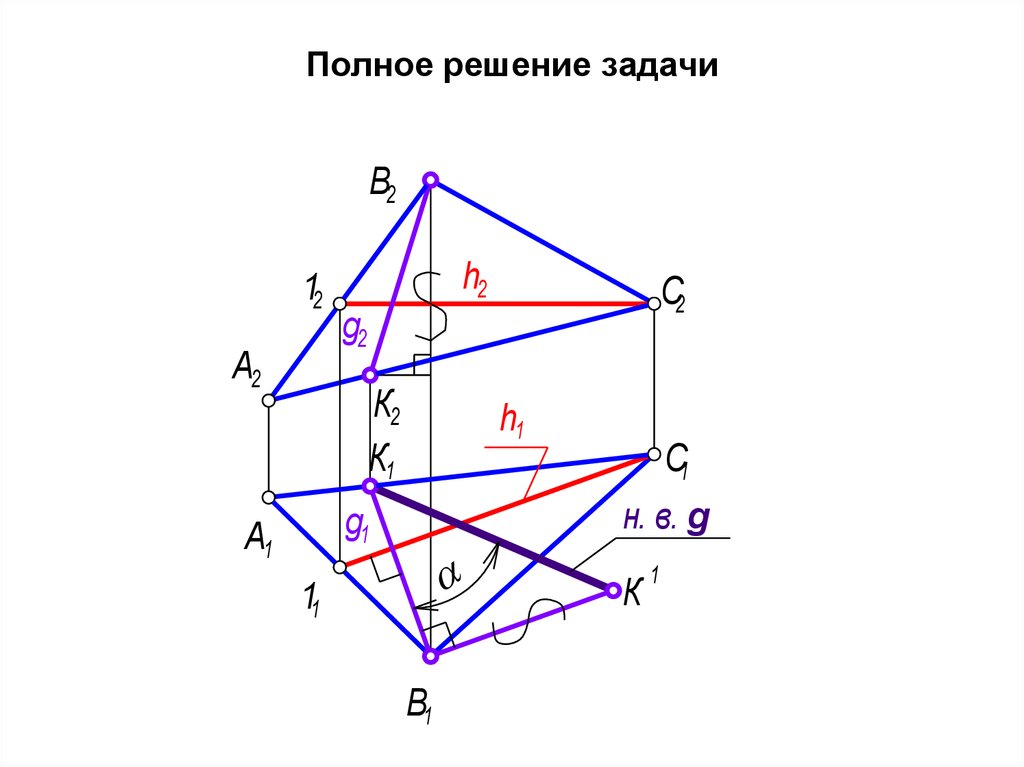
45. Полное решение задачи
В212
А2
h2
g2
К2
К1
h1
g1
А1
С2
11
В1
С1
н. в. g
К
1
46. Аналогично можно решить задачу на определение угла наклона плоскости Ф к П2. Для этого в плоскости Ф нужно взять фронталь,
линию наибольшего наклонаплоскости к П2 - е строить перпендикулярно фронтали
(е2 f2 е) и находить натуральную величину е на П2.
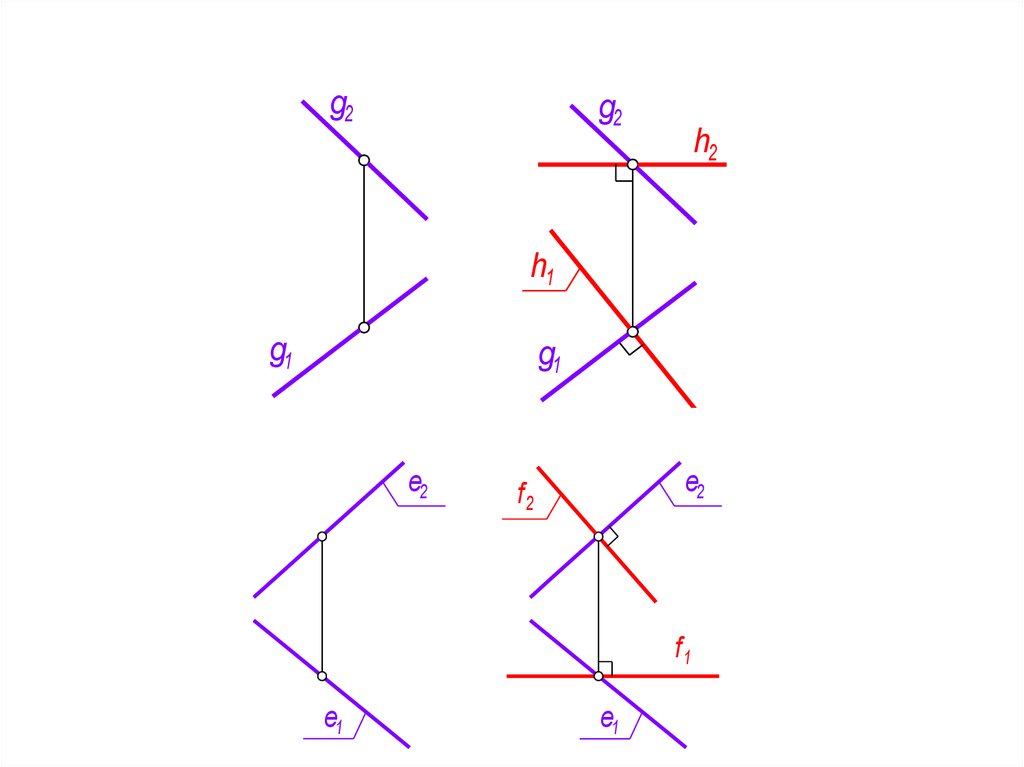
Если плоскости заданы с помощью линии ската g и
линии наибольшего наклона плоскости к П2 – е, то:
в первом случае к линии ската необходимо добавить
горизонталь (h2 линиям связи, h1 g1) ;
во втором к линии наибольшего наклона е добавляют
фронталь (f1 линиям связи, f2 е2)
. В обоих случаях плоскость получается заданной
пересекающимися прямыми.
47.
g2g2
h2
h1
g1
g1
e2
e2
f2
f1
e1
e1
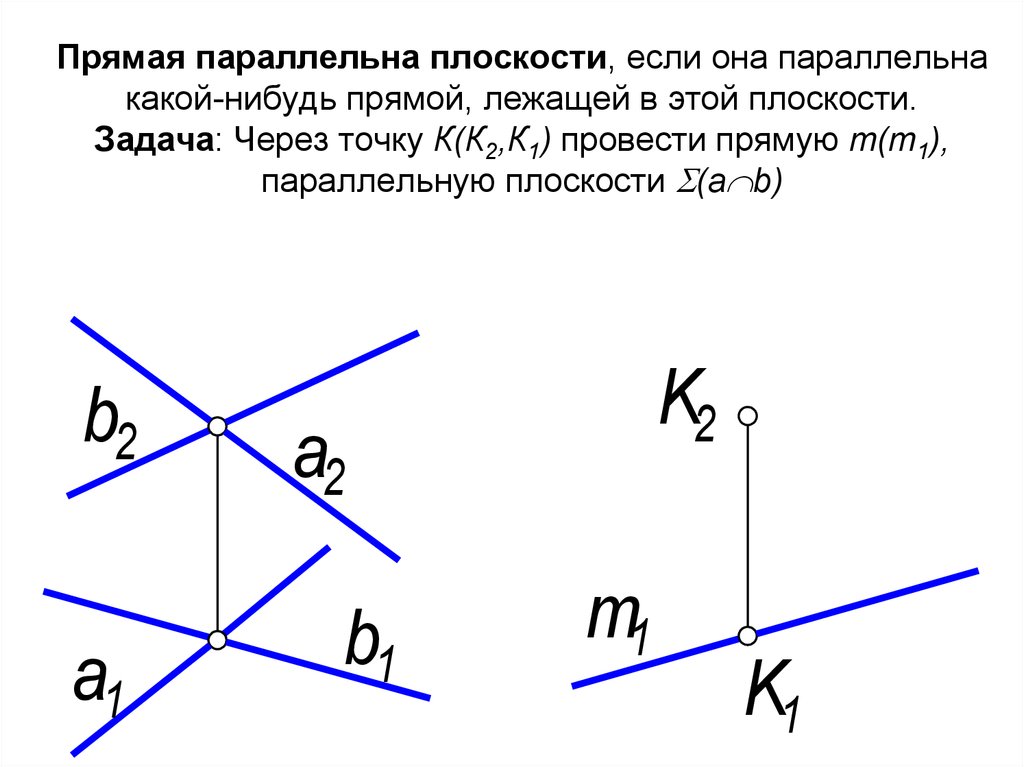
48. Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости. Задача: Через точку К(К2,К1)
провести прямую m(m1),параллельную плоскости (a b)
b2
a1
K2
а2
b1
m1
K1
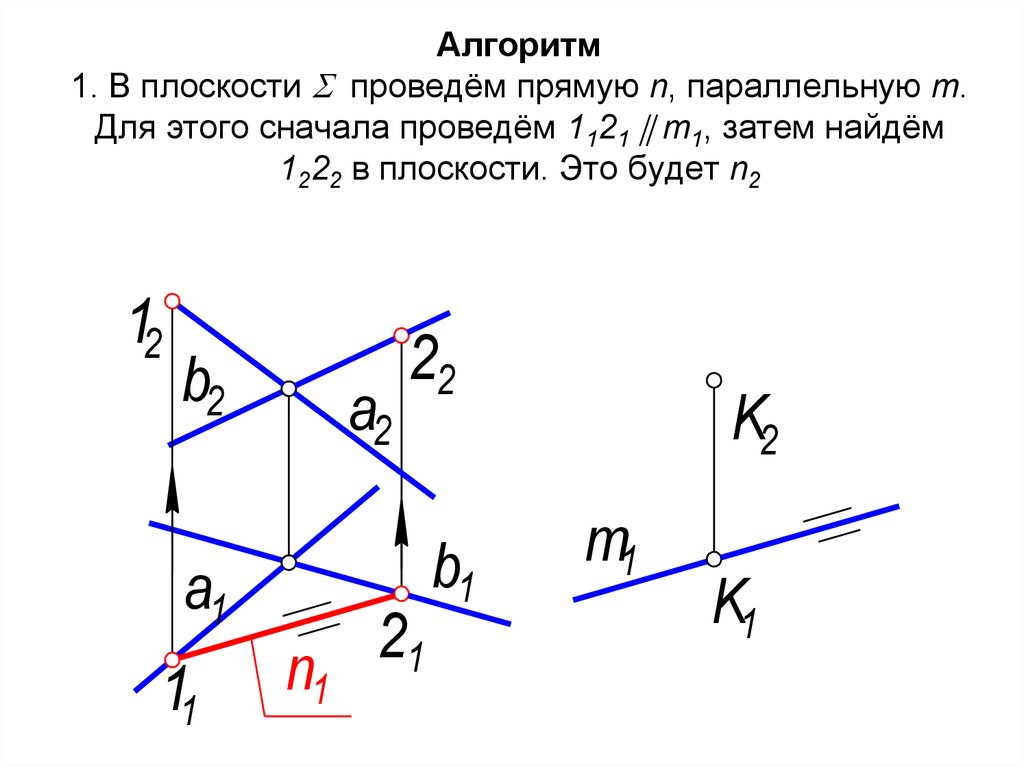
49. Алгоритм 1. В плоскости проведём прямую n, параллельную m. Для этого сначала проведём 1121 m1, затем найдём 1222 в
Алгоритм1. В плоскости проведём прямую n, параллельную m.
Для этого сначала проведём 1121 m1, затем найдём
1222 в плоскости. Это будет n2
12
b2
а2
b1
a1
11
22
n1
21
K2
m1
K1
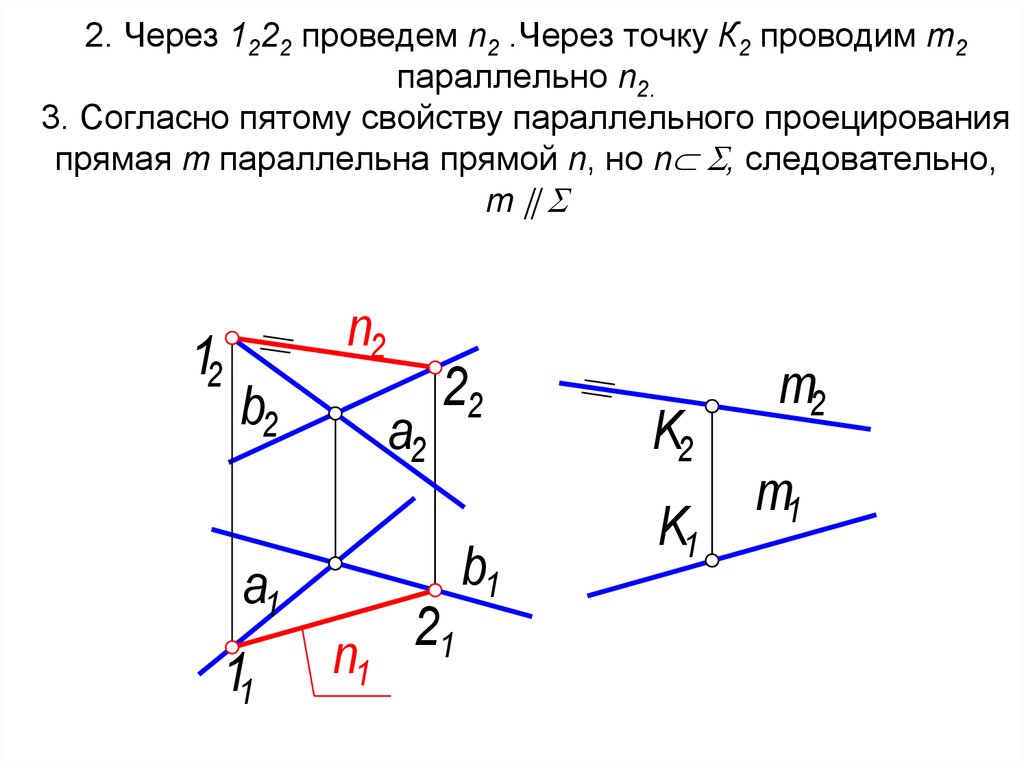
50. 2. Через 1222 проведем n2 .Через точку К2 проводим m2 параллельно n2. 3. Согласно пятому свойству параллельного проецирования
прямая m параллельна прямой n, но n , следовательно,m
12
n2
b2
а2
b1
a1
11
22
n1
21
K2
K1
m2
m1
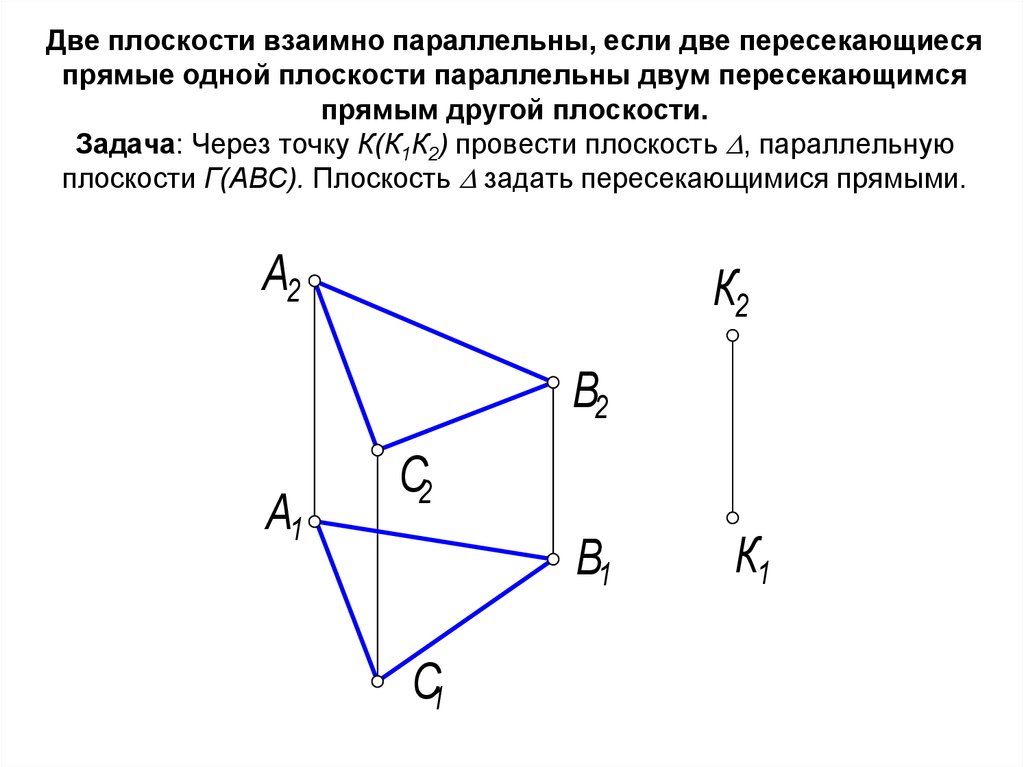
51. Две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой
плоскости.Задача: Через точку К(К1К2) провести плоскость , параллельную
плоскости Г(АВС). Плоскость задать пересекающимися прямыми.
А2
К2
В2
А1
С2
В1
С1
К1
52. Алгоритм: 1. Плоскость зададим прямыми m n = K. 2. Прямую m возьмём параллельно стороне СВ треугольника. Если m СВ, то
Алгоритм:1. Плоскость зададим прямыми m n = K.
2. Прямую m возьмём параллельно стороне СВ треугольника.
Если m СВ, то m1 C1B1, a m2 C2B2
3. Прямую n возьмём параллельно стороне АВ треугольника.
Если n AB, mo n1 A1B1, a n2 A2B2.
4. Таким образом, плоскости (АВС) и (m n) параллельны.
А2
К2
В2
А1
С1
п2
т1
п1
С2
В1
т2
К1
53. Задание поверхности на комплексном чертеже
Существует несколько способов заданияповерхности: аналитический, графический,
кинематический.
Любое тело ограничивается своей
поверхностью. Тело - конечно и состоит из
конкретного материала - металла,
пластмассы, древесины.
Поверхность является абстрактной фигурой,
не имеющей толщины, т.е. образно говоря,
это тонкая пленка, натянутая на каркас
поверхности. Например, шар - тело, которое
ограничено сферой - поверхностью.
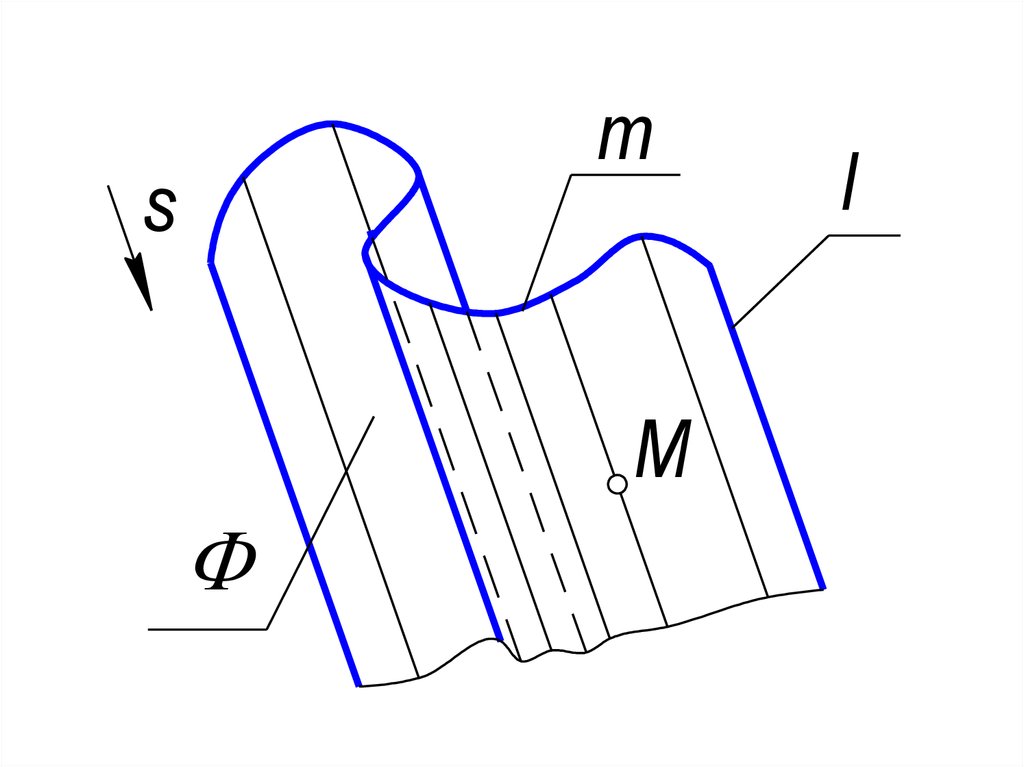
54. В начертательной геометрии поверхность задают кинематически - как множество всех положений перемещающейся по определенному
закону линии впространстве. Эта линия называется образующей - l.
Как правило, она скользит по некоторой неподвижной
линии, называемой направляющей - m,
направляющих может быть одна или несколько.
Образующая l , скользя по неподвижной
направляющей m, создает плотную сеть линий.
Такое упорядоченное множество линий
поверхности называется ее каркасом:
• Каркасы бывают непрерывными – поверхность
задана всем множеством образующих, или
дискретными, когда имеется конечное число
образующих.
• При построении дискретного каркаса поверхности
необходимо учитывать закон каркаса.
• Закон каркаса - это закон движения образующей.
55.
тs
М
l
56. Определитель поверхности
• Определитель состоит из двух частей: D = G+ А.
• Геометрическая часть - G устанавливает
набор геометрических фигур (геометрических
элементов), участвующих в образовании
поверхности, например: (m,s)
• Алгоритмическая часть - А устанавливает
закон (характер) взаимодействия
геометрических фигур в процессе
образования поверхности, например: l m, l
s.
• При построении чертежа поверхности
алгоритмической частью определителя
является закон каркаса поверхности.
57.
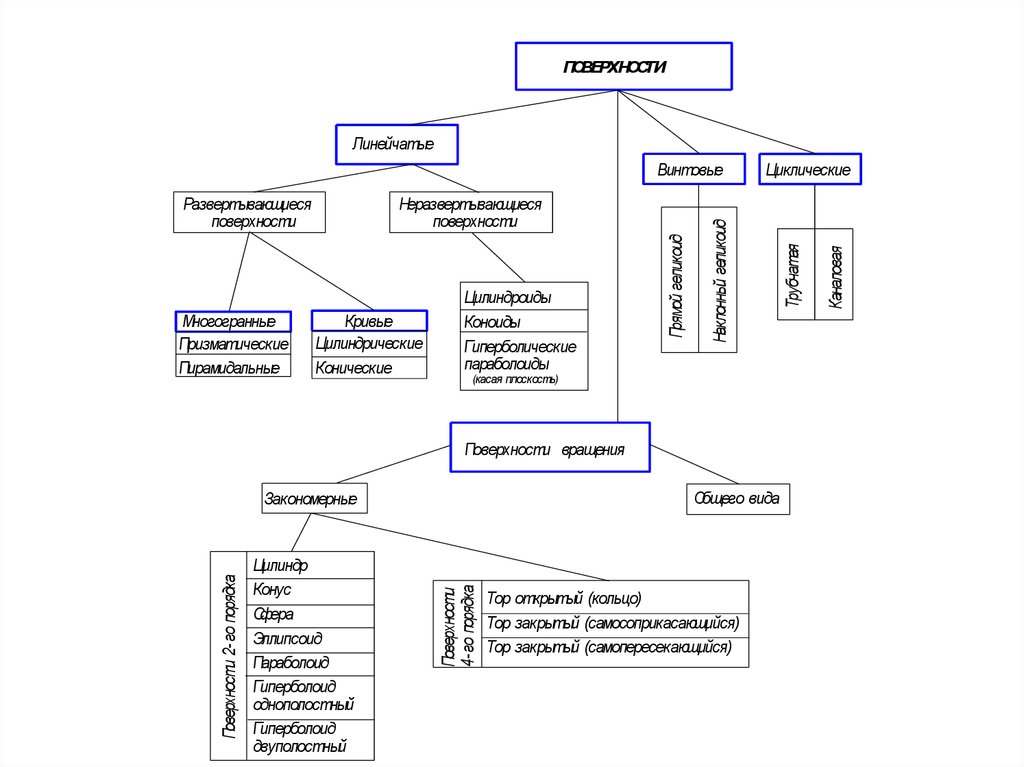
ПОВЕРХНОСТИЛинейчатые
Многогранные
Призматические
Пирамидальные
Кривые
Цилиндрические
Конические
(касая плоскость)
Поверхности вращения
Общего вида
Цилиндр
Конус
Сфера
Эллипсоид
Параболоид
Гиперболоид
однополостный
Гиперболоид
двуполостный
Поверхности
4- го порядка
Поверхности 2- го порядка
Закономерные
Тор открытый (кольцо)
Тор закрытый (самосоприкасающийся)
Тор закрытый (самопересекающийся)
Каналовая
Цилиндроиды
Коноиды
Гиперболические
параболоиды
Трубчатая
Неразвертывающиеся
поверхности
Прямой геликоид
Развертывающиеся
поверхности
Циклические
Наклонный геликоид
Винтовые
58. Поверхность считается графически заданной на комплексном чертеже, если можно построить точку на поверхности.
• Точка принадлежит поверхности, если онапринадлежит линии, лежащей на поверхности.
Для линейчатых поверхностей выбирают
образующую - прямую линию. Для других
поверхностей выбирают графически простые
линии, к которым относят прямую и
окружность.
59. Рассмотрим пример задания треугольной призмы проекциями геометрической части определителя (АВС,S)
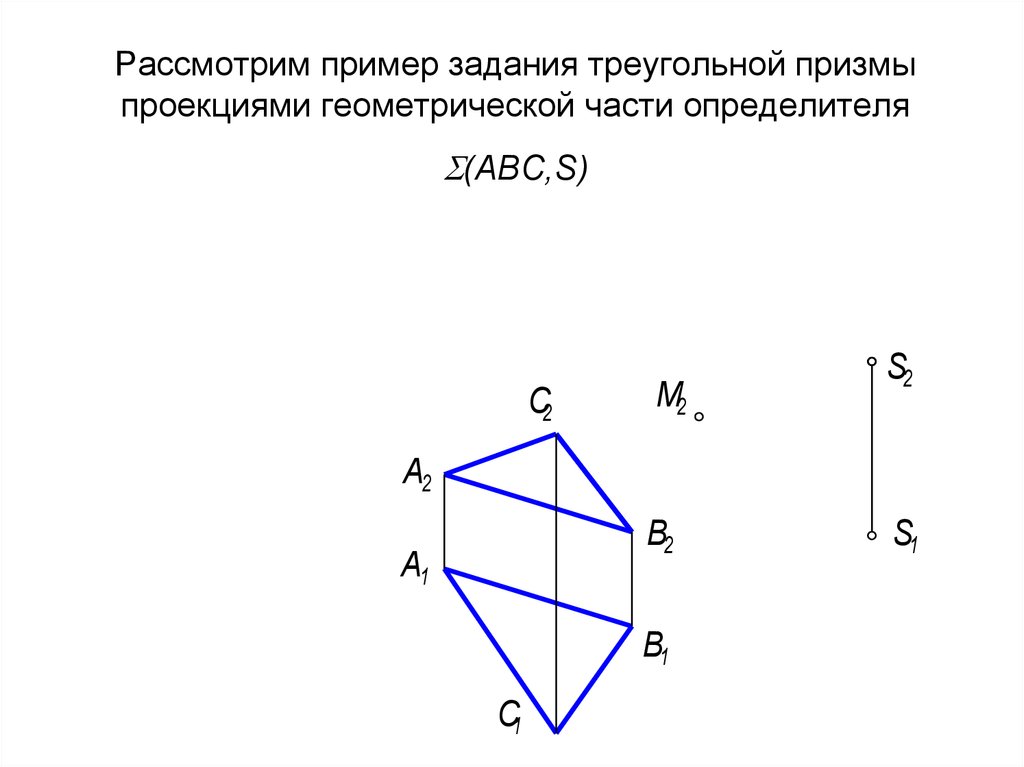
Рассмотрим пример задания треугольной призмыпроекциями геометрической части определителя
(АВС,S)
С2
М2
S2
А2
В2
А1
В1
С1
S1
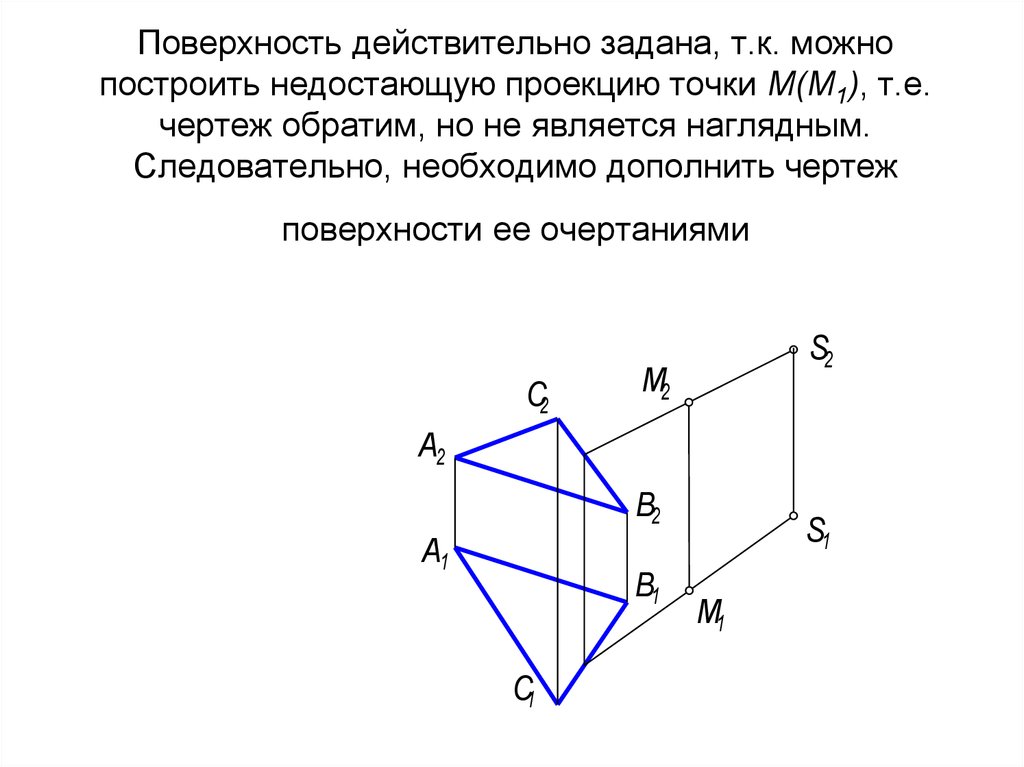
60. Поверхность действительно задана, т.к. можно построить недостающую проекцию точки М(М1), т.е. чертеж обратим, но не является
наглядным.Следовательно, необходимо дополнить чертеж
поверхности ее очертаниями
С2
S2
М2
А2
В2
А1
В1
С1
S1
М1
61. Поэтому конструировать поверхности мы будем с помощью построения дискретного каркаса, проекции которого обеспечат обратимость и
наглядность чертежа поверхности.Сконструировать поверхность - это
значит построить проекции
поверхности, состоящие из проекций
определителя и проекций характерных
линий, к которым относятся линии
контура и линии обреза.
62. Алгоритм (последовательность построения чертежа любой поверхности):
1. Задать проекции элементов определителя (будемиметь в виду задание проекций геометрической части
определителя).
2. Построить проекции дискретного каркаса, состоящего
из конечного числа графически простых линий.
3. Построить проекции линии обреза, которые для
образования поверхности существенной роли не
играют, они лишь ограничивают, обрезают
поверхность.
4. Определить видимость проекций поверхности.
5. Обвести видимые линии проекций поверхности
сплошной толстой линией.



























 drafting
drafting








