Комплексные чертежи плоскостей. Аксиомы

1. Комплексные чертежи плоскостей

Аксиомы
Через любые три точки не принадлежащие одной
прямой проходит одна и только одна плоскость
Следствия
1.
2.
3.
Через прямую и не принадлежащую ей точку проходит одна
и только одна плоскость
Через две пересекающиеся прямые проходит одна и только
одна плоскость
Через две различные параллельные прямые проходит одна
и только одна плоскость
Если две точки прямой принадлежат плоскости, то
вся прямая принадлежит плоскости
Две плоскости пересекаются по прямой

2. Обозначения

Плоскости (поверхности) обозначают
на комплексных чертежах прописными
буквами греческого алфавита:
Г (гамма), Δ (дельта), Λ (ламбда),
Σ (сигма), Т (тау), Ψ (пси), Φ (фи)
и другими.
Нет обозначения – нет плоскости!

3. Положение плоскостей в пространстве Плоскости, как и прямые, могут быть общего и частного положения

Плоскости общего положения- не параллельны и не
перпендикулярны ни одной плоскости проекций
Плоскости уровня – параллельны плоскостям проекций
Горизонтальная плоскость уровня - параллельна П1
Фронтальная плоскость уровня - параллельна П2
Профильная плоскость уровня - параллельна П3
Проецирующие плоскости - перпендикулярны плоскостям
проекций
Горизонтально-проецирующая – перпендикулярна П1
Фронтально-проецирующая – перпендикулярна П2
Профильно-проецирующая – перпендикулярна П3

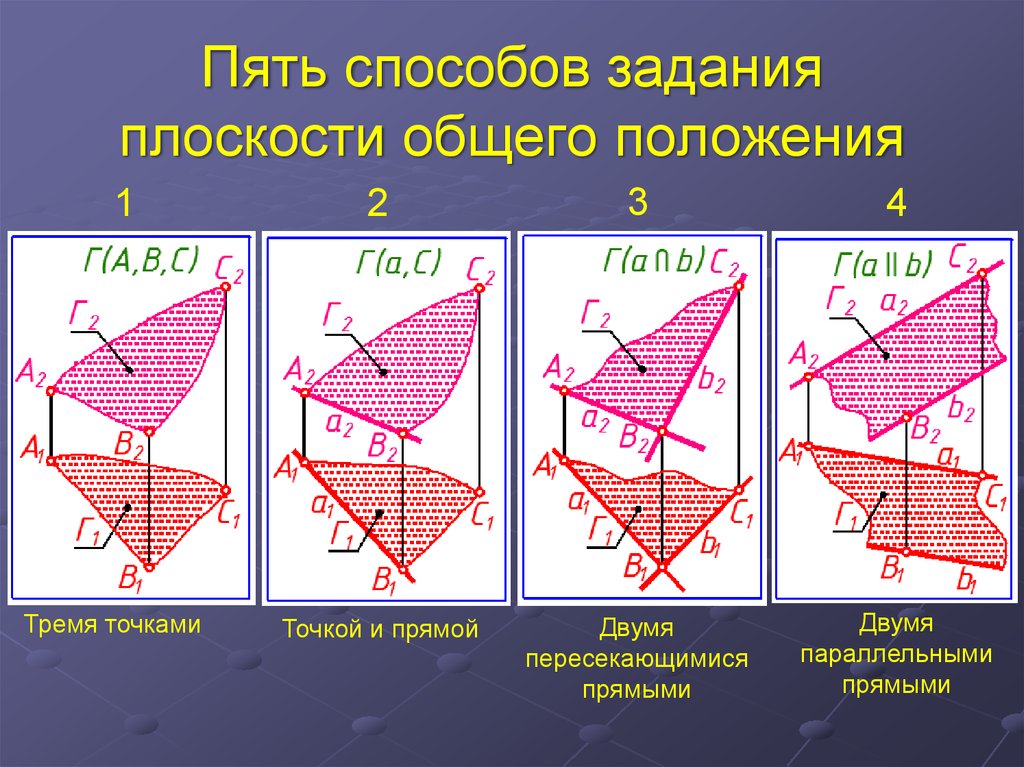
4. Пять способов задания плоскости общего положения

1
Тремя точками
2
3
4
Точкой и прямой
Двумя
пересекающимися
прямыми
Двумя
параллельными
прямыми

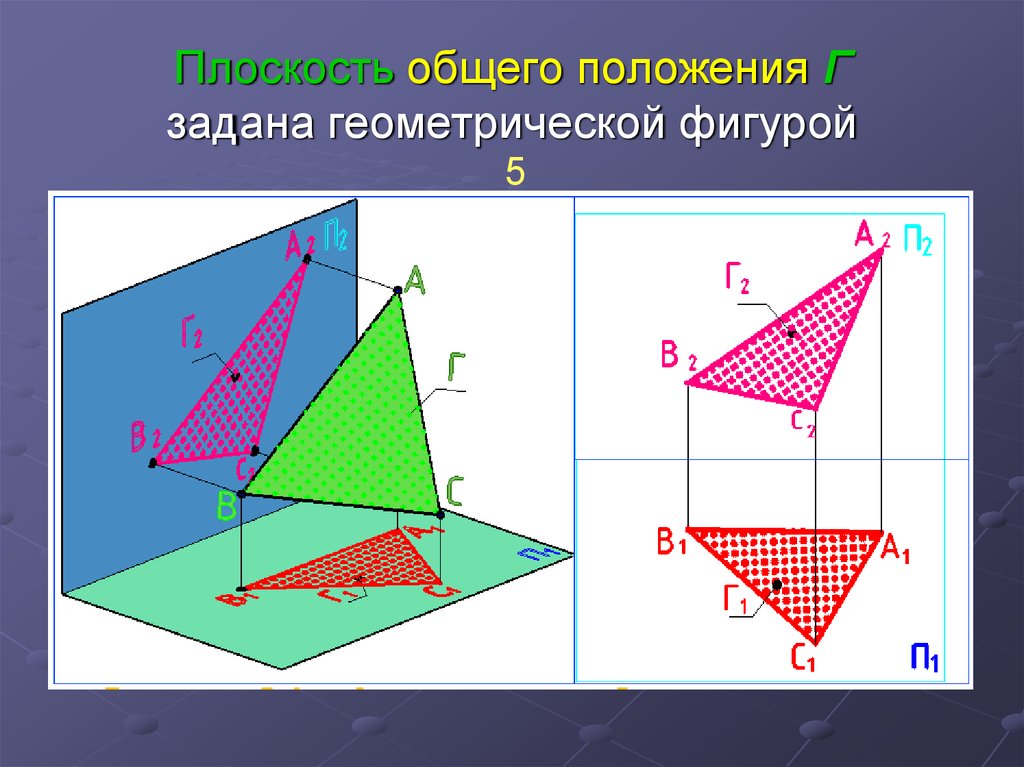
5. Плоскость общего положения Г задана геометрической фигурой

5

6.

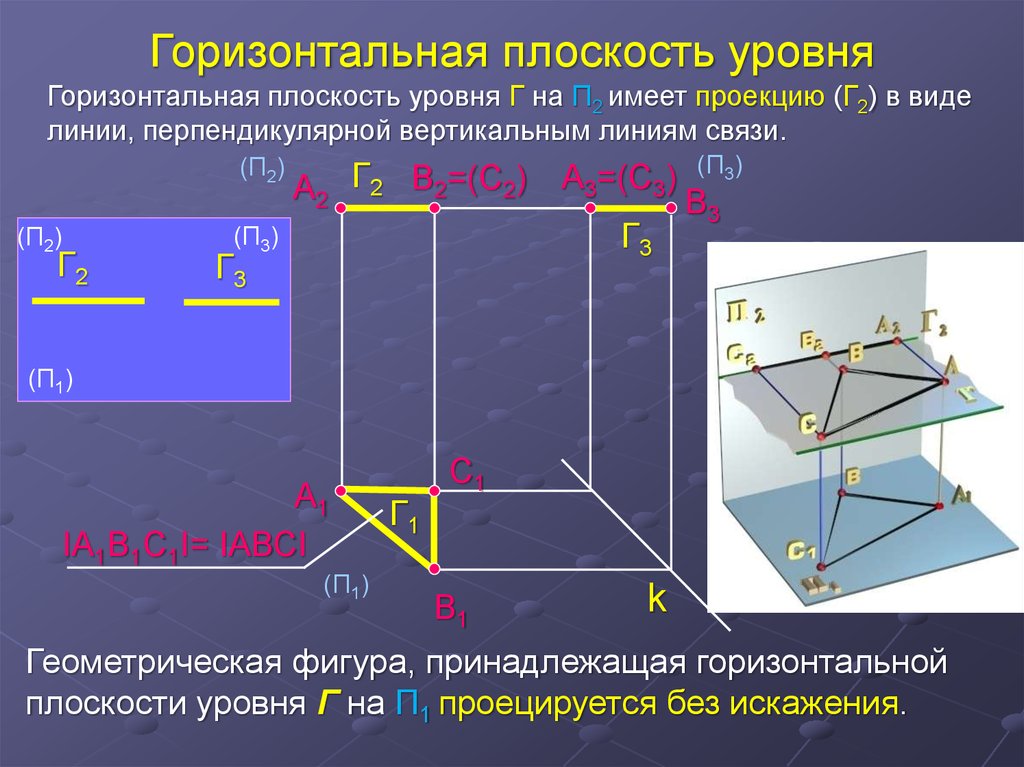
Горизонтальная плоскость уровня
Горизонтальная плоскость уровня Г на П2 имеет проекцию (Г2) в виде
линии, перпендикулярной вертикальным линиям связи.
(П2)
(П2)
Г2
A2
Г2 В2=(С2) A3=(С3)
Г3
(П3)
Г3
(П3)
В3
(П1)
A1
IA1В1С1I= IAВСI
(П1)
Г1
С1
В1
k
Геометрическая фигура, принадлежащая горизонтальной
плоскости уровня Г на П1 проецируется без искажения.

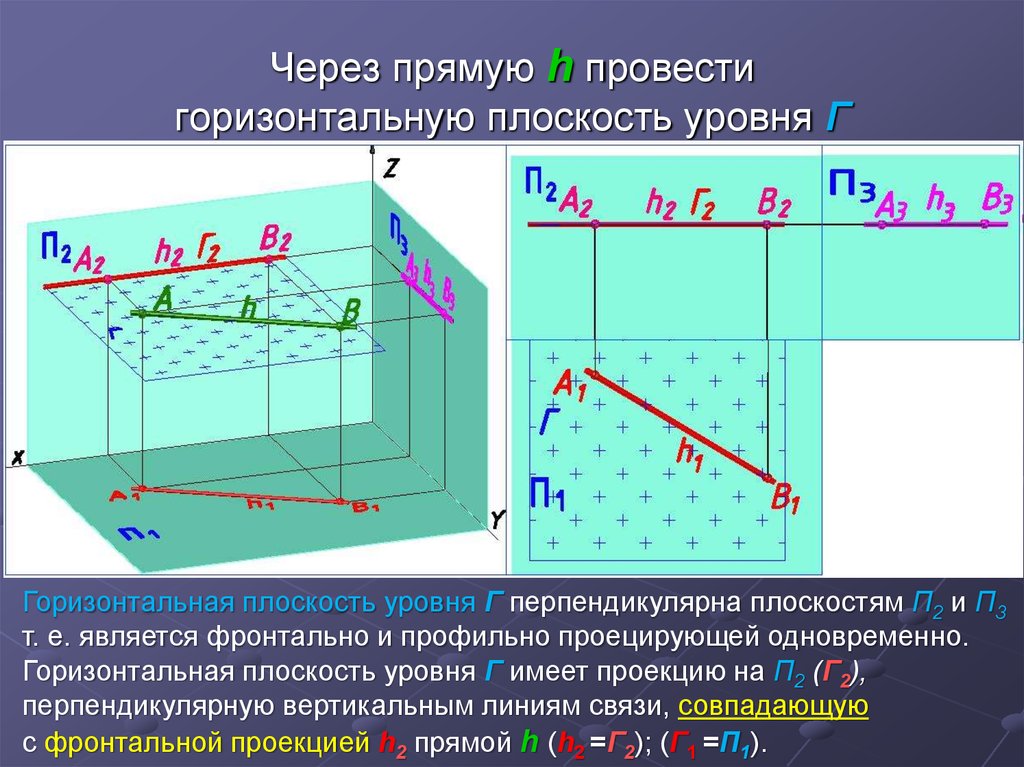
7. Через прямую h провести горизонтальную плоскость уровня Г

Горизонтальная плоскость уровня Г перпендикулярна плоскостям П2 и П3
т. е. является фронтально и профильно проецирующей одновременно.
Горизонтальная плоскость уровня Г имеет проекцию на П2 (Г2),
перпендикулярную вертикальным линиям связи, совпадающую
с фронтальной проекцией h2 прямой h (h2 =Г2); (Г1 =П1).

8.

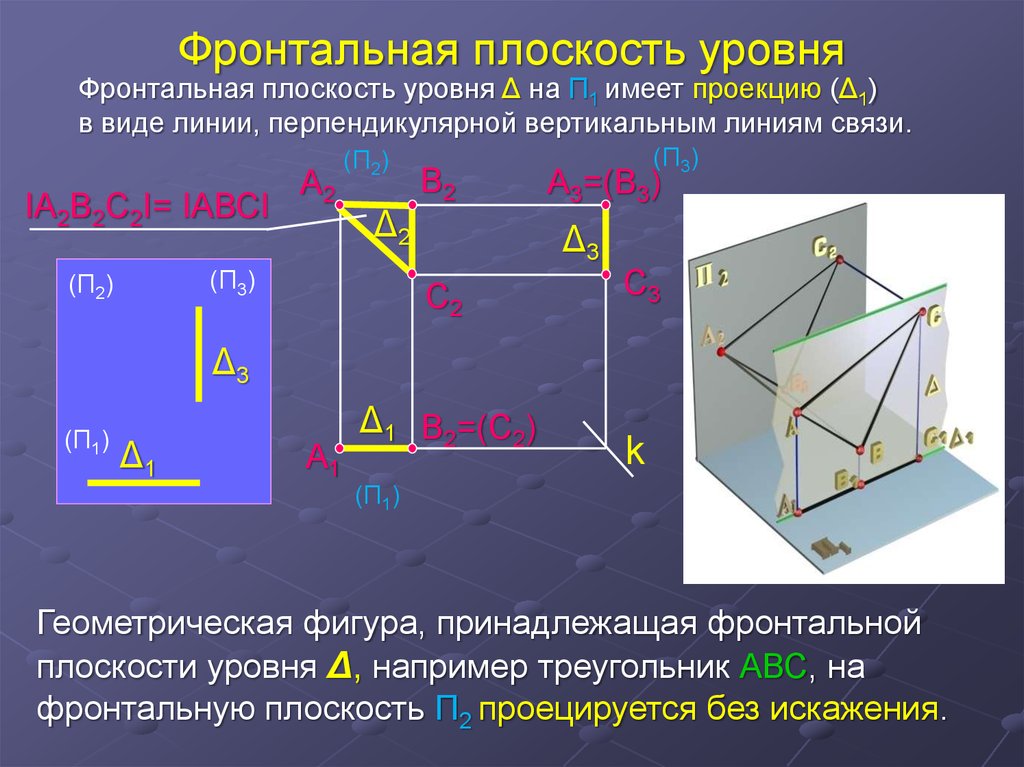
Фронтальная плоскость уровня
Фронтальная плоскость уровня Δ на П1 имеет проекцию (Δ1)
в виде линии, перпендикулярной вертикальным линиям связи.
IA2В2С2I= IAВСI
A2
(П2)
Δ2
(П3)
(П2)
В2
(П3)
A3=(В3)
Δ3
С2
С3
Δ3
(П1)
Δ1
A1
Δ1 В2=(С2)
k
(П1)
Геометрическая фигура, принадлежащая фронтальной
плоскости уровня Δ, например треугольник АВС, на
фронтальную плоскость П2 проецируется без искажения.

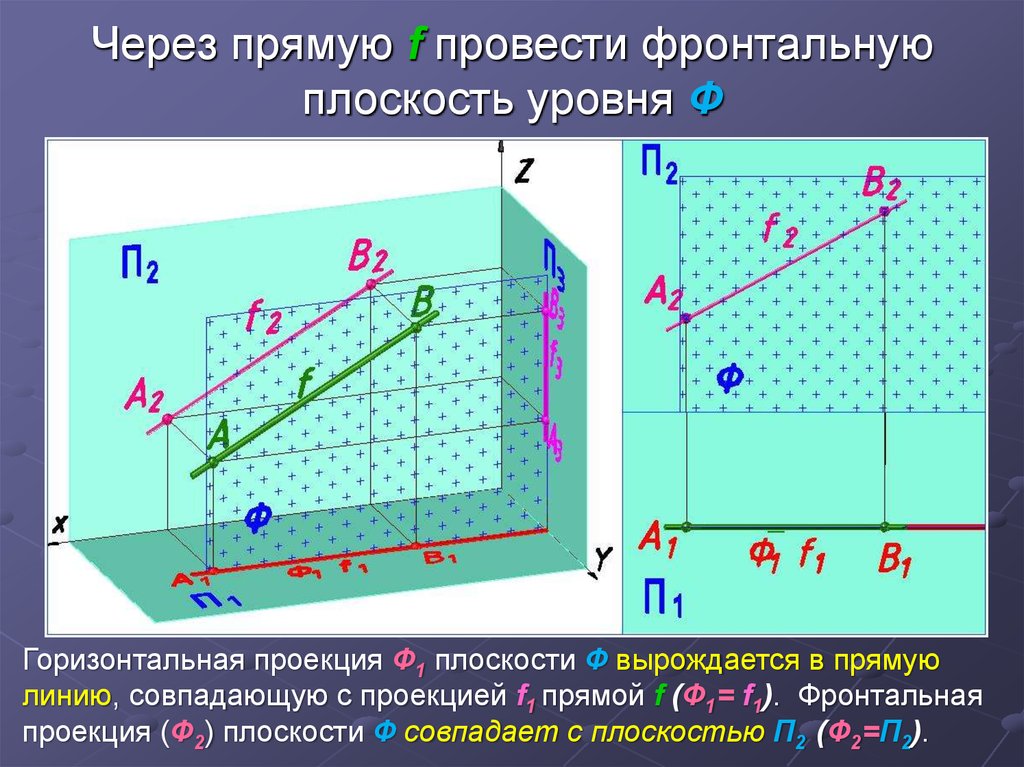
9. Через прямую f провести фронтальную плоскость уровня Ф

Горизонтальная проекция Ф1 плоскости Ф вырождается в прямую
линию, совпадающую с проекцией f1 прямой f (Ф1= f1). Фронтальная
проекция (Ф2) плоскости Ф совпадает с плоскостью П2 (Ф2=П2).

10.

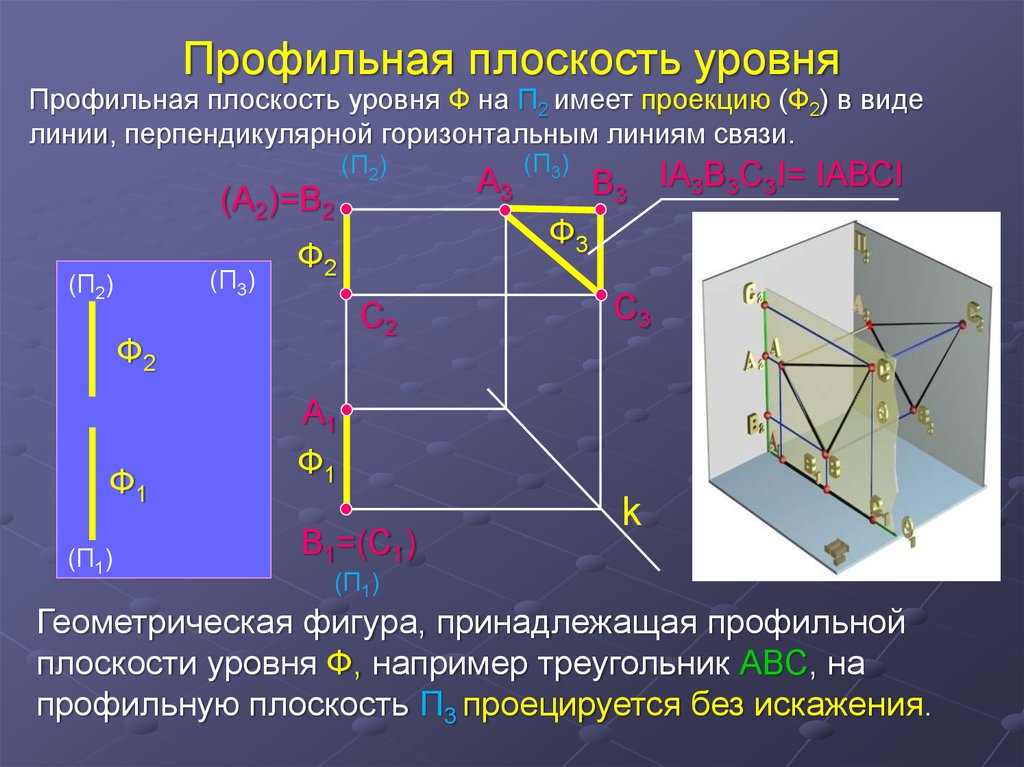
Профильная плоскость уровня
Профильная плоскость уровня Ф на П2 имеет проекцию (Ф2) в виде
линии, перпендикулярной горизонтальным линиям связи.
(П2)
(A2)=В2
(П3)
(П2)
Ф1
(П1)
(П3)
В3 IA3В3С3I= IAВСI
Ф3
Ф2
С2
Ф2
A3
С3
A1
Ф1
В1=(С1)
k
(П1)
Геометрическая фигура, принадлежащая профильной
плоскости уровня Ф, например треугольник АВС, на
профильную плоскость П3 проецируется без искажения.

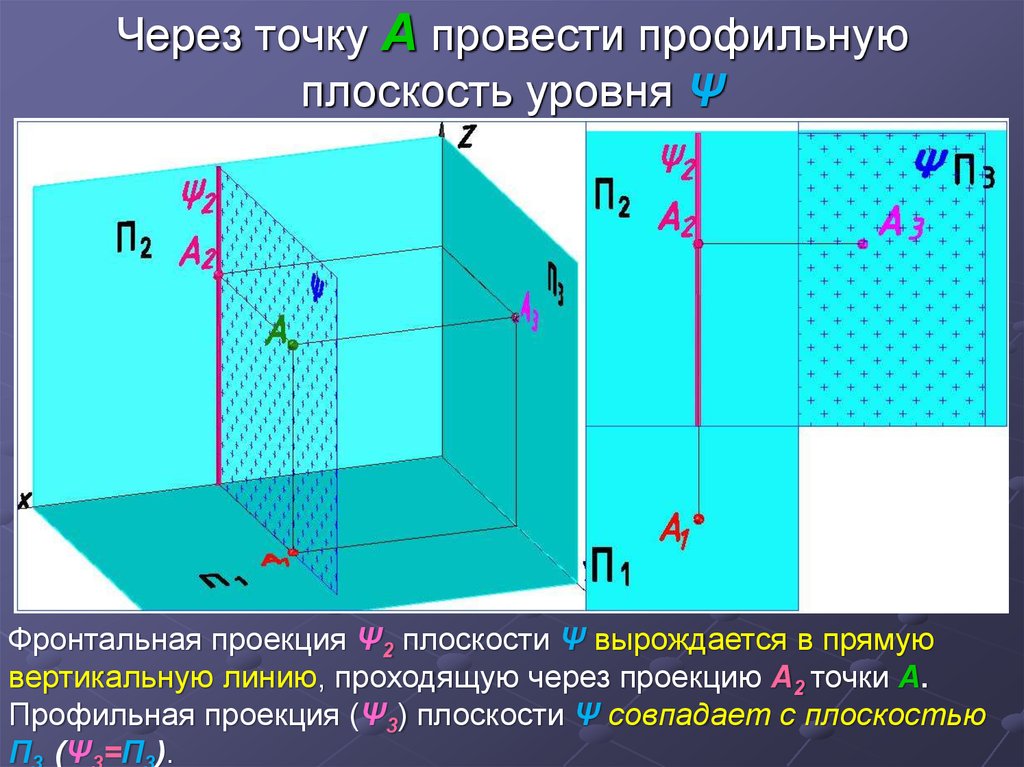
11. Через точку А провести профильную плоскость уровня Ψ

Фронтальная проекция Ψ2 плоскости Ψ вырождается в прямую
вертикальную линию, проходящую через проекцию А2 точки А.
Профильная проекция (Ψ3) плоскости Ψ совпадает с плоскостью
П (Ψ =П ).

12.

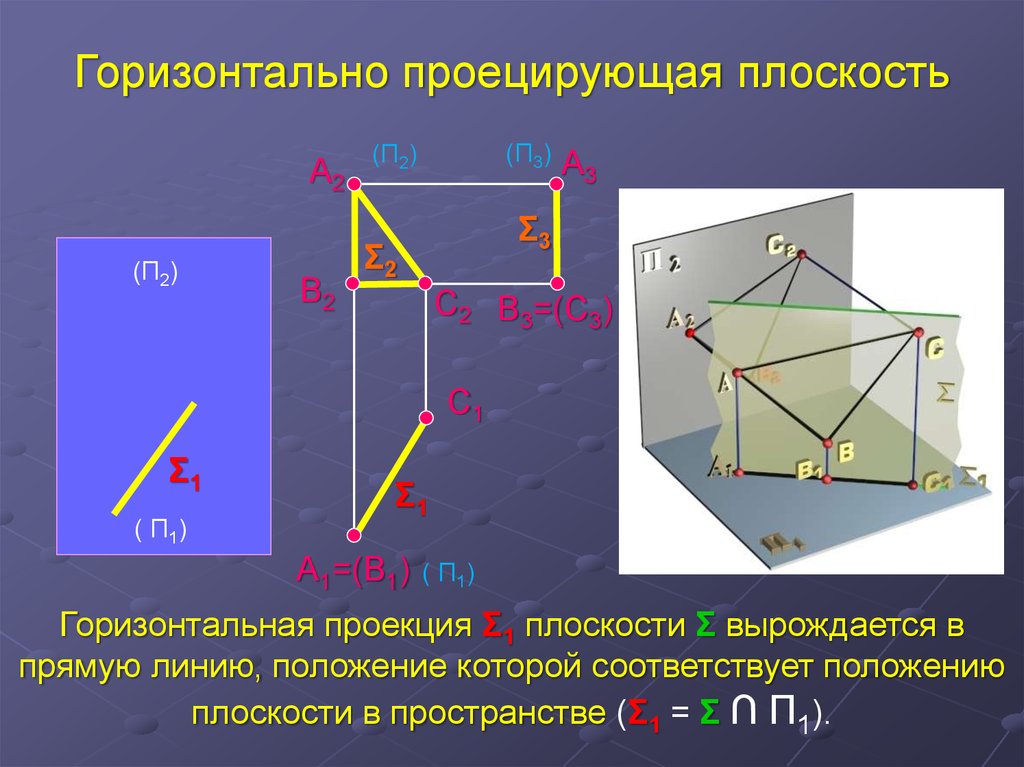
Горизонтально проецирующая плоскость
A2
(П2)
В2
(П3)
(П2)
A3
Σ3
Σ2
С2 В3=(С3)
С1
Σ1
( П1)
Σ1
А1=(В1)
( П1)
Горизонтальная проекция Σ1 плоскости Σ вырождается в
прямую линию, положение которой соответствует положению
плоскости в пространстве (Σ1 = Σ ∩ П1).

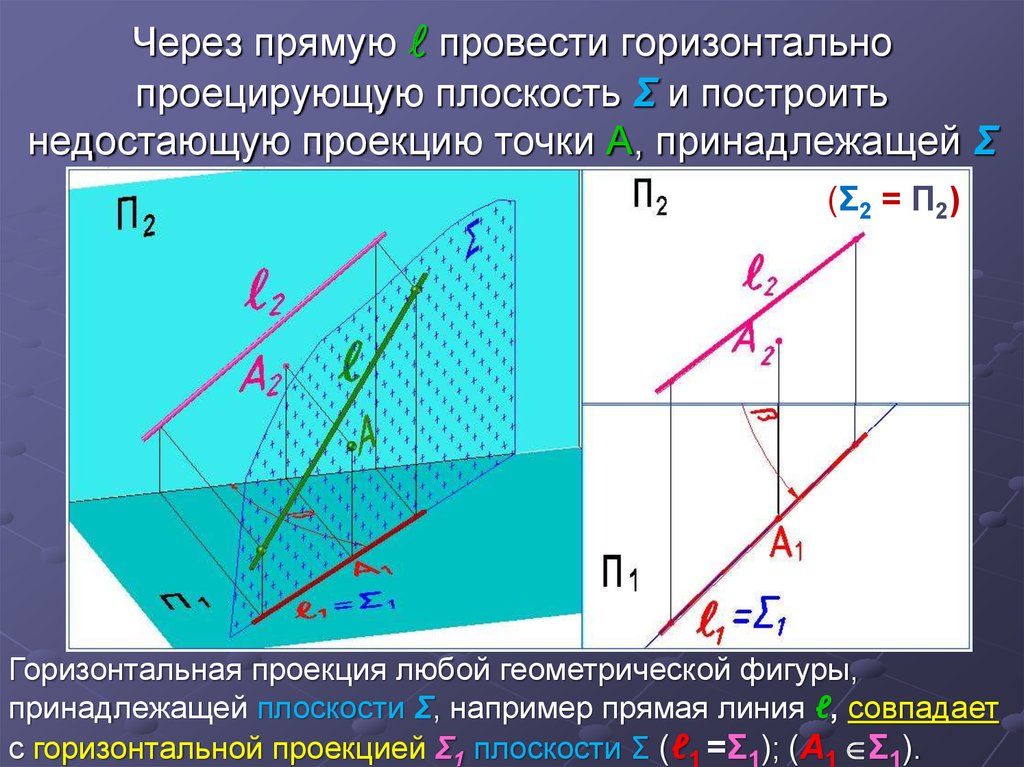
13. Через прямую l провести горизонтально проецирующую плоскость Σ и построить недостающую проекцию точки А, принадлежащей Σ

(Σ2 = П2)
Горизонтальная проекция любой геометрической фигуры,
принадлежащей плоскости Σ, например прямая линия ℓ, совпадает
с горизонтальной проекцией Σ1 плоскости Σ (ℓ1 =Σ1); (А1 Σ1).

14.

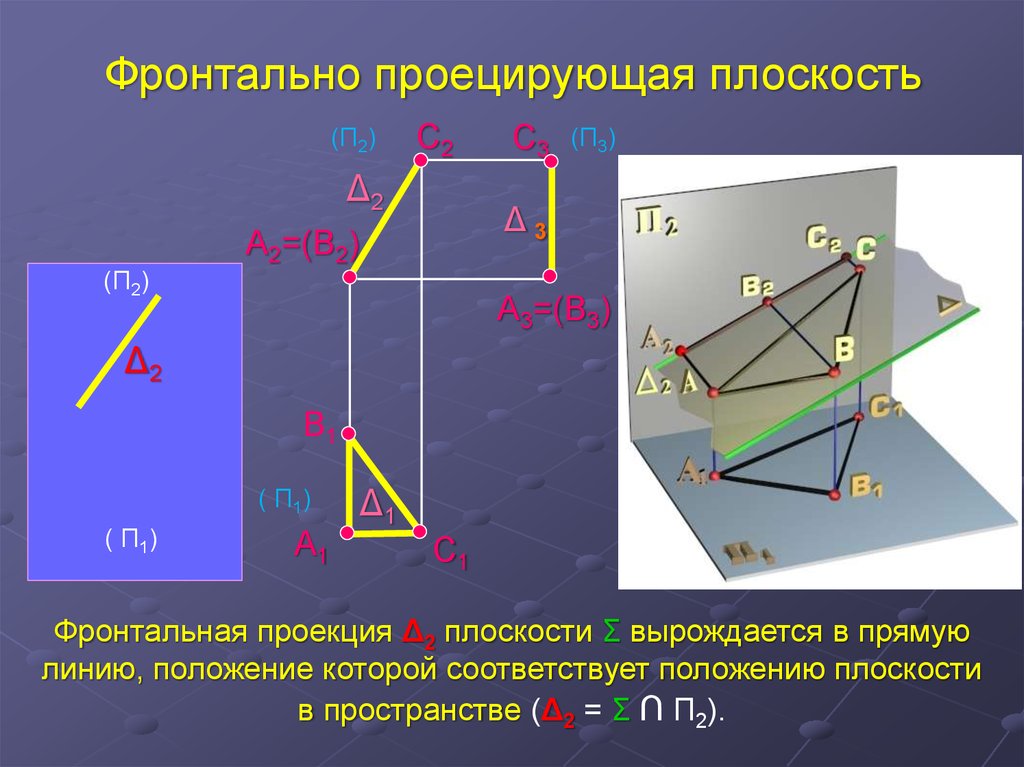
Фронтально проецирующая плоскость
(П2)
С2
Δ2
(П2)
С3
(П3)
Δ3
А2=(В2)
A3=(B3)
Δ2
В1
( П1)
( П1)
A1
Δ1
С1
Фронтальная проекция Δ2 плоскости Σ вырождается в прямую
линию, положение которой соответствует положению плоскости
в пространстве (Δ2 = Σ ∩ П2).

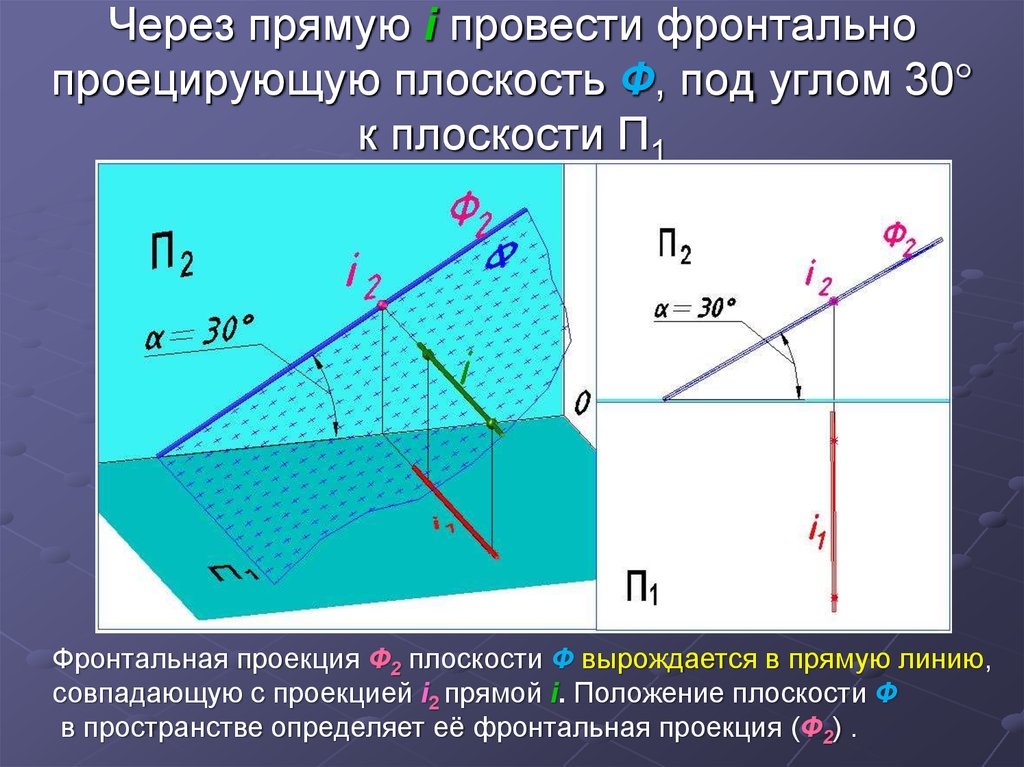
15. Через прямую i провести фронтально проецирующую плоскость Ф, под углом 30 к плоскости П1

Через прямую i провести фронтально
проецирующую плоскость Ф, под углом 30
к плоскости П1
Фронтальная проекция Ф2 плоскости Ф вырождается в прямую линию,
совпадающую с проекцией i2 прямой i. Положение плоскости Ф
в пространстве определяет её фронтальная проекция (Ф2) .

16.

Профильно проецирующая плоскость
С2
(П2)
(П2)
С3
Г3
(П3)
Г3
В2
Г2
(П3)
A2
(A3)=В3
С1
( П 1)
Г1
В1
( П 1)
А1
k
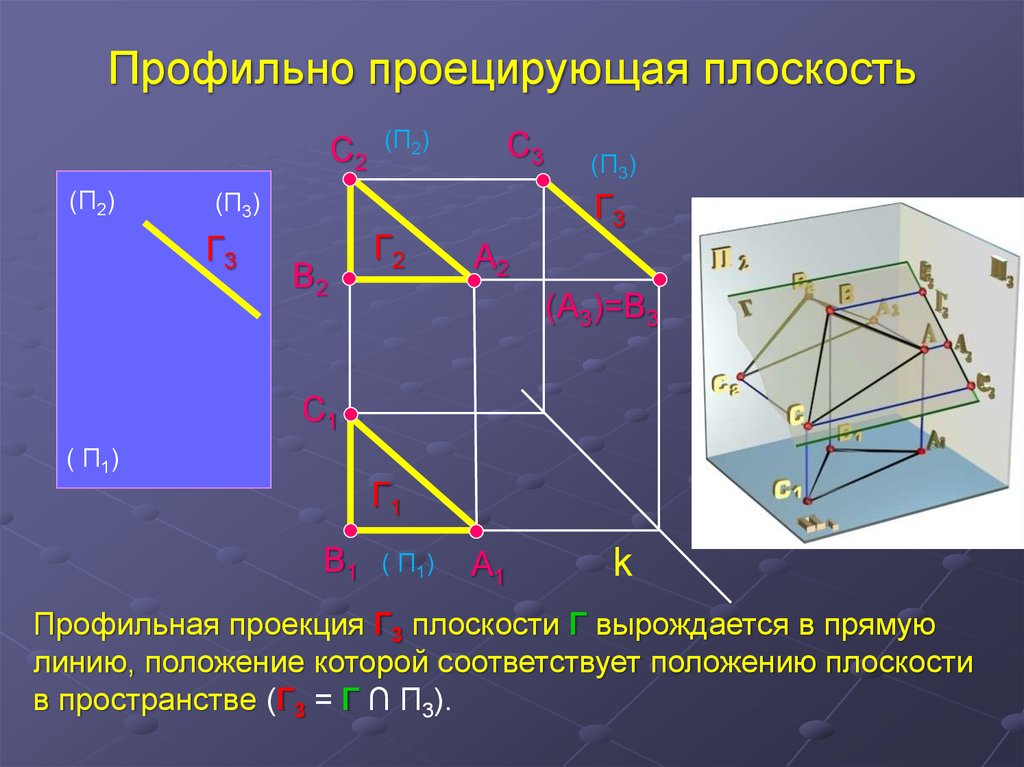
Профильная проекция Г3 плоскости Г вырождается в прямую
линию, положение которой соответствует положению плоскости
в пространстве (Г3 = Г ∩ П3).

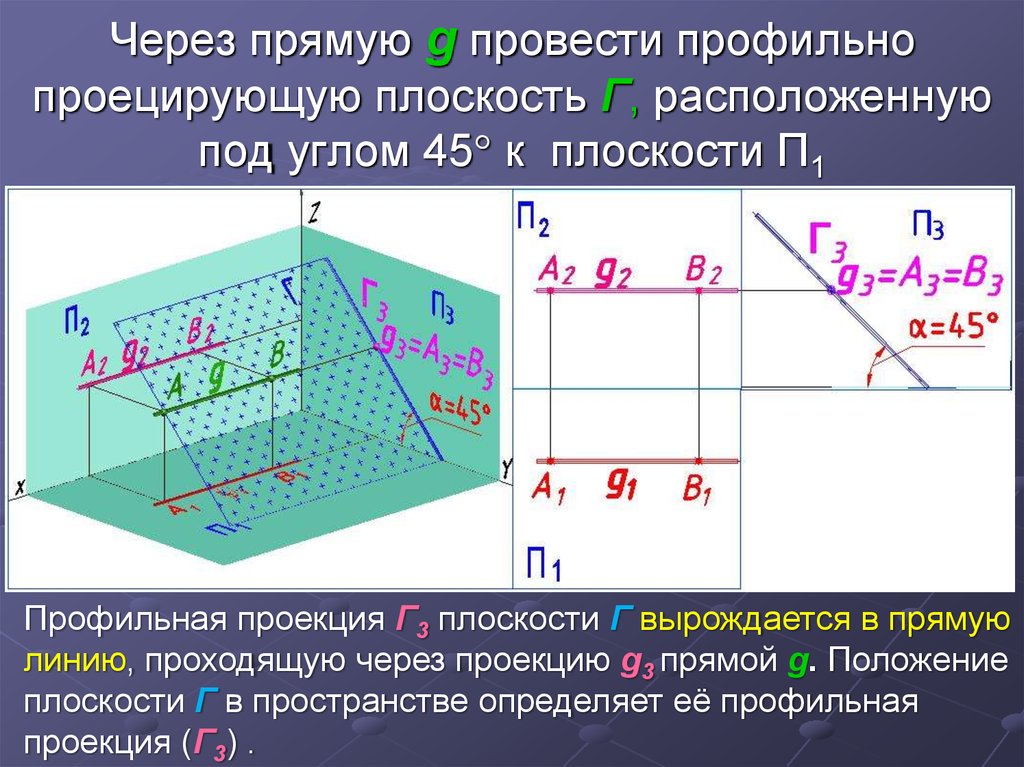
17. Через прямую g провести профильно проецирующую плоскость Г, расположенную под углом 45 к плоскости П1

Через прямую g провести профильно
проецирующую плоскость Г, расположенную
под углом 45 к плоскости П1
Профильная проекция Г3 плоскости Г вырождается в прямую
линию, проходящую через проекцию g3 прямой g. Положение
плоскости Г в пространстве определяет её профильная
проекция (Г3) .

18. Принадлежность прямой и точки плоскости

Аксиомы
1. Вся прямая принадлежит плоскости, если
две точки прямой принадлежат плоскости.
2. Прямая принадлежит плоскости, если она
имеет одну общую точку с плоскостью
и параллельна какой-либо прямой,
принадлежащей плоскости.
3. Точка принадлежит плоскости, если через нее
можно провести прямую, принадлежащую
плоскости.

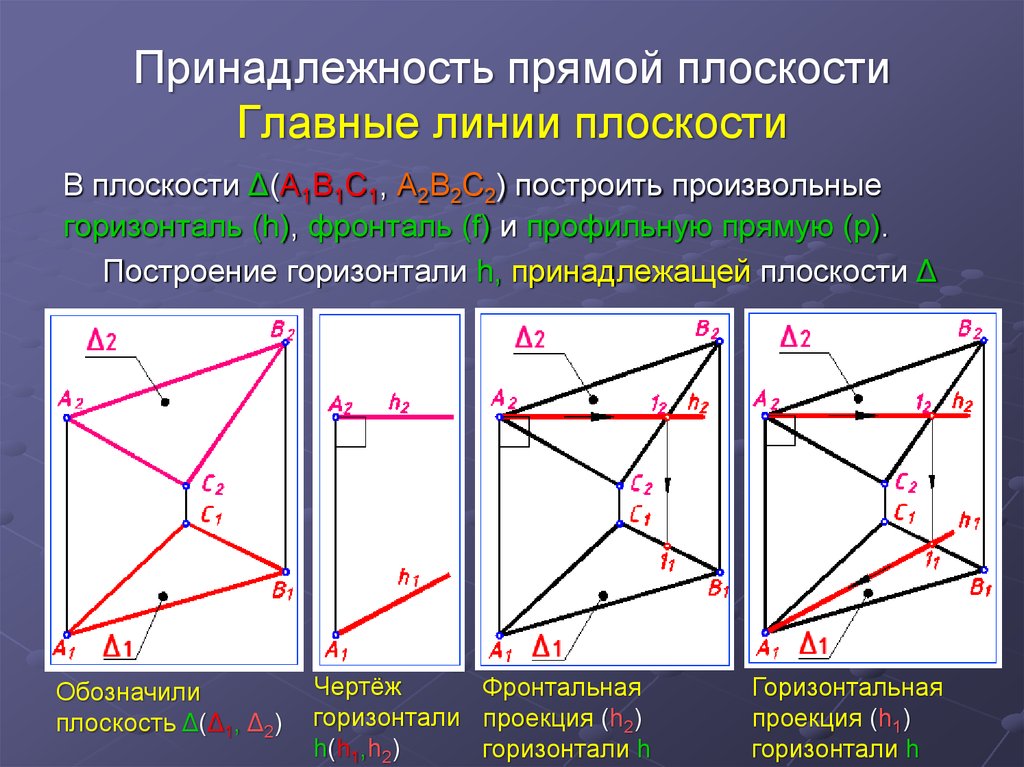
19. Принадлежность прямой плоскости Главные линии плоскости

В плоскости Δ(А1В1С1, А2В2С2) построить произвольные
горизонталь (h), фронталь (f) и профильную прямую (p).
Построение горизонтали h, принадлежащей плоскости Δ
Обозначили
плоскость Δ(Δ1, Δ2)
Чертёж
Фронтальная
горизонтали проекция (h2)
h(h1,h2)
горизонтали h
Горизонтальная
проекция (h1)
горизонтали h

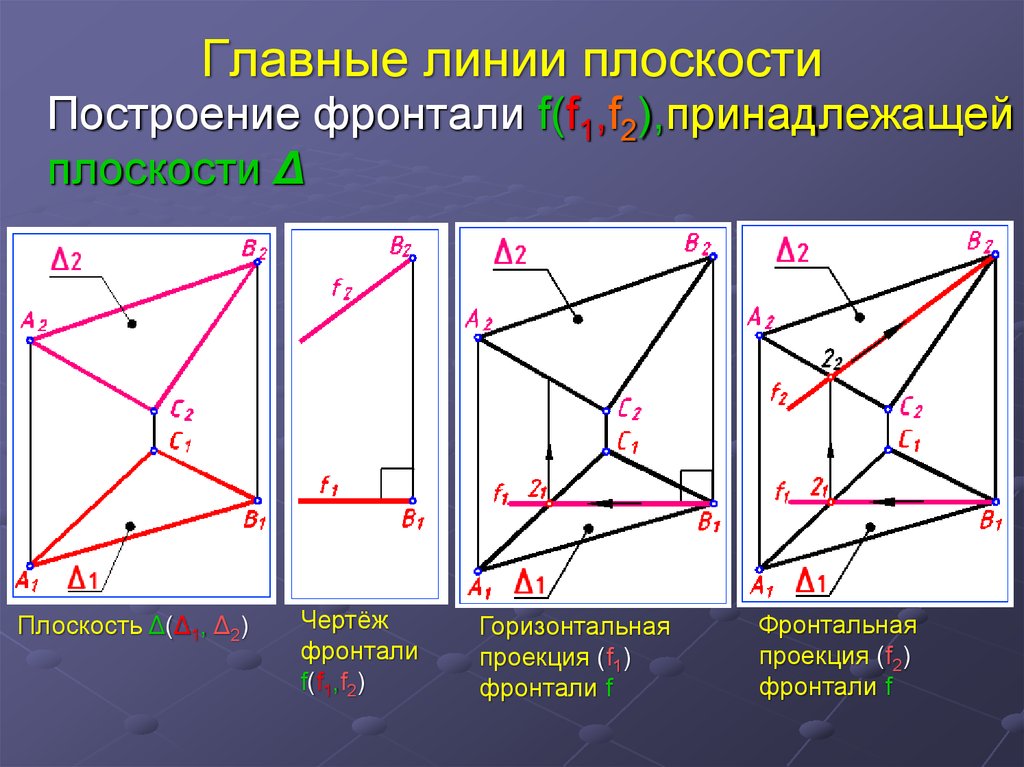
20. Главные линии плоскости

Построение фронтали f(f1,f2),принадлежащей
плоскости Δ
Плоскость Δ(Δ1, Δ2)
Чертёж
фронтали
f(f1,f2)
Горизонтальная
проекция (f1)
фронтали f
Фронтальная
проекция (f2)
фронтали f

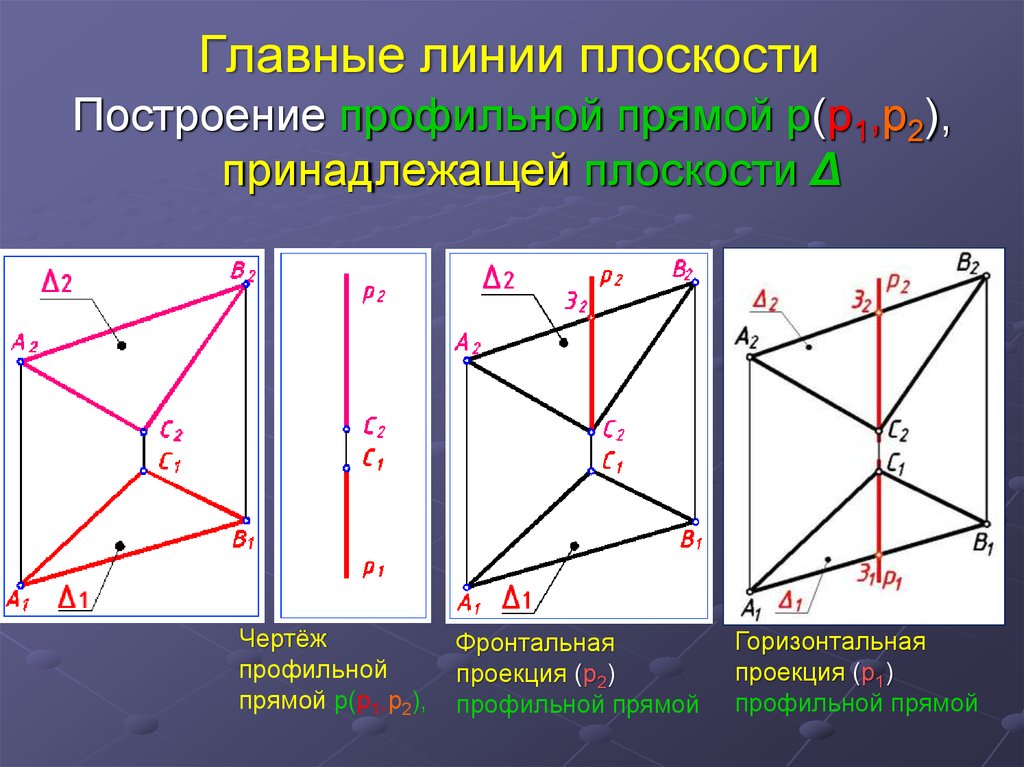
21. Главные линии плоскости

Построение профильной прямой p(p1,p2),
принадлежащей плоскости Δ
Чертёж
профильной
прямой p(p1,p2),
Фронтальная
проекция (p2)
профильной прямой
Горизонтальная
проекция (p1)
профильной прямой

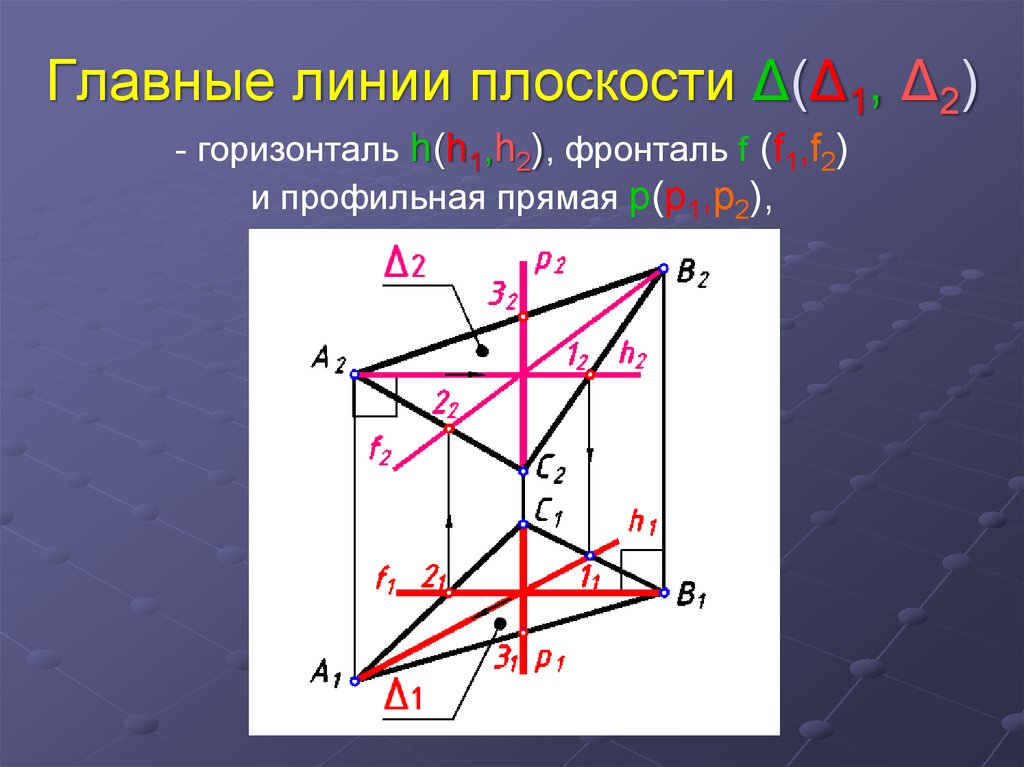
22. Главные линии плоскости Δ(Δ1, Δ2)

- горизонталь h(h1,h2), фронталь f (f1,f2)
и профильная прямая p(p1,p2),

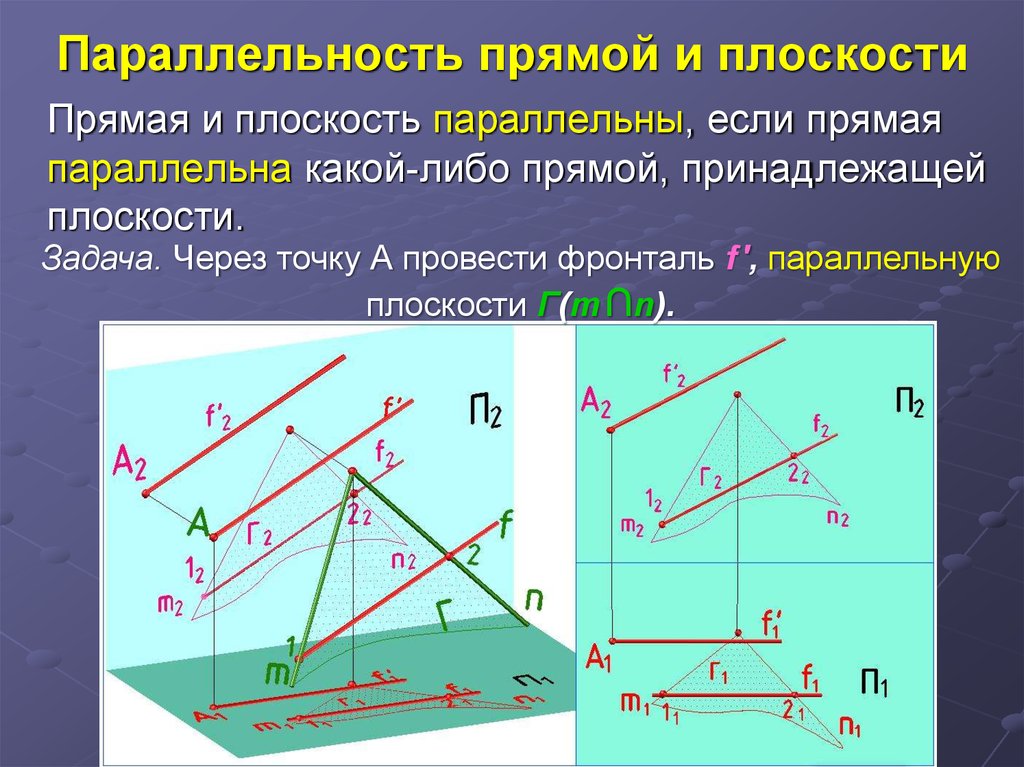
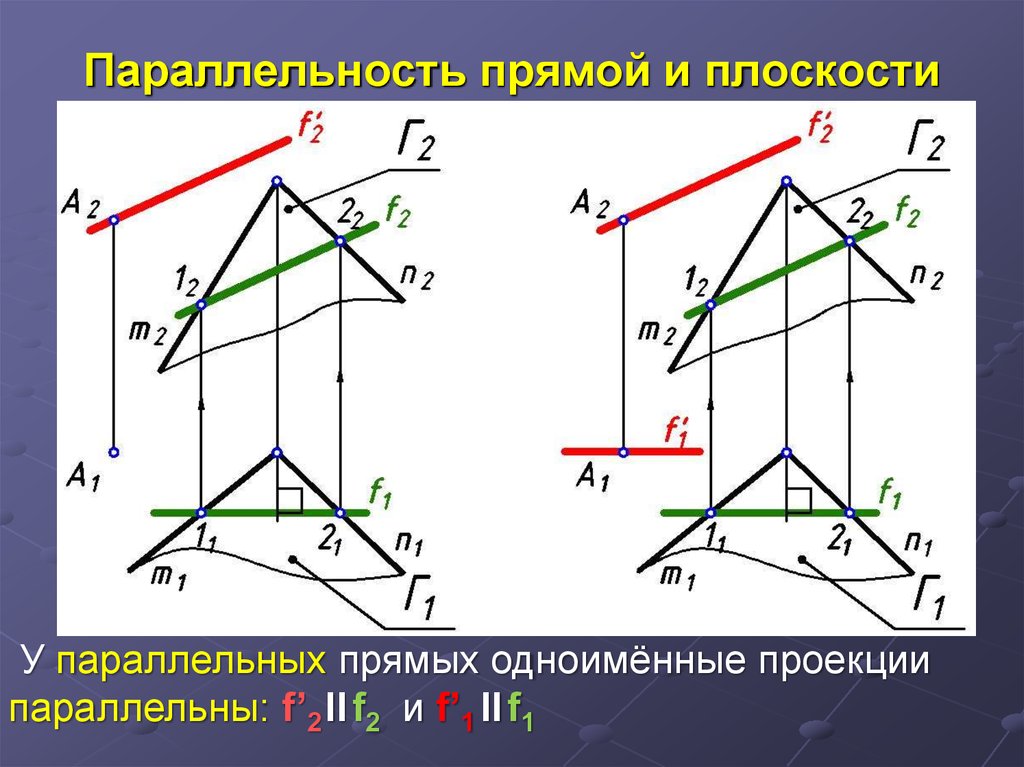
23. Параллельность прямой и плоскости

Прямая и плоскость параллельны, если прямая
параллельна какой-либо прямой, принадлежащей
плоскости.
Задача. Через точку А провести фронталь f ′, параллельную
плоскости Г(m ∩n).

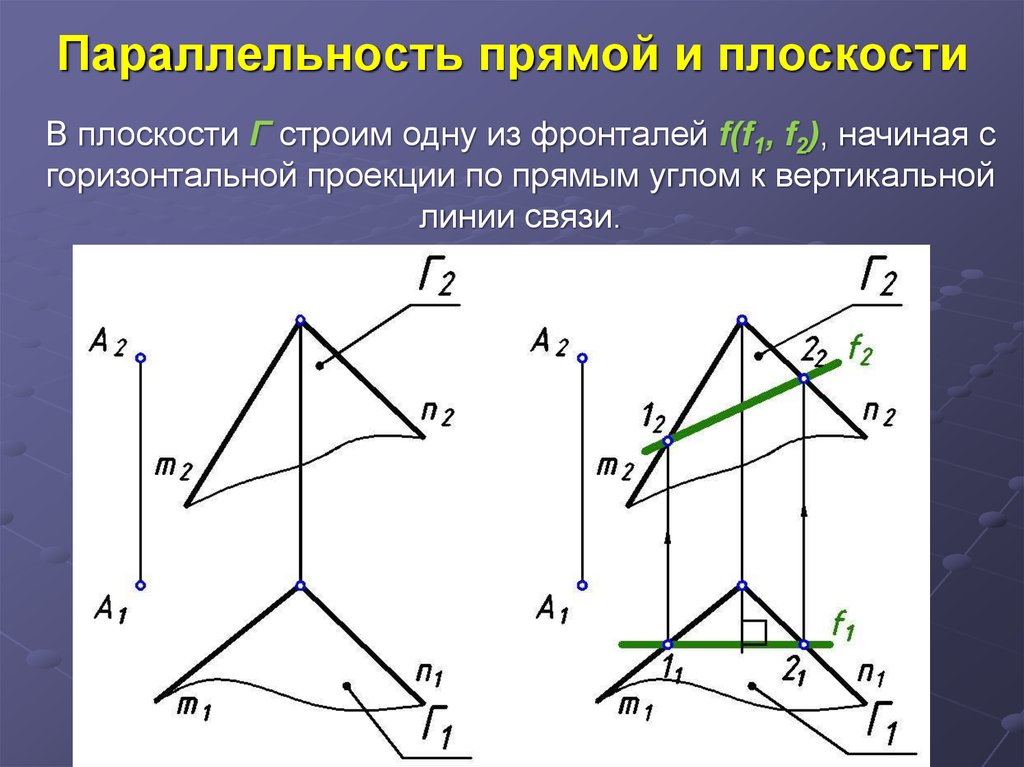
24. Параллельность прямой и плоскости

В плоскости Г строим одну из фронталей f(f1, f2), начиная с
горизонтальной проекции по прямым углом к вертикальной
линии связи.

25. Параллельность прямой и плоскости

У параллельных прямых одноимённые проекции
параллельны: f’2 II f2 и f’1 II f1

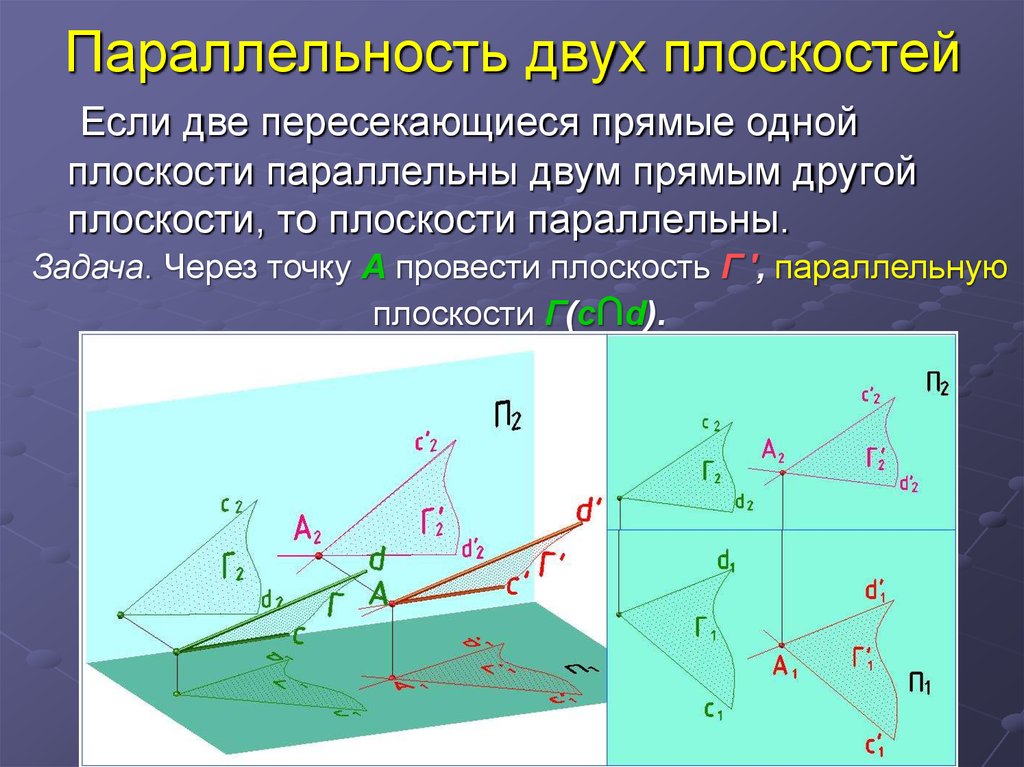
26. Параллельность двух плоскостей

Если две пересекающиеся прямые одной
плоскости параллельны двум прямым другой
плоскости, то плоскости параллельны.
Задача. Через точку А провести плоскость Г ′, параллельную
плоскости Г(c∩d).

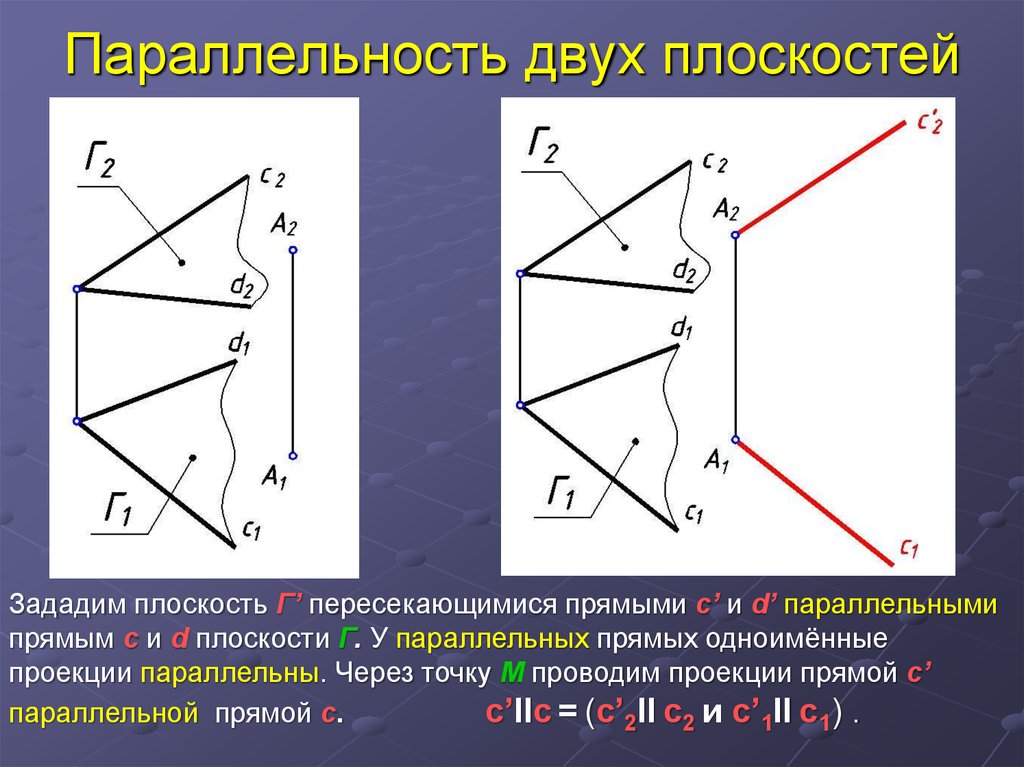
27. Параллельность двух плоскостей

Зададим плоскость Г’ пересекающимися прямыми c’ и d’ параллельными
прямым c и d плоскости Г. У параллельных прямых одноимённые
проекции параллельны. Через точку М проводим проекции прямой c’
параллельной прямой c.
c’IIc = (c’2II c2 и c’1II c1) .

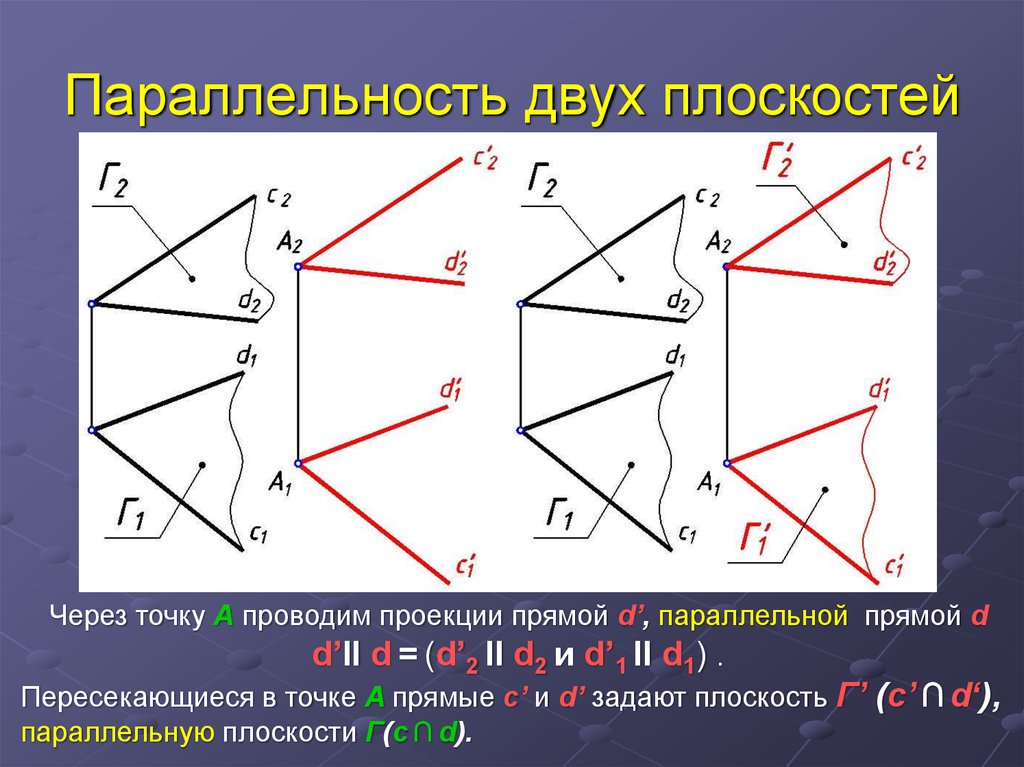
28. Параллельность двух плоскостей

Через точку A проводим проекции прямой d’, параллельной прямой d
d’II d = (d’2 II d2 и d’1 II d1) .
Пересекающиеся в точке A прямые c’ и d’ задают плоскость Г’ (c’ ∩ d‘),
параллельную плоскости Г(c ∩ d).