Similar presentations:
Задачи ЕГЭ и олимпиад по молекулярной физике и термодинамике
1.
Волгоградский государственныйсоциально-педагогический университет
26 декабря 2020 г
Глазов Сергей Юрьевич, доктор
физико-математических
наук,
профессор,
кафедра
высшей
математики и физики ВГСПУ
2.
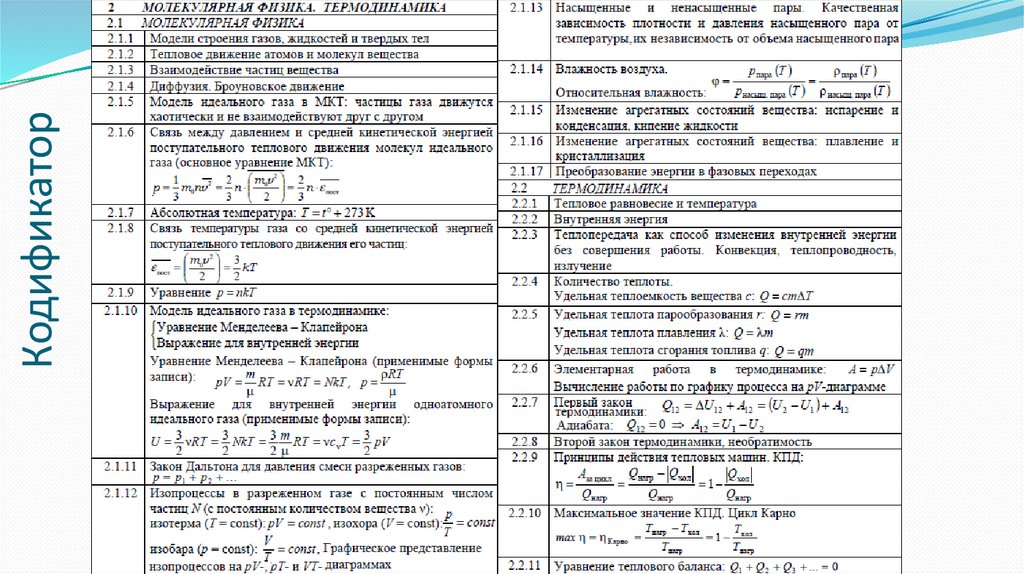
Кодификатор3.
Уравнение Менделеева-КлапейронаЗадача 1: Сосуд объемом V1 = 50 л соединен с сосудом объемом V2 = 18 л с помощью короткой трубки, в
которой есть специальный клапан, позволяющий газу переходить из большего сосуда в малый, если
разность давления в сосудах превышает p = 1,1 105 Па. В большом сосуде находится газ при давлении
p0 = 105 Па и температуре T0 = 300 К, в малом сосуде - вакуум. Каким будет давление в малом сосуде,
если систему нагреть до температуры t = 167 C?
Дано:
V1 = 50 л
V2 = 18 л
p = 1,1 105 Па
p0 = 105 Па
T0 = 300 К
T1 = 167+273 К
p1 ?
Решение:
1. Рассмотрим два состояния системы, выполним
рисунок и расставим параметры системы.
2. Для начального состояния уравнение МенделееваКлапейрона
p0
V1
T0
V2
p0V1 RT0 (1)
3. После нагрева уравнения состояния для газов в
двух сосудах
( p1 p )V1 1 RT1 (2)
p1V2 ( 1 ) RT1 (3)
4. Решив систему уравнений, получим
p1
Ответ: p1 27 кПа.
( p0T1 pT0 )V1
(V1 V2 )T0
p2 =p1+ p
T1
1
p1
T1
2= - 1
4.
Уравнение Менделеева-КлапейронаЗадача 2: В баллоне объемом V = 1,5 л находится воздух при нормальном давлении. За сколько ходов
поршня разряжающего насоса, имеющего объем цилиндра V1 = 100 см3, можно понизить давление в
баллоне в k = 100 раз. Температуру считать постоянной.
Решение:
Дано:
V = 1,5 л
V1 = 100 см3
k = 100
1. Рассмотрим два состояния системы, выполним
рисунок и расставим параметры системы.
2. Начальное состояние p0V RT (1)
p0
V
T
V1
3. Первый ход поршня насоса
p1V ( 1 ) RT (2)
p1V1 1 RT (3)
4. Решив систему, получим
n ?
1
V1
V V1
1 1
5. После 2-го хода поршня
V
V V1
p1 p0
V
V V1
V
V
p2 p1
p0
V V1
V V1
n
V
p0
6. После n-го хода поршня pn p0 V V k
1
lg k
n
7. Выражая n, имеем
V
lg(1 1 )
V
V
V1V
2 1 1
V V1
(V V1 ) 2
Ответ: n = 71.
V
2 1 2
V V1
2
2
p1
1= 1
V
T
p1
V1
T
1
5.
Уравнение Менделеева-КлапейронаЗадача 3: В вертикальном закрытом с обоих торцов цилиндре находится массивный поршень, по обе
стороны которого – по одному молю воздуха. При температуре T1 = 300 К отношение верхнего объема к
нижнему n1 = 4. При какой температуре это отношение станет равным n2 = 3? Трение не учитывать.
Решение:
Дано:
= 1 моль
T1 = 300 К
n1 = 4
n2 = 3
T2 ?
1. Рассмотрим два состояния системы, выполним
рисунок и расставим параметры системы.
2. Условие равновесия поршня
F1н F1в mg 0
F2 н F2 в mg 0
p1н S p1в mg (1)
p2 н S p2 в mg (2)
3. Связь между объемами
V2в V1в V
V2 в V1в V
n1
V1в
(3)
V1н
n2
p1в
F1н
F1в
mg
V2 в V1в V
( 4)
V2 н V1н V
p1нV1н RT1 (6)
p2 в (V1в V ) RT2 (7)
5. Решив систему уравнений, получим
Ответ: T2 = 420 К.
T2 T1
F1н
p2 н (V1н V ) RT2 (8)
(n12 1)n2
(n22 1)n1
p1н
V1н
T1
p2в
4. Уравнение Менделеева-Клапейрона
p1вV1в RT1 (5)
V1в
T1
F1в
mg
V2в
T2
p2н
V2н
T2
6.
Колебания поршняЗадача 4: Найти период малых колебаний поршня массой m, разделяющего гладкий цилиндрический
сосуд сечения S на две части длиной L каждая. По обе стороны от поршня находится газ при давлении
p0 и температуре T0. Считать, что при колебаниях температура газа не меняется.
Решение:
Дано:
m
S
L
p0, T0
T ?
1. Выведем поршень из положения равновесия. Под
действием сил со стороны
газов поршень
будет совершать
колебания.
ma F F mg N
1
2
p0
p0
V
T0
V
T0
2. В проекции на ось ох
ma x F1 F2
ma x ( p1 p2 ) S (1)
L
3. Уравнение Менделеева-Клапейрона
p0 LS RT0 (2)
p1 ( L x) S RT0 (3)
4. Воспользуемся приближением
p2 ( L x) S RT0 (4)
p1 p2 2 p0 (5)
5. Решив систему уравнений, получим уравнение гармонических
2p S
колебаний
ax 2 х 0
ax 0 х 0
mL
L
p1
p2
V+ V
T0
V- V
T0
F1
F2
6. Тогда период колебаний
Ответ:
T 2
mL
2 p0 S
0 x
x
7.
ТермодинамикаЗадача 5: В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный
идеальный газ. Первоначальное давление газа р1 = 4 105 Па. Расстояние от дна сосуда до поршня равно
L. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газ получил
количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние x = 10 см. При движении поршня
на него со стороны стенок действует сила трения величиной Fтр =3 103 Н. Найдите L. Считать, что сосуд
находится в вакууме.
Решение:
Дано:
p1
p2
i=3
1. Рассмотрим первоначальное равновесие поршня.
T1
T3
р1 = 4 105 Па
S = 25 см2
Q = 1,65 кДж
x = 10 см
Fтр =3 103 Н
L ?
p1S 4 105 25 10 4 103 Н Fтр
2. При нагревании поршень будет оставаться в покое
до тех пор, пока
p2 S Fтр (1)
L
L
x
3. Затем поршень будет сдвигаться при
постоянном давлении p2
4. Количество теплоты, полученное газом, складывается из количества теплоты, полученного при
изохорном нагревании газа и количества теплоты, полученного при изобарном расширении газа
3
A12 p2 Sx Fтр x (4)
U13 R(T3 T1 ) (3)
2
5. Уравнения Менделеева-Клапейрона
p1 LS RT1 (5)
p2 ( L x) S RT3 (6)
Q Q12 Q23 U13 A23 (2)
6. Решив систему уравнений, получим
Q
Ответ:
L
5
Fтр x
2
3
( Fтр p1 S )
2
= 0,3 м.
8.
ВлажностьЗадача 6: Человек при частоте дыхания n = 10 раз в минуту при каждом вдохе вдыхает воздух объемом
V = 1 л при температуре t1 = 27 C и относительной влажности 1 = 30%, а выдыхает при температуре
t2 = 36 C и относительной влажности 2 = 100%. Определите массу воды, которая теряется организмом
за сутки в процессе дыхания. Давления насыщенного пара при температурах t1 и t2 равны
соответственно pнп1 = 3,6 кПа и pнп2 = 6 кПа.
Дано:
n = 10
V=1л
t1 = 27 C
1 = 30%
t2 = 36 C
2 = 100%
pнп1 = 3,6 кПа
pнп2 = 6 кПа
m ?
Решение:
1. Человек с воздухом вдыхает массу водяного пара
mвдох вп1V, а выдыхает
mвыдох вп 2V
2. Масса воды, теряемая за один вдох и выдох
m mвыдох mвдох ( вп 2 вп1 )V (1)
3. Плотности вдыхаемого и выдыхаемого пара
вп1
1
100%
нп1 (2)
вп 2
2
100%
нп 2 (3)
4. Давление связано с плотностью уравнением Менделеева-Клапейрона
5. За сутки человек делает N = 24 60 n (5) вздохов
6. Таким образом за сутки человек теряет m N m (6)
7. Решив систему уравнений, получим
Ответ:
m
1440 n 2 pнп 2 1 pнп1 MV
0,5 кг.
100% T2
T1 R
pнп
нп
M
RT (4)
9.
Спасибо за внимание!Литература для подготовки к ЕГЭ
Кабардин О.Ф. Физика: справочник для школьников и поступающих в вузы. Курс подготовки к ГИА, ЕГЭ и
дополнительным вступ. испытаниям в вузы – М.: Арт-пресс школа, 2019. – 528 с.
Демидова М.Ю. ЕГЭ 2020. Банк заданий. 1000 задач. – М.: Изд. “Экзамен”, 2020. – 430 с.
Кабардин О.Ф. Физика. Подготовка к ЕГЭ. Вступительные испытания.–М.: Изд.“Экзамен”, 2011.– 477 с.
Турчина Н.В. и др. 3800 задач по физике для школьников и поступающих в ВУЗы. – М.: Дрофа, 2000. – 672 с.
Вишнякова Е.А. и др. Отличник ЕГЭ. Физика. Решение сложных задач. М.: Интеллект-Центр, 2010.– 368 с.
Парфентьева Н.А. Задачи по физике для поступающих в вузы. – М.: Просвещение, 2008. – 303 с.
Гольдфарб Н.И. Физика. Задачник. 10-11 кл. : учеб. пособие. – М.: Дрофа, 2018. – 398 с.
Физика. Углубленный курс с решениями и указаниями. ЕГЭ, олимпиады, экзамены в вуз [Электронный
ресурс] / Е. А. Вишнякова [и др.]; под ред. В. А. Макарова, С. С. Чеснокова. — М. : БИНОМ. Лаборатория
знаний, 2015. – 419 с.
ЕГЭ. Физика: типовые экзаменационные варианты : 30 вариантов / под ред. М. Ю. Демидовой. — М. : Изд.
Национальное образование, 2020. – 400 с.








 physics
physics








