Similar presentations:
Задачи. Термодинамические циклы
1.
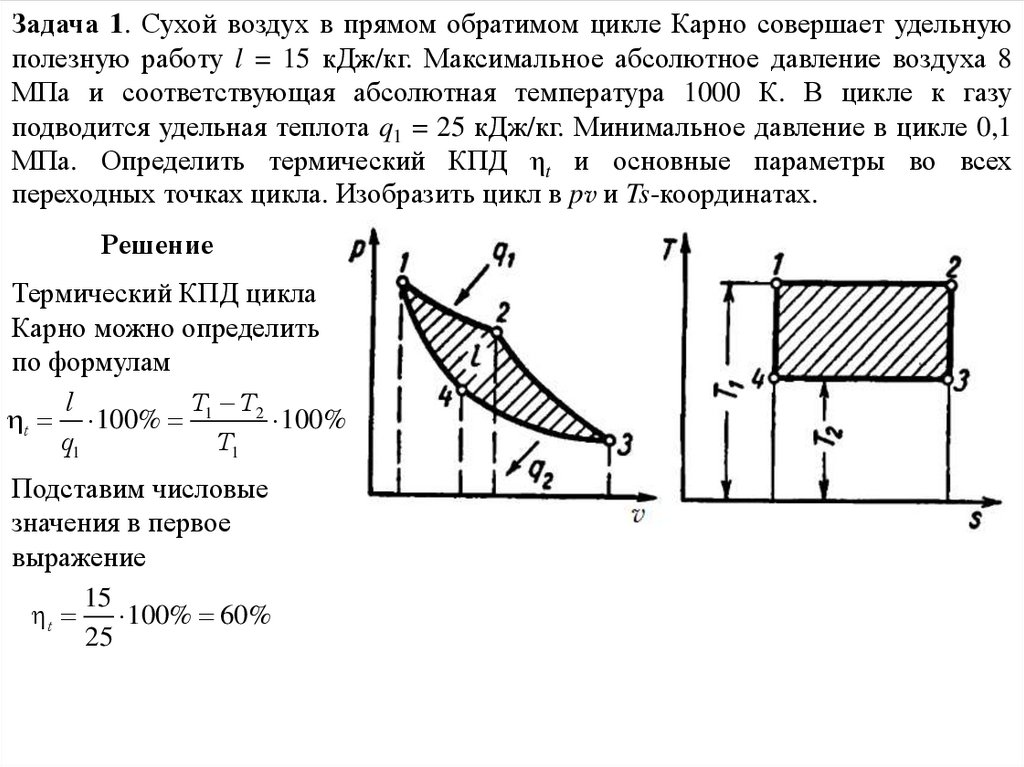
Задача 1. Сухой воздух в прямом обратимом цикле Карно совершает удельнуюполезную работу l = 15 кДж/кг. Максимальное абсолютное давление воздуха 8
МПа и соответствующая абсолютная температура 1000 К. В цикле к газу
подводится удельная теплота q1 = 25 кДж/кг. Минимальное давление в цикле 0,1
МПа. Определить термический КПД ηt и основные параметры во всех
переходных точках цикла. Изобразить цикл в pv и Ts-координатах.
Решение
Термический КПД цикла
Карно можно определить
по формулам
l
T T
t 100% 1 2 100%
q1
T1
Подставим числовые
значения в первое
выражение
15
t
100% 60%
25
2.
Выразим из формул для КПД температуру Т2l
T
1 2
q1
T1
T2
l
1
T1
q1
l
T2 T1 1
q1
Подставим числовые значения
15
T2 1000 1 400 К
25
Удельный объём воздуха v1 в состоянии 1 определим из уравнения состояния
RT1
v1
p1v1 RT1
p1
Газовую постоянную для воздуха найдём из таблицы R 287 Дж/(кг К)
287 1000
v1
0,036 м3 /кг
6
8 10
Удельный объём воздуха v3 в состоянии 3 определим из уравнения состояния
RT2
v3
p3v 3 RT2
p3
Подставим числовые значения
v3
287 400
1,148 м3 /кг
5
10
3.
Молекулярные массы, плотности, молярные объёмы при нормальных условиях и газовые постоянныеважнейших газов
1
Химическое
обозначение
Молекулярная
масса , кг/кмоль
Плотность
, кг/м3
Молярный объём
v , м3/кмоль
Газовая постоянная
R, Дж/(кг К)
−
28,96
1,293
22,40
287,0
3
Кислород
O2
32,00
1,439
22,39
259,8
4
Азот
N2
28,026
1,251
22,40
296,8
5
Атмосферный азот
N2
28,16
1,257
22,40
295,3
6
Гелий
He
4,003
0,179
22,42
2078,0
Аргон
Ar
39,994
1,783
22,39
208,2
Водород
H2
2,016
0,090
22,43
4124,0
Окись углерода
CO
28,01
1,250
22,40
296,8
Углекислый газ
CO2
44,01
1,977
22,26
188,9
Сернистый газ
SO2
64,06
2,926
21,89
129,8
Метан
CH4
16,032
0,717
22,39
518,8
Этилен
C2H4
28,052
1,251
22,41
296,6
−
11,50
0,515
22,33
721,0
Аммиак
NH3
17,032
0,771
22,08
488,3
Водяной пар
H2O
18,016
0,804
22,40
461
Вещество
Воздух
Коксовый газ
2
4.
Запишем выражение для удельного количества теплоты, которое получает воздухпри изотермическом расширении
v
q1 RT1 ln 2
v1
Выразим отсюда объём v2 в состоянии 2
q
v 2 v1 exp 1
RT1
Подставляем числовые значения
25000
3
v 2 0,036 exp
0,039 м /кг
287 1000
Давление воздуха в состоянии 2 определим, записав закон Бойля-Мариотта для
изотермического процесса 1-2
v
p2 p1 1
p1v1 p2v 2
v2
Найдём числовое значение
0,036
p2 8 106
7,4 106 Па 7,4 МПа
0,039
5.
Чтобы определить удельный объём воздуха в состоянии 4, запишем выражениедля удельного количества теплоты, передаваемого газом в окружающую среду в
процессе 3-4
v
q 2 q1 l RT2 ln 3
v4
Выразим отсюда удельный объём в состоянии 4
l q1
v 4 v 3 exp
RT2
Подставим числовые значения
15000 25000
3
v 4 1,148 exp
1,052 м /кг
287 400
Давление воздуха в состоянии 4 определим, записав закон Бойля-Мариотта для
изотермического процесса 3-4
v
p 4 p3 3
p3v 3 p4v 4
v4
Подставим числовые значения
1,148
p4 105
1,1 105 Па 0,11 МПа
1,052
6.
Определим удельную энтропию воздуха в переходных точках цикла. В состоянии1 энтропию определим по формуле
T
p
p 0 p3
s1 c p ln 1 R ln 1
T0 273 К
T
p
0
0
Удельную теплоёмкость воздуха при постоянном давлении определим по
формуле
kR
cp
k 1
Тогда выражение для удельной энтропии будет иметь вид
k
p
T
p
kR T1
ln R ln 1 R
ln 1 ln 1
k 1 T0
p0
p0
k 1 T0
Подставим числовые значения
s1
1,4
8 106
1000
s1 287
ln
46 Дж/(кг К)
ln
5
1,4
1
273
10
Поскольку процесс 4-1 является адиабатным, то можно записать
s 4 s1 46 Дж/(кг К)
7.
Изменение удельной энтропии в изотермическом процессе 1-2 и, соответственно,удельную энтропию в состоянии 2 найдём по формулам
q
q
s12 1
s 2 s1 s12 s1 1
T1
T1
Подставим числовые значения
25000
s 2 46
71 Дж/(кг К)
1000
Так как процесс 2-3 тоже является адиабатным, то можно записать
s3 s 2 71 Дж/(кг К)
Определим удельную энтальпию воздуха в переходных точках цикла. В
состоянии 1 энтропию определим по формуле
kRt1
h1 c pt1
k 1
Подставим числовые значения
1,4 287 727
h1
730 кДж/кг
1,4 1
Поскольку процесс 1-2 изотермический, то
h2 h1 730 кДж/кг
8.
Энтальпию в состоянии 3 найдём по выражениюkRt 2
h3 c pt 3
k 1
Рассчитаем эту величину
1,4 287 127
h3
128 кДж/кг
1,4 1
Энтальпии в состояниях 3 и 4 будут равны между собой
h4 h3 128 кДж/кг
9.
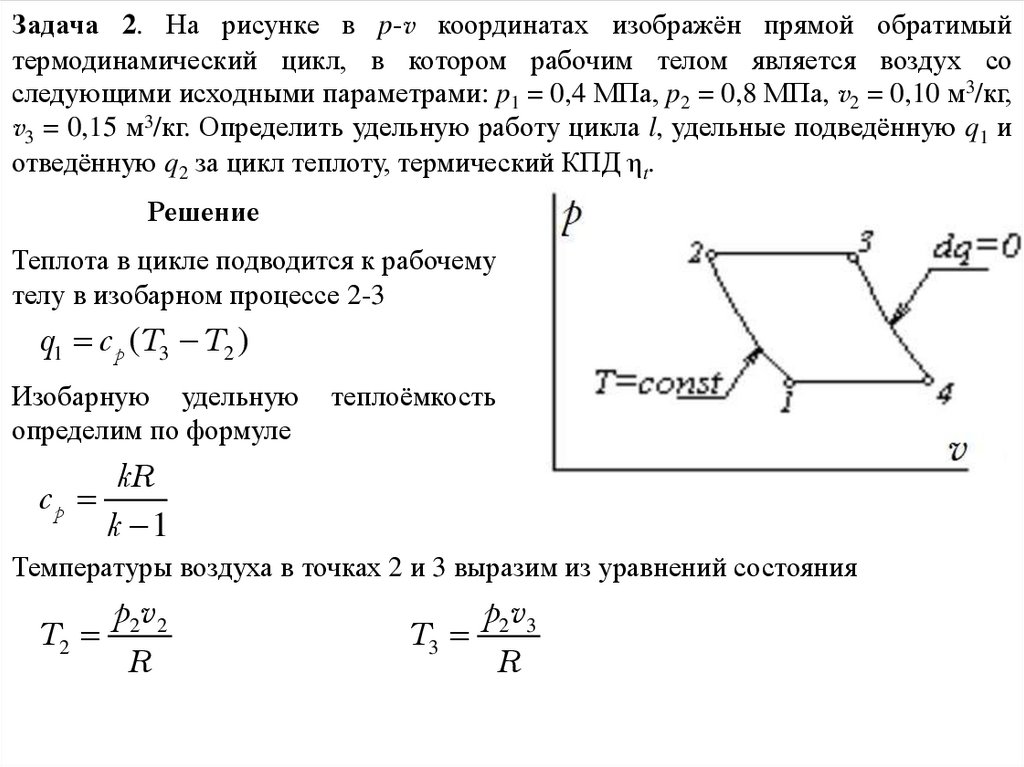
Задача 2. На рисунке в p-v координатах изображён прямой обратимыйтермодинамический цикл, в котором рабочим телом является воздух со
следующими исходными параметрами: p1 = 0,4 МПа, p2 = 0,8 МПа, v2 = 0,10 м3/кг,
v3 = 0,15 м3/кг. Определить удельную работу цикла l, удельные подведённую q1 и
отведённую q2 за цикл теплоту, термический КПД ηt.
Решение
Теплота в цикле подводится к рабочему
телу в изобарном процессе 2-3
q1 c p (T3 T2 )
Изобарную удельную
определим по формуле
cp
теплоёмкость
kR
k 1
Температуры воздуха в точках 2 и 3 выразим из уравнений состояния
T2
p2v 2
R
T3
p2v 3
R
10.
Подставим эти выражения в формулу для подведённой теплотыq1
kR p2v 3 p2v 2 kp2
(v 3 v 2 )
k 1 R
R k 1
Подставим числовые значения
1,4 8 105
q1
(0,15 0,1) 140 кДж/кг
1,4 1
Теплота в цикле отводится в процессах 4-1 и 1-2, поэтому она равна
q 2 q 41 q12
Теплоту, отдаваемую рабочим телом при изобарном сжатии найдём
kp2v 2 T4
kR
kRT1 T4
q 41 c p (T4 T1 )
(T4 T1 )
1
1
k 1
k 1 T1
k
1
T1
Так как процесс 4-1 изобарный, то для него можно записать
v 4 v1
T4 T1
T4 v 4
T1 v1
11.
Удельный объём v1 выразим из закона Бойля-Мариоттаv1
p1v1 p2v 2
p2
v2
p1
Для определения удельного объёма v4 запишем уравнение адиабаты
p
v 4 v3 2
p1
p1v 4k p2v 3k
1
k
Тогда отношение удельных объёмов в 4 и 1 состояниях равно
1
k
v 4 v 3 p2 p1 v 3 p2
v1 v 2 p1 p2 v 2 p1
1 k
k
Тогда отвод теплоты в процессе 4-1 равен
k 1
k
kp v v p
q 41 2 2 3 1 1
k 1 v 2 p2
12.
Теплота, отдаваемая рабочим телом в изотермическом процессе 1-2, равнаp2
v1
q12 RT1 ln p2v 2 ln
v2
p1
Тогда количество отданной за цикл теплоты равно
k 1
k
k v 3 p1
ln p2
q 2 p2v 2
1
k 1 v p
p1
2 2
Подставим числовые значения
1,4 1
1,4
1,4 0,15 0,4
ln 0,8
q 2 8 105 0,1
1
0,4
1,4 1 0,1 0,8
120 кДж/кг
13.
Удельная работа за цикл равнаl q1 q 2
Подставим числовые значения
l 140 120 20 кДж/кг
Термический КПД цикла определим по формуле
t
l
100%
q1
Подставим числовые значения
t
20
100% 14%
140
14.
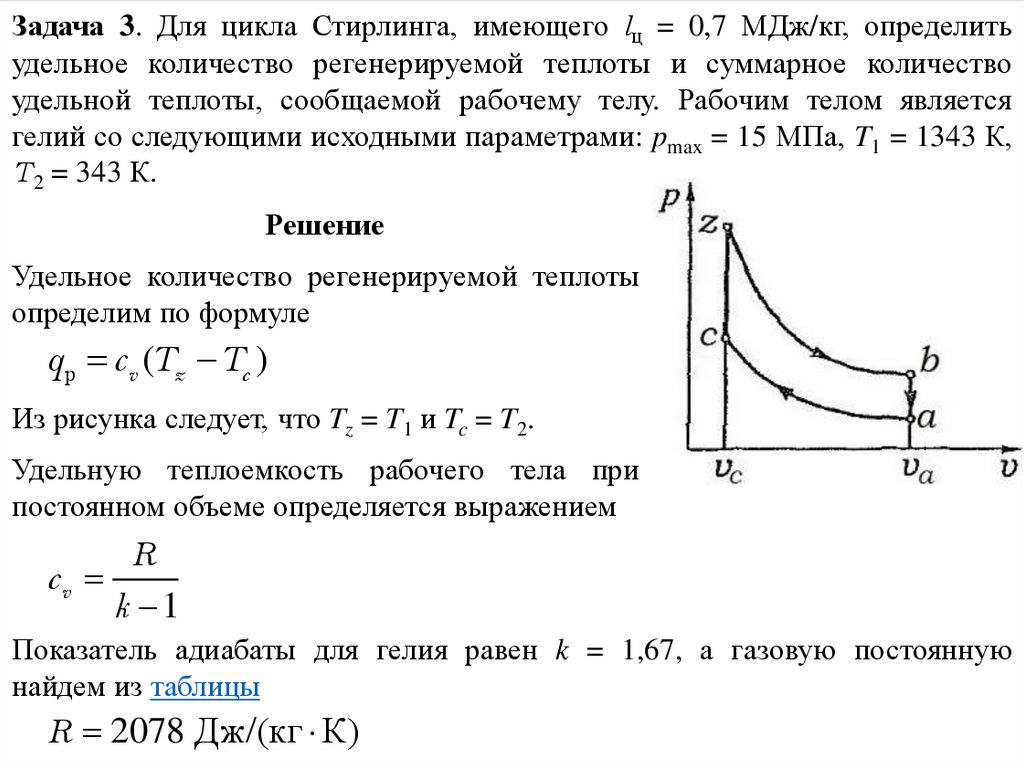
Задача 3. Для цикла Стирлинга, имеющего lц = 0,7 МДж/кг, определитьудельное количество регенерируемой теплоты и суммарное количество
удельной теплоты, сообщаемой рабочему телу. Рабочим телом является
гелий со следующими исходными параметрами: pmax = 15 МПа, T1 = 1343 К,
T2 = 343 К.
Решение
Удельное количество регенерируемой теплоты
определим по формуле
q р c v (Tz Tc )
Из рисунка следует, что Tz = T1 и Tc = T2.
Удельную теплоемкость рабочего тела при
постоянном объеме определяется выражением
cv
R
k 1
Показатель адиабаты для гелия равен k = 1,67, а газовую постоянную
найдем из таблицы
R 2078 Дж/(кг К)
15.
Тогда формула для количества теплоты будет иметь видqр
R (T1 T2 )
k 1
Подставим числовые значения
qр
2078 (1343 343)
3,10 106 Дж/кг 3,10 МДж/кг
1,67 1
Удельное количество теплоты, которое получает рабочее тело при
изотермическом расширении определяется равенством
v
q1 RTz ln a
vc
va
RT
ln
1
vc
С другой стороны, удельная работа за цикл определяется формулой
v
l ц R (Tz Tc )ln a
vc
va
R
(
T
T
)ln
1
2
vc
Выразим отсюда логарифм отношения объемов и подставим в формулу для
q1
16.
vln a
vc
lц
R (T1 T2 )
lц
T1
q1 RT1
lц
R (T1 T2 )
T1 T2
Суммарное удельное количество теплоты, передаваемое рабочему телу,
определим по формуле
q q р q1 q р l ц
T1
T1 T2
Подставим числовые значения
q 3,1 0,7
1343
4,04 МДж/кг
1343 343













 physics
physics








