Similar presentations:
Теплопередача. Задачи
1.
Задание 1. Определить плотность теплового потока, температуры на внешней ивнутренней поверхности слоя асбеста толщиной δ = 0,5 м и теплопроводностью
λ= 0,15 Вт/(м∙К). «Горячая» среда имеет параметры tж1 = 200°С и α1 = 9 Вт/(м2∙К).
«Холодная» среда – tж2 = 20°С и α2 = 14 Вт/(м2∙К).
Решение
Определим плотность теплового потока по формуле:
(t ж1 t ж2 )
q
1 1
1 2
(200 20)
q
51 Вт/м 2
1 0,5 1
9 0,15 14
С другой стороны, плотность теплового потока через поверхность стенки равна:
q k (t ж1 t ж2 ) 1 (t ж1 t с1 ) 2 (t с2 t ж2 )
Отсюда температуры на внутренней и внешней поверхности асбеста равны:
q
t с1 t ж1
1
q
t с2 t ж2
2
51
t с1 200 194 C
9
51
t с2 20 24 C
14
2.
Задание 2. Определить потери теплоты через 1 м2 кирпичной обмуровки котлатолщиной = 250 мм и температуры стенок tс1 и tс2, если температура газов tж1 =
600°С, температура воздуха tж2 = 30°С, коэффициент теплоотдачи со стороны
газов α1 = 20 Вт/(м2∙°С), коэффициент теплоотдачи со стороны воздуха α2 = 8
Вт/(м2∙°С) и коэффициент теплопроводности обмуровки λ = 0,7 Вт/(м∙°С).
Решение
Коэффициент теплопередачи от газов к воздуху определим по формуле:
1
k
1 1
1 2
1
k
1,88 Вт/(м 2 С)
1 0,25 1
20 0,7 8
Потерю теплоты определим по выражению:
q k (t ж1 t ж2 )
q 1,88 (600 30) 1070 Вт/м2
Температуры на внутренней и внешней стенок обмуровки равны:
q
t с1 t ж1
1
q
t с2 t ж2
2
1070
t с1 600
547 C
20
1070
t с2 30
164 C
8
3.
Задание 3. Паропровод диаметром 200/216 мм покрыт слоем совелитовойизоляции толщиной 2 = 120 мм, коэффициент теплопроводности которой λ2 =
=0,1 Вт/(м∙°С). Температура пара tж1 = 300°С и окружающего воздуха tж2 = 25°С.
Кроме того, заданы коэффициент теплопроводности стенки λ1 = 40 Вт/(м∙°С), α1 =
= 100 Вт/(м2∙°С) и α2 = 8,5 Вт/(м2∙°С). Требуется определить линейный
коэффициент теплопередачи, линейную плотность теплового потока и
температуру в месте соприкосновения паропровода с изоляцией.
Решение
Согласно условию задачи диаметры будут равны:
d1 0,2 м
d 3 d 2 2
d 2 0,216 м
d 3 0,216 2 0,12 0,456 м
Линейный коэффициент теплопередачи определим по
формуле:
kl
1
1
1
1
1
0,216
0,456
ln
ln
100 0,2 2 40 0,2 2 0,1 0,216 8,5 0,456
0,247 Вт/(м С)
4.
Определим линейную плотность теплового потока:ql kl (t ж1 t ж2 )
ql 3,14 0,247 (300 25) 213 Вт/м
Температуру в месте соприкосновения паропровода с изоляцией определим по
формуле:
213
1
1
0,216
t с2 300
ln
296,5 C
3,14 100 0,2 2 40 0,2
5.
Задание 4. Определить плотность теплового потока через стенку, холоднаясторона которой оребрена и коэффициент оребревания F2/F1 = 13. Толщина
стенки = 10 мм и коэффициент теплопроводности материала λ = 40 Вт/(м∙°С).
Коэффициенты теплоотдачи соответственно α1 = 200 Вт/(м2∙°С) и α2 = 10
Вт/(м2∙°С) и температуры tж1 = 75°С и tж2 = 15°С.
Решение
Определим коэффициент теплопередачи по формуле:
1
k1
77 Вт/(м2 С)
1
0,01
1
200 40 10 13
Плотность теплового потока определим по формуле:
q k1 (t ж1 t ж2 )
q 77 (75 15) 4620 Вт/м2
При отсутствии рёбер имели бы:
1
k
1 1
1 2
k
1
9,5 Вт/(м 2 С)
1
0,01 1
200 40 10
Таким образом, оребривание поверхности позволяет увеличить теплопередачу
более чем в 8 раз.
6.
Задание 5. Определить потери теплоты трубопровода при следующих условиях:диаметр трубы d = 100 мм, длина трубопровода l = 100 м, температура воды t1 =
=130°С, глубина заложения трубопровода h = 1,5 м. Влагонепроницаемая
изоляция имеет толщину δ = 0,05 м и теплопроводность λиз = 0,15 Вт/(м∙К).
Теплопроводность грунта λгр = 0,7 Вт/(м∙К). Средняя температура грунта t0 = 3°С.
Коэффициент теплоотдачи с поверхности грунта α2 = 12 Вт/(м2∙К). Учитывая, что
для воды α1→∞, температуру стенки трубы можно принять равной температуре
воды.
Решение
По таблице П.1.1 приложения 1 (п.1) полное
термическое сопротивление для одиночной
трубы в полуограниченном пространстве,
(м∙К)/Вт:
1
R
2 l
*
1 Rиз 1 2
гр
ln h
ln
2
из R гр R
Учтём, что:
R d 2
Rиз d из 2
d из d 2
7.
Получаем:1
R
2 l
*
1 d 2 1 4
гр
ln h
ln
2
из d гр d
Потери теплоты трубопровода равны:
Q
t1 t 0
*
R
1
2 l
t1 t 0
1 d 2 1 4
гр
ln h
ln
2
из d гр d
130 3
Q
1
1
4
0,7
0,1 2 0,05 1
ln
ln
1,5
2 3,14 100 0,15
0,1
0,7
0,1
12
7580 Вт
8.
Задание 6. Определить минимальную глубину h0 заложения неизолированнойтрубы диаметром d = 76 мм, по которой течёт вода температурой tтр = 130°С.
Учитывая, что для воды α → ∞, температуру стенки трубы можно принять равной
температуре воды. Теплопроводность грунта λгр = 1,16 Вт/(м∙К), температура
наружного воздуха tн = −29°С, теплоотдача с поверхности грунта αн= 23 Вт/(м2∙К).
Удельные тепловые потери принять равными не более ql = 310 Вт/м. Определить
температуру в точке M, расположенной над трубой на поверхности грунта.
Решение
Удельные потери теплоты трубопровода равны:
ql
t тр t н
R *l
Выразим отсюда полное линейное термическое
сопротивление для одиночной трубы в полуограниченном пространстве при отсутствии изоляции:
R
*
l
t тр t н
ql
9.
Для которого можно записать следующее выражение:2
гр
1
R
ln h
2 гр r
н
*
l
или
t тр t н
ql
2
гр
1
ln h
2 гр r
н
Выразим отсюда глубину закладки оси трубопровода:
2 гр
гр
r
h exp
(t тр t н )
2
ql
н
Учитывая, что h
h0 r
r d 2
получим
2 гр
гр d
d
h0 exp
(t тр t н )
4
ql
н 2
Подставим числовые значения:
0,076
2 3,14 1,16
1,16 0,076
h0
exp
(130 ( 29))
0,71 м
4
310
2
23
10.
Температура в точке, расположенной над трубой на поверхности грунта равна:t м t тр ql Rl*
2
1
h
h
Rl*
ln 1 − линейное термическое сопротивление грунта
2 гр r
r
2
2h d
ql
2
h
d
t м t тр
ln 0
0
1
2 гр d
d
Подставим числовые значения:
2
2 0,71 0,076
310
2
0,71
0,076
t м 130
ln
1 26 C
2 3,14 1,16
0,076
0,076
11.
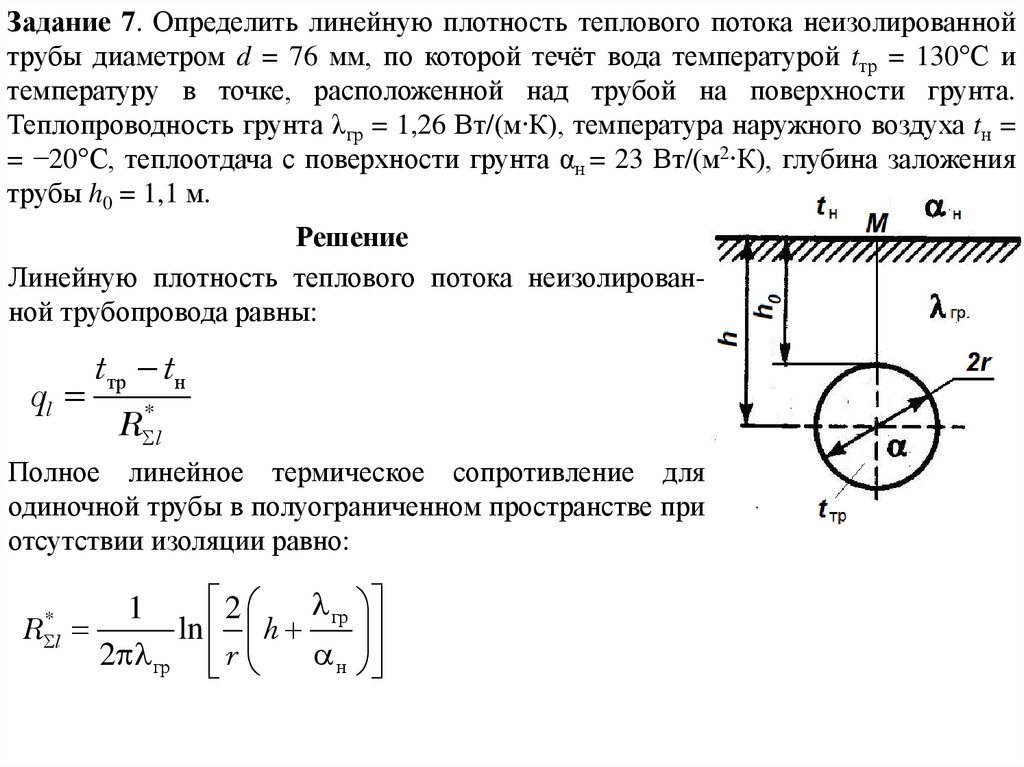
Задание 7. Определить линейную плотность теплового потока неизолированнойтрубы диаметром d = 76 мм, по которой течёт вода температурой tтр = 130°С и
температуру в точке, расположенной над трубой на поверхности грунта.
Теплопроводность грунта λгр = 1,26 Вт/(м∙К), температура наружного воздуха tн =
= −20°С, теплоотдача с поверхности грунта αн = 23 Вт/(м2∙К), глубина заложения
трубы h0 = 1,1 м.
Решение
Линейную плотность теплового потока неизолированной трубопровода равны:
ql
t тр t н
R *l
Полное линейное термическое сопротивление для
одиночной трубы в полуограниченном пространстве при
отсутствии изоляции равно:
2
гр
1
R
ln h
2 гр r
н
*
l
12.
h h0 r r d 22 гр (t тр t н )
ql
4
d гр
ln h0
2 н
d
Учитывая, что
получим
Подставим числовые значения:
2 3,14 1,26 (130 ( 20))
ql
287 Вт/м
4
0,076 1,26
ln
1,1
0,076
2
23
Температура в точке, расположенной над трубой на поверхности грунта равна:
t м t тр ql Rl*
2
1
h
h
Rl*
ln 1 − линейное термическое сопротивление грунта
2 гр r
r
2
2h d
ql
2
h
d
t м t тр
ln 0
0
1
2 гр d
d
13.
Подставим числовые значения:2
2 1,1 0,076
287
2
1,1
0,076
t м 130
ln
1 18 C
2 3,14 1,26
0,076
0,076
14.
Задание 8. Определить тепловые потоки от нагретой вертикальной поверхности впомещение за счет конвекции, излучения и полный тепловой поток. Найти их
отношение = Qл/Qк. Исходные данные: температура нагретой поверхности t1 =
55 С; температура на поверхности стены t2 = 15 С; температура воздуха в
помещении tв = 18 С; площадь нагретой поверхности F1 = 5 м2; высота нагретой
поверхности h1 = 0,5 м; приведённый коэффициент теплового излучения пр =
0,80; угловой коэффициент 12 = 1.
Решение
Определим радиационный тепловой поток по формуле
Q л пр 12 (T14 T24 )F1
Подставим числовые значения
Q л 0,8 5,67 10 8 1 (3284 2884 ) 5 1065 Вт
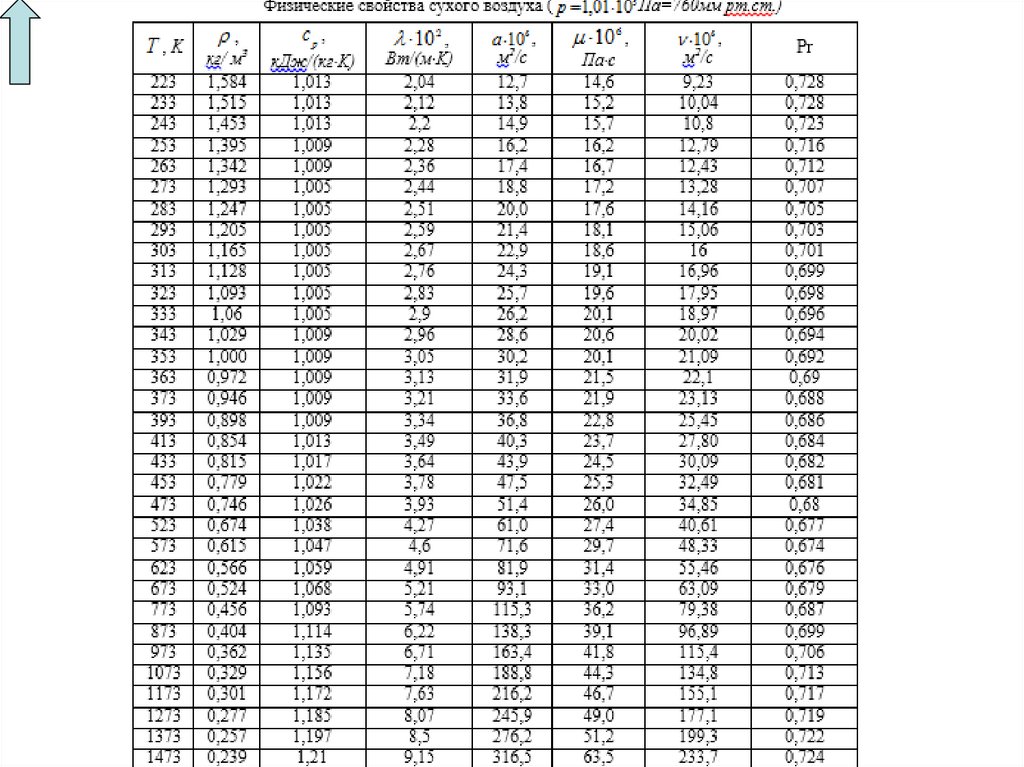
Найдём для воздуха коэффициент теплопроводности, кинематическую вязкость и
число Прандтля при температуре воздуха по таблице
0,0257 Вт/(м К)
14,88 10 6 м 2 /с
Определим критерий Нуссельта по формуле
Nu C (Gr Pr)n
Pr 0,703
15.
Число Грасгофа определим по формулеg (t1 t в )h13
Gr
2
Коэффициент объёмного расширения воздуха определим по равенству
1
t в 273
Определим произведение числа Грасгофа на число Прандтля по выражению
g (t1 t в )h13
Gr Pr
Pr
2
(t в 273)
Подставим числовые значения
9,81 (55 18) 0,53 0,703
8
Gr Pr
4,95
10
(18 273) (14,88 10 6 ) 2
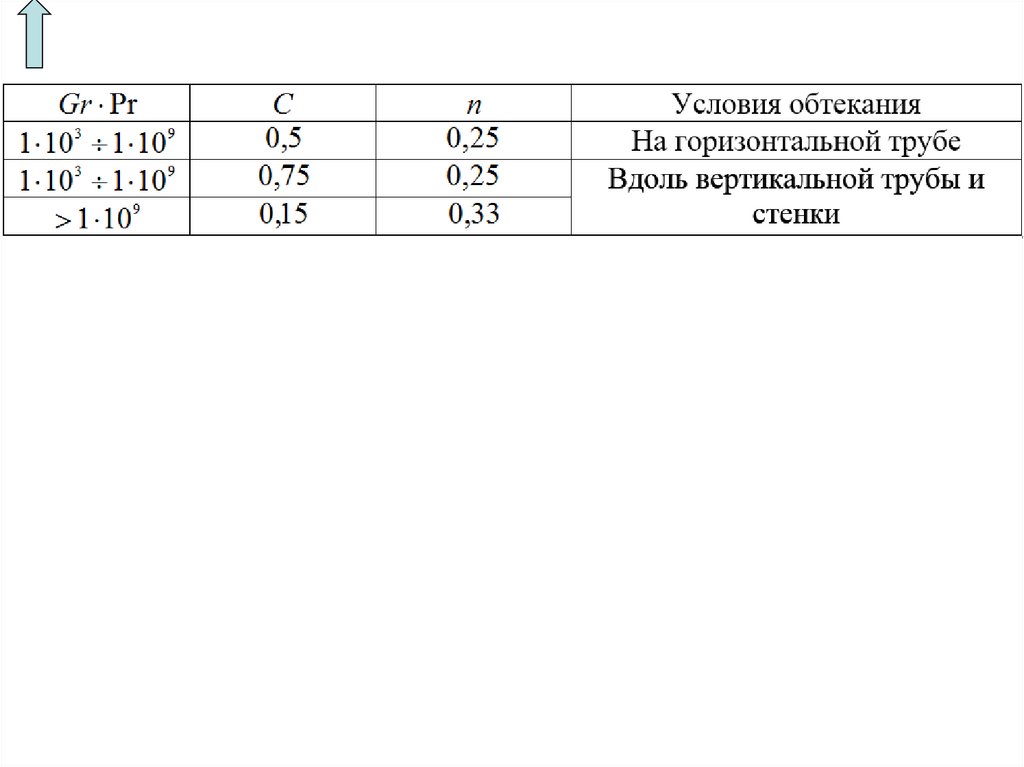
Постоянные C и n определим по таблице
C 0,75
n 0,25
16.
Подставим числовые значения в формулу для критерия НуссельтаNu 0,75 (4,95 108 )0,25 111,9
Коэффициент теплоотдачи определим по выражению
Nu
h1
0,0257
111,9
5,75 Вт/(м 2 К)
0,5
Конвективный тепловой поток определим по формуле Q к (t1 t в ) F1
Рассчитаем эту величину
Подставим числовые значения
Q к 5,75 (55 18) 5 1064 Вт
Рассчитаем суммарный тепловой поток
Q 1065 1064 2129 Вт
Вычислим отношение радиационного теплового потока к конвукционному
1065
1,001
1064
17.
18.
19.
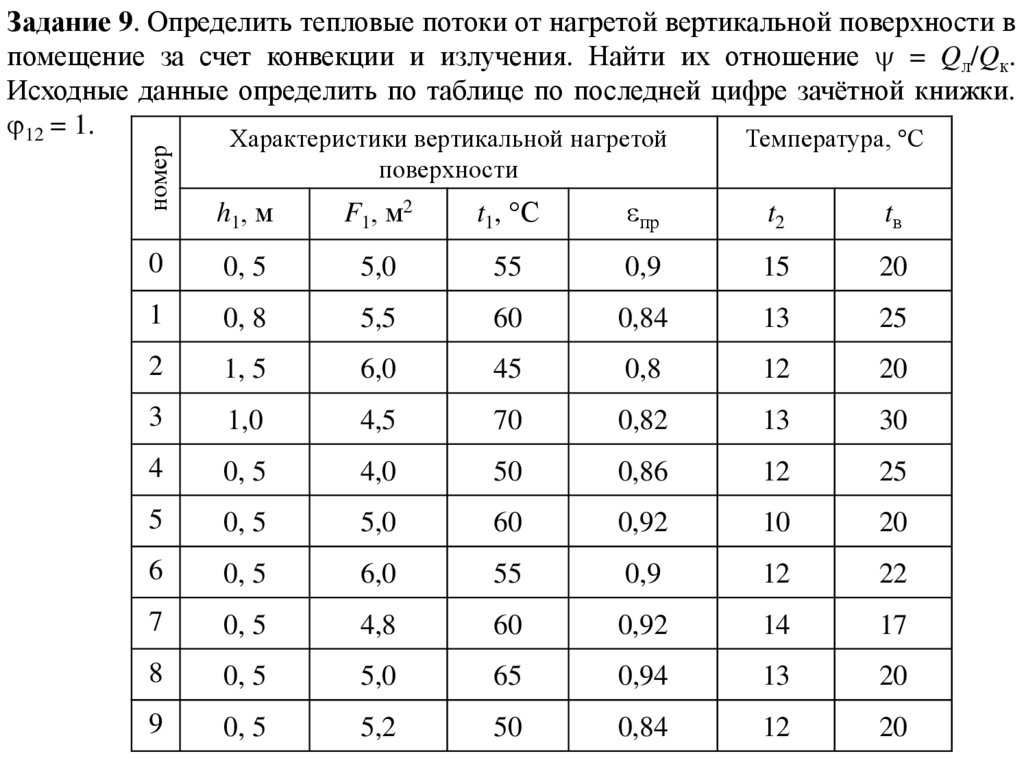
номерЗадание 9. Определить тепловые потоки от нагретой вертикальной поверхности в
помещение за счет конвекции и излучения. Найти их отношение = Qл/Qк.
Исходные данные определить по таблице по последней цифре зачётной книжки.
12 = 1.
Характеристики вертикальной нагретой
Температура, С
поверхности
h1, м
F1, м2
t1, С
пр
t2
tв
0
0, 5
5,0
55
0,9
15
20
1
0, 8
5,5
60
0,84
13
25
2
1, 5
6,0
45
0,8
12
20
3
1,0
4,5
70
0,82
13
30
4
0, 5
4,0
50
0,86
12
25
5
0, 5
5,0
60
0,92
10
20
6
0, 5
6,0
55
0,9
12
22
7
0, 5
4,8
60
0,92
14
17
8
0, 5
5,0
65
0,94
13
20
9
0, 5
5,2
50
0,84
12
20















 physics
physics








