Similar presentations:
Динамика вращательного движения твердого тела. Момент импульса частицы. Момент силы
1.
Физика ч.I«Механика.
Молекулярная
физика и
термодинамика»
2.
Лекция №6Динамика
вращательного
движения твердого
тела
3.
Тема 6. Элементы динамики вращательногодвижения твердого тела.
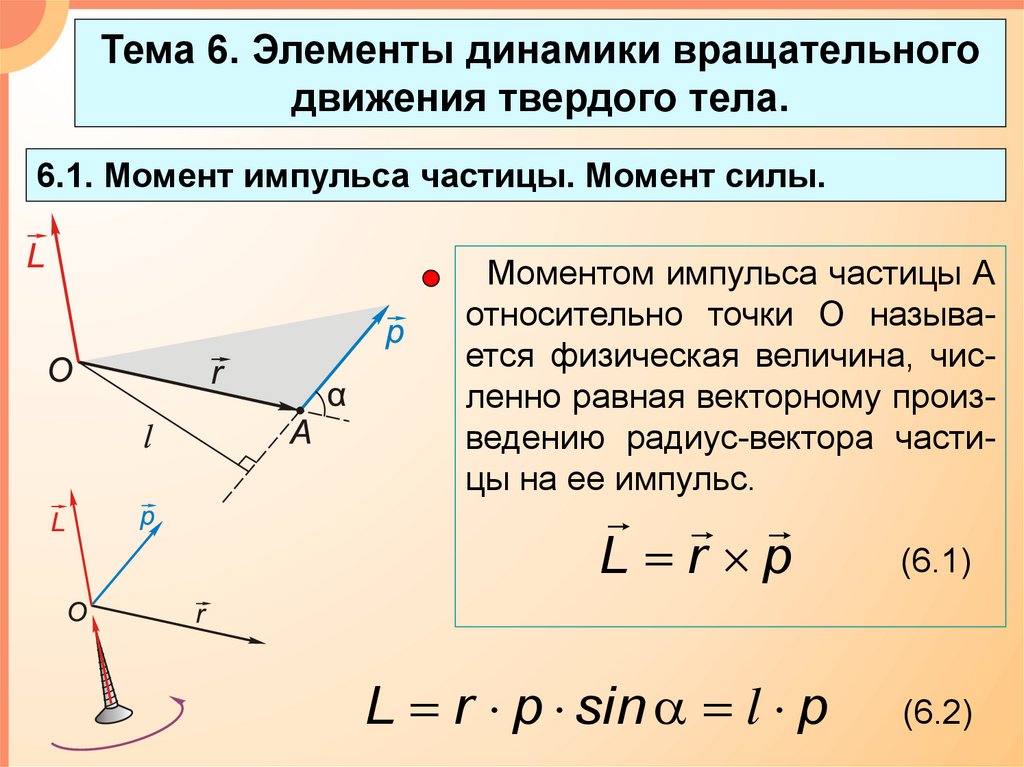
6.1. Момент импульса частицы. Момент силы.
Моментом импульса частицы А
относительно точки О называется физическая величина, численно равная векторному произведению радиус-вектора частицы на ее импульс.
L r p
L r p sin l p
(6.1)
(6.2)
4.
Единицы системы СИ:момент импульса – 1м·1кг·м/с=1 кг·м2/с
d L d r dp
p r
dt
dt
dt
(6.3)
dr
dr
v p
p 0
dt
dt
dp
F
dt
- момент силы F относительно точки О
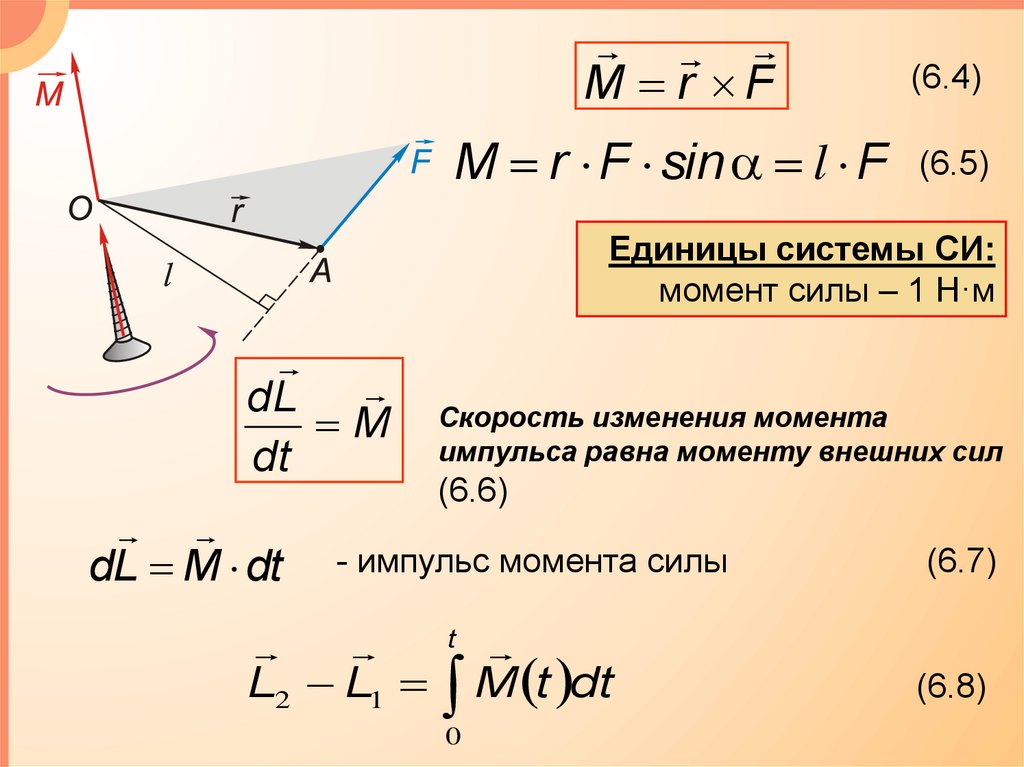
M r F
5.
M r F(6.4)
M r F sin l F
(6.5)
Единицы системы СИ:
момент силы – 1 Н·м
dL
M
dt
dL M dt
Скорость изменения момента
импульса равна моменту внешних сил
(6.6)
- импульс момента силы
L2 L1
M t dt
(6.7)
t
0
(6.8)
6.
Задача 6.1Момент импульса частицы относительно
точки
2
некоторой
меняется со временем t по закону L t a b t , где a и b
- некоторые постоянные
векторы, причем a b . Найти
момент силы M , действующий
на частицу, когда угол
между векторами L и M окажется равным 45°.
dL
M
2b t
dt
a b t 02
t0 a b
M 2 a b b
7.
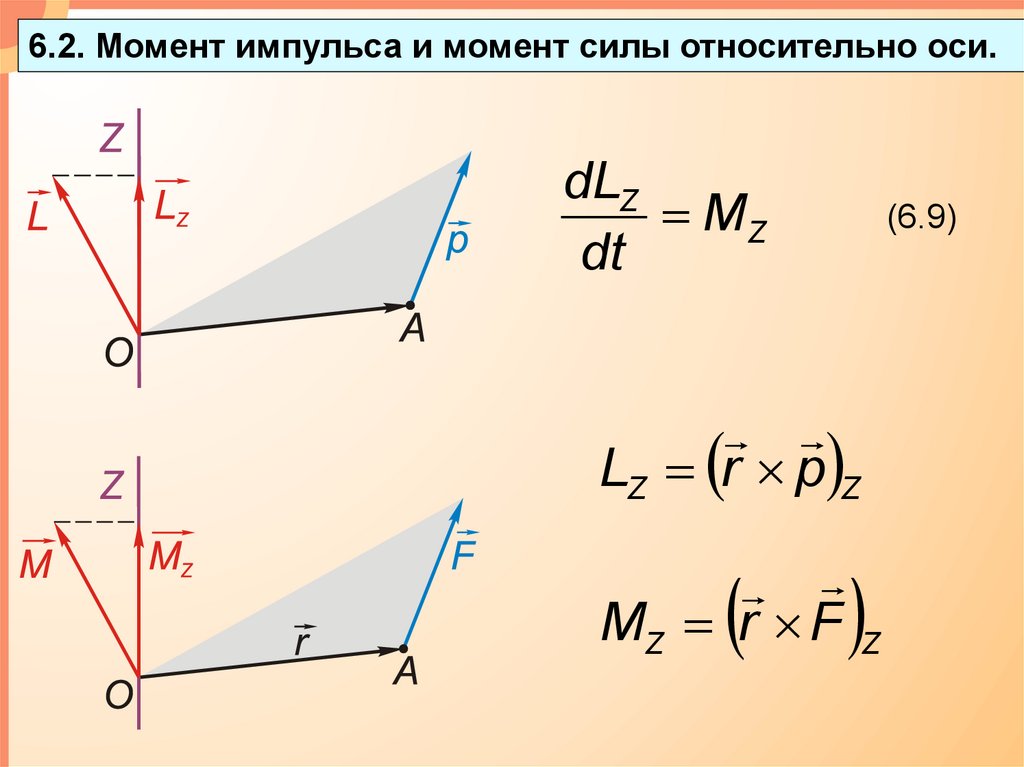
6.2. Момент импульса и момент силы относительно оси.dLZ
MZ
dt
(6.9)
LZ r p Z
MZ r F
Z
8.
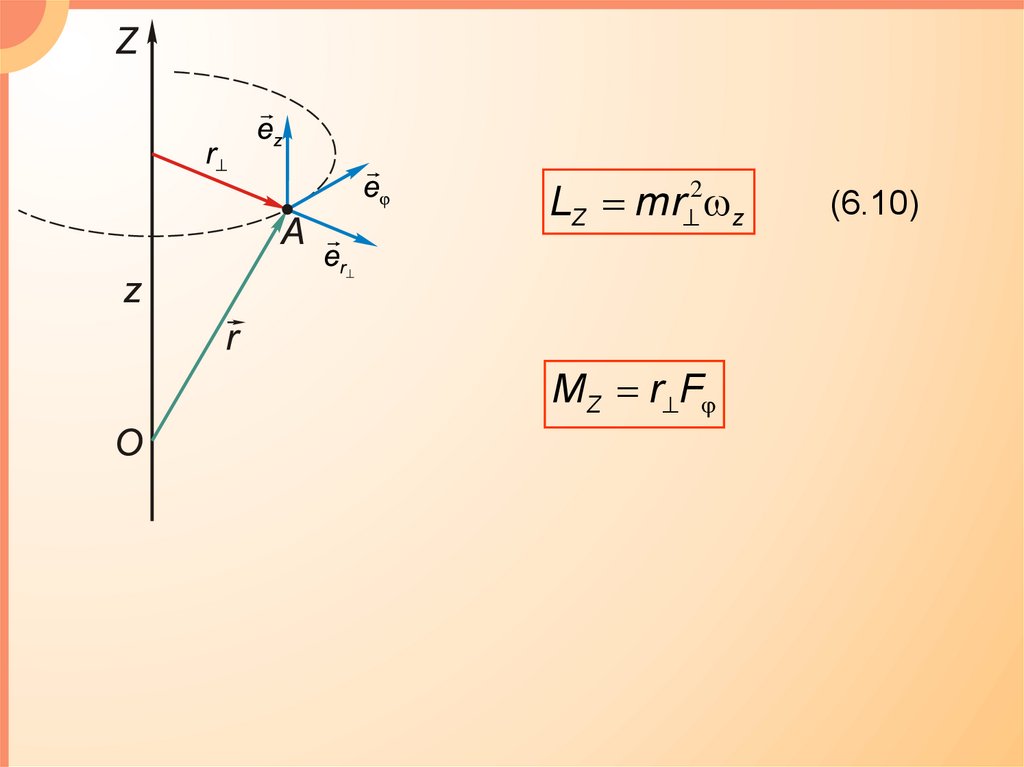
LZ mr z2
MZ r F
(6.10)
9.
6.3. Закон сохранения момента импульса.Моментом импульса системы тел или частиц называется
векторная сумма моментов импульсов всех тел, образующих систему.
L Li
(6.11)
в ну тр
в неш
dL
dLi
Mi
Mi
dt
dt
M ik M ki
dL
Mв неш
dt
(6.12)
10.
tL2 L1 Mвнеш t dt
(6.13)
0
Если система замкнутая, то на неё
внешние силы не действуют, и их
момент равен нулю.
Поэтому справедлив:
Закон сохранения момента импульса.
Момент импульса замкнутой системы тел не меняется
с течением времени.
L Li t const
11.
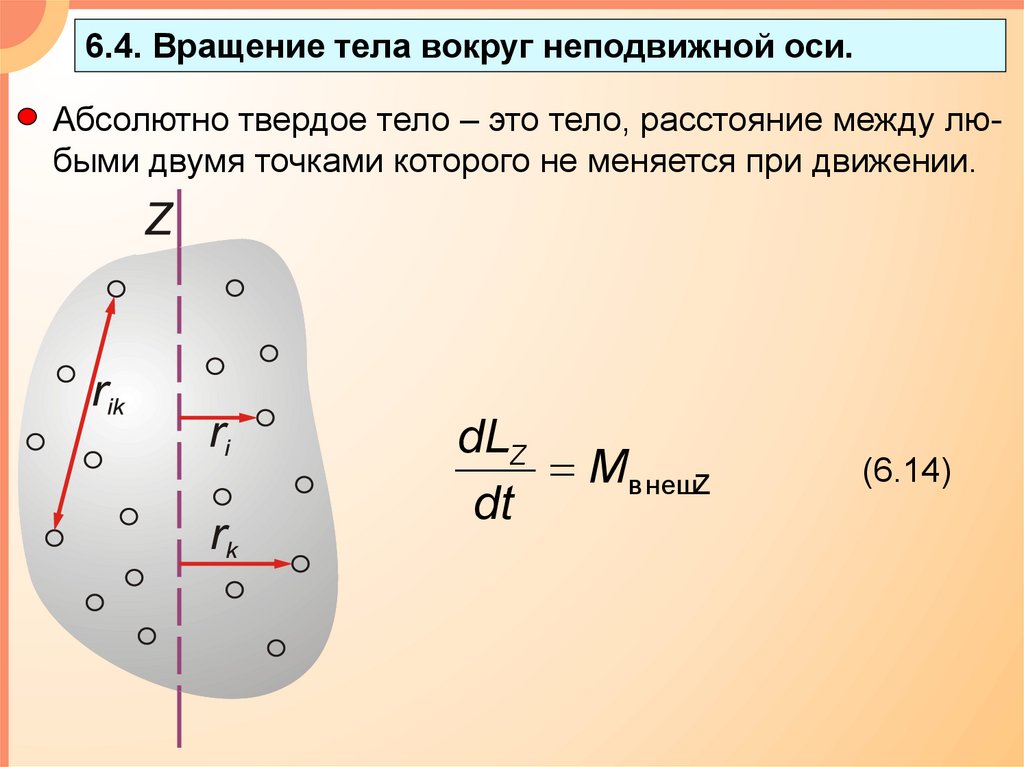
6.4. Вращение тела вокруг неподвижной оси.Абсолютно твердое тело – это тело, расстояние между любыми двумя точками которого не меняется при движении.
dLZ
Mв нешZ
dt
(6.14)
12.
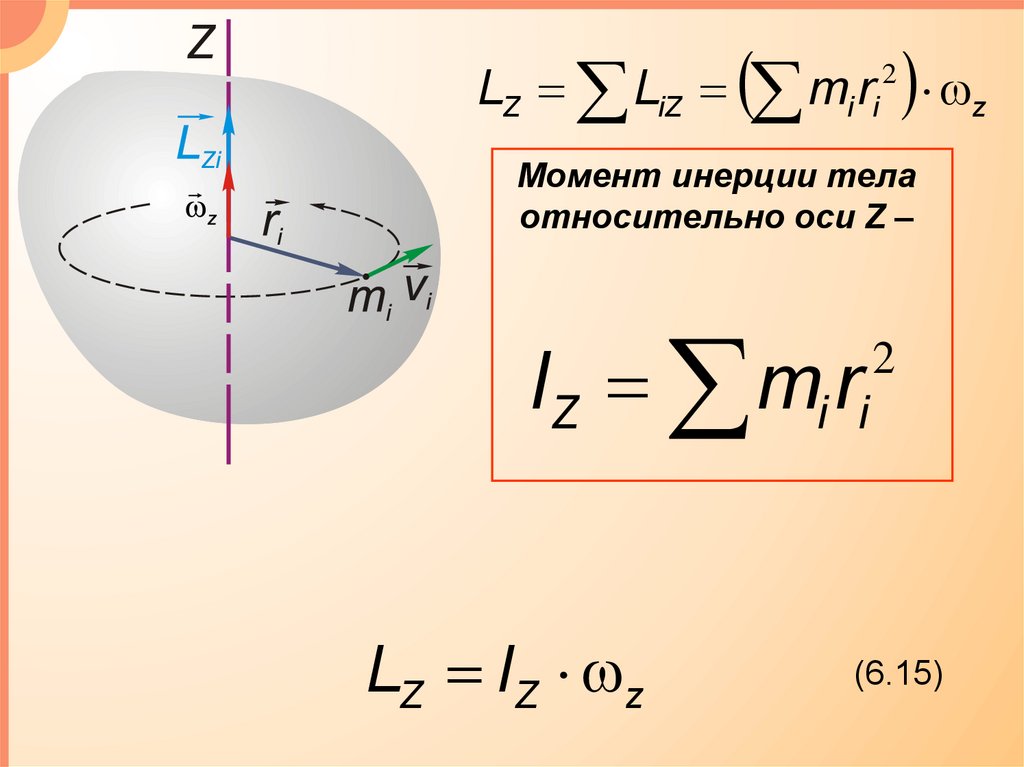
LZ LiZm r
2
i i
Момент инерции тела
относительно оси Z –
IZ mi ri
LZ IZ z
2
(6.15)
z
13.
6.4.1. Моменты инерции некоторых тел.IZ mi ri r dm r dv
2
2
2
Единицы системы СИ:
момент инерции – 1 кг·м2
IZ r dm R
2
2
dm mR
2
14.
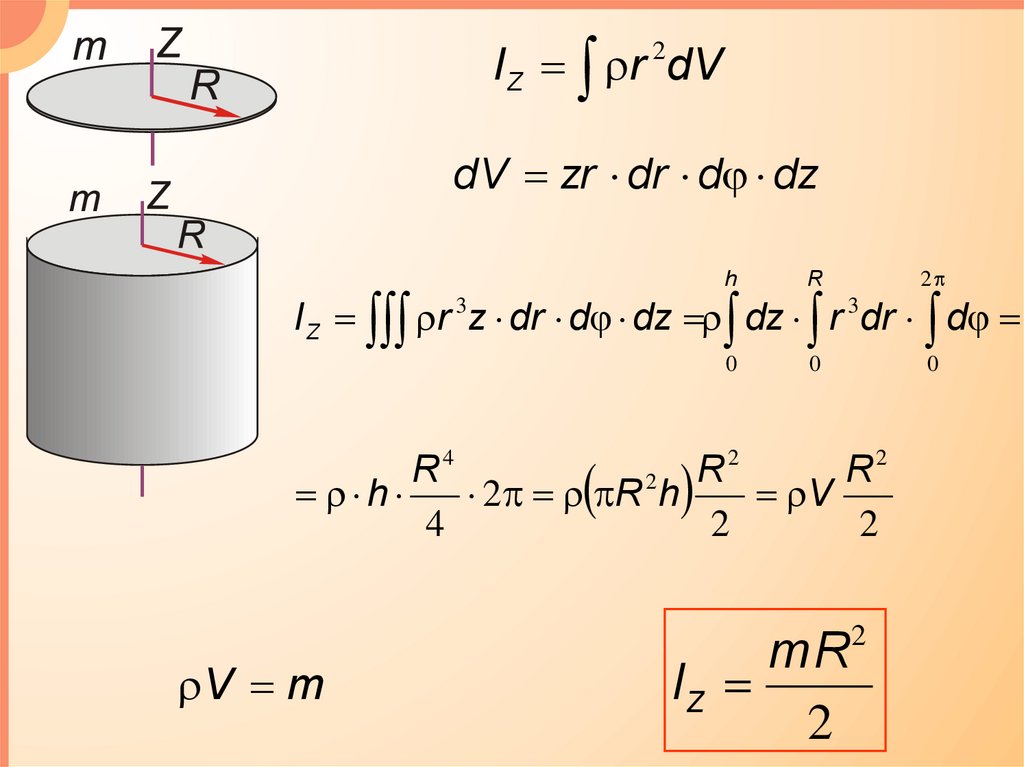
IZ r dV2
dV zr dr d dz
h
R
2
0
0
0
I Z r 3 z dr d dz dz r 3dr d
2
2
R4
R
R
h
2 R 2 h
V
4
2
2
V m
mR
IZ
2
2
15.
IZ 2 IZ1 IZI Z I Z 2 I Z1
IZ 2
1
1
2
2
2
m2R2 R2 hR2
2
2
1
1
4
4
h R2 R1 h R22 R12 R22 R12
2
2
h R R m
2
2
I Z1
1
1
2
m1R1 R12hR12
2
2
2
1
1
2
2
IZ m R2 R1
2
16.
2I Z mR 2
5
IZ r 2dV
l
2
3
3
1 l
1 l
2
I Z r Sdr S
3 2
l
3 2
2
l2
Sl
12
1
2
IZ ml
12
17.
Теорема Штайнера:Момент инерции IZ относительно произвольной оси Z равен
моменту инерции IC относительно оси С, параллельной данной и проходящей через центр масс С тела, плюс произведение массы m тела на квадрат расстояния a между осями.
IZ IC ma
2
(6.16)
ri ri a
2
IZ mi ri mi ri a
2
2
IZ mi ri 2a mi ri mi a
2
(6.17)
18.
IZ mi ri 2a mi ri mi a22
2
m
r
i i IC
mi ri mrC 0
IZ IC ma
2
2
m
a
ma
i
2
2
1
1 2
l
2
I Z ml m ml
12
3
2
19.
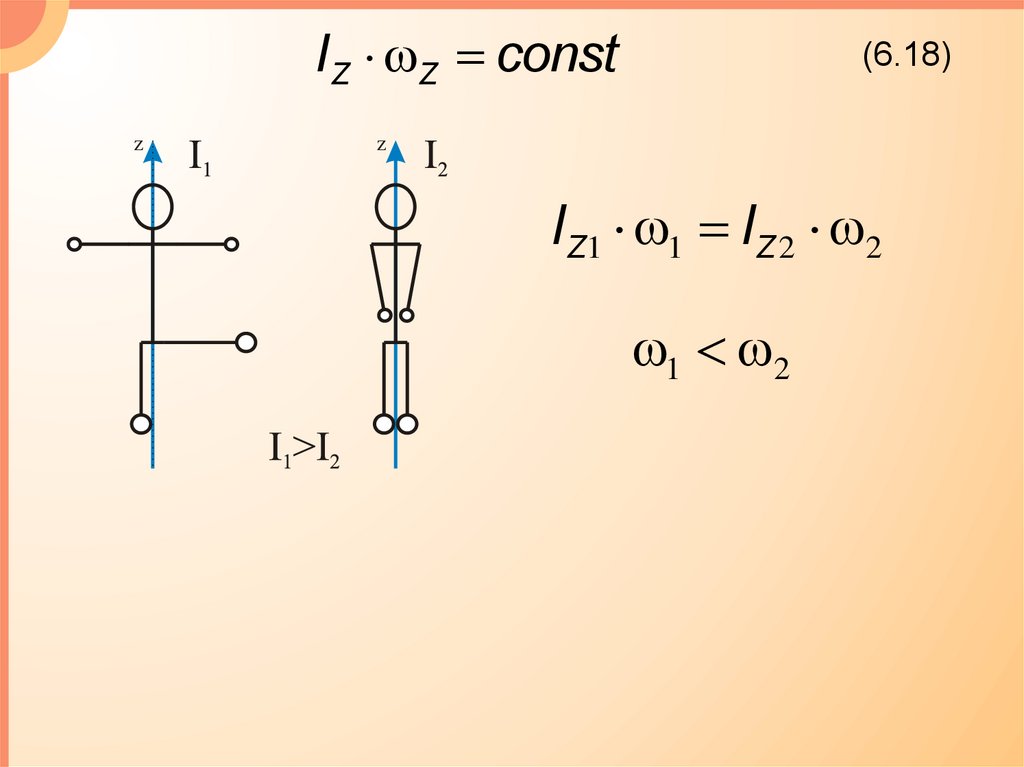
IZ Z const(6.18)
IZ1 1 IZ 2 2
1 2
20.
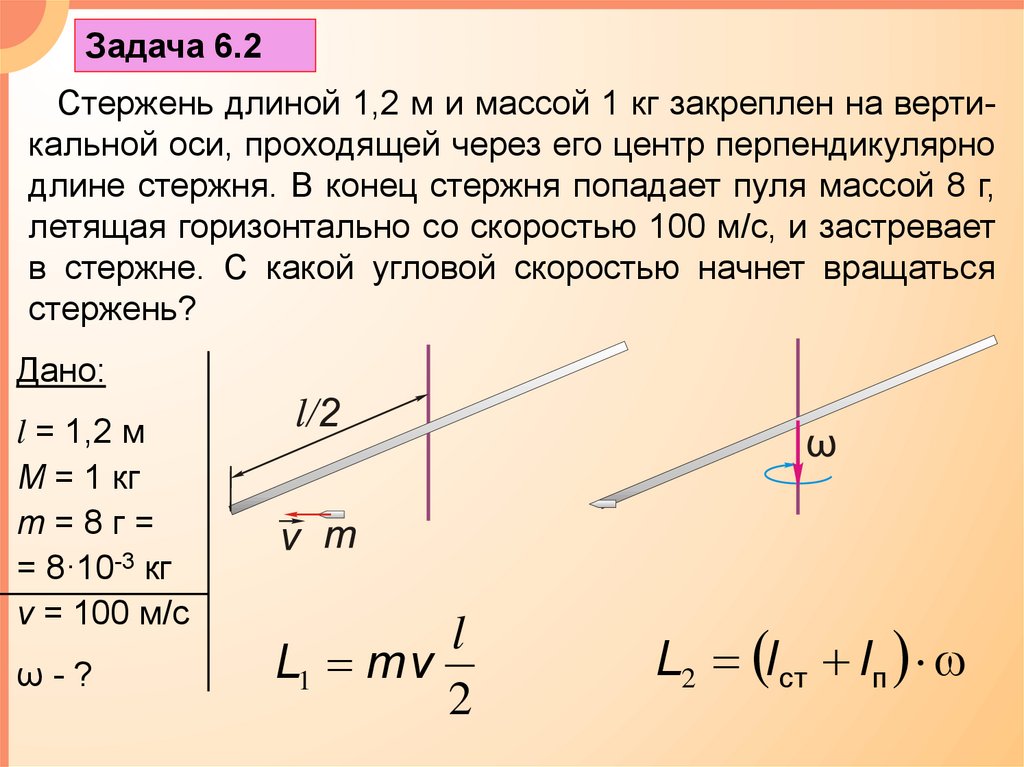
Задача 6.2Стержень длиной 1,2 м и массой 1 кг закреплен на вертикальной оси, проходящей через его центр перпендикулярно
длине стержня. В конец стержня попадает пуля массой 8 г,
летящая горизонтально со скоростью 100 м/с, и застревает
в стержне. С какой угловой скоростью начнет вращаться
стержень?
Дано:
l = 1,2 м
M = 1 кг
m=8г=
= 8·10-3 кг
v = 100 м/с
ω-?
l
L1 mv
2
L2 Iст Iп
21.
22
1
l
l
2
L2
Ml m
M 3m
12
2
12
L1 L2
l l 2
M 3m
mv
2 12
6mv
6 8 10 3 кг 100 м с
3,9 рад с
-3
l M 3m 1,2 м 1кг 3 8 10 кг
22.
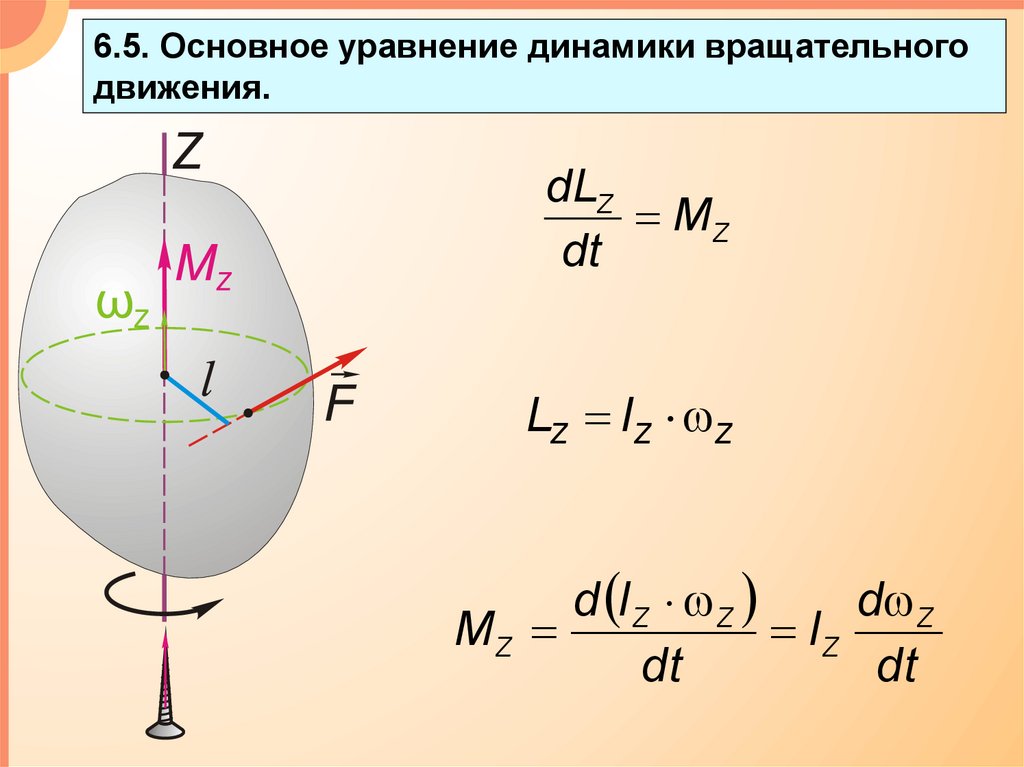
6.5. Основное уравнение динамики вращательногодвижения.
dLZ
MZ
dt
LZ IZ Z
d IZ Z
d Z
MZ
IZ
dt
dt
23.
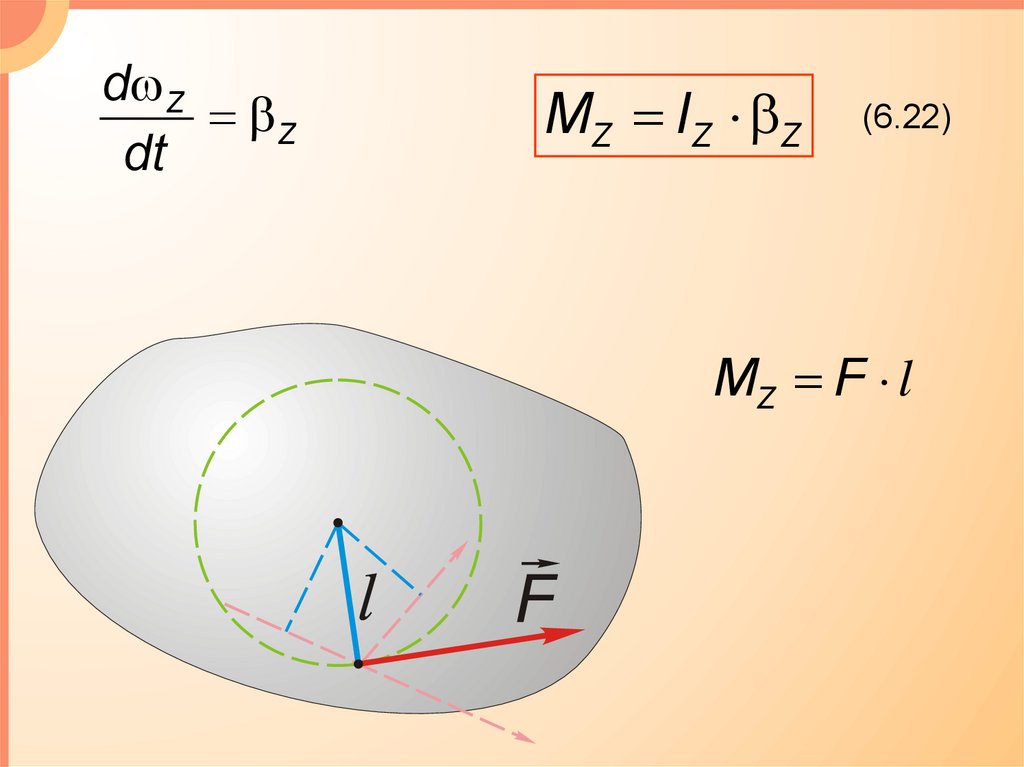
d ZZ
dt
MZ IZ Z
(6.22)
MZ F l
24.
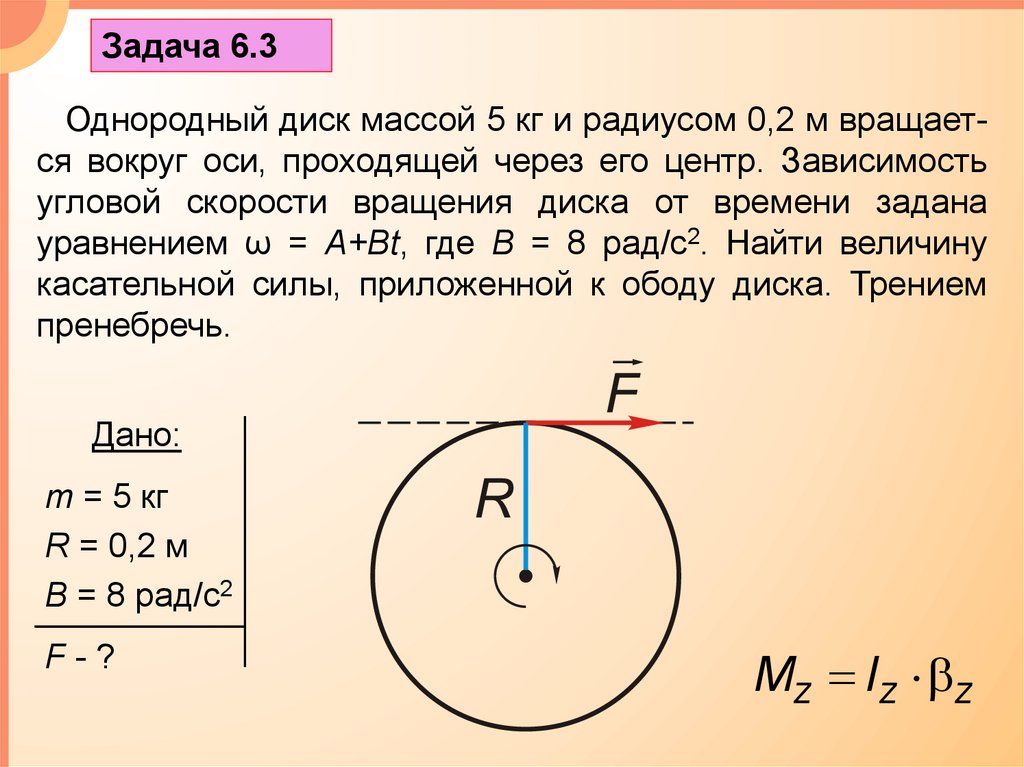
Задача 6.3Однородный диск массой 5 кг и радиусом 0,2 м вращается вокруг оси, проходящей через его центр. Зависимость
угловой скорости вращения диска от времени задана
уравнением ω = A+Bt, где В = 8 рад/с2. Найти величину
касательной силы, приложенной к ободу диска. Трением
пренебречь.
Дано:
m = 5 кг
R = 0,2 м
В = 8 рад/с2
F-?
MZ IZ Z
25.
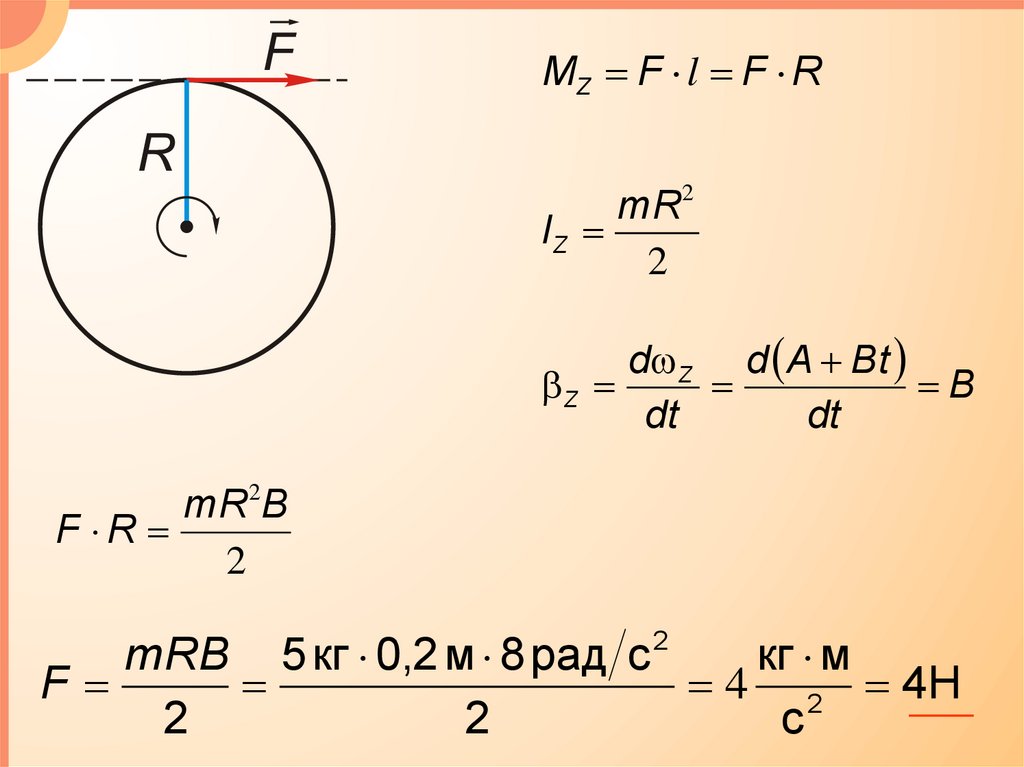
MZ F l F RmR2
IZ
2
d Z d A Bt
Z
B
dt
dt
2
mR B
F R
2
mRB 5 кг 0,2 м 8 рад с 2
кг м
F
4 2 4Н
2
2
с
26.
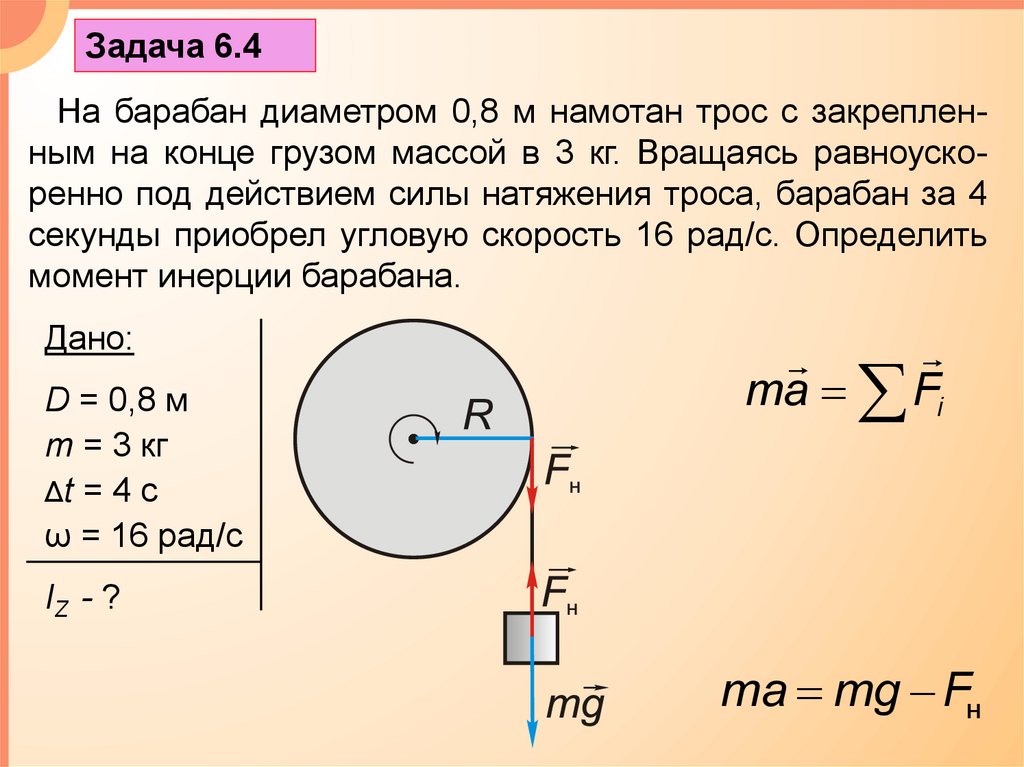
Задача 6.4На барабан диаметром 0,8 м намотан трос с закрепленным на конце грузом массой в 3 кг. Вращаясь равноускоренно под действием силы натяжения троса, барабан за 4
секунды приобрел угловую скорость 16 рад/с. Определить
момент инерции барабана.
Дано:
D = 0,8 м
m = 3 кг
Δt = 4 c
ω = 16 рад/с
ma Fi
IZ - ?
ma mg Fн
27.
a aFн m(g a )
(6.23)
IZ Z MZ Fн R m g a R
a Z R
m g Z R R
IZ
Z
0
Z
t
t
28.
Dm g
D
m 2g t D D
t 2
IZ
4
2
t
3кг 2 9,81м с 4с - 16 рад с 0,8м 0,8м
IZ
4 16рад с
2
кг м с м с м
2,46
2,46 кг м2
1с
29.
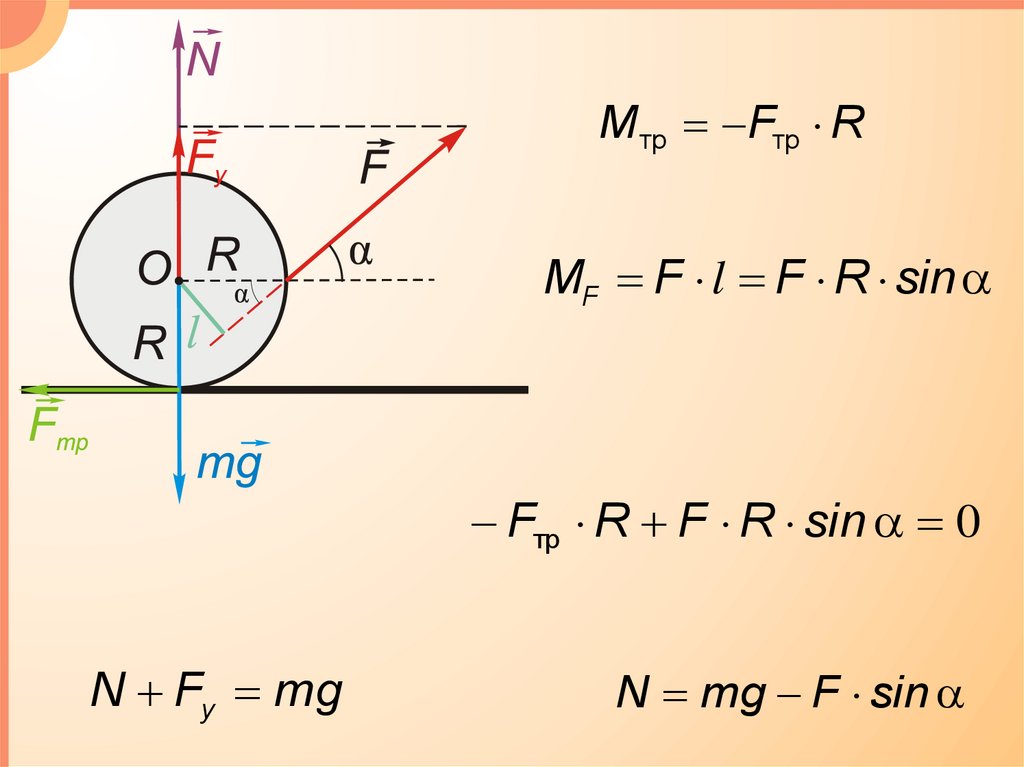
Задача 6.5Однородный
шар
массы
m=4,0
кг
движется
поступательно по поверхности стола под действием
постоянной силы , приложенной, как показано на рисунке,
где угол α=30º. Коэффициент трения между шаром и
столом k=0,20. Найти силу F .
Дано:
m = 4 кг
α = 30˚
k = 0,2
F-?
Mтр MF 0
30.
M тр Fтр RMF F l F R sin
Fтр R F R sin 0
N Fy mg
N mg F sin
31.
Fтр kN k mg F sinF sin Fтр kmg kF sin
F 1 k sin kmg
kmg
0,2 4 9,8
F
13 Н
1 k sin 1,2 0,5
32.
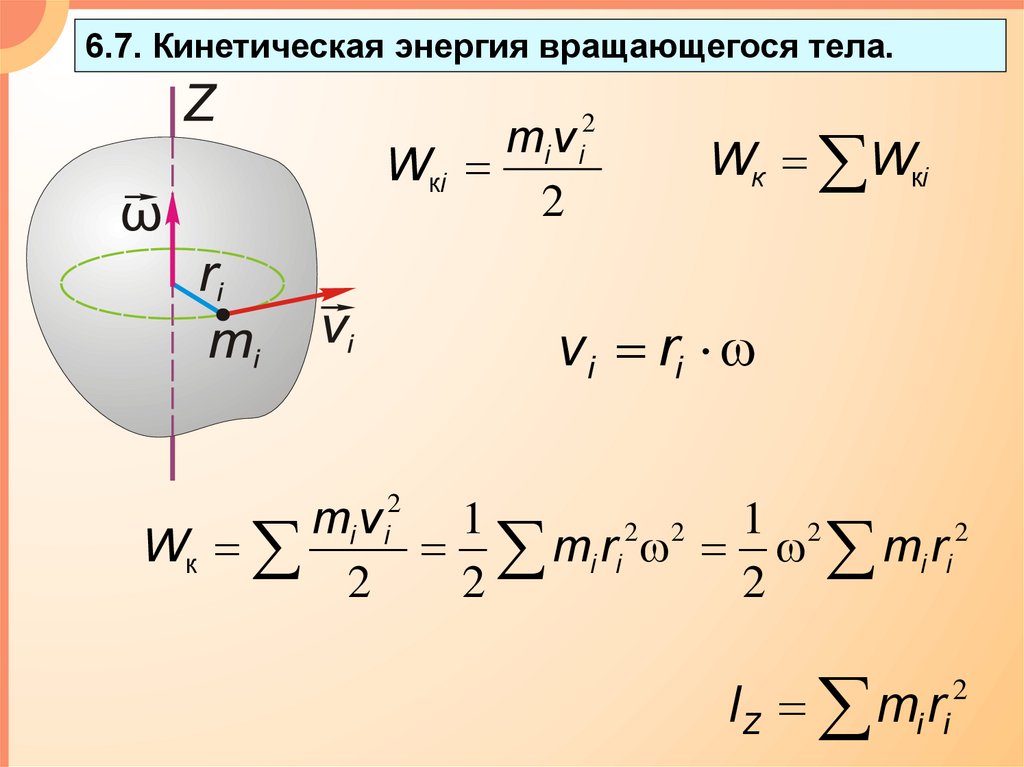
6.7. Кинетическая энергия вращающегося тела.mi v i2
Wкi
2
Wк Wкi
v i ri
mi v i2 1
1 2
2 2
Wк
mi ri mi ri 2
2
2
2
IZ mi ri
2
33.
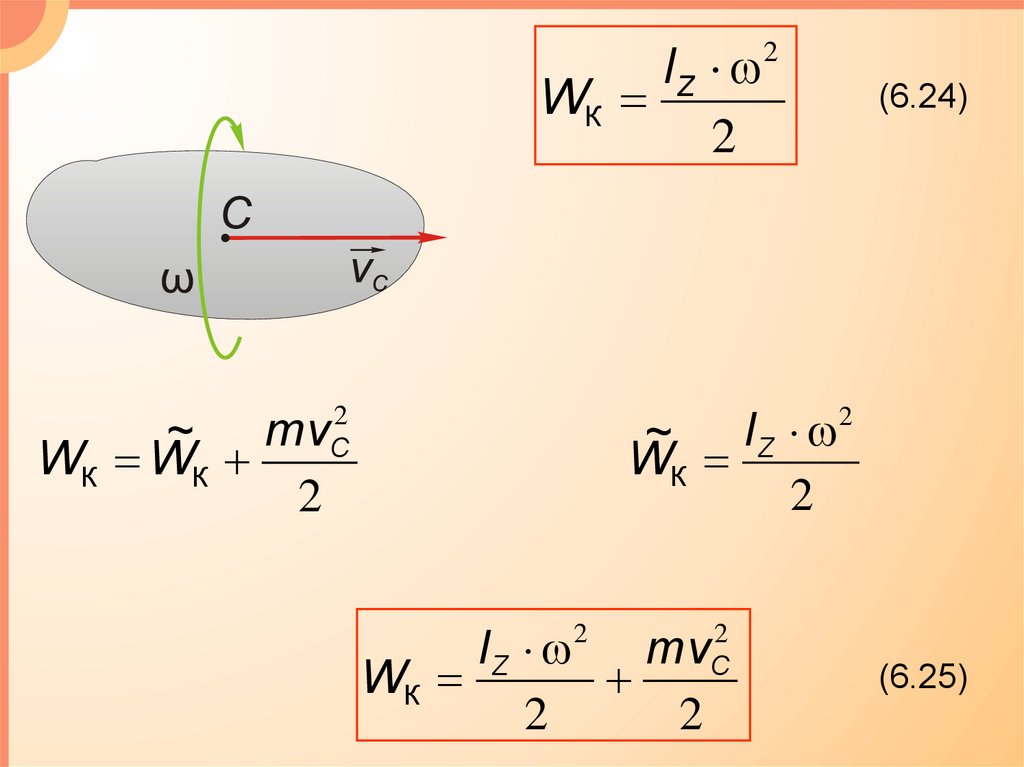
IZ 2WК
2
(6.24)
IZ
~
WК
2
2
C
2
mv
~
WК WК
2
IZ
mv
WК
2
2
2
2
C
(6.25)
34.
dA F dr F r d MZ ddLZ
d
MZ
IZ
dt
dt
2
IZ 2
d
d
dA IZ
d IZ
dt IZ d IZ d d
dt
dt
2
2
A1 2
IZ
2
2
кон
IZ
2
2
нач
(6.26)
35.
Задача 6.6К ободу диска массой 5 кг приложена постоянная касательная сила 2 Н. Какую кинетическую энергию будет иметь диск
через 5 секунд после начала действия силы?
Дано:
m = 5 кг
F=2Н
t0 = 5 с
WК - ?
К Н
t
t0
I Z 2
WК
2
FR
IZ
MZ FR IZ
2
t 0
2 2
0
2
2 2
0
FRt0
IZ
2 2
0
IZ F R t
F Rt
F t
WК
2
1
2IZ
m
2
2 mR
2
36.
Н Н м4 Н2 25 с 2
20 Н м 20 Дж
20
WК
м
5 кг
кг 2
с
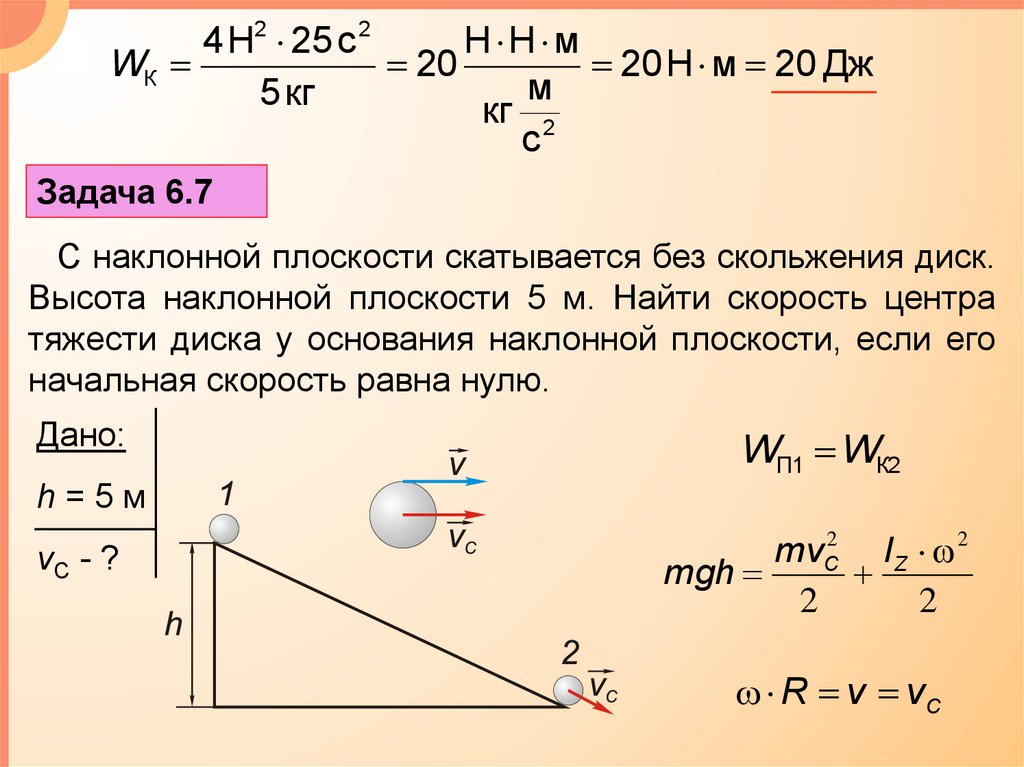
Задача 6.7
С наклонной плоскости скатывается без скольжения диск.
Высота наклонной плоскости 5 м. Найти скорость центра
тяжести диска у основания наклонной плоскости, если его
начальная скорость равна нулю.
Дано:
h=5м
vC - ?
WП1 WК2
mvC2 IZ 2
mgh
2
2
R v vC
37.
12
2
mR v C
mvC2 2
mvC2 mvC2 3mvC2
mgh
2
2
2R
2
4
4
4gh
4 9,81 5
vC
8,1м с
3
3








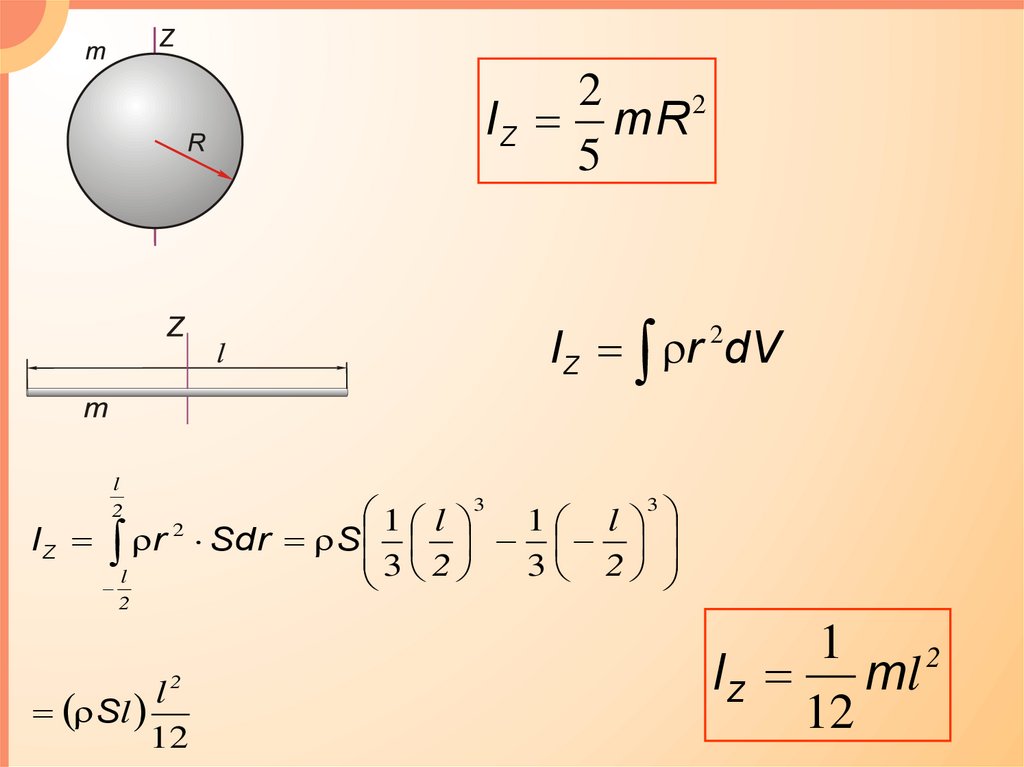



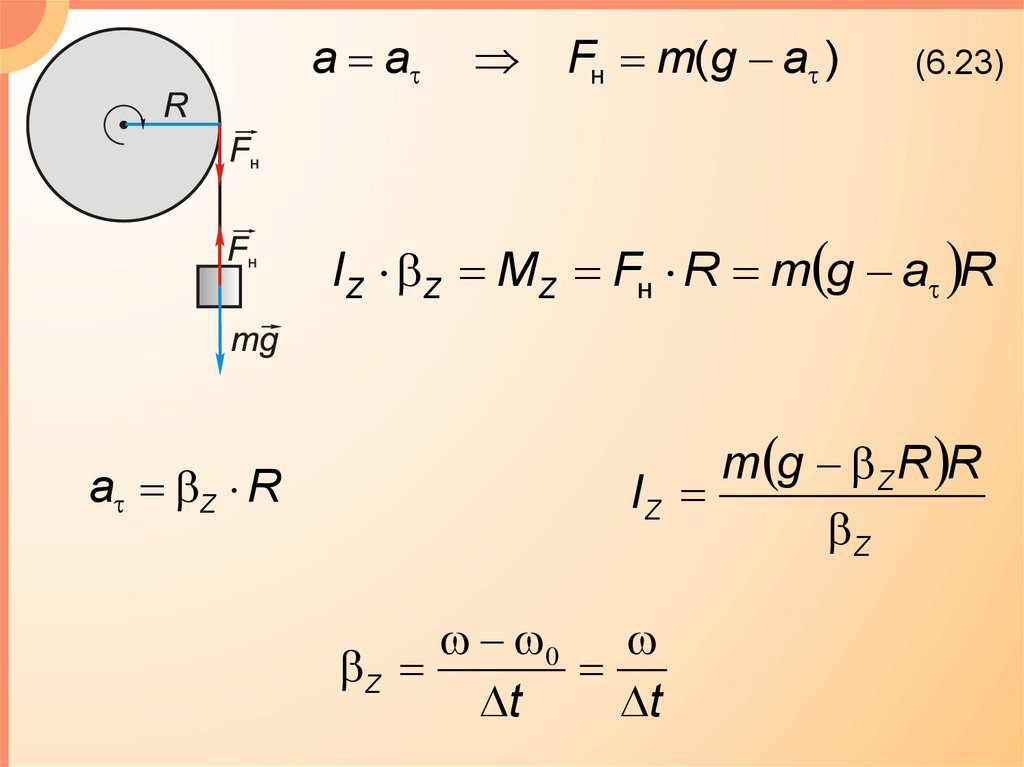



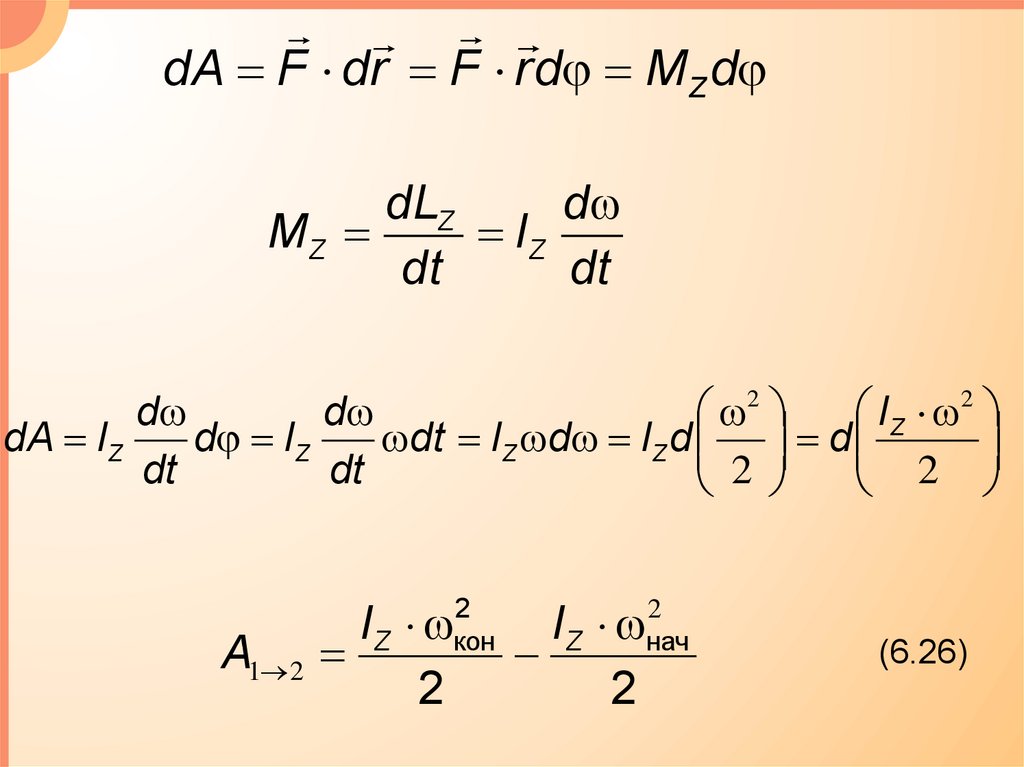


 physics
physics








