Similar presentations:
Гармонические колебания
1.
Гармонические колебания.2.
d 2x2
x 0
2
dt
Процесс удовлетворяющий условию:
называется гармоническими колебаниями.
Решением диф. уравнения является уравнение:
где:
x
Дифференциальное
уравнение
гармонических
колебаний.
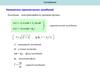
x X m sin t 0
- смещение (мгновенное значение колеблющейся величины)
X m - амплитуда (максимальное значение смещения)
t 0 - фаза (величина определяющая смещение в данный момент времени)
0
- начальная фаза (фаза в начальный момент времени, т.е. при t=0
- циклическая частота
3.
constx
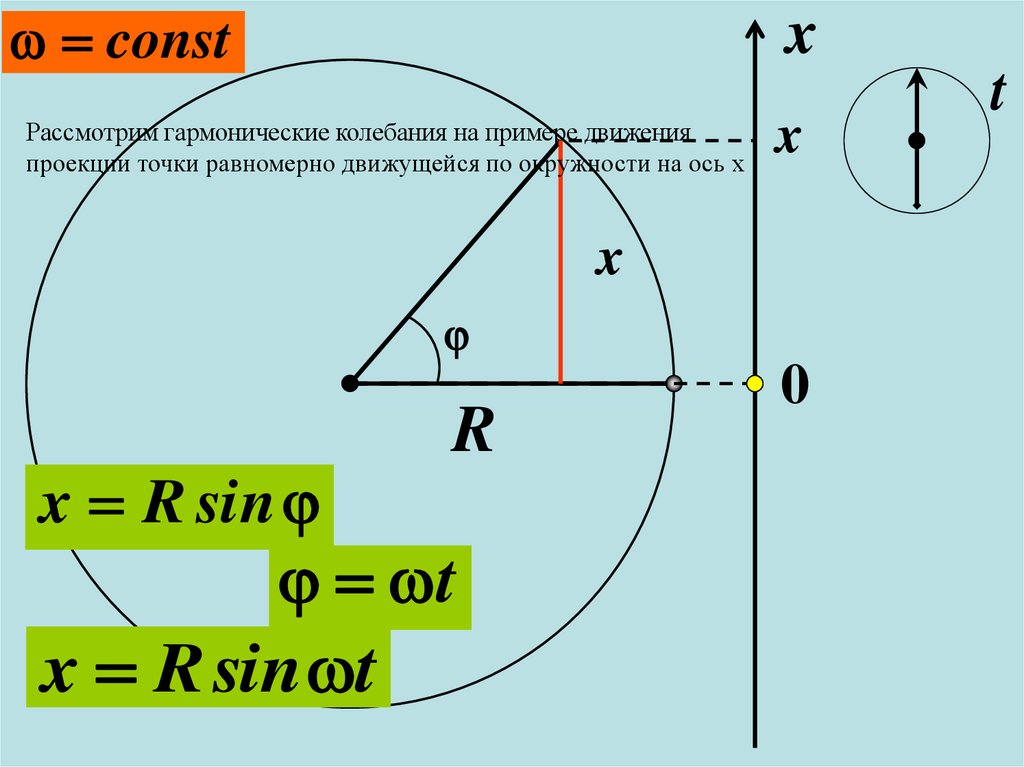
Рассмотрим гармонические колебания на примере движения
проекции точки равномерно движущейся по окружности на ось х
x
x
x R sin
R
t
x R sin t
0
t
4.
constx
Xm
x
R
x0
1
0
0
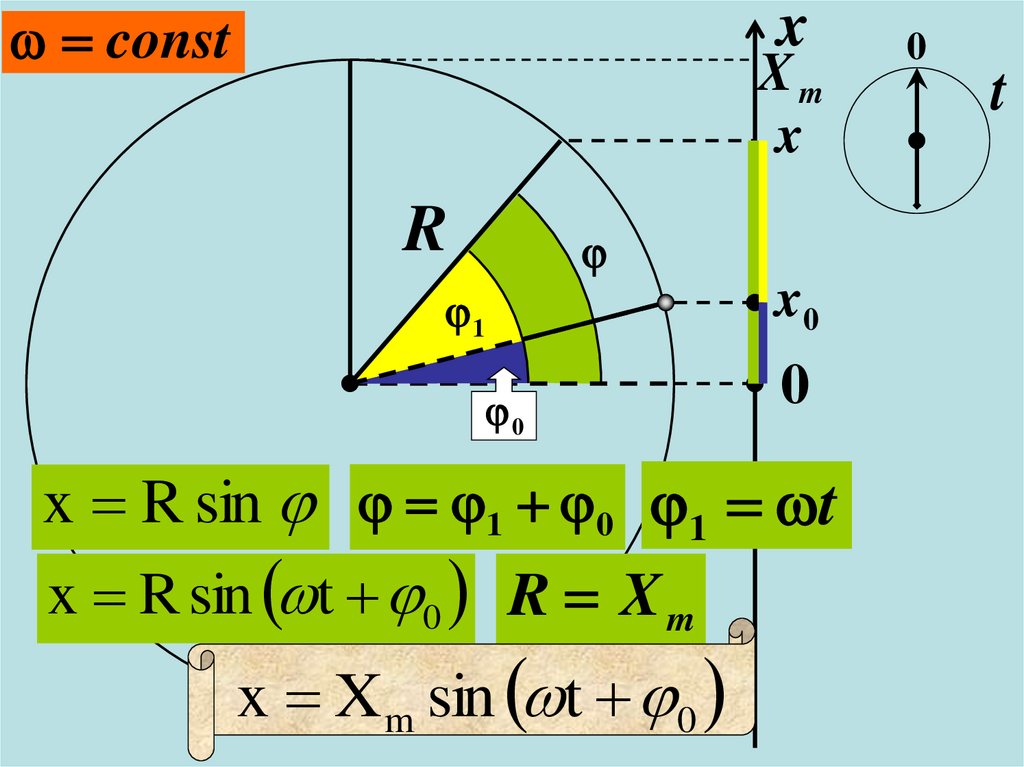
x R sin 1 0 1 t
x R sin t 0 R X m
x X m sin t 0
0
t
5.
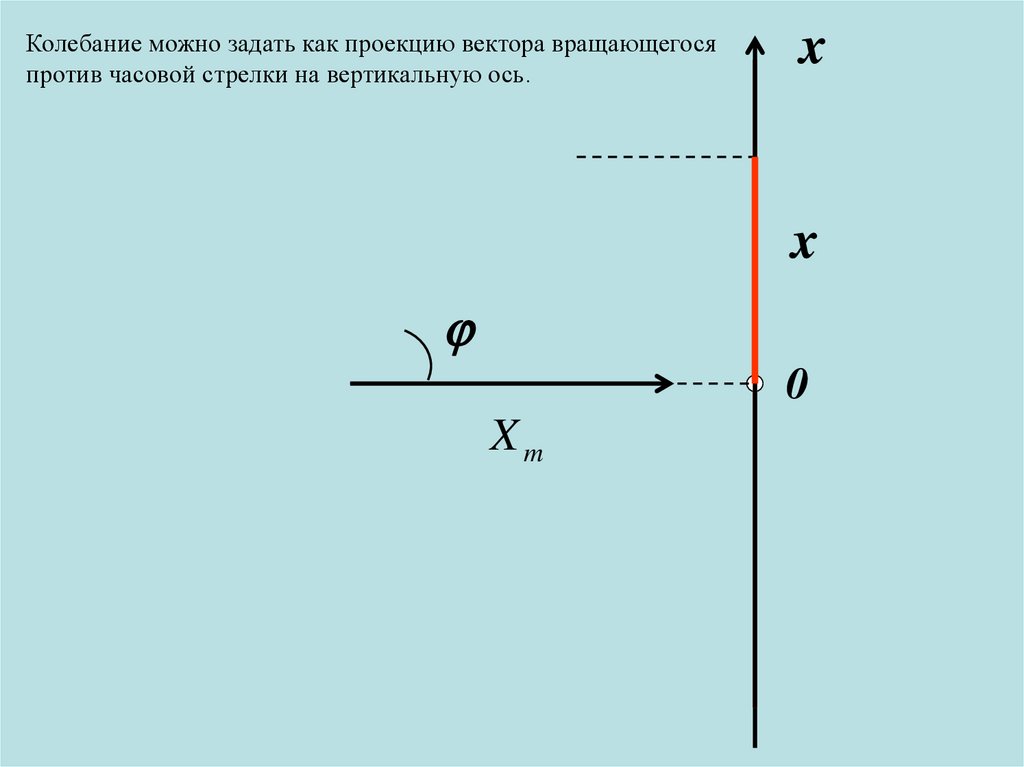
Колебание можно задать как проекцию вектора вращающегосяпротив часовой стрелки на вертикальную ось.
x
x
0
Xm
6.
Гармонические осцилляторы.Гармонические осцилляторы – это система колебания которой удовлетворяют
дифференциальному уравнению гармонических колебаний.
Свободными называются колебания системы предварительно выведенной из
положения равновесия и предоставленной самой себе.
Частота свободных не затухающих колебаний называется собственной частотой
колебаний системы.
2
d x
2
0 x 0
2
dt
Собственная частота
7.
Рассмотрим пружинный маятник. ( система из абсолютно упругой пружиныи материальной точки).
Возвращающей силой является сила упругости.
F kx
d 2x
m 2 kx
dt
d 2x
F ma m 2
dt
2
2
d x
d
x
k
или
m 2 kx o
x 0
2
dt
dt
m
2
d x
2
0 x 0
2
dt
Период колебаний пружинного маятника:
m
T 2
k
или
k
m
2
0
8.
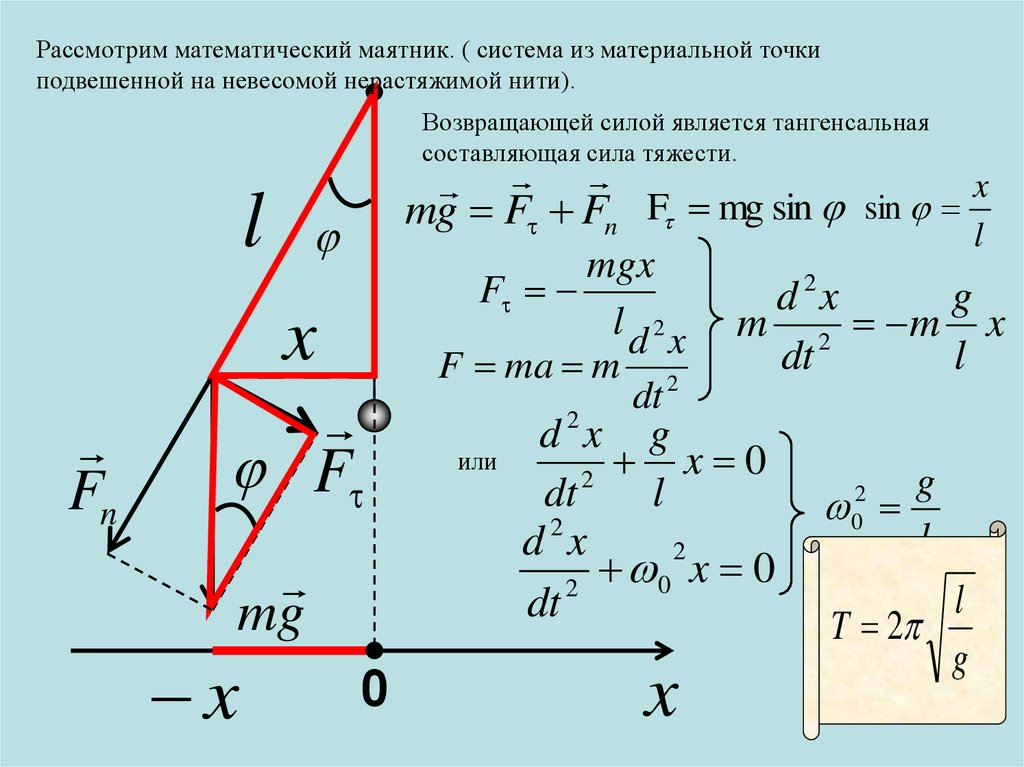
Рассмотрим математический маятник. ( система из материальной точкиподвешенной на невесомой нерастяжимой нити).
Возвращающей силой является тангенсальная
составляющая сила тяжести.
l
x
mg F Fn F mg sin sin
l
x
Fn
F
mg
x
mgx
F
d 2x
g
l d 2 x m 2 m x
dt
l
F ma m 2
dt
d 2x g
или
x 0
2
g
2
dt
l
0
2
l
d x
2
dt
0
2
0 x 0
x
l
T 2
g
9.
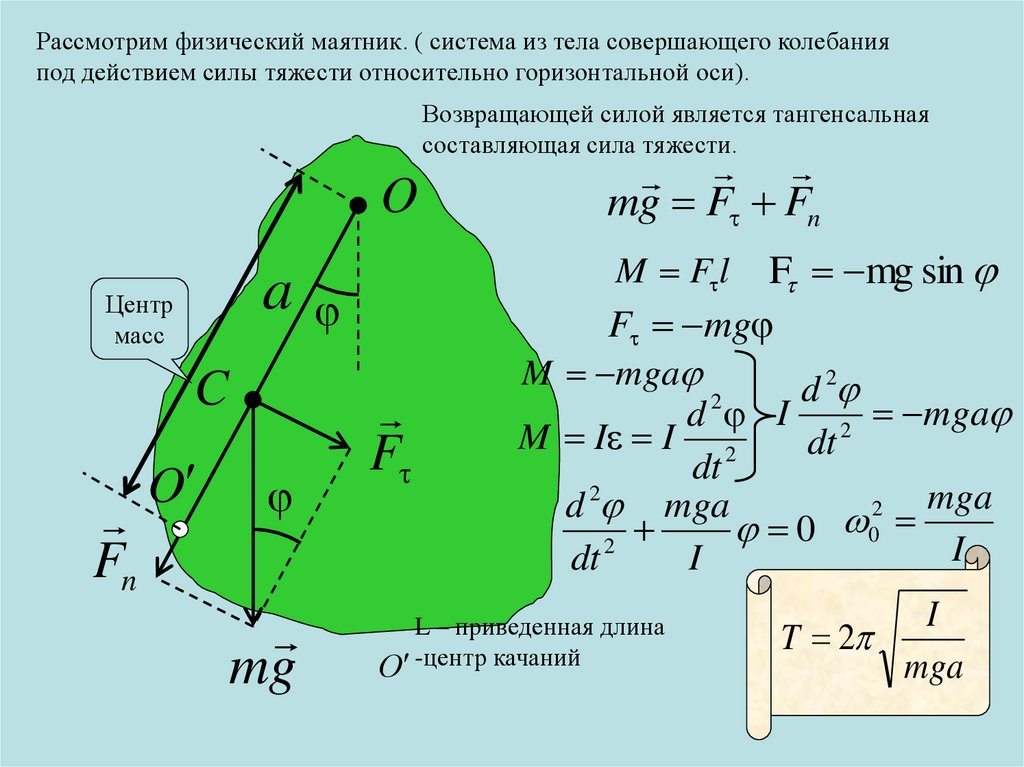
Рассмотрим физический маятник. ( система из тела совершающего колебанияпод действием силы тяжести относительно горизонтальной оси).
Возвращающей силой является тангенсальная
составляющая сила тяжести.
O
a
Центр
масс
L
C
Fn
O
mg
F
mg F Fn
M F l F mg sin
F mg
2
M mga
d
2
d I 2 mga
M I I 2
dt
dt
2
mga
2
d mga
0
0
I
dt 2
I
L – приведенная длина
О -центр качаний
I
T 2
mga





 physics
physics