Similar presentations:
Свободные колебания простых одномерных осцилляторов
1.
Курс: “Колебания и волны.Волновая оптика”
“В науке необходимо воображение.
Она не исчерпывается целиком ни
математикой, ни логикой, в ней есть
что-то от красоты и поэзии”
М. Митчелл, 1860
1
2.
Часть I. Колебания и волныhttp://vega.phys.msu.ru/
Лекция 1. Свободные колебания простых одномерных
осцилляторов
3.
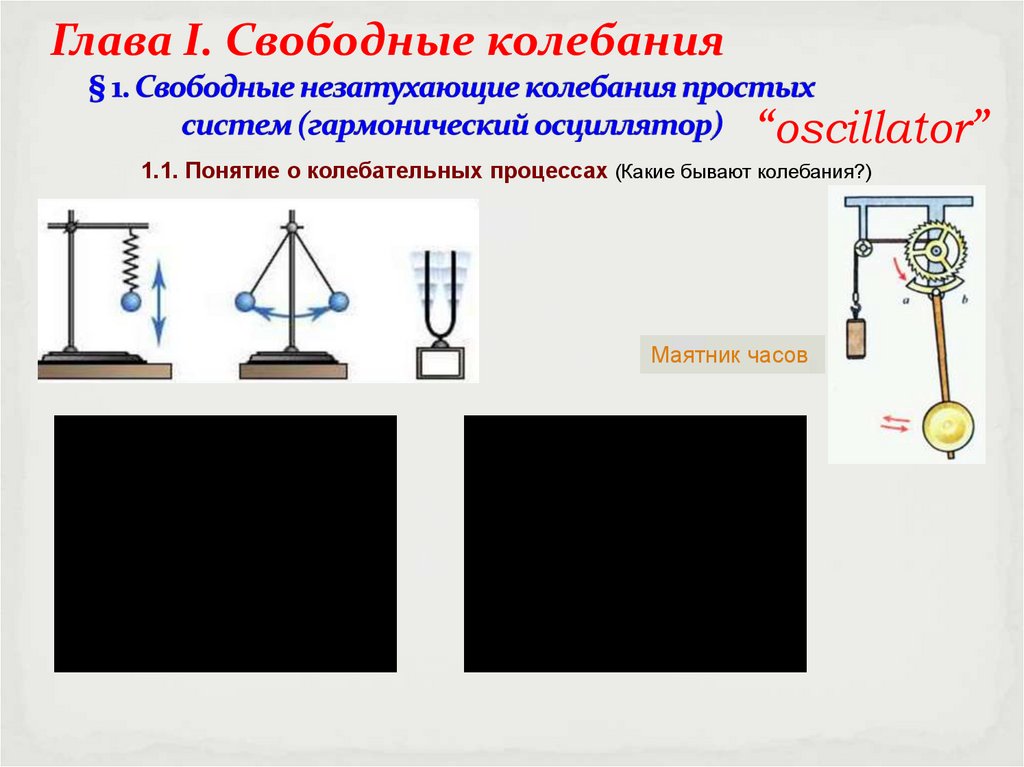
Глава I. Свободные колебания“oscillator”
1.1. Понятие о колебательных процессах (Какие бывают колебания?)
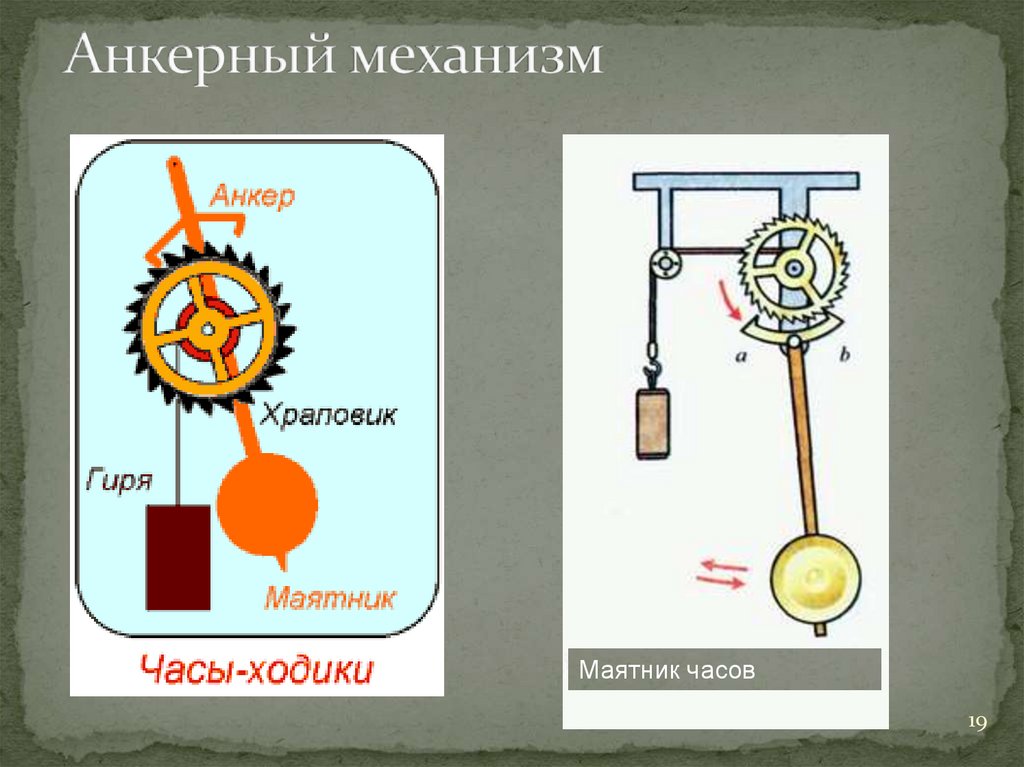
Маятник часов
4.
Колебания???
4
5.
Колебания “бегут” – “Волны”5
6.
Колебания???
6
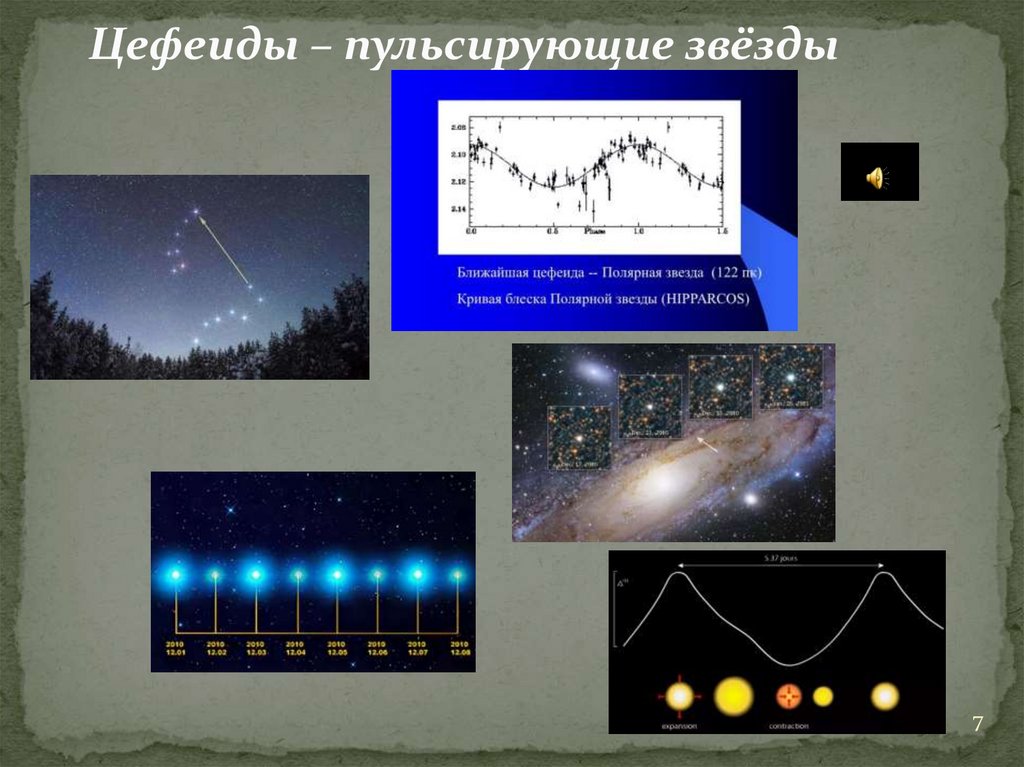
7.
Цефеиды – пульсирующие звёзды7
8.
Реакция Белоусова (1951 г.) –Жаботинского (теория)
Симон Шноль - История открытия:
https://www.youtube.com/watch?v=Op066Iof2sE
9.
Реакция Белоусова –Жаботинского
10.
Волны при протекании реакцииБелоусова - Жаботинского
11.
Ещё волны …12.
“Опр.” Колебаниями называются процессы, обладающиев той или иной мере свойством повторяемости во времени
Замечания:
1. Почему так
«расплывчато»?
2. Какие-такие «процессы?
…
?!
12
13.
“Визуализация” колебанийОсциллограф
13
14.
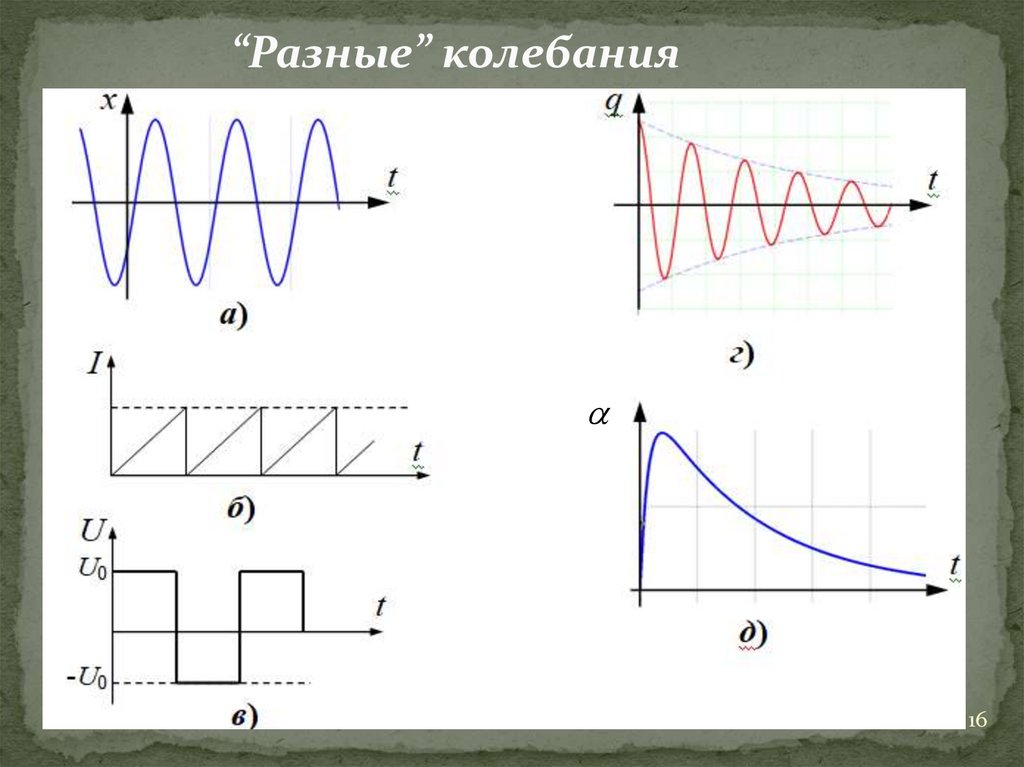
“Разные” колебания14
15.
Апериодический режим - “Релаксация”15
16.
“Разные” колебания16
17.
“Опр.” Колебаниями называются процессы, обладающиев той или иной мере свойством повторяемости во времени
Замечания:
1. Почему так
«расплывчато»?
2. Какие-такие «процессы? Что там по оси … ?
x, x , q, I, u, …, а ещё E , B , …
“Кси”:
?!
(t )
“теория колебаний”
3. “Классификация”
(какие бывают колебания)
??
17
18.
Физический маятник. Анимация18
19.
Маятник часов19
20.
2021.
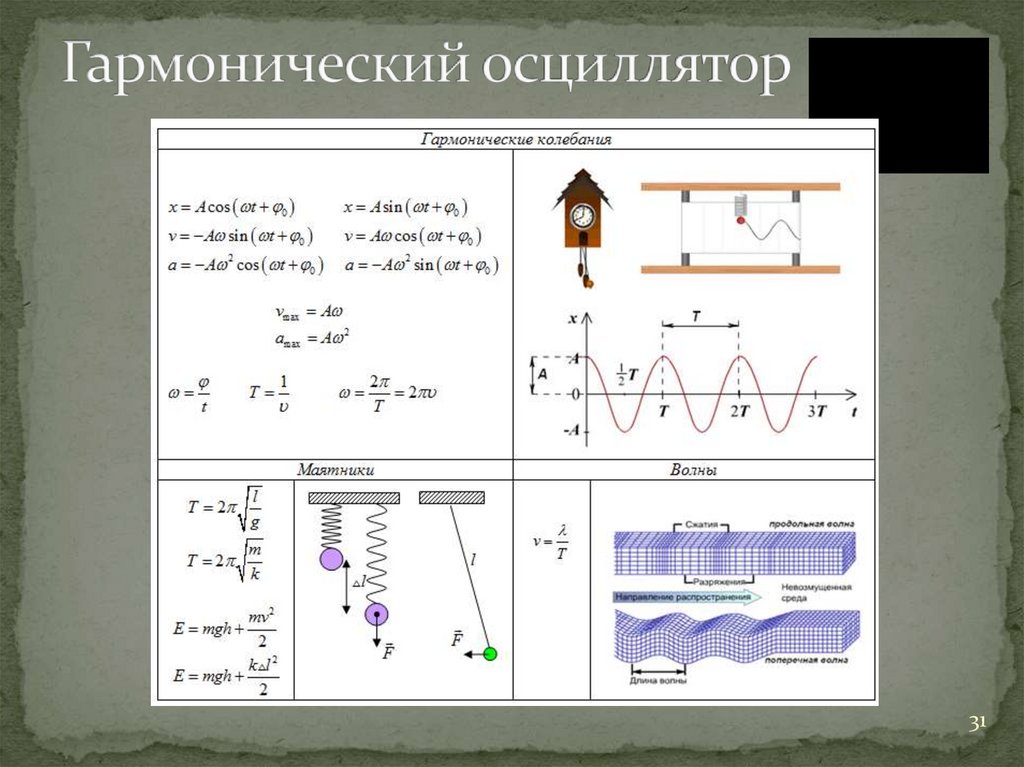
4. «Одномерный осциллятор»Свободные колебания
1.2. Модель гармонический осциллятор. “Кинематика” гармонических колебаний
“Опр.” Колебания называются гармоническими, если
они происходят по закону синуса или косинуса:
(t ) A sin( t 0 )
cos ?
~
0
(t ) 2 A cos( t 0 )
(t ) 2 (t )
2
21
22.
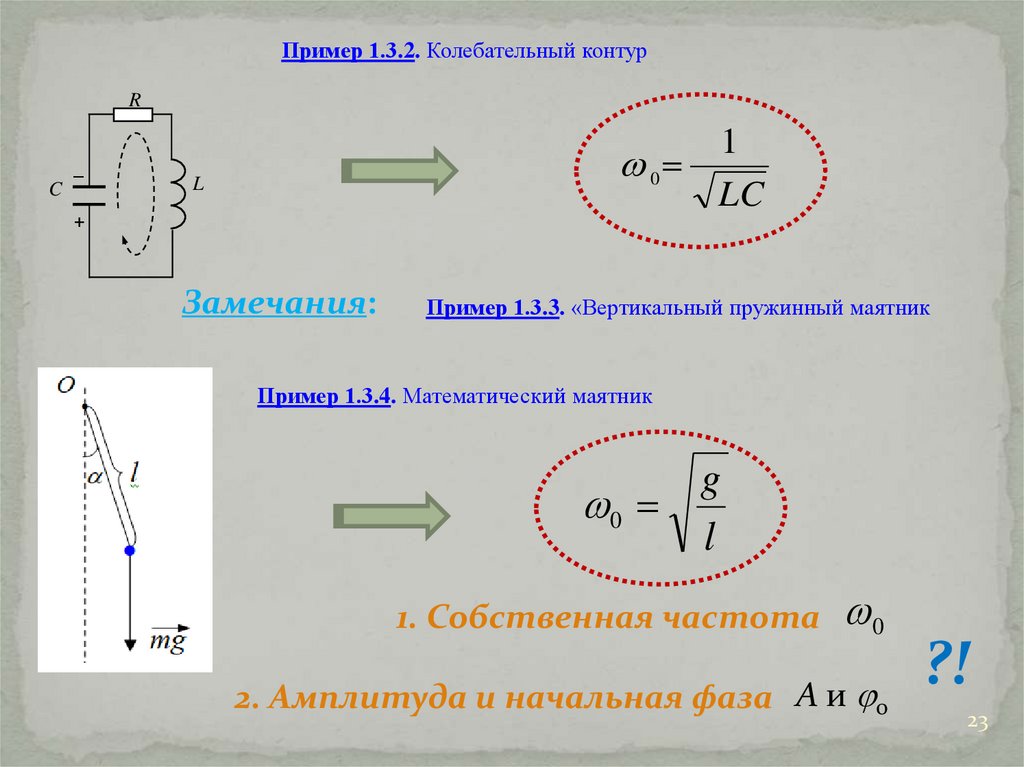
1.3. Динамика гармонических колебаний.Примеры
k
ω
m
02 0
2
0
(t ) A cos( 0t 0 )
Примеры простейших механических и электрических
гармонические осцилляторов
Пример 1.3.1. Пружинный маятник
m
k
0
x
ω0
X
k
m
22
23.
Пример 1.3.2. Колебательный контурR
C
–
1
0
LC
L
+
Замечания:
Пример 1.3.3. «Вертикальный пружинный маятник
Пример 1.3.4. Математический маятник
0
g
l
1. Собственная частота
0
2. Амплитуда и начальная фаза А и 0
?!
23
24.
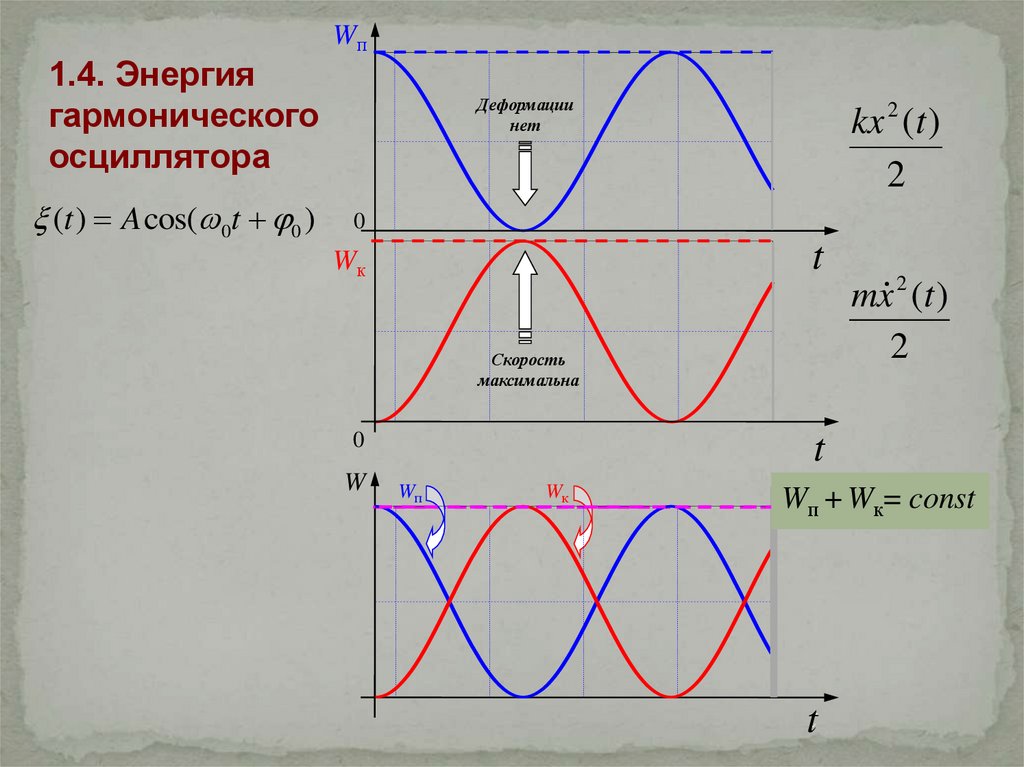
1.4. Энергиягармонического
осциллятора
(t ) A cos( 0t 0 )
Wп
Деформации
нет
kx 2 (t )
2
0
t
Wк
Скорость
максимальна
0
W
mx 2 (t )
2
t
Wп
Wк
W0 п + Wк=
W
tt
const
25.
ПолезныеТаблица 1.1.
Механический
осциллятор
Смещение, x ( )
скорость,
аналогии
Электрический
осциллятор
Заряд, q
x ( )
Сила тока, I ( q )
kx 2 Энергия электрического поля q 2
U
We
конденсатора
2
2С
Потенциальная энергия
Кинетическая энергия T mv
2
масса, m
жёсткость пружины, k
Сила (момент силы)
2
Энергия магнитного поля
LI 2
Wм
катушки
2
индуктивность, L
величина, обратная
электроёмкости конденсатора, 1/C
ЭДС
26.
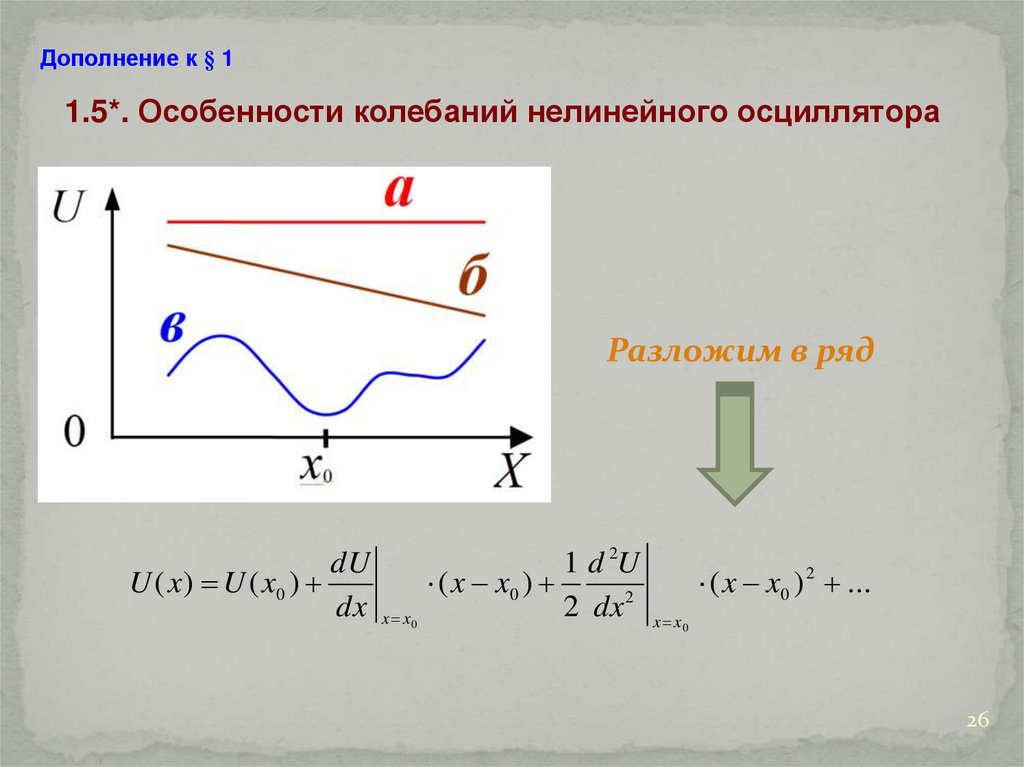
Дополнение к § 11.5*. Особенности колебаний нелинейного осциллятора
Разложим в ряд
dU
U ( x ) U ( x0 )
dx
x x0
1 d 2U
( x x0 )
2 dx 2
( x x0 ) 2 ...
x x0
26
27.
Нелинейный осциллятор:f ( ) 0
f( ) = –k + k2 2 + k3 3 + …
(t) = A1 cos( 0t + 0) + A2 cos(2 0t + 02) + A3 cos(3 0t + 03) + …
Ангармонизм
Неизохронность
! ??
27
28.
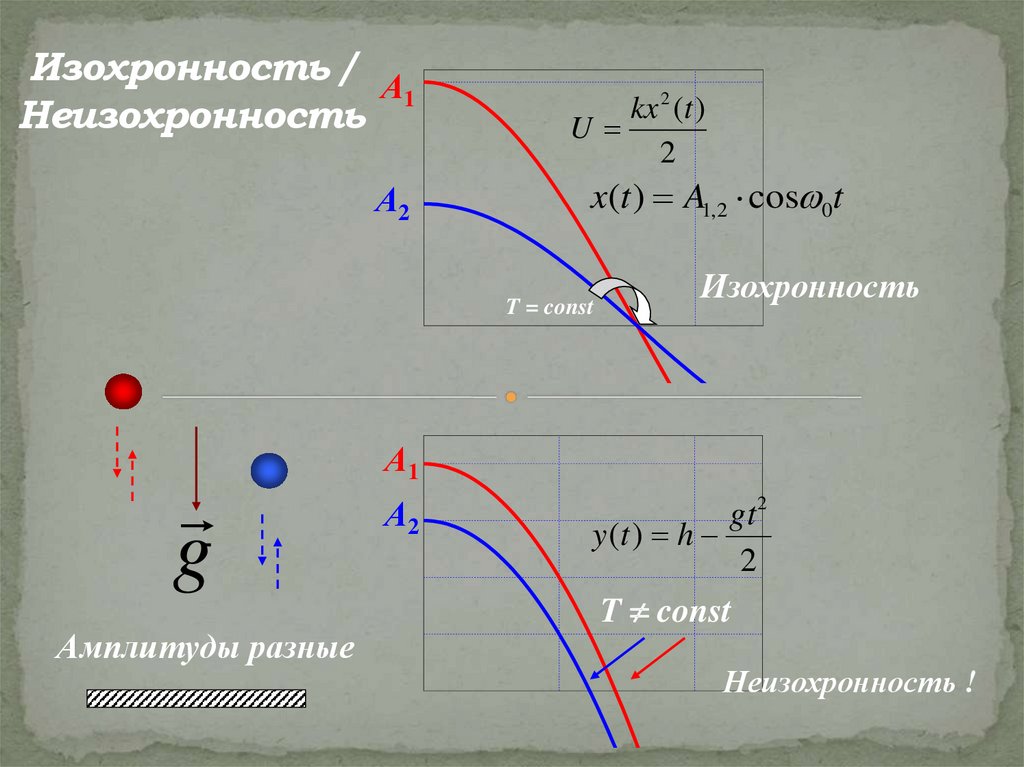
Изохронность / А1
Неизохронность
А2
kx 2 (t )
U
2
x(t ) A1,2 cos 0t
T = const
g
Амплитуды разные
Изохронность
А1
А2
gt 2
y (t ) h
2
T const
Неизохронность !
29.
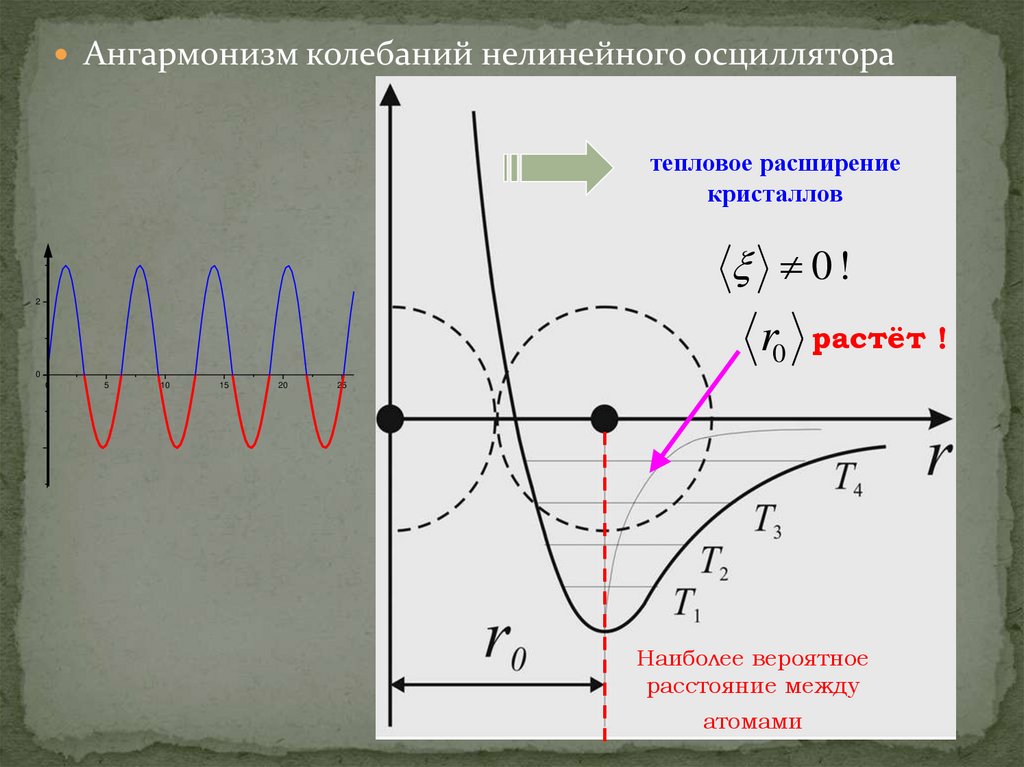
Ангармонизм колебаний нелинейного осцилляторатепловое расширение
кристаллов
0!
2
r0
растёт !
0
0
5
10
15
20
25
Наиболее вероятное
расстояние между
атомами
30.
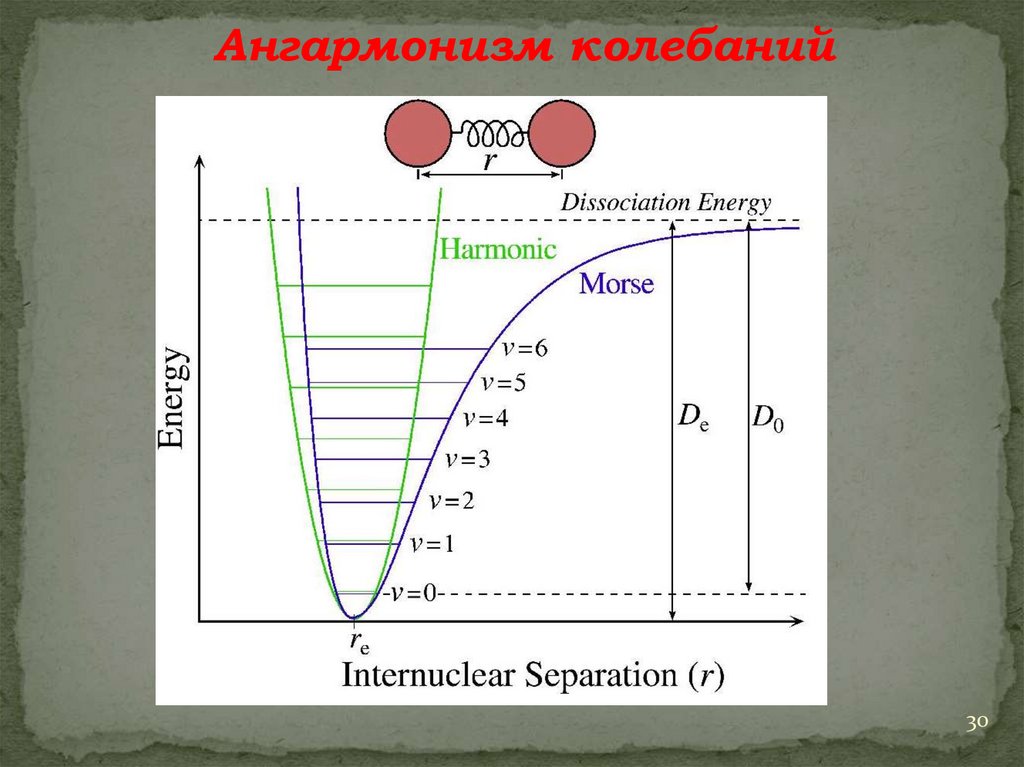
Ангармонизм колебаний30



















 physics
physics








