Колебания связанных осцилляторов. Колебания молекул. Лекция 2

1.

2.

§ 1. продолжение …

3.

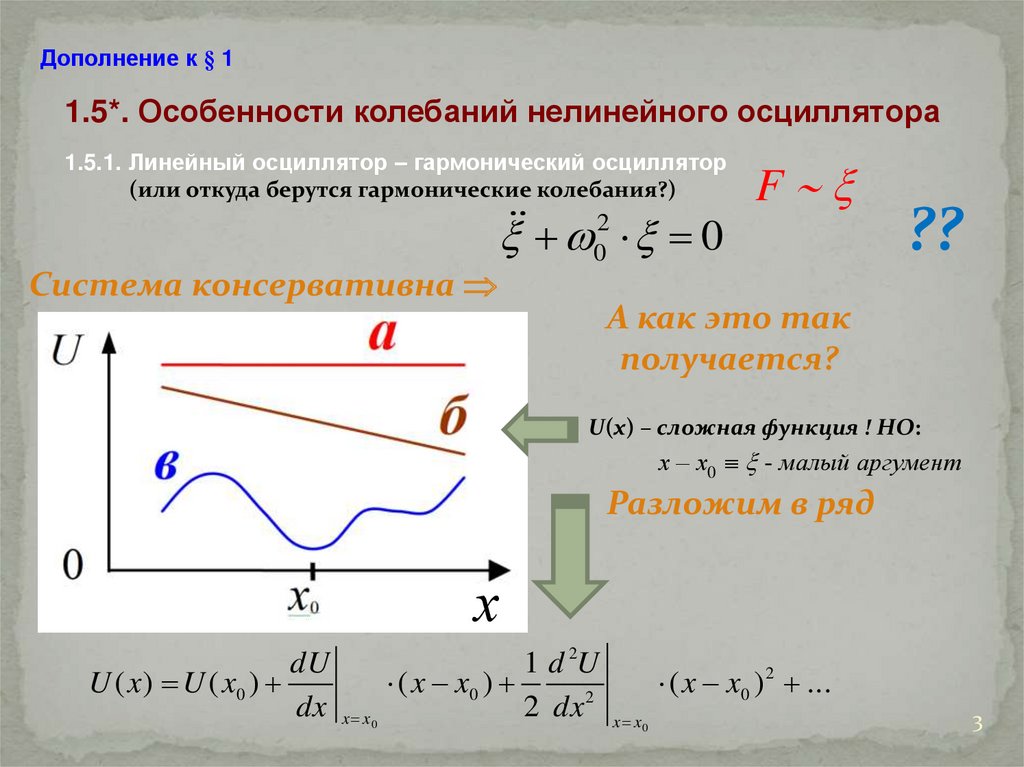
Дополнение к § 1
1.5*. Особенности колебаний нелинейного осциллятора
1.5.1. Линейный осциллятор – гармонический осциллятор
(или откуда берутся гармонические колебания?)
Система консервативна
2
0 0
F
??
А как это так
получается?
U(x) – сложная функция ! НО:
х – х0 - малый аргумент
Разложим в ряд
х
dU
U ( x ) U ( x0 )
dx
x x0
1 d 2U
( x x0 )
2 dx 2
( x x0 ) 2 ...
x x0
3

4.

dU
U ( ) U (0)
dx
1 d 2U
2 dx 2
0
2 ...
0
мала ! Тогда:
Но:
Fx
dU
dx
и тогда
1 d 2U
k 2
2
U( ) U(0)
U(0)
2
2 dx 0
2
Fx k
«Возвращающая сила», линейный, гармонический
осциллятор !!!
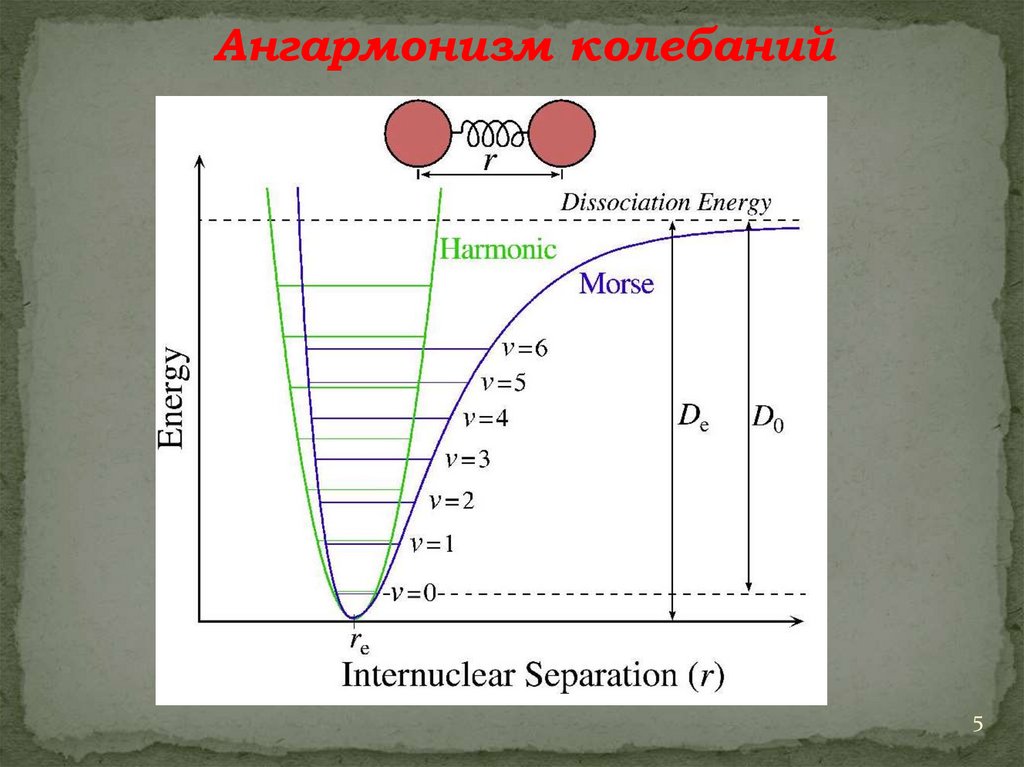
Примеры: “Потенциал Морзе”,
d 2U
k
dx 2
0
“Ленннард-Джонса” (6/12), “Бакингема”, …
1.5.2. Нелинейный («ангармонический») осциллятор
растёт нельзя «аппроксимировать» параболой
f( ) = –k + k 2 + k 3 + …
f ( ) 0
2
3
(t) = A1 cos( 0t + 0) + A2 cos(2 0t + 02) + A3 cos(3 0t + 03) + …
Ангармонизм
Неизохронность
! ??
4

5.

Ангармонизм колебаний
5

6.

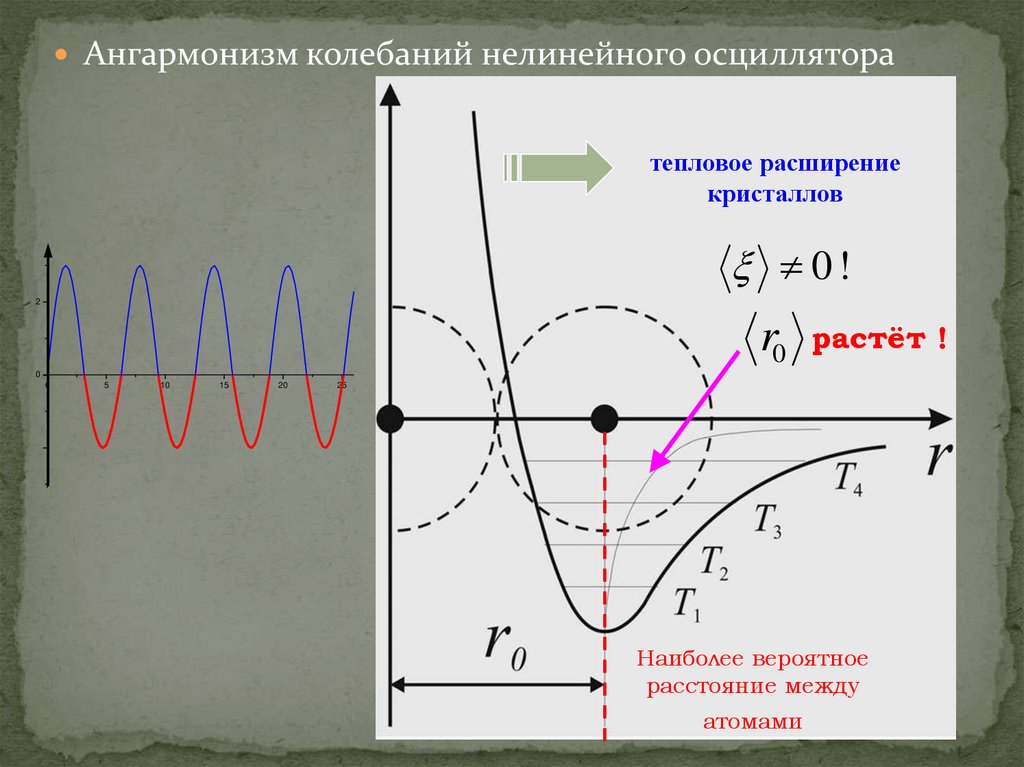
Ангармонизм колебаний нелинейного осциллятора
тепловое расширение
кристаллов
0!
2
r0
растёт !
0
0
5
10
15
20
25
Наиболее вероятное
расстояние между
атомами

7.

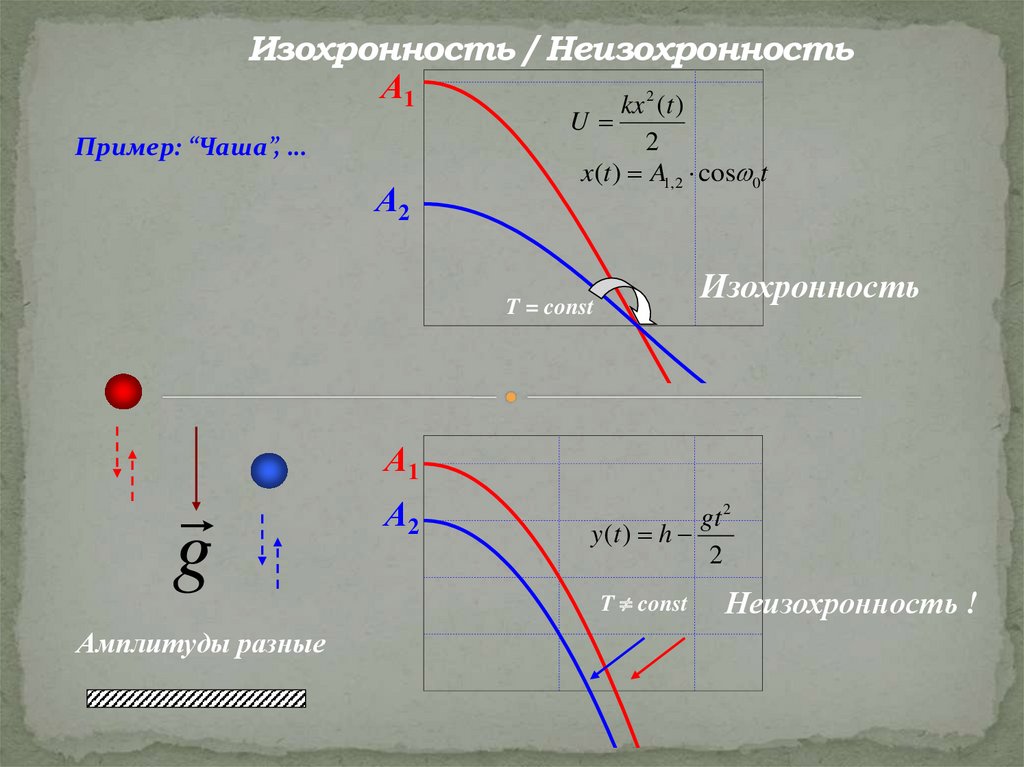
Изохронность / Неизохронность
А1
kx 2 (t )
U
Пример: “Чаша”, …
А2
2
x(t ) A1,2 cos 0t
Изохронность
T = const
g
Амплитуды разные
А1
А2
gt 2
y (t ) h
2
T const
Неизохронность !

8.

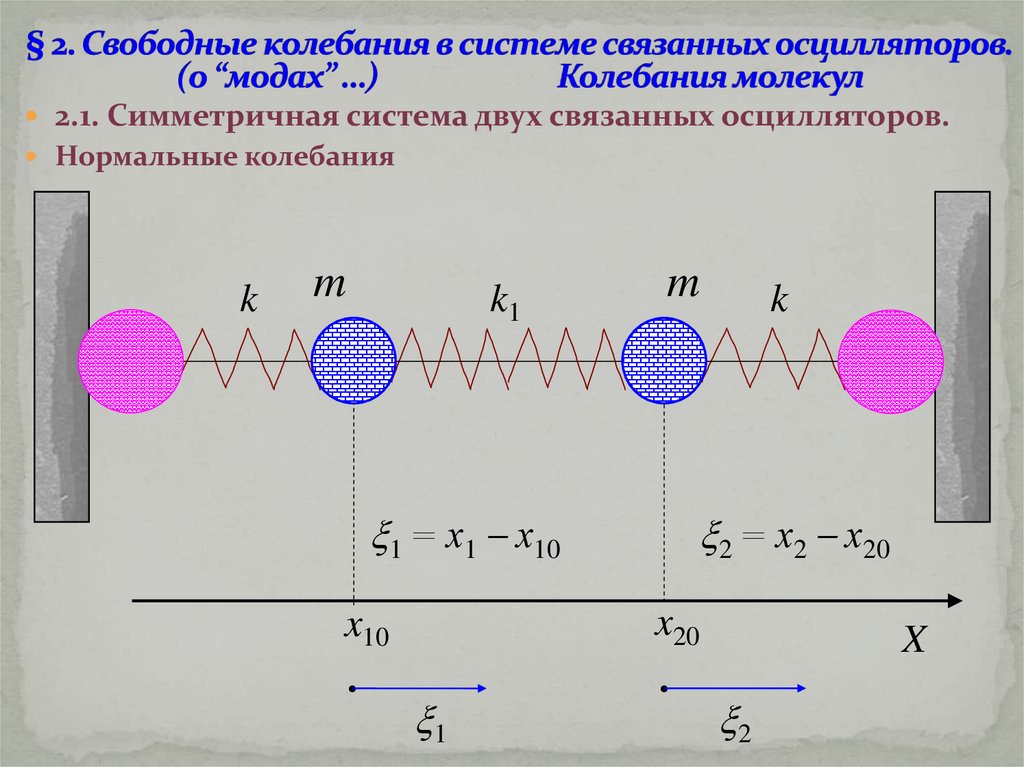
2.1. Симметричная система двух связанных осцилляторов.
Нормальные колебания
k
m
k1
m
1 = х1 х10
2 = х2 х20
x10
x20
1
k
X
2

9.

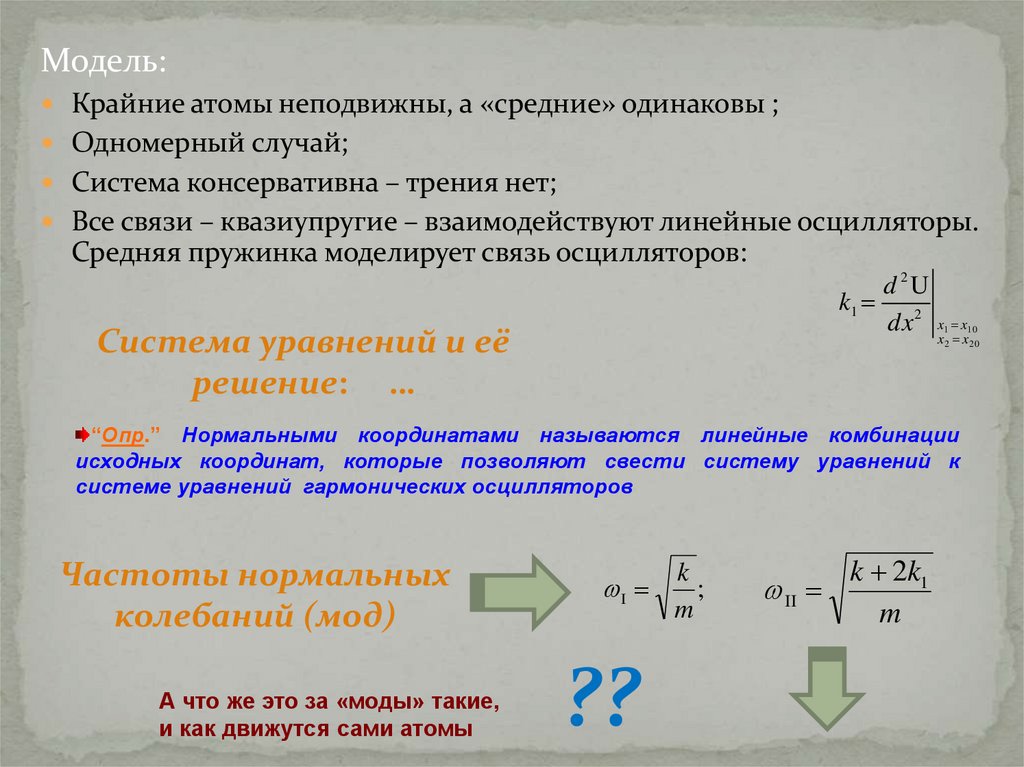
Модель:
Крайние атомы неподвижны, а «средние» одинаковы ;
Одномерный случай;
Система консервативна – трения нет;
Все связи – квазиупругие – взаимодействуют линейные осцилляторы.
Средняя пружинка моделирует связь осцилляторов:
d 2U
k1
dx 2
Система уравнений и её
решение: …
x1 x10
x 2 x 20
“Опр.” Нормальными координатами называются линейные комбинации
исходных координат, которые позволяют свести систему уравнений к
системе уравнений гармонических осцилляторов
Частоты нормальных
колебаний (мод)
А что же это за «моды» такие,
и как движутся сами атомы
I
??
k
;
m
k 2k1
II
m

10.

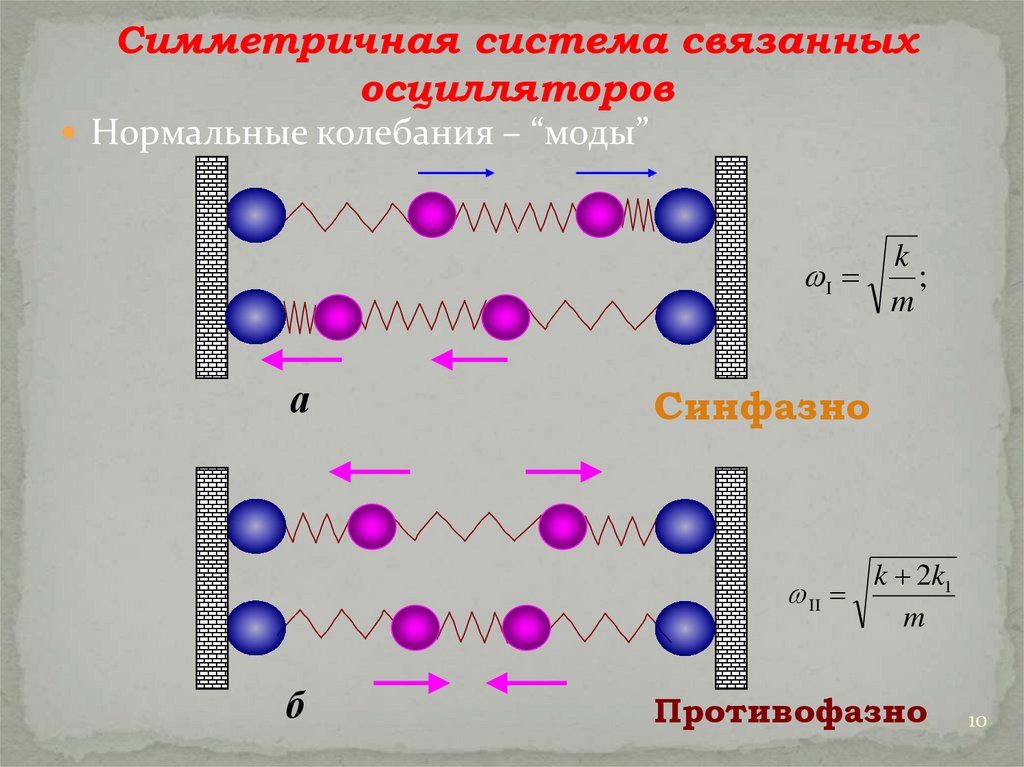
Симметричная система связанных
осцилляторов
Нормальные колебания – “моды”
k
I
;
m
а
Синфазно
II
б
k 2k1
m
Противофазно
10

11.

Антракт

12.

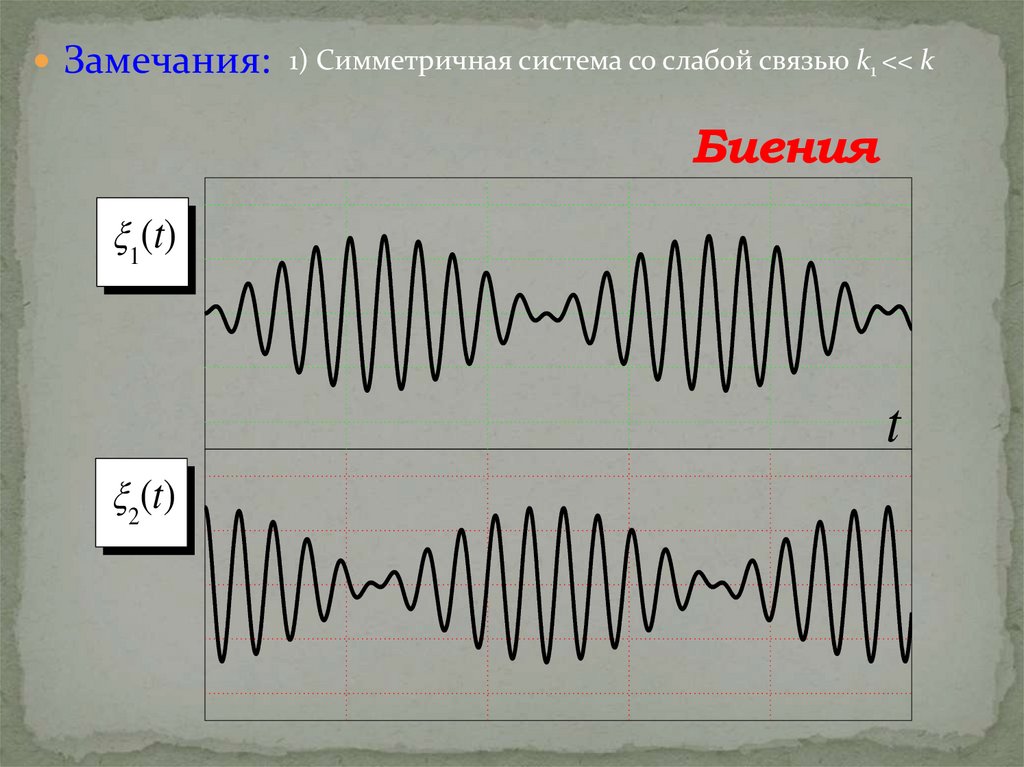
Замечания: 1) Симметричная система со слабой связью k1 << k
“Биения”
2) Моды энергетически независимы !!
3) Несимметричные системы
??

13.

Замечания: 1) Симметричная система со слабой связью k1 << k
Биения
1(t)
t
2(t)

14.

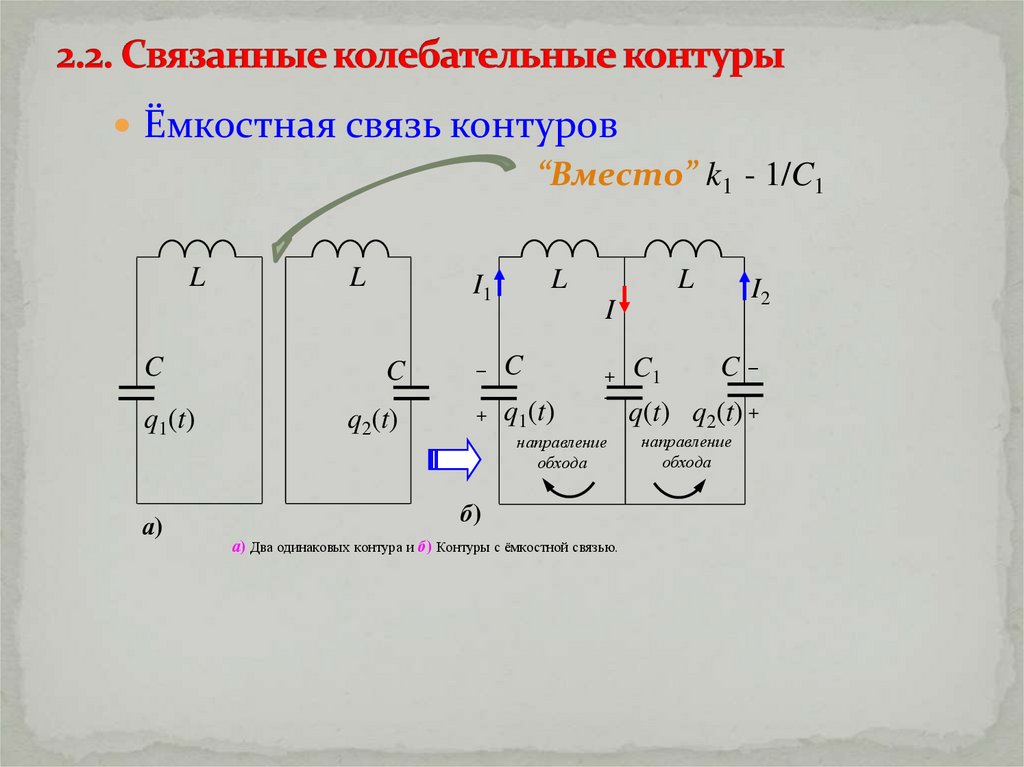
Ёмкостная связь контуров
“Вместо” k1 - 1/C1
L
C
q1(t)
а)
L
L
I1
C
q2(t)
L
I2
I
–
C
+
q1(t)
+
–
направление
обхода
б)
а) Два одинаковых контура и б) Контуры с ёмкостной связью.
C1
C
–
q(t) q2(t) +
направление
обхода

15.

Ёмкостная связь контуров
L
I1
2-е правило Кирхгофа
и “-/+”:
qI :
I
qII :
II
–
q1
1 1 2
L C C1
Противофазно
+
C
I2
направление
обхода
направление
обхода
1
LC
Синфазно
L
+
–
C1
q
C
–
+
q2

16.

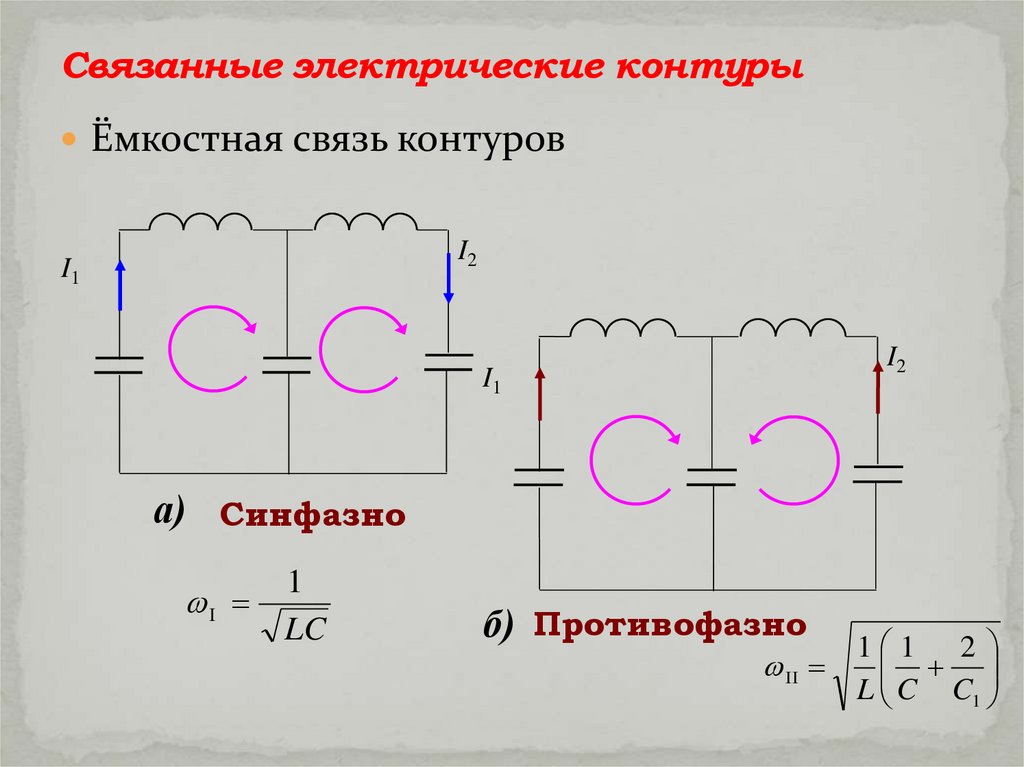
Связанные электрические контуры
Ёмкостная связь контуров
I2
I1
I2
I1
а) Синфазно
I
1
LC
б) Противофазно
II
1 1 2
L C C1

17.

2.3. Колебания молекул
(колебательная/молекулярная спектроскопия)
2.3.1. Двухатомная молекула
ц.м.
x1
Внутримолекулярные колебания свободной
двухатомной молекулы (Модель «гармонический
осциллятор» в химии)
Задачи 2.3 – 2.5 :
= х2 х1 l0
Одна “колебательная степень
свободы”
??
k
0
k
m2
А где её “увидеть”
X
m1
x2
m1m2
m1 m2
Пример 1. Изотопные сдвиги в колебательных спектрах
0OH
OD
mD (mO mH )
1,37
OD
0
OH
mH (mO mD )
Пример 2. Свободные и связанные гидроксилы
0своб
(mO mH )
1,031
связ
0
mO
2.3.2. Многоатомные молекулы. Колебательные степени свободы
молекул:
3N – 6 / 3N – 5
??
проверим

18.

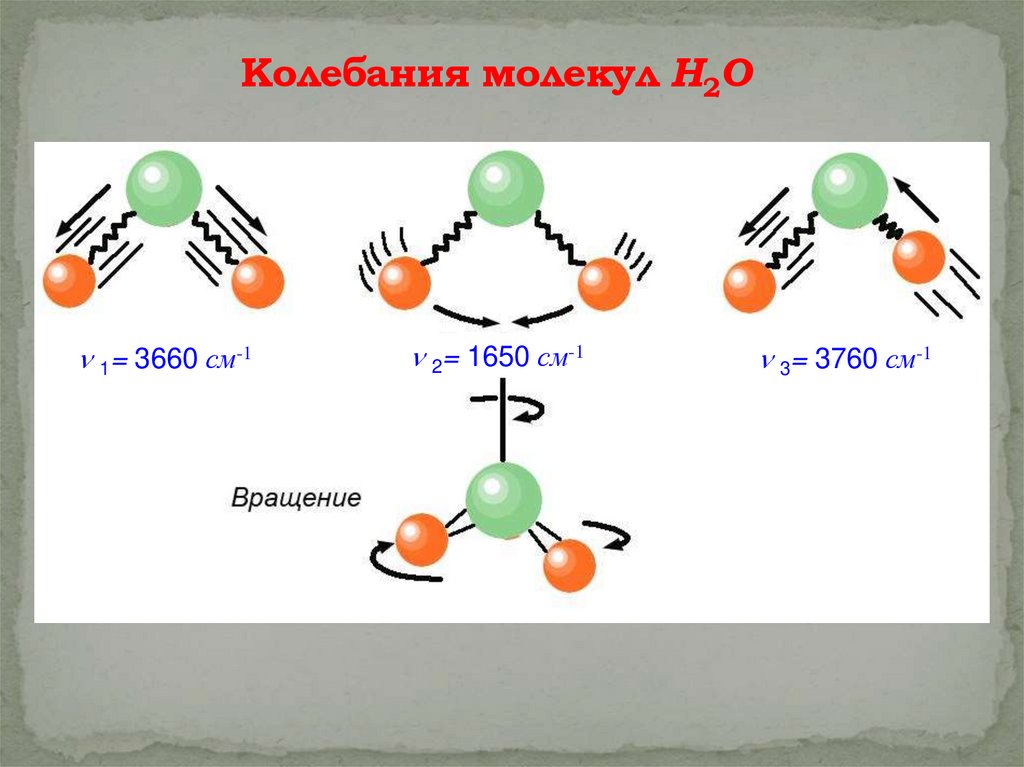
Колебания молекул Н2О
1= 3660 см-1
2= 1650 см-1
3= 3760 см-1

19.

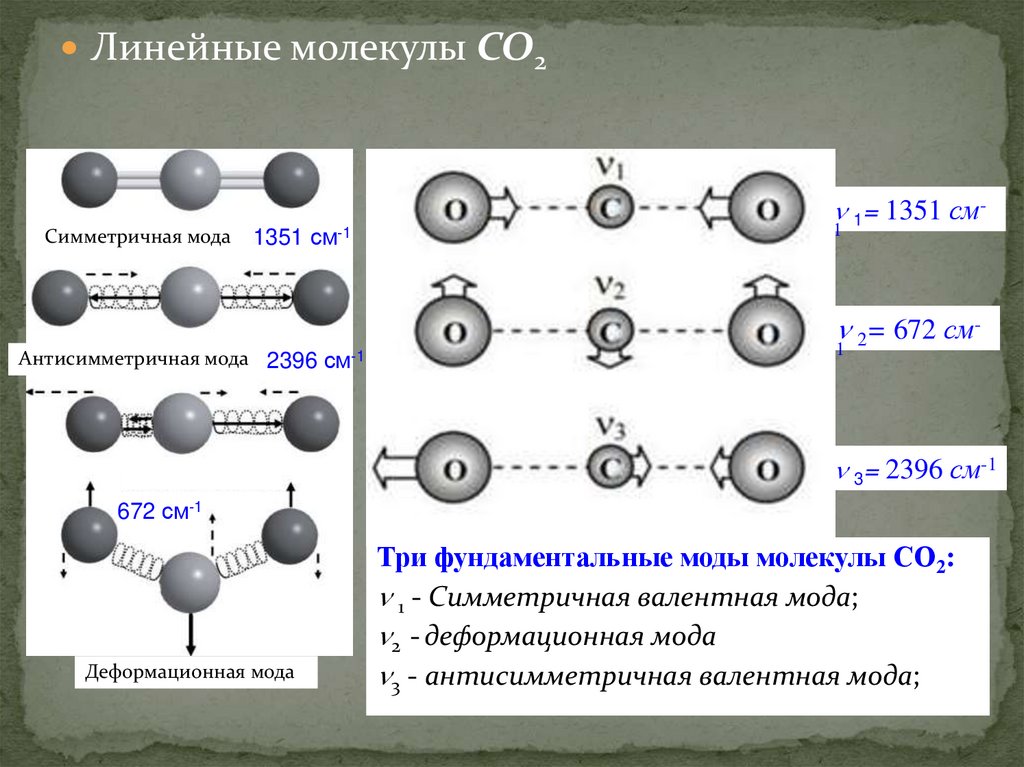
Линейные молекулы CO2
Симметричная мода
1351 см-1
Антисимметричная мода 2396 см-1
1= 1351 см1
2= 672 см1
3= 2396 см-1
672 см-1
Деформационная мода
Три фундаментальные моды молекулы СО2:
1 - Симметричная валентная мода;
2 - деформационная мода
3 - антисимметричная валентная мода;

20.

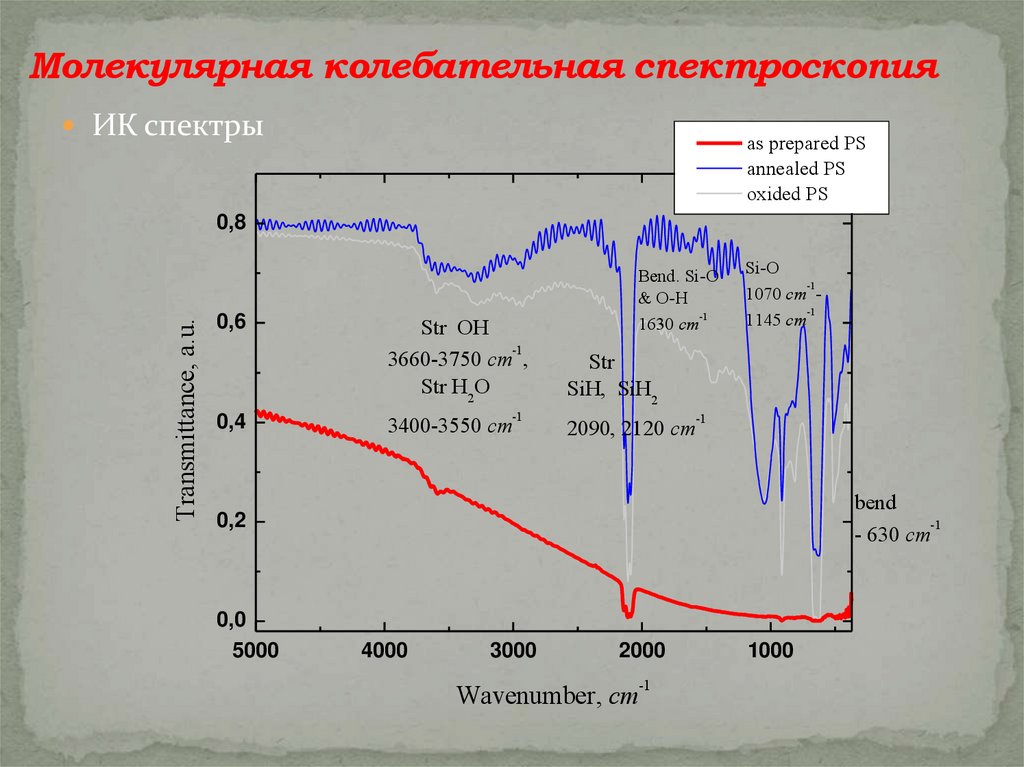
Молекулярная колебательная спектроскопия
ИК спектры
as prepared PS
annealed PS
oxided PS
Transmittance, a.u.
0,8
0,6
0,4
Str OH
-1
3660-3750 cm ,
Str H2O
-1
3400-3550 cm
Bend. Si-O
& O-H
-1
1630 cm
Si-O
-1
1070 cm -1
1145 cm
Str
SiH, SiH2
-1
2090, 2120 cm
bend
-1
- 630 cm
0,2
0,0
5000
4000
3000
2000
Wavenumber, cm
-1
1000

21.

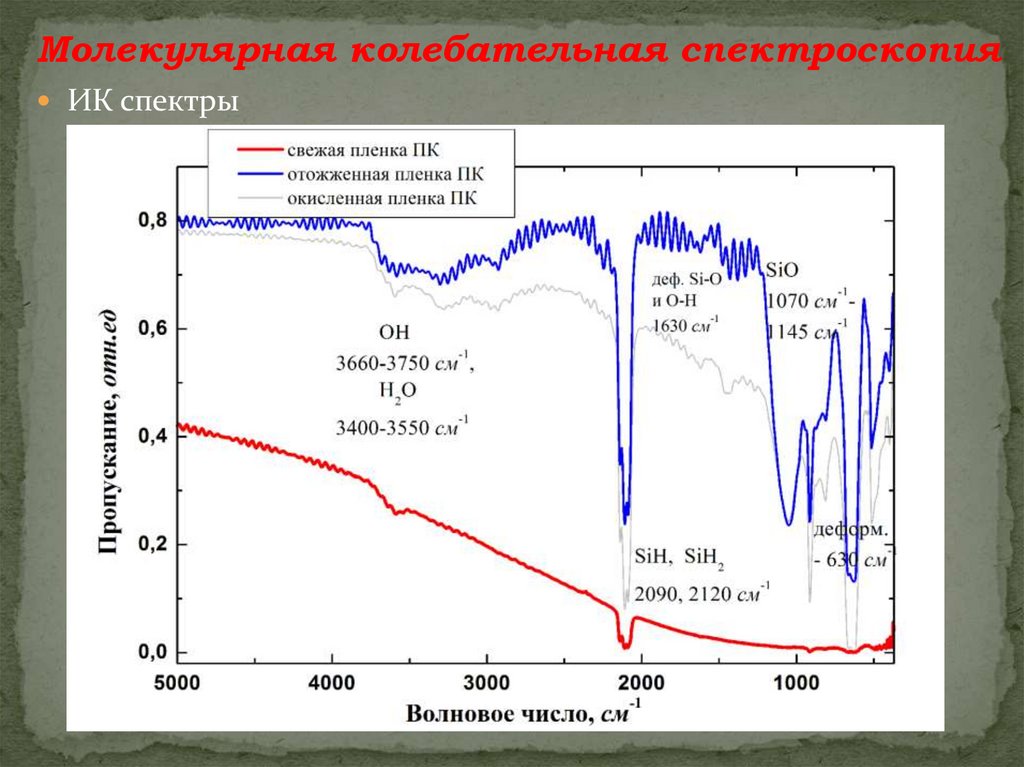
Молекулярная колебательная спектроскопия
ИК спектры

22.

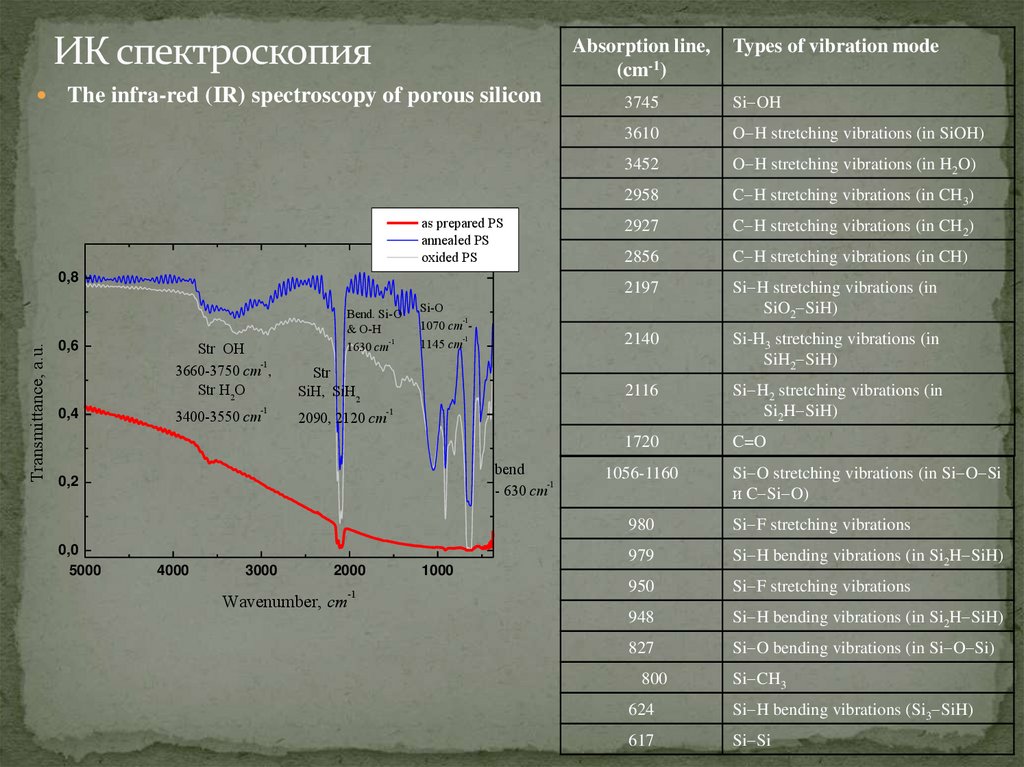
ИК спектроскопия
Absorption line,
(cm-1)
The infra-red (IR) spectroscopy of porous silicon
as prepared PS
annealed PS
oxided PS
Transmittance, a.u.
0,8
0,6
0,4
Str OH
-1
3660-3750 cm ,
Str H2O
-1
3400-3550 cm
Bend. Si-O
& O-H
-1
1630 cm
Si-O
-1
1070 cm -1
1145 cm
Str
SiH, SiH2
0,0
5000
3000
Si OH
3610
O H stretching vibrations (in SiOH)
3452
O H stretching vibrations (in H2O)
2958
C H stretching vibrations (in CH3)
2927
C H stretching vibrations (in CH2)
2856
C H stretching vibrations (in CH)
2197
Si H stretching vibrations (in
SiO2 SiH)
2140
Si-H3 stretching vibrations (in
SiH2 SiH)
2116
Si H2 stretching vibrations (in
Si2H SiH)
1720
C=O
2090, 2120 cm
bend
-1
- 630 cm
4000
3745
-1
0,2
2000
Wavenumber, cm
-1
Types of vibration mode
1056-1160
Si O stretching vibrations (in Si O Si
и C Si O)
980
Si F stretching vibrations
979
Si H bending vibrations (in Si2H SiH)
950
Si F stretching vibrations
948
Si H bending vibrations (in Si2H SiH)
827
Si O bending vibrations (in Si O Si)
1000
800
Si CH3
624
Si H bending vibrations (Si3 SiH)
617
Si Si

23.

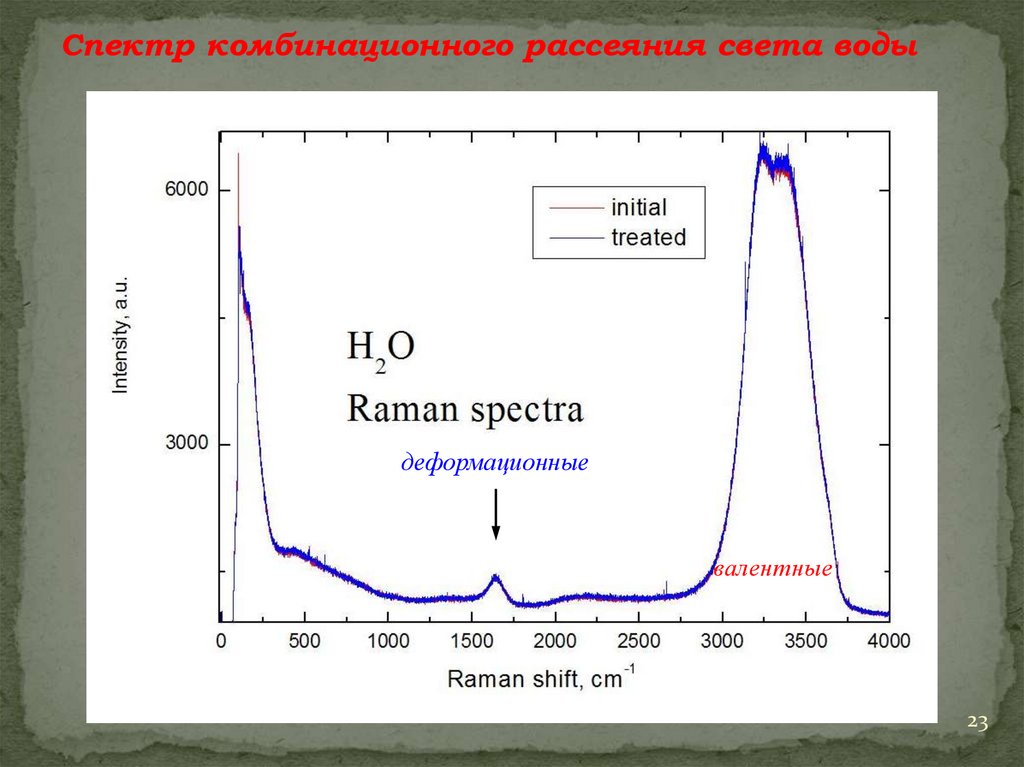
Спектр комбинационного рассеяния света воды
деформационные
валентные
23

24.

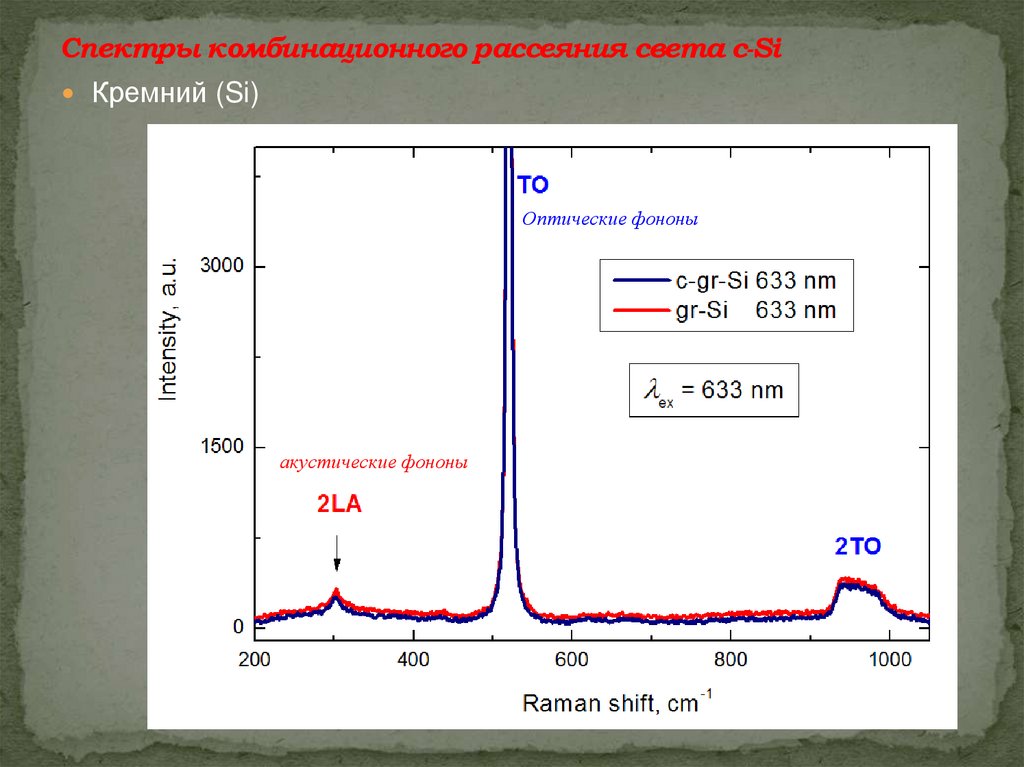
Спектры комбинационного рассеяния света c-Si
Кремний (Si)
Оптические фононы
акустические фононы

25.

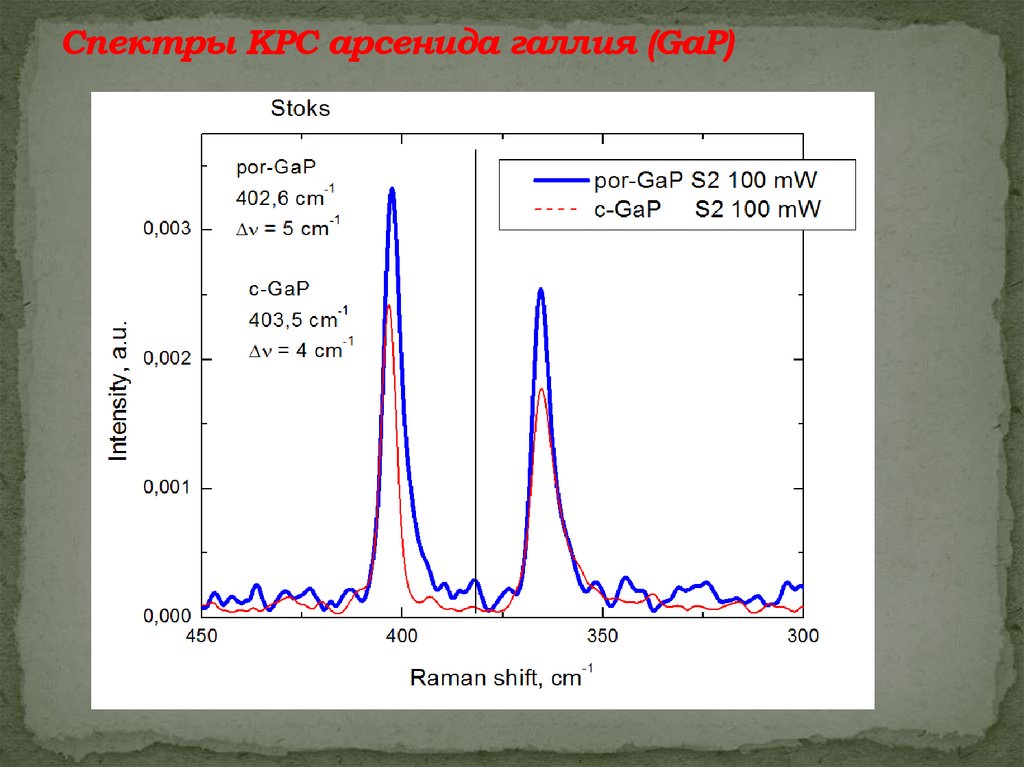
Спектры КРС арсенида галлия (GaP)

26.

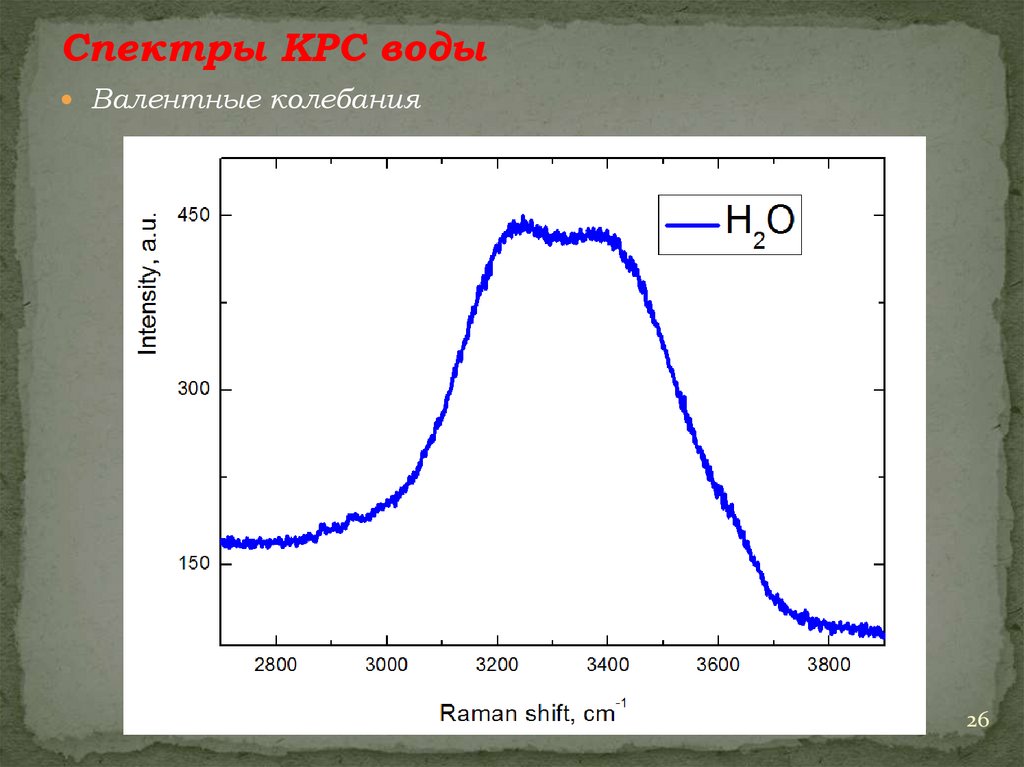
Спектры КРС воды
Валентные колебания
26

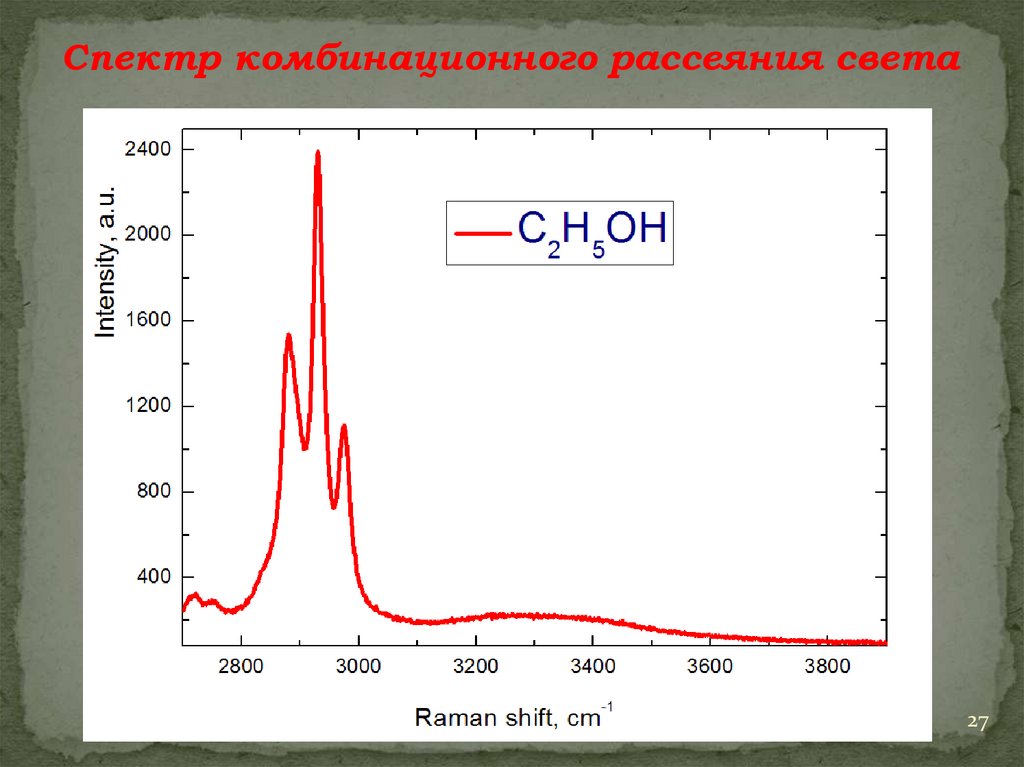
27.

Спектр комбинационного рассеяния света
27

28.

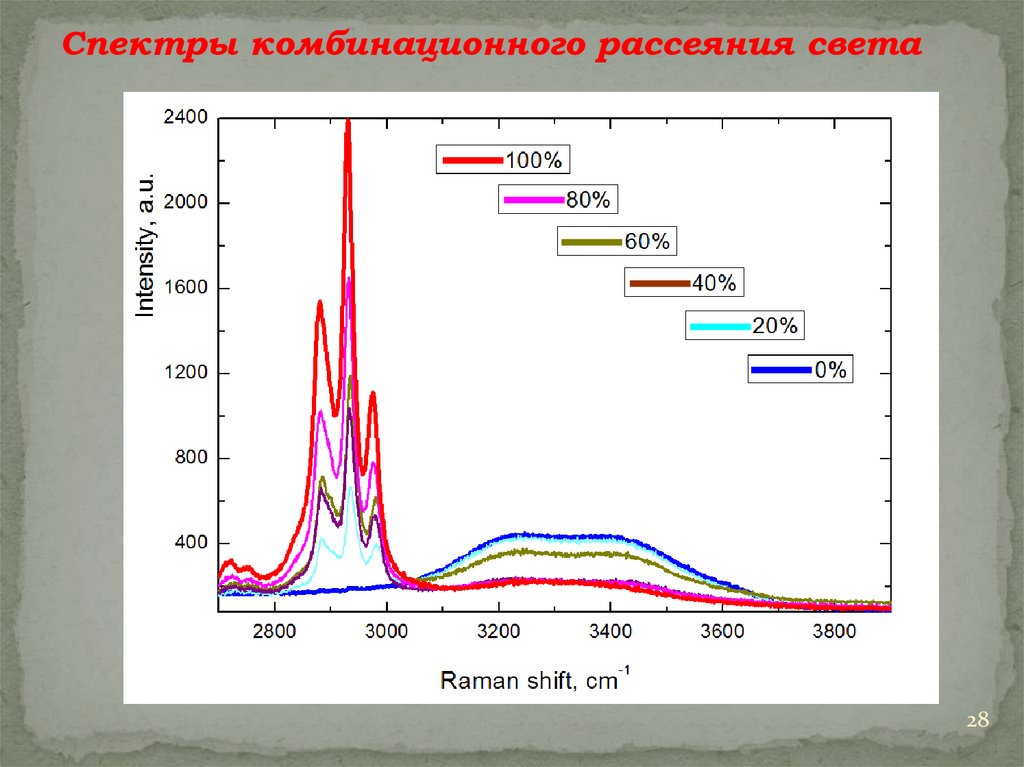
Спектры комбинационного рассеяния света
28