Колебания. Колебательный контур

1.

Колебания
бывают
механические,
электромагнитные,
химические,
термодинамические
и различные другие.
Несмотря
на
такое
разнообразие, все они
имеют между собой
много
общего.

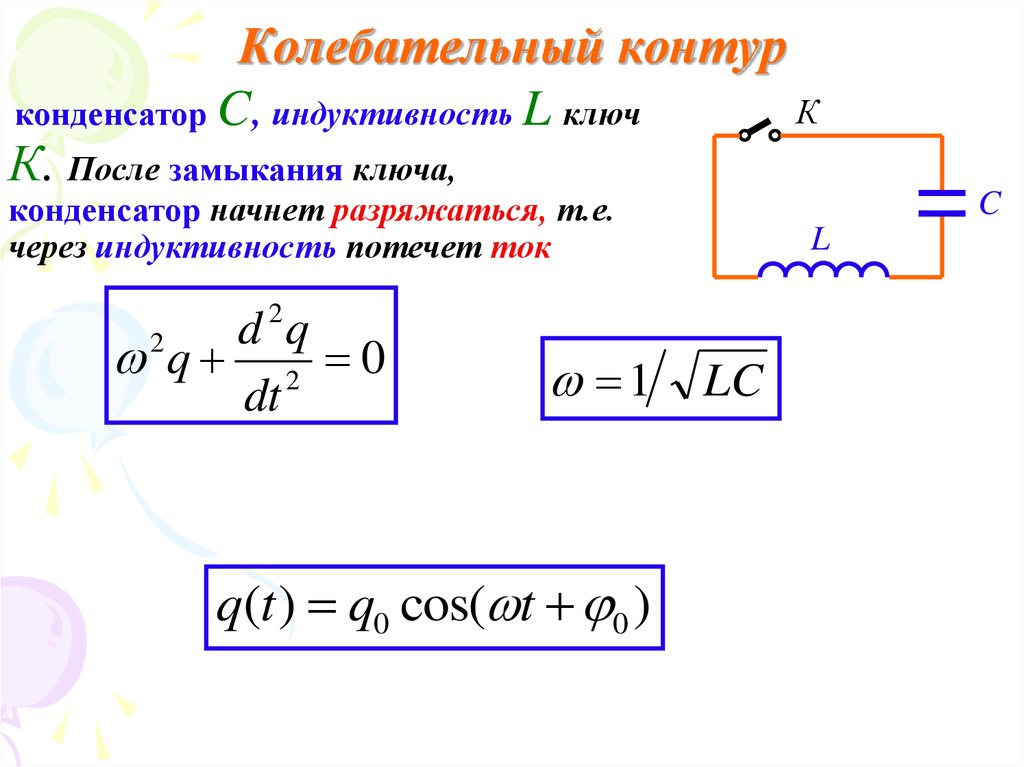
2. Колебательный контур

К
конденсатор C, индуктивность L ключ
К. После замыкания ключа,
конденсатор начнет разряжаться, т.е.
через индуктивность потечет ток
L
2
d q
q 2 0
dt
2
1
q(t ) q0 cos( t 0 )
LC
C

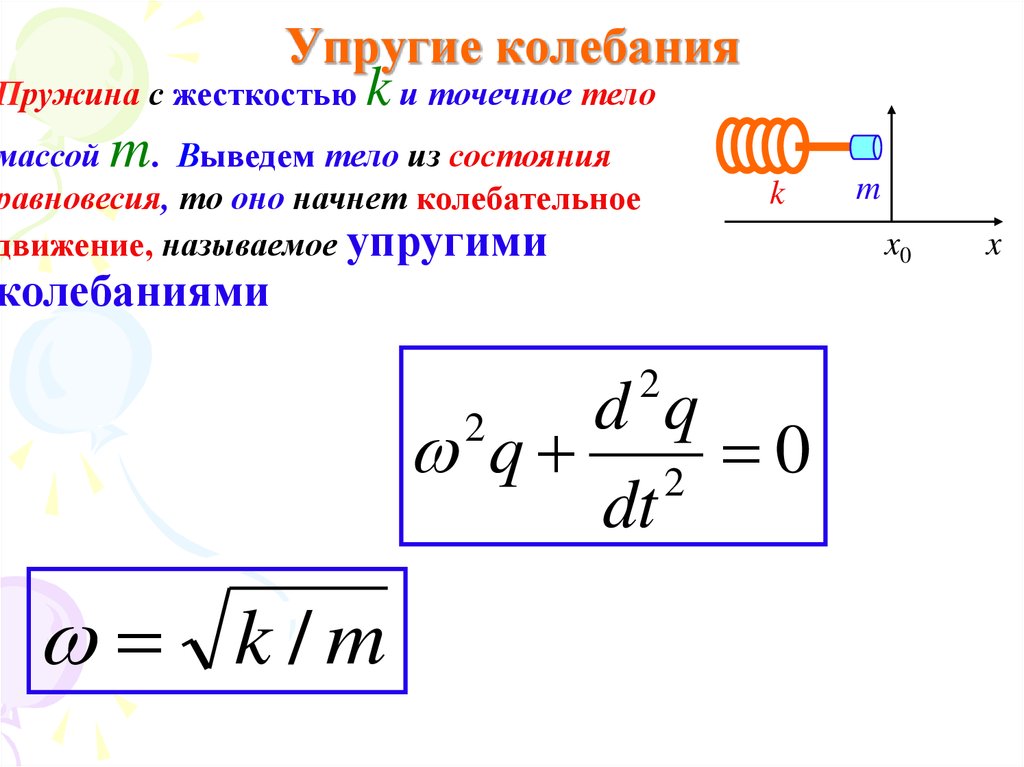
3. Упругие колебания

Пружина с жесткостью
k и точечное тело
m
массой . Выведем тело из состояния
равновесия, то оно начнет колебательное
движение, называемое упругими
k
колебаниями
2
d q
q 2 0
dt
2
k/m
m
x0
x

4. Упругие колебания

Изменение заряда (в любой точке
колебательного контура) и изменение
координаты точечного тела под действием
упругой силы описывается уравнением
гармонических колебаний

5. Математический маятник

точечное тело массой m,
подвешено на невесомой,
нерастяжимой нити длиной l.
lα
m
d
2
0
2
dt
2
g /l
l
T
m
FT

6. Гармонические колебания

q - физическая величина,
2
характеризующая движение
физической системы,
ω - (круговая) частота
d q
2
q 0
2
dt
2
T 1 /
гармонических колебаний
ν - (линейная) частота,
T - период колебаний
Решение
Фаза
начальная фаза
q(t ) q0 cos( t 0 )
(t ) t 0
0 (0)

7.

• Смещение описывается уравнением
x Acos (ω0t φ)
тогда, по определению:
dx
скорость υ x
ω0 Asin (ω0t φ)
dt
dυ x
ускорение ax
ω02 Acos(ω0t φ)
dt
ω0 A υ m
– амплитуда скорости;
2
ω0 A
– амплитуда ускорения.
am
7

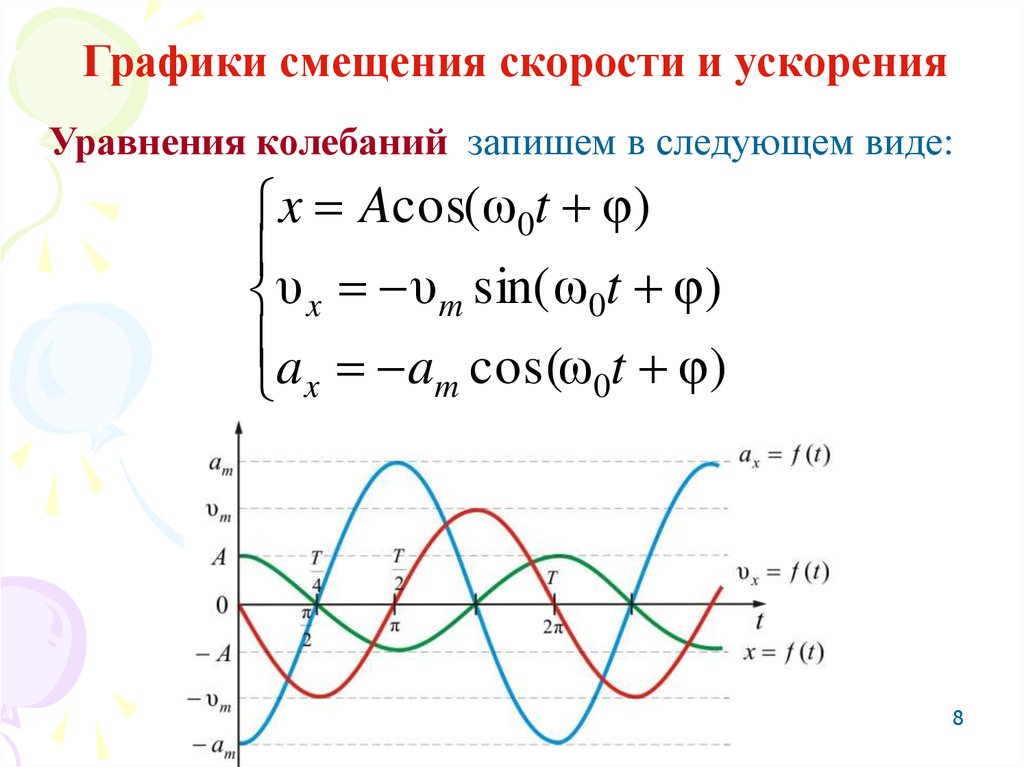
8.

Графики смещения скорости и ускорения
Уравнения колебаний запишем в следующем виде:
x Acos(ω0t φ)
υ x υ m sin( ω0t φ)
a a cos(ω t φ)
m
0
x
8

9. Когерентные колебания

Два гармонические колебания называют
когерентными, если разность фаз
этих колебаний не меняется с течением
времени
d
12 0
dt

10. Произвольные гармонические колебания

Гармонические колебания, создаваемые одинаково
направленными плоскими монохроматическими
волнами будем называть одинаково
направленными колебаниями

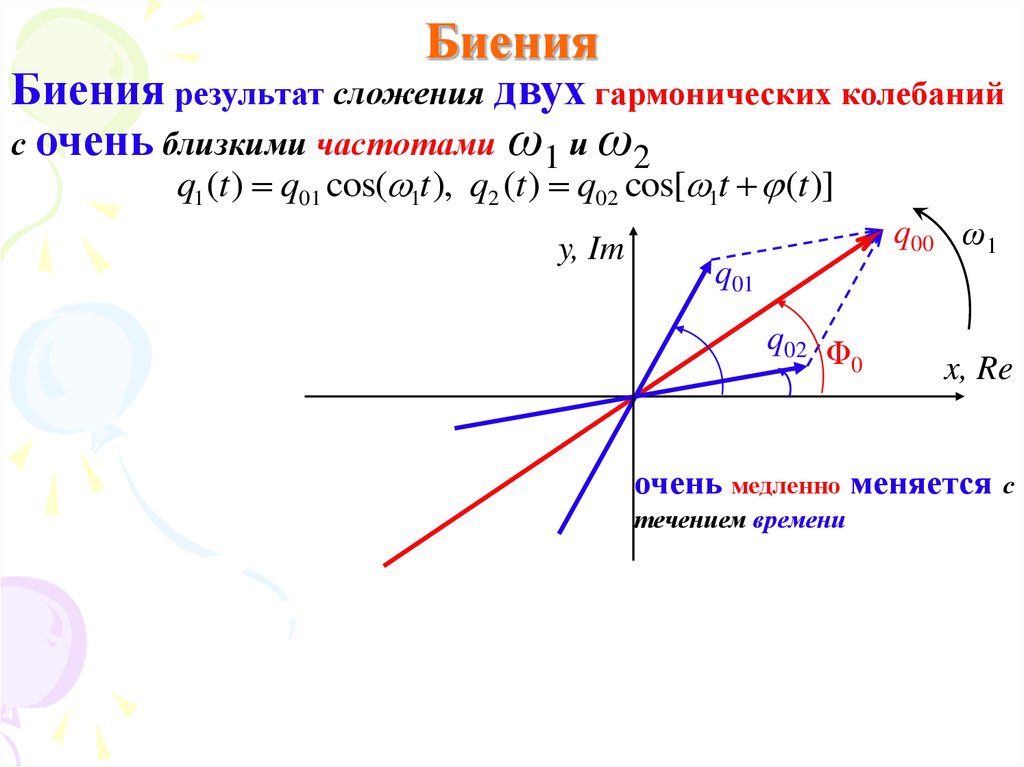
11. Биения

Биения результат сложения двух гармонических колебаний
с очень близкими частотами ω1 и ω2
q1 (t ) q01 cos( 1t ), q2 (t ) q02 cos[ 1t (t )]
y, Im
q00 ω1
q01
q02 Φ
0
x, Re
очень медленно меняется с
течением времени

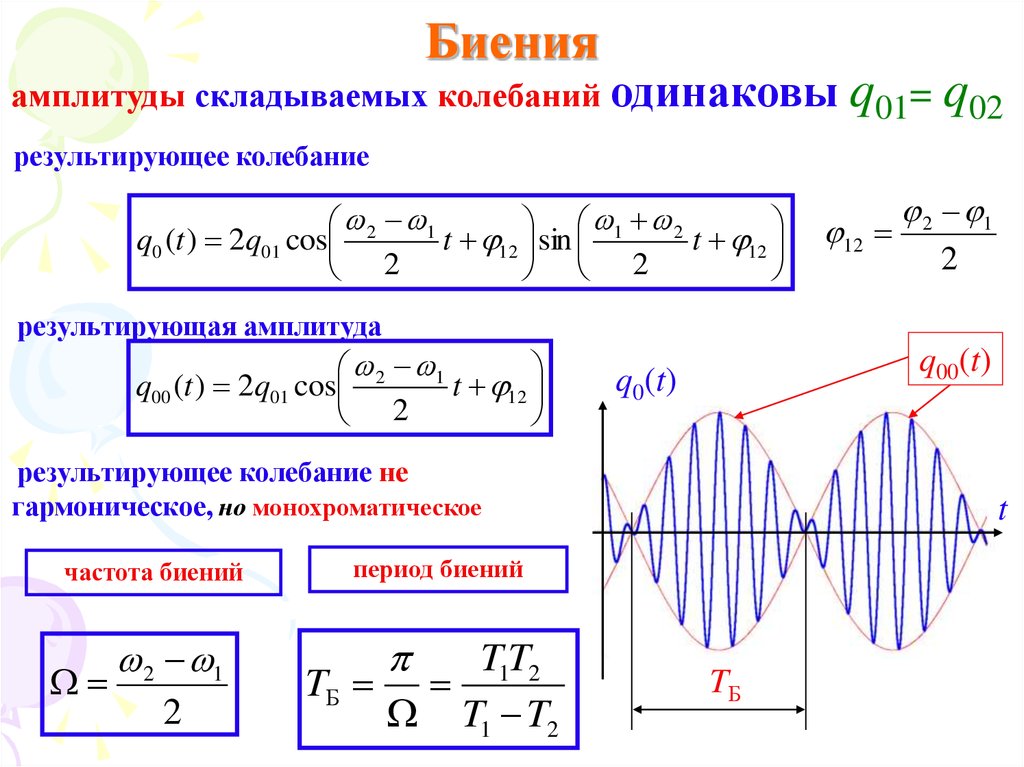
12. Биения

амплитуды складываемых колебаний одинаковы
q01= q02
результирующее колебание
2 1
1 2
q0 (t ) 2q01 cos
t 12 sin
t 12
2
2
12
2 1
2
результирующая амплитуда
1
q00 (t ) 2q01 cos 2
t 12
2
q00(t)
q0(t)
результирующее колебание не
гармоническое, но монохроматическое
частота биений
2 1
2
t
период биений
T1T2
TБ
T1 T2
TБ

13. Затухающие колебания

колебательный контур, состоит из
К
конденсатора C, индуктивности L и
ключа
К сопротивление R
I
C
R
L
2
dq d q
q 2
2 0
dt dt
2
0
0 1 LC
R
2L
собственная частота
колебательного контура
коэффициент
уравнение затухающих колебаний
затухания

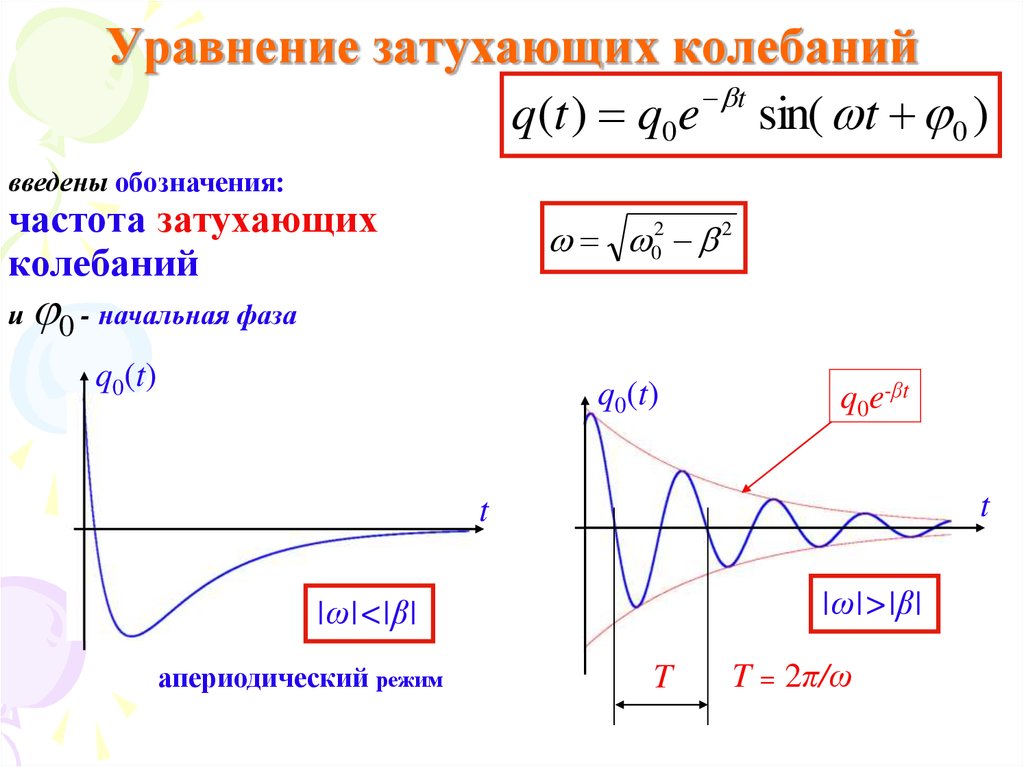
14. Уравнение затухающих колебаний

q(t ) q0 e t sin( t 0 )
введены обозначения:
частота затухающих
колебаний
и
02 2
0 - начальная фаза
q0(t)
q0(t)
q0e-βt
t
t
|ω|>|β|
|ω|<|β|
апериодический режим
T
T = 2π/ω

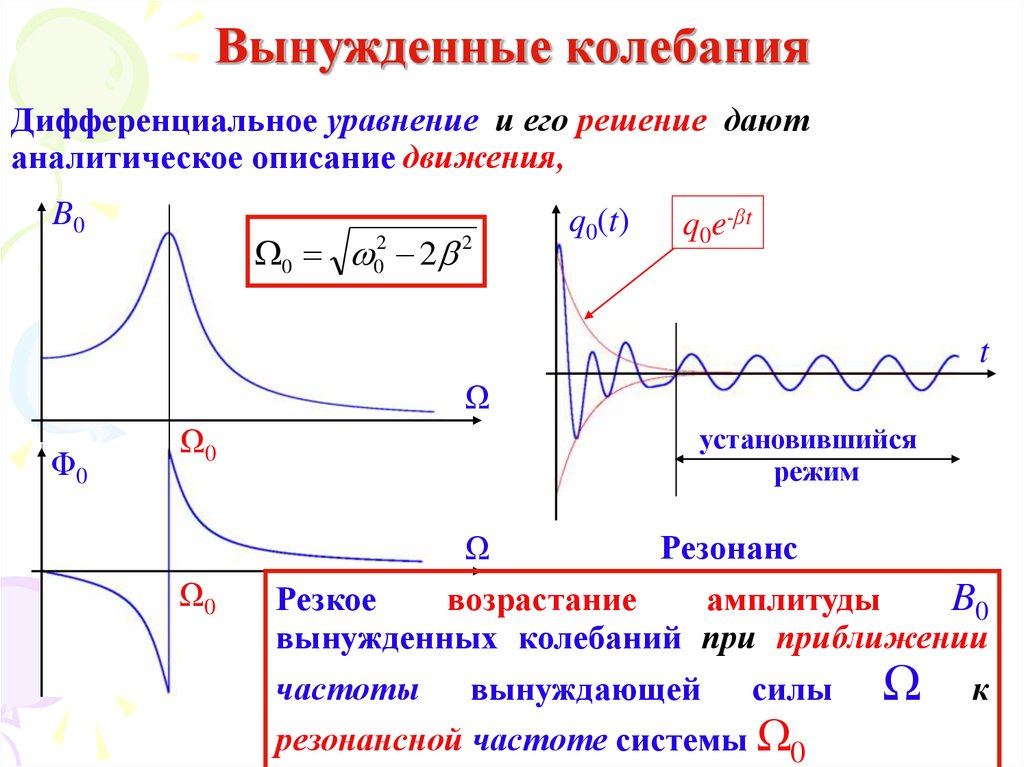
15. Вынужденные колебания

Вынужденными колебаниями будем называть
затухающие колебания + вынуждающая сила
k
dx F (t )
a ( x-x0 ) b
m
dt
m
2
dq
d
q
2
0 q 2
2 A(t ) (*)
dt dt
A(t) = F(t)/m и F(t) = F(t+T) - вынуждающая сила
Уравнение называют уравнением
вынужденных колебаний
2
dq
d
q
2
0 q 2
2 A0 cos( t )
dt dt

16. Вынужденные колебания

Дифференциальное уравнение является неоднородным
дифференциальным уравнением, решение
В2
В3
q(t ) q0 e t sin( t 0 ) B0 cos( t 0 )
B0
A0
( 02 2 ) 2 4 2 2
02 2
2
tg 0 2
02
амплитуда
фаза
вынужденных
колебаний
вынужденных
колебаний
В4

17. Вынужденные колебания

Решение В2 имеет смысл только если затухание β не
слишком мало (β ~ ω0) В этом случае первое слагаемое
в решении В2 достаточно быстро убывает и остается
только частное решение (второе слагаемое) -
установившийся режим
qу (t ) B0 cos( t 0 )
В2'

18. Вынужденные колебания

Дифференциальное уравнение и его решение дают
аналитическое описание движения,
B0
0 02 2 2
q0(t)
q0e-βt
t
Ω
Φ0
Ω0
Ω0
установившийся
режим
Резонанс
Ω
Резкое
возрастание
амплитуды
B0
вынужденных колебаний при приближении
частоты вынуждающей силы
резонансной частоте системы Ω0
Ω
к

19. Волна – возмущения, распространяющиеся в среде (вакууме) и несущие с собой энергию.

Гармоническая
волна
Цуг
волн
Одиночная волна (импульс)

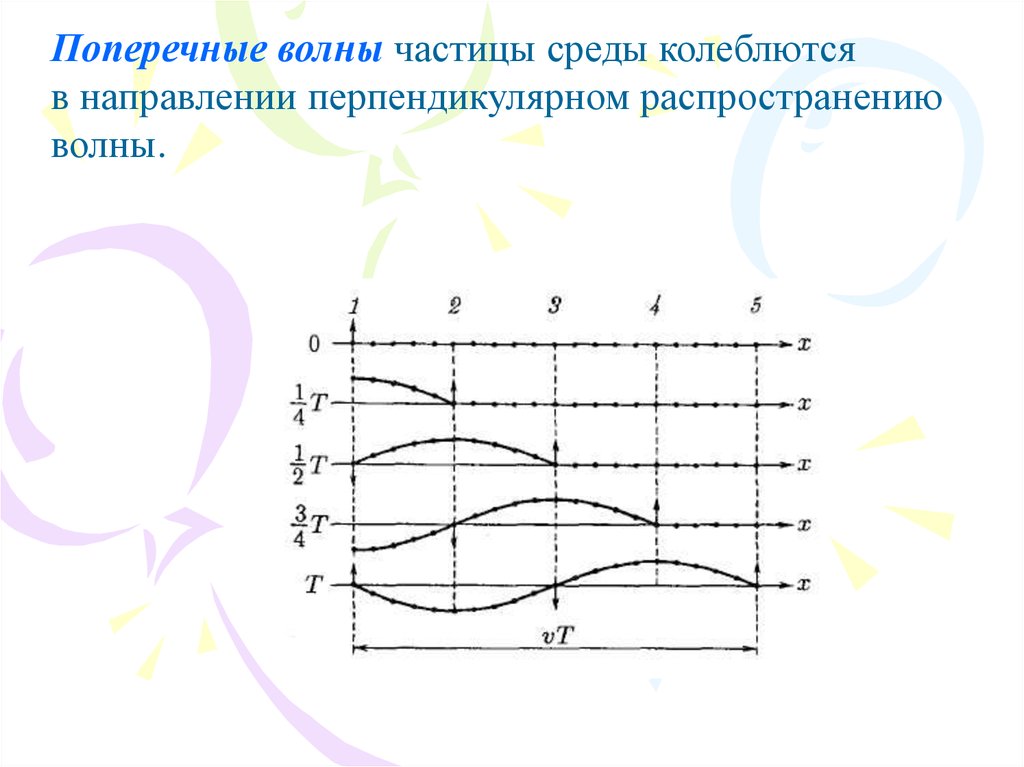
20.

Поперечные волны частицы среды колеблются
в направлении перпендикулярном распространению
волны.

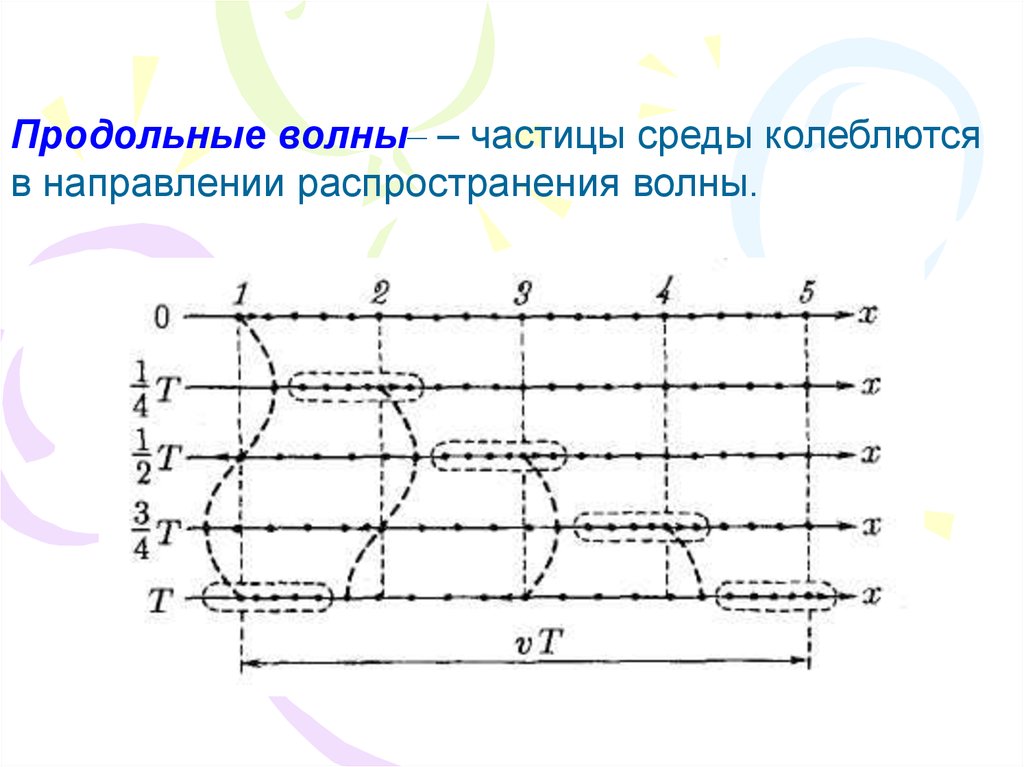
21.

Продольные волны– – частицы среды колеблются
в направлении распространения волны.

22.

Волновой фронт (фронт волны) – геометрическое
место точек, до которого дошли колебания.
Волновая поверхность – геометрическое место точек,
колеблющихся в одинаковой фазе.

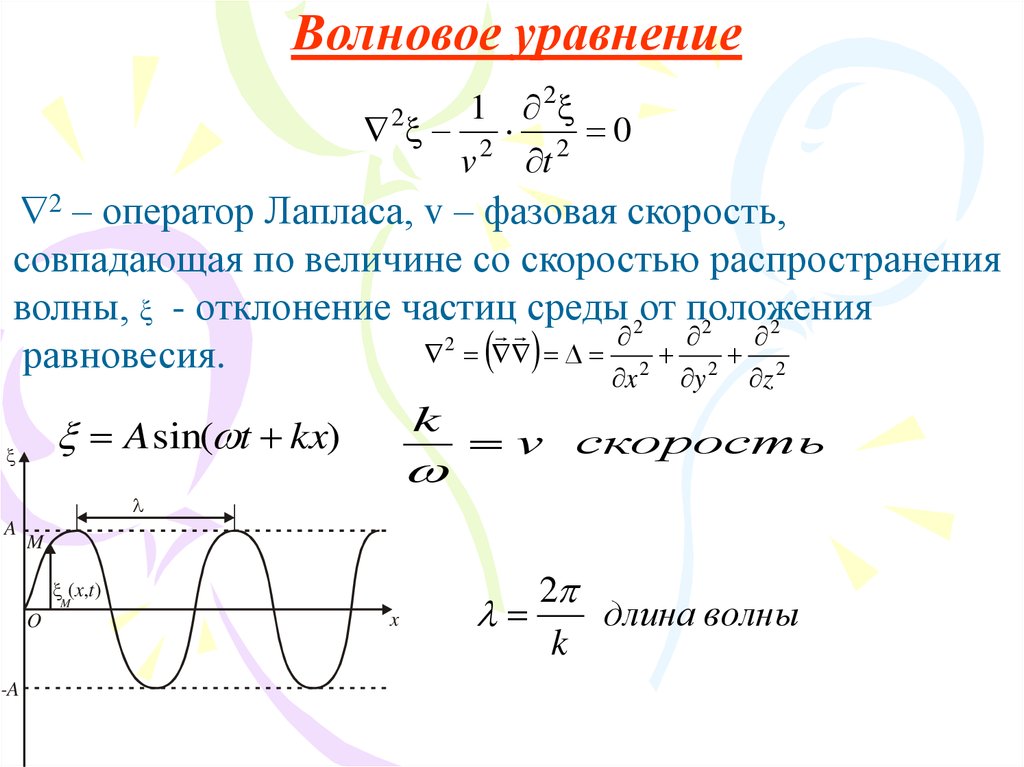
23.

Волновое уравнение
2
1
2
2 2 0
v t
2 – оператор Лапласа, v – фазовая скорость,
совпадающая по величине со скоростью распространения
волны, ξ - отклонение частиц
среды 2от положения
2
2
2
2 2 2
равновесия.
x
y
z
k
A sin( t kx)
v скорость
A
M
(x,t)
M
O
-A
x
2
длина волны
k

24.

Стоячие волны возникают при наложении
(интерференции) двух встречных плоских
когерентных волн с равными амплитудами:
1 A cos( t kx 1 ),
2 A cos( t kx 2 ). Амплитуда 2 A cos( 2 x )
x
(2 A cos( 2 )) cos t
X узл
X пучн n
2
(n 0 ,1, 2 ,...)
1
(n ) , (n 0,1, 2,...)
2 2
Стоячая волна в отличие от бегущей
не переносит энергии!

25.

Эффект Доплера
c vr
0
c vs
Если расстояние между источником и приемником
уменьшается, то воспринимаемая частота больше
испущенной.
Если расстояние между источником и приемником
увеличивается, то воспринимаемая частота меньше
испущенной.

26. Электромагнитные волны

уравнения Максвелла в отсутствии зарядов и токов имеют в
этом случае следующий вид
1
3
1 D
, H
c t
B 0
B
, E
t
D 0
2
4

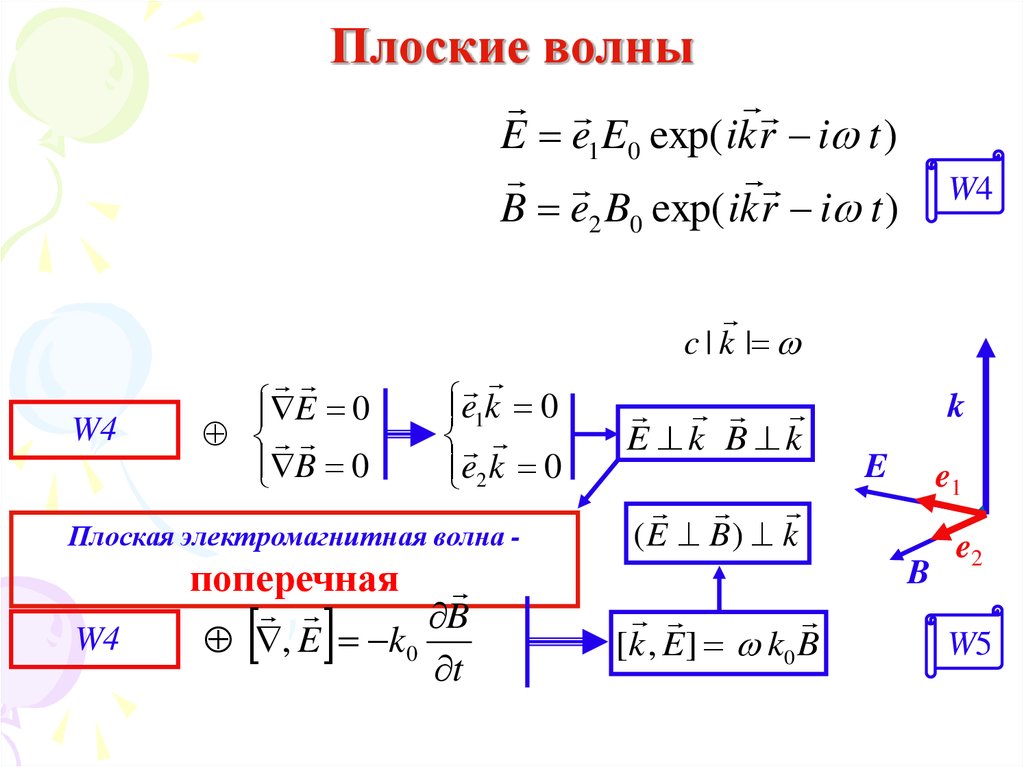
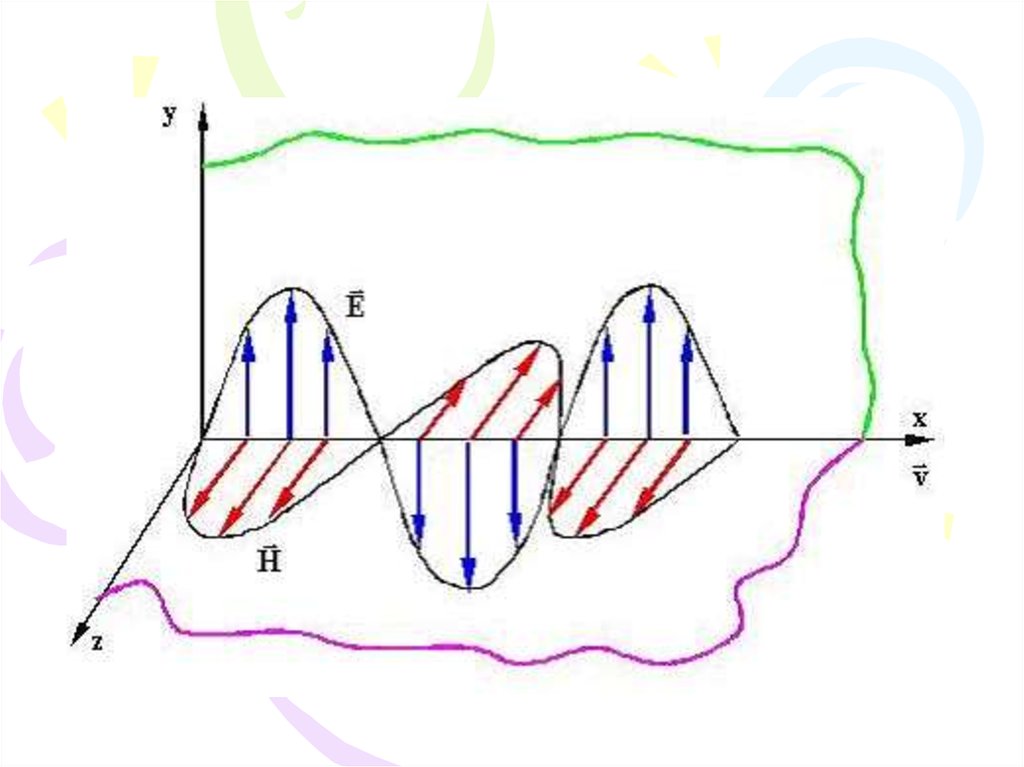
27. Плоские волны

E e1 E0 exp( ik r i t )
B e2 B0 exp( ik r i t )
W4
E 0
B 0
e1k 0
e2 k 0
Плоская электромагнитная волна -
поперечная
W4
B
, E k0
t
W4
c | k |
E k B k
k
E
e1
( E B) k
B
[k , E] k0 B
e2
W5

28.

29.

ВОЛНОВАЯ ОПТИКА
Свет – сложное явление: в одних случаях это поток
частиц (фотонов), в других – ЭМ (электромагнитная
волна) волна
Свойства света определяются вектором
- световым вектором.
E Em cos t kr
абсолютный показатель преломления
n
E
Так как обычно
c
n
v
1

30.

Видимый свет:
= 0.40-0.70 мкм
15
v 0.39 1.75 10 Гц
Частоты:
Модуль среднего по времени плотности потока энергии –
интенсивностью света:
I S EH
I n E2m A2

31. ВОЛНОВЫЕ СВОЙСТВА излучений

Интерференция
Совокупность явлений, возникающих в каждой
точке пространства при сложении (в заданной
точке) нескольких волн, называют
,
интерференцией
Пусть две волны накладываются . друг на друга в некоторой точке
пространства.
A1 cos t 1
A2 cos t 2
Если разность фаз между волнами остается
постоянной то волны называются когерентными

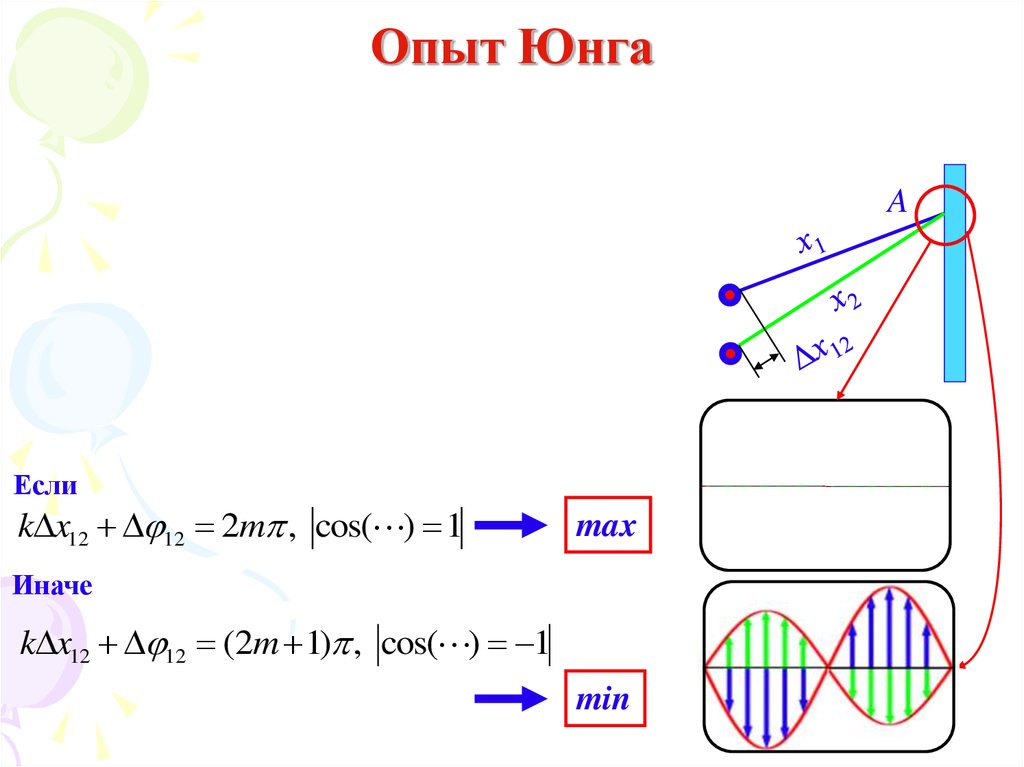
32. Опыт Юнга

A
Если
k x12 12 2m , cos( ) 1
max
Иначе
k x12 12 (2m 1) , cos( ) 1
min

33. Опыт Юнга

y
ym
d
12 n x12
оптической разность хода (волн 1 и 2)
(λ0 - длина волны излучения в вакууме)
L
max 12 m 0 12 0
2
И1
0 12
12 (2m 1)
0
min
2
2
Совокупность явлений, возникающих в
каждой точке пространства при сложении
(в заданной точке) нескольких волн,
называют интерференцией
В 1805 году Юнг провел опыт по интерференции волн от двух
когерентных источников
L
y
m 0
max
max
d
L d y L
0
L
В силу симметрии
m
12
min ymin d (2m 1) 2
d
Δ 12 = 0

34. Зоны Френеля

Принцип Гюйгенса - Френеля
1. Любой источник волн F можно
заменить системой вторичных
источников G, охватывающих исходный
2. Все вторичные источники когерентны
3. Амплитуда волны, излученной
ограниченным количеством вторичных
источников, в заданной точке
пространства A
G
F
L
A
пропорциональна площади S,
источниками
занимаемой вторичными
и обратно пропорциональна расстоянию L
от вторичных источников до заданной точки
S
E0
L
S

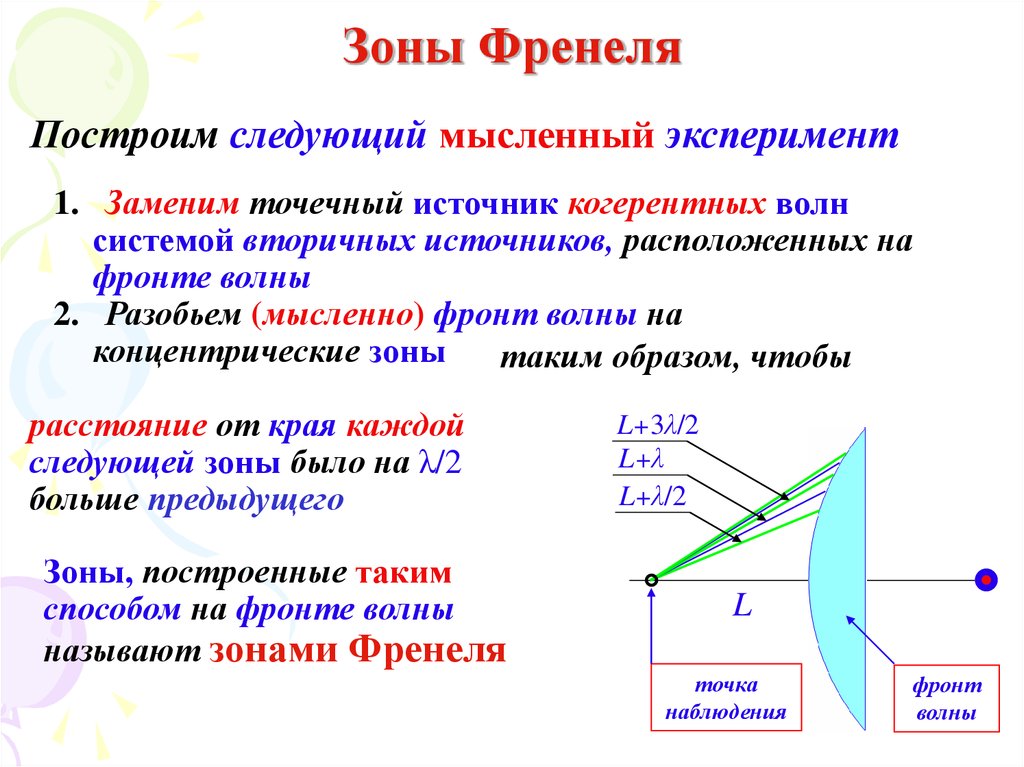
35. Зоны Френеля

Построим следующий мысленный эксперимент
1. Заменим точечный источник когерентных волн
системой вторичных источников, расположенных на
фронте волны
2. Разобьем (мысленно) фронт волны на
концентрические зоны
таким образом, чтобы
расстояние от края каждой
следующей зоны было на λ/2
больше предыдущего
Зоны, построенные таким
способом на фронте волны
называют зонами Френеля
L+3λ/2
L+λ
L+λ/2
L
точка
наблюдения
фронт
волны

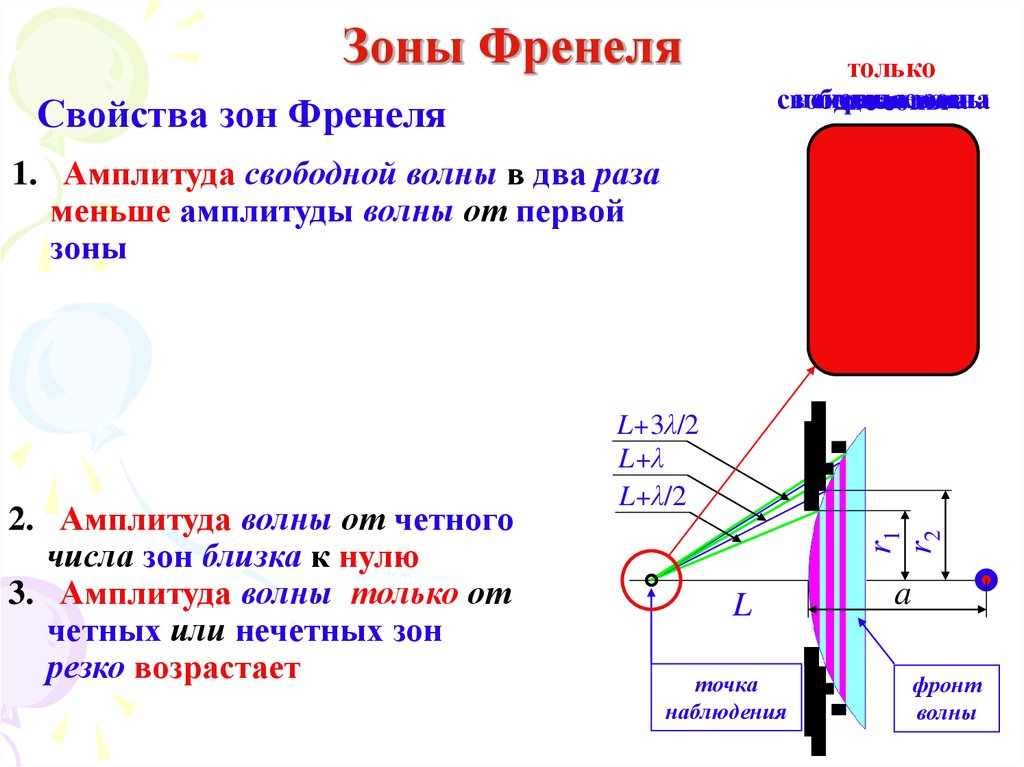
36. Зоны Френеля

только
нечетные
зоны
свободная
первая
зона
волна
две зоны
Свойства зон Френеля
1. Амплитуда свободной волны в два раза
меньше амплитуды волны от первой
зоны
r1
r2
2. Амплитуда волны от четного
числа зон близка к нулю
3. Амплитуда волны только от
четных или нечетных зон
резко возрастает
L+3λ/2
L+λ
L+λ/2
L
точка
наблюдения
a
фронт
волны

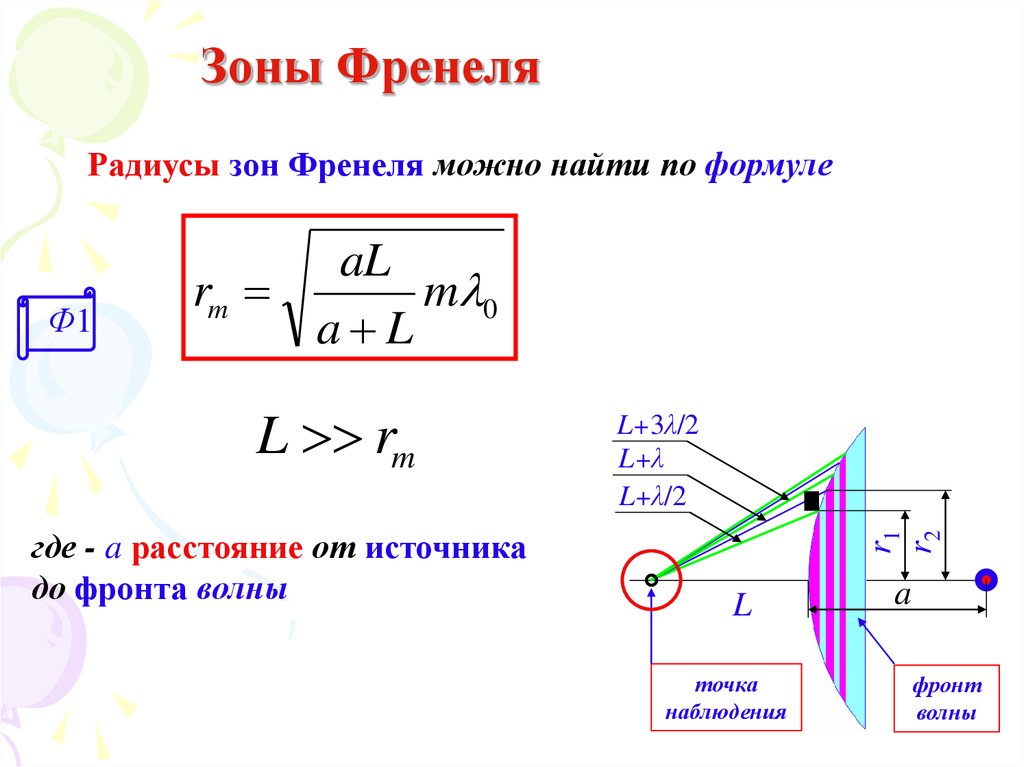
37. Зоны Френеля

Радиусы зон Френеля можно найти по формуле
L rm
где - a расстояние от источника
до фронта волны
L+3λ/2
L+λ
L+λ/2
r1
r2
Ф1
aL
rm
m 0
a L
L
точка
наблюдения
a
фронт
волны

38. Дифракция Френеля

Дифракцией Френеля называют дифракцию сферической
волны (от точечного источника)
Дифракция на круглом отверстии
Рассмотрим дифракцию когерентной
сферической волны от точечного источника на
круглом отверстии, диаметр которого
значительно (~100 раз) превосходит длину волны
λ

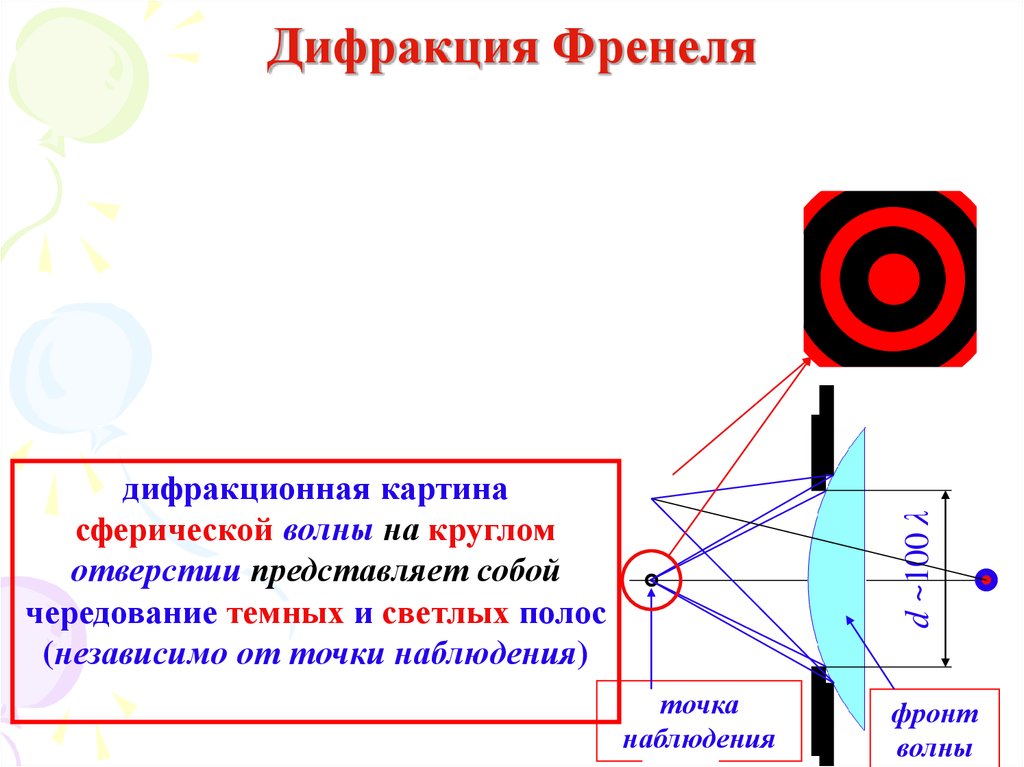
39. Дифракция Френеля

d ~100 λ
дифракционная картина
сферической волны на круглом
отверстии представляет собой
чередование темных и светлых полос
(независимо от точки наблюдения)
точка
наблюдения
фронт
волны

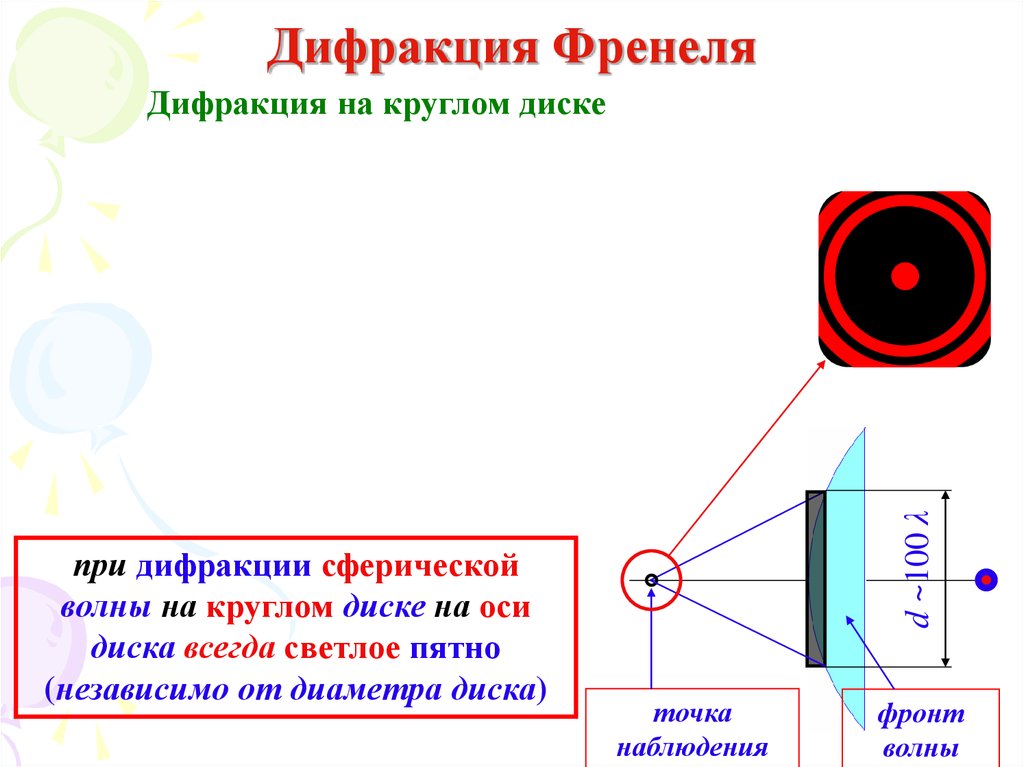
40. Дифракция Френеля

при дифракции сферической
волны на круглом диске на оси
диска всегда светлое пятно
(независимо от диаметра диска)
d ~100 λ
Дифракция на круглом диске
точка
наблюдения
фронт
волны

41. Дифракция Фраунгофера

Дифракцией Фраунгофера называют дифракцию волны с
плоским фронтом
Дифракция на щели
Рассмотрим дифракцию когерентной волны
с плоским фронтом на щели, ширина b
которой незначительно превосходит длину
волны λ (b > mλ, где - m > 0 целое число)

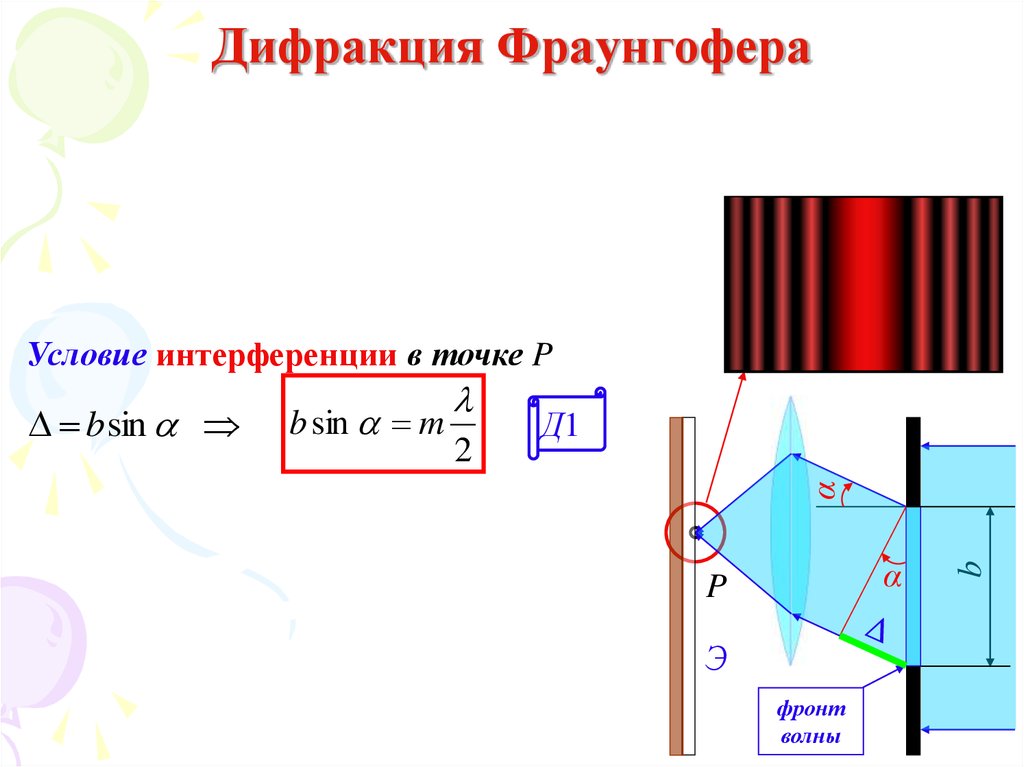
42. Дифракция Фраунгофера

Условие интерференции в точке P
2
Д1
α
P
Э
фронт
волны
b
b sin m
α
b sin

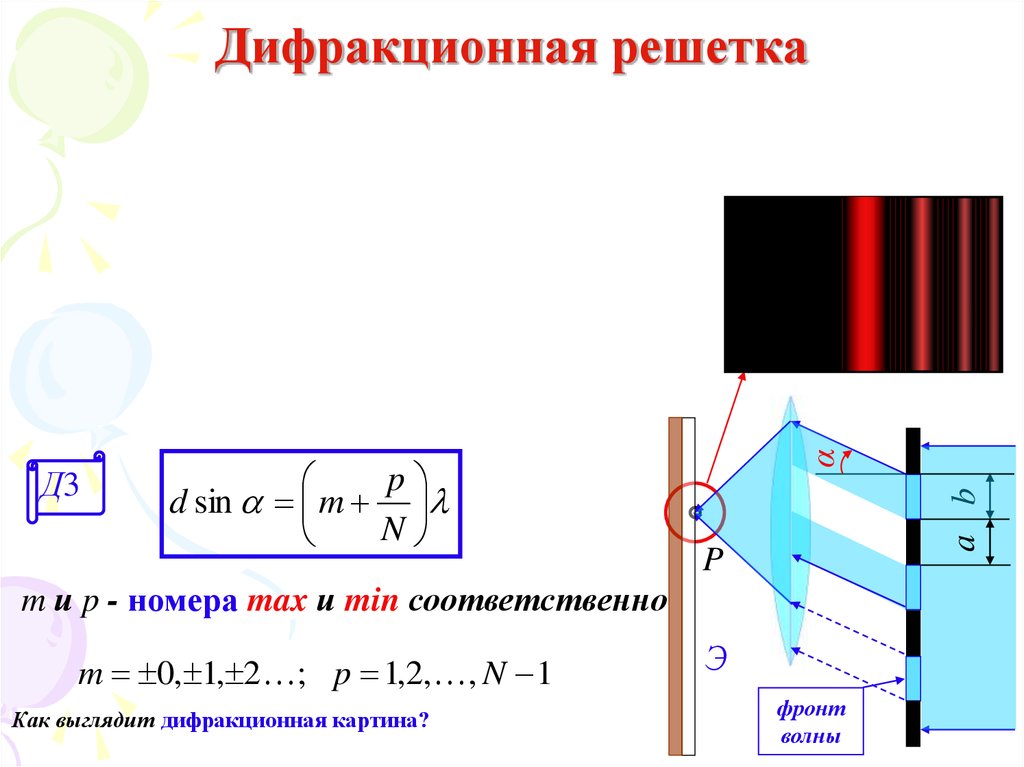
43. Дифракционная решетка

Дифракционной решеткой называют плоскую непрозрачную
пластинку с большим (= N) количеством параллельных щелей
шириной b, расположенных на одинаковом расстоянии a
Дифракция на отдельной щели решетки с последующей
интерференцией волн от различных щелей

44. Дифракционная решетка

p
d sin m
N
a b
Д3
α
Дифракционная решетка
P
m и p - номера max и min соответственно
m 0, 1, 2 ; p 1,2, , N 1
Как выглядит дифракционная картина?
Э
фронт
волны

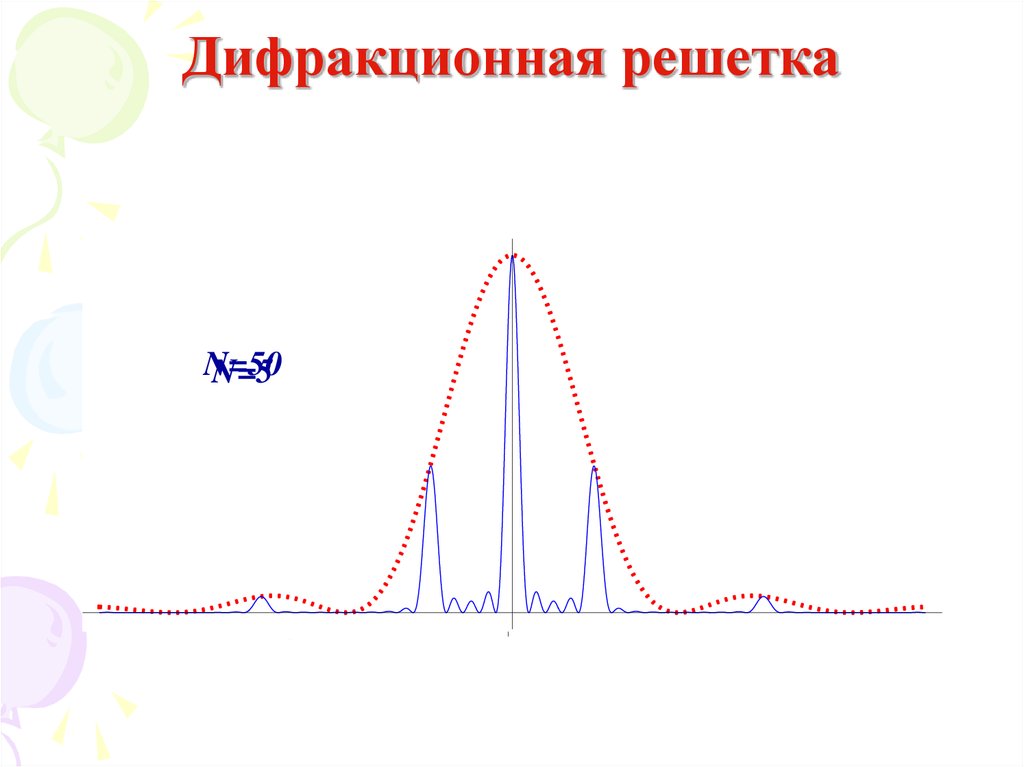
45. Дифракционная решетка

N=50
N=5

46.

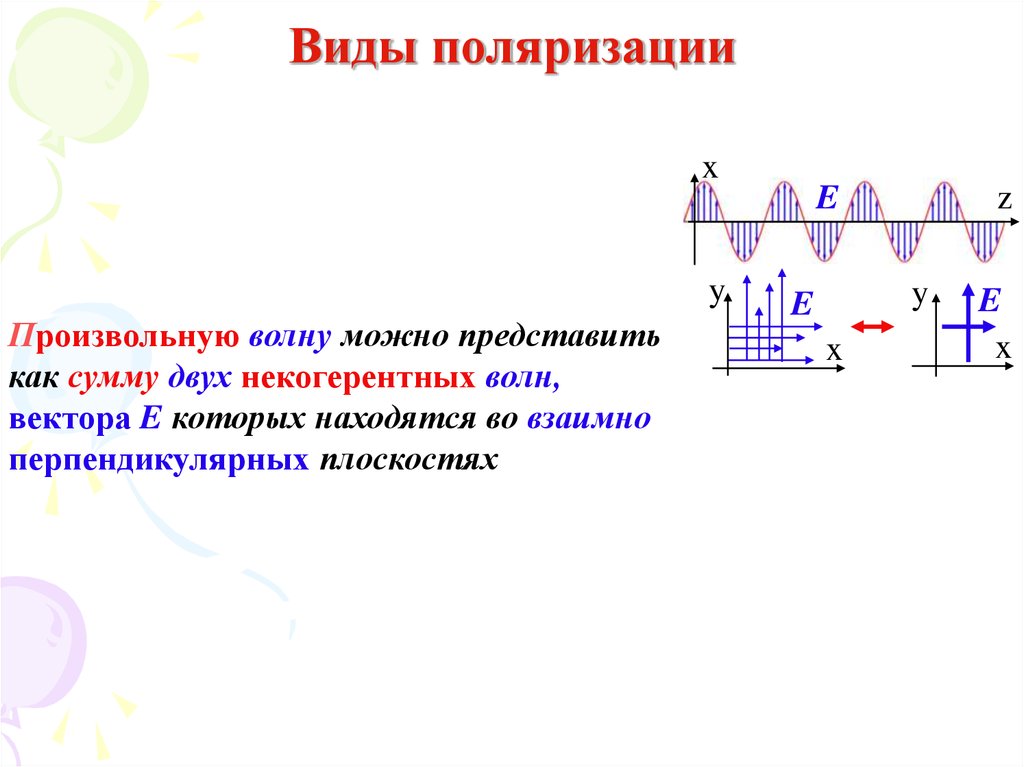
Поляризация волн

47. Виды поляризации

x
E
y
Произвольную волну можно представить
как сумму двух некогерентных волн,
вектора E которых находятся во взаимно
перпендикулярных плоскостях
z
y
E
x
E
x

48. Виды поляризации

Волну, у которой в одной из плоскостей
результирующий вектор E больше,
называют частичнополяризованной
При этом, степень поляризации такой
волны определяют величиной
2
2
Emax
Emin
P 2
2
Emax Emin
P1

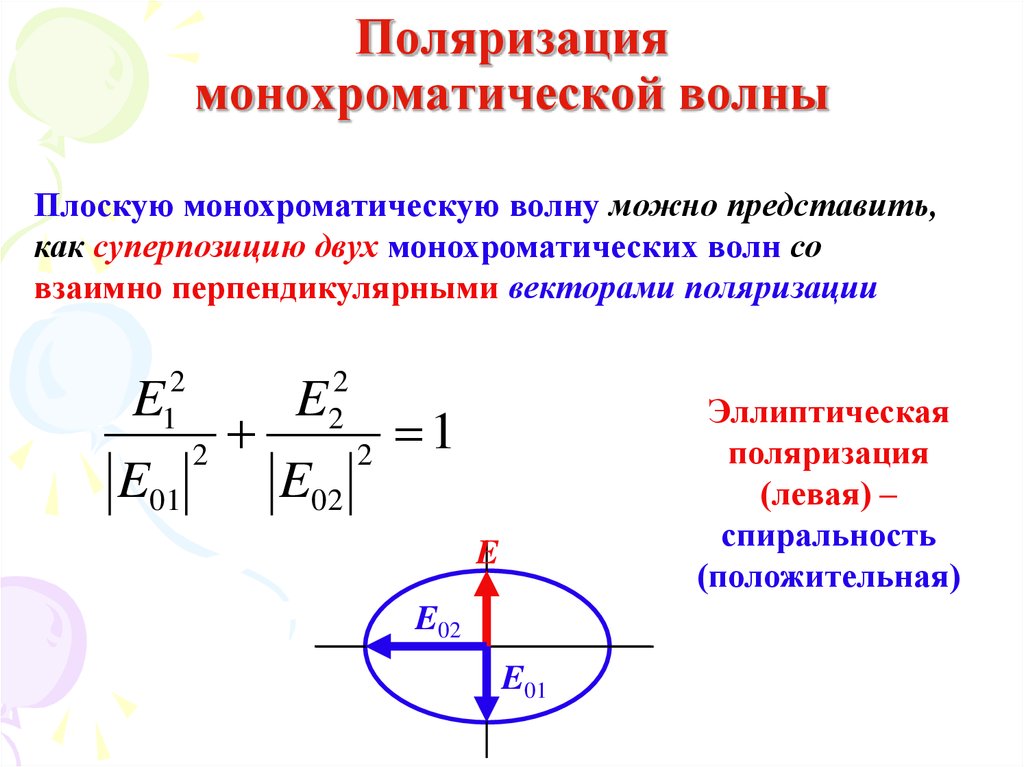
49. Поляризация монохроматической волны

Плоскую монохроматическую волну можно представить,
как суперпозицию двух монохроматических волн со
взаимно перпендикулярными векторами поляризации
2
1
E
E01
2
E
2
2
E02
2
Эллиптическая
поляризация
(левая) –
спиральность
(положительная)
1
E
E02
E01

50. Закон Брюстера

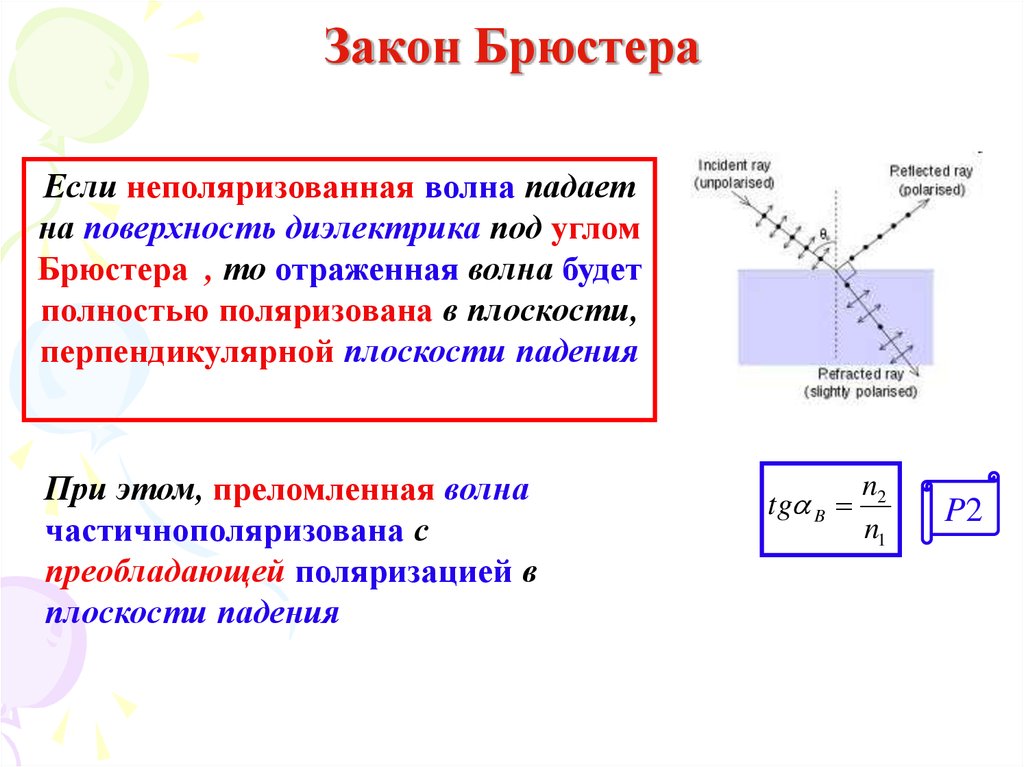
Если неполяризованная волна падает
на поверхность диэлектрика под углом
Брюстера , то отраженная волна будет
полностью поляризована в плоскости,
перпендикулярной плоскости падения
При этом, преломленная волна
частичнополяризована с
преобладающей поляризацией в
плоскости падения
n2
tg B
n1
P2

51. Закон Малю

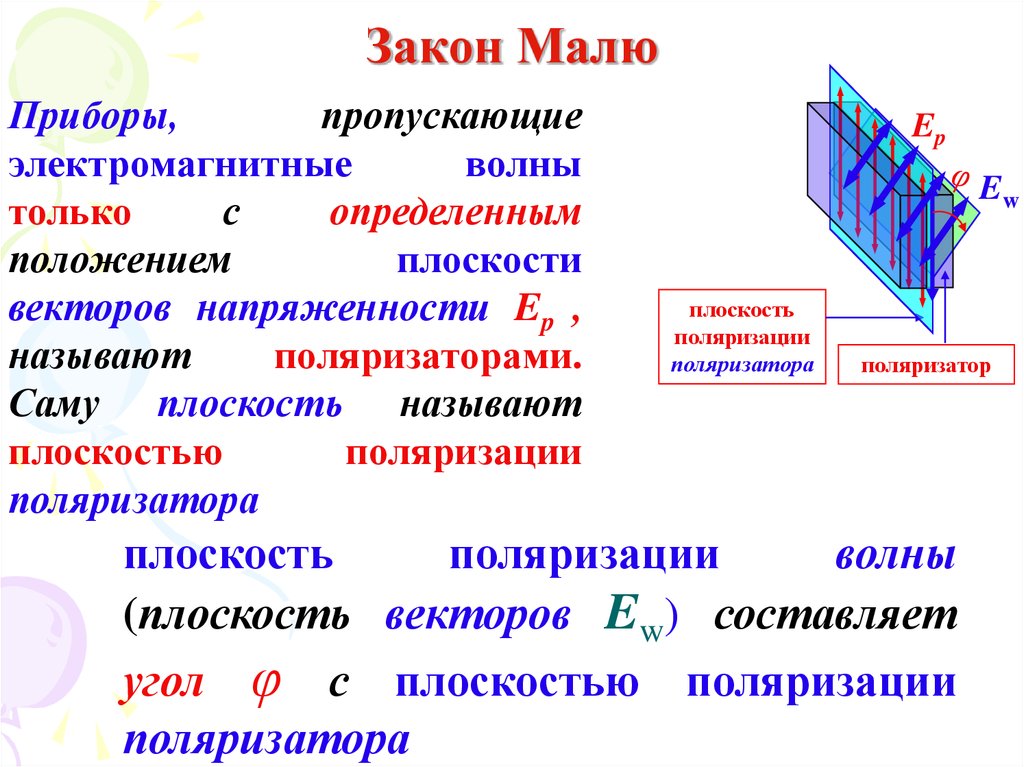
Приборы,
пропускающие
электромагнитные
волны
только
с
определенным
положением
плоскости
векторов напряженности Ep ,
называют
поляризаторами.
Саму плоскость называют
плоскостью
поляризации
поляризатора
Ep
Ew
плоскость
поляризации
поляризатора
поляризатор
плоскость
поляризации
волны
(плоскость векторов Ew) составляет
угол φ с плоскостью поляризации
поляризатора

52. Закон Малю

Через поляризатор пройдет только часть
падающей электромагнитной волны с
векторами напряженности электрического
поля Eout , являющимися проекцией векторов
Ew на плоскость поляризации поляризатора
Eout Ew cos I I 0 cos 2
I~E
2
P3

53. Закон Малю

Если неполяризованная электромагнитная
волна последовательно проходит через два
поляризатора, плоскости поляризации которых
расположены под углом φ
Здесь I - интенсивность
волны
P4
1
2
I I 0 cos
2

54. Характеристики равновесного излучения

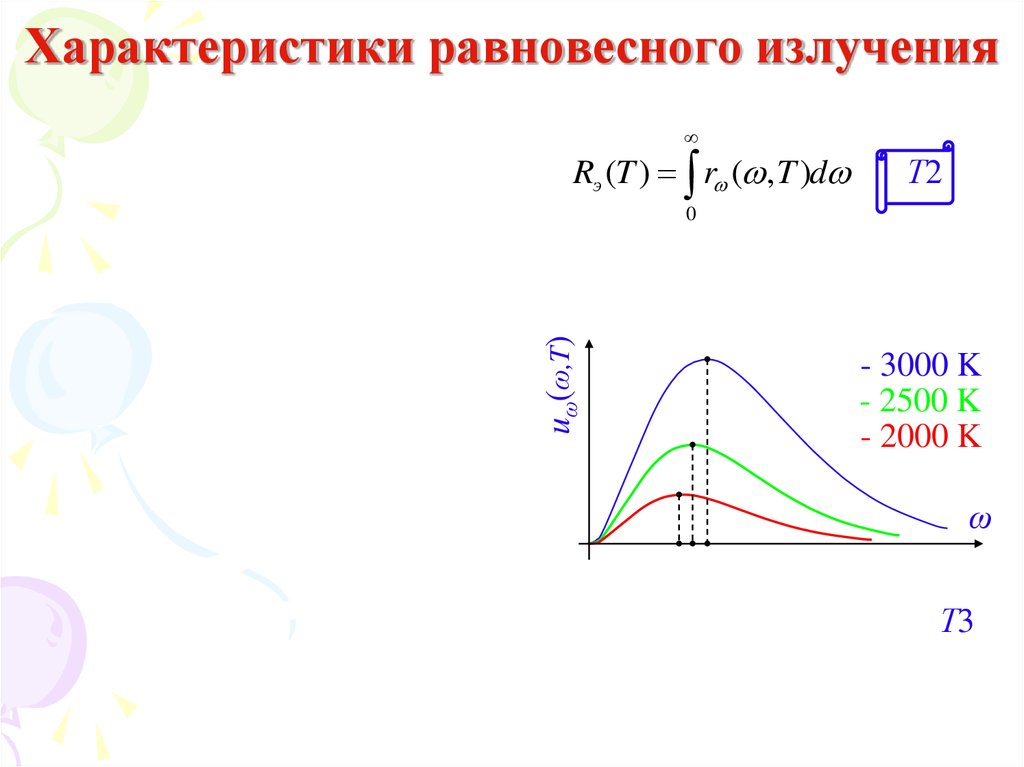
Rэ (T ) r ( , T )d
Т2
uω(ω,T)
0
- 3000 K
- 2500 K
- 2000 K
ω
Т3

55. Закон Кирхгофа

r d
f ( , T )
a d
Т4
dФ
абсолютно черное
тело - BB
a 1
dRэ
T
r f ( , T )
Отношение излучательной способности тела к
его поглощательной способности не зависит от
свойств тела и равно излучательной
способности абсолютно черного тела
V
dФотр

56. Теорема и закон смещения Вина

Теорема Вина
равновесное излучение абсолютно черного тела
(BB), заключенное в оболочку с идеально
отражающими стенками остается равновесным
при квазистатическом сжатии или растяжении
оболочки
u ( , T ) T
T
3
Т4

57. Теорема и закон смещения Вина

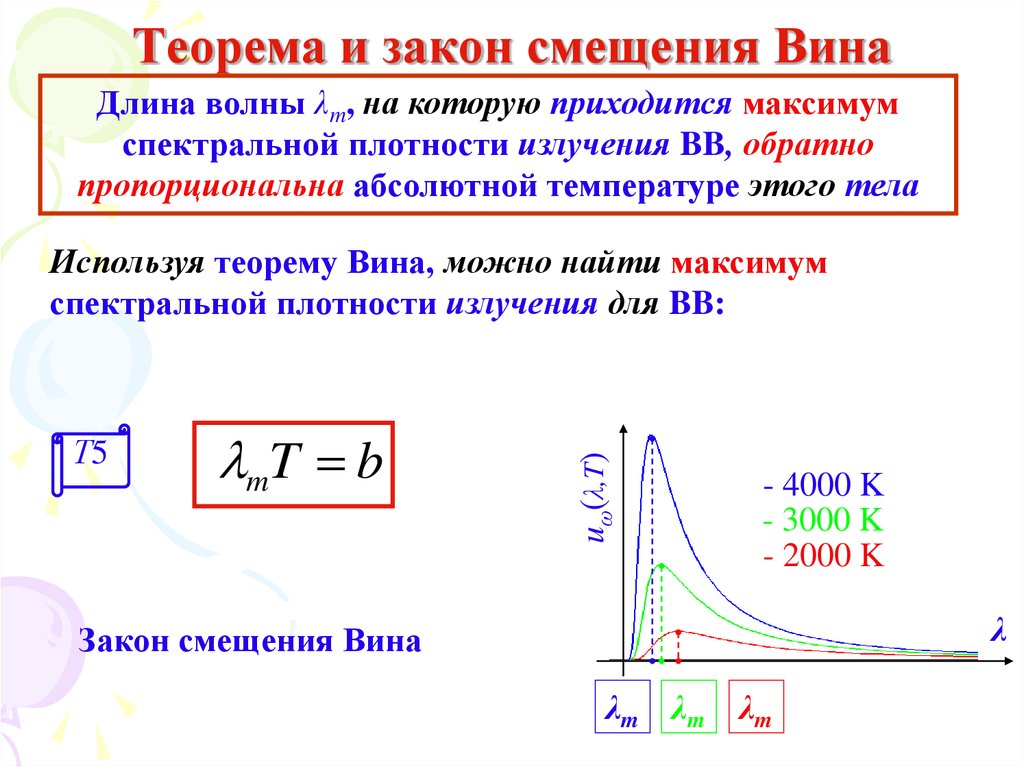
Длина волны λm, на которую приходится максимум
спектральной плотности излучения BB, обратно
пропорциональна абсолютной температуре этого тела
Т5
mT b
uω(λ,T)
Используя теорему Вина, можно найти максимум
спектральной плотности излучения для BB:
- 4000 K
- 3000 K
- 2000 K
λ
Закон смещения Вина
λm λm
λm

58. Закон Стефана-Больцмана Закон Стефана-Больцмана

4
Закон Стефана-Больцмана Rэ (T ) T
Т6
постоянная Стефана-Больцмана 5,67032 10 8 Вт м 2 К 4
Энергетическая светимость Rэ абсолютно
черного тела (BB) пропорциональна
четверной степени абсолютной температуры
этого тела

59. формула Рэлея-Джинса

формула Рэлея-Джинса
Т7
2
u ( , T ) 2 3 kT
c

60. Формула Планка

f , T
, T
3
1
4 2 c 3 e / kT 1
4 2 c 3
1
5
e 2 c / kT 1

61. Фотоэффект

Законы фотоэффекта:
Максимальная энергия электронов не зависит от
интенсивности света, а висит от частоты.
От интенсивности света зависит число вылетевших
электронов.

62. Фотоэффект

me v
Aвых
2
2
Здесь ħω - энергия фотона, Aвых - работа выхода электрона из
металла, me - масса электрона (соответственно mev2/2 кинетическая энергия электрона)

63.

Корпускулярно – волновой дуализм:
свет в некоторых случаях ведёт себя как волна,
в других как частица.
Для квантов электромагнитного излучения, как и для обычных
частиц можно ввести динамические характеристики
энергия
масса
импульс
mфc
m
2
ф
c
2
pф mф
c
c
2
c
c

64. Эффект Комптона

Эффектом Комптона называют
рассеяние фотонов электромагнитного
излучения на свободных электронах
p'ф
φ
pθ
= '- = C(1-cosφ).

65. Корпускулярно-волновой дуализм

Мы убедились, что электромагнитное излучение проявляет как
волновые свойства (интерференция, дифракция), так и
корпускулярные (фотоэффект, эффект Комптона)
Такая двойственность свойств электромагнитного излучения
названа корпускулярно-волновым дуализмом
В 1924 Л. де Бройль высказал гипотезу о том, что
корпускулярно-волновой дуализм присущ всем без исключения
объектам

66. Корпускулярно-волновой дуализм

Постулат Л. Де Бройля
Любую микрочастицу можно
моделировать волновым
процессом с длиной волны λБ
h
Б
p
Q1
где h - постоянная Планка, p - относительный импульс
микрочастицы (т.е. импульс, измеренный относительно другого
объекта с которым взаимодействует микрочастица)

67. Корпускулярно-волновой дуализм

Принцип неопределенности: произведение
неопределённостей значений двух сопряжённых
переменных не могут быть по порядку величины
больше постоянной Планка
E t / 2
Это соотношение означает, что определение энергии с
точностью ΔЕ должно занять интервал времени
t ~ / E

68. Рассеяние  частиц. Опыт Резерфорда

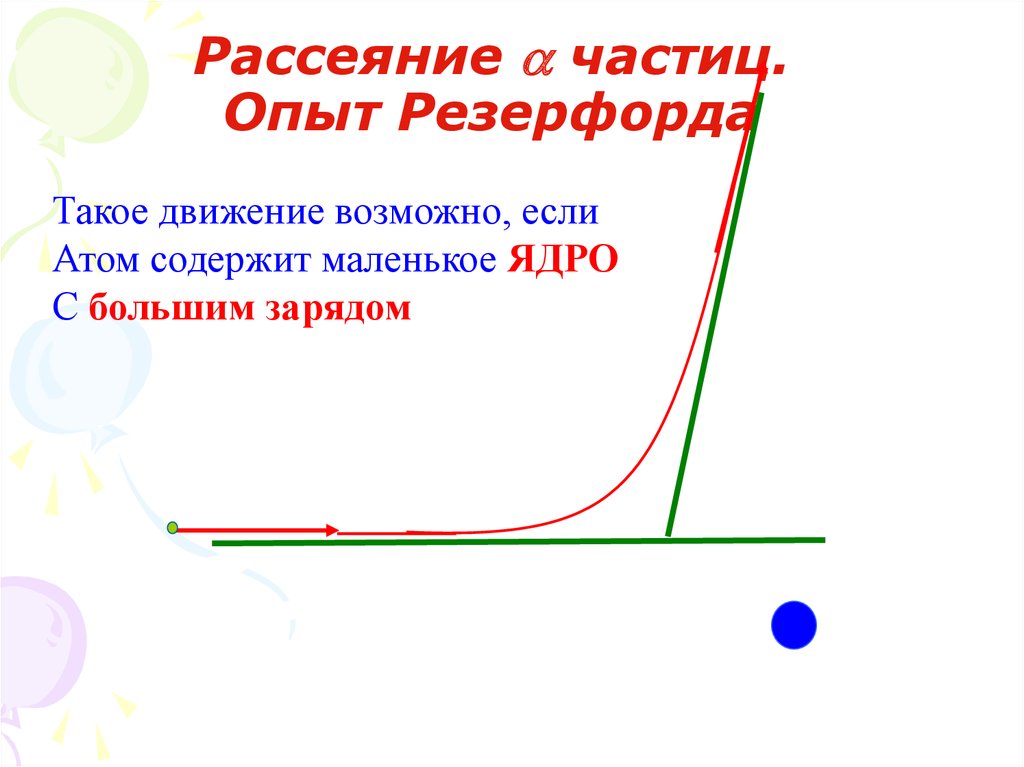
Рассеяние частиц.
Опыт Резерфорда
Такое движение возможно, если
Атом содержит маленькое ЯДРО
С большим зарядом

69. Модель атома Резерфорда

• Внутри атома – малое положительно заряженное
ядро, вокруг которого вращаются электроны –
планетарная модель атома.
• Недостатки – вращаясь вокруг ядра электрон
движется с ускорением и в конце концов должен
излучать и упасть на ядро.

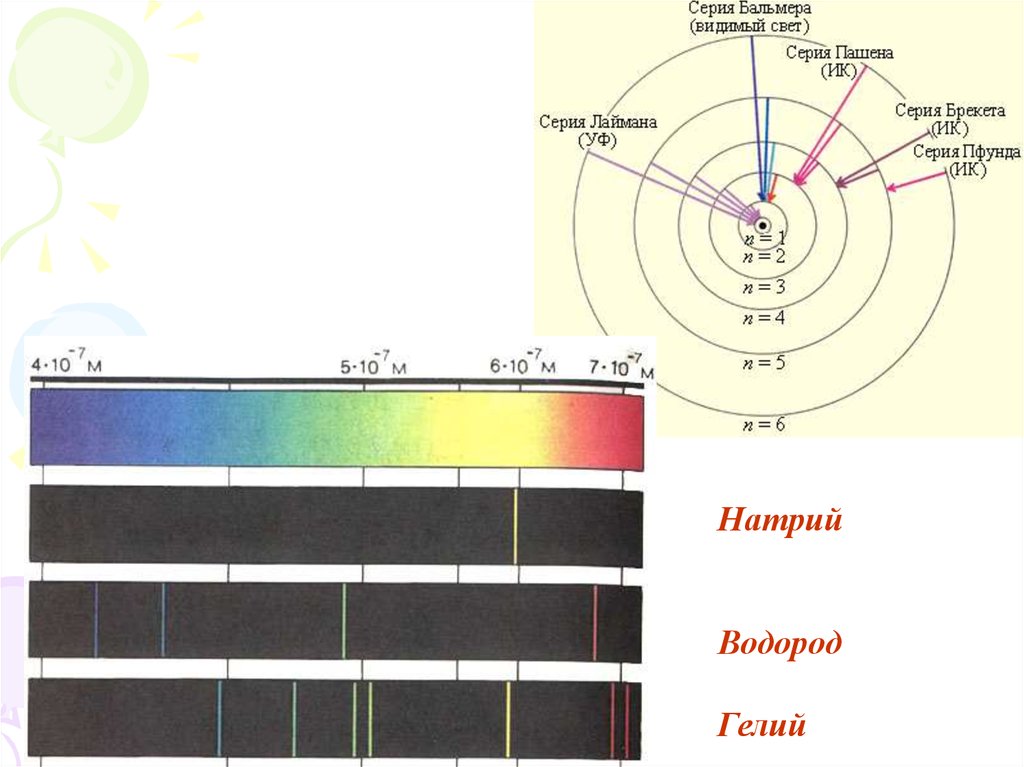
70. Спектр атома водорода

Для спектра атома водорода
в 1885 году Бальмером была
получена
(эмпирически)
формула,
где m и n - целые числа
(m>n), R - постоянная
Ридберга
Группы линий с
одинаковым n называют
серией
1
1
R 2 2
m
n
R 3,2921193 1015 c 1
n=1 → серия Лаймана
n=2 → серия Бальмера
n=3 → серия Пашена
А1

71.

Натрий
Водород
Гелий

72. Теория Бора

Планетарная модель атома имеет недостатки - электрон (за
счет электромагнитного излучения при движении по круговой
орбите) падает на атом

73. Теория Бора

Для спасения - постулаты Бора (1913)
• Электроны в атоме существуют
стационарных состояниях
только
в
• Момент импульса электрона в стационарном
состоянии равен
mvnrn = nћ, где n - номер стационарного состояния
• При переходе из одного стационарного состояния с
энергией En в другое - Em , электрон излучает (либо
поглощает) энергию ћω = En - Em в виде фотонов

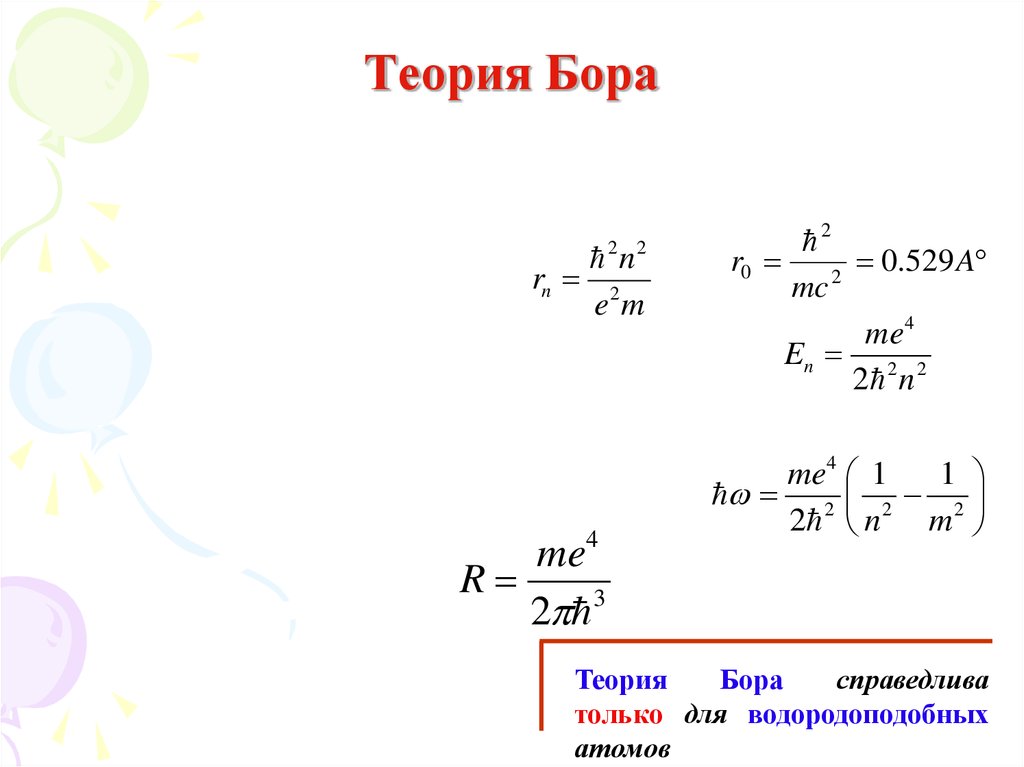
74. Теория Бора

rn
2
2
n
e2m
me4
R
2 3
2
r0
0.529 A
2
mc
me4
En 2 2
2 n
me4 1
1
2 2 2
2 n m
Теория
Бора
справедлива
только для водородоподобных
атомов

75. Уравнение Шредингера

В 1926 Э. Шредингер
предложил уравнение,
описывающее поведение
микрочастицы (массой
m) во внешнем силовом
поле
2
ˆ
2
ˆ
i
H , H
U (r )
t
2m
Q2
здесь ћ = h/2π - постоянная Дирака, 2 - квадрат оператора
«набла» (лапласиан), U(r) - потенциальная функция внешнего
поля, Ĥ - оператор Гамильтона, Ψ- «пси» функция - функция,
полностью определяющая состояние микрочастицы

76. Уравнение Шредингера

2 2m
E U (r ) (r )
(r )
Q3
стационарное уравнение Шредингера
где E = ћω - полная механическая энергия микрочастицы в
стационарном состоянии

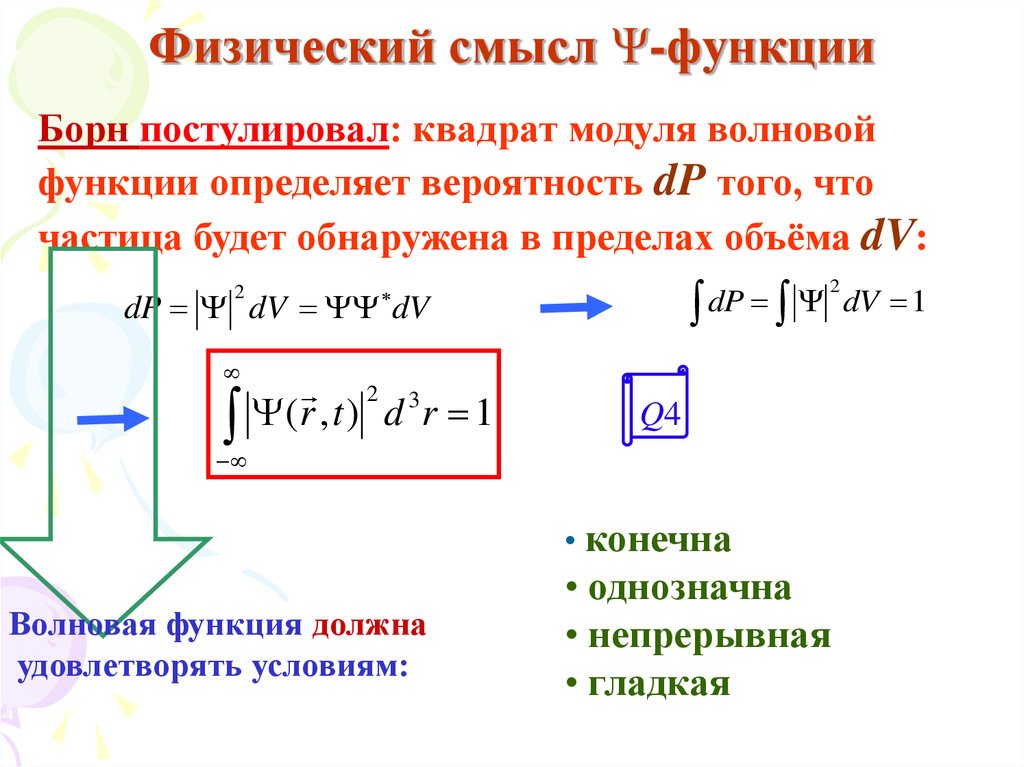
77. Физический смысл Ψ-функции

Борн постулировал: квадрат модуля волновой
функции определяет вероятность dP того, что
частица будет обнаружена в пределах объёма dV:
2
dP dV 1
2
dP dV dV
2 3
(r , t ) d r 1
Q4
• конечна
Волновая функция должна
удовлетворять условиям:
• однозначна
• непрерывная
• гладкая

78. Основной постулат

Оператор - это правило, по которому одной функции
сопоставляется другая функция
функция 1
оператор
функция 2
В квантовой механике принято оператор
физической величины обозначать той же
буквой, но со «шляпкой»
S
Sˆ
Любой физической величине можно поставить в
соответствие линейный самосопряженный оператор так,
что спектр собственных значений оператора совпадет со
спектром допустимых значений физической величины

79. Правила сопоставления операторов

Правила сопоставления Неймана
Нейман доказал, что сопоставление взаимнооднозначно
Физическая
величина S
1.
2.
3.
4.
Линейный
самосопряженный
S1 Sˆ1
ˆ ˆ
S1 S 2 S1 S 2
S 2 Sˆ2
S Sˆ S Sˆ
S Sˆ f ( S ) f ( Sˆ )
1 1ˆ
оператор Ŝ
O2
O1

80. Правила сопоставления операторов

Принцип соответствия
(Неймана)
1.
2.
3.
Операторы, сопоставляемые
физическим величинам,
подчиняются тем же
соотношениям, что и сами
физические величины
H T U (r ) Hˆ Tˆ Uˆ (rˆ )
T mv 2 / 2 p 2 /( 2m) Tˆ mvˆ 2 / 2 pˆ 2 /( 2m)
ˆ
ˆ ˆ
M [r , p] M [r , p]

81. Правила сопоставления операторов

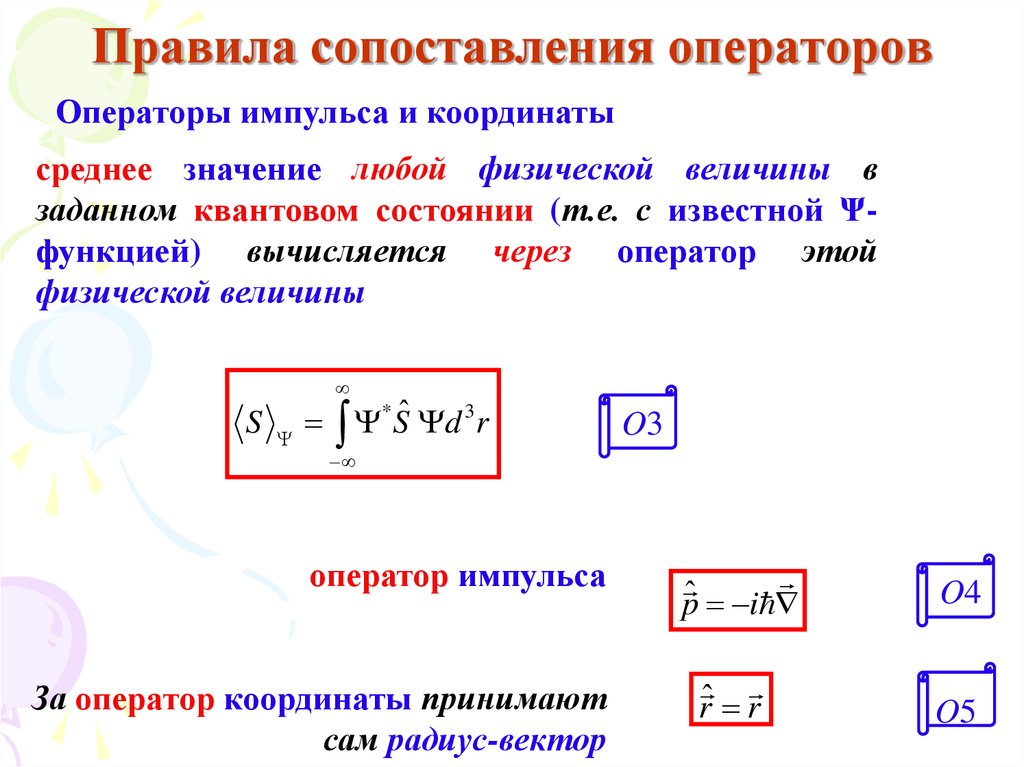
Операторы импульса и координаты
среднее значение любой физической величины в
заданном квантовом состоянии (т.е. с известной Ψфункцией) вычисляется через оператор этой
физической величины
S
*Sˆ d 3r
O3
оператор импульса
За оператор координаты принимают
сам радиус-вектор
ˆ
p i
O4
rˆ r
O5

82. Правила сопоставления операторов

Практический рецепт (сопоставления операторов)
Если физическая величина имеет классический аналог,
то для сопоставления ей оператора нужно
представить эту физическую величину как функцию
координаты и импульса
O6
S f кл (r , p)
ˆ ˆ
ˆ
S f кл (r , p)
2
2
p2
ˆ
p
Tˆ
1. T
2m
2m
2m
ˆ ˆ
ˆ
2. M [ r , p ] M [r , p ] i [r , ]

83. Проблема измерения

Если физической величины, например S, измеримы сколь угодно
точно
тогда
Sˆ s
т.е. Ψ-функция является собственной функцией оператора Ŝ
если можно создать такие условия - «приготовить»
состояние - при которых Ψ-функция этого состояния
будет собственной функцией оператора Ŝ, то
собственные значения s физической величины S
измеримы сколь угодно точно

84. Проблема измерения

Пусть S1 и S2 , измеримы сколь угодно точно
Если операторы Ŝ1 и Ŝ2 физических величин S1 и S2
удовлетворяют условию коммутации, то собственные
значения s1 и s2 измеримы сколь угодно точно

85. Принцип суперпозиции

Пусть квантовая система может находится в состояниях:
Ψ1 и Ψ2 ,тогда квантовая система может находиться и в
состоянии:
c1 1 c2 2
Если в состоянии Ψ1 физическая
величина, описываемая оператором Ŝ
равна s1
А в состоянии Ψ2 физическая величина,
описываемая оператором Ŝ равна s2
S 1 s1 1
S 2 s2 2
Тогда в состоянии Ψ физическая величина Ŝ будет
принимать значения: s1 либо s2 с вероятностью равной
|c1|2 для s1 и |c2|2 для s2

86. Принцип суперпозиции

Общий случай: рассмотрим совокупность
собственных функций Ψi и собственных
значений
si
физической величины,
описываемой оператором Ŝ
:
Тогда любая волновая функция
может быть разложена по
собственным волновым функциям
оператора Ŝ
:
s1 , s2 , ... si , ...
1 , 2 , ... i , ...
ci i
i
Тогда в состоянии Ψ физическая величина Ŝ будет
принимать значения: si с вероятностью равной |ci|2

87. Принцип суперпозиции

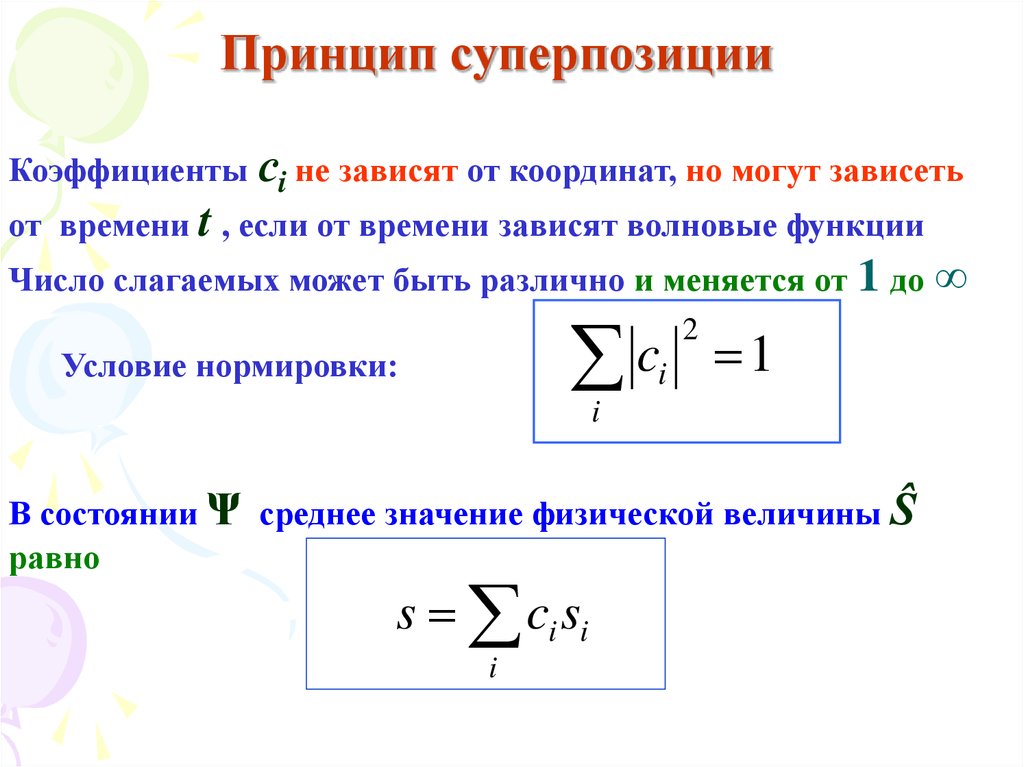
Коэффициенты сi не зависят от координат, но могут зависеть
от времени t , если от времени зависят волновые функции
Число слагаемых может быть различно и меняется от 1 до ∞
c
Условие нормировки:
i
2
1
i
В состоянии Ψ среднее значение физической величины Ŝ
равно
s ci si
i

88. Простейшие задачи

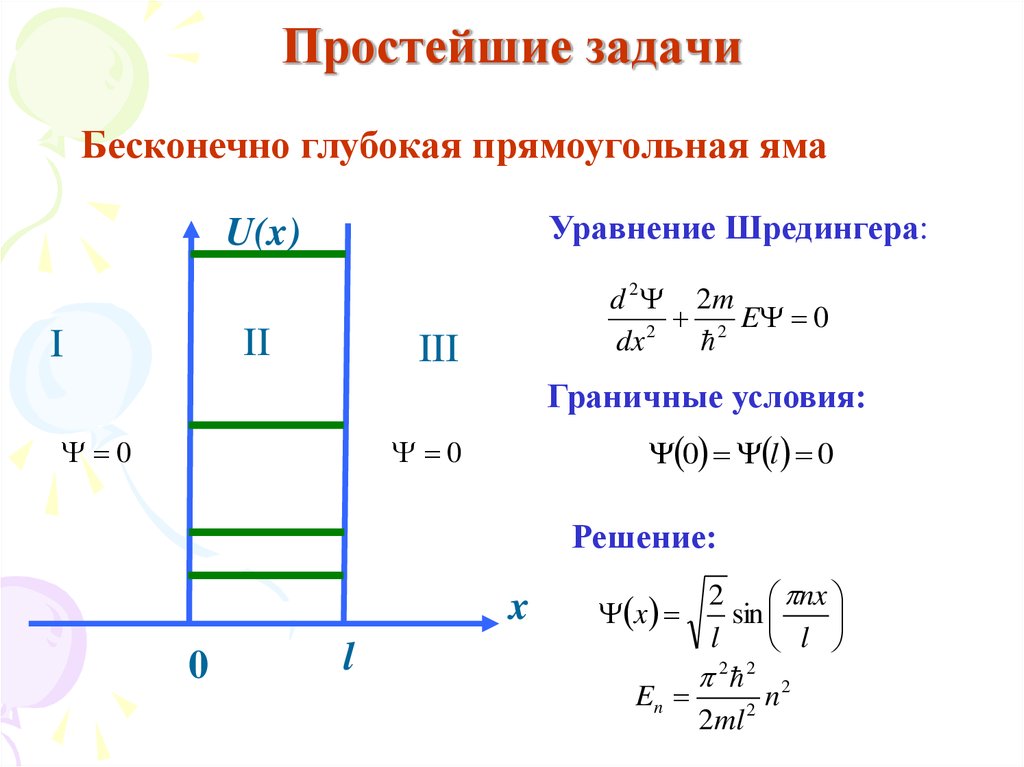
Бесконечно глубокая прямоугольная яма
Уравнение Шредингера:
U(x)
II
I
d 2 2m
2 E 0
2
dx
III
Граничные условия:
0
0 l 0
0
Решение:
x
0
l
2 nx
sin
l
l
2 2 2
En
n
2
2ml
x

89. Простейшие задачи

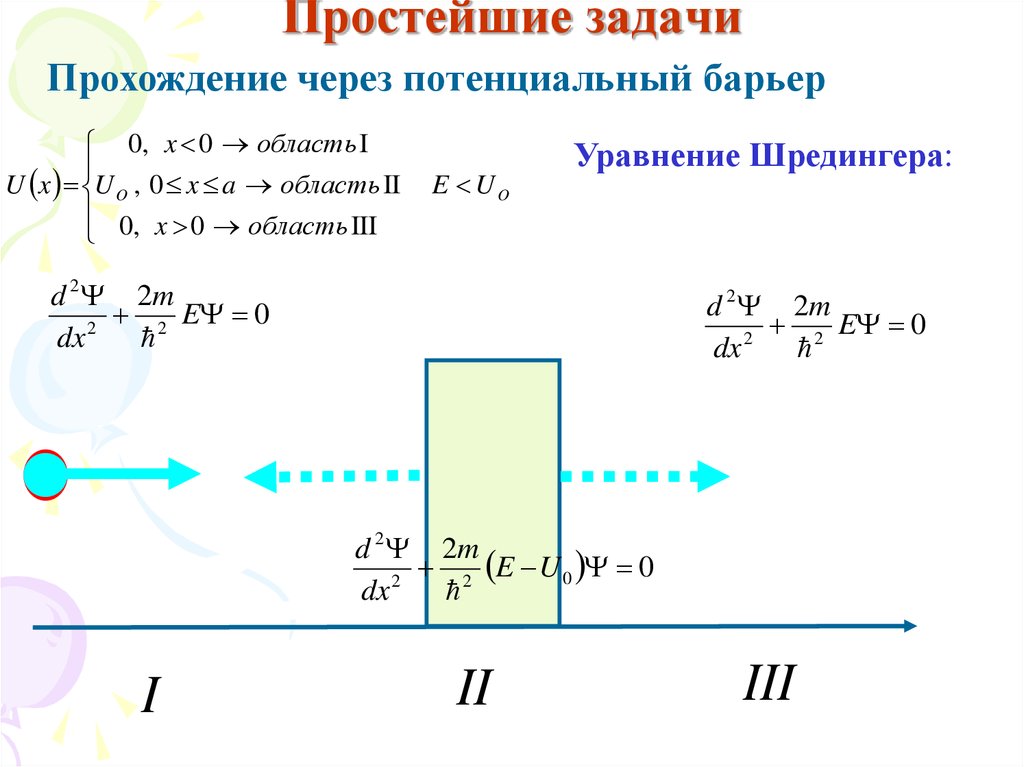
Прохождение через потенциальный барьер
0, x 0 область I
U x U O , 0 x a область II
0, x 0 область III
E UO
Уравнение Шредингера:
d 2 2m
2 E 0
2
dx
d 2 2m
2 E 0
2
dx
d 2 2m
2 E U 0 0
2
dx
I
II
III

90. Простейшие задачи

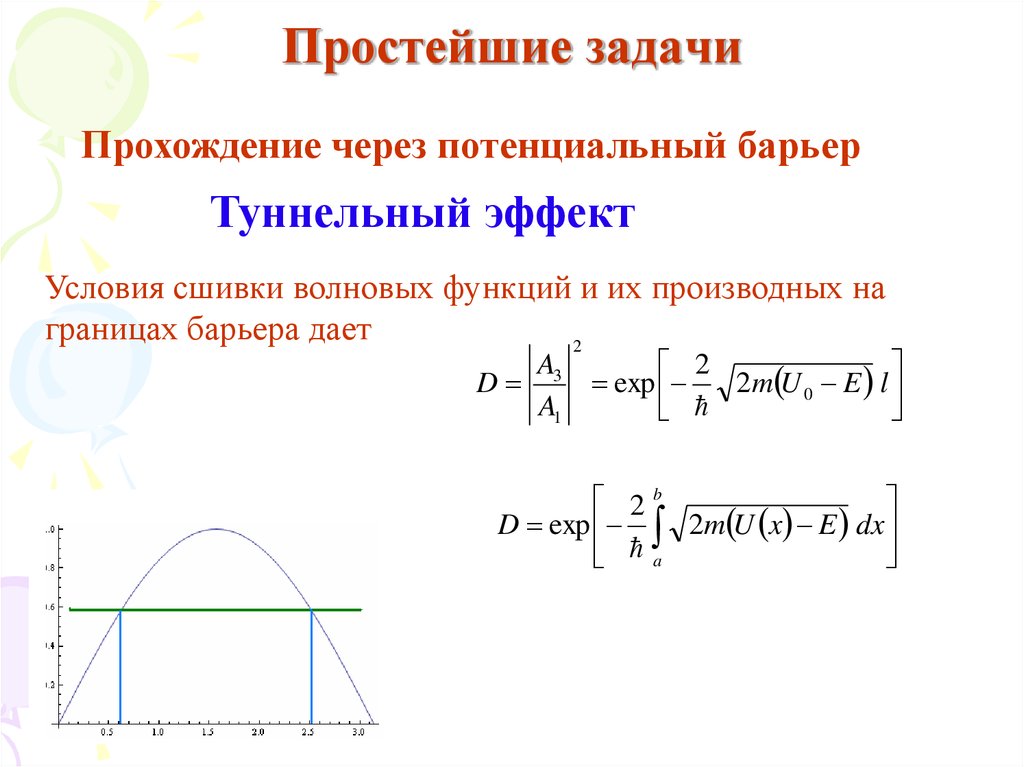
Прохождение через потенциальный барьер
Туннельный эффект
Условия сшивки волновых функций и их производных на
границах барьера дает
2
A3
2
D
exp
2m U 0 E l
A1
2b
D exp 2m U x E dx
a

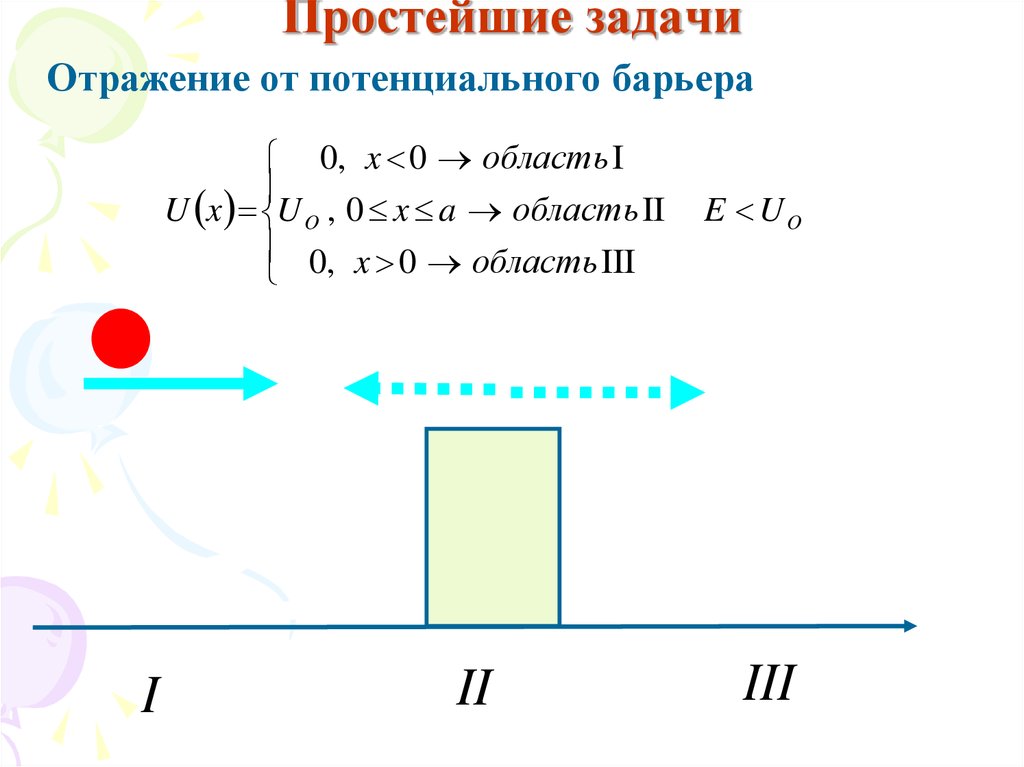
91. Простейшие задачи

Отражение от потенциального барьера
0, x 0 область I
U x U O , 0 x a область II
0, x 0 область III
I
II
E UO
III

92. Простейшие задачи

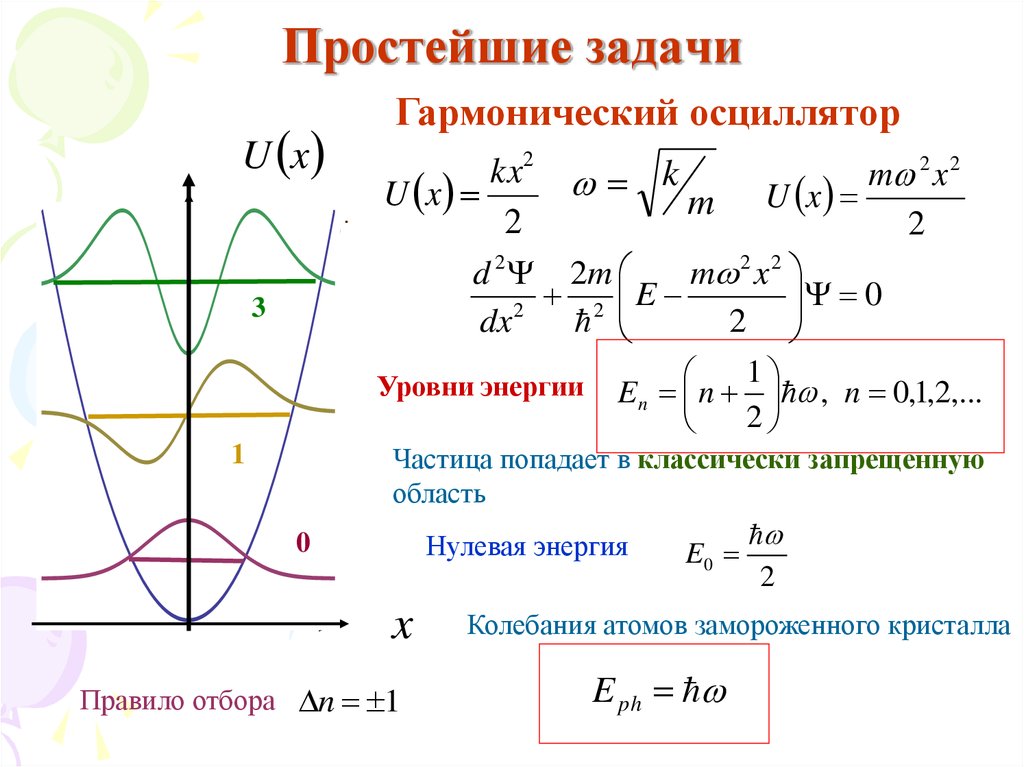
U x
Гармонический осциллятор
m 2 x 2
m U x
2
d 2 2m
m 2 x 2
0
2 E
2
dx
2
kx2
U x
2
3
k
Уровни энергии
1
0
1
En n , n 0,1,2,...
2
Частица попадает в классически запрещенную
область
Нулевая энергия
E0
2
x
Правило отбора n 1
Колебания атомов замороженного кристалла
E ph

93. Простейшие задачи

Атом водорода
Исторически именно для атома водорода было впервые решено
уравнение Шредингера (самим Шредингером)
2 2m
e2
e2
E (r ) 0
( r )
U (r )
| r |
|r |
me4
En 2 2 , n 1,2,3,...
2 n
- допустимые значения энергии
электрона в атоме H1
уровни энергии вырождены
n ,l ,m r Rnl r lm ,
Кратность вырождения
n
- главное квантовое число (КЧ)
l 0,1,2,..., n 1
- орбитальное КЧ
m 0, 1, 2,..., l
- магнитное КЧ
n 1
2l 1 n
l 0
2

94. Магнитный момент атома

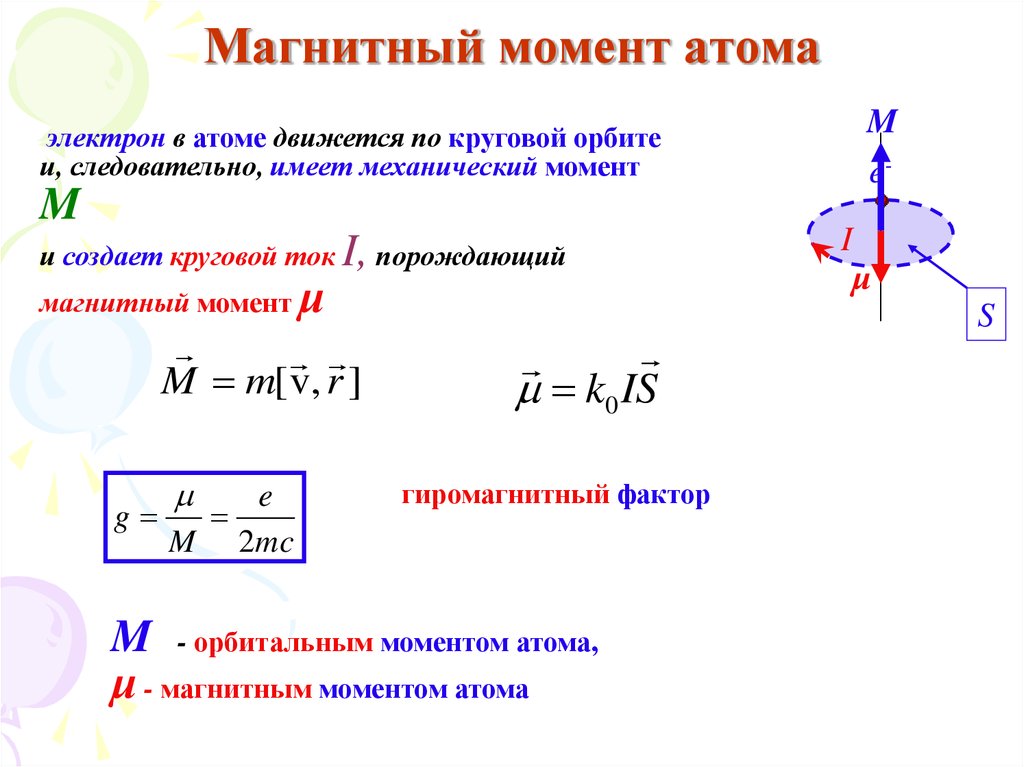
электрон в атоме движется по круговой орбите
и, следовательно, имеет механический момент
M
и создает круговой ток I, порождающий
магнитный момент μ
M m[ v, r ]
e
g
M 2mc
k0 IS
гиромагнитный фактор
M - орбитальным моментом атома,
μ - магнитным моментом атома
M
e-
I
μ
S

95. Магнитный момент атома

Из уравнения квантования для орбитального
момента и его проекции на ось Z
Mˆ M ,
Mˆ M
z
z
следует, что
где l = 0, 1, … - орбитальное кч,
m = 0, ±1, ±2, … , ±l - магнитное кч
M l (l 1) ,
для магнитного момента получим,
M z m
0 l (l 1) , z 0m, 0 e (2mc)
μ0 - магнетон Бора

96. Атом в магнитном поле (эффект Зеемана)

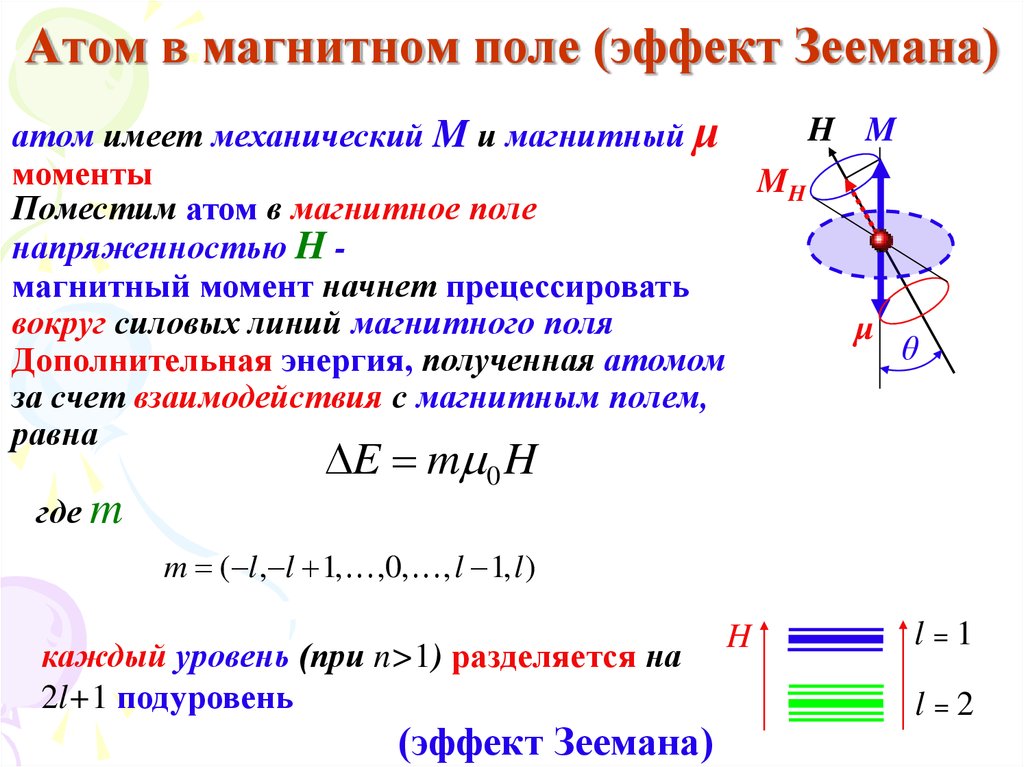
H M
атом имеет механический M и магнитный μ
моменты
MH
Поместим атом в магнитное поле
напряженностью H магнитный момент начнет прецессировать
вокруг силовых линий магнитного поля
μ
θ
Дополнительная энергия, полученная атомом
за счет взаимодействия с магнитным полем,
равна
E m 0 H
где m
m ( l , l 1, ,0, , l 1, l )
каждый уровень (при n>1) разделяется на
2l+1 подуровень
(эффект Зеемана)
H
l =1
l =2

97. Спин электрона

Позже было замечено, что в магнитном поле
каждый подуровень (эффект Зеемана)
состоит из двух уровней
H
в 1925 Уленбек и Гаудсмит предположили, что
электрон имеет собственный механический
момент Ms - спин
При этом, измеренный гиромагнитный фактор
для электрона
e
s
Ms
mc
2g
, где μs - магнитный и Ms - механический моменты
электрона
l =1
l =2

98. Спин электрона

Из уравнения квантования для
механического момента Ms и его
проекции на ось Z
- Msz следует, что
где s = 1/2 , ms = ±1/2 - спиновые
квантовые числа
Тогда для магнитного момента μs
электрона получим
M s s( s 1) ,
M sz ms
s 2 0 s( s 1) ,
sz 2 gM sz 0

99. Принцип Паули

Согласно квантовой механике, состояние
электрона в атоме описывается 4 (четырьмя)
квантовыми числами
главное КЧ
орбитальное КЧ
магнитное КЧ
спиновое КЧ
n 1, 2, 3, ,
l 0,1, 2, 3, , n 1
mz l , -l 1, -l 2, , 1, 0, 1, , l 1, l
1
1
ms , s
2
2

100. Принцип Паули

Электроны являются фермионами и согласно
принципу Паули
в атоме (в любой квантовой системе), не может
быть двух электронов, имеющих одинаковый
набор квантовых чисел
Электроны с одинаковым значением главного КЧ n
(находящиеся на одной орбите) образуют оболочку
1 2 3 4
n
обозн. K L M N
Электроны с одинаковым значением орбитального КЧ l
образуют подоболочку
0 1 2 3
l
обозн. s p d f

101. Строение ядра

Ядром называют положительно
заряженную центральную часть
атома не содержащую электронов
n
n
4
2
He
α-частица
Ядро состоит из нуклонов - положительно
заряженных протонов (p) и не заряженных частиц –
нейтронов (n)
Электрический заряд ядра qя = Ze, где e - величина
заряда протона (= заряду электрона), Z - номер
элемента (в таблице Менделеева), равный числу p в
ядре

102. Строение ядра

Соответственно, общее количество нуклонов в
ядре равно A=N+Z , где N - число n (A массовое число)
A1
Z
X,
A
Z
A2
Z
X,
X
A3
Z
X,
A4
Z
X
Ядра одного элемента (т.е. с одинаковым Z) с
различным числом n называют изотопами
Ядра различных элементов с одинаковым
числом нуклонов A называют изобарами
A
Z1
X,
A
Z2
Y,
A
Z3 Z ,
A
Z4
V

103. Энергия связи и свойства ядерных сил

Энергией связи нуклона в ядре
численно равна работе удаления
нуклона из ядра
Энергией связи ядра Aсв численно
равна работе разделения ядра на
нуклоны
n
n
M я c 2 Aсв c 2 M нукл
Wя Aсв c 2 M нукл M я
При образовании ядра происходит
выделение энергии (ядерной энергии)
Δm = Aсв /c2 называют дефектом массы ядра
Aсв
m 2 M нукл M я Zm p ( A Z )mn M я ZmH1 ( A Z )mn M at
c

104. Энергия связи и свойства ядерных сил

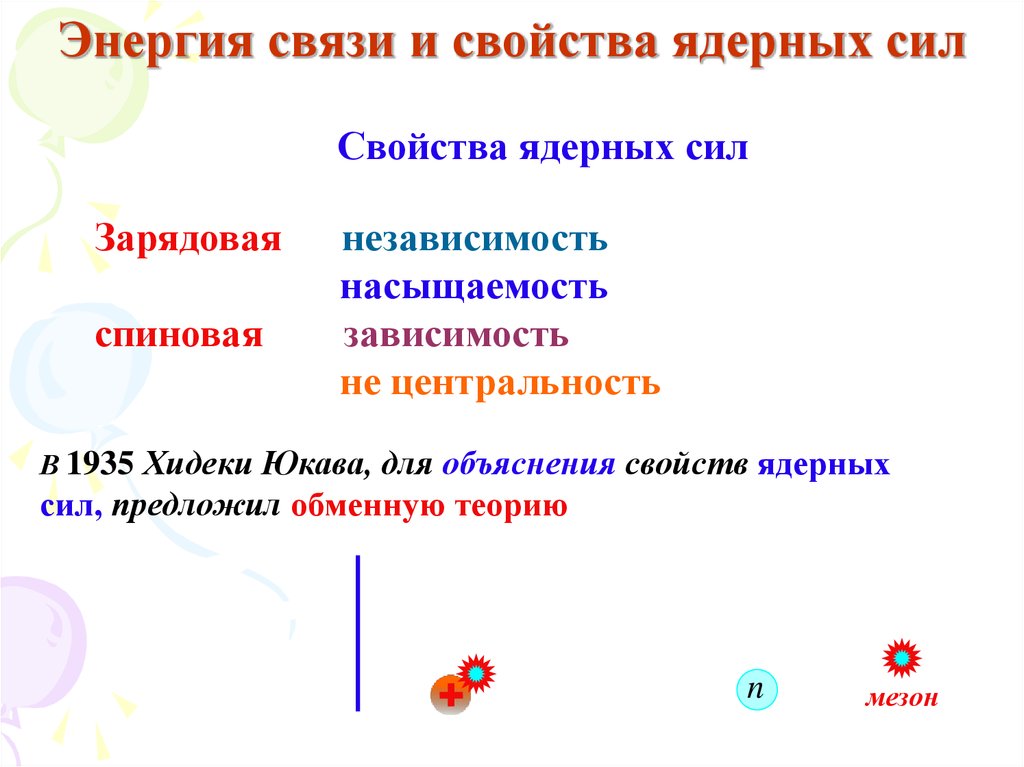
Свойства ядерных сил
Зарядовая
спиновая
независимость
насыщаемость
зависимость
не центральность
В 1935 Хидеки Юкава, для объяснения свойств ядерных
сил, предложил обменную теорию
n
мезон

105. Радиоактивность ядер

Радиоактивностью называют превращение неустойчивых изотопо
одного химического элемента в изотопы другого химического
элемента
К радиоактивности относят и взаимные превращения
элементарных частиц
Различают два вида радиоактивности:
естественная
радиоактивность
неустойчивых природных
изотопов
искусственная
радиоактивность изотопов,
полученных из ядерных
реакций
Все виды радиоактивности (кроме превращения
элементарных частиц) сопровождаются испусканием
γ-лучей

106. Радиоактивность ядер

Закон самопроизвольного радиоактивного распада :
- постоянная распада λ (вероятность распада)
зависит от внешних условий
- распад является случайной величиной
dP
dN
dP
dt
N
dN
dt
N
не
N N 0 e t
Закон самопроизвольного
радиоактивного распада
Т - время, за которое распадется половина ядер (период
полураспада)
N0
T ln 2
N 0 e T
2

107. Радиоактивность ядер

α - и β - распады
α – распад - радиоактивный распад ядер с испусканием
α-частиц (ядра Не)
α - распад характерен для ядер тяжелых элементов (с
массовым числом A > 200)
Различают 3 вида β - распада:
- электронный
или β – - распад
- позитронный или β + - распад
- K-захват (электронный захват)
n p e
p n e~
p e n

108. Радиоактивность ядер

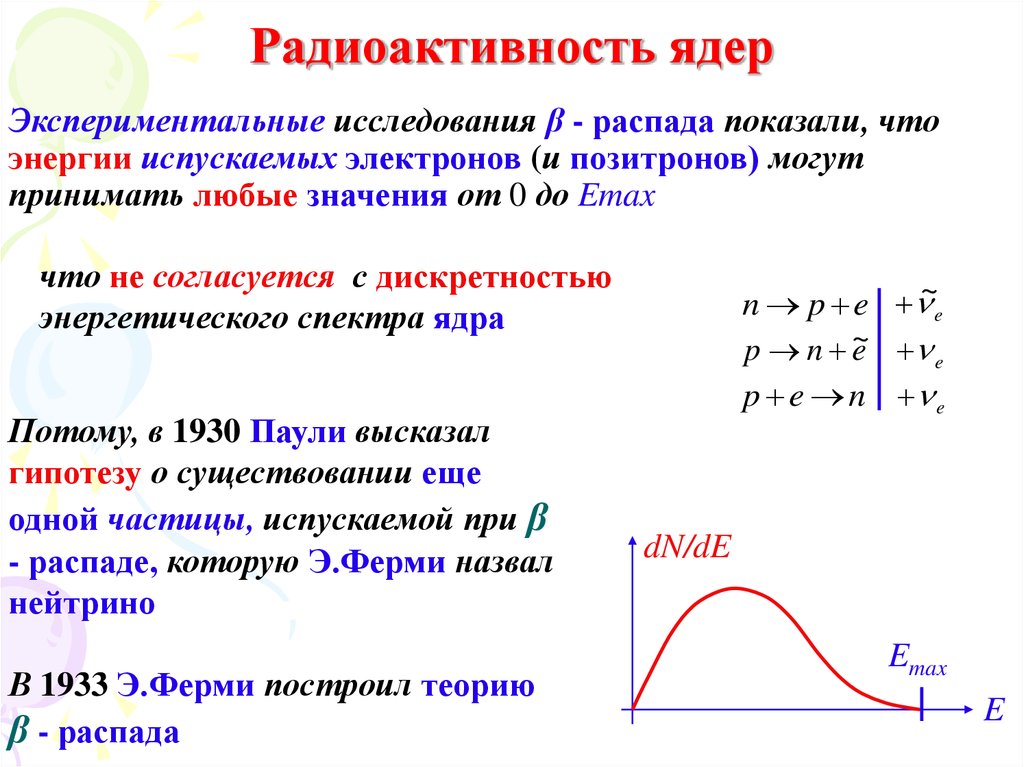
Экспериментальные исследования β - распада показали, что
энергии испускаемых электронов (и позитронов) могут
принимать любые значения от 0 до Emax
что не согласуется с дискретностью
энергетического спектра ядра
Потому, в 1930 Паули высказал
гипотезу о существовании еще
одной частицы, испускаемой при β
- распаде, которую Э.Ферми назвал
нейтрино
В 1933 Э.Ферми построил теорию
β - распада
n p e ~e
p n e~ e
p e n e
dN/dE
Emax
E

109. Деление ядер

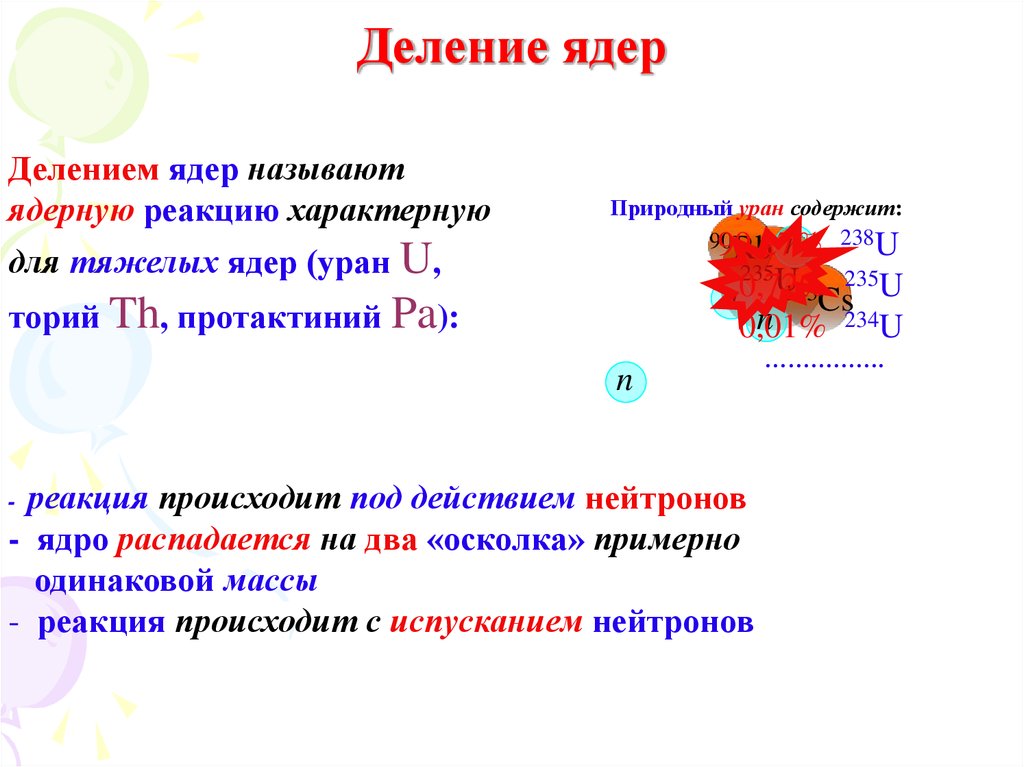
Делением ядер называют
ядерную реакцию характерную
для тяжелых ядер (уран U,
торий Th, протактиний Pa):
Природный уран содержит:
90
99,27%
Rb n 238U
235U
235U
0,72%
143
n
Cs234
n
0,01%
U
n
реакция происходит под действием нейтронов
- ядро распадается на два «осколка» примерно
одинаковой массы
- реакция происходит с испусканием нейтронов
-
…………….