Similar presentations:
Волновые свойства частиц. Понятие вероятности обнаружения частицы
1.
МИЭТ.Кафедра обшей физики.
Л.В.В.
Волновые свойства частиц
Понятие вероятности
обнаружения частицы
Уравнение Шредингера
для частиц, скорость движения
которых мала по сравнению
со скоростью света.
2.
Корпускулярно-волновойдуализм
Корпускулярно-волновой дуализм
электромагнитного излучения
Фотоны.
p k ,E
• Гипотеза Луи де Бройля о волновых
свойствах микрочастиц
Дифракция микрочастиц
Волновая
ˆ
H i
t
функция
Уравнение
Шредингера
3. Ф о т о н
ФотонСвет и любое электромагнитное излучение – поток фотонов.
Корпускулярные свойства излучения.
1. Энергия и импульс фотонов: ,
p k,
p
2
c
2. Собственная масса m0 0 (масса покоя).
8
Фотон всегда движется со скоростью света с 3 10 м с
(в любой системе отсчета) и не может находиться в состоянии покоя.
3. Энергия и импульс связаны соотношением
Частный случай релятивистского
соотношения для частицы массы m0 :
E
p c
p2c2 (m0c2 )2
4. Фотон – стабильная элементарная частица, время жизни
которой определяется взаимодействием с веществом.
4.
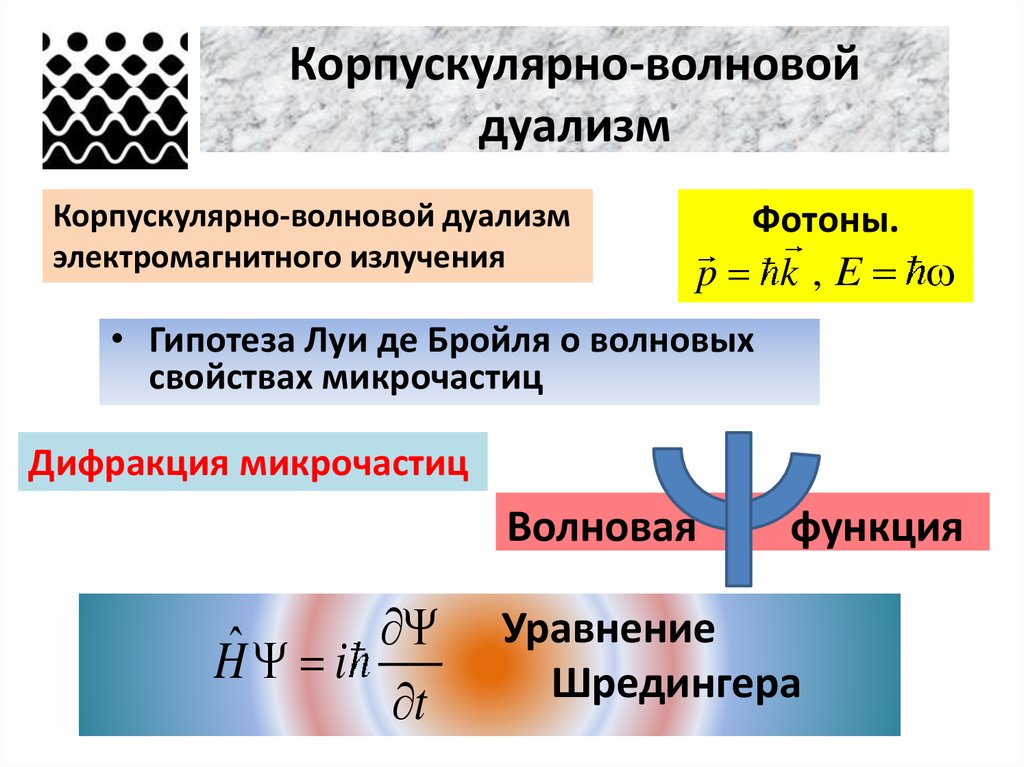
5. Фотон - неделимая частица. Поглощается и испускаетсяцеликом в процессе квантового скачка из состояния вещества с
энергией Em в состояние с энергией En .
Em
En
Фотон
Поглощение
Em
Фотон
Испускание
En
6. Интенсивность светового монохроматического пучка
(средняя плотность потока энергии электромагнитного излучения)
I w c nФ с jФ
, где jФ nФ c
- плотность потока фотонов
w - средняя плотность энергии излучения : nФ
среднее число фотонов в единице объема (концентрация);
7. В квантовой физике отсутствует наглядный образ фотона.
5. Корпускулярно – волновой дуализм электромагнитного излучения
«Противоположности не противоречия, а дополнения» (Нильс Бор)Такие явления, как интерференция, дифракция, поляризация света, были
объяснены, исходя из представлений о волновой природе света: свет – это
распространяющиеся в пространстве электромагнитные волны. Световая волна
не локализована в пространстве. Объемная плотность энергии электромагнитной
волны пропорциональна квадрату её амплитуды и изменяется непрерывно.
В явлениях взаимодействия с веществом свет ведет себя
как поток частиц
– фотонов, обладающих
энергией и импульсом
p k ,c p 2
(фотоэффект, тепловое равновесное излучение, эффект Комптона и др.).
Световая энергия изменяется не непрерывно, а только
дискретно в виде порций ( квантов) энергии.
Электромагнитное излучение обладает двойственной природой,
получившей название «корпускулярно-волновой дуализм».
Явления, в которых участвует свет, объясняются с учетом двух ,
дополняющих друг друга, понятий: «волна – частица»
6.
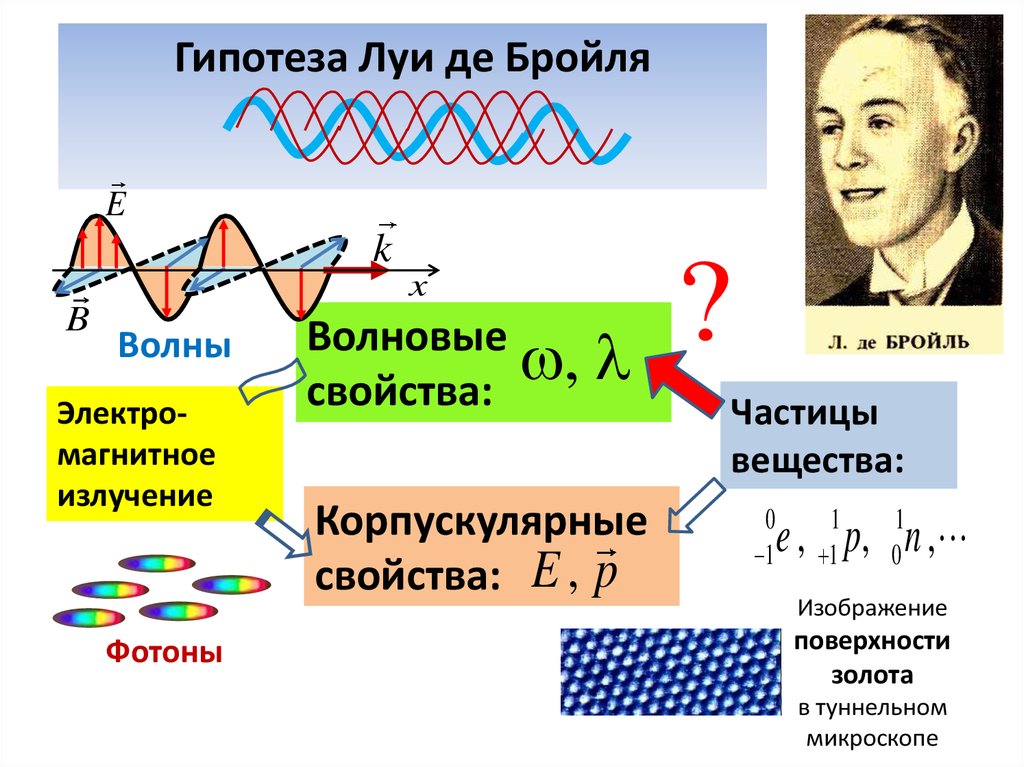
Гипотеза Луи де БройляE
k
x
B
Волны
Электромагнитное
излучение
Фотоны
Волновые
,
свойства:
Корпускулярные
свойства: E , p
?
Частицы
вещества:
0
1
e , p, n ,
1
1
1
0
Изображение
поверхности
золота
в туннельном
микроскопе
7. Гипотеза де Бройля
В 1923 г. Французский физик Луи де Бройль выдвинулчрезвычайно смелую гипотезу:
Электромагнитное излучение и вещество, состоящее из
микрочастиц, равноправны в отношении проявления
корпускулярно-волновых свойств.
Микрочастицы должны проявлять волновые свойства.
Свет с длиной волны и частотой ведет себя
как поток частиц (фотонов)
с импульсом p 2 и энергией E
Частице с импульсом p и энергией E
соответствует некий волновой процесс
с длиной волны =2 p и частотой = E
8. Плоская волна де Бройля
Свободной частице с энергией E и импульсом p,P
x
движущейся вдоль оси x, соответствует плоская
волна де Бройля:
E
p
( x, t ) A exp i ( t kx) A exp i ( x t )
где
k p
- волновое число,
E
- частота .
Волна распространяется в том же направлении, что и
частица, и описывает её волновые свойства.
9. Групповая скорость волны де Бройля
Групповая скорость световой волны: v гр kГрупповая скорость волны де Бройля:
( ) E
vгр
k ( k ) p
Дифференцируя формулу связи между энергией E и импульсом
p релятивистской частицы: E 2 p 2 c 2 (me c 2 ) 2 , получим
vгр pc2 E
1
Учитывая, что E me c , p me v , где =
2
2
1
v
c
для групповой скорости находим
2
vгр v
Групповая скорость волны де Бройля равна
скорости движения частицы v .
10.
Волна де Бройля не является волной, движущейся.
вместе с частицей.
Волна де Бройля и частица – это один и тот же объект !
Понятие длины волны де Бройля характеризует этот объект с
волновой точки зрения, а понятие импульса определяет свойства
объекта как частицы, и эти два понятия связаны соотношением
p k
, где
k 2 Б
2
или Б
p
mc 2 и EK p 2 2m
Для частицы с кинетической энергией EK
длина волны де Бройля равна
Для релятивистской частицы:
2
p
2
2mEK
2
Б
2mEK
EK
1
2mc 2
Б
EK
1
2mc 2
11. Эксперименты по дифракции микрочастиц
Опыты К. Дэвиссона и Л. Джермера (Америка, 1927 г.)Электроны
Детектор
e
eU 54 эВ
2 500
Кристалл
Ni
Ni
Картина
Дифракция лазерного
света ( 632,8 нм )
на прямоугольной
проволочной сетке
d = 30 мкм
дифракции
электронов на
монокристалле
12.
Отражение электронов от атомных плоскостей в кристалле.Атомная структура кристаллов была известна из опытов по
дифракции рентгеновских волн. Еще в 1912 – 1913 гг.
английские физики Г. Брэгг и Л. Брэгг (отец и сын) предложили
вместо сложной дифракции от множества атомов
рассматривать отражение волн от параллельных атомных
плоскостей в кристалле и интерференцию отраженных волн.
Б
2d sin n
0,165 нм
d 0,091 нм
2
Б
0,166 нм
2meeU
Атомные плоскости в
кристалле
d
d1
13.
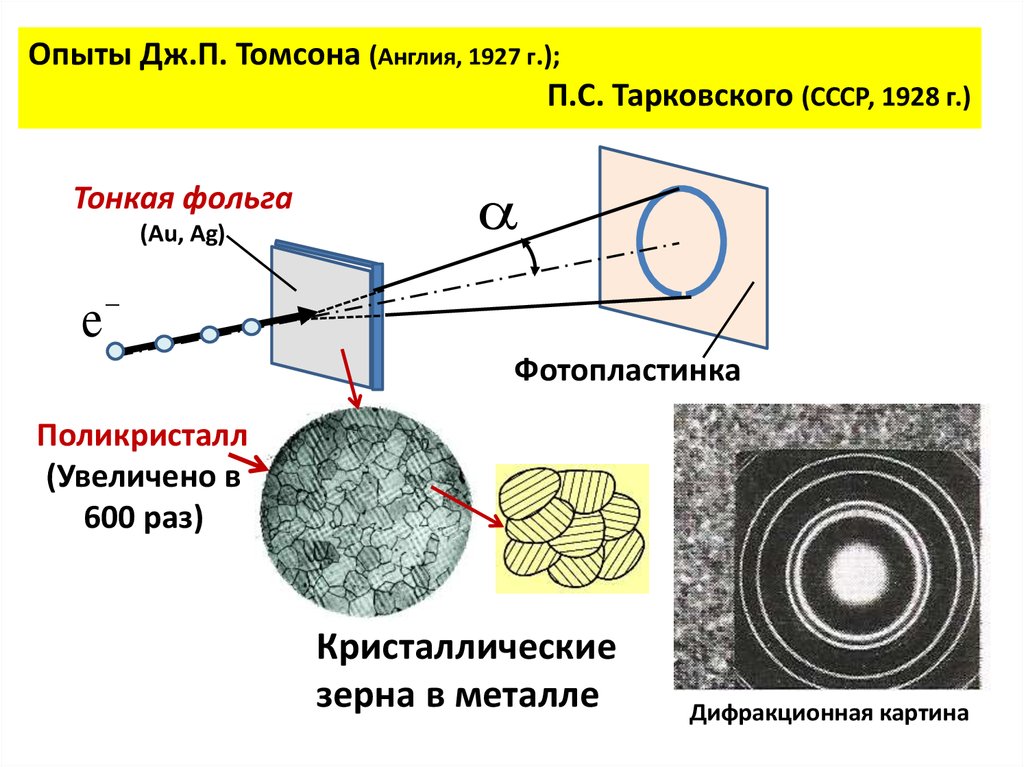
Опыты Дж.П. Томсона (Англия, 1927 г.);П.С. Тарковского (СССР, 1928 г.)
Тонкая фольга
(Au, Ag)
e
Фотопластинка
Поликристалл
(Увеличено в
600 раз)
Кристаллические
зерна в металле
Дифракционная картина
14.
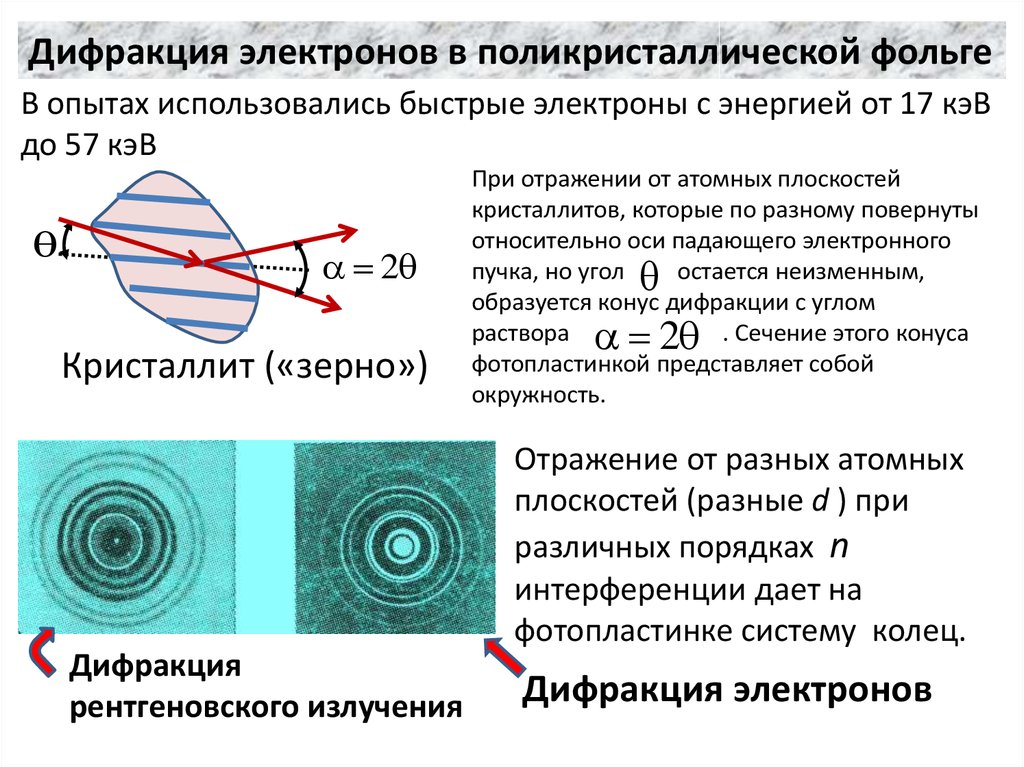
Дифракция электронов в поликристаллической фольгеВ опытах использовались быстрые электроны с энергией от 17 кэВ
до 57 кэВ
2
Кристаллит («зерно»)
При отражении от атомных плоскостей
кристаллитов, которые по разному повернуты
относительно оси падающего электронного
пучка, но угол
остается неизменным,
образуется конус дифракции с углом
раствора
. Сечение этого конуса
фотопластинкой представляет собой
окружность.
2
Отражение от разных атомных
плоскостей (разные d ) при
различных порядках n
интерференции дает на
фотопластинке систему колец.
Дифракция
рентгеновского излучения
Дифракция электронов
15. Дифракция одиночных электронов
Группа физиков во главе с В.А.Фабрикантом в СССР выполнила в 1949гдифракционные исследования с очень слабым электронным пучком.
В этих опытах интервал времени между двумя последовательными
прохождениями электронов через поликристалл в 81 раз превышал
время, затрачиваемое одним электроном на прохождение всего
прибора. Таким образом, взаимодействие электронов друг с другом
полностью исключалось, и электроны дифрагировали поодиночке.
Дифракция
одиночных
электронов
Волновые свойства присущи отдельному
электрону.
16.
«Некоторые исследователи приступили к выполнению опыта за которыйещё несколько лет назад их бы посадили в психиатрическую больницу для
наблюдения за их душевным состоянием. Но они добились успеха !»
Эрвин Шредингер о первых
опытах по дифракции электронов
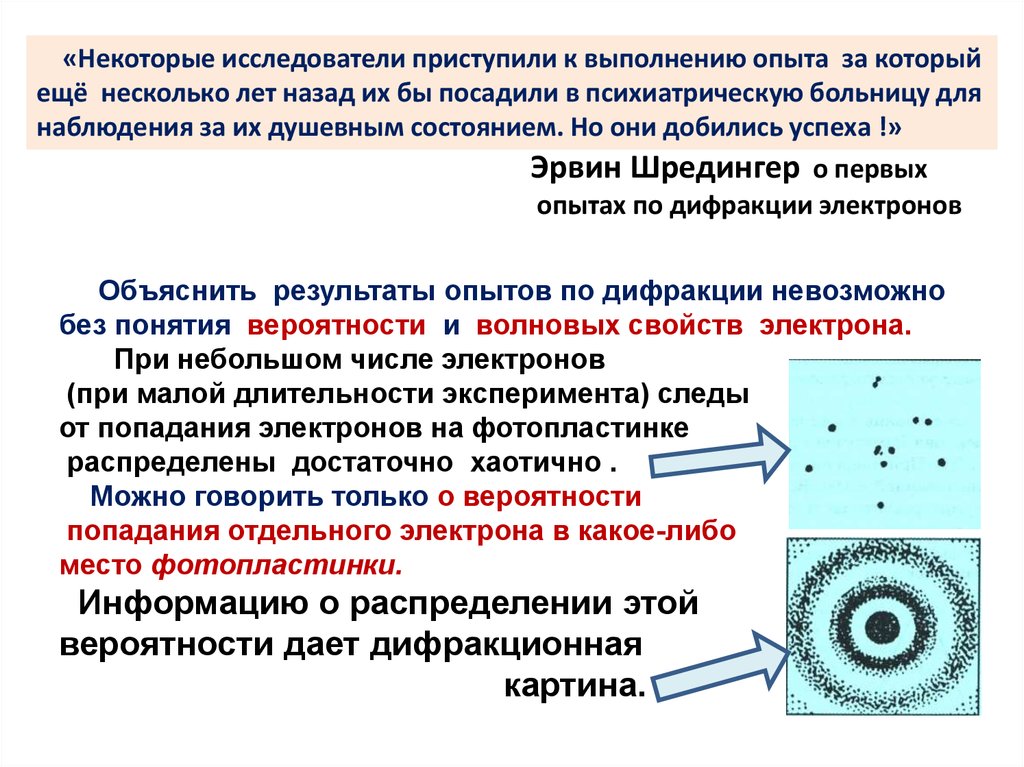
Объяснить результаты опытов по дифракции невозможно
без понятия вероятности и волновых свойств электрона.
При небольшом числе электронов
(при малой длительности эксперимента) следы
от попадания электронов на фотопластинке
распределены достаточно хаотично .
Можно говорить только о вероятности
попадания отдельного электрона в какое-либо
место фотопластинки.
Информацию о распределении этой
вероятности дает дифракционная
картина.
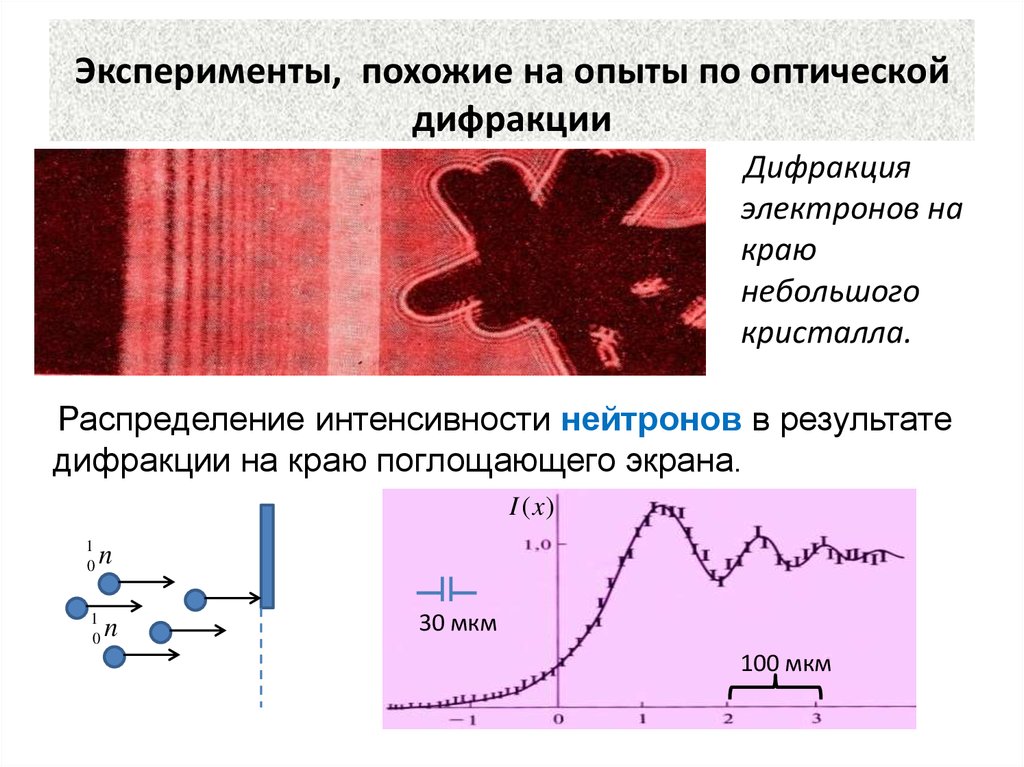
17. Эксперименты, похожие на опыты по оптической дифракции
Дифракцияэлектронов на
краю
небольшого
кристалла.
Распределение интенсивности нейтронов в результате
дифракции на краю поглощающего экрана.
I ( x)
1
0
n
1
0
n
30 мкм
100 мкм
18.
О новой механике движения микрочастиц –квантовой механике
На заре квантовой механики (1920-е годы) физики
пытаются найти законы, определяющие движение
микрочастицы (электрона) в различных условиях, не
прибегая к моделям внутренней структуры.
Так например, электрон в дифракционных экспериментах
с поликристаллической фольгой с некоторой вероятностью
меняет свое направление движения после фольги, но
фиксируется на фотопластинке как точечная частица.
Задача: Выяснить особенности физического и
математического описания движения микрообъекта,
совмещающего в себе каким-то образом
корпускулярные и волновые свойства.
19.
Уравнение ШредингераЕще до начала экспериментов по дифракции электронов
физики-теоретики Вернер Гейзенберг в Германии
и Эрвин Шредингер в Австрии начали разрабатывать новую
механику, позволяющую рассчитывать волновое движение не только
свободных микрочастиц, как это было у де Бройля, но и частиц ,
находящихся во внешнем потенциальном поле.
В 1926 г. Шредингер получил свое знаменитое уравнение для
волновой пси-функции ( r , t ) и применил его к атому
водорода, в котором единственный электрон находится в
электрическом поле протона .
U ( x, y , z ) i
,
2m
t
2
2
2
где ex
,
ey ez
x
y
z
2 2 2
2 2 .2
x
y
z
2
20.
Принцип дополнительности Н. Бора.Соотношения неопределенностей
1927г. Нильс Бор в Дании сформулировал
принцип дополнительности в квантовых явлениях,
а мысленные эксперименты Вернера Гейзенберга в Германии привели
к соотношениям неопределенностей, которые являются математическим
воплощением общей идеи дополнительности в квантовых явлениях.
Принцип дополнительности Бора: В области квантовых явлений
наиболее общие физические свойства какой-либо системы описываются
с помощью дополняющих друг друга пар независимых переменных ,
каждая из которых может быть лучше определена только за счет
уменьшения степени определенности другой.
Такими переменными являются: импульс
– координата ; энергия –
время; частица – волна; непрерывность – дискретность; … .
«Физическая картина явления и его математическое описание дополнительны.
Создание физической картины требует пренебрежения деталями и уводит от
математической точности. И наоборот, попытка точного математического описания
явления затрудняет ясное понимание» (А. Б. Мигдал)
21.
Соотношения неопределенностей.Примеры мысленных экспериментов.
1
Для определения положения электрона надо осветить его и посмотреть
в микроскоп. В этом случае неопределенность в координате x порядка
длины волны света , то есть x . Для уточнения положения электрона
надо уменьшать . Но свет передает электрону импульс. Чтобы уменьшить
передаваемый импульс надо ослабить интенсивность света так,
чтобы с электроном сталкивался один фотон с импульсом p 2 .
Появляется неконтролируемое изменение импульса электрона
px p 2 . Заменяя на x , получаем
p .
x px 2
x
2 Частица пролетает через отверстие в экране, открываемое
p
на время . Момент взаимодействия частицы с краями отверстия
имеет неопределенность t . Неопределенность координаты
x
частицы в направлении оси x равна x v t ,
где v – скорость частицы. Предполагается, что скорость частицы мало
изменилась при прохождении отверстия. Из соотношения неопределенностей
x px 2 находим неопределенность в импульсе px 2 x 2 v . t
2
Учитывая, что E (mv 2)
v px ,
получаем
E t 2
22.
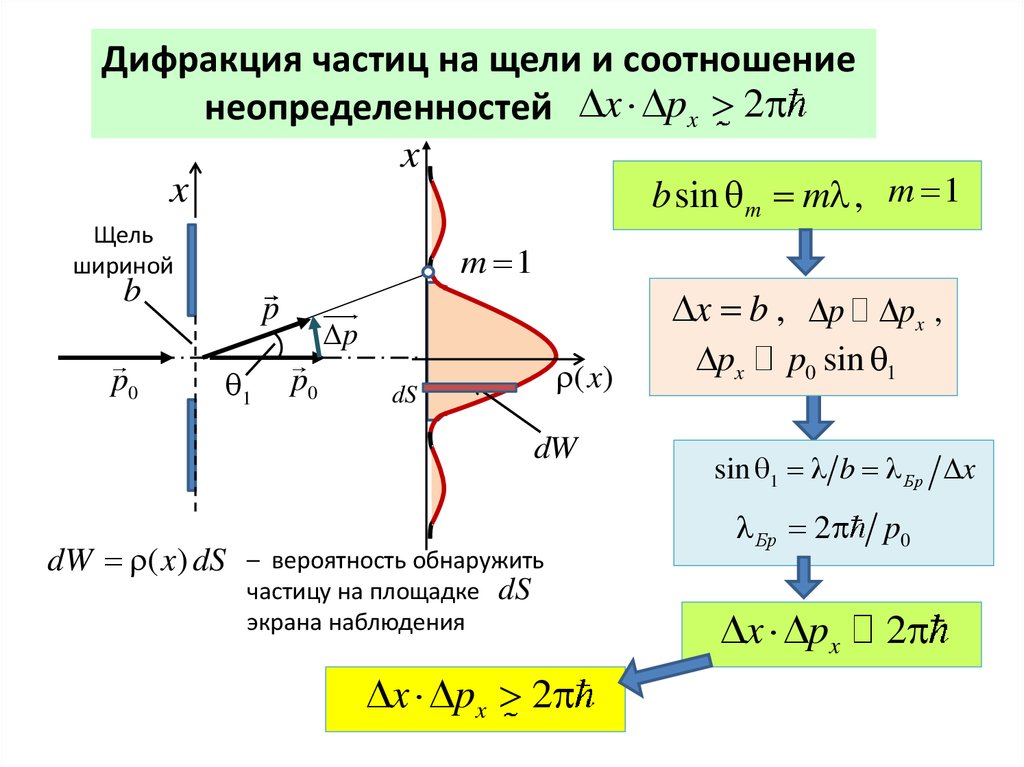
Дифракция частиц на щели и соотношениенеопределенностей x px 2
x
x
b sin m m , m 1
Щель
шириной
m 1
b
p0
p
1
x b , p px ,
p
p0
( x)
dS
dW
dW ( x) dS
– вероятность обнаружить
частицу на площадке dS
экрана наблюдения
x px 2
px
p0 sin 1
sin 1 b Бр x
Бр 2
x px
p0
2
23.
Соотношения неопределенностей В. Гейзенберга1)
Координатная ось x в полученных соотношениях неопределенностей
физически ничем не выделена , поэтому они справедливы и для осей y и z :
x px 2
y p y 2
z pz 2
При получении этих соотношений использовались некоторые упрощающие
предположения, и достаточно произвольные критерии для оценки
неопределенностей . Поэтому их следует считать приближенными.
Есть соотношения неопределенностей, которые строго могут быть
2)
получены методами квантовой физики , исходя из того, что частица
находится в определенном состоянии с волновой функцией ,
которая является решением уравнения Шредингера.
Пример. Если под неопределенностями координаты и импульса
понимать их среднеквадратичные отклонения от средних величин,
то xкв ( x)2 ( x x )2 , px, кв ( px )2 ( px px )2
xкв px ,кв
2
Соотношения неопределенностей – частный случай и конкретное
выражение принципа дополнительности Н. Бора.
24.
Следствия из соотношений неопределенностей1 Координата и импульс не могут одновременно иметь определенные
значения.
2 Для микрочастиц теряется понятие траектории движения:
например, если точно известна координата ( x 0 ), то px .
Несмотря на отсутствие траектории, движение частиц происходит
по определенному закону , который проявляется в неизменности
результата при повторении опытов в одних и тех же условиях.
Н.Бор часто вспоминал, как в 50-х годах к нему после лекции
подошел студент и спросил: « Неужели действительно были такие
идиоты, которые думали, что электрон в атоме вращается по
орбите»
3
Микрочастица не может находится в состоянии полного покоя: если
положение частицы ограничено областью x a, то
px 2a.
25. В о л н о в о е у р а в н е н и е
1 Волновое уравнение для электромагнитных волнв одномерном случае, когда напряженность электрического
поля E зависит только от координаты x и времени t , имеет вид:
E
1
E
;
2
2
2
x
v t
2
2
v 1
,
0 0 c n ,
где v - фазовая скорость волны, n – показатель преломления
среды, c 1 0 0 - скорость света в вакууме.
Частным решением этого волнового уравнения является
плоская электромагнитная волна:
E
k
i(kx- t)
E E0 e
x
B
26. Волновое уравнение Шредингера
2В 1926 г. австрийский физик-теоретик Эрвин Шредингер разработал теорию
движения микрочастиц, в основу которой положил уравнение
U ( x) i
2
2m x
t
2
2
Одномерное
движение: ( x, t )
Движение в трехмерном пространстве;
U ( x, y , z ) i
, где ( x, y, z, t );
2m
t
2
2
ex
2
ey ez
x
y
z
2
2
2
2
2 2 2
x
y
z
27. Вероятностный смысл
функцииПочти вся теория Шредингера заключена в его волновом уравнении,
если мы знаем, как интерпретировать волновую функцию .
В том же 1926 г. немецкий физик – теоретик Макс Борн
предложил статистический (вероятностный) смысл
функции :
dW dV dV
2
- вероятность dW
обнаружения частицы в элементарном объёме dV .
Величина
dW dV
2
- плотность вероятности
Функцию называют
амплитудой вероятности
28.
Вероятность в классической физикеВ классической физике статистические методы, использующие
понятие вероятности, рассматриваются как вспомогательные,
и применяются в тех случаях, когда недостаточно знаний
о подробностях того или иного события.
Так обстоит дело, например, в кинетической теории газов, где
предполагается, что каждая частица во всякий данный момент
времени имеет определенное значение скорости.
Но частиц много, уследить за всеми невозможно,
и единственный реальный путь заключается в том,
чтобы найти закономерности в этом хаотичном
движении многих частиц – вычислить вероятность
распределения частиц по скоростям.
29.
Вероятность в квантовой физикеВ квантовой физике, согласно М.Борну, ситуация совсем иная.
Электронам, протонам, фотонам и другим частицам присущи
волновые свойства.
Нет смысла, например, говорить о локализации световой волны
после дифракции на щели или траектории фотонов.
Фотон может попасть в любое место экрана наблюдения
с той или иной вероятностью. Это касается и микрочастиц, для
описания движения которой понятие определенной и
непрерывной траектории оказывается неприменимым.
При рассмотрении процессов , происходящих в микромире,
неизбежно приходится использовать понятие
волны вероятности
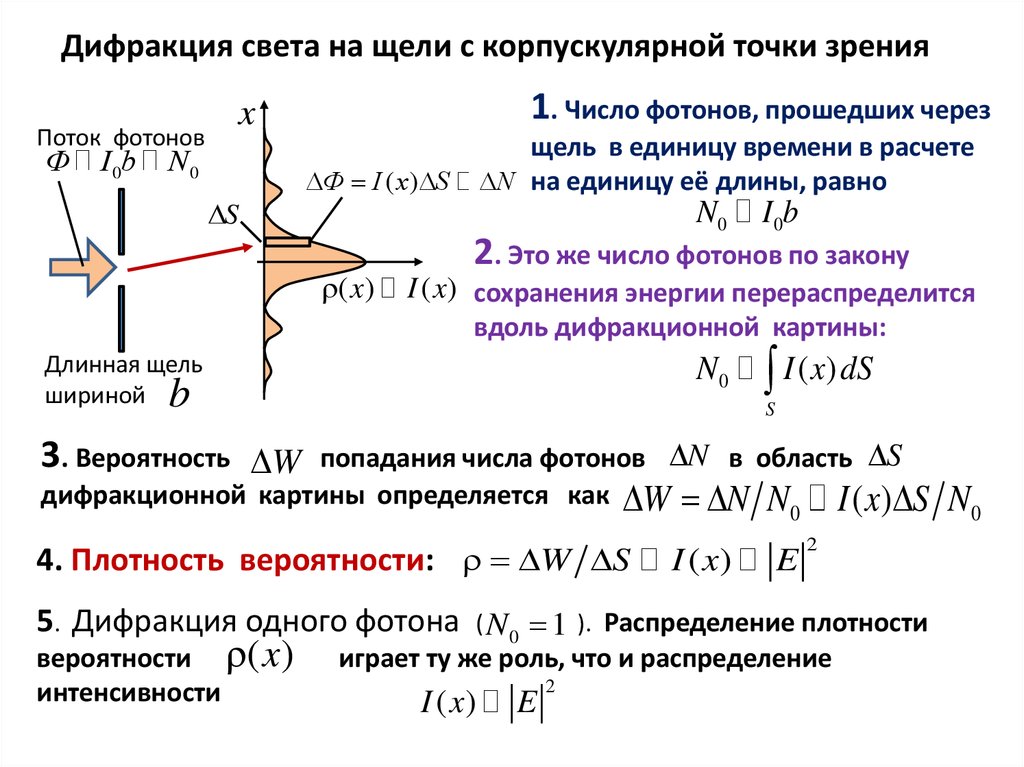
30.
Дифракция света на щели с корпускулярной точки зренияПоток фотонов
Ф
I 0b
1. Число фотонов, прошедших через
x
N0
S
щель в единицу времени в расчете
N на единицу её длины, равно
Ф I ( x) S
N0
( x)
I 0b
2. Это же число фотонов по закону
I ( x) сохранения энергии перераспределится
вдоль дифракционной картины:
Длинная щель
шириной
N0
b
I ( x) dS
S
попадания числа фотонов N в область S
дифракционной картины определяется как W N N
I ( x) S
3. Вероятность W
0
4. Плотность вероятности: W S
I ( x)
E
2
5. Дифракция одного фотона ( N0 1 ). Распределение плотности
вероятности ( x)
интенсивности
играет ту же роль, что и распределение
I ( x)
E
2
N0
31.
О вероятности обнаружения электрона,который свободно движется в направлении оси
e
S
x
x
( x, t ) A cos(kx t ) i sin(kx t , или
p
i ( x E t )
( x, t ) A e
A
2
Почему нельзя представить плоскую волну де Бройля
в вещественной форме ( x, t ) A cos(kx t ?
В этом случае 2 A2 cos2 (kx t ) . Если наблюдатель
находится в любой из плоскостей, где 0 , он никогда не
зафиксирует летящую навстречу ему частицу , что
противоречит здравому смыслу !
2
32. Уравнение Шредингера в символическом представлении
1. Об идее М. Борна и операторах в математике.Макс Борн в том же 1926 году высказал идею , суть
которой состояла в сопоставлении классической физической
величине некоторого линейного оператора, обладающего
определенными свойствами.
В математике оператором называют правило, с помощью которого
одной функции f ( x ) может быть сопоставлена другая функция F ( x ) .
Символически это правило записывается так: F Df
,
ˆ
где оператор обозначен «шляпкой» .
Пример. Функции f ( x) sin ax
F ( x) a cos ax
сопоставим функцию
с помощью оператора дифференцирования Dˆ x :
ˆ
F ( x) Df ( x) a cos ax sin ax
x
33.
2. Уравнение ШредингераКлассический закон сохранения энергии :
2
p
U ( x) E (кинетическая энергия + потенциальная
энергия равна полной энергии частицы)
2m
В соответствии с идеей М.Борна введем операторы,
которые действуют на волновую функцию :
p p pˆ pˆ ;
2
2
ˆˆ
pp
ˆ
ˆ
ˆ
U ( x) Uˆ ; 2m ( x) U ( x) H ( x) ; E E
Тогда можно записать квантовое уравнение
в символической форме 1
2m
pˆ ( pˆ ) U Eˆ ,
где потенциальная энергия – функция координат,
ей соответствует оператор умножения: Uˆ U .
34.
Операторы импульса и энергииВыясним вид операторов,
i ( p x Et )
используя плоскую волну де Бройля, которая является
x
решением уравнения Шредингера в случае U = 0 : ( x, t ) Ae
Найдем производную этой функции по координате x :
i
px , i
px , pˆ x px
x
x
Оператор импульса p px ex p y ey pz ez
pˆ ( i
)ex ( i
)ey ( i
)ez i ;
x
y
z
p2 pˆ x pˆ x pˆ y pˆ y pˆ z pˆ z 2 2
pˆ x i
x
и квадрата импульса:
где градиент
(оператор «набла»)
Eˆ i
t
Дифференцируя волну де Бройля по времени.
можно найти оператор Eˆ полной энергии:
При таких операторах квантовое уравнение в символической
форме является уравнением Шредингера
где
Hˆ (
2
Hˆ i
U ) оператор Гамильтона
2
2m
(оператор полной энергии).
t
























 physics
physics