Корпускулярно-волновой дуализм. Тема 3

1.

Тема 3. КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ
3.1. Гипотеза Луи де Бройля
3.2. Эксперименты по дифракции микрочастиц
3.3. Волны де Бройля и принцип неопределенности
3.4. Волновое уравнение Шредингера
3.5. Свойства
функции

2. О границах применимости квантовой механики

• Диаграмма расстояние — скорость для наглядной иллюстрации
областей применимости физических теорий:
классической механики, специальной теории относительности (СТО),
квантовой механики (КМ),
общей теории относительности (ОТО) и квантовой теории поля (КТП).
Точка показывает электрон в атоме — в сфере действия квантовой
механики

3. Ф о т о н

Свет и любое электромагнитное излучение – поток фотонов.
Корпускулярные свойства излучения.
1. Энергия и импульс фотонов: E p k , p 2
c
2. Собственная масса
m0 0
(масса покоя).
Фотон всегда движется со скоростью света
с 3 108 м с
(в любой системе отсчета) и не может находиться в состоянии покоя.
3. Энергия и импульс связаны соотношением E p c
(частный случай релятивистского соотношения для
частицы массы m0 :
E p 2c2 (m0c2 )2
).
4. Фотон – стабильная элементарная частица, время жизни
которой определяется взаимодействием с веществом.

4.

5. Фотон неделим. Поглощается и испускается целиком в процессе квантового
скачка из состояния вещества с энергией Em в состояние с энергией En .
Поглощение
Em
En
Фотон
Em
Фотон
En
Испускание
6. Интенсивность светового монохроматического пучка (средняя плотность
потока энергии электромагнитного излучения)
I w c nФ с jФ
, где jФ nФ c плотность потока фотонов
w - средняя плотность энергии излучения : nФ - среднее
число фотонов в единице объема (концентрация);
7. В квантовой физике отсутствует наглядный образ фотона.

5. Корпускулярно – волновой дуализм электромагнитного излучения

«Противоположности не противоречия, а дополнения» (Нильс Бор)
Такие явления, как интерференция, дифракция, поляризация света, были
объяснены, исходя из представлений о волновой природе света: свет – это
распространяющиеся в пространстве электромагнитные волны. Световая волна
не локализована в пространстве. Объемная плотность энергии электромагнитной
волны пропорциональна квадрату её амплитуды и изменяется непрерывно.
В явлениях взаимодействия с веществом свет ведет себя
как поток частиц – фотонов, обладающих
энергией E
и импульсом
p k ,c p 2
(фотоэффект, тепловое равновесное излучение, эффект Комптона и др.).
Световая энергия изменяется не непрерывно, а только
дискретно в виде порций ( квантов) энергии.
Электромагнитное излучение обладает двойственной природой,
получившей название «корпускулярно-волновой дуализм».
Явления, в которых участвует свет, объясняются с учетом двух ,
дополняющих друг друга, понятий: «волна – частица»

6. Луи Де Бройль (1892-1987)

3.1. Гипотеза де Бройля
Луи Де Бройль
(1892-1987)
1924 г.
Выдвинул
гипотезу
о
корпускулярно-волновом
дуализме электронов, атомов и
других микрочастиц
Нобелевская премия 1929 г.

7. Лабораторная работа №15 Волны де Бройля

8.

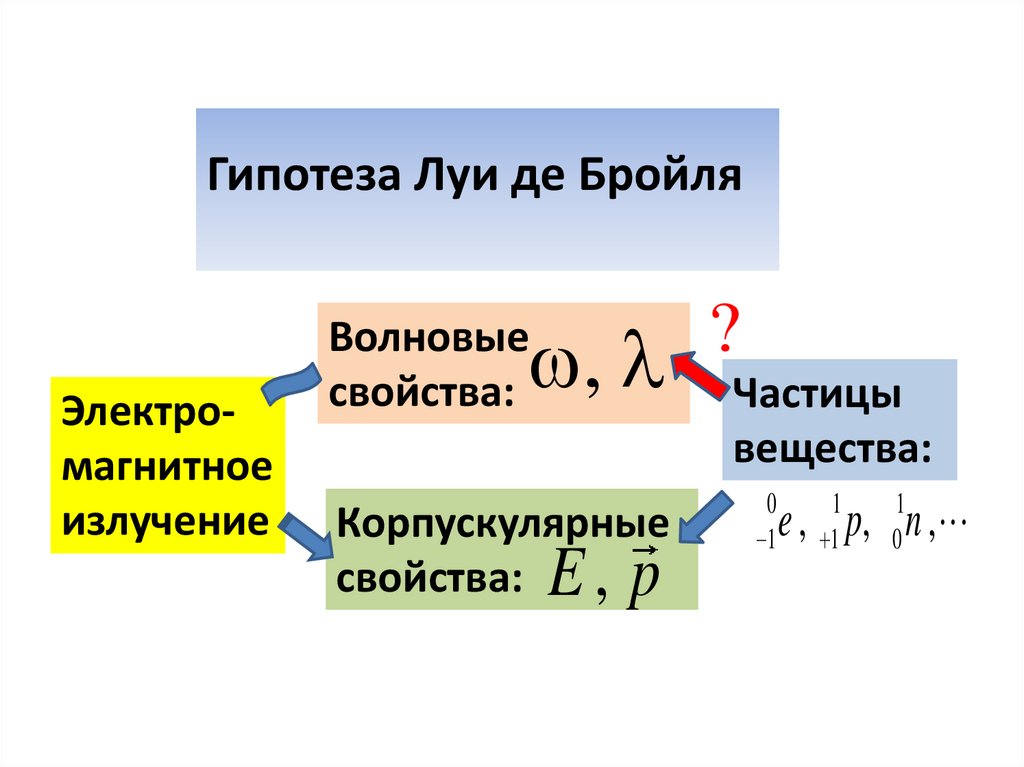
Гипотеза Луи де Бройля
Электромагнитное
излучение
?
,
Волновые
свойства:
Корпускулярные
свойства: E , p
Частицы
вещества:
0
1
e , p, n ,
1
1
1
0

9. Гипотеза де Бройля

В 1923 г. Французский физик Луи де Бройль выдвинул чрезвычайно смелую гипотезу:
Электромагнитное излучение и вещество, состоящее из
микрочастиц, равноправны в отношении проявления
корпускулярно-волновых свойств. Микрочастицы должны
проявлять волновые свойства.
Свет с длиной волны и частотой ведет себя
как поток частиц (фотонов)
с импульсом p 2
и энергией E
Частице с импульсом p и энергией E
соответствует некий волновой процесс
с длиной волны = 2 p
и частотой = E

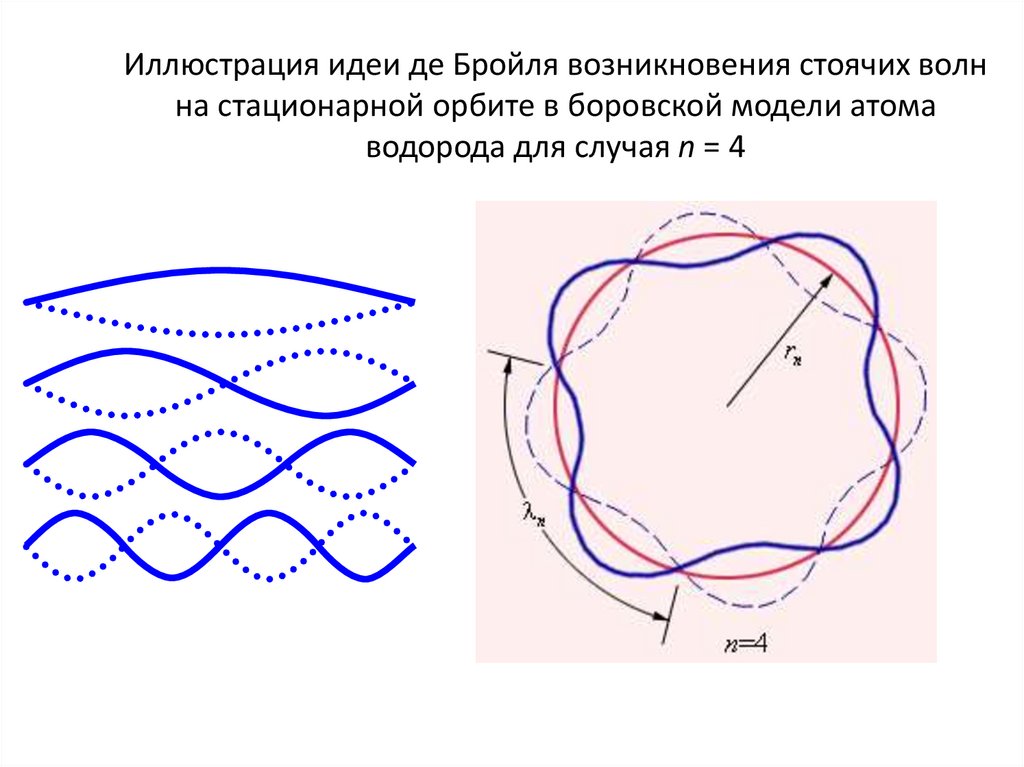
10. Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите в боровской модели атома водорода для случая n = 4

Иллюстрация идеи де Бройля возникновения стоячих волн
на стационарной орбите в боровской модели атома
водорода для случая n = 4

11. Плоская волна де Бройля

Свободной частице с энергией E и импульсом p,
P
x
движущейся вдоль оси x, соответствует плоская
волна де Бройля:
E
p
( x, t ) A exp i ( t kx) A exp i ( x t )
где
k p
- волновое число
E
- частота .
Волна распространяется в том же направлении, что и
частица, и описывает её волновые свойства.

12. Групповая скорость волны де Бройля

Групповая скорость световой волны:
Vгр k
Групповая скорость волны де Бройля:
( ) E
Vгр
k ( k ) p
Дифференцируя формулу связи между энергией E и импульсом
p релятивистской частицы: E 2 p 2 c 2 (me c 2 ) 2 , получим
V .pc2 E
гр
1
Учитывая, что E me c , p me V , где =
2
2
1
V
c
для групповой скорости находим
2
Vгр V
Групповая скорость волны де Бройля равна
скорости движения частицы V.

13.

Волна де Бройля не является волной, движущейся вместе с
частицей.
.
Волна де Бройля и частица – это один и тот же
объект. Понятие длины волны де Бройля характеризует
этот объект с волновой точки зрения, а понятие импульса
определяет свойства объекта как частицы, и эти два
понятия связаны соотношением
p
k , где
k 2 Б
2
Б
p
или
mc 2 и EK p 2 2m
Для частицы с кинетической энергией EK
длина волны де Бройля равна
2
p
2
2mEK
2
Для релятивистской частицы: Б
2mEK
EK
1
2mc 2
Б
EK
1
2mc 2

14. 3.2.Эксперименты по дифракции микрочастиц

1927 г.
Дэвиссон и Джермер

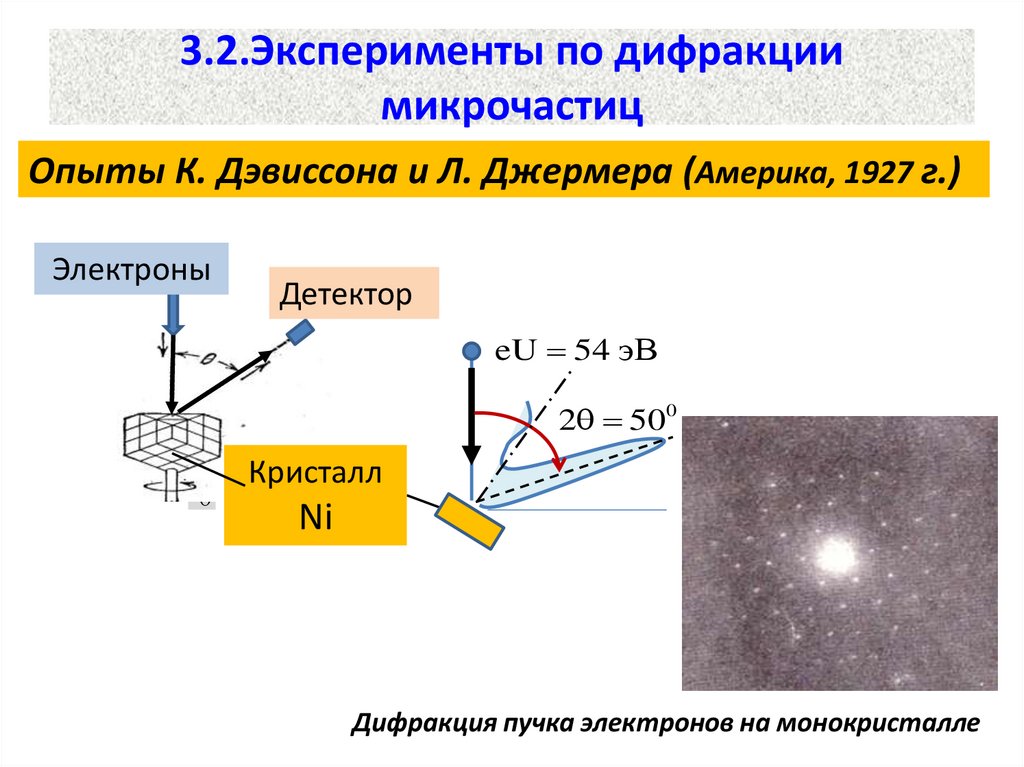
15. 3.2.Эксперименты по дифракции микрочастиц

Опыты К. Дэвиссона и Л. Джермера (Америка, 1927 г.)
Электроны
Детектор
eU 54 эВ
2 500
Кристалл
Ni
Дифракция пучка электронов на монокристалле

16.

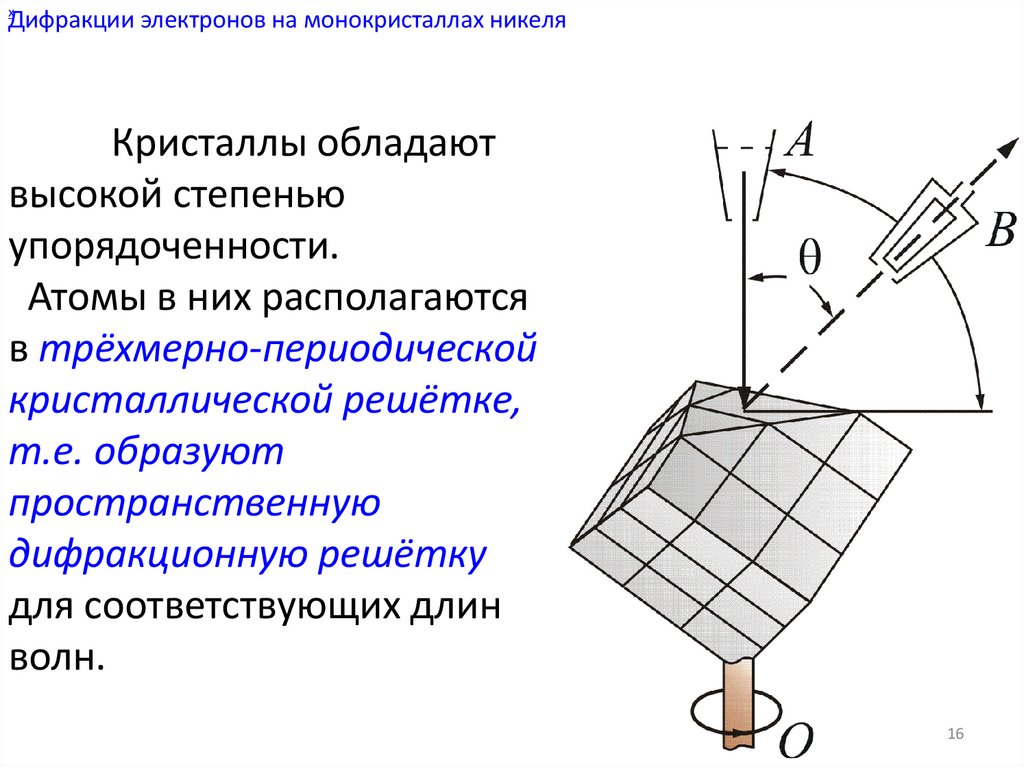
х
Дифракции электронов на монокристаллах никеля
Кристаллы обладают
высокой степенью
упорядоченности.
Атомы в них располагаются
в трёхмерно-периодической
кристаллической решётке,
т.е. образуют
пространственную
дифракционную решётку
для соответствующих длин
волн.
16

17.

х
Дифракции электронов на монокристаллах никеля
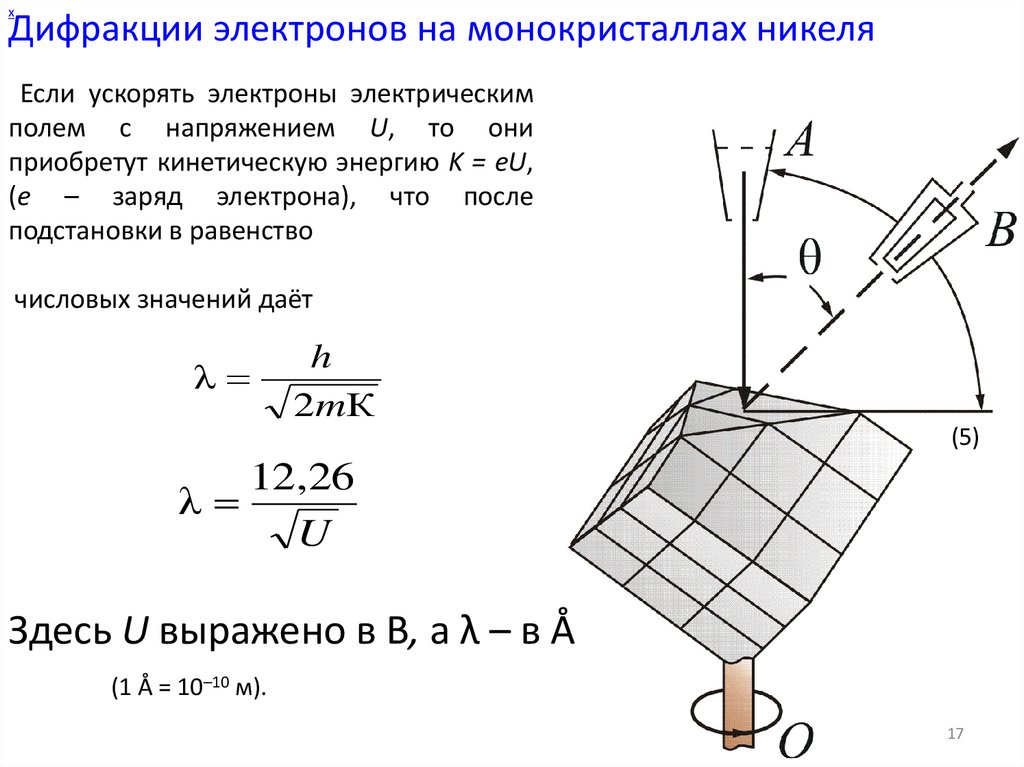
Если ускорять электроны электрическим
полем с напряжением U, то они
приобретут кинетическую энергию K = eU,
(е – заряд электрона), что после
подстановки в равенство
числовых значений даёт
λ
h
2 mК
(5)
12,26
λ
U
Здесь U выражено в В, а λ – в Å
(1 Å = 10–10 м).
17

18.

х
Дифракции электронов на монокристаллах никеля
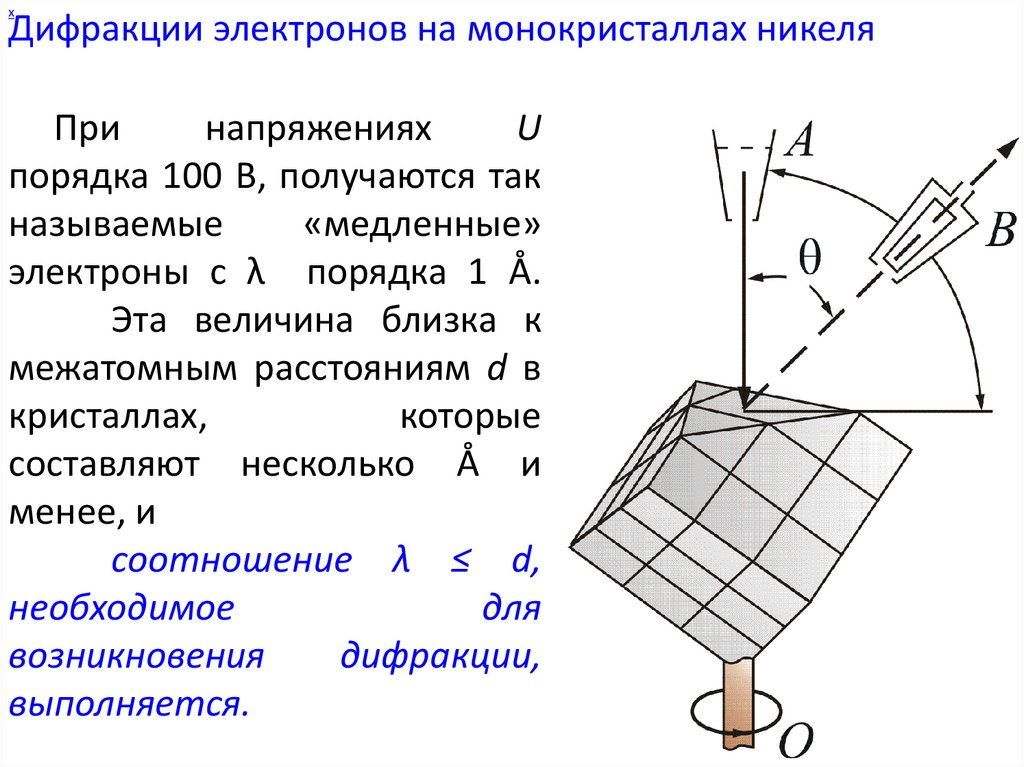
При
напряжениях
U
порядка 100 В, получаются так
называемые
«медленные»
электроны с λ порядка 1 Å.
Эта величина близка к
межатомным расстояниям d в
кристаллах,
которые
составляют несколько Å и
менее, и
соотношение λ ≤ d,
необходимое
для
возникновения
дифракции,
выполняется.
18

19. Тест на экзамене

20.

U

21.

Отражение электронов от атомных плоскостей в
кристалле.
Атомная структура кристаллов была известна из опытов по
дифракции рентгеновских волн. Еще в 1912 – 1913 гг. английские
физики Г. Брэгг и Л. Брэгг (отец и сын) предложили вместо
сложной дифракции от множества атомов рассматривать
отражение волн от параллельных атомных плоскостей в
кристалле и интерференцию отраженных волн.
Атомные плоскости в
Б
2
d
sin
n
кристалле
0,165 нм
d 0,091 нм
2
Б
0,166 нм
2meeU
d
d1

22. Дифракция электронов на кристаллической решетке

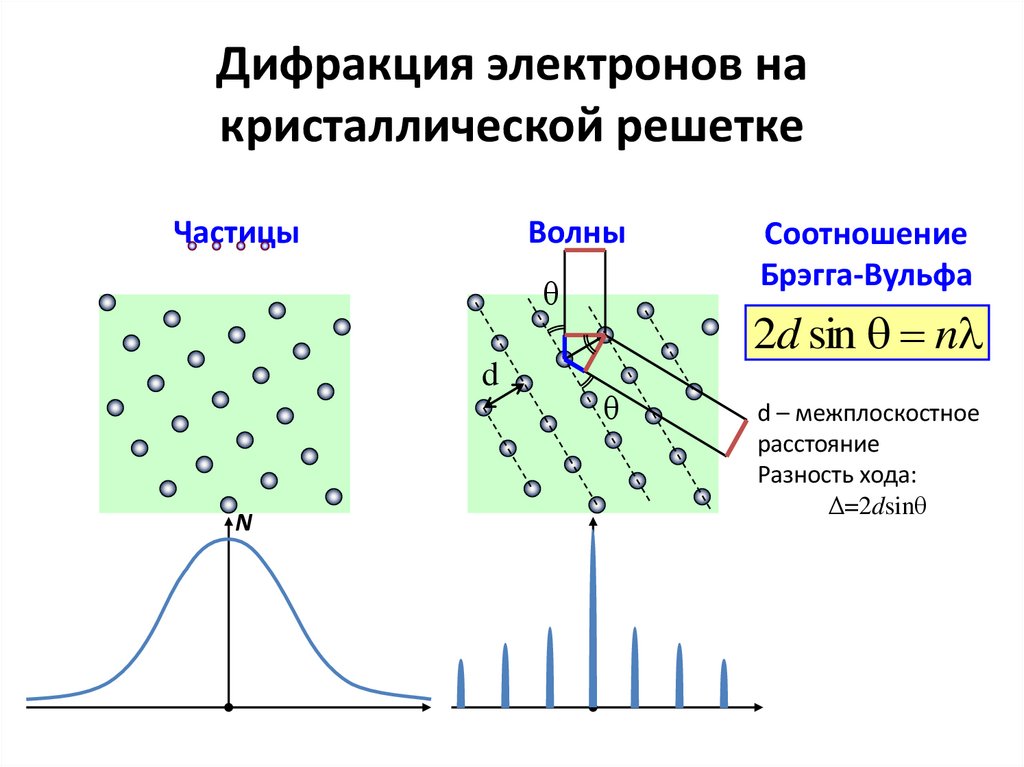
Частицы
Волны
θ
d
N
Соотношение
Брэгга-Вульфа
2d sin n
θ
d – межплоскостное
расстояние
Разность хода:
Δ=2dsinθ

23.

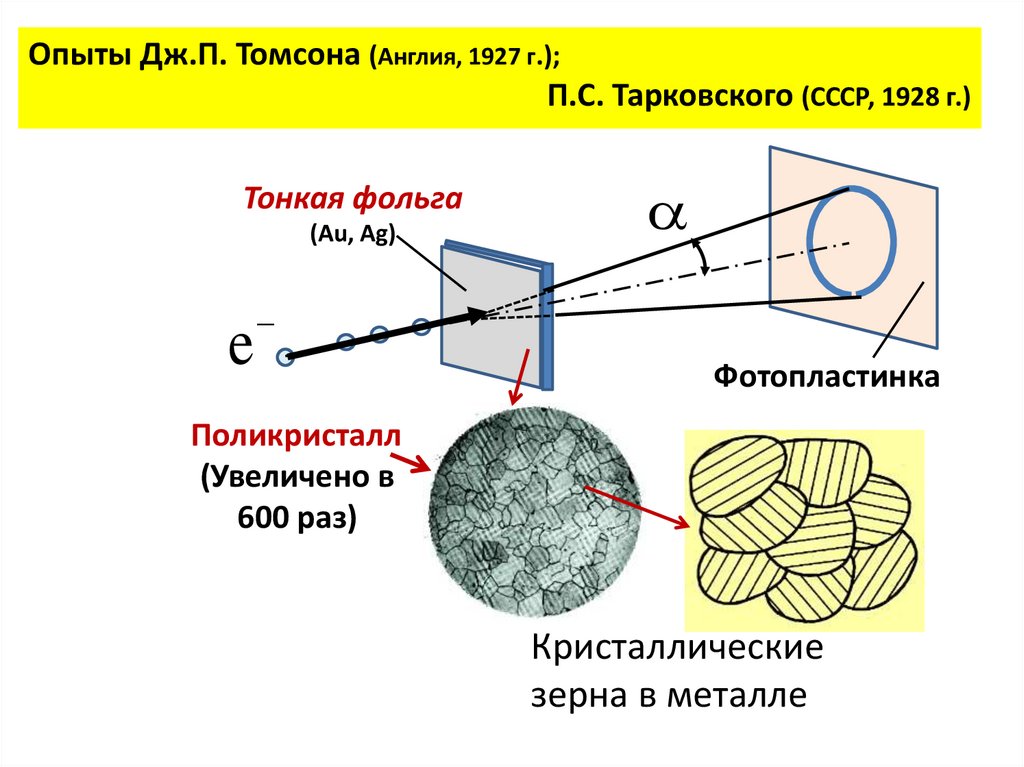
Опыты Дж.П. Томсона (Англия, 1927 г.);
П.С. Тарковского (СССР, 1928 г.)
Тонкая фольга
(Au, Ag)
e
Фотопластинка
Поликристалл
(Увеличено в
600 раз)
Кристаллические
зерна в металле

24.

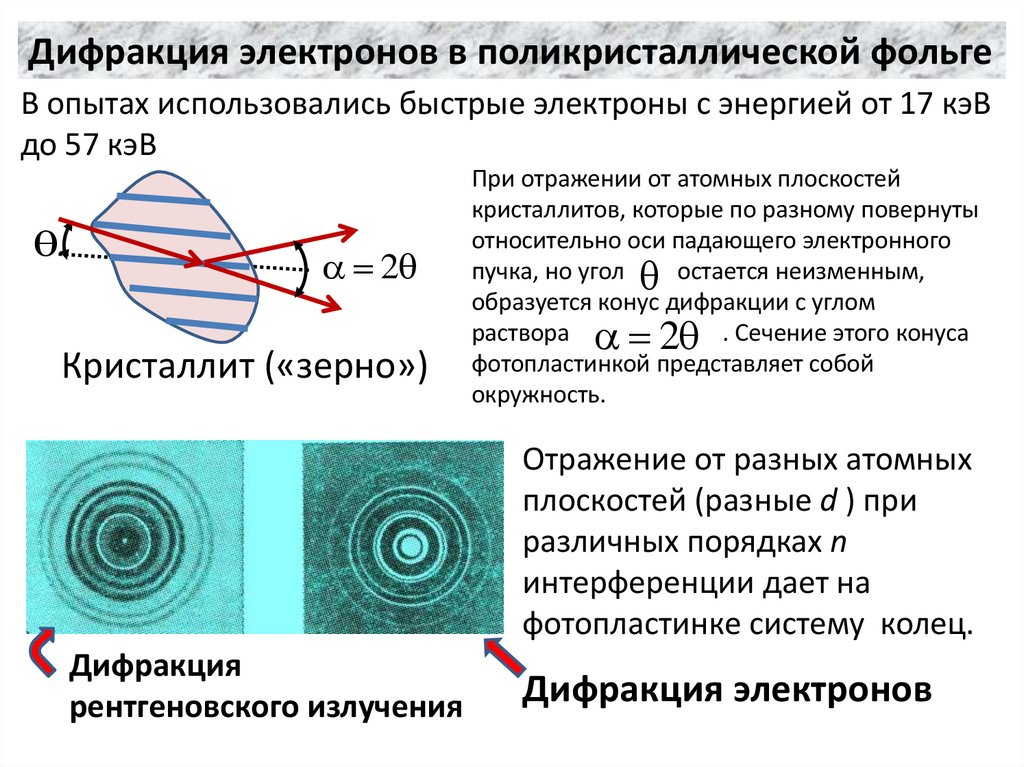
Дифракция электронов в поликристаллической фольге
В опытах использовались быстрые электроны с энергией от 17 кэВ
до 57 кэВ
2
Кристаллит («зерно»)
При отражении от атомных плоскостей
кристаллитов, которые по разному повернуты
относительно оси падающего электронного
пучка, но угол
остается неизменным,
образуется конус дифракции с углом
раствора
. Сечение этого конуса
фотопластинкой представляет собой
окружность.
2
Отражение от разных атомных
плоскостей (разные d ) при
различных порядках n
интерференции дает на
фотопластинке систему колец.
Дифракция
рентгеновского излучения
Дифракция электронов

25. Дифракция одиночных электронов

Группа физиков во главе с В.А.Фабрикантом в СССР выполнила в 1949г
дифракционные исследования с очень слабым электронным пучком. В
этих опытах интервал времени между двумя последовательными
прохождениями электронов через поликристалл в 81 раз превышал
время, затрачиваемое одним электроном на прохождение всего прибора.
Таким образом, взаимодействие электронов друг с другом полностью
исключалось, и электроны дифрагировали поодиночке.
Дифракция
одиночных
электронов
Волновые свойства присущи отдельному
электрону.

26.

27.

Картина дифракции
электронов на слюде

28.

Картина дифракции
нейтронов на кварце

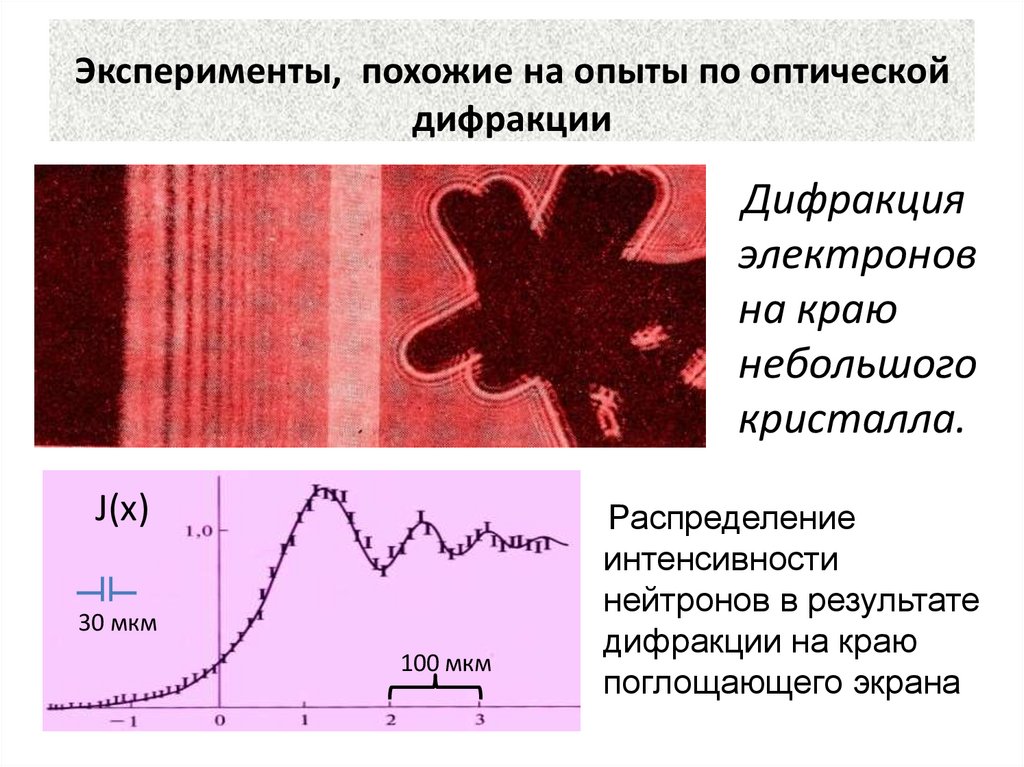
29. Эксперименты, похожие на опыты по оптической дифракции

Дифракция
электронов
на краю
небольшого
кристалла.
J(x)
30 мкм
100 мкм
Распределение
интенсивности
нейтронов в результате
дифракции на краю
поглощающего экрана

30. Тест на экзамене

31.

О новой механике движения микрочастиц – квантовой
механике
На заре квантовой механики (1920-е годы) физики
пытаются
найти
законы,
определяющие
движение
микрочастицы (электрона) в различных условиях, не прибегая
к моделям внутренней структуры. Так например, электрон в
дифракционных экспериментах
с поликристаллической
фольгой с некоторой вероятностью меняет свое направление
движения после фольги, но фиксируется на фотопластинке как
точечная частица.
Задача: Выяснить особенности физического и
математического описания движения микрообъекта,
совмещающего в себе каким-то образом
корпускулярные и волновые свойства.

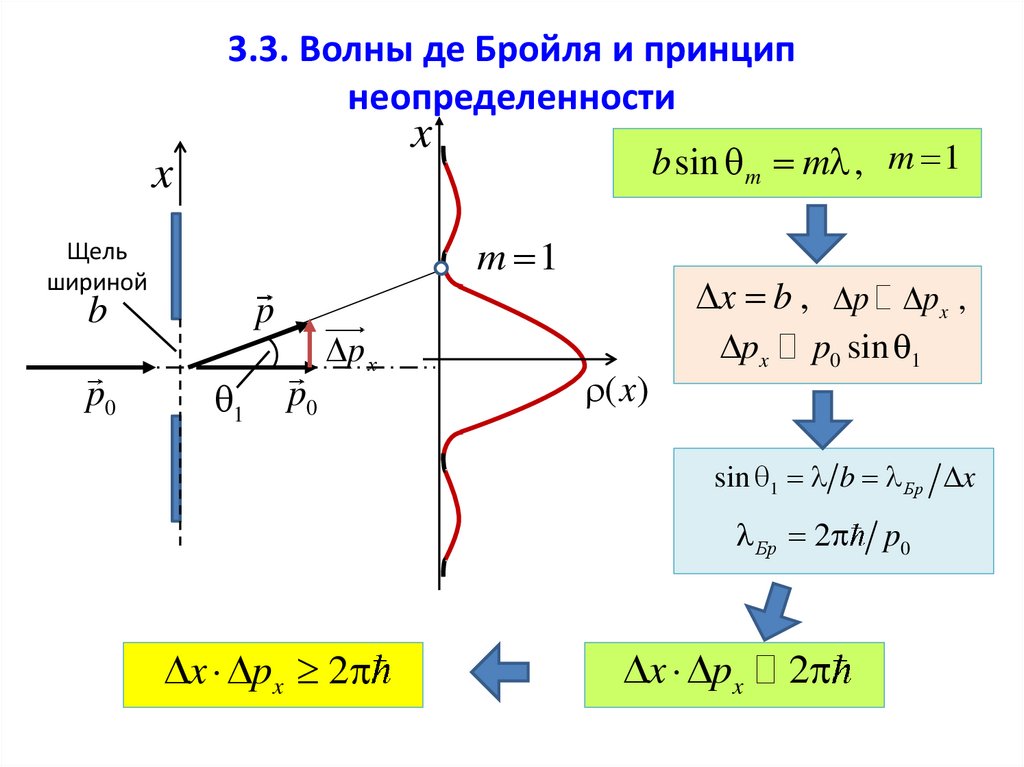
32. 3.3. Волны де Бройля и принцип неопределенности

x
x
m 1
Щель
шириной
p
b
p0
b sin m m , m 1
1
p х
p0
x b , p px ,
( x)
px
p0 sin 1
sin 1 b Бр x
Бр 2
x px 2
x px
2
p0

33. Строгое соотношение Гейзенберга для среднеквадратичных отклонений

xкв x ( x x )
2
2
pкв p ( p p )
2
xкв pкв
2
2

34.

Еще до начала экспериментов о дифракции электронов физики-теоретики
Вернер Гейзенберг в Германии и Эрвин Шредингер в Австрии начали
разрабатывать новую механику, позволяющую рассчитывать волновое движение
не только свободных микрочастиц, как это было у де Бройля, но и частиц ,
находящихся во внешнем потенциальном поле.
Одним из важных физических принципов такого описания является
соотношения неопределенностей Гейзенберга:
x px
2
y p y
2
z pz
В 1926 г. Шредингер получил свое знаменитое уравнение для волновой
пси-функции (r , t ) и применил его к атому водорода, в котором
единственный электрон находится в электрическом поле протона .
Шредингер о первых опытах по дифракции:
электронов:
«Некоторые исследователи приступили к выполнению
опыта за который ещё несколько лет назад их бы посадили
в психиатрическую больницу для наблюдения за их
душевным состоянием. Но они добились успеха !»
2

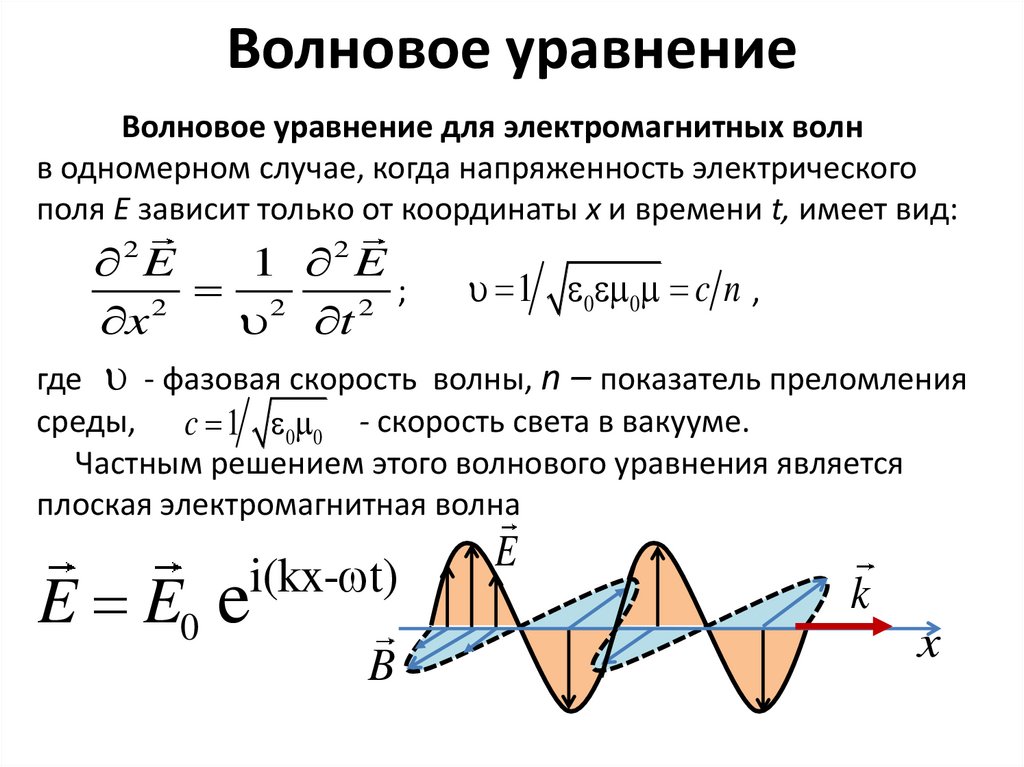
35. Волновое уравнение

Волновое уравнение для электромагнитных волн
в одномерном случае, когда напряженность электрического
поля E зависит только от координаты x и времени t, имеет вид:
2 E
1 2 E
2
;
2
2
x
t
1 0 0 c n ,
где - фазовая скорость волны, n – показатель преломления
среды, c 1 0 0 - скорость света в вакууме.
Частным решением этого волнового уравнения является
плоская электромагнитная волна
i(kx- t)
E E0 e
B
E
k
x

36. 3.4.Волновое уравнение Шредингера

В 1926 г. австрийский физик-теоретик Эрвин Шредингер разработал теорию
движения микрочастиц, в основу которой положил уравнение
2
U ( x) i
2
2m x
t
2
Одномерное
движение: ( x, t )
U ( x, y , z ) i
,
2m
t
2
2
где ( x, y, z, t );
2
2
2
2
2 2 2
x
y
z

37.

х
Если силовое поле, в котором движется частица
потенциально, то функция U не зависит явно от времени
и имеет смысл потенциальной энергии.
В этом случае решение уравнения Шредингера
распадается на два сомножителя, один из которых
зависит только от координаты, а другой – только от
времени.
E
i t
Ψ( x, y, z, t ) Ψ( x, y, z )e
Здесь E – полная энергия частицы, которая в случае
стационарного поля остается постоянной.

38.

Уравнение Шредингера для стационарных состояний
2m
Ψ 2 ( E U )Ψ 0
2
Е - полная энергия электрона
U - потенциальная энергия
-волновая функция электрона
( x , y, z )

39.

х
Уравнение Шредингера для стационарных
состояний
2m
Ψ 2 ( E U )Ψ 0
2
можно переписать в виде:
H Ψ EΨ
2
– оператор Гамильтона,
U H равный сумме операторов
2m
Гамильтониан является оператором энергии E.

40.

Какой смысл имеет пси-функция ???
В свое время среди физиков была популярной
эпиграмма на Шредингера:
Erwin with his psi can do
Calculations quite a few.
But one thing has not been seen
Just what does psi really means
Эрвин с помощью своей пси-функции
Может многое вычислить.
Но одно лишь неясно –
Что в действительности она означает?

41. Вероятностный смысл

функции
Почти вся теория Шредингера заключена в его волновом уравнении,
если мы знаем, как интерпретировать волновую функцию .
В том же 1926 г. немецкий физик – теоретик Макс Борн
предложил статистический (вероятностный) смысл
функции :
2
dW dV dV - вероятность dW
обнаружения частицы в элементарном объёме dV .
Величина dW
dV - плотность вероятности
2
Функцию называют амплитудой вероятности

42.

2

43.

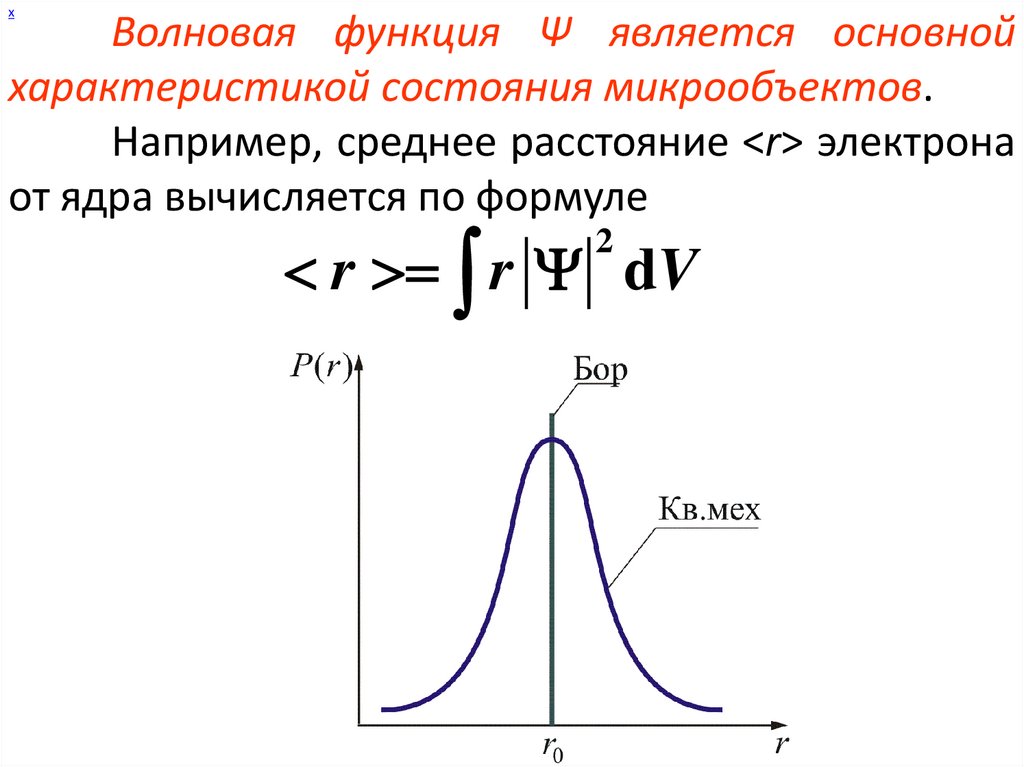
х
Волновая функция Ψ является основной
характеристикой состояния микрообъектов.
Например, среднее расстояние <r> электрона
от ядра вычисляется по формуле
r r dV
2

44.

dV
1
2
V

45.

Вероятность в классической физике
В классической физике статистические методы, использующие
понятие вероятности, рассматриваются как вспомогательные,
и применяются в тех случаях, когда недостаточно знаний
о подробностях того или иного события.
Так обстоит дело, например, в кинетической теории газов, где
предполагается, что каждая частица во всякий данный момент
времени имеет определенное значение скорости.
Но частиц много, уследить за всеми невозможно,
и единственный реальный путь заключается в том,
чтобы найти закономерности в этом хаотичном
движении многих частиц – вычислить вероятность
распределения частиц по скоростям.

46.

Вероятность в квантовой физике
В 1926 г. немецкий физик-теоретик Макс Борн предложил
статистический смысл волны де Бройля:
« Интенсивность волны де Бройля в каком-либо месте пространства
пропорциональна вероятности обнаружения частицы в этом месте».
В квантовой физике, согласно М.Борну, ситуация совсем иная.
Электронам, протонам, фотонам и другим частицам присущи
волновые свойства.
Нет смысла, например, говорить о локализации световой волны
после дифракции на щели или траектории фотонов.
Фотон может попасть в любое место экрана наблюдения
с той или иной вероятностью. Это касается и микрочастиц, для
описания движения которой понятие определенной и
непрерывной траектории оказывается неприменимым.
При рассмотрении процессов , происходящих в микромире,
неизбежно приходится использовать понятие
волны вероятности

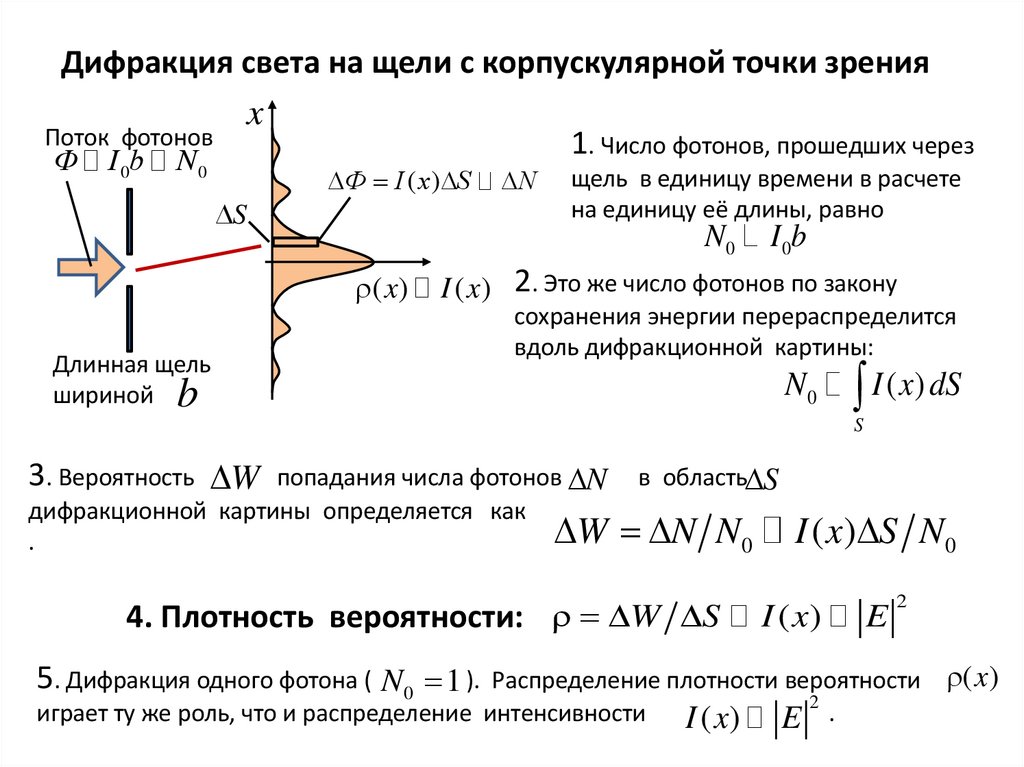
47.

Дифракция света на щели с корпускулярной точки зрения
Поток фотонов
Ф
I 0b
x
N0
S
1. Число фотонов, прошедших через
Ф I ( x) S
щель в единицу времени в расчете
на единицу её длины, равно
N0
( x)
Длинная щель
шириной
N
I 0b
I ( x) 2. Это же число фотонов по закону
сохранения энергии перераспределится
вдоль дифракционной картины:
N0
b
I ( x) dS
S
3. Вероятность W попадания числа фотонов N
дифракционной картины определяется как
.
в область S
W N N0
4. Плотность вероятности: W S
I ( x) S N0
I ( x)
E
2
5. Дифракция одного фотона ( N 0 1 ). Распределение плотности вероятности ( x)
2
играет ту же роль, что и распределение интенсивности
I ( x) E .

48.

О вероятности обнаружения электрона,
который свободно движется в направлении оси x
e
S
( x, t ) A cos(kx t ) i sin(kx t , или
p
i ( x E t )
( x, t ) A e
x
A
2
2

49.

Макс Борн: «Интенсивность волны де Бройля в каком-либо месте
пространства пропорциональна вероятности обнаружения частицы
в этом месте».
e
S
2
( x, t ) A e
x
Пусть через S 1 м 2 за время
t 1 c
W V S t 1
2
A
p
i ( x E t )
2
2
проходит один электрон, тогда
A me p
2
В классической физике статистические методы, использующие понятие
вероятности, рассматриваются как вспомогательные, и применяются в тех
случаях, когда недостаточно знаний о подробностях того или иного события.
В квантовой физике, согласно М.Борну, ситуация совсем иная.
Электронам, протонам, фотонам и другим частицам присущи волновые свойства.
Нет смысла, например, говорить о локализации световой волны после дифракции
на щели или траектории фотонов. Фотон может попасть в любое место экрана
наблюдения с той или иной вероятностью. Это касается и микрочастиц, для
описания движения которой понятие определенной и непрерывной траектории
оказывается неприменимым. При рассмотрении процессов, происходящих в
микромире, неизбежно приходится использовать понятие волны вероятности.

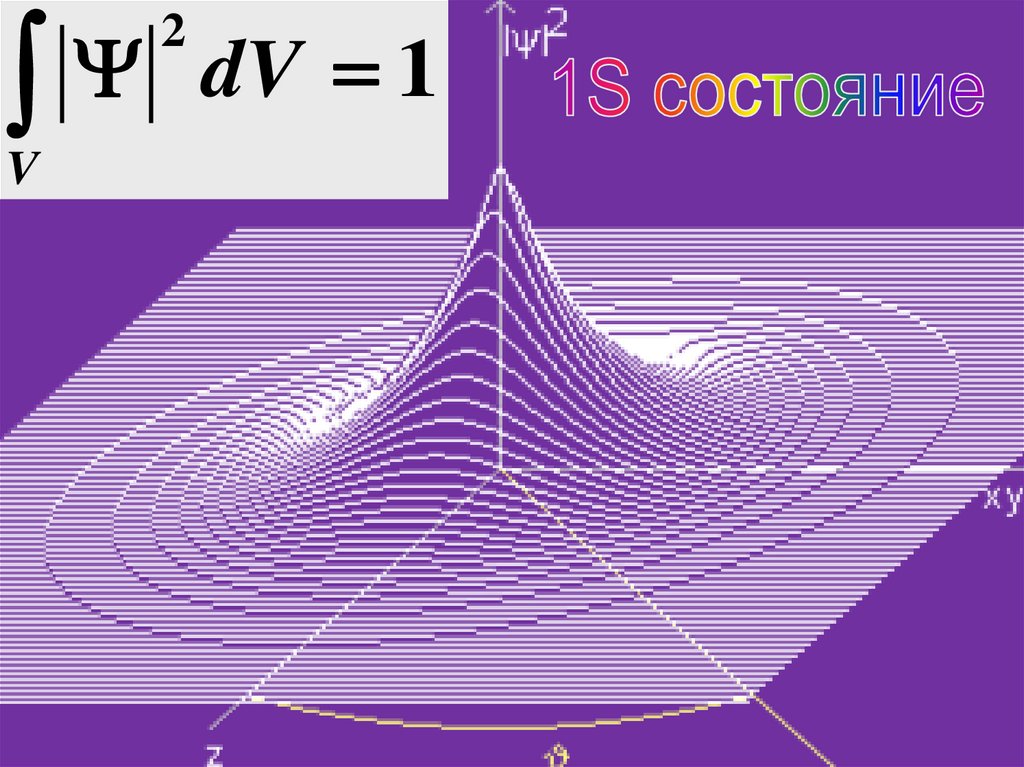
50. 3.5. Свойства волновой функции

1. Из понятия плотности вероятности
2
следует условие
нормировки:
Если известно, что частица находится в объеме V
(достоверное событие), то
2
dV 1
V
2.
dV
V
функция должна быть конечной и однозначной. Только при
этом её физическая интерпретация как амплитуда вероятности имеет
смысл.
3.
непрерывная и гладкая функция.
1 ( x0 ) 2 ( x0 )
1
x0
x
2
1
2
x x
x x
0
1
0
x0
x
2

51. Свойства волновой функции

4. Волновая функция описывает квантовое состояние
частиц. Она содержит в себе всю возможную информацию о
состоянии частицы.
Допускает опытную проверку в том смысле, что позволяет
вычислить вероятности возможных результатов
экспериментальных измерений
5.Кроме указанных стандартных ограничений на функцию
могут накладываться дополнительные условия из
соображений симметрии.