Similar presentations:
Корпускулярно-волновой дуализм
1. Корпускулярно-волновой дуализм
1924 г. Луи де БройльE
,
2
,
p
k
p
Луи Виктор Пьер Раймон, 7-й герцог де Бройль
Свободная частица плоская волна
i
( r, t ) exp i( t kr) exp ( Et pr)
Нобелевская премия 1929 г.
© К.К.Боярский 2009
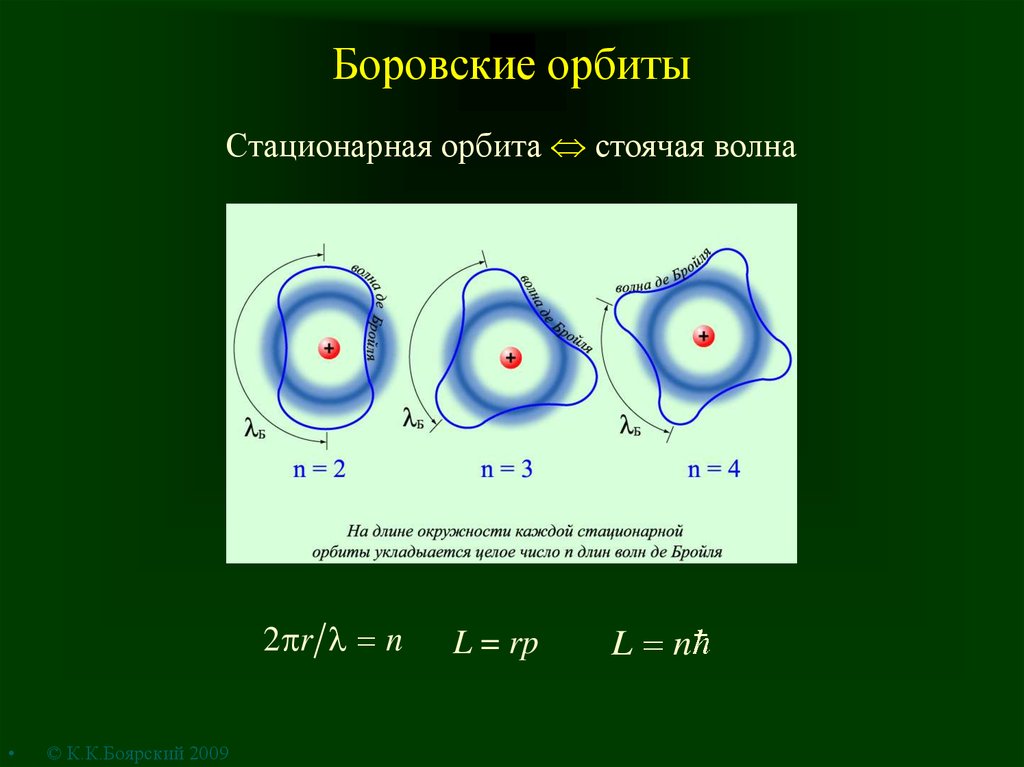
2. Боровские орбиты
Стационарная орбита стоячая волна2 r n
© К.К.Боярский 2009
L = rp
L n
3. Волновая функция
1926 г. Макс БорнКвадрат модуля волновой функции
определяет вероятность обнаружения
частицы в данном состоянии.
dP A r, t dV A dV
2
Условие нормировки
E
vф ,
p
E p 2 2m
E
p2c2 m02c4 mc2
© К.К.Боярский 2009
2
dV 1
dE
u Нобелевская премия 1954 г.
dp
u dE dp p m v
c2 p
u
E
uvф c2
4. Принцип суперпозиции
Если частица может находиться в квантовом состоянии,описываемом волновой функцией 1, а также в другом
квантовом состоянии, описываемом волновой функцией 2,
то эта частица может также находиться в состоянии,
описываемом волновой функцией = C1 1+ C2 2
Величина |Ci|2 определяет вероятность того, что при измерении,
проведенном над системой с волновой функцией , мы
обнаружим ее в квантовом состоянии, описываемом волновой
функцией i.
© К.К.Боярский 2009
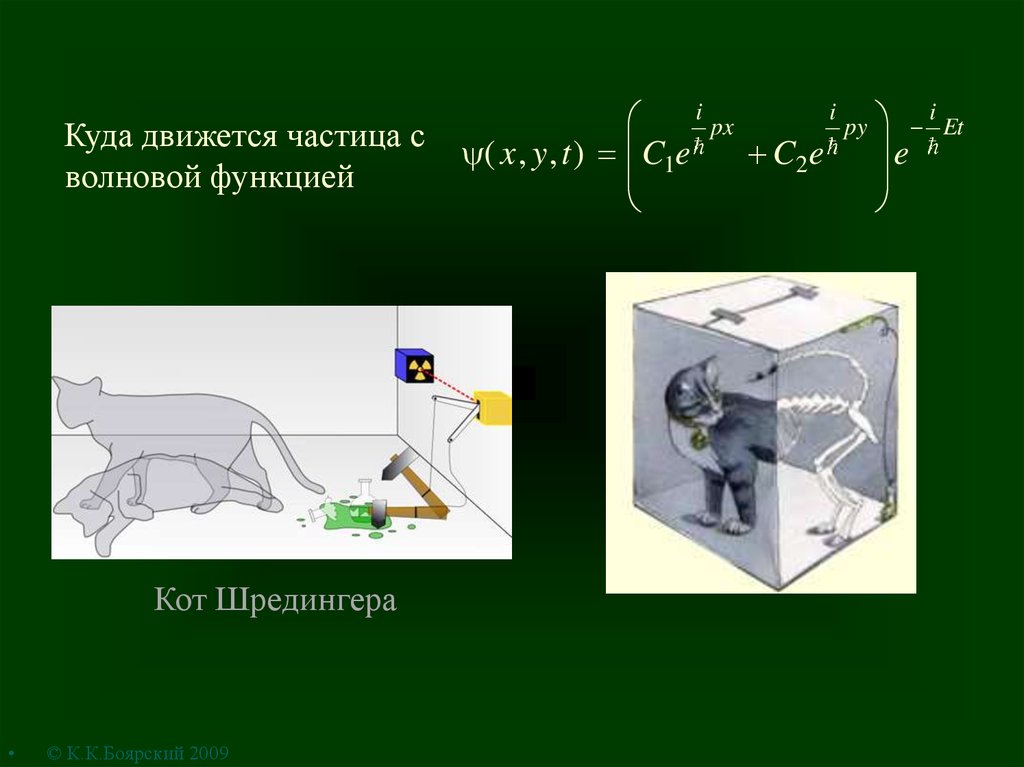
5.
Куда движется частица сволновой функцией
Кот Шредингера
© К.К.Боярский 2009
i
i
i
px
py Et
e
( x , y , t ) C1e
C2 e
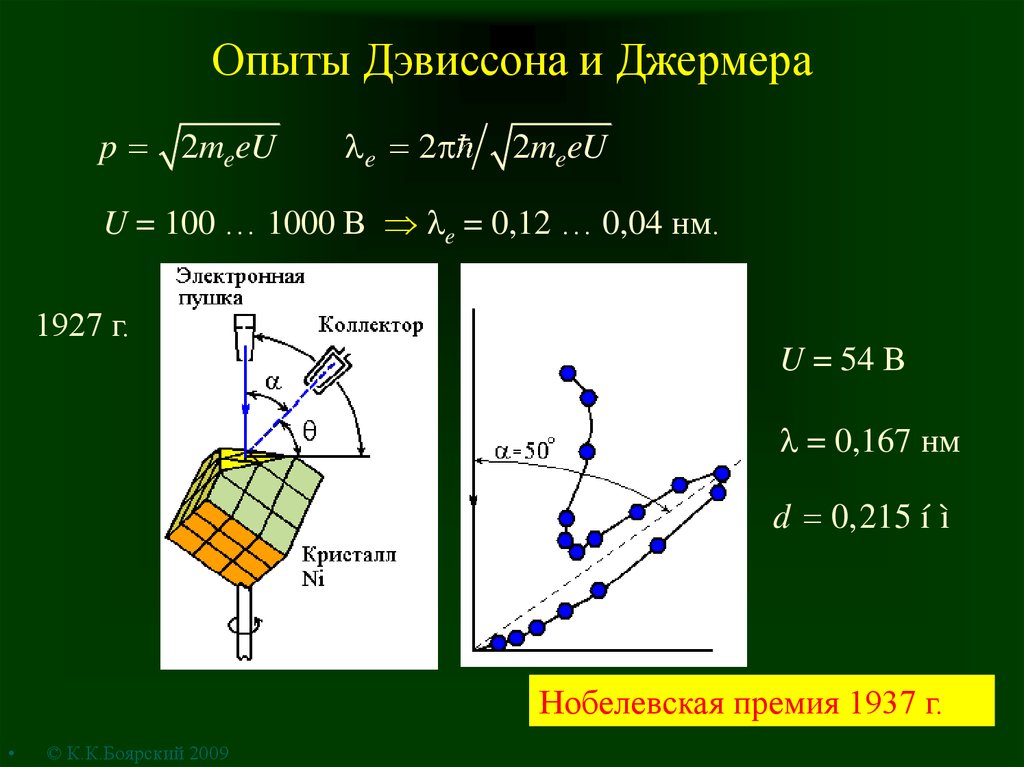
6. Опыты Дэвиссона и Джермера
p 2meeUe 2
2meeU
U = 100 … 1000 В e = 0,12 … 0,04 нм.
1927 г.
U = 54 В
= 0,167 нм
d 0,215 í ì
Нобелевская премия 1937 г.
© К.К.Боярский 2009
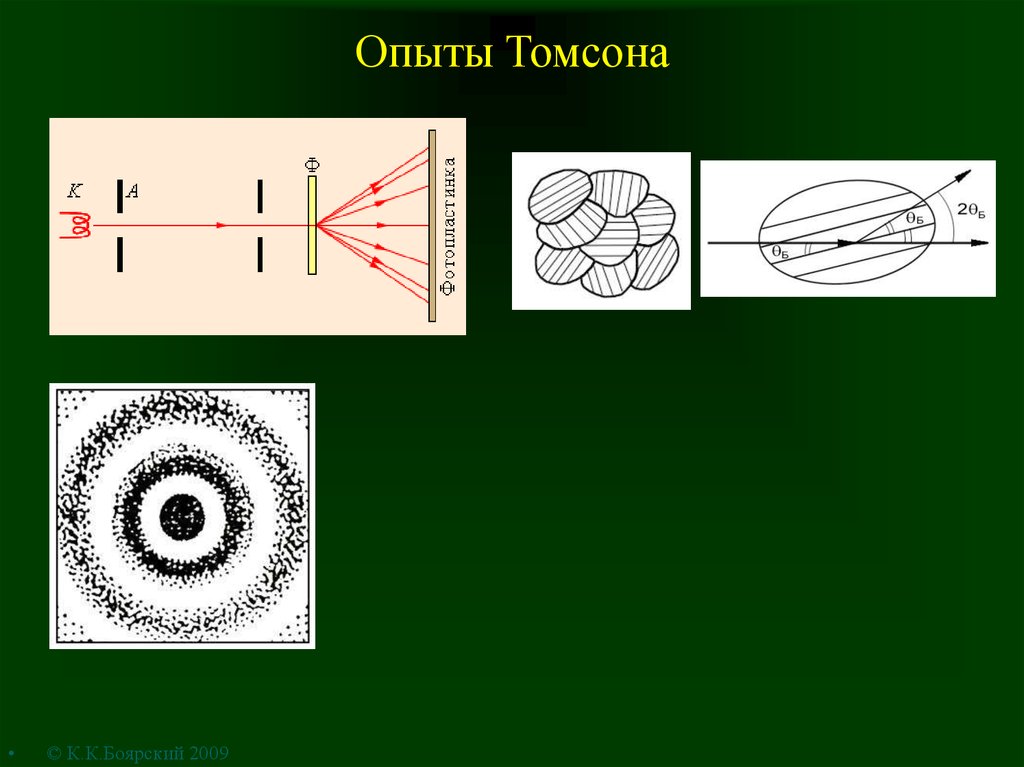
7. Опыты Томсона
© К.К.Боярский 2009
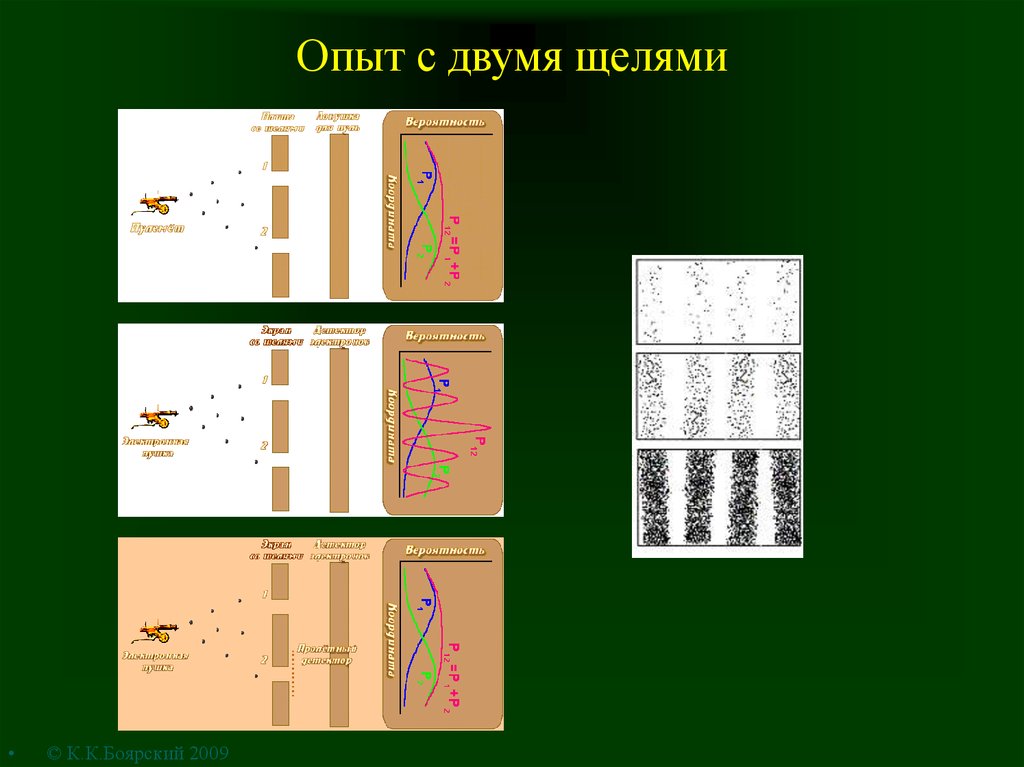
8. Опыт с двумя щелями
© К.К.Боярский 2009
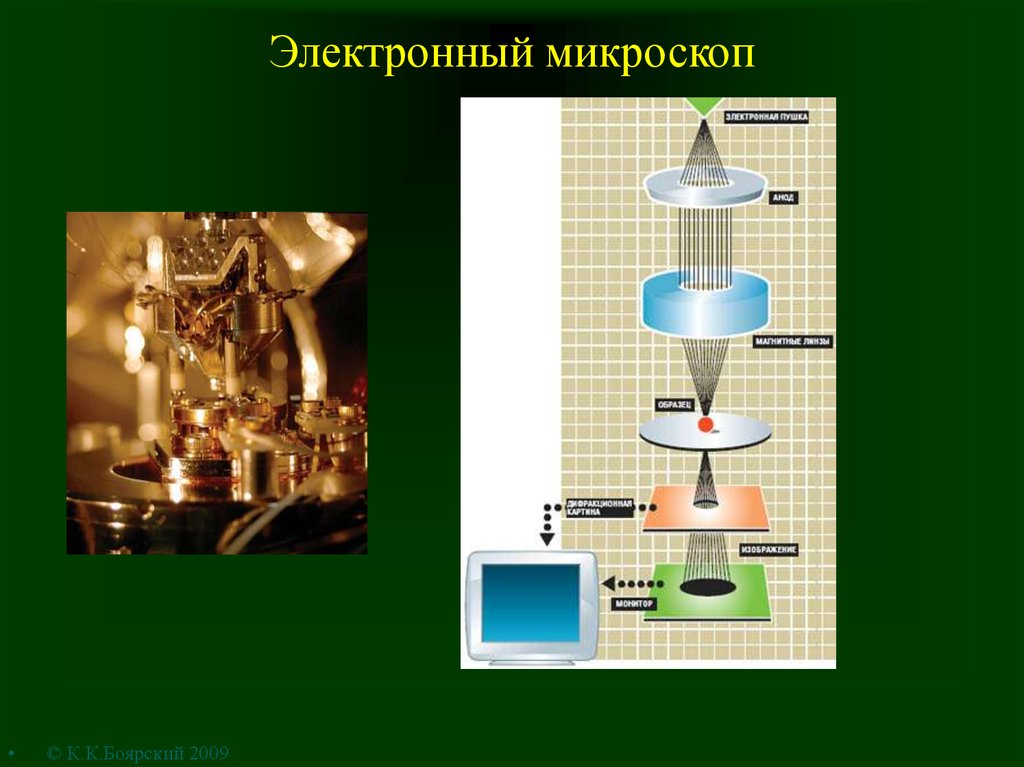
9. Электронный микроскоп
© К.К.Боярский 2009
10. Принцип неопределенности
Вернер Гейзенберг, 1927 г.sin px p x
x px
2
t E
2
1928 г. Н. Бор выдвинул принцип дополнительности, в соответствии с
которым описание состояния в квантовой механике распадается на два
взаимоисключающих класса, совокупность которых могла бы дать в
классическом понимании полное описание системы.
Нобелевская премия 1932 г.
© К.К.Боярский 2009




 physics
physics