Similar presentations:
Лекция 21 (4). Корпускулярно-волновой дуализм. Уравнение Шрёдингера
1. Корпускулярно-волновой дуализм Уравнение Шрёдингера
ВоГТУЛекция 21 (4)
Корпускулярно-волновой
дуализм
Уравнение Шрёдингера
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.
1
2. План
1. Экспериментальное обоснование основных идей квантовой теории1.1. Коротковолновая граница сплошного рентгеновского спектра
1.2. Опыт Боте
2. Связь между волновой и корпускулярной картинами
3. Гипотеза де Бройля
4. Микрочастица в двухлучевом интерферометре
5. Соотношение неопределённостей
6. Волновая функция, её вероятностная интерпретация и свойства
7. Уравнение Шрёдингера
7.1. Нестационарное (временное) уравнение Шрёдингера
7.2. Стационарное уравнение Шрёдингера
7.3. Собственные функции, собственные значения
8. Применение уравнения Шрёдингера
9.1. Одномерное движение свободной частицы
9.2. Частица в одномерной потенциальной яме с бесконечно высокими стенками
9.3. Линейный гармонический осциллятор
а) Классический
б) Квантовый
9.4. Ангармонический осциллятор
а) Классический
б) Квантовый
2
9.5. Туннельный эффект
3.
Экспериментальное обоснованиеосновных идей квантовой теории
Волновые свойства света проявляются в явлениях:
•интерференции,
•дифракции,
•поляризации
Явления:
•фотоэффекта,
•комптоновского рассеяния,
•тепловое излучение
могут быть объяснены только корпускулярными свойствами.
К экспериментальному обоснованию квантовых свойств
относятся:
1. существование коротковолновой границы сплошного
рентгеновского спектра;
2. опыт Боте
4.
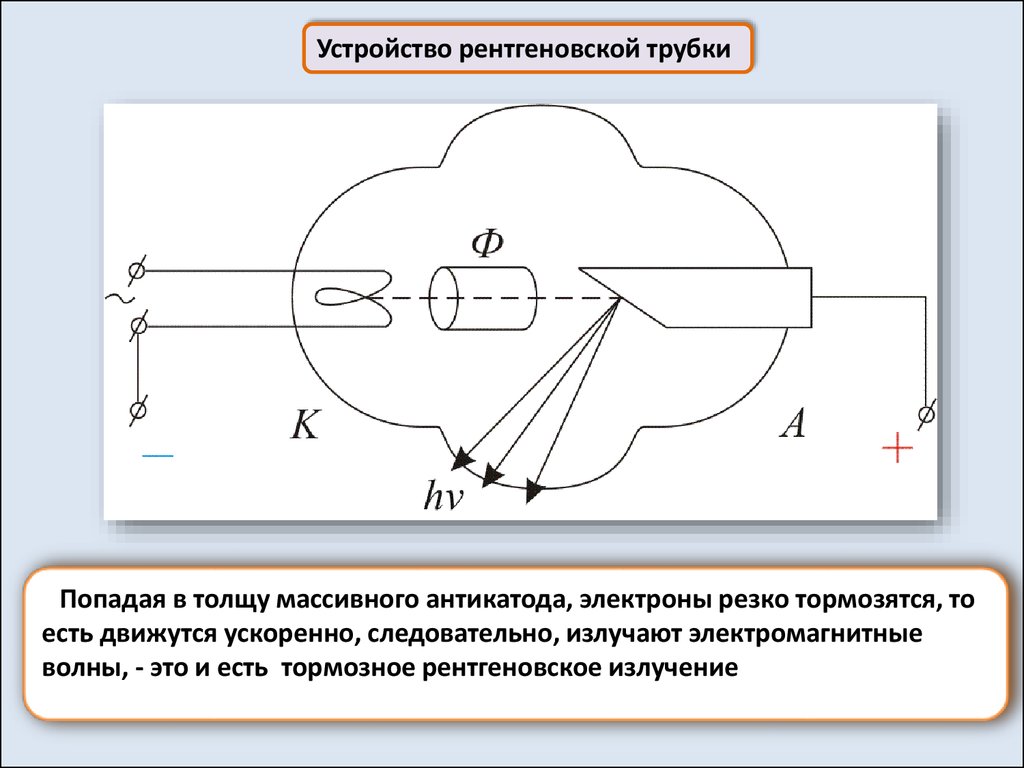
Устройство рентгеновской трубкиПопадая в толщу массивного антикатода, электроны резко тормозятся, то
есть движутся ускоренно, следовательно, излучают электромагнитные
волны, - это и есть тормозное рентгеновское излучение
5.
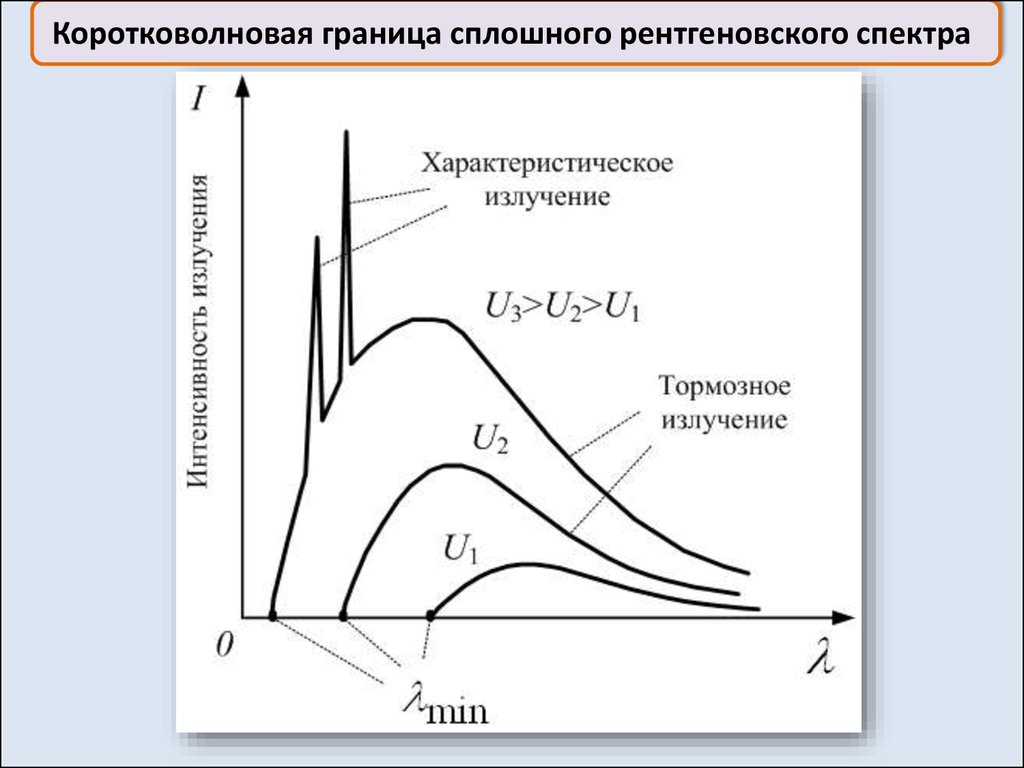
Коротковолновая граница сплошного рентгеновского спектра6.
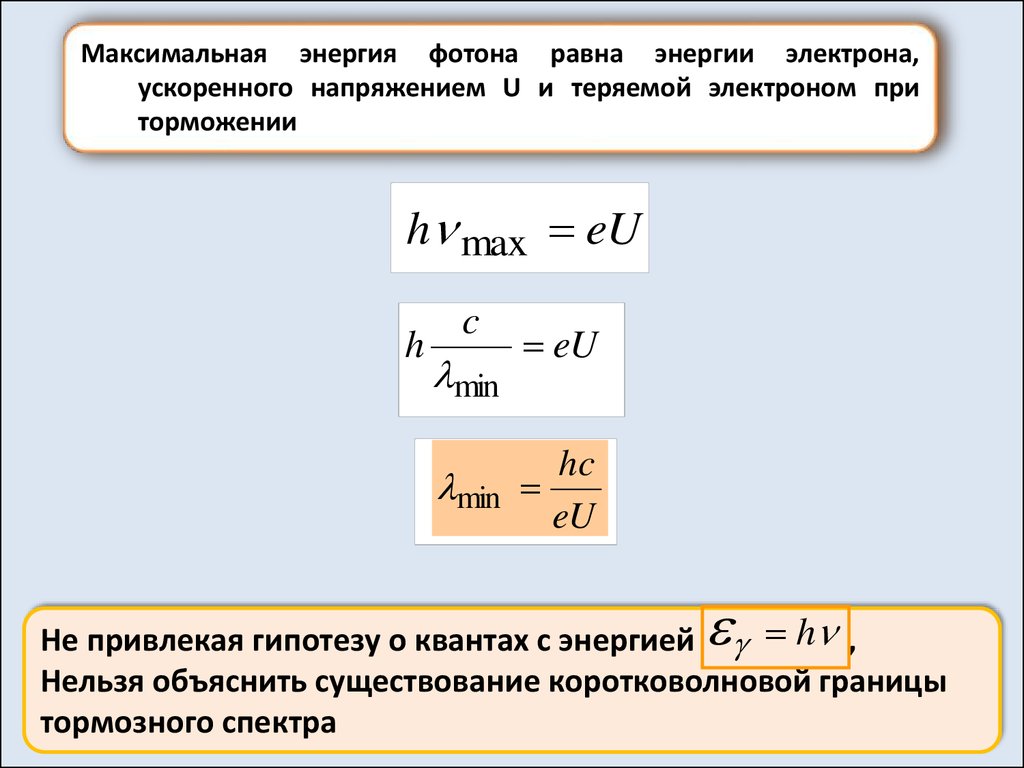
Максимальная энергия фотона равна энергии электрона,ускоренного напряжением U и теряемой электроном при
торможении
h max eU
h
c
min
eU
hc
min
eU
Не привлекая гипотезу о квантах с энергией h ,
Нельзя объяснить существование коротковолновой границы
тормозного спектра
7.
Опыт Боте8.
Опыт БотеЭтот опыт должен был дать ответ на вопрос, как же происходит
электромагнитное излучение: как волна или как поток дискретных частиц –
фотонов
Металлическая фольга облучается рентгеновским излучением и сама, в
свою очередь, становится источником рентгеновского излучения
Счётчики Гейгера, расположенные симметрично, фиксируют вторичные Rлучи
Если бы вторичное излучение распространялось в виде сферических
волн, оба счётчика должны срабатывать одновременно, и на ленте
самописца отметки слева и справа совпадали бы
Опыт дал другие результаты: счётчики срабатывали случайным
образом, неодновременно
Это значит, что при излучении возникали отдельные фотоны,
попадавшие либо в один счётчик, либо в другой
9.
Связь между волновой и корпускулярной картинамиСвет обнаруживает корпускулярно-волновой дуализм:
обладает и свойствами волн, и свойствами частиц
Эти свойства с макроскопической точки зрения
противоречат друг другу:
волна непрерывна, частица – дискретна;
волна – безгранична, частица – ограничена в пространстве
Установить связь между волновой и корпускулярной
картинами можно с помощью статистического подхода
10.
Связь между волновой и корпускулярной картинамиЭлектромагнитная волна:
E E0 cos t k r
Вероятность dp того, что фотон будет обнаружен в малом
объёме dV вблизи точки с радиус-вектором r
(или координатами x,y,z),
пропорциональна квадрату амплитуды волны и объёму:
dp E02 dV
Распределение фотонов носит статистический характер
Квадрат амплитуды волны определяет вероятность попадания
фотона в данную точку
11.
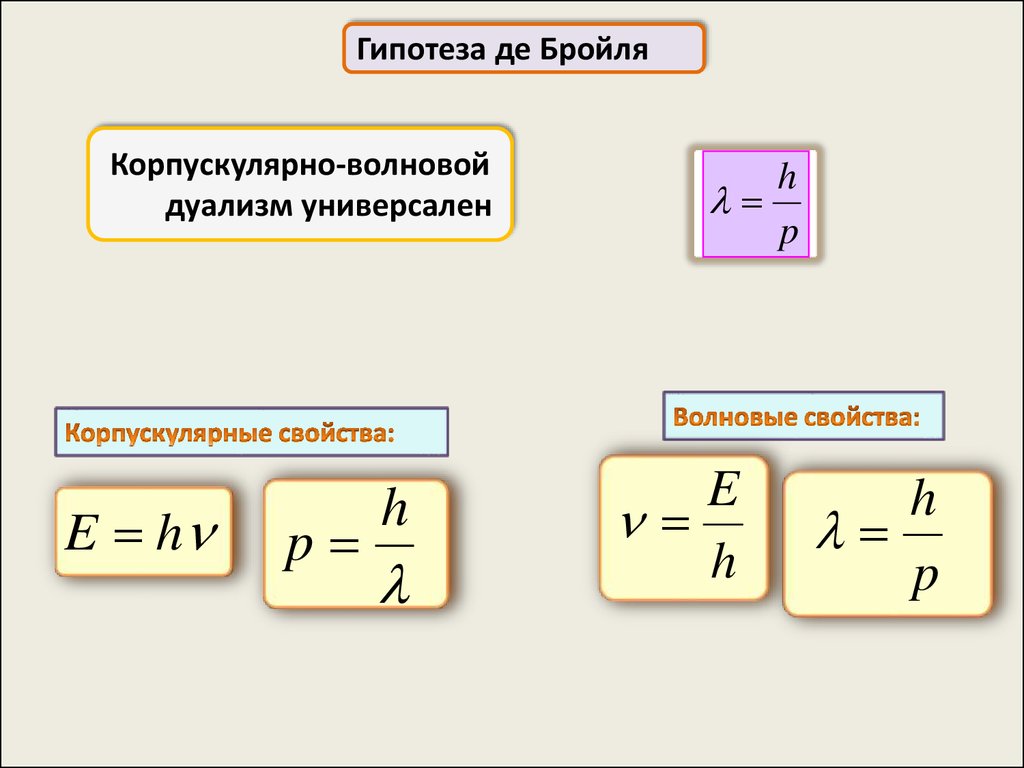
Гипотеза де БройляКорпускулярно-волновой
дуализм универсален
Частицы обладают
волновыми свойствами
Существует симметрия: если свет (волна) обладает корпускулярными
свойствами, то почему бы частицам не проявлять свойства волновые?
Движущейся частице с импульсом р и энергией Е
сопоставлена волна длиной
h
p
12.
Гипотеза де БройляКорпускулярно-волновой
дуализм универсален
E h
p
h
h
p
E
h
h
p
13.
Движущейся частице с импульсом р и энергией Есопоставлена волна
0 cos t k r
Из энергии получаем частоту:
h
E h
2
2
E
Из импульса получаем волновой вектор:
2
2
2 p p
k
h
h
p
14.
Гипотеза де Бройля0 cos t k r
p
k
E
p
E
0 cos t r
Для волны, бегущей вдоль оси OX
(частицы, движущейся
параллельно оси OX):
p
E
( x) 0 cos t x
15.
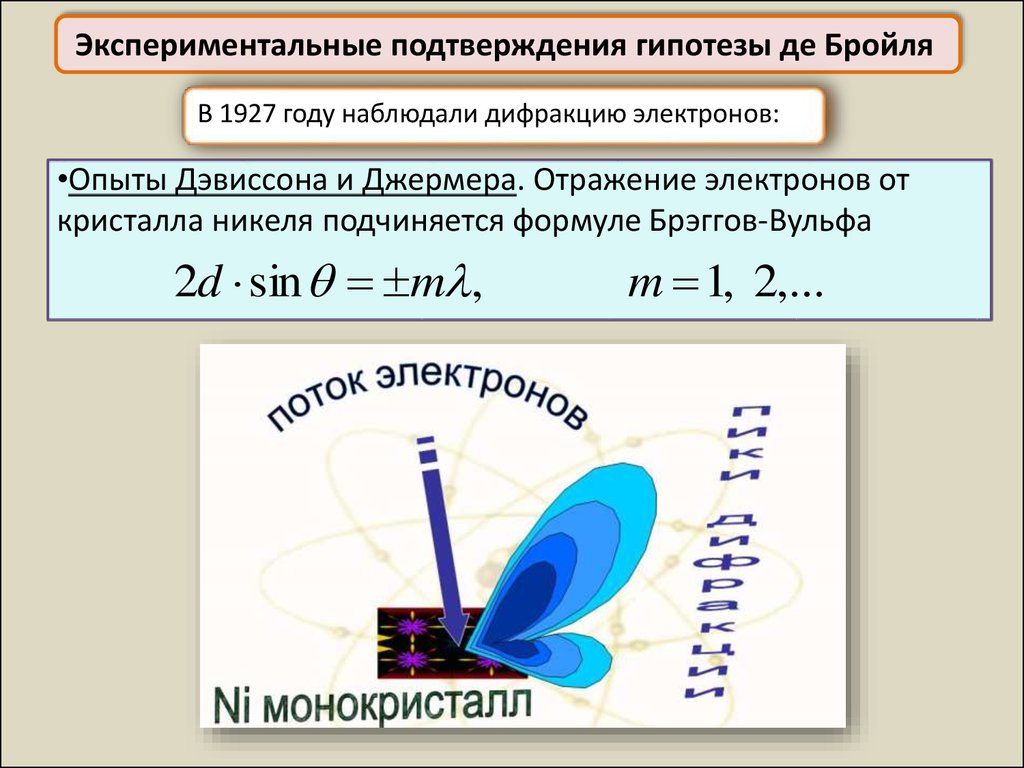
Экспериментальные подтверждения гипотезы де БройляВ 1927 году наблюдали дифракцию электронов:
•Опыты Дэвиссона и Джермера. Отражение электронов от
кристалла никеля подчиняется формуле Брэггов-Вульфа
2d sin m ,
m 1, 2,...
16.
Экспериментальные подтверждения гипотезы де Бройля•В опытах Дж.Томсона исследовалась дифракция электронов на
тонкой металлической поликристаллической фольге
На фотопластинке появлялась
дифракционная картина в
виде концентрических колец
me 2
p2
eU
2
2me
h
h
p
2meeU
17.
Экспериментальные подтверждения гипотезы де БройляВолновые свойства электрона обнаружились и в других экспериментах.
Более того, удалось наблюдать дифракцию нейтронов на кристаллах (1936
год), а также атомов (гелий) и молекул (водород). Есть эксперименты по
дифракции больших молекул красителя фталоцианина на специально
созданной дифракционной решётке
18.
Экспериментальные подтверждения гипотезы де БройляВолновые свойства присущи каждой частице: дифракционная картина
наблюдается и в случае очень слабых пучков, когда частицы летят
поодиночке. Со временем по мере выпуска всё новых и новых молекул на
финальной пластине всё ярче и ярче проступает интерференционная
картина. Благодаря дифракции случайно прибывающие на финиш
массивные частицы проявляют свои волновые свойства
a
б
в
г
19.
Микрочастица в двухщелевом интерферометреИллюстрацией двойственности свойств микрочастиц является опыт с
двухщелевым интерферометром.
Диафрагма с двумя щелями обстреливается потоком микрочастиц
(электронов), которые затем попадают на экран
Если открыта одна щель, напротив неё на экране получается полоса
20.
Микрочастица в двухщелевом интерферометреОткрывая вторую щель, ожидаем
получить на экране две полосы, то есть
простое сложение картинок при одной и
второй открытой щелях, как это было бы
в макромире при обстреле диафрагмы с
щелями обычными пулями
В опытах с микрочастицами на экране появляется интерференционная
картина, характерная для световых волн в аналогичном опыте Юнга.
Электроны интерферируют при прохождении через две щели
21.
Микрочастица в двухщелевом интерферометре22.
Микрочастица в двухщелевом интерферометреПули дискретны, неделимы: каждая проходит через какую-то одну из
двух щелей; никакой интерференции нет
Электрон, как и пуля, дискретен, он не может разделиться и пройти
одновременно через обе щели
Проделаем тот же эксперимент с
волнами: волна проходит через
обе щели, она непрерывна
Для волн нет дискретности; есть
интерференция
Электроны (и любые микрочастицы) дискретны, как
пули, но испытывают интерференцию, как волны
23.
Микрочастица в двухщелевоминтерферометре
Могло создаться впечатление, что микрочастицы интерферируют, потому
что взаимодействуют друг с другом. Но даже для очень слабых пучков,
когда микрочастицы летят поодиночке, интерференционная картина
сохранялась, только нужно было подождать достаточно долго, чтобы
картина достаточно проявилась. Электроны как будто «знают», что
открыты обе щели, и попадают в нужные места экрана: туда, где должны
быть интерференционные максимумы. Электрон интерферирует сам с
собой? На движение одиночного, дискретного и неделимого электрона
оказывают влияние обе щели.
Как это понять? Приходится принять, что микрочастица обладает
принципиально иными свойствами, чем макрочастица. У микрочастиц нет
траектории.
Электрон не может «разделиться» на половинки и пролететь сразу через
обе щели.
24.
Микрочастица в двухщелевом интерферометреВсё-таки хотелось бы знать, через какую щель пролетел электрон.
«Подсмотрим» за электроном, поставив сразу за каждой из щелей
источник света. Электрон, прошедший через данную щель, будет
рассеивать свет, и мы это «увидим», то есть будем точно знать, через какую
из щелей прошёл электрон; а если он, разделившись, пройдёт сразу через
две щели, вспышки у каждой из щелей произойдут одновременно
Если «подсматривать» за электронами , то
никакой интерференции нет
Если « не подсматривать» (выключаем источники
света), картинка интерференции появляется снова
25.
Соотношение неопределённостейЕсли не знаем координату (неизвестно, через какую щель пролетела
микрочастица), то интерференция есть; тогда знаем длину волны де
Бройля, знаем импульс частицы
p
h
де Бройля
Если будем фиксировать, через какую щель прошёл электрон
(включили лампочку), то не получим интерференции
Если знаем координату электрона (пролетел через данную щель),
то не знаем длину волны, не знаем импульс
Нельзя одновременно точно знать координату частицы
и её импульс
Нельзя сказать: длина волны в данной точке
Если точно знаем импульс частицы, то знаем длину волны де Бройля,
но совершенно не знаем, где находится наша частица:
гармоническая волна в пространстве бесконечна
26.
Принцип неопределённостей Гейзенберга1927 г.
Произведение неопределённостей координаты и
соответствующей проекции импульса частицы не меньше
постоянной Планка:
p x x
p y y
h
2
p z z
Есть и другие пары сопряжённых динамических переменных:
E t
L
Принцип неопределённостей Гейзенберга не связан
с несовершенством приборов или методов измерения;
является спецификой микрочастиц –
проявлением корпускулярно-волнового дуализма
27.
Волновая функция,её вероятностная интерпретация
Квантовая механика была создана в начале 20-го века
В ней учитываются волновые свойства микрочастиц
Авторы квантовой механики:
Планк,
Гейзенберг,
Шрёдингер,
Борн
Состояние микрообъекта в квантовой механике
описывается волновой функцией (пси-функция):
x, y , z , t
В общем случае Ψ – функция координат и времени;
значения функции – комплексные
28.
Волновая функция,её вероятностная интерпретация
Смысл функции:
Квадрат модуля волновой функции определяет
вероятность нахождения частицы в данной точке, то есть
вероятность dp обнаружить частицу в объёме dV вблизи
заданной точки с координатами x, y, z в момент времени t
равна
dp x, y, z, t dV
2
*
dp dV
Плотность вероятности обнаружения
частицы в данной точке равна
квадрату модуля волновой функции:
dp
dV
2
29.
x, y , z , tСвойства волновой функции
1) Однозначна, конечна, непрерывна, дифференцируема
2) Вероятность pV найти частицу в конечном объёме V равна:
2
3) Условие нормировки:
dV 1
2
pV dV
V
4) Волновую функцию можно домножить на любое комплексное число С:
Ψ и С∙Ψ описывают одно и то же состояние
5) Принцип суперпозиции
Если частица может находиться в состоянии, описываемом функциями Ψ1,
Ψ2,… Ψi, …, то возможно состояние частицы, описываемое любой линейной
комбинацией этих функций:
N
Ci i
i 1
6) Зная волновую функцию состояния, можно найти среднее значение любой
физической величины В
B
*
B
dV
по области
определения
функции
2
B dV
30.
Волновая функция. Уравнение ШрёдингераОписание состояния частицы с помощью волновой функции
не позволяет найти ни координаты частицы, ни её
траекторию. Однако утверждается, что волновая функция
даёт исчерпывающее описание поведения микрочастицы.
Волновая функция не даёт информации о том, чего нет: у
микрочастиц нет траектории, нет точных значений
координат в любой момент времени
Волновую функцию находят решением
уравнения Шрёдингера
Уравнение Шрёдингера –
основное уравнение квантовой механики
Уравнение не доказывается теоретически и не
может быть выведено из других соотношений
Справедливость уравнения Шрёдингера доказывается
тем, что следствия из него согласуются с опытом
31.
Временное уравнение Шрёдингера:2
U i
2m
t
i 2 1 – мнимая единица
2
x
2
2
y
2
2
z
U U x, y , z , t
2
– оператор Лапласа
– потенциальная функция
32.
Стационарное уравнение ШрёдингераЕсли потенциальная функция не зависит от времени:
U=U(x,y,z), то
i
t
x, y, z, t x, y, z e
i t
i
t
x, y , z e
i e
t
t
i
t
x, y, z, t e
x, y, z
33.
Стационарное уравнение Шрёдингераx, y, z, t x, y, z e i t
i
t
i e
t
i
t
x, y, z, t e
x, y, z
2
U i
2m
t
2 i t
i
t
i
t
e
U e
i i e
2m
34.
Стационарное уравнение Шрёдингера2
e i t U e i t i i e i t
2m
2
U i i
2m
E
2
U E
2m
E U
2
2m
0
35.
Собственные функции, собственные значенияE U
2
2m
Решение уравнения Шрёдингера существует не для любых
значений энергии Е
Значения энергии, при которых решение существует,
называются собственными значениями
Соответствующие им волновые функции тоже называются
собственными функциями
Совокупность собственных значений энергии – спектр
(энергетический спектр)
Спектр энергии может быть дискретным (набор конкретных
значений) или непрерывным, сплошным
0
36.
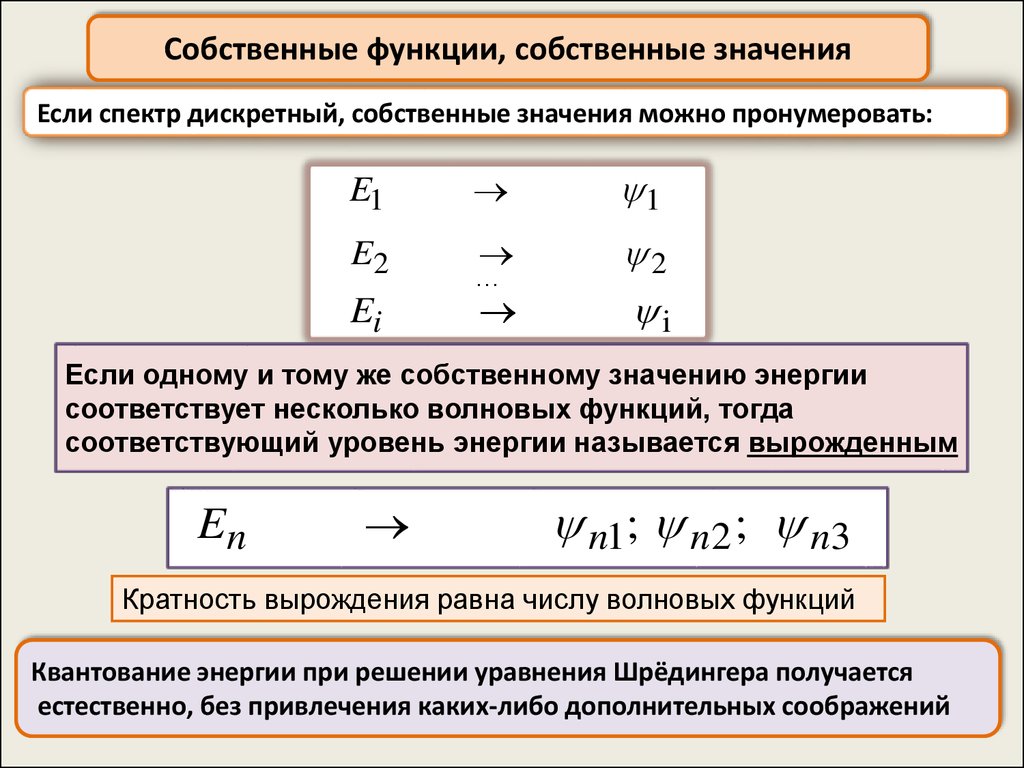
Собственные функции, собственные значенияЕсли спектр дискретный, собственные значения можно пронумеровать:
E1
1
E2
2
i
Ei
…
Если одному и тому же собственному значению энергии
соответствует несколько волновых функций, тогда
соответствующий уровень энергии называется вырожденным
En
n1; n 2 ; n3
Кратность вырождения равна числу волновых функций
Квантование энергии при решении уравнения Шрёдингера получается
естественно, без привлечения каких-либо дополнительных соображений
37.
Применение уравнения ШрёдингераОдномерное движение свободной частицы
x
Пусть частица движется в постоянном потенциальном поле, причём
потенциальная энергия частицы меньше её полной энергии: U<E
d 2
dx2
Обозначение:
2
E U
2
2m
k
2m
2
0
E U 0
d 2
dx
Одно из возможных решений:
2
k 0
2
x A cos k x
38.
Одномерное движение свободной частицыОбщее решение:
k
2m
2
E U
i k x
x A e
k
2
B e
i k x
– волновое число
i
t
i
k
x
i
k
x
i
t
x, t x e
A e
B e
e
i
t
k
x
i
t
k
x
x, t A e
B e
В положительном
направлении оси OX
В отрицательном
направлении оси OX
39.
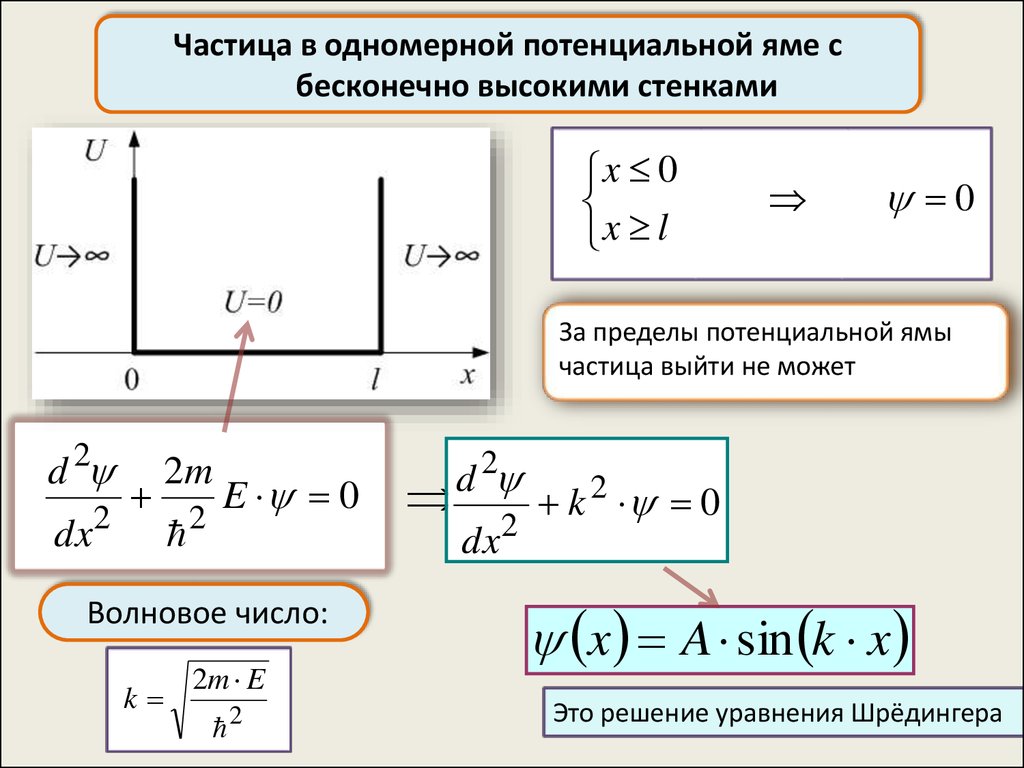
Частица в одномерной потенциальной яме сбесконечно высокими стенками
x 0
x l
0
За пределы потенциальной ямы
частица выйти не может
d 2
dx
2
2m
2
E 0
Волновое число:
k
2m E
2
d 2
dx2
k 2 0
x A sin k x
Это решение уравнения Шрёдингера
40.
Частица в одномерной потенциальной яме сбесконечно высокими стенками
x A sin k x
Функция непрерывна:
0 0
l A sin k l 0
k l n
k
n
l
(n 1, 2, 3, ....)
Квантовое число
41.
Частица в одномерной потенциальной яме сбесконечно высокими стенками
x A sin k x
Получили квантование энергии:
k l n
2m E
En
2
k
2m E
2
l n
2 2
2m l 2
n
2
Emin E1
2 2
2m l 2
42.
Частица в одномерной потенциальной яме с бесконечно высокими стенкамиВолновые функции:
k l n
n
n x A sin
x
l
1 x A sin x
l
2
2 x A sin x
l
3
3 x A sin x
l
x A sin k x
43.
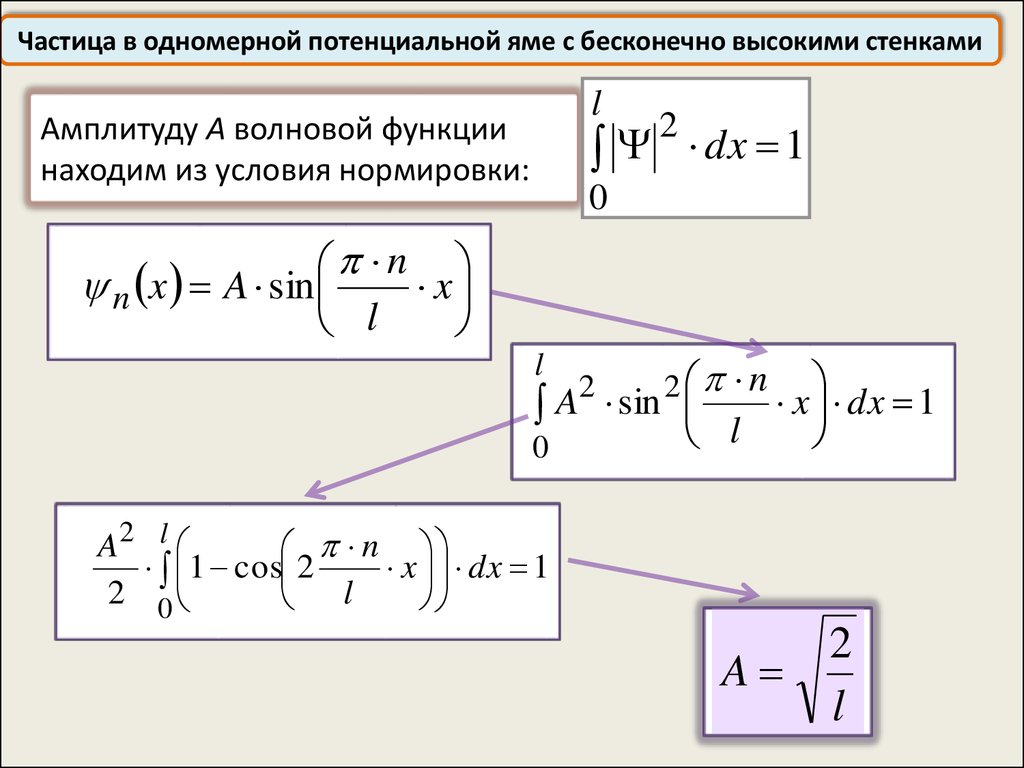
Частица в одномерной потенциальной яме с бесконечно высокими стенкамиl
Амплитуду А волновой функции
находим из условия нормировки:
2
dx 1
0
n
n x A sin
x
l
l
2 n
A
sin
x
dx 1
l
0
A2
2
2
n
1 cos 2
x dx 1
l
0
l
A
2
l
44.
Частица в одномерной потенциальной яме с бесконечно высокими стенкамиРасстояние между соседними уровнями энергии:
En En 1 En
2 2
2m l
n 1 2
2
2 2
2m l
2
n2
2 2
2m l
2
2n 1
Относительное расстояние между уровнями
уменьшается при увеличении квантового числа n :
1
2
En 2n 1
2
n
0
2
En
n
n
n
45.
Частица в одномерной потенциальной яме с бесконечно высокими стенками1
Для больших квантовых чисел n
2
E
2
n
1
дискретность уровней энергии уже
n 2 0
n
не играет роли
En
n
n
n2
Это – проявление принципа соответствия:
при больших квантовых числах (большая энергия) законы квантовой
механики дают тот же результат, что и классическая механика;
энергию можно считать изменяющейся непрерывно
Расстояние между уровнями энергии при n=1:
1) для электрона в потенциальной яме шириной 0.1 нм:
En 1.8 10 17 Дж 100 эВ
2) для макротела размером 0.1 м:
En 10 16 эВ
В первом случае дискретность уровней энергии существенна;
во втором случае уровни так близки, что энергию можно считать
изменяющейся непрерывно
46.
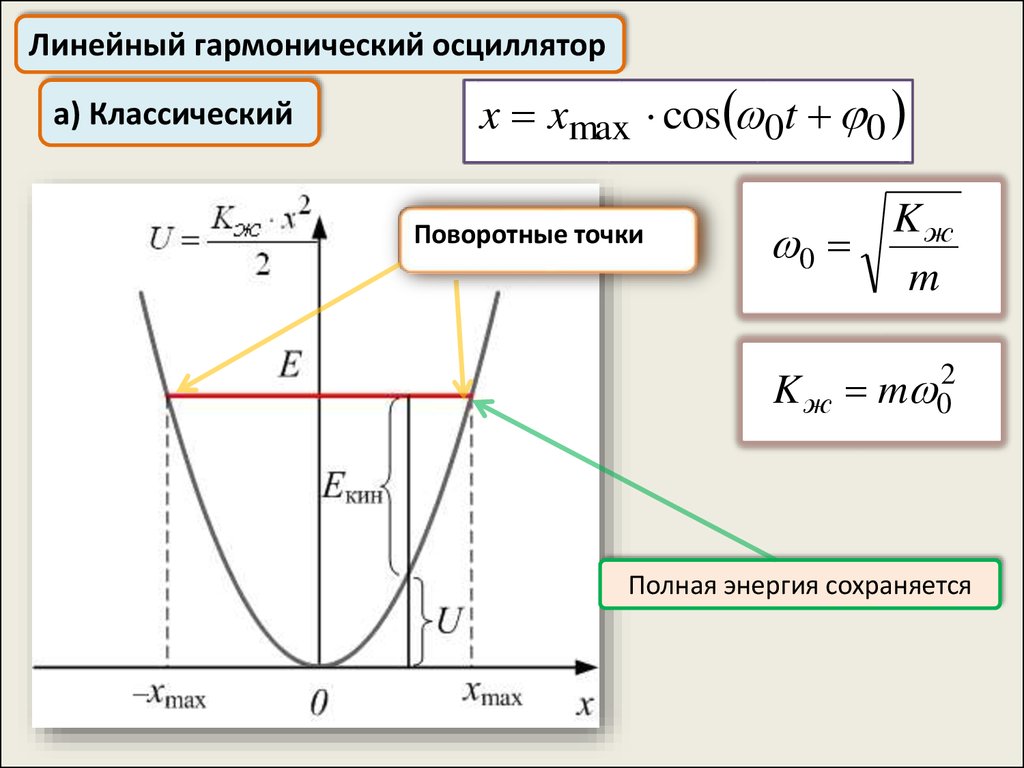
Линейный гармонический осциллятора) Классический
x xmax cos 0t 0
Поворотные точки
0
Kж
m
K ж m 02
Полная энергия сохраняется
47.
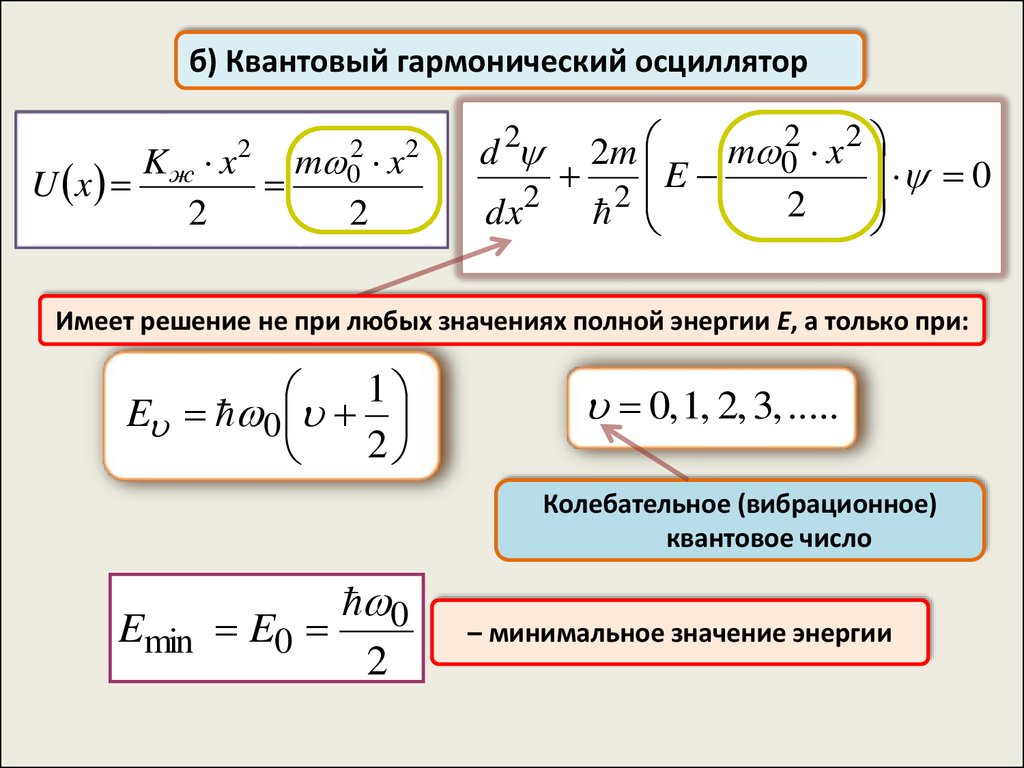
б) Квантовый гармонический осцилляторKж x
U x
2
2
m 02
x
2
2
m 02 x 2
2m
E
0
2
dx2 2
d 2
Имеет решение не при любых значениях полной энергии E, а только при:
1
E 0
2
0, 1, 2, 3, .....
Колебательное (вибрационное)
квантовое число
0
Emin E0
2
– минимальное значение энергии
48.
б) Квантовый гармонический осцилляторВсе уровни энергии отстоят
друг от друга на одинаковом
расстоянии:
E 0
Волновая функция
основного состояния:
m 0 2
x
0 0 A e 2
49.
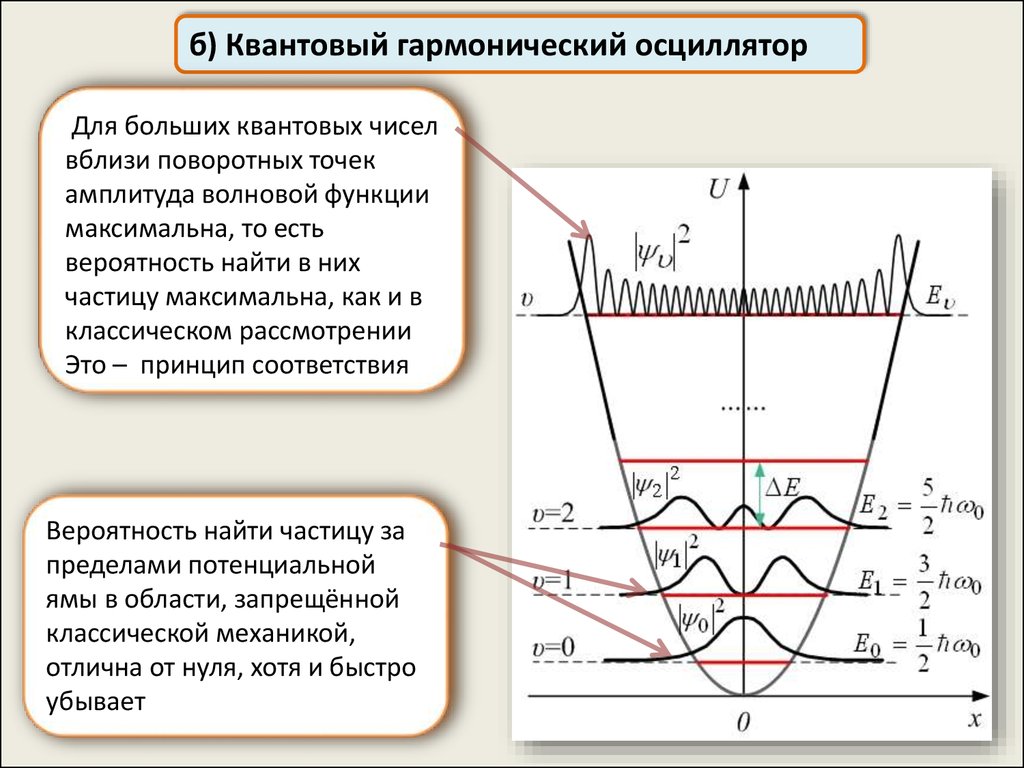
б) Квантовый гармонический осцилляторДля больших квантовых чисел
вблизи поворотных точек
амплитуда волновой функции
максимальна, то есть
вероятность найти в них
частицу максимальна, как и в
классическом рассмотрении
Это – принцип соответствия
Вероятность найти частицу за
пределами потенциальной
ямы в области, запрещённой
классической механикой,
отлична от нуля, хотя и быстро
убывает
50.
Ангармонический осциллятора) Классический
dU
F
K x x2
dx
K x 2 x3
U x
2
3
K
F K x x 2 m a m x
K
2
x x x 0
2
2
x
x
x
0
m
m
0
0
Решение дифф.уравнения:
x A sin t A sin 2 t ...
Частота зависит от амплитуды
2 02 1 f A
Примеры:
Колебания математического, физического, пружинного маятников будут
ангармоническими при большой амплитуде колебаний, то есть если угол
отклонения большой или не выполняется закон Гука
51.
б) Квантовый ангармонический осцилляторK x 2 x3
U x
2
3
K
Расстояния между уровнями
энергии неодинаковы:
K x 2 x3
2m
0
E
2
3
dx2 2
d 2
2
1
1
E 0
2
2
E 0 1 2 1
0
Уровни энергии «сбегаются» кверху:
чем больше энергия,
тем ближе уровни друг к другу
52.
Туннельный эффектЧастица налетает на прямоугольный потенциальный барьер шириной l и
высотой U0, большей, чем полная энергия частицы E
Классическая частица отразится от барьера
Квантовая частица
с ненулевой вероятностью
проникнет сквозь барьер
53.
Туннельный эффектU x 0
U x U 0
при x 0; x l
при 0 x l
I
d 2
dx
2
2m
2
E 0
i k I x
I x AI e
2m
kI
2
E
2 2m
kI
E 0
2
Re I x AI cos k I x
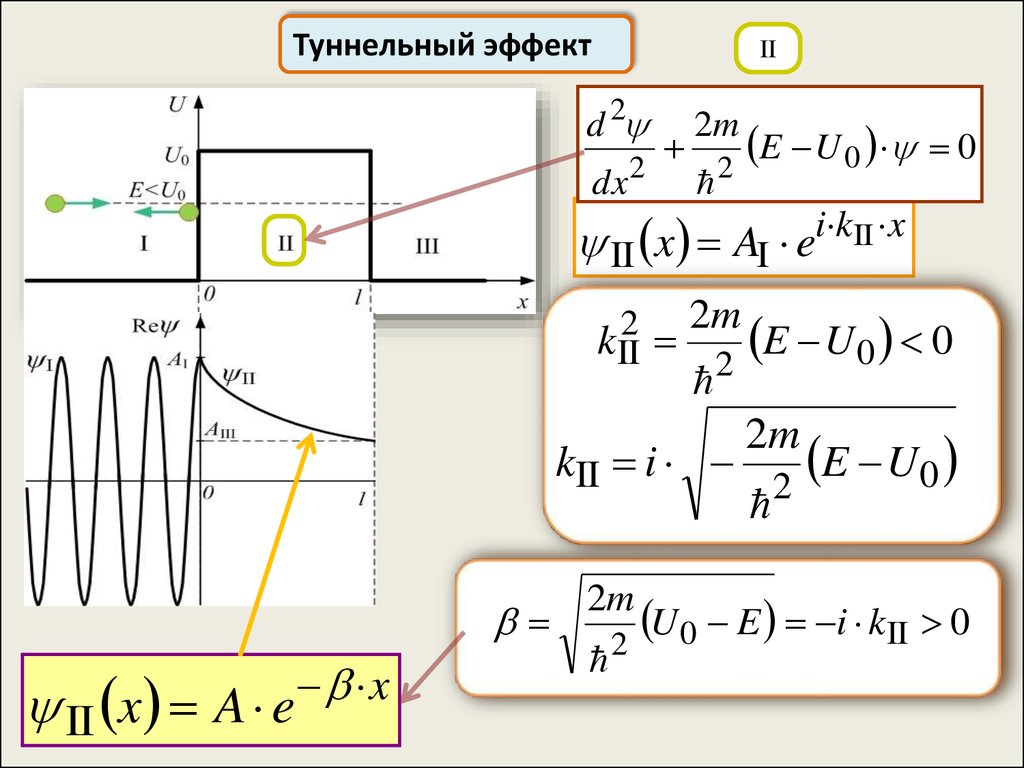
54.
Туннельный эффектII
d 2
dx2
E U 0
2
2m
0
II x AI ei kII x
2 2m
kII
E U0 0
2
kII i
II x A e
x
E U0
2
U 0 E i kII 0
2
2m
2m
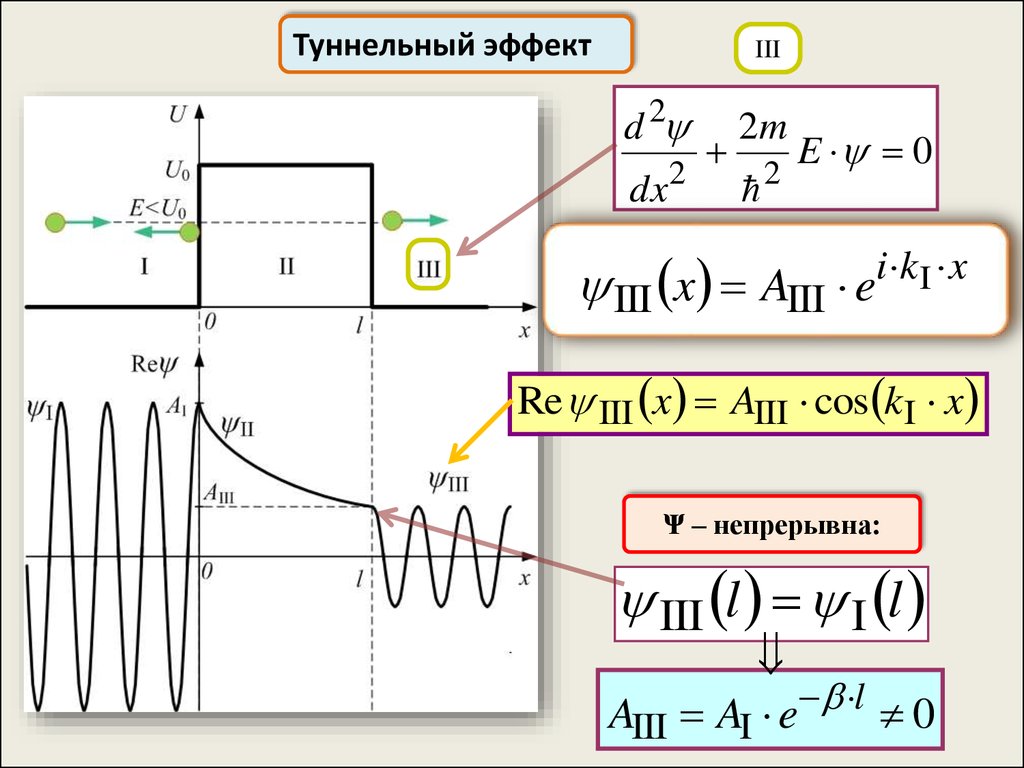
55.
Туннельный эффектIII
d 2
dx2
2m
2
E 0
III x AIII e
i k I x
Re III x AIII cos k I x
Ψ – непрерывна:
III l I l
AIII AI e l 0
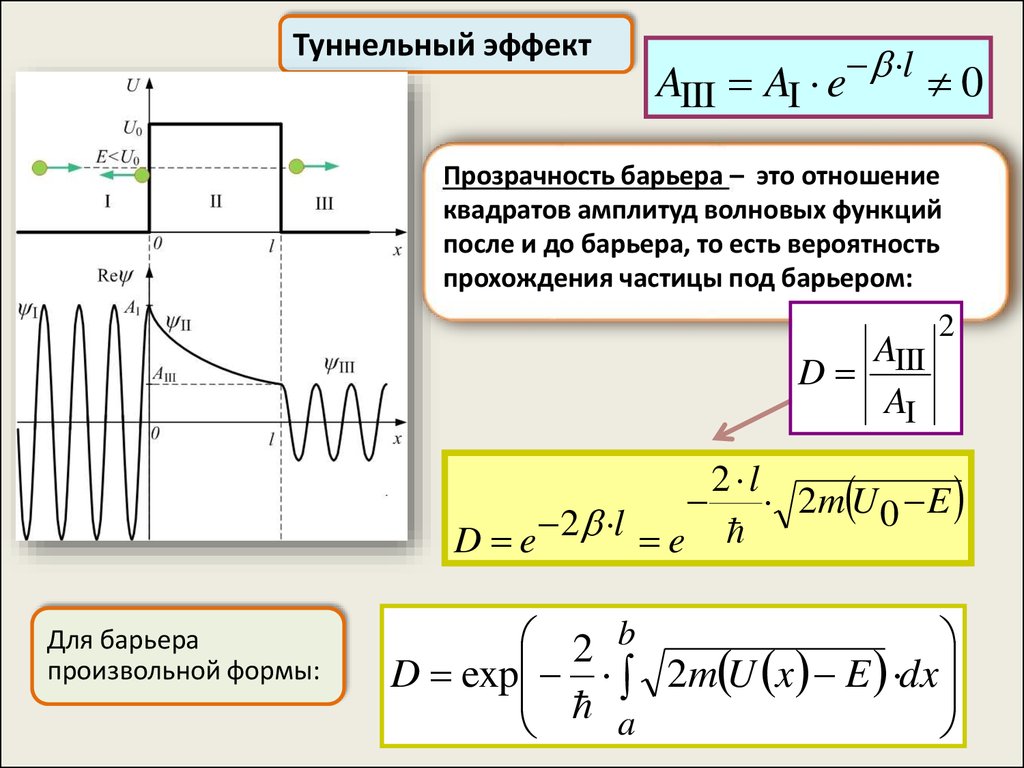
56.
Туннельный эффектAIII AI e l 0
Прозрачность барьера – это отношение
квадратов амплитуд волновых функций
после и до барьера, то есть вероятность
прохождения частицы под барьером:
AIII
D
AI
2
2 l
2m U 0 E
D e 2 l e
Для барьера
произвольной формы:
2 b
D exp 2m U x E dx
a
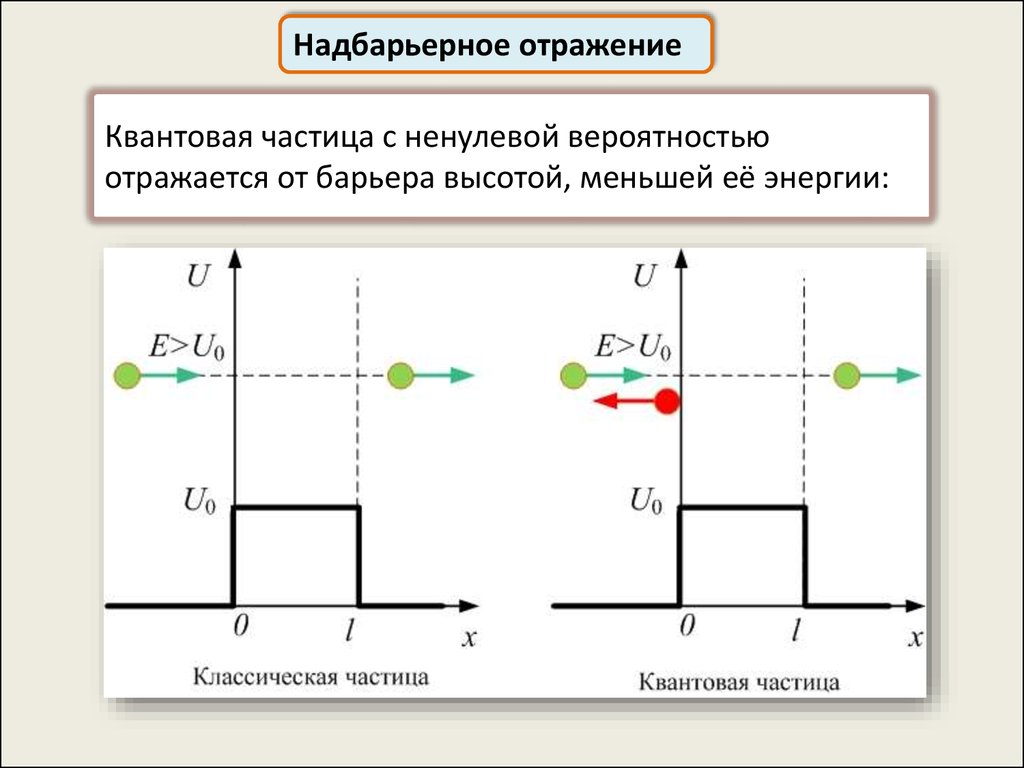
57.
Надбарьерное отражениеКвантовая частица с ненулевой вероятностью
отражается от барьера высотой, меньшей её энергии:










































 physics
physics