Similar presentations:
Уравнение Шрёдингера для стационарных состояний. Лекция 11
1. Проф. КОПЫТИН И.В.
Лекционный курс «Квантовая механика»Направление 03.03.03. – «Радиофизика»
Бакалавры, 3 курс
2. Задание на период с 17 по 28 марта 2020 г. Разобрать прилагающиеся ниже лекции 11-13
3. Лекция 11 УРАВНЕНИЕ ШРЁДИНГЕРА ДЛЯ СТАЦИОНАРНЫХ СОСТОЯНИЙ
4.
Для нахождения волновой функции временнымуравнением Шрёдингера имеет смысл пользоваться
только тогда, когда явно зависит от времени
ˆ ξ,t) . В нем такая зависимость
гамильтониан H(
возникает только через потенциальную функцию
U( ξ,t) . Если зависимость гамильтониана от времени
отсутствует, т.е. U = U( ) , то волновую функцию
находят из уравнения Шредингера для стационарных
состояний (часто говорят – из «уравнения Шрёдингера»
без слова «временное»).
ˆ ) .
Пусть гамильтониан не зависит от времени: Hˆ = H(
Тогда в нем можно разделить переменные ξ и t. Имеем:
∂
Ψ( ξ
, t)
ˆ ξ) Ψ( ξ,t)
i
= H(
.
(11.1)
∂
t
Ищем волновую функцию в виде:
Ψ( ξ,t) =Ψ( ξ) f( t) .
(11.2)
5.
Подставим (11.2) в (11.1) и разделим переменные.df( t)
ˆ ξ) Ψ( ξ)
i Ψ( ξ )
= f( t) H(
;
dt
ˆ ξ) Ψ( ξ)
1 df( t) H(
i
=
=E .
(11.3)
f( t) dt
Ψ( ξ)
Величина E – константа с размерностью энергии.
Введена она потому, что в (11.3) левая сторона зависит
только от t, а правая сторона – только от ξ. Поэтому
равенство возможно, только если и правая, и левая
стороны будут константами.
Из (11.3) получаются два уравнения:
1 df( t)
df( t)
i
i
=E
E dt ;
(11.4)
f( t) dt
f( t)
6.
ˆ ξ) Ψ( ξ) = E Ψ( ξ) .H(
(11.5)
Интегрирование в (11.4) дает:
f( t) = e
i
- Et
(11.6)
.
Константа интегрирования положена равной 1, так как
общая константа в (11.2) все равно будет находиться
из условия нормировки.
Уравнение (11.5) позволяет найти волновую функцию
Ψ( ξ) и величину E. Так как гамильтониан от времени
не зависит, то, следовательно, в нем вместо
потенциальной функции U( ξ,t) будет потенциальная
энергия микросистемы U( ) . Это означает, что
гамильтониан Hˆ становится оператором энергии и
уравнение (11.5) есть уравнение на его собственные
функции и собственные значения. Последние – это
энергии соответствующих состояний системы,
имеющие определенные значения.
7.
Состояние с определенным значением энергии Eназывается стационарным, а уравнение (11.5)
называется уравнением Шрёдингера для стационарных
состояний. Итак, в случае одной микрочастицы ( ξ = r )
это уравнение имеет вид:
ĤΨ( r) = E Ψ( r) ,
Hˆ = -
(11.7)
2
∇2 + U ( r) .
2m
(11.8)
Обычно интерес представляет именно волновая
функция Ψ( r) , так как зависимость от времени полной
волновой функции определена ф-лой (11.6). Но в ряде
случаев требуется знание именно полной волновой
функции стационарного состояния системы, и в
соответствии с (11.2) она имеет вид:
Ψ( ξ,t) =Ψ( ξ) e
i
- Et
,
(11.9)
8.
а величины Ψ( ξ) и E находятся из уравнения (11.5)или из уравнения (11.7) с гамильтонианом (11.8), если
ξ = r . Спектр энергий может быть дискретным или
непрерывным. В первом случае волновые
функции (11.9) принимают вид
Ψ(n ξ,t) =Ψ(n ξ) e
i
- E nt
, n = 1, 2, …
Во втором случае –
Ψ( E ,ξ,t) =Ψ( E ,ξ) e
(11.10)
i
- Et
.
(11.11)
Свойства стационарных состояний
1. Волновые функции в виде (11.10) или (11.11)
образуют полную систему, т.е. допускают
разложение произвольной функции Ψ( ξ,t) :
9.
Ψ( ξ,t) = a(n t) Ψ(n ξ,t) =a(
n
n
t) Ψ(n ξ) e
i
- E nt
n
если спектр энергий дискретный, и
Ψ( ξ,t) =
=
a(
E ,t) Ψ( E ,ξ,t)dE =
a( E ,t) Ψ( E ,ξ) e
i
- Et
dE
,
если спектр энергий непрерывный.
2.Плотность вероятности ρ( r,t) и плотность
тока вероятности j( r,t) не изменяются с
течением времени.
По определению (см. (4.3)) и с учетом (11.9)
получаем:
ρ( ξ, t) = Ψ( ξ, t)
= Ψ(* ξ) e
i
2
= Ψ(* ξ, t) Ψ( ξ, t) =
Et
Ψ( ξ) e
= Ψ( ξ) Ψ( ξ) = Ψ( ξ)
*
2
i
- Et
=
= ρ( ξ, t = 0)
,
,
10.
что и требовалось доказать. Аналогично сиспользованием формул (10.5) и (11.9) (в этом
случае ξ = r ) доказывается, что j( r,t) = j( r,t = 0) .
3.Среднее значение физической величины от
времени не зависит.
Если микросистема находится в состоянии с волновой
функцией Ψ( ξ, t) , то по определению (8.1) среднее
значение физической величины F
F ( t) = Ψ(* ξ,t)FˆΨ( ξ,t) dξ .
Подстановка в это выражение волновой функции в виде
(11.9) дает утверждаемое выше:
F ( t) = Ψ(* ξ,t)FˆΨ( ξ,t) dξ =
= Ψ(* ξ)FˆΨ( ξ) dξ = F ( t = 0) .
11.
4.Вероятность результата измерения физическойвеличины не изменяется с течением времени.
Пусть микросистема находится в стационарном состоянии
i
- Et
Ψ( ξ,t) =Ψ( ξ) e
. Рассмотрим, например, физическую
величину F с дискретным спектром. Тогда вероятность того,
что F = Fn , будет (см. (8.9)):
2
W(n F = F n ,t) = φ( ξ) Ψ( ξ,t) dξ =
*
n
2
= φ( ξ) Ψ( ξ) dξ e
*
n
i
- Et
2
=
2
= φ( ξ) Ψ( ξ) dξ =W(n F = F n ,t = 0)
*
n
что и требовалось доказать.
,
12.
ПРОВЕРОЧНЫЕ ВОПРОСЫ К ЛЕКЦИИ 111.Какое состояние называется стационарным?
2.Когда следует решать не временное уравнение
Шрёдингера, а уравнение Шрёдингера для стационарных
состояний?
3.Какой вид имеет зависящий от времени фактор в
волновой функции стационарного состояния и откуда
можно найти параметры, входящие в него?
4.Что такое «условия сшивания» для волновой функции?
Когда необходимо их использовать?
5.Запишите общий вид уравнения Шредингера для
стационарных состояний водородоподобного атома
(атомное ядро с зарядовым числом Z и электрон).
6.Запишите общий вид уравнения Шредингера для
стационарных состояний атома гелия (атомное ядро с
зарядовым числом 2 и два электрона; движением ядра
пренебречь).
7.Запишите общий вид уравнения Шредингера для
стационарных состояний атома лития (атомное ядро с
зарядовым числом 3 и три электрона).
13. Лекция 12 СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
14.
Предположим, что нас интересуют две физических2
величины F и G, например, Lz и L , или x и px,
или Lx и Ly и пр. Соответственно предполагается, что
известны их операторы F̂ и Ĝ , а также коммутатор
ˆ .
[ Fˆ , Gˆ ] Fˆ Gˆ Gˆ Fˆ iM
(12.1)
Оператор M̂ может быть любым - нулем (тогда операторы
F̂ и Ĝ коммутируют), константой или оператором.
ˆ2
ˆ
L
L
коммутируют и M̂ = 0 , для
Например, операторы z и
операторов x и pˆ x M̂ , а для операторов Lˆ и Lˆ y
x
ˆ Lˆ .
M
z
15.
Если известно состояние микрочастицы, т.е. ееволновая функция Ψ( ξ) (включать в аргумент время не
будем), то можно будет вычислить средние значения
F и G по формуле (8.1):
ˆ
F = Ψ(* ξ)FΨ(
ξ) dξ ;
ˆ
G = Ψ(* ξ)GΨ(
ξ) dξ .
Можно ввести операторы отклонения от среднего
значения: ΔFˆ = Fˆ - F и ΔGˆ = Gˆ -G . Так как средние
значения F и G - это константы, то коммутатор
операторов ΔFˆ и ΔGˆ будет таким же, как и
операторов F̂ и Ĝ :
ˆ ≡ΔFˆ ΔGˆ - ΔGˆ ΔFˆ = iMˆ .
[ΔF,ˆ ΔG]
(12.2)
16.
С помощью операторов ΔFˆ и ΔGˆ можно рассчитатьˆ 2
ˆ 2 и ( ΔG)
среднеквадратичные отклонения ( ΔF)
для физических величин F и G:
( ΔFˆ) 2 =( Fˆ - F ) 2 = Ψ(* ξ() Fˆ - F ) 2 Ψ( ξ) dξ ;
ˆ 2 =( Gˆ -G) 2 = Ψ(* ξ() Gˆ -G) 2Ψ( ξ) dξ
( ΔG)
.
Именно они используются для количественной
характеристики разброса, т.е. неопределенности,
значений физических величин F и G при их
экспериментальном измерении. Если, например,
ˆ 2 = 0 , то разброс отсутствует и величина F имеет
( ΔF)
вполне определенное значение. В классической физике
2
2
ˆ
ˆ
(
ΔF)
(
ΔG)
никак не связаны друг с
величины
и
другом. Однако в квантовой механике такая
взаимосвязь может возникнуть, и именно она
фиксируется соотношением неопределенностей.
17.
Получим это соотношение. Пусть есть три линейныхэрмитовых оператора Â , B̂ и Ĉ , и они связаны
коммутационным соотношением
Aˆ Bˆ - Bˆ Aˆ = iCˆ ,
или
ˆ .
Cˆ = i ( Bˆ Aˆ - Aˆ B)
Введем очевидное неравенство:
2
ˆ
ˆ
αAΨ( ξ) - iBΨ( ξ) dξ ≥0 .
(12.3)
(12.3*)
(12.4)
Здесь Ψ( ξ) - волновая функция микрочастицы (время
включать в аргумент не будем), α – произвольный
параметр (будем считать его действительным, т.е.
α = α*). Очевидность неравенства (12.4) в том, что под
знаком интеграла стоит всюду неотрицательная
величина, а потому и сам интеграл будет
неотрицательным. Раскроем неравенство (12.4):
18.
2ˆ
ˆ
ˆ
ˆ
ξ) - iBΨ(
ξ) dξ = ( αAΨ(
ξ) - iBΨ(
ξ) ) ×
αAΨ(
ˆ
×( αAˆ*Ψ(* ξ) + iBˆ*Ψ(* ξ) ) dξ = α 2 AΨ(
ξ)Aˆ*Ψ(* ξ) dξ +
ˆ
ˆ
+ BΨ(
ξ)Bˆ*Ψ(* ξ) dξ - iα[ BΨ(
ξ)Aˆ*Ψ(* ξ) dξ ˆ
- AΨ(
ξ)Bˆ*Ψ(* ξ) dξ] = α 2 Ψ(* ξ)Aˆ 2Ψ( ξ) dξ +
ˆ ˆ ( ξ) dξ + Ψ(* ξ)Bˆ 2Ψ( ξ) dξ - iα[ Ψ(* ξ)ABΨ
.
ˆˆ
- Ψ(* ξ)BAΨ(
ξ) dξ] = α 2 Aˆ 2 + Bˆ 2 +
ˆ ˆ - AB)
ˆ ˆ Ψ( ξ) dξ = α 2 Aˆ 2 + Bˆ 2 + α Cˆ ≥0
+α Ψ(* ξ)i ( BA
Здесь для подчеркнутых операторов были
использованы их свойства эрмитовости (см. (5.6)),
определение среднего значения (см. (8.1), знак ...
означает усреднение), а также соотношение (12.3*).
Итак, получено:
ˆ 2 α 2 + Cˆ α + Bˆ 2 ≥0 .
y( α) = A
(12.5)
19.
Функция y (α) имеет вид параболы и, если еенарисовать в плоскости (α, y), то ни при каких
значениях α она не должна пересекать ось абсцисс
( y( α) 0 ), но может ее касаться сверху ( y( α) = 0 ).
Иными словами, квадратное уравнение по параметру α,
т.е. уравнение y( α) = 0 , не должно иметь
действительных корней, но их величины могут и
совпадать. Как известно из алгебры, два корня x1 и x2
2
квадратного уравнения ax bx c 0 имеют вид:
b b2 4ac
x1,2
.
2a
Отсюда следует, что, если
b2 4ac 0 → ac b2 / 4 ,
действительных корней либо не будет (знак “>”), либо они
будут совпадать (знак “=”). Соответственно,
20.
ˆ , b Cˆ , c Bˆ , получаем условие
полагая a A
выполнения соотношения (12.5):
ˆ 2
C
2
2
ˆ Bˆ ≥
A
(12.6)
.
4
2
2
Операторы Â , B̂ и Ĉ - произвольные, и можно выбрать
ˆ = ΔFˆ , Bˆ = ΔGˆ и Cˆ = Mˆ .
их как физические операторы: A
Подставляя их в (12.6), получаем соотношение
неопределенностей для физических величин F и G:
2
ˆ
M
ˆ 2 ≥
( ΔFˆ) 2 ( ΔG)
(12.7)
.
4
Из него следует, что среднеквадратичные значения
ˆ 2 действительно не
ˆ 2 и ( ΔG)
физических величин ( ΔF)
ˆ 0 . Более того,
будут независимы, если величина M
2
если, например, величина ( ΔFˆ) = 0 , т.е. F имеет
ˆ 2 , т.е. G
определенное значение, то ( ΔG)
21.
не будет иметь определенного значения. И, наоборот,ˆ = 0 , то ( ΔF)
ˆ , и физическая
если ( ΔG)
величина F не будет иметь определенного значения.
В классической физике такого не бывает!
Рассмотрим частный случай соотношения
неопределенностей (12.7), положив F = x и G = px.
Поскольку коммутатор xpˆ x - pˆ x x = i , то M̂ =
и
2
ˆ =
M
2
. Соотношение неопределенностей (12.7) тогда
принимает вид:
ˆx )2 ≥
( Δx) 2 ( Δp
2
4
.
(12.8)
Это соотношение неопределенностей Гейзенберга,
полученное им в 1925 г. Иногда его записывают
в упрощенном виде:
Δx Δp x
,
(12.9)
22.
подразумевая подвеличинами Δx и Δpx
неточности в значениях
координаты x и проекции
импульса px на ось x при
их экспериментальном
измерении у
микрочастицы. Из (12.9)
прямо следует, что у микрочастицы понятие траектории
отсутствует в классическом ее понимании.
Действительно, движение частицы по траектории
означает, что в любой момент времени для точно
заданной координаты x можно указать точное значение
проекции импульса px и наоборот. А из соотношения
(12.9) следует, что чем точнее измеряется координата,
т.е. Δx→0, тем неопределеннее будет проекция
импульса, так как Δpx → . И, наоборот, если Δpx →0,
то Δx→ .
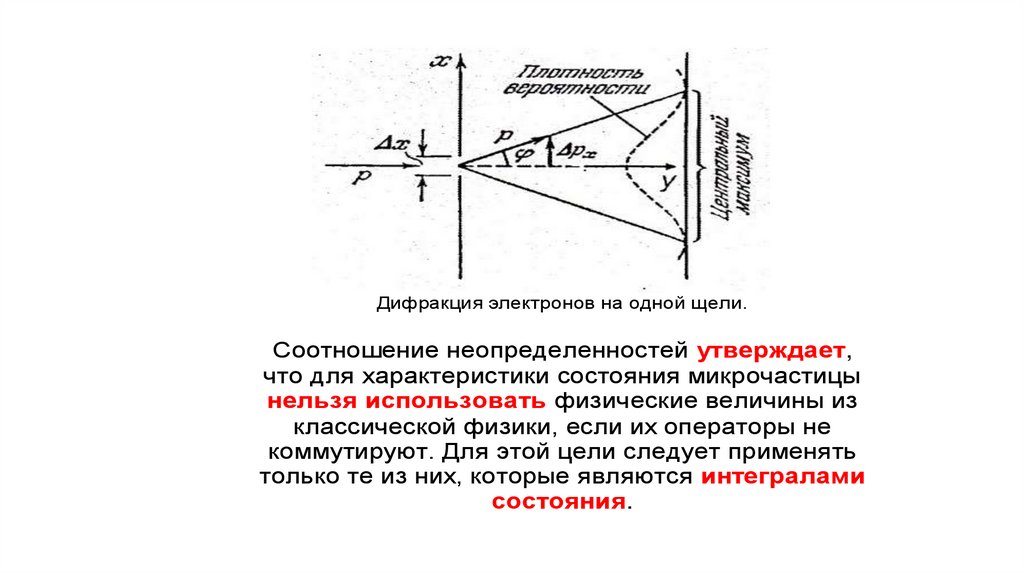
23.
Дифракция электронов на одной щели.Соотношение неопределенностей утверждает,
что для характеристики состояния микрочастицы
нельзя использовать физические величины из
классической физики, если их операторы не
коммутируют. Для этой цели следует применять
только те из них, которые являются интегралами
состояния.
24.
ПРОВЕРОЧНЫЕ ВОПРОСЫ К ЛЕКЦИИ 121. Как можно объяснить отсутствие понятия траектории у
микрочастицы, исходя из соотношения
неопределенностей?
2. Почему можно видеть траекторию альфа-частицы в
камере Вильсона?
3. Запишите соотношение неопределенностей для
операторов проекции импульса pˆ x и проекции момента
импульса Lˆ y .
4. Запишите соотношение неопределенностей для
операторов проекций момента импульса Lˆ x и Lˆ y .
5. Запишите соотношение неопределенностей для
ˆ2
ˆ
L
L
.
операторов момента импульса y и
25.
Лекция 13ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАТОРОВ ПО
ВРЕМЕНИ И ИНТЕГРАЛЫ СОСТОЯНИЯ
КВАНТОВОЙ СИСТЕМЫ
26.
Предположим, что оператор физической величиныдействует не только на координаты микрочастиц ξ, но
еще зависит и от времени t, т.е. Fˆ = F(ˆ ξ,t) . Если
известна волновая функция системы Ψ(ξ, t), можно
вычислить среднее значение F :
*
F( t) = Ψ( ξ,t) F(ˆ ξ,t) Ψ( ξ,t) dξ .
(13.1)
Продифференцируем это соотношение по времени:
dF
ˆ
*
= Ψ( ξ,t) F ( ξ,t) Ψ( ξ,t) dξ +
dt
t
*
ˆ
+ Ψ( ξ,t) F ( ξ,t) Ψ( ξ,t) dξ +
t
.
*
ˆ
+ F ( ξ,t) Ψ( ξ,t) Ψ( ξ,t) dξ
t
27.
Для удобства в последнем интеграле производная*
Ψ( ξ,t) переставлена с функцией Fˆ Ψ( ξ,t) .
t
*
Подставим сюда производные t Ψ( ξ,t) и t Ψ( ξ,t) , взяв
∂Ψ ˆ
их из временного уравнения Шрёдингера i ∂t = HΨ
( Hˆ - гамильтониан):
*
∂Ψ 1 ˆ
∂Ψ
1 ˆ* *
= HΨ ;
=- H Ψ .
∂t i
∂t
i
28.
dFFˆ
1
*
ˆ
= Ψ( ξ, t)
Ψ( ξ, t) dξ + Ψ(* ξ, t) FˆHΨ(
ξ, t) dξ dt
t
i
1
Fˆ
*
*
*
ˆ
ˆ
F Ψ( ξ, t) H Ψ( ξ, t) ) dξ = Ψ( ξ, t)
Ψ( ξ, t) dξ +
i
t
1
1
*
ˆ
ˆ ˆΨ( ξ, t) dξ =
+ Ψ(* ξ, t) FˆHΨ(
ξ, t) dξ Ψ(
ξ, t) HF
i
i
Fˆ
1
*
ˆ ˆ) ]Ψ( ξ, t) dξ.
= Ψ( ξ, t) [
+ ( FˆHˆ - HF
t
i
dF
Fˆ
1
*
ˆ ˆ) ]Ψ( ξ,t) dξ.
= Ψ( ξ,t) [
+ ( FˆHˆ - HF
dt
t
i
(13.2)
ˆ
dF
Введем оператор dt , который называется
«производной оператора по времени»:
dFˆ
∂
Fˆ
1
∂
Fˆ
1
ˆ
ˆ
ˆ
ˆ
ˆ
=
+ ( F H - HF ) =
+
[ Fˆ, H]
. (13.3)
dt
∂
t
i
∂
t
i
29.
ˆ ˆ - коммутатор операторов Fˆ и Ĥ .Здесь [ F,H]
Сравнивая (13.2) и (13.3), получаем:
dF
dFˆ
=
.
(13.4)
dt
dt
Это соотношение позволяет вычислять величину
dF / dt , используя определение (13.3) оператора dFˆ / dt .
Если среднее значение физической величины F не
изменяется с течением времени, то такая физическая
величина называется интегралом состояния системы.
Из соотношения (13.4) следует, что это будет тогда,
dFˆ
когда dt = 0 . Как видно из (13.3), для этого от
оператора Fˆ требуется выполнение двух условий:
∂
Fˆ
= 0 , т.е. оператор Fˆ не должен явно зависеть
1. ∂
t
от времени;
30.
ˆ ˆ = 0 , т.е. оператор Fˆ должен2. [ F,H]
коммутировать с гамильтонианом Hˆ .
ˆ2 ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
p
,
p
,
p
,
L
,
L
,
L
,
L
,K
Для физических операторов x y z x y z
первое условие выполняется, поэтому необходимо
вычислять их коммутаторы с гамильтонианом. Если
для каких-то из них коммутаторы будут равны нулю,
то эти физические величины и будут интегралами
состояния микросистемы.
31.
ПРОВЕРОЧНЫЕ ВОПРОСЫ К ЛЕКЦИИ 131.Какие интегралы движения будут у свободно движущейся
микрочастицы, если оно описывается в декартовой системе
координат? А если в сферической системе координат?
2. Какие интегралы движения будут у свободно движущейся
микрочастицы, если оно описывается в сферической
системе координат?
3.Определите, какие интегралы движения будут у частицы,
движущейся в центральном поле (потенциальная энергия
частицы зависит только от расстояния до центра силы).






























 physics
physics








