Строение и физические свойства вещества

1. Лекция № 7 (2.05.12г.) Раздел IV «СТРОЕНИЕ И ФИЗИЧЕСКИЕ СВОЙСТВА ВЕЩЕСТВА» Тема «Основы атомной физики»

1)
2)
3)
4)
5)
6)
7)
Опыты Резерфорда по изучению строения атома.
Квантовые постулаты Бора. Закономерности
спектров излучения атомов водорода.
Дискретность энергетических уровней в атоме.
Опыты Франка и Герца .
Недостатки теории Бора. Волновая функция и ее
свойства. Уравнение Шредингера.
Уравнение Шредингера для атома водорода.
Главное, орбитальное и магнитное квантовые
числа.
Кратность вырождения уровней энергии.

2. Опыты Резерфорда по изучению строения атома

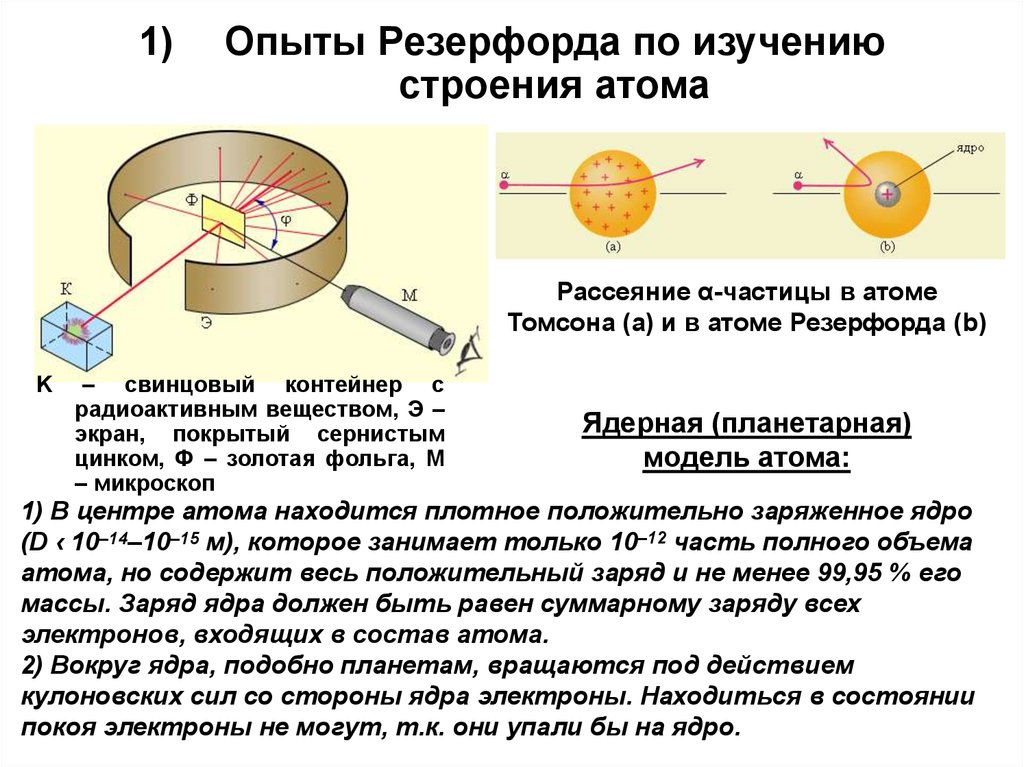
1)
Опыты Резерфорда по изучению
строения атома
Рассеяние α-частицы в атоме
Томсона (a) и в атоме Резерфорда (b)
K
– свинцовый контейнер с
радиоактивным веществом, Э –
экран, покрытый сернистым
цинком, Ф – золотая фольга, M
– микроскоп
Ядерная (планетарная)
модель атома:
1) В центре атома находится плотное положительно заряженное ядро
(D ‹ 10–14–10–15 м), которое занимает только 10–12 часть полного объема
атома, но содержит весь положительный заряд и не менее 99,95 % его
массы. Заряд ядра должен быть равен суммарному заряду всех
электронов, входящих в состав атома.
2) Вокруг ядра, подобно планетам, вращаются под действием
кулоновских сил со стороны ядра электроны. Находиться в состоянии
покоя электроны не могут, т.к. они упали бы на ядро.

3. 2) Квантовые постулаты Бора

Первый постулат Бора (постулат стационарных состояний):
Атомная система может находится только в особых стационарных или
квантовых состояниях, каждому из которых соответствует определенная
энергия En. В стационарных состояниях атом не излучает
Согласно первому постулату Бора, атом
характеризуется системой энергетических уровней,
каждый из которых соответствует определенному
стационарному состоянию.
Величина |E1| называется энергией ионизации.
Состояние с энергией E1 называется основным
состоянием атома.
Второй постулат Бора (правило частот):
Энергетические уровни
атома и условное
изображение
процессов поглощения
и испускания фотонов
При переходе атома из одного
стационарного состояния с энергией En в
другое стационарное состояние с энергией
Em излучается или поглощается квант,
энергия которого равна разности энергий
стационарных состояний:
hνnm = En – Em

4. 2) Закономерности спектров излучения атомов водорода

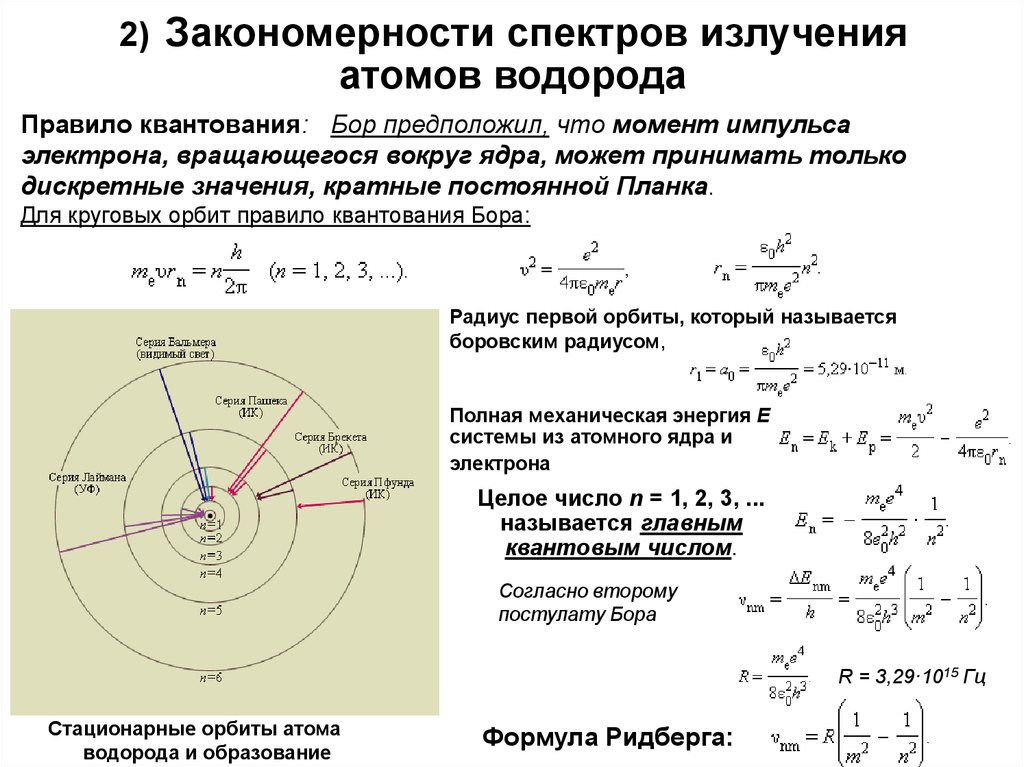
Правило квантования: Бор предположил, что момент импульса
электрона, вращающегося вокруг ядра, может принимать только
дискретные значения, кратные постоянной Планка.
Для круговых орбит правило квантования Бора:
Радиус первой орбиты, который называется
боровским радиусом,
Полная механическая энергия E
системы из атомного ядра и
электрона
Целое число n = 1, 2, 3, ...
называется главным
квантовым числом.
Согласно второму
постулату Бора
R = 3,29·1015 Гц
Стационарные орбиты атома
водорода и образование
Формула Ридберга:

5. 3) Дискретность энергетических уровней в атоме.

Физическая интерпретация правила квантования на основе представлений о волновых свойствах
частиц (гипотеза де Бройля).
Иллюстрация идеи де Бройля
возникновения стоячих волн
на стационарной орбите для
случая n = 4
Де Бройль предложил, что каждая орбита в атоме
водорода соответствует волне,
распространяющейся по окружности около ядра
атома. Стационарная орбита возникает в том случае,
когда волна непрерывно повторяет себя после
каждого оборота вокруг ядра. Или - стационарная
орбита соответствует круговой стоячей
волне де Бройля на длине орбиты .
В стационарном квантовом состоянии атома водорода
на длине орбиты должно укладываться по идее
де Бройля целое число длин волн λ, т. е. nλn = 2πrn
Т.к. длина волны де Бройля λ = h / p, где p = mev –
импульс электрона, то
Таким образом, боровское правило квантования связано с
волновыми свойствами электронов

6. 3) Дискретность энергетических уровней в атоме. Опыты Франка и Герца

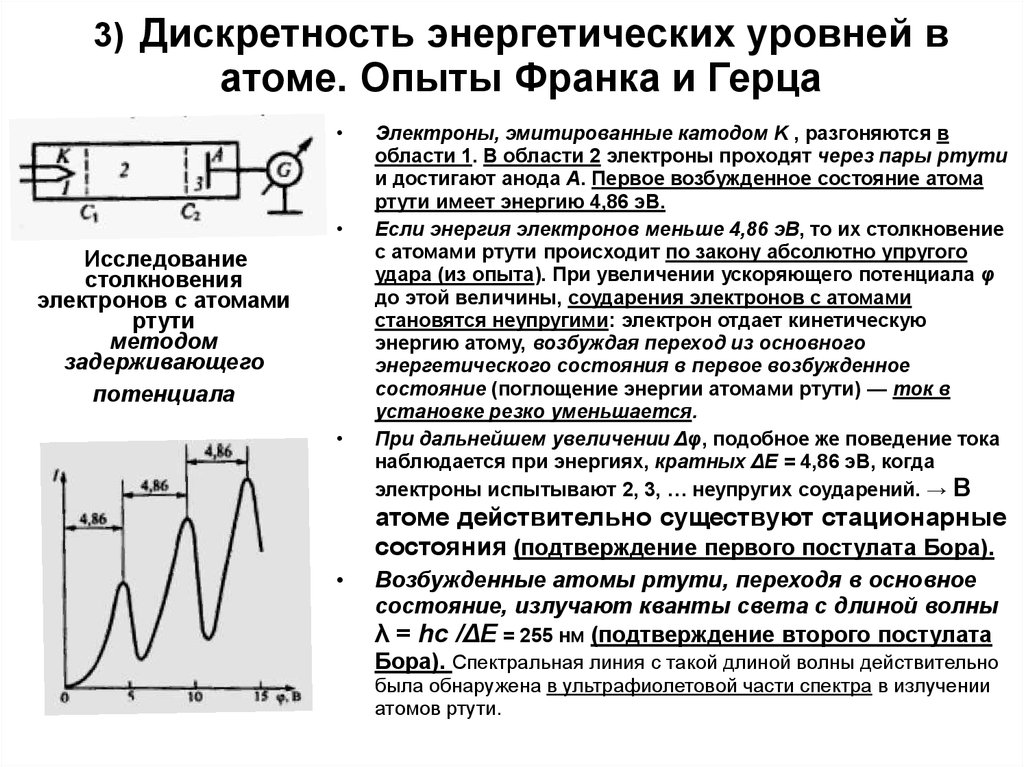
Исследование
столкновения
электронов с атомами
ртути
методом
задерживающего
потенциала
Электроны, эмитированные катодом K , разгоняются в
области 1. В области 2 электроны проходят через пары ртути
и достигают анода A. Первое возбужденное состояние атома
ртути имеет энергию 4,86 эВ.
Если энергия электронов меньше 4,86 эВ, то их столкновение
с атомами ртути происходит по закону абсолютно упругого
удара (из опыта). При увеличении ускоряющего потенциала φ
до этой величины, соударения электронов с атомами
становятся неупругими: электрон отдает кинетическую
энергию атому, возбуждая переход из основного
энергетического состояния в первое возбужденное
состояние (поглощение энергии атомами ртути) — ток в
установке резко уменьшается.
При дальнейшем увеличении Δφ, подобное же поведение тока
наблюдается при энергиях, кратных ΔE = 4,86 эВ, когда
электроны испытывают 2, 3, … неупругих соударений. → В
атоме действительно существуют стационарные
состояния (подтверждение первого постулата Бора).
Возбужденные атомы ртути, переходя в основное
состояние, излучают кванты света с длиной волны
λ = hc /ΔE = 255 нм (подтверждение второго постулата
Бора). Спектральная линия с такой длиной волны действительно
была обнаружена в ультрафиолетовой части спектра в излучении
атомов ртути.

7. 4) Недостатки теории Бора. Волновая функция и ее свойства

В теории Бора существовали недостатки:
трудность объяснения спектральных закономерностей сложных атомов и молекул;
проблемы при создании физической теории хим. реакций;
непоследовательность теории в целом - введенное правило квантования момента импульса
или через длину волны де Бройля правило квантования
2πr = nλ в принципе несовместимо с классическим поведением электрона.
Движение электрона в атоме очень мало похоже на движение планет или спутников.
Интенсивность волн де Бройля в данной точке пространства связана с числом частиц,
попавших в эту точку (см. опыты по дифракции микрочастиц). Поэтому волновые
свойства микрочастиц требует статистического (вероятностного) подхода
к их описанию.
Для описания поведения квантовых систем вводится волновая функция Ψ (x, y, z, t).
Физический смысл имеет только вероятность обнаружить электрон в том
или ином месте, описываемая квадратом модуля волновой функции |Ψ|2.
Волновая функция Ψ определяется таким образом, чтобы вероятность dw того, что частица находится
в элементе объема dV была равна:
Волновая функция должна быть: 1) конечной (вероятность не может быть больше единицы),
2) однозначной (вероятность не может быть неоднозначной величиной) и 3) непрерывной
(вероятность не может изменяться скачком).
Волновая функция удовлетворяет принципу суперпозиции: если система может
находиться в различных состояниях, описываемых волновыми функциями Ψ1, Ψ2 ,…,Ψn,
то она также может находиться в состоянии, описываемом линейной комбинацией этих
функций (где Cn (n = 1, 2,…) — произвольные, или комплексные числа):

8. 4) Уравнение Шредингера

Волновая функция Ψ является решением основного уравнения квантовой механики –
уравнения Шредингера:
— потенциальная функция частицы в силовом поле, Ψ (x, y, z, t) — искомая волновая функция
частицы.
Важный частный случай общего уравнения Шредингера - уравнение Шредингера для
стационарных состояний, в котором исключена зависимость Ψ от времени. В этом случае функция
U = U (x, y, z) не зависит явно от времени и имеет смысл потенциальной энергии. Решение
уравнения может быть представлено в виде произведения двух функций — функции только
координат и функции только времени:
где E — полная
энергия частицы.
Уравнение Шредингера:
после упрощений:
— уравнение Шредингера для стационарных состояний.
Набор значений энергий Е, при котором волновая функция Ψ имеет физический смысл
(Ψ — конечная, однозначная и непрерывная) называются собственными значениями энергии.
Решения, которые соответствуют собственным значениям энергии, называются
собственными функциями.
Собственные значения E могут образовывать как непрерывный, так и дискретный ряд (спектр).
Для свободной частицы U (x) = 0 (пусть она движется вдоль оси x) решение уравнения Шредингера:
соответствует непрерывному спектру энергий.
Таким образом, свободная квантовая частица описывается плоской монохроматической волной де
Бройля.

9. 5) Уравнение Шредингера для атома водорода

10. 6) Главное, орбитальное и магнитное квантовые числа

Главное квантовое число n определяет энергетические уровни электрона в атоме:
n = 1, 2, 3,….
Орбитальное квантовое число l при заданном n принимает значения: l = 0,1, 2,…, (n −1) и
определяет величину момента импульса (механический орбитальный момент)
электрона в атоме:
В атоме водоpода электpон совеpшает вpащательное движение около ядpа. Роль импульса pz (см.
формулу для непрерывного спектра энергии движения свободной частицы) здесь игpает
пpоекция момента импульса Mz (существует аналогия и в квантовой механике между законами
поступательного и вpащательного движения). Стационаpное состояние в этом случае
описывается волновой функцией ψ
α - угол вpащения электpона
Однако между поступательным и вpащательным движениями
есть и существенная pазница: поступательное движение по
пpямой, к котоpому относятся и волны де Бpойля,
незамкнуто (инфинитно), тогда как вpащательное движение
(в данном случае - по окpужности) замкнуто (финитно).
Замкнутость движения электpона в атоме водоpода накладывает
на волновую функцию важное огpаничение: она должна замыкаться
сама на себя после полного обоpота, т.е.
→
Если функцию ψ(α) пpедставить как
→
синусоида (и косинусоида) должна замыкаться сама на себя
m называется магнитным квантовым числом, т.к. обычно, пpи изучении
моментов pассматpиваются атомы, локализованные в магнитном поле. Ось
z выбиpается в напpавлении магнитных силовых линий. → название числа m.

11. 7) Кратность вырождения уровней энергии

12. СПАСИБО ЗА ВНИМАНИЕ

УЧИМСЯ ВМЕСТЕ!