Строение атома. Физические модели строения атома

1.

Химия - теоретические основы
Анатолий Анатольевич БАРУНИН - лектор
Литература:
1,2. А.П.КИСЕЛЕВ, А.А.КРАШЕНИННИКОВ. Основы общей химии:
1-Уч.пос.2012 г. одной книгой(1262) 2-Уч.пос.(ч.1,2,3)2002-2007г.
2 – Уч.пос. Часть 1 Строение вещества 2002 г.(552)
Часть 2 Термодин.и кинетика химического процесса 2003(599)
г.(599)
Часть 3 Электрохим. и коррозионные процессы 2007(837)
3. Учебные пособия и метод.указания кафедры
4. А.И. Горбунов, А.А. Гуров и др.Теоретические основы общей
химии 5. А.В. Суворов, А.Б.Никольский 6. В.В.Фролов
7.Н.В.Коровин - учебники для вузов

2. Химия

Строение вещества
Химический процесс
Строение атома
Химическая
термодинамика
Химическая связь
Химическая кинетика
Строение твердого
тела
Равновесие в
химических системах
Электрохимия;
Коррозия

3. I. Строение атома

3 этапа развития учения о строении атома
1 – Натурфилософские представления об атомном строении материи.
(5 в.до н.э.) Демокрит – понятие «атом». Эпикур, Аристотель
2 – Химическая гипотеза об атоме, как наименьшей частице химического
элемента. Атомы отличаются массой. Парацельс, Бойль, Берцелиус
(16-17 в.)
3 – Физические модели. Описывают сложное строение атома (на рубеже 1920 в. по настоящее время) на основании:
Исследование электролиза(1832) Майкл Фарадей
Открытие каналовых (1886) и катодных лучей (1896) Уильям Крукс
Открытие и измерение свойств электрона (1897) Джозеф Джон Томсон
Открытие естественной радиоактивности (1896) Анри Беккерель
Атомы содержат разноименно заряженные частицы

4. Строение атома. Физические модели строения атома

Эрнест Резерфорд - Планетарная модель атома (1911 г.)
Атом - сложная частица, состоящая из положительно заряженного
ядра (~10-15 м) и отрицательно заряженных электронов вращающихся
вокруг ядра на расстоянии ~10-10 м (по характеру рассеяния α-частиц
тонкими Pt, Ag и Cu металлическими фольгами)
Нильс Бор – теория (модель) строения атома
водорода (постулаты) (1913 г.)
En = - 2π2e4k2m / h2 ∙ 1/n2 (n=1 E1= -13,6 эВ; En = - E1 / n2
rn = h2 / 4π2e2km ∙ n2 n = 1,2,3…..
Эрвин Шредингер - [квантово-механическая модель]
Квантовая (волновая) механика - теория, устанавливающая способ
описания и законы движения микрочастиц (1926 г.)

5. Корпускулярно-волновой дуализм свойств материи [проблема природы лучистой энергии - эл.магн.излучения(ЭМИ)]

Частица: m - масса
p = mv - импульс
E= mv2/2 - кинетическая энергия
Волна: l - длина волны
n- частота
Т - период
Электромагнитное излучение
Макс Планк E = h n h n – энергия кванта ЭМИ нагретого
1900 г.
тела (дискретная порция)
h = 6,6262 10-34 Дж с - постоянная Планка
n- частота излучения [с–1]
квант энергии любого ЭМИ– частица фотон
Альберт Эйнштейн E =
1905 г.
m - масса фотона, кг
c = 2,9979 108 м/сек - скорость света
m c2
hn = mc2 n с
Корпускулярно- l
h
m
cl
волновой дуализм
ЭМИ:фотон - частица и/или волна
h
l
m c
h
l
p
p = m c - импульс
фотона

6. Луи де Бройль

(дуализм-общее свойство материи, Частица: m - масса, v – скорость
а не только ЭМИ) - гипотезапостулат о связи импульса P любого
h
движущегося матер.объекта с
m v
длиной волны λ, представляющей
волновой хар-р его движения (1924)
2
m
v
г.
Кинетическая энергия - E k
2
электрон
h
Длина волны - l
m = 9,11 10-31 кг
2 m Ek
h
l
p
Ek = 100 эВ (1эВ=1,602 10-19Дж) , l = 1.2 Å (1 Å =10-10 м)
Дифракционная
решеткакристалл.плоскости Ме
монокристаллов
l= 1.2 Å
(Ni фольга)
α- постоянная
решетки

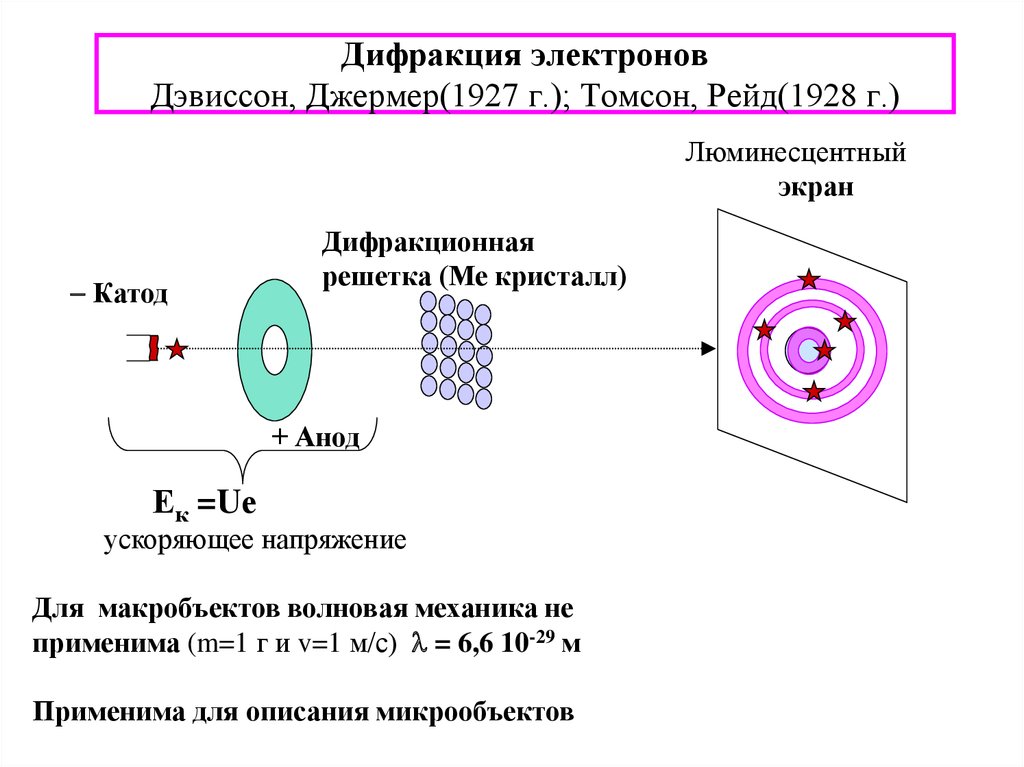
7. Дифракция электронов Дэвиссон, Джермер(1927 г.); Томсон, Рейд(1928 г.)

Люминесцентный
экран
Катод
Дифракционная
решетка (Ме кристалл)
+ Анод
Ек =Uе
ускоряющее напряжение
Для макробъектов волновая механика не
применима (m=1 г и v=1 м/с) l = 6,6 10-29 м
Применима для описания микрообъектов

8. Принцип неопределенности [для микрочастиц(электрона)]

Вернер Гейзенберг постулировал
этот принцип в 1927 г.
h
x p x
2
Точное определение координат частицы и ее импульса невозможно и
заменяется определением вероятности нахождения частицы в какой-то
области пространства
Р - вероятность
0 Р 1
Эрвин Шредингер – квантово-механическая модель строения атома на
основе квантовой (волновой) механики - теории, устанавливающей способ
описания и законы движения микрочастиц - базируется на 2-х основных
гипотезах-постулатах Л. Де Бройля и В. Гейзенберга

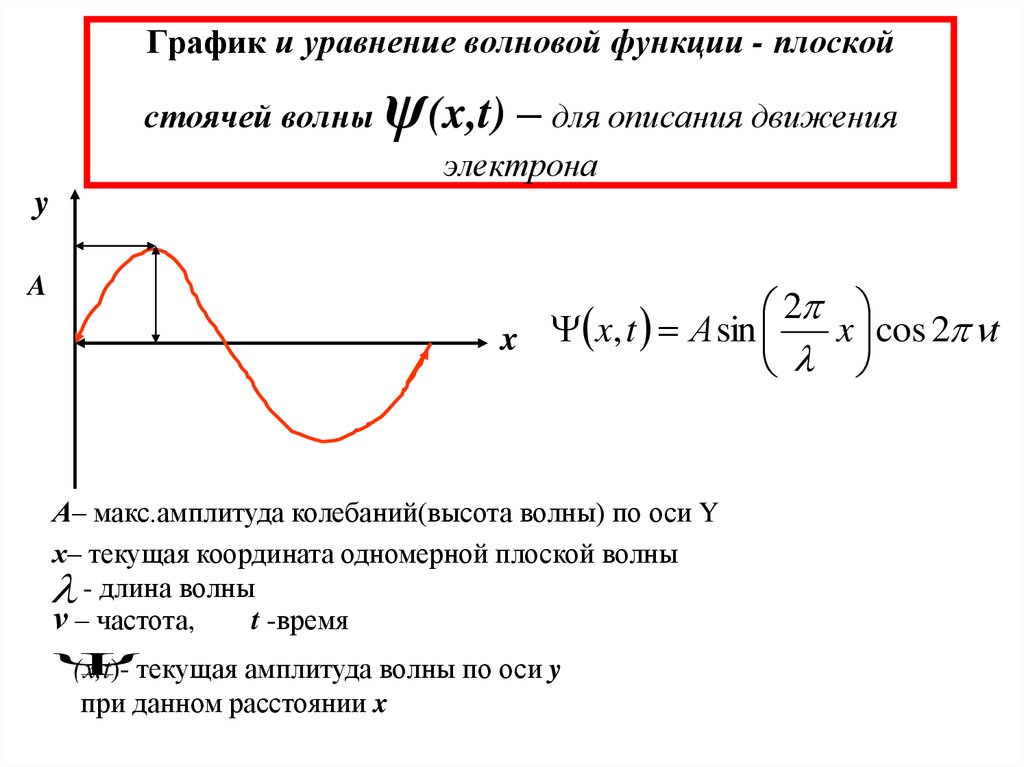
9. График и уравнение волновой функции - плоской стоячей волны ψ(x,t) – для описания движения электрона

y
A
2
x cos 2 nt
x x, t А sin
l
А– макс.амплитуда колебаний(высота волны) по оси Y
х– текущая координата одномерной плоской волны
l - длина волны
ν – частота,
t -время
(x,t)- текущая амплитуда волны по оси y
при данном расстоянии x

10. Уравнение Шредингера

1. Уравнение отображает волновой характер движения электрона в
пространстве с координатами (x,y,z)
(x,y,z,t) - волновая функция - пси функция (стоячая волна)
- Текущая амплитуда, функция координат (x,y,z) и времени (t)
(x,y,z) – (стоячая волна)стационарный процесс
– Текущая амплитуда, функция координат (x,y,z); пусть cos2πνt=1
Дифф.уравнение 2-го порядка стоячей волны для стационарного процесса
2 (x, y, z) 2 (x, y, z) 2 (x, y, z) 4 2
2 (x, y, z) 0
2
2
2
x
y
z
l
l - длина волны
2 2 2
2
2
2
2
x
y
z
2 - оператор Лапласа(набла два)

11. 2. Уравнение должно содержать в себе характеристики электрона как волны - , так и частицы - m (дуализм микромира)

2. Уравнение должно содержать в себе характеристики электрона как
волны - l, так и частицы - m (дуализм микромира)
l m, Ek
l
Длина волны де Бройля
h
h
h
p m v
2 m Ek
2
h
λ2
2 m Ek
Волновое уравнение движения свободного электрона:
8 2 m
(x, y, z)
E k (x, y, z) 0
2
h
E - полная энергия
V- потенциальная энергия
2
E = Ek + V
Эрвин Шрeдингер: Волновое уравнение микрочастицы(электрона) в
потенциальном поле(в атоме)
1926 г.
8 m
(x, y, z) 2 (E V) (x, y, z) 0
h
2
2

12. Физический смысл волновой функции

Макс Борн, 1926 г.
(x,y,z) - пси функция - волновая функция
•волновая функция(амплитудная) и физического смысла не имеет
• 2(x,y,z) - квадрат волновой функции пропорционален вероятности
(dP) нахождения частицы в элементарном объеме (dV)
dP = 2(x,y,z) dV
Вероятность Pv нахождения частицы в объеме V:
PV 2 (x, y, z)dV
V
Плотность вероятности (электронная плотность) вероятность нахождения в элементарном объеме dV с
коордиатами dx, dy, dz:
dP
2 (x, y, z)
dV
Принцип нормирования волновых функций
PV = ∫v A2 |Ψ(x,y,z) |2 dV = 1,
А –нормирующий множитель

13. Электрон в одномерном потенциальном ящике(яме). Решение ур. Шредингера.

Потенциальная яма (ящик) - область пространства, вне которой
потенциальная энергия электрона обращается в бесконечность, т.е
электрон не может выйти за границы ящика (связанное состояние)V 0
модель для электрона в атоме
a
•Одномерный потенциальный ящик
Граничные условия:
внутри ящика:
на границах ящика:
V=0
V=
(x)
(0)=0; (а)=0
d 2 (x) 8 2m
E (x) 0
dx 2
h2
Решение – нахождение собственных функций(конечны, однозначны,
непрерывны) и расчет соответствующих этим функциям значений
собственных энергий
x

14. Нахождение волновой функции состояния электрона в потенц.ящике

•Нахождение волновой функции состояния
электрона в потенц.ящике
d 2 (x) 8 2m
E (x) 0
dx 2
h2
Общее решение
ур.Шредингера
(x) A sin
(0) A sin
Граничные условия
A 0
sin
2
l
a 0
2a
n
(x) A sin
x
l
a
n
2
n
(x)
sin
x
a
a
2
2
l
x
0 0
l
2
(a) A sin
a 0
l
2
a n
n=1,2,3…..
l
Из условия
нормировки
a
A sin
2
0
2
(
n
a
x)dx 1
Решение в явном виде - набор
волн.функций Ψ(х), где a параметр потенциального ящика,
n = 1,2,3…- квантовое число

15. Нахождение энергии электрона

•Нахождение энергии электрона
(x) A sin
n
a
x 0
d 2 (x)
2 n2
n
A
( sin
x)
2
2
dx
a
a
2 n2
d (x)
n
n
A
cos
x
dx
a
a
d 2 (x) 8 2m
E (x) 0
2
2
dx
h
8 2 m
n
A
( sin
x)
E A sin
x 0
2
2
a
a
h
a
n
2 n 2 8 2 m
A (sin
x) [
E] 0
2
2
a
a
h
2 n2
a2
n
8 2 m
E 0
2
h
h2
E 2
n2
8a m
Набору ᴪ(x) соответствует набор Е, n = 1,2,3…- квантовое число

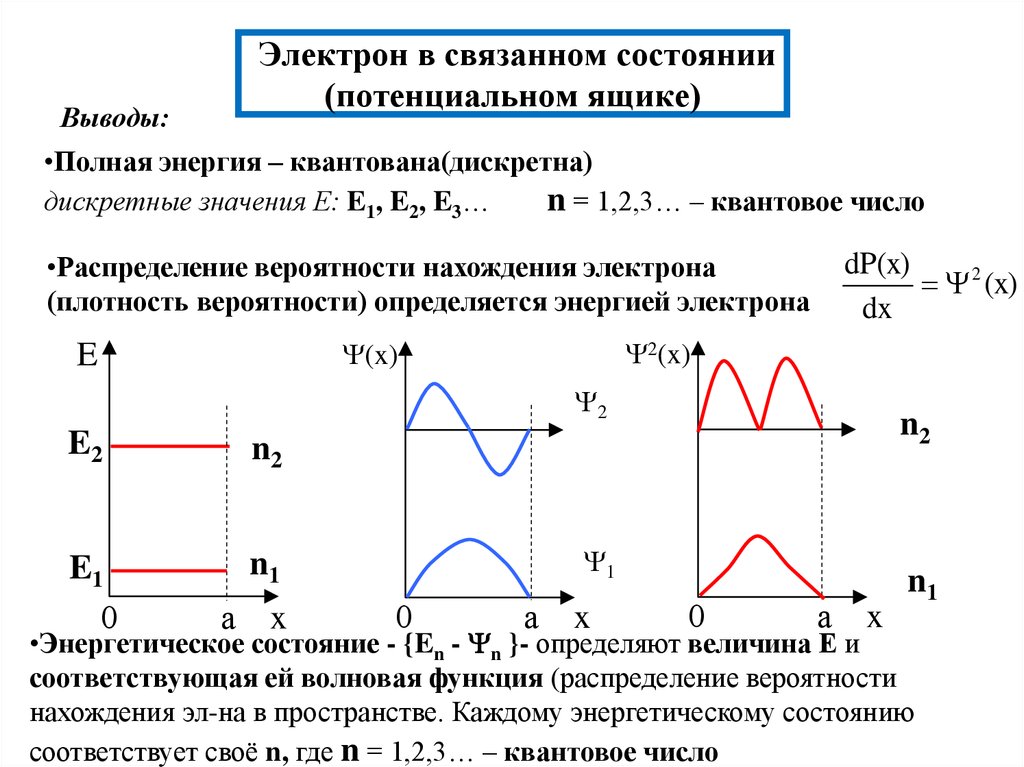
16. Электрон в связанном состоянии (потенциальном ящике)

Выводы:
•Полная энергия – квантована(дискретна)
дискретные значения Е: E1, E2, E3…
n = 1,2,3… – квантовое число
•Распределение вероятности нахождения электрона
(плотность вероятности) определяется энергией электрона
2(x)
(x)
E
dP(x)
2 (x)
dx
2
E2
n2
E1
0
n1
а
x
n2
1
0
а
x
0
а
x
n1
•Энергетическое состояние - {En - n }- определяют величина Е и
соответствующая ей волновая функция (распределение вероятности
нахождения эл-на в пространстве. Каждому энергетическому состоянию
соответствует своё n, где n = 1,2,3… – квантовое число

17. Электрон в трехмерном потенциальном ящике

Решение:
•Набор волновых функций:
n y
8
n x
n
(x, y, z)
sin(
x) sin(
y) sin( z z)
a b c
a
b
c
nx, ny, nz – квантовые числа
a,b,c – параметры ящика
2
•Набор энергий:
2
ny
2
2
h
n
n
E
( x2 2 z2 )
8m a
b
c
Выводы:
1. Энергия электрона квантована.
2. Энергетическое состояние определяется набором целочисленных
параметров - трех квантовых чисел nx. ny, nz.

18. Вырожденные энергетические состояния

одно значение энергии – несколько наборов квантовых чисел несколько волновых функций
h2
2
2
2
E
(n
n
n
x
y
z )
2
8m a
а=b=c
2
h
Е,
8m a 2
Е5 = 12
Е4 = 11
[2,2,2]
[3,1,1] [1,3,1] [1,1,3]
Е3 = 9
[2,2,1] [1,2,2] [2,1,2]
Е2 = 6
[2,1,1] [1,2,1] [1,1,2]
Е1 = 3
[1,1,1]
Трехкратная
степень
вырождения

19. Квантово-механическая модель атома. Основное состояние атома водорода [k=1/4πε0] - константа в з-не Кулона

-ē
r
+ē
k e
V
r
2
(x, y, z)
z
r
y
x = r sin cos
y = r sin sin
z = r cos
x
2
2
8
m
k
e
2 (x, y, z) 2 (E
) (x, y, z) 0
h
r
(r, , )
Основное состояние
Еmin
(r)
2 (r) 2 (r) 8 2 m
k e2
(E
) (r) 0
2
2
r
r r
h
r
(r) A e a r
Ψ(r) – волновая функция (собственная функция), явл.
решением ур.Шредингера,
а – const, А – нормирующий коэффициент

20. Решение уравнения Шредингера для основного состояния атома водорода

(r) A e a r 0
(r)
A a e a r
r
2 (r)
2
a r
A
a
e
r 2
подставляем в уравнение Шредингера
A a 2 e a r
A e a r 0
2
2
2
8
m
k
e
a r
A a e a r
(E
)
A
e
0
2
r
h
r
2
2
2
2
a
8
m
8
m
k
e
a2
E
0
2
2
r
h
h
r
2
2
2
8
m
1
8
m
k
e
a2
E (2 a
)
2
2
h
r
h

21. Решение системы

2 2 m k 2 e4
E
h2
2
8
m
2
a
E 0
2
h
8 2 m k e 2
2 a
0
2
h
4 2 m k e 2
a
h2
(r) A e a r
Из принципа нормировки:
Сходимость значений Е расчетной и
экспериментальной (-13,6 эВ) – модель
имеет право на существование
A
1
a 3

22. Радиальное распределение электронной плотности. Понятие электронной орбитали

Наглядно вероятность нахождения электрона в пространстве характеризует
функция распределения эл.плотности (вероятность в элементарном объеме dV)
dP = 2 dV
P 2 dV 1
V
r
dr
s( r)
dP(r)= 2 4 r2dr P(r)=∫r0 2 4 r2dr
dV = 4 r2dr
Объём сферич.слоя Радиальное распределение электронной
тощиной dr
плотности (зависимость вероятности
нахождения эл-на в сферическом слое от r):
dP(r) =
s(r) = 2 4 r2
dr
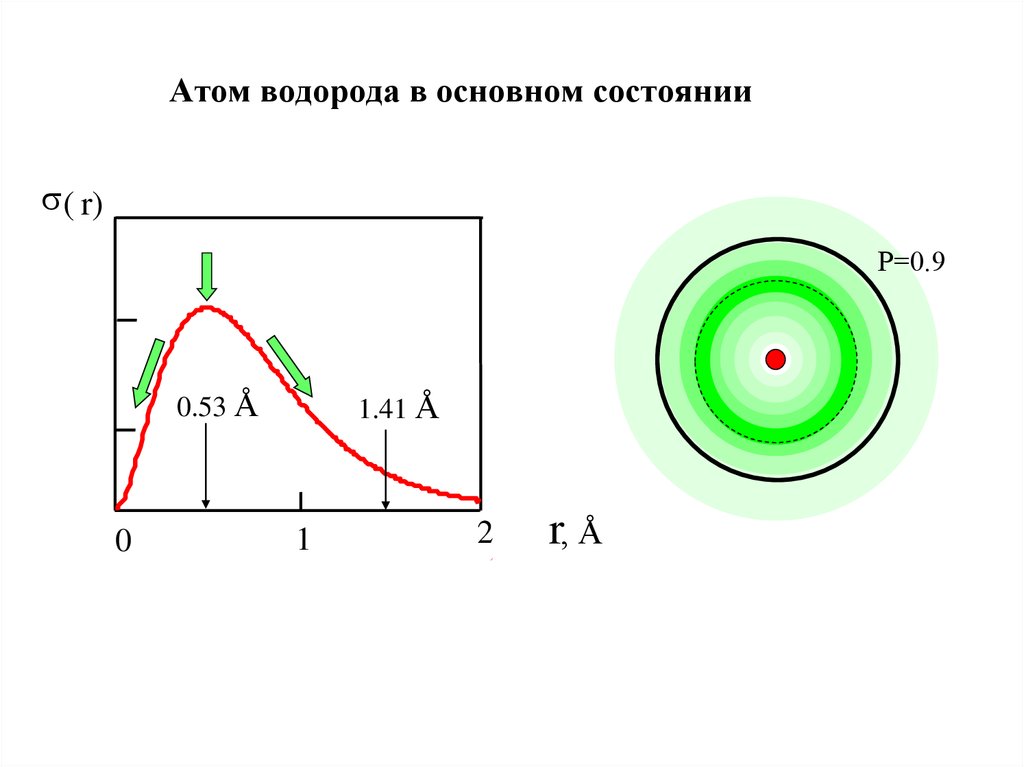
Орбиталь электрона –
s ( r)-max
P=0.90
P=0.33
0
0.53 Å
1
1.41 Å 2 r, Å
(объём) область пространства
(для атома водорода в основном
состоянии это сфера) в которой
вероятность нахождения
электрона P=0.90
(90 %)

23. Атом водорода в основном состоянии

s( r)
Р=0.9
0.53 Å
0
1.41 Å
1
2
r, Å

24. Возбужденные состояния атома водорода

Общий вид волновой функции - (r, , ). Используя метод разделения
переменных (r, , ) представляют в виде R(r) Y( , )
R(r)n, l -функция радиального распределения электронной плотности в
явном виде(получают при решении ур. Шреденгера) содержит n и l
Y( , )l,m -функция углового распределения электронной плотности в
явном виде(получают при решении ур. Шреденгера) содержит l и m
n, l, m - целочисленные параметры волновых функций в явном виде – наз.
квантовыми числами
Определяют набор собственных волн.функций(решений ур.Шредингера) и
соответствующий им набор энергетических состояний{En- n,l,m } в атоме
водорода
Квантовые числа:
главное – n = 1,2,3,4…
орбитальное – l = 0,1,2,3...(n -1)
магнитное – m = -l, (-l+1),...,0,...,(+l–1), +l
спиновое – ms =±1/2 (1933 г.) Поль Дирак, модель Уленбека и Гаудсмита

25. Квантовые числа

главное : n = 1,2,3,4…
Определяет разрешенные (квантованные, дискретные)
2 2 m k 2 e 4 1
En
2
значения полной энергии электрона, размер
2
h
n
орбитали(расстояния е до ядра)
орбитальное : l = 0,1,2,3...(n-1) Возможные квантовые значения орбитального
момента кол.движения электрона(Екин -форма орбитали)
l=2
l=0
l=1
s- орбиталь
р- орбиталь
магнитное : m = -l, (-l+1),...,0,..., (l-1), +l Разрешенные
направления в пространстве вектора орбит.момента
кол.движения-число орбиталей(Епот –зависит от положения е
в пространстве)
р- орбиталь m = 1, 0,-1
s- орбиталь- m = 0
cпиновое : ms ±1/2 Собственный момент кол.движения
d- орбиталь
pz
px
py

26.

Электрон.орбитали ат. водорода(комбинация 3-х кв.ч.)
n l = 0,1…(n-1)
1
2
3
4
m = -l,…0,…+l
Число
орбиталей
Энергия Еn
0 – 1s
0 – 2s
1 – 2p
0 – 3s
1 – 3p
2 – 3d
0
0
+1, 0, -1
1
E1
1
3
E2
0
+1, 0, -1
+2, +1, 0, -1, -2
0 – 4s
1 – 4p
2 – 4d
3 – 4f
0
+1, 0, -1
+2, +1, 0, -1, -2
+3,+2,+1,0,-1,-2,-3
1
3
5
1
3
5
7
E3
E4

27. Энергетическая диаграмма орбиталей в атоме водорода

Е
n=4
n=3
n=2
n=1
4s
4p
4d
3s
3p
3d
2s
2p
4f
1s
E1s < E2s = E2p< E3s = E3p = E3d < E4s = E4p = E4d = E4f < E5s …
(вырождение по орбит.кв.ч. l и по магн.кв.ч. m, Е электрона
зависит только от значения главного кв.ч. n)

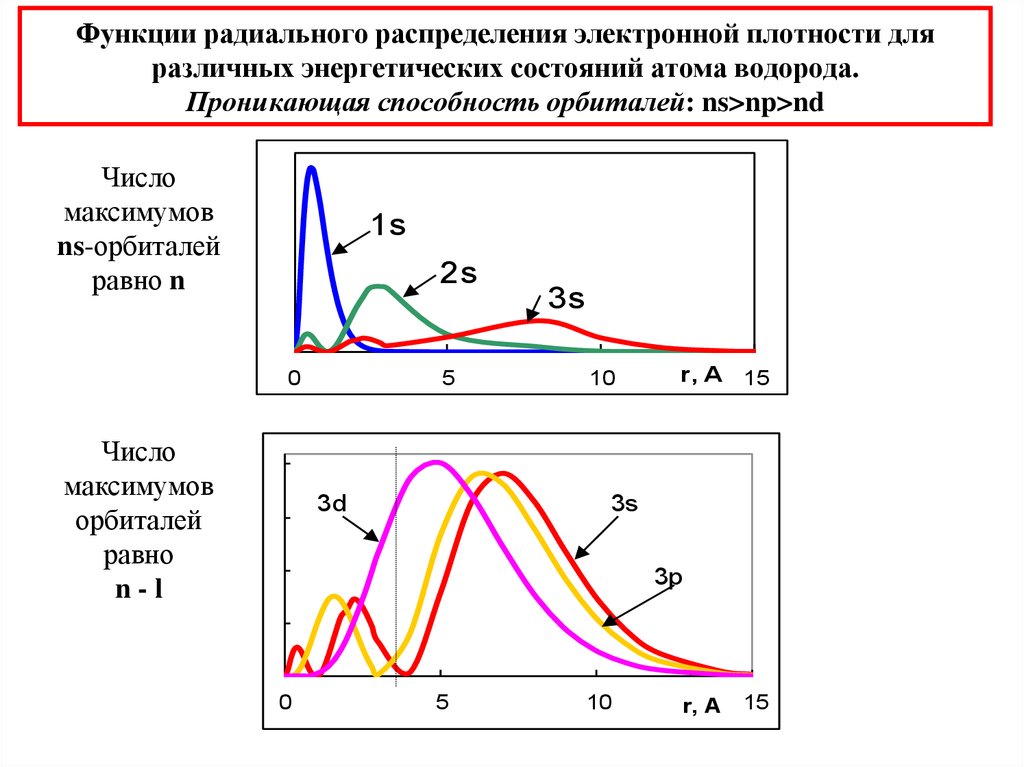
28. Функции радиального распределения электронной плотности для различных энергетических состояний атома водорода. Проникающая способность

орбиталей: ns>np>nd
Число
максимумов
ns-орбиталей
равно n
1s
2s
0
Число
максимумов
орбиталей
равно
n-l
5
3d
3s
10
r, A 15
3s
3p
0
5
10
r, A
15

29. 1.7 Многоэлектронный атом (одноэлектронное приближение - водородоподобная система)

Z
э
+Z
Zэ = Z - sn,l
Z – заряд ядра
Zэ - эффективный заряд ядра
sn,l - константа экранирования
ē
-(Z-1)
Атом
Z
sn,l
Zэ=Z - s
H
1
0
1
He Li Be
B
C
2
3
4
5
6
0.3 2.70 2.05 2.40 2.75
1.7 1.30 1.95 2.60 3.25

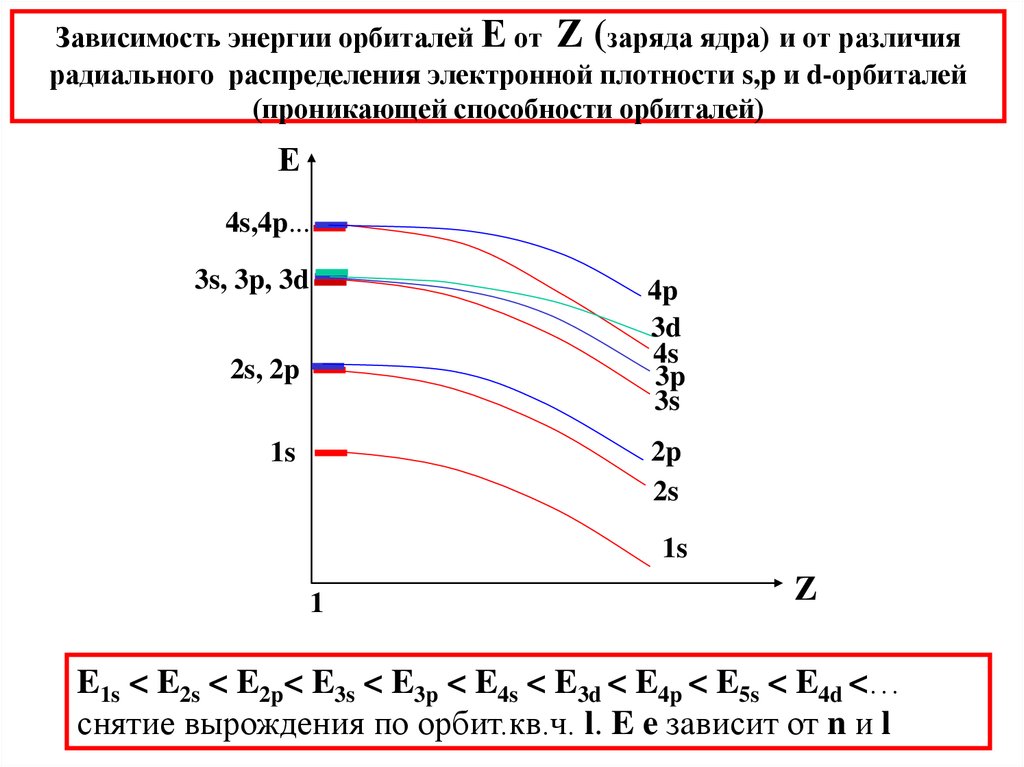
30. Зависимость энергии орбиталей Е от Z (заряда ядра) и от различия радиального распределения электронной плотности s,p и d-орбиталей (проникающ

Зависимость энергии орбиталей Е от Z (заряда ядра) и от различия
радиального распределения электронной плотности s,p и d-орбиталей
(проникающей способности орбиталей)
Е
4s,4p...
3s, 3p, 3d
4p
3d
4s
3p
3s
2s, 2p
2p
2s
1s
1s
1
Z
E1s < E2s < E2p< E3s < E3p < E4s < E3d < E4p < E5s < E4d <…
снятие вырождения по орбит.кв.ч. l. E e зaвисит от n и l

31. Таблица электронных орбиталей многоэлектронных атомов

1 1s
2 2s
2p
3 3s
3p
4 4s
3d
4p
5 5s
4d
5p
6 6s
* 5d
6p
7 7s
**6d
7p
*4f
**5f

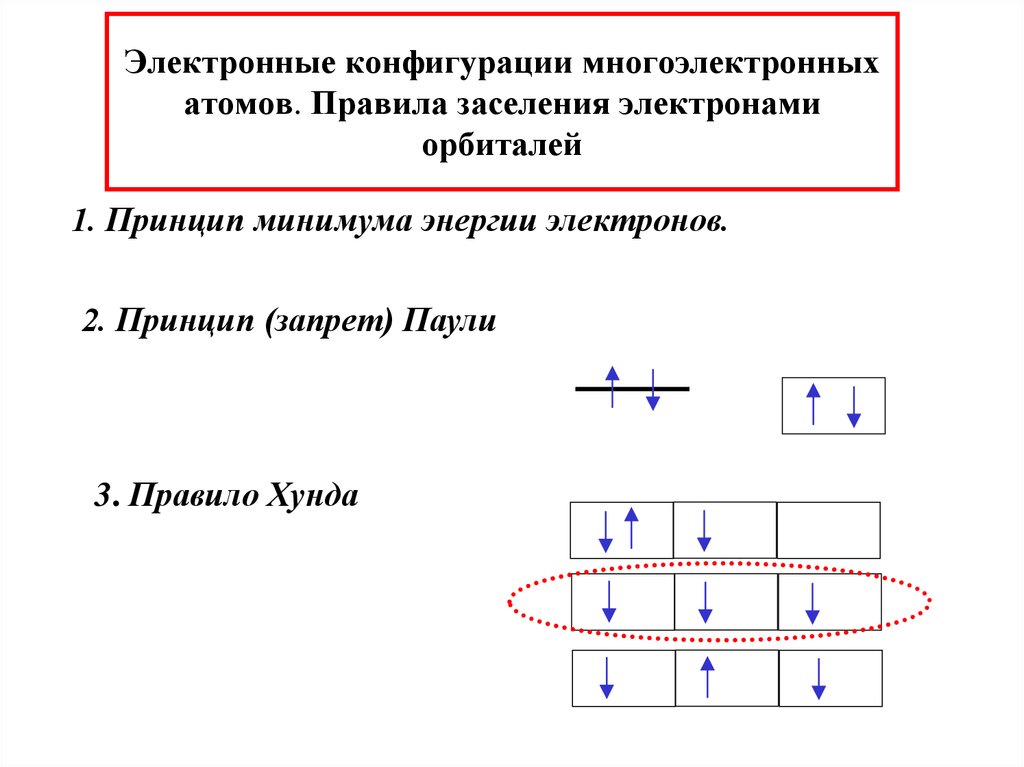
32. Электронные конфигурации многоэлектронных атомов. Правила заселения электронами орбиталей

1. Принцип минимума энергии электронов.
2. Принцип (запрет) Паули
3. Правило Хунда

33. 1.8 Периодическая таблица элементов (1869)

ГРУППЫ
ПЕРИОДЫ
1 1s 1
1 1ВодородH
2 2s1,0079
2 3 Li
3 3sЛитий
6,941
3 11 Na
4 4sНатрий
22,9898
2
3
4
5
6
7
8
9
10
11
4 Be
5
3pБор
Бериллий
9,0122
12Mg
4p26,9815
Алюминий
Кальций
4d
40,08
Скандий
44,9559
Титан
47,88
Ванадий
50,9415
Железо
Кобальт
Никель
Медь
Цинк
54,9380
55,847
58,933
58,69
63,546
65,39
56 Ba 57 La 72 Hf 73 Ta 74 W 75 Re 76 Os 77 Ir
**6dЛантан
138,9055
45Rh
46 Pd 47 Ag 48Cd
Цирконий
Ниобий
Молибден
Технеций
Рутений
Палладий
Серебро
91,22
92,9064
95,94
Родий
[97]
101,07
102,91
106,4
107,868
Барий
Гафний
137,33
178,49
87 Fr 88 Ra 89 Ac 104Rf
Тантал
180,9479
Азот
Кислород
Фтор
Неон
12,011
14,0067
15,9994
18,9984
20,179
39,948
72,59
Мышьяк
74,9216
34 Se 35 Br 36 Kr
Селен
Бром
Криптон
78,96
79,904
83,80
49 In 50 Sn 51 Sb 52 Te 53
Кадмий
6pИндий
112,41 114,82
Олово
Сурьма
Теллур
118,69
121,75
127,60
I 54 Xe
Иод
126,9044
Ксенон
131,29
Свинец
Астат
Радон
186,207
190,2
192,2
195,08
207,21
Висмут
208,9804
Полоний
183,85
[209]
[210]
[222]
111
112
114
115
116
117
118
[223]
226,03
227,03
[261]
[262]
[263]
[262]
[265]
232,038
35,453
7pТаллий
200,59 204,3
Хассий
231,036
32,06
Ртуть
Борий
Протактиний
Аргон
30,9738
80Hg
Сиборгий
Торий
Хлор
28,0855
Золото
196,9665
Дубний
140,908
Сера
Платина
Резерфордий
140,12
17 Cl 18 Ar
Фосфор
78 Pt 79Au
Актиний
Празеодим
15 P 16 S
Кремний
Иридий
105Db 106 Sg 107Bh 108Hs 109Mt 110
58 Ce 59 Pr
F 10 Ne
Осмий
Радий
Церий
5pГаллий
69,72
9
Рений
81 Tl 82 Pb 83 Bi 84 Po 85 At 86Rn
113
Майтнерий
[266]
60 Nd 61Pm 62Sm 63 Eu 64 Gd 65 Tb 60 Dy 61 Ho 62 Er 68 Tm 69 Yb 71 Lu
Неодим
Прометий
Самарий
Европий
Гадолиний
144,24
[145]
150,36
151,96
157,25
90 Th 91 Pa 92 U
p
d
f
0
2 He
Вольфрам
Франций
**5f
40,08s
17
Углерод
Германий
Марганец
6 55 Cs
7 7sЦезий
132,9054
Кальций
16
N 8 O
32 Ge 3 As
51,996
42Mo 43 Tc 44Ru
Стронций
*4f
C 7
30 Zn 31Ga
Хром
* 5dИттрий
87,62
88,9059
20 Ca
15
4,0026
B 6
13 Al 14 Si
3d
24,305
Магний
38 Sr 39 Y 40 Zr 41Nb
Номер
14
Гелий
10,81
5 37Rb
6 6sРубидий
85,4678
7
13
2p
19 K 20 Ca 21 Sc 22 Ti 23 V 24 Cr 25Mn 26 Fe 27 Co 28 Ni 29Cu
4
5 5sКалий
39,0983
12
Уран
238,029
Символ
Название
Атомная масса, относительная
Тербий
158,925
Диспрозий
Гольмий
162,50
Эрбий
164,930
167,26
93 Np 94 Pu 95Am 96Cm 97 Bk 98 Cf
Нептуний
237,048
Плутоний
Америций
[244]
[243]
Кюрий
Брклий
[247]
[247]
Тулий,
168,934
Иттербий
Лютеций
173,04
174,967
99 Es 100Fm 101Md 102No 103Lr
Калифорний
Эйнштейний
[251]
[252]
Фермий
[257]
Менделевий
Нобелий
Лоуренсий
[258]
[259]
[260]

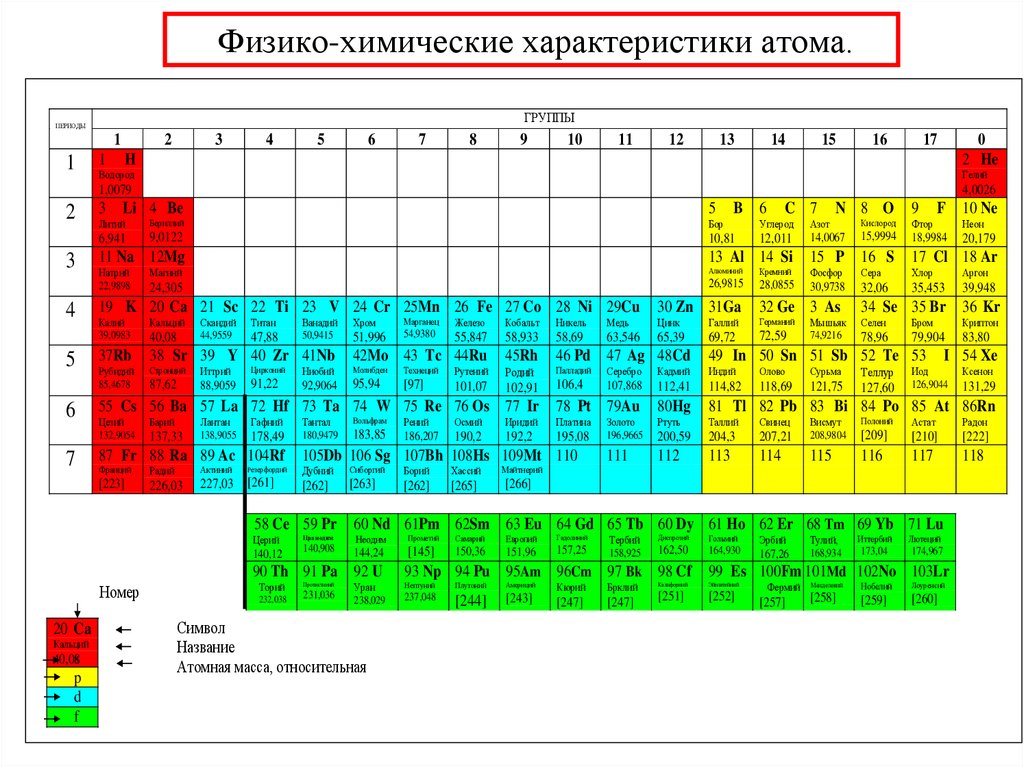
34. Физико-химические характеристики атома.

ПЕРИОДЫ
1
1
1
2
3
4
5
ГРУППЫ
•Радиус атома
и иона
6
7
8
9
10
11
12
13
14
15
16
17
0
2 He
H
Водород
Гелий
1,0079
2
3
4
5
6
7
4,0026
3 Li 4 Be
5
Литий
Бериллий
Бор
Углерод
Азот
Кислород
Фтор
Неон
6,941
9,0122
10,81
12,011
14,0067
15,9994
18,9984
20,179
11 Na 12Mg
Натрий
22,9898
Магний
Ковалентный радиус атомов, A
13 Al
2,5
24,305
Хлор
Аргон
28,0855
30,9738
32,06
35,453
39,948
Хром
Марганец
Железо
Кобальт
Никель
Медь
Цинк
Rb
32 Ge 3 As
Галлий
Германий
51,996
54,9380
55,847
58,933
58,69
63,546
65,39
69,72
72,59
42Mo 43 Tc 44Ru
45Rh
46 Pd 47 Ag 48Cd
Родий
Палладий
Серебро
Кадмий
Индий
Олово
Сурьма
Теллур
106,4
107,868
112,41
114,82
118,69
121,75
127,60
Иод
126,9044
Ксенон
102,91
Золото
196,9665
Ртуть
Таллий
Свинец
Астат
Радон
204,3
207,21
Висмут
208,9804
Полоний
200,59
[209]
[210]
[222]
111
112
113
114
115
116
117
118
Рубидий
85,4678
Стронций
Иттрий
Цирконий
87,62
88,9059
91,22
Цезий
132,9054
Барий
Лантан
138,9055
Гафний
47,88
Li
Na
101,07
Ниобий
Молибден
Технеций
92,9064
95,94
[97]
Рутений
Тантал
180,9479
Вольфрам
Рений
Осмий
Иридий
Платина
183,85
186,207
190,2
192,2
195,08
Мышьяк
74,9216
34 Se 35 Br 36 Kr
Селен
Бром
78,96
79,904
49 In 50 Sn 51 Sb 52 Te 53
Криптон
83,80
I 54 Xe
131,29
1,5
55 Cs 56 Ba 57 La 72 Hf 73 Ta 74 W 75 Re 76 Os 77 Ir 78 Pt 79Au 80Hg 81 Tl 82 Pb 83 Bi 84 Po 85 At 86Rn
137,33
178,49
87 Fr 88 Ra 89 Ac1 104Rf
105Db 106 Sg 107Bh 108Hs 109Mt 110
Франций
Радий
Актиний
Резерфордий
Дубний
Сиборгий
Борий
Хассий
[223]
226,03
227,03
[261]
[262]
[263]
[262]
[265]
Номер
p
d
f
26,9815
Сера
38 Sr 39 Y 40 Zr 41Nb
2
140,12
40,08s
17 Cl 18 Ar
Фосфор
37Rb
40,08
Церий
Кальций
K
F 10 Ne
15 P 16 S
Кальций
Ванадий
50,9415
9
Кремний
Калий
39,0983
Титан
N 8 O
14 Si
30 Zn 31Ga
Скандий
44,9559
C 7
Алюминий
19 K 20 Ca 21 Sc 22 Ti 23 V 24 Cr 25Mn 26 Fe 27 Co 28 Ni 29Cu
0,5 58 Ce 59 Pr 60 Nd
20 Ca
B 6
0
Празеодим
140,908
232,038
Протактиний
231,036
[266]
63 Eu 64 Gd 65 Tb 60 Dy 61 Ho 62 Er 68 Tm 69 Yb 71 Lu
Прометий
Самарий
Европий
Гадолиний
144,24
[145]
150,36
151,96
157,25
Тербий
158,925
Диспрозий
Гольмий
162,50
Эрбий
164,930
167,26
93 Np 94 Pu 95Am 96Cm 97 Bk 98 Cf
Уран
238,029
0
Символ
Название
Атомная масса, относительная
Kr
Ar
Неодим
90 Th 91 Pa 92 U
Торий
Ne
61Pm 62Sm
Майтнерий
Нептуний
Плутоний
Америций
237,048
[244]
[243]
10
20
Кюрий
Брклий
[247]
[247]
Заряд ядра, Z
Иттербий
Лютеций
173,04
174,967
99 Es 100Fm 101Md 102No 103Lr
Калифорний
Эйнштейний
[251]
[252]
30
Тулий,
168,934
Фермий
[257]
Менделевий
Нобелий
Лоуренсий
[258]
[259]
[260]
40

35. Ковалентный радиус ( RA = rсв /2) и радиус иона

R A R A0 R A
Частица
Радиус, Å
Частица
Радиус, Å
Na0
1.54
Sr0
1.91
Na+
1.02
Sr+2
1.18
Cl0
0.99
S0
1.02
Cl1.81
S-2
1.84

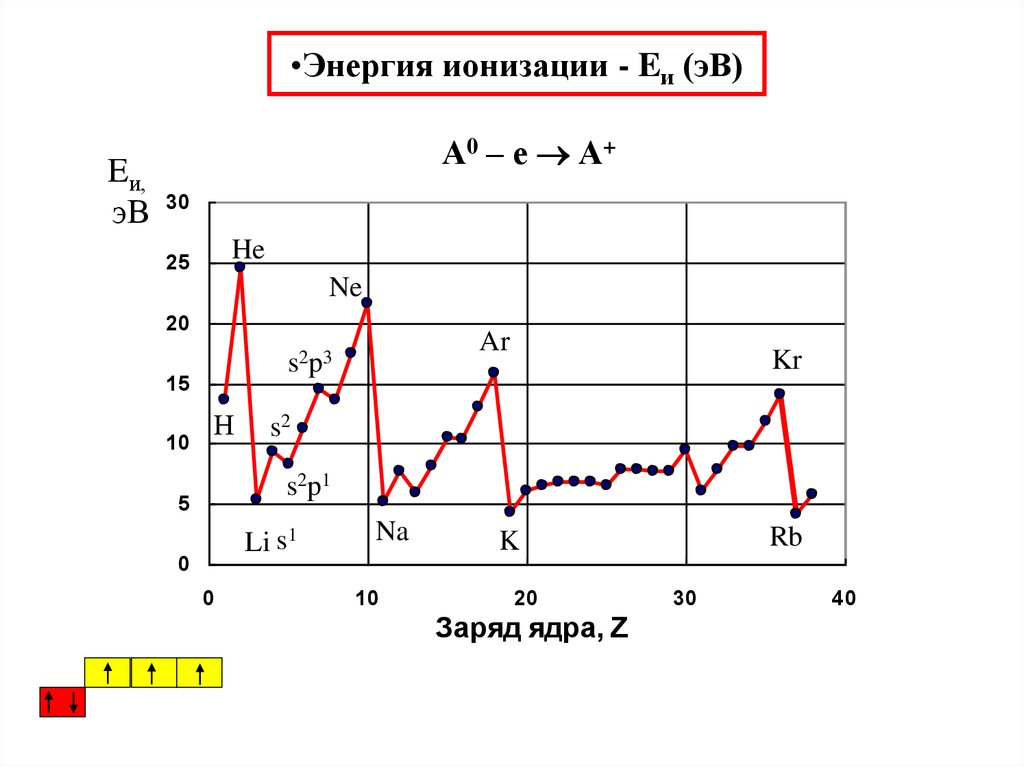
36. Энергия ионизации - Eи (эВ)

•Энергия ионизации - Eи (эВ)
Eи,
эВ
А0 – е А+
30
He
25
Ne
20
15
10
Ar
s2 p 3
Н
Kr
s2
s2 p 1
5
Li s1
0
0
Na
10
Rb
K
20
Заряд ядра, Z
30
40

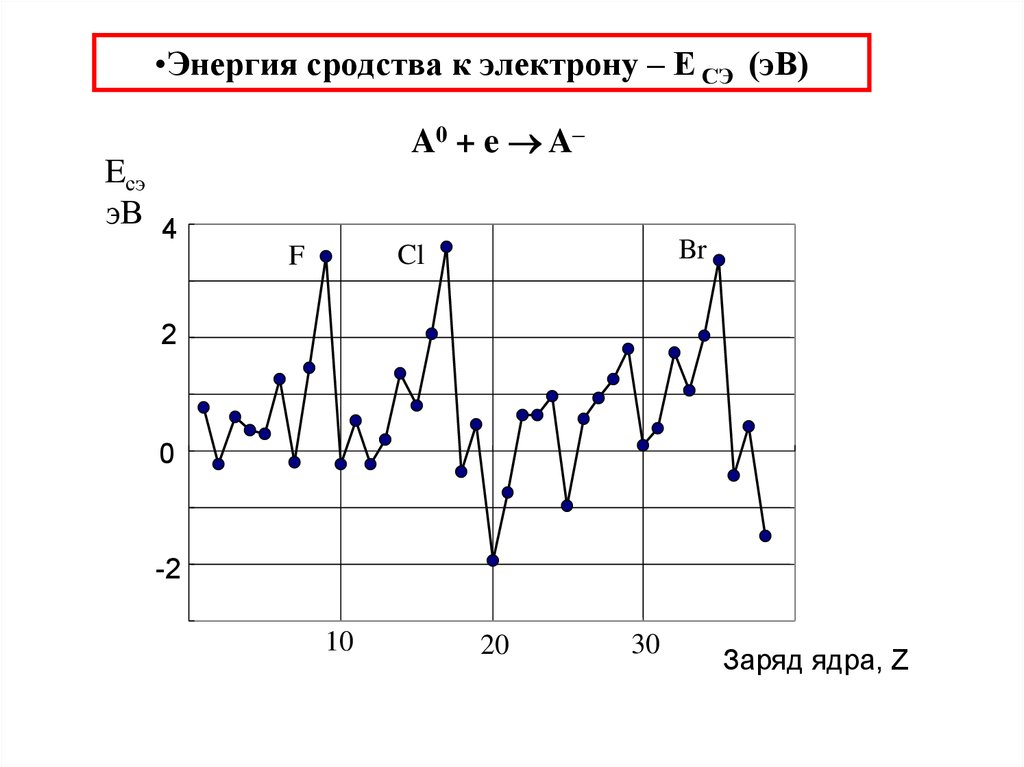
37. Энергия сродства к электрону – Е СЭ (эВ)

•Энергия сродства к электрону – Е СЭ (эВ)
A0 + e A–
Eсэ
эВ 4
Br
Cl
F
2
0
-2
10
20
30
Заряд ядра, Z

38. Электроотрицательность (способность атома притягивать к себе элетронную плотность при образовании хим.связи с другим атомом)

•Электроотрицательность (способность атома притягивать к себе
элетронную плотность при образовании хим.связи с другим атомом)
• по Малликену
• Шкала Олреда-Рохова
• по Полингу
М
П
М
П
Eи Есэ
2
(эВ)
F = 1.0, F = 4.0 (у.е.)
Li
Be
B
C
N
O
F
2.96 2.86 3.83 5.61 7.34 9.99 12.3
1.0 1.5 2.0 2.5 3.0 3.5 4.0
Na Mg Al
Si
P
S
Cl
2.94 2.47 2.97 4.35 5.72 7.60 9.45
0.9 1.2 1.5 1.8 2.1 2.5 3.0