Квантовомеханическая модель атома водорода

1. Омский государственный технический университет Кафедра физики

Калистратова Л.Ф.
Электронные лекции по разделам оптики,
квантовой механики, атомной и ядерной физики
9 лекций
(18 аудиторных часов)

2. Лекция 7. Квантовомеханическая модель атома водорода

План лекции
7.1. Квантование энергии. Главное квантовое число.
7.2. Распределение электронного заряда в атоме.
Орбитальное квантовое число.
7.3. Квантование орбитального момента импульса.
7.4. Пространственное квантование. Магнитное
квантовое число.
7.5. Квантование собственного момента импульса.
Спиновое квантовое число.
7.6. Энергетический спектр атома водорода.

3. 7.1. Квантование энергии. Главное квантовое число

С точки зрения квантовой механики, электрон в атоме
водорода находится в трёхмерной
потенциальной яме сложной формы.
Потенциальная энергия определяет взаимодействие
электрона с положительно заряженным ядром:
r – расстояние электрона от ядра;
Ze – заряд ядра: Z = 1 для водорода;
e – заряд электрона.
kZe
U
r
2

4.

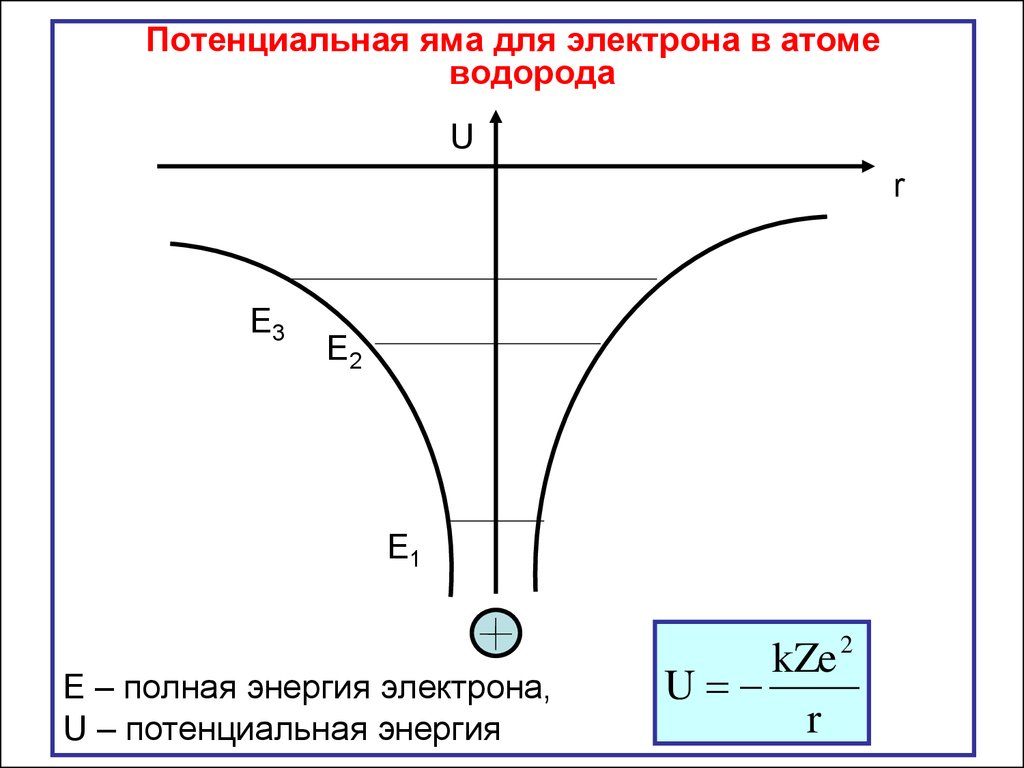
Потенциальная яма для электрона в атоме
водорода
U
r
E3
E2
E1
Е – полная энергия электрона,
U – потенциальная энергия
kZe
U
r
2

5.

Уравнение Шредингера для стационарных состояний
имеет вид:
2
2m
kZe
0
2 E
r
Электрон находится в центральном, сферически
симметричном электрическом поле, поэтому при
решении этого уравнения целесообразно
использовать сферическую системой координат.
x r cos sin
у r sin sin
z r cos

6.

Сферическая система координат
z
r
у
x r cos sin
у r sin sin
x
z r cos

7.

Уравнение Шредингера в сферических координатах
имеет сложный вид, но более простое
математическое решение.
1 2
1
r
2
sin
2
r r r r sin
1
2m
kZe
2 2 2 2 E
r sin
r
2
Е – полная энергия электрона;
- волновая функция.
2
0

8.

При решении уравнения Шредингера в сферических
координатах получены следующие результаты:
собственные значения полной энергии электрона Е
и собственные волновые функции ψ зависят от
целых чисел.
E E(n, l, m)
nlm r, ,
Эти целые числа получили название:
n – главное квантовое число,
l – орбитальное квантовое число;
m – магнитное квантовое число.

9.

Уравнение Шредингера имеет требуемые
однозначные конечные и непрерывные решения в
следующих случаях:
-
при любых положительных Е;
- при дискретных отрицательных значениях
энергии, определяемых формулой:
2
2 4
k Zem 1
En
2
2
2
n

10.

1. Случай Е = 0 соответствует отрыву электрона от
атома.
2. Случай E > 0 соответствует свободному электрону,
пролетающему вблизи ядра и снова удаляющемуся
на бесконечность.
3. Случай E < 0 соответствует электрону, связанному с
ядром атома.
Последнее выражение для полной энергии
совпадает с формулой для энергии по теории
Бора.

11.

Однако в квантовой механике данные значения энергии
получаются как следствие основных положений этой
науки, т.е. решения уравнения Шредингера.
Бору же для получения такого результата пришлось
постулировать о наличии стационарных состояний
атома.
Значения энергии
E1
En 2
n
соответствуют энергиям стационарных состояний
атома.
Число n называют главным квантовым числом.

12.

Главное квантовое число:
- принимает целочисленные значения:
n = 1, 2, 3, …
- определяет номер стационарных состояний
атома;
- определяет значения полной энергии
стационарных состояний атома.

13.

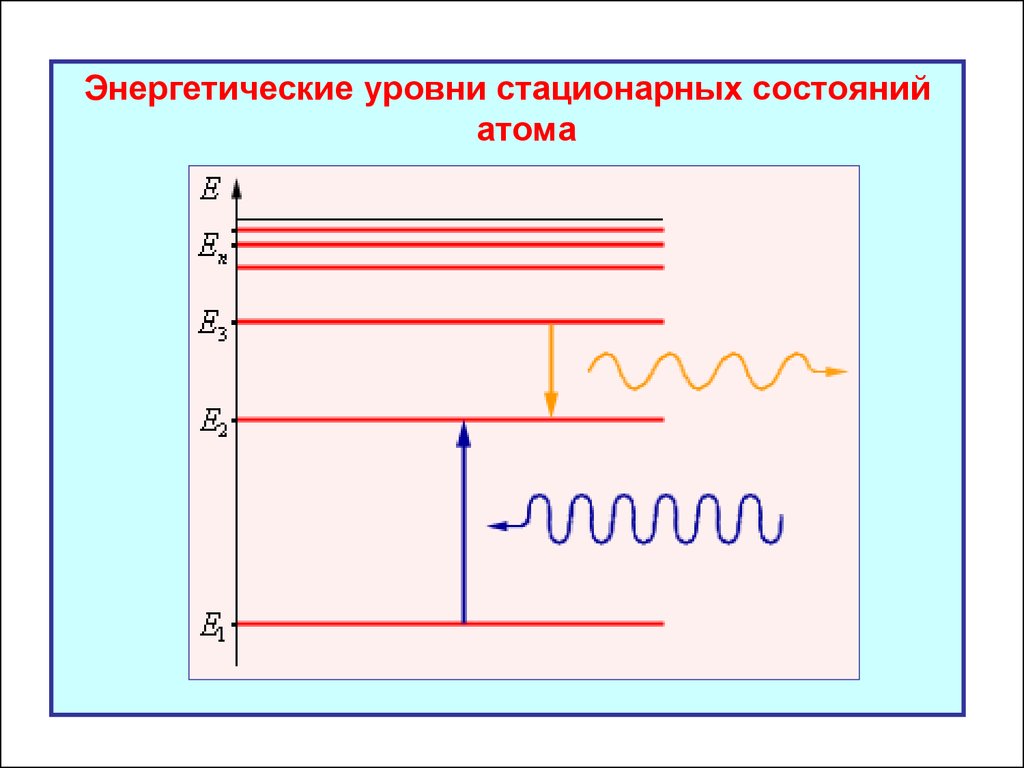
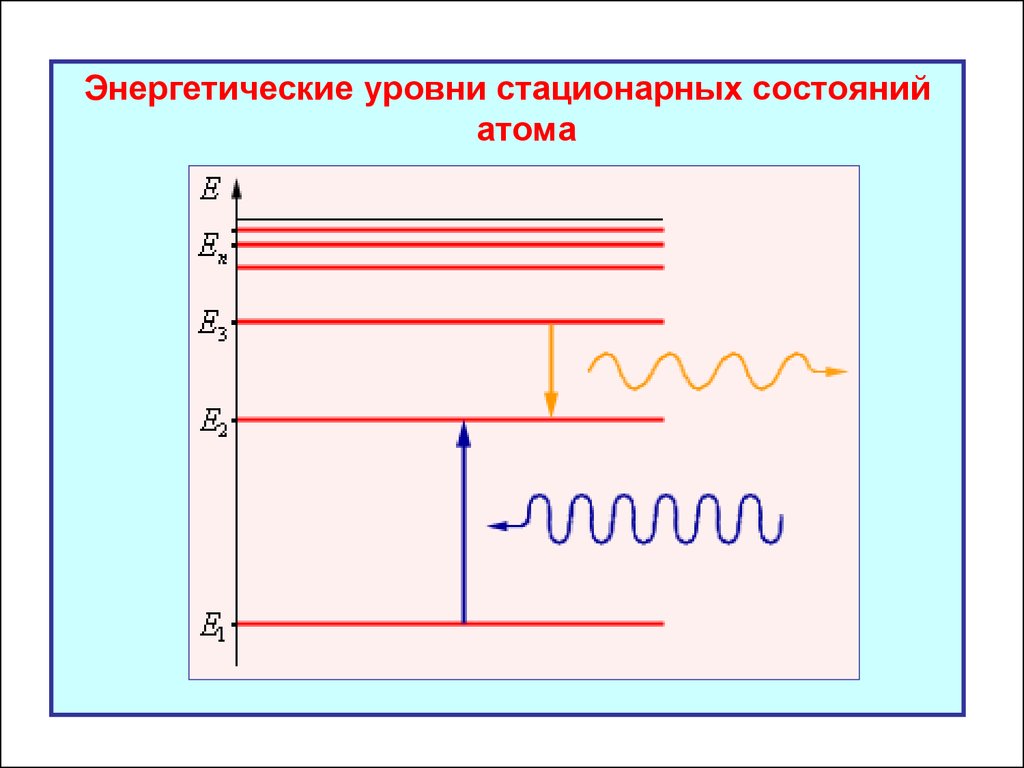
Энергетические уровни стационарных состояний
атома

14. 7.2. Распределение электронного заряда в атоме. Орбитальное квантовое число

Рассмотрим собственные волновые функции
электрона, которые зависят от трёх целочисленных
параметров n, l, m:
nlm r, ,
Волновые функции можно представить в виде
произведения отдельных функций:
(r, , ) R (r ) ( ) Ф( )

15.

Радиальная часть волновой функции:
R ( r ) f ( n , l)
Угловые части волновой функции:
( ) f (l, m)
Ф( ) f (m)
Квадрат модуля волновых функций определяет
вероятность обнаружения электрона в единице
объёма атома.

16.

Эта вероятность различна в разных частях объёма
атома.
Заряд электрона «размазан» по всему объёму атома,
образуя так называемое электронное облако.
Объёмная плотность электрического заряда атома
для стационарных состояний зависит только от
расстояния r электрона от ядра:
(r )
e
Vатома
(r ) C e
r
r1
С – некоторая постоянная величина, r1 = 0,0529 нм –
радиус первой стационарной орбиты.

17.

Для стационарных состояний атома волновые
функции также зависят от расстояния r электрона
от ядра атома.
Существует прямая зависимость между объёмной
плотностью заряда атома и квадратом модуля
радиальной волновой функции.
(r ) (r ) R(r )
2
2
Орбиталь – форма распределения объёмной
плотности электрического заряда в атоме.
Классическое понятие орбит пропадает.

18.

Радиальная часть волновой функции (форма
орбитали) зависят от двух квантовых чисел: n, l.
R(r ) (r ) f (n, l )
2
Орбитальное квантовое число
- принимает целочисленные значения:
l: 0, 1, 2, …, (n-1);
- определяет форму распределения
электронного заряда (форму орбитали);
- определяет значения орбитального момента
импульса электрона.

19.

При условии n = 1, 2, 3… и l = 0 форма электронного
облака обладает сферической симметрией.
При этих условиях плотность вероятности
нахождения электрона в тонком шаровом слое
радиуса r и толщины dr определяется по формуле
dP
2
2
2
R(r ) dV R(r ) 4 r
dr
Величина dP / dr оказывается максимальной на
расстояниях от ядра, соответствующих радиусам
«боровских» стационарных орбит: r1, r2 = 4r1,
r3= 9r1,… и т.д.

20.

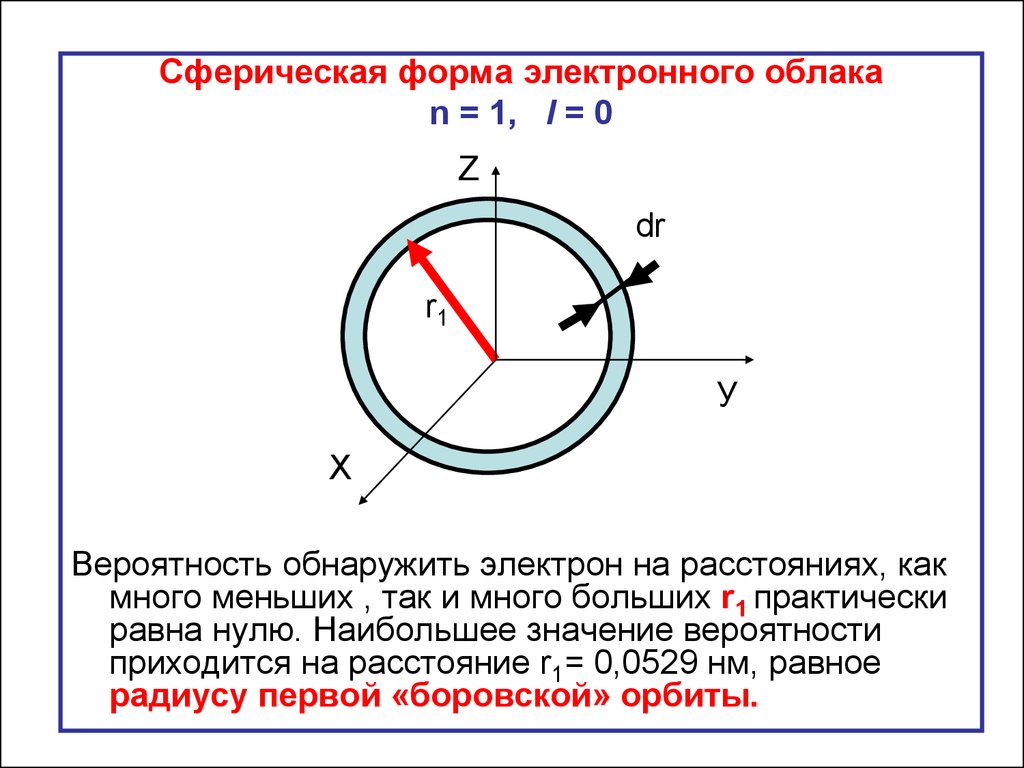
Сферическая форма электронного облака
n = 1, l = 0
Z
dr
r1
У
X
Вероятность обнаружить электрон на расстояниях, как
много меньших , так и много больших r1 практически
равна нулю. Наибольшее значение вероятности
приходится на расстояние r1= 0,0529 нм, равное
радиусу первой «боровской» орбиты.

21.

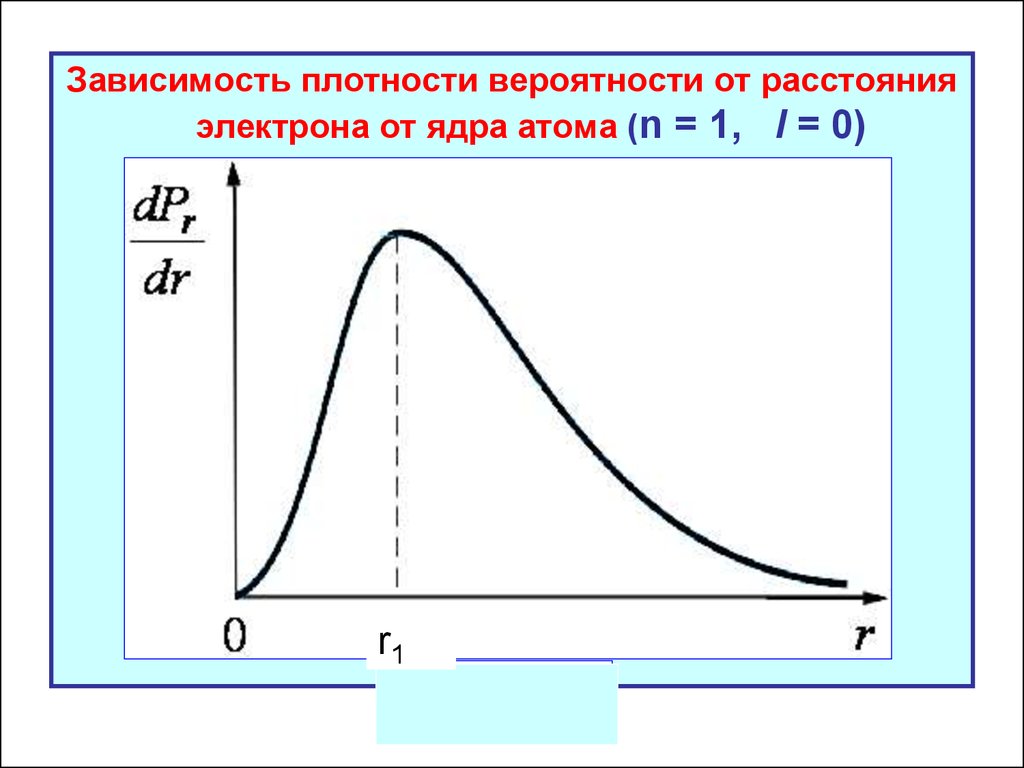
Зависимость плотности вероятности от расстояния
электрона от ядра атома (n = 1, l = 0)
r1

22.

В состоянии с квантовыми числами
n=2и l=0
максимальная вероятность приходится на расстояние
r2 = 4r1, которое соответствует радиусу второй
стационарной орбиты.
Принято называть состояния атома, в которых:
- l = 0 s - состоянием;
- l = 1 p - состоянием;
- l = 2 d – состоянием;
- l = 3 f - состоянием и т д.

23.

Распределение вероятности обнаружения
электрона в атоме водорода в состояниях 1s и 2s

24.

Для р -, d -, f - состояний плотность электронного
облака зависит не только от расстояния r от ядра,
но и от направлений, определяемых углами , .
В таких состояниях форма распределения объёмного
заряда имеет форму эллипса.
Чем больше орбитальное квантовое число , тем
более вытянутым является эллипс.

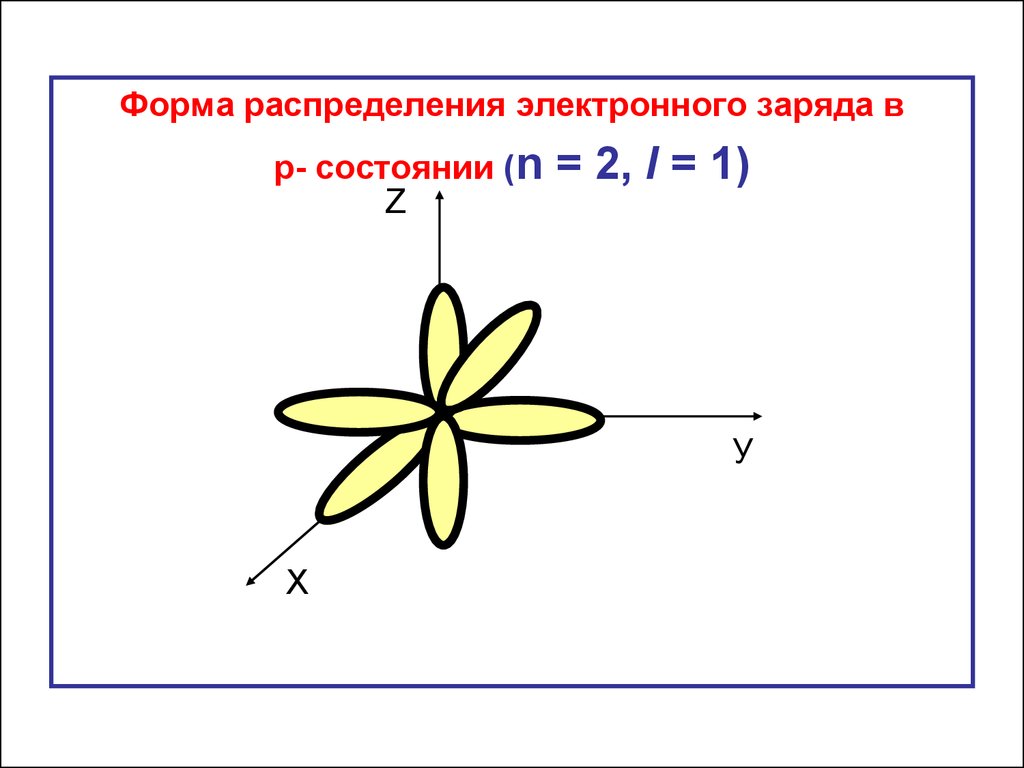
25.

Форма распределения электронного заряда в
р- состоянии (n
Z
= 2, l = 1)
У
Х

26.

За радиус атома принято считать расстояние r, на
которое приходится 95 % объёмной плотности
заряда.
Самый маленький размер атом имеет в основном
состоянии.
Если атом возбудить, то его размеры возрастают, атом
как бы «разбухает».

27.

Таким образом, волновой характер движения
электрона приводит к тому, что понятие орбиты
теряет классический смысл.
Заряд электрона становится пространственно
распределённым.
Можно говорить лишь об электронном облаке,
имеющем различную форму в разных квантовых
состояниях электрона в атоме.

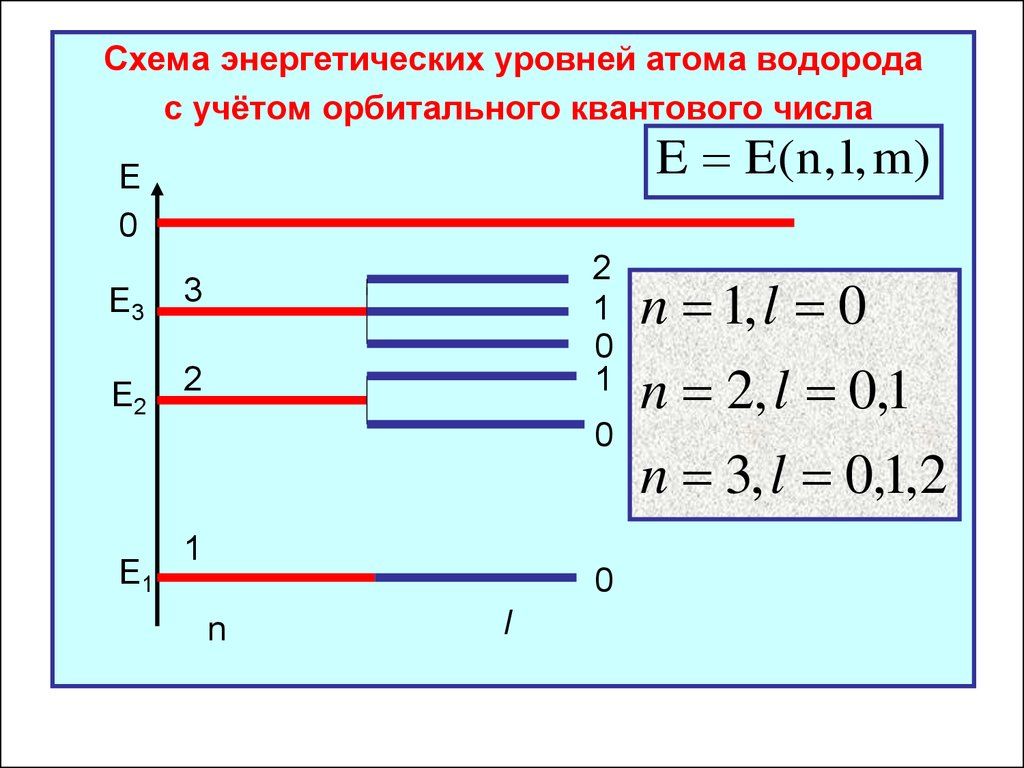
28.

Схема энергетических уровней атома водорода
с учётом орбитального квантового числа
E E(n, l, m)
Е
0
Е3
3
Е2
2
2
1
0
1
0
Е1
1
0
n
l
n 1, l 0
n 2, l 0,1
n 3, l 0,1,2

29. 7.3. Квантование орбитального момента импульса.

Согласно первому постулату Бора момент импульса
электрона (L = mvr) квантуется по условию:
L n
где n – главное квантовое число.
Условием квантования момента импульса электрона
согласно квантовой механики является формула, в
которой участвует орбитальное квантовое число l.
L l (l 1)

30.

При больших значениях n (l ~n ) обе формулы
практически дают одинаковый ответ.
Магнитный момент импульса Pm электрона и его
механический момент импульса L связаны между
собой соотношением:
e
Pm
L
2me
.
Условие квантования для магнитного момента
электрона:
e
Pm
l (l 1) Á l (l 1)
2me

31.

Единицей квантования орбитального механического
момента импульса L является перечёркнутая
постоянная Планка.
1,05 10
34
Дж с
Единицей квантования орбитального магнитного
момента импульса Pm является магнетон Бора.
e
24
Á
9,23 10 Äæ / Òë
2me

32. 7.4. Пространственное квантование. Магнитное квантовое число

Рассмотрим атом, помещённый в магнитное поле.
Направления как механического , так и магнитного
моментов электрона в пространстве не может быть
произвольным.
Ориентация векторов L и Pm может быть только
вполне определённой по отношению к направлению
внешнего магнитного поля.

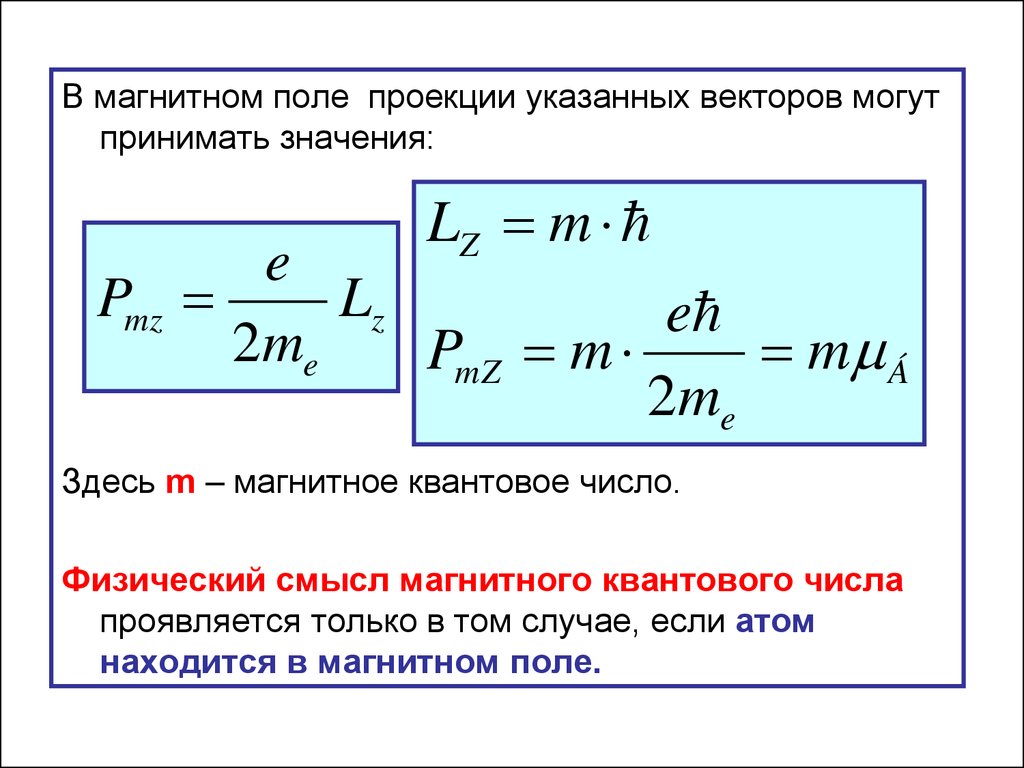
33.

В магнитном поле проекции указанных векторов могут
принимать значения:
LZ m
e
Pmz
Lz
e
2me
PmZ m
m Á
2me
Здесь m – магнитное квантовое число.
Физический смысл магнитного квантового числа
проявляется только в том случае, если атом
находится в магнитном поле.

34.

Магнитное квантовое число
- принимает целочисленные значения:
m : l ,...,0,..., l
- принимает всего (2l +1) значение при заданном
значении орбитального квантового числа l;
- квантует проекции орбитальных механического и
магнитного моментов.
Явление квантования проекций векторов L
получило название пространственного
квантования.
и
Pm

35.

l 0:m 0
l 1 : m 1,0, 1
l 2 : m 2, 1,0, 1, 2
l 3 : m 3, 2, 1,0, 1, 2, 3
Рассмотрим случай, когда l = 2. Магнитное число
примет всего (2l +1)
= 5 значений.
Значит векторы моментов импульсов на направление
магнитного поля могут принять только 5 положений в
пространстве.

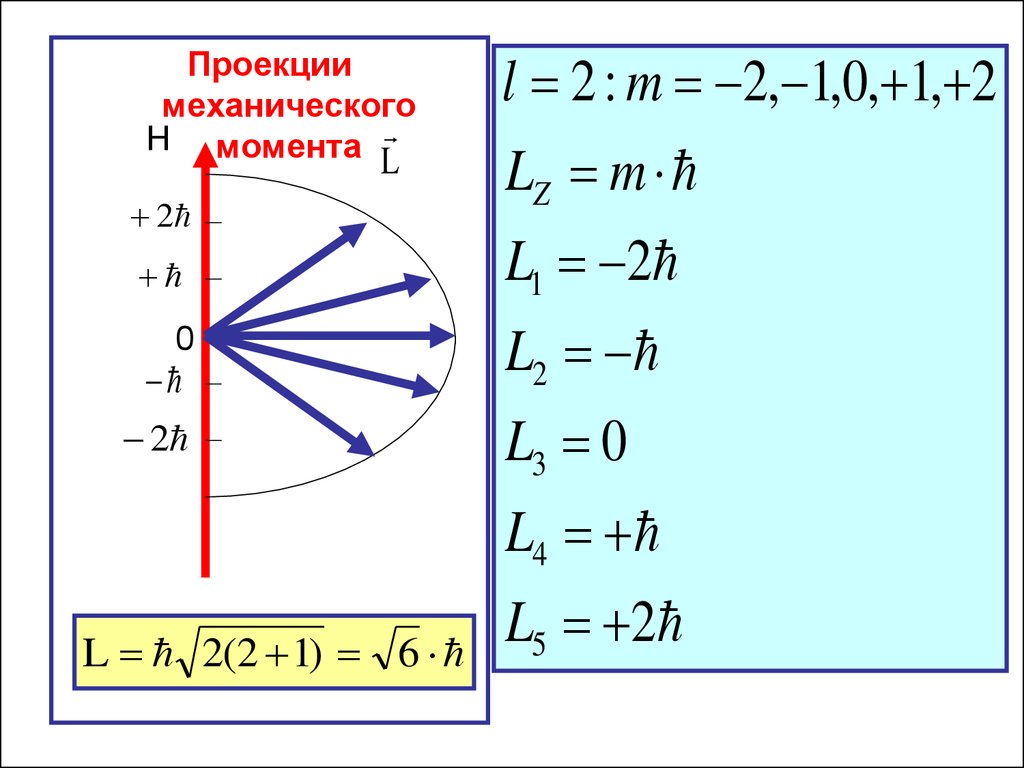
36.

Проекции
механического
Н момента
L
2
0
2
l 2 : m 2, 1,0, 1, 2
LZ m
L1 2
L2
L3 0
L4
L 2(2 1) 6
L5 2

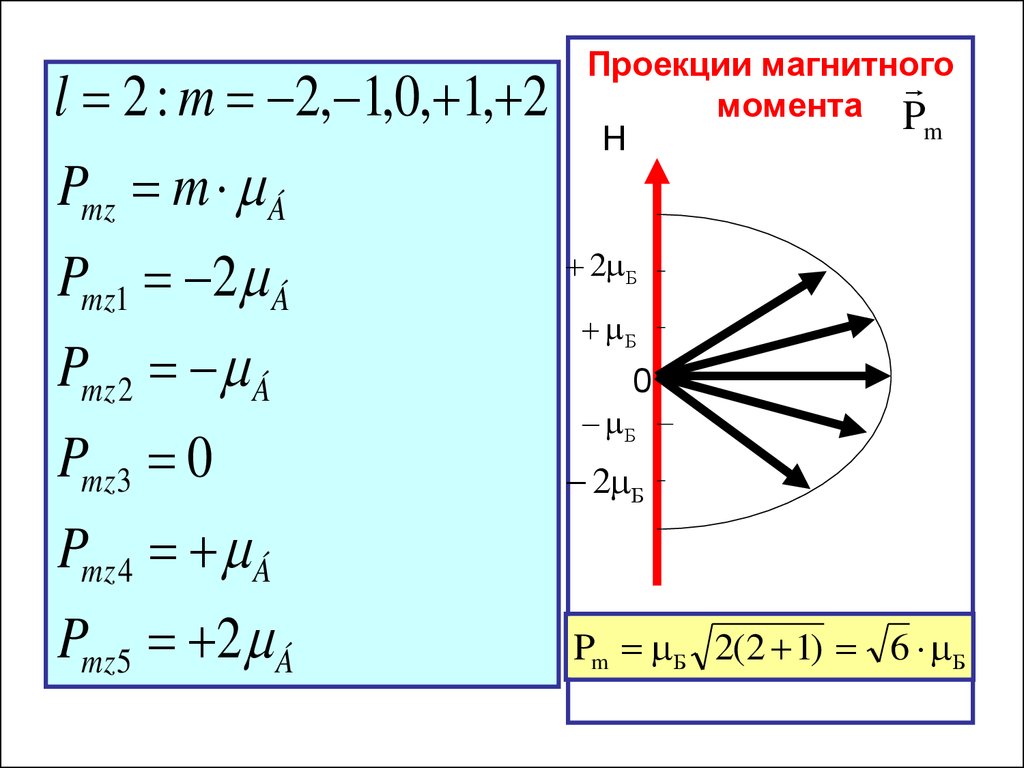
37.

l 2 : m 2, 1,0, 1, 2
Pmz m Á
Pmz1 2 Á
Pmz 2 Á
Pmz3 0
Pmz 4 Á
Pmz5 2 Á
Проекции магнитного
момента P
m
H
2 Б
Б
0
Б
2 Б
Pm Б 2(2 1) 6 Б

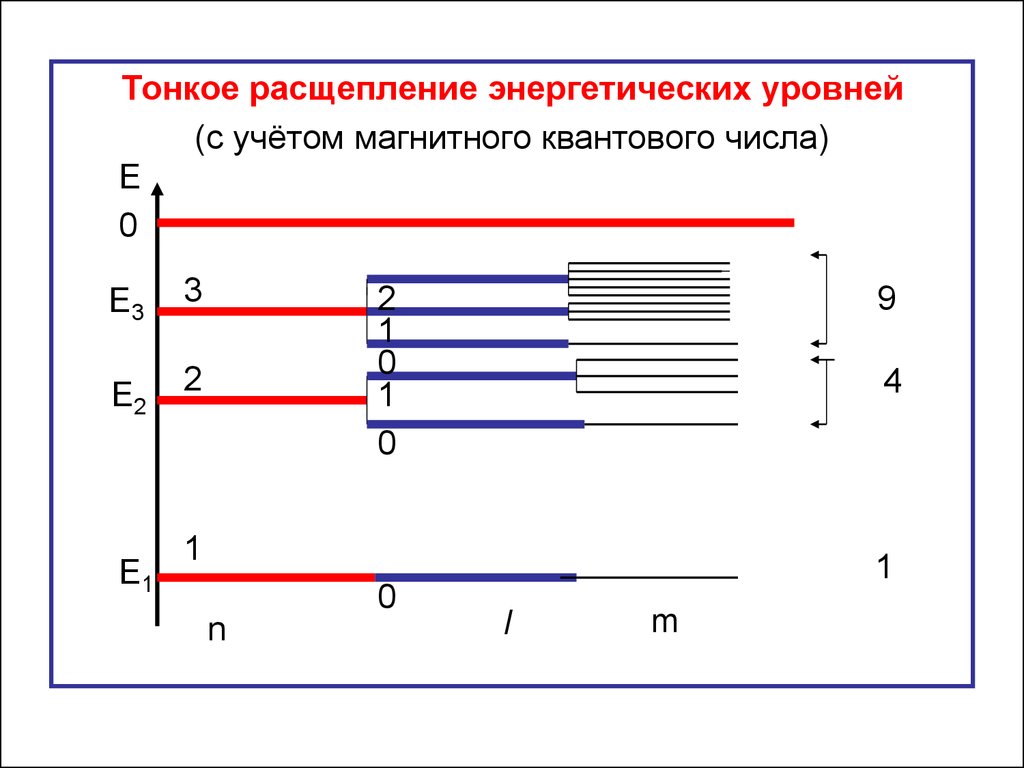
38.

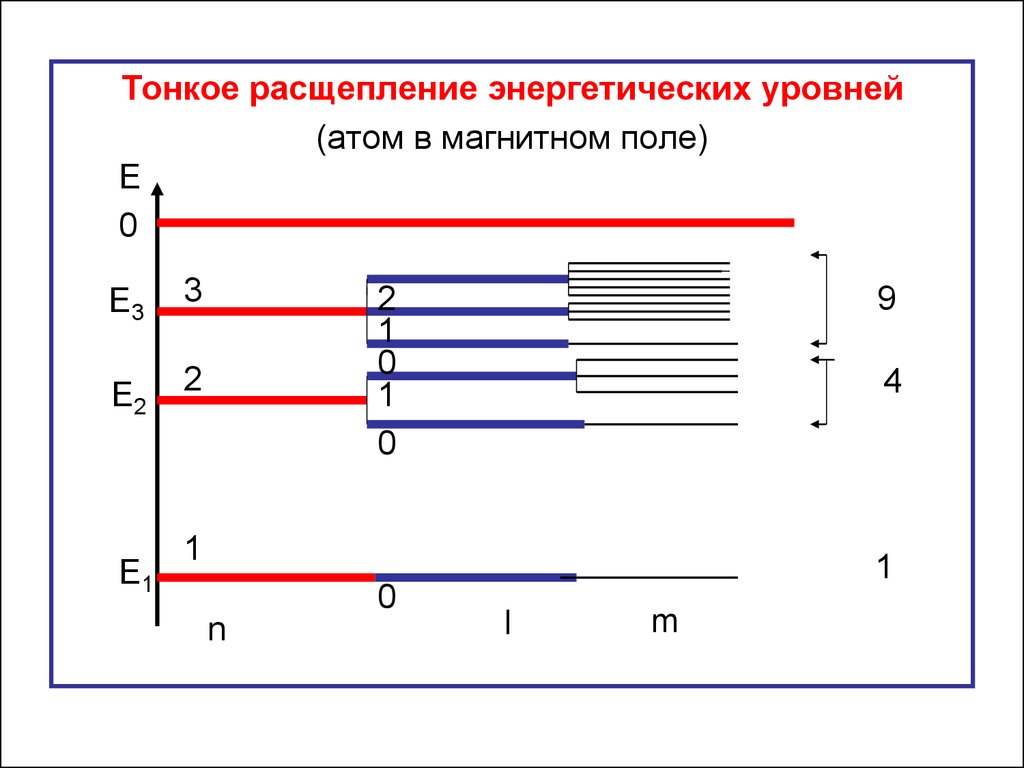
Тонкое расщепление энергетических уровней
(с учётом магнитного квантового числа)
Е
0
Е3
3
Е2
2
Е1
2
1
0
1
0
9
4
1
0
n
1
l
m

39. 7.5. Квантование собственного момента импульса. Спиновое квантовое число

В 1925 году американские физики Уленбек и Гоудсмит
для объяснения некоторых экспериментальных
результатов, не объясняемых с точки зрения
классической физики, ввели понятие спинового
движения электрона.
Предполагалось, что спиновое движение
обусловлено как бы вращением электрона
вокруг своей оси (электрон уподоблялся волчку).

40.

По современным представлениям всем элементарным
частицам природы (микрочастицам) приписывают
наличие спина.
Спин:
- следует считать внутренним свойством,
присущим микрочастице подобно тому, как ей
присущи заряд и масса;
- является свойством одновременно квантовым и
релятивистским.
Спином обладают многие элементарные частицы
(электроны, протоны, нейтроны, фотоны), кроме
мезонов.

41.

Спин:
- собственный момент импульса частицы;
- имеет одно единственное значение:
LS s(s 1)
..
S – спиновое квантовое число.
По значению спинового квантового числа микрочастицы
делятся на два класса: фермионы и бозоны.

42.

К фермионам относятся микрочастицы с полуцелым
спином:
1 3
S
,
2 2
,...
К ним принадлежат электроны, протоны, нейтроны и
другие элементарные частицы.
К бозонам относятся микрочастицы с нулевым или
целым спином:
S 0,1,...
К ним принадлежат фотоны, фононы и другие
элементарные частицы.

43.

Для электрона:
1
S
2
Собственный механический момент импульса
электрона имеет одно единственное значение:
LS s( s 1)
1 1
3
LS ( 1)
2 2
2

44.

Собственные магнитный и механический
моменты электрона связаны соотношением:
Pm S
e
LS
me
Тогда для собственного магнитного момента имеем:
Pm S
e
e
2e
LS
s ( s 1)
S ( S 1)
me
me
2me
e
Á
2me
PmS 2 Á s ( s 1) 2 Á
1 1
( 1) 3 Á
2 2

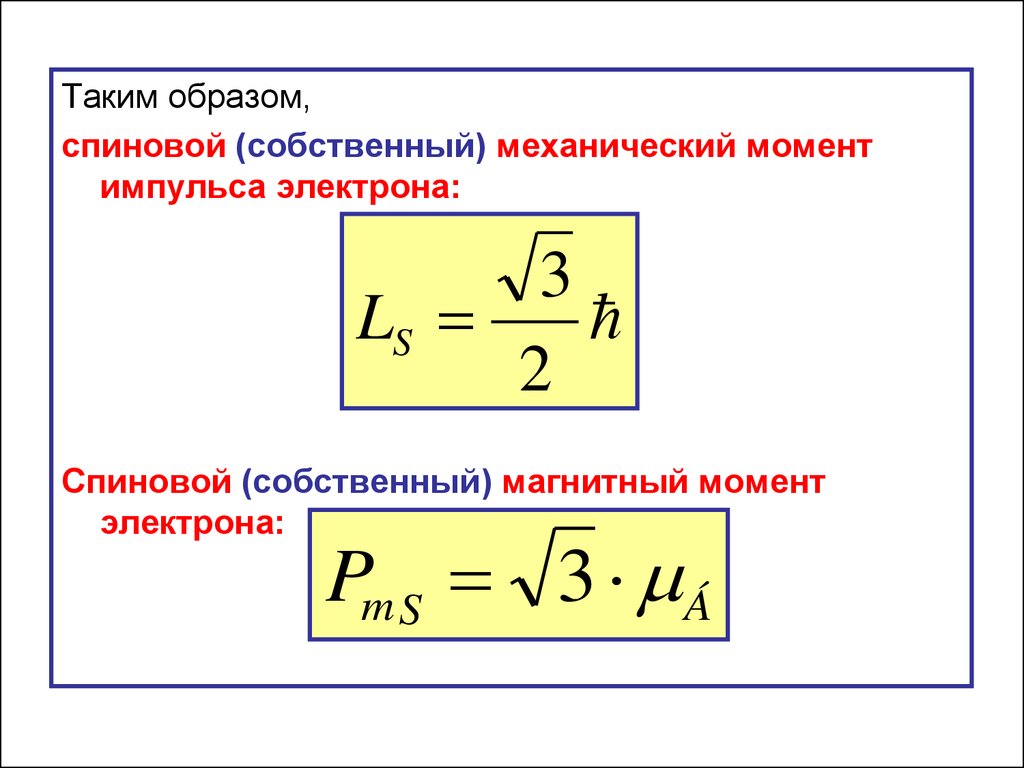
45.

Таким образом,
спиновой (собственный) механический момент
импульса электрона:
3
LS
2
Спиновой (собственный) магнитный момент
электрона:
Pm S 3 Á

46.

В пространстве спин электрона на направление
внешнего магнитного поля принимает только две
проекции.
LSZ mS
1
mS _ ñïèíîâîå
2
1
LS
2
_ êâàíòîâîå _ ÷èñëî

47.

В пространстве спиновой магнитный момент
электрона на направление внешнего магнитного
поля принимает только две проекции.
e
PmS
LS
me
LSZ mS
1
mS _ ñïèíîâîå _ êâàíòîâîå _ ÷èñëî
2
e
2e
PmS
mS
mS 2 Á mS Á
me
2me

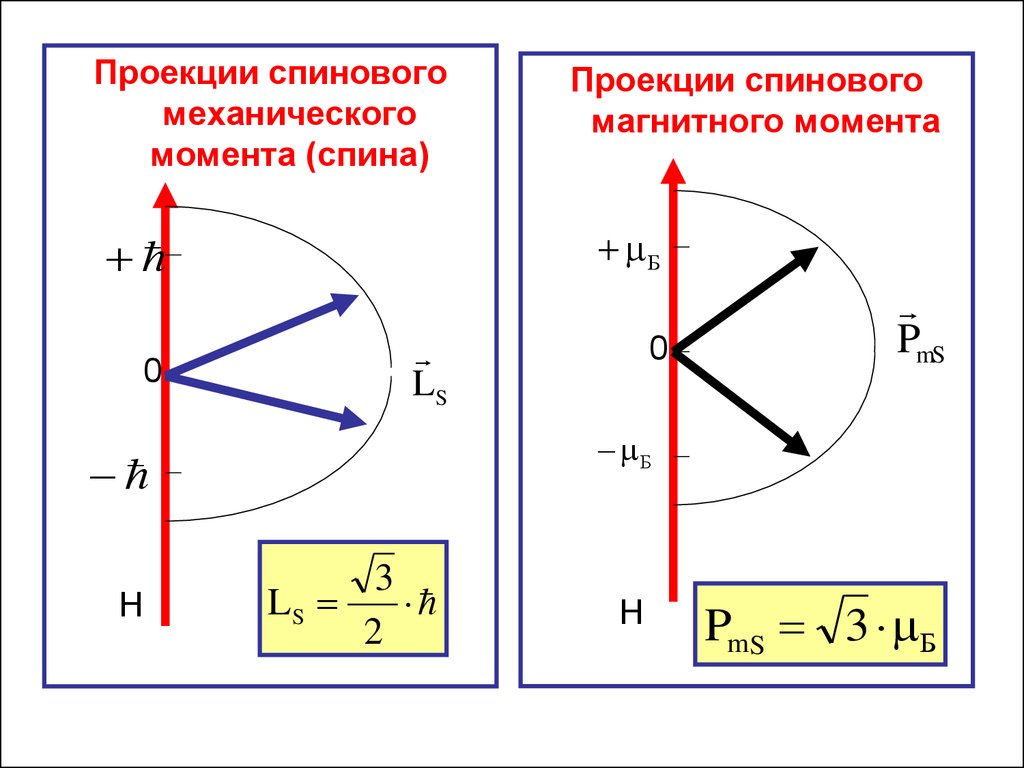
48.

Проекции спинового
механического
момента (спина)
Б
0
LS
0
PmS
Б
Н
Проекции спинового
магнитного момента
3
LS
2
Н
PmS 3 Б

49.

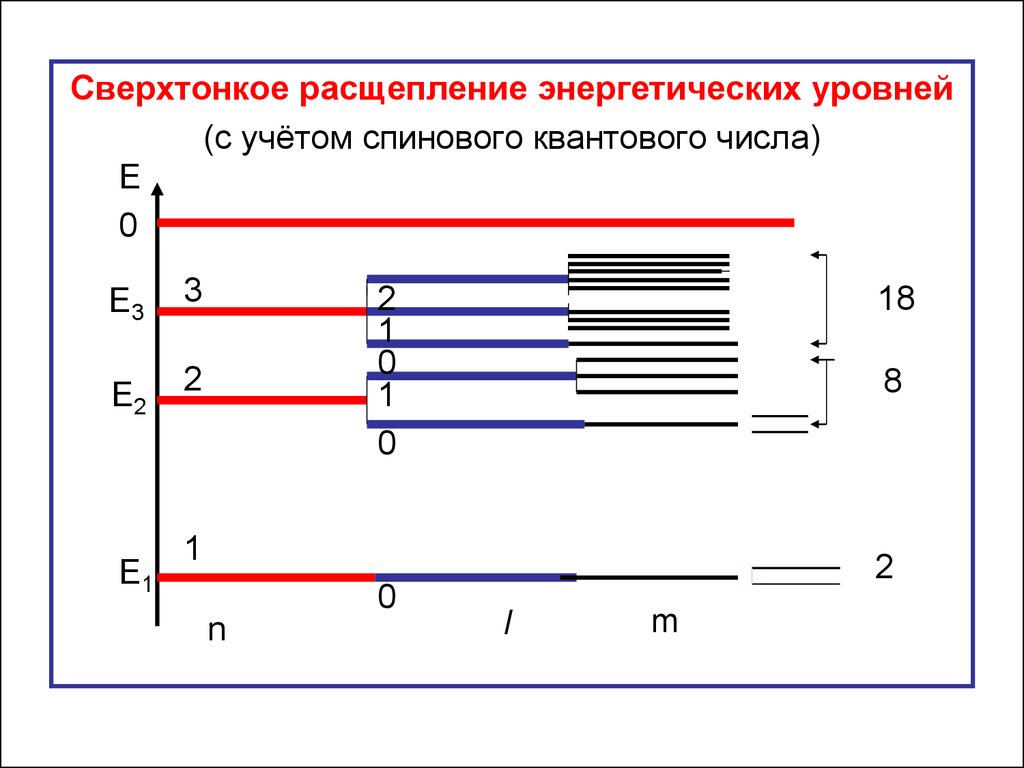
Сверхтонкое расщепление энергетических уровней
(с учётом спинового квантового числа)
Е
0
Е3
3
Е2
2
Е1
2
1
0
1
0
18
8
1
0
n
2
l
m

50.

Число возможных энергетических состояний атома
( с учётом всех четырёх квантовых чисел)
2n
2
где n – главное квантовое число.
n 1, N 2
n 2, N 8
n 3, N 18

51. 7.6. Энергетический спектр атома водорода

Значения полной энергии электрона в атоме водорода
зависят от всех четырёх квантовых чисел:
E E(n, l, m, s)
n – главное квантовое число: 1,
2, 3, ….
l - орбитальное квантовое число: 0, 1, 2, …, n -1
m – магнитное квантовое число: - l, …,0, …, + l
s – спиновое квантовое число: 1/2

52.

Главное квантовое число определяет энергию
стационарных состояний:
.
E1
En 2
n
Принято говорить, что энергетические уровни с
данным числом «n» расщепляются с учётом
остальных квантовых чисел на подуровни.
Если:
n = 1, то l = 0 – данный уровень не расщепляется;
n = 2, то l = 0, 1 – данный уровень расщепляется на
два подуровня;
n = 3, то l = 0, 1, 2 – данный уровень расщепляется
на три подуровня и т.д.

53.

Энергетические уровни стационарных состояний
атома

54.

Расщепление уровней
по орбитальному квантовому числу
Е
0
Е3
3
Е2
2
2
1
0
1
0
Е1
1
0
n
l

55.

Расщепление энергетических уровней по магнитному
квантовому числу происходит в магнитном поле и
названо тонким расщеплением.
Такое расщепление было обнаружено в 1896 году
голландским учёным П. Зееманом.
Если:
l = 0, то m = 0 – уровень не расщепляется;
l = 1, то m = -1, 0, +1 – уровень расщепляется на три
подуровня;
l = 2, то m = -2, -1, 0, +1, +2 – уровень расщепляется
на пять подуровней.

56.

Тонкое расщепление энергетических уровней
(атом в магнитном поле)
Е
0
Е3
3
Е2
2
Е1
2
1
0
1
0
9
4
1
0
n
1
l
m

57.

С учётом трёх квантовых чисел уровень с заданным
числом n расщепляется на n2 подуровней.
Число возможных состояний определяется
формулой:
n
2
l n 1
(2l 1)
l 0
Вырожденными называются состояния с
одинаковой энергией.
Кратностью вырождения называется число
различных состояний с одинаковым значением
главного квантового числа.

58.

Кратность тонкого вырождения уровней:
первого: n = 1 равна 1;
l n 1
2
второго: n = 2 равна 4;
третьего: n = 3 равна 9;
l 0
четвёртого: n = 4 равна 16.
n
(2l 1)
Тонкое вырождение снимается магнитным полем.
В зависимости от числа m ориентации векторов Pm
в поле различны, поэтому и энергии, соответствующие
квантовым состояниям с разными проекциями Pm
на направление поля, оказываются различными.

59.

Сверхтонким называется расщепление
энергетических уровней по спиновому
квантовому числу.
Оно было обнаружено П. Зееманом в слабых
магнитных полях при применении очень
чувствительных спектральных приборов с большой
разрешающей способностью.
Поскольку спиновой магнитный момент электрона PmS
принимает только две проекции, то каждый уровень в
слабом магнитном поле расщепляется на два
подуровня.

60.

Сверхтонкое расщепление энергетических уровней
(с учётом спинового квантового числа)
Е
0
Е3
3
Е2
2
Е1
2
1
0
1
0
18
8
1
0
n
2
l
m

61.

С учётом всех четырёх квантовых чисел число
возможных энергетических состояний электрона
в атоме водорода и любом другом атоме равно
2n
2
Состояние 1s (n = 1, l = 0) является основным
состоянием атома водорода.
В этом состоянии атом может находиться бесконечно
долго, обладая минимальной энергией.
Все остальные состояния называются
возбуждёнными.

62.

Чтобы перевести атом из основного состояния в
возбужденное, ему необходимо сообщить энергию.
Это может быть осуществлено за счет:
- теплового соударения атомов;
- столкновения атома с быстрым электроном;
- за счет поглощения атомом фотона.