Лекция 22 (5). Строение атома

1. Строение атома

ВоГТУ
Лекция 22 (5)
Строение атома
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.
1

2. План

2

3.

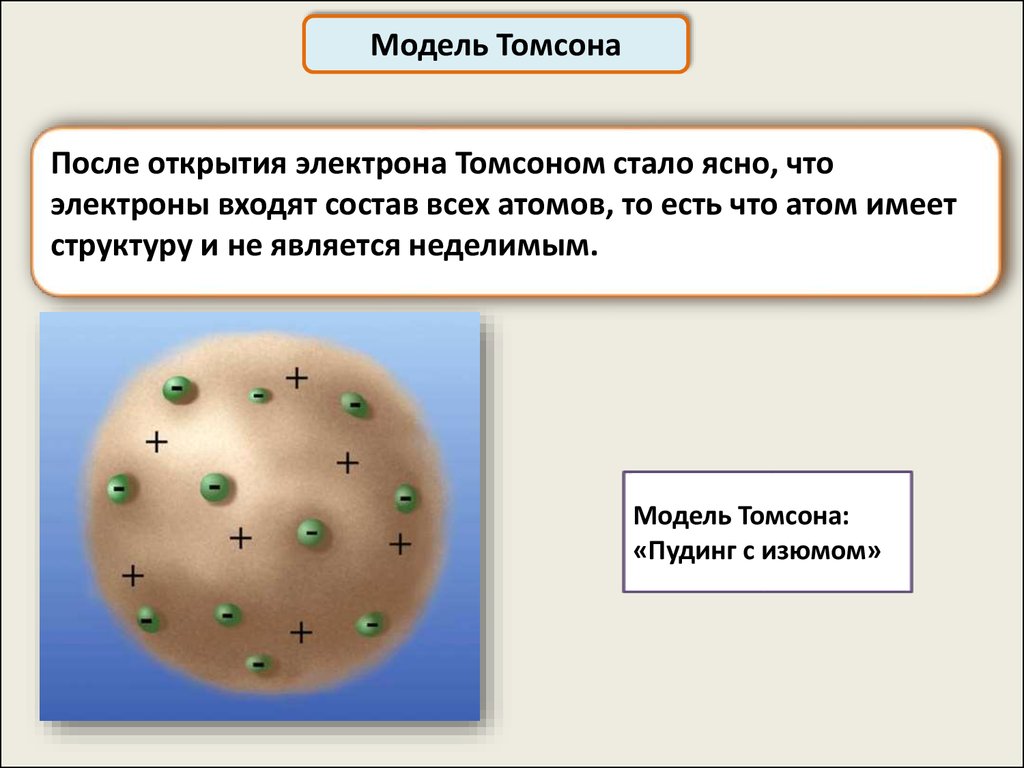
Модель Томсона
После открытия электрона Томсоном стало ясно, что
электроны входят состав всех атомов, то есть что атом имеет
структуру и не является неделимым.
Модель Томсона:
«Пудинг с изюмом»

4.

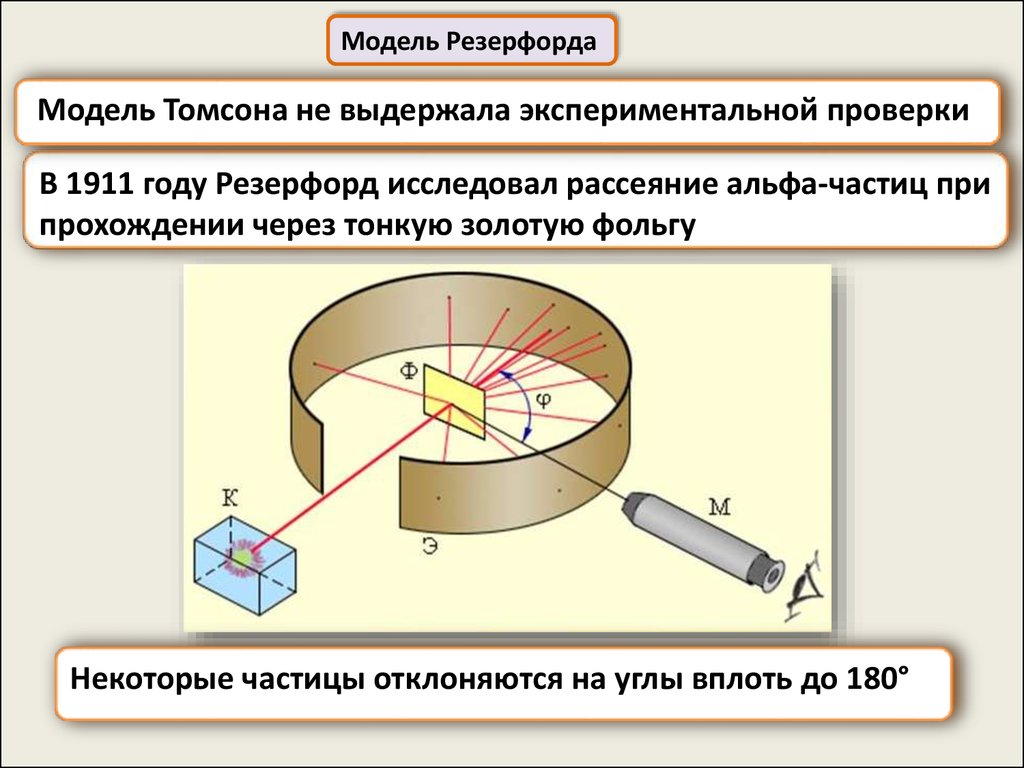
Модель Резерфорда
Модель Томсона не выдержала экспериментальной проверки
В 1911 году Резерфорд исследовал рассеяние альфа-частиц при
прохождении через тонкую золотую фольгу
Некоторые частицы отклоняются на углы вплоть до 180°

5.

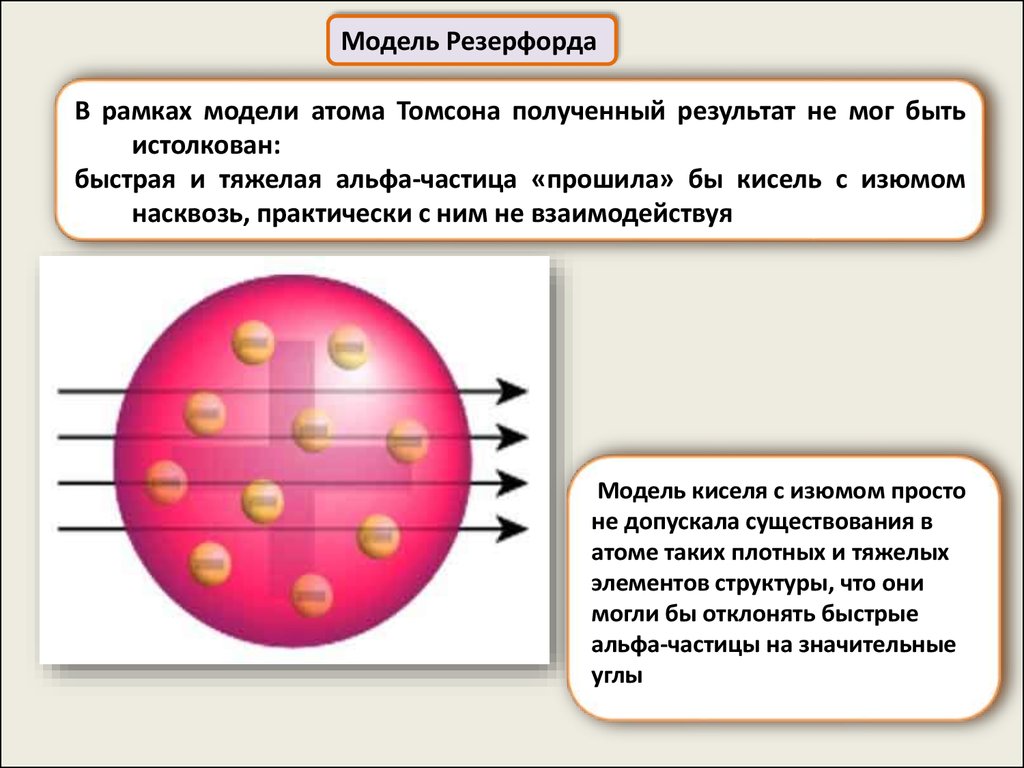
Модель Резерфорда
В рамках модели атома Томсона полученный результат не мог быть
истолкован:
быстрая и тяжелая альфа-частица «прошила» бы кисель с изюмом
насквозь, практически с ним не взаимодействуя
Модель киселя с изюмом просто
не допускала существования в
атоме таких плотных и тяжелых
элементов структуры, что они
могли бы отклонять быстрые
альфа-частицы на значительные
углы

6.

Модель Резерфорда
Чтобы отбросить частицу назад, требуется компактное массивное
очень плотное положительно заряженное ядро

7.

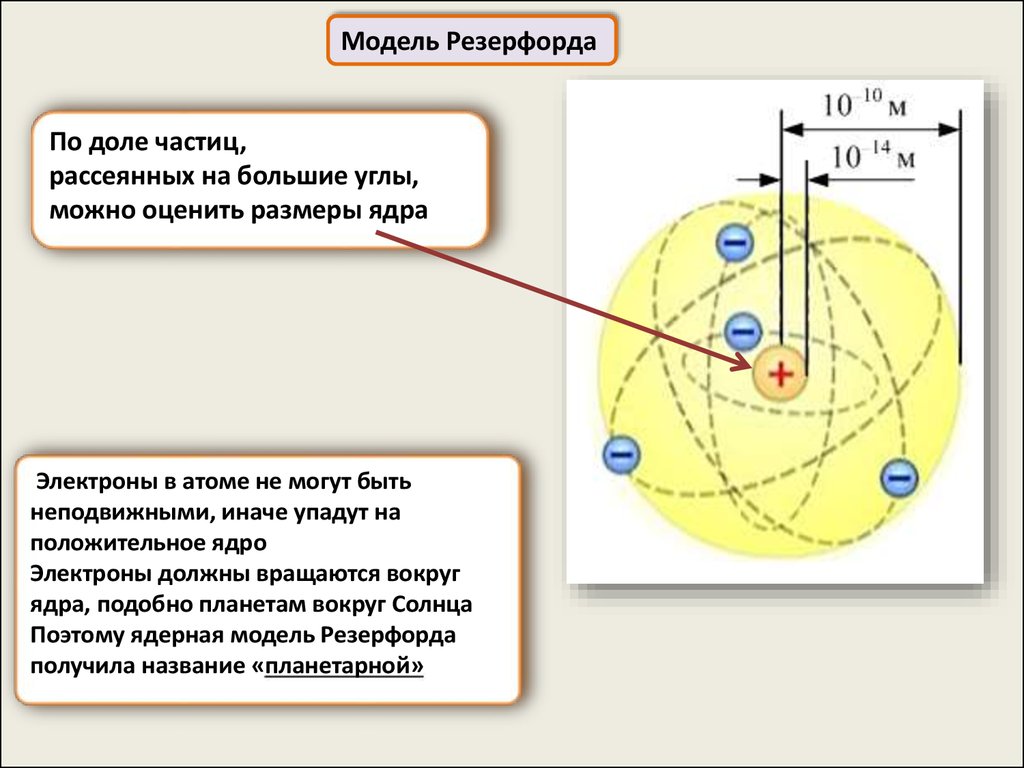
Модель Резерфорда
По доле частиц,
рассеянных на большие углы,
можно оценить размеры ядра
Электроны в атоме не могут быть
неподвижными, иначе упадут на
положительное ядро
Электроны должны вращаются вокруг
ядра, подобно планетам вокруг Солнца
Поэтому ядерная модель Резерфорда
получила название «планетарной»

8.

Трудности планетарной модели Резерфорда
1. Неустойчивость атомов
Электрон движется вокруг ядра, следовательно, имеет
центростремительное ускорение
Любая заряженная частица, движущаяся с ускорением, излучает
электромагнитные волны
Электрон излучает, поэтому теряет энергию, теряет скорость и падает на
ядро

9.

Трудности планетарной модели Резерфорда
2. Спектр излучения атома должен быть сплошным
Ничто не мешает электрону в атоме Резерфорда иметь любую энергию и
терять на излучение тоже любую энергию
Опыт показывает, что спектры излучения невзаимодействующих
атомов
(паров металлов, атомарных газов)
дискретные, состоят из отдельных спектральных линий

10.

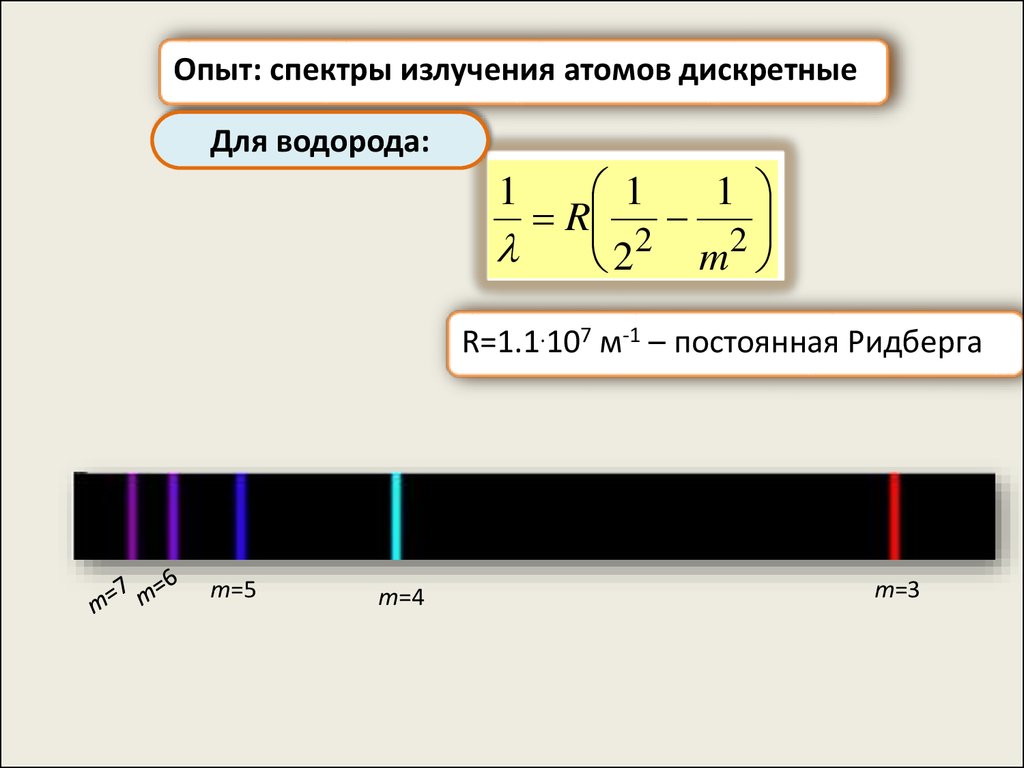
Опыт: спектры излучения атомов дискретные
Для водорода:
1
1
R
22 m2
1
R=1.1.107 м-1 – постоянная Ридберга
m=5
m=4
m=3

11.

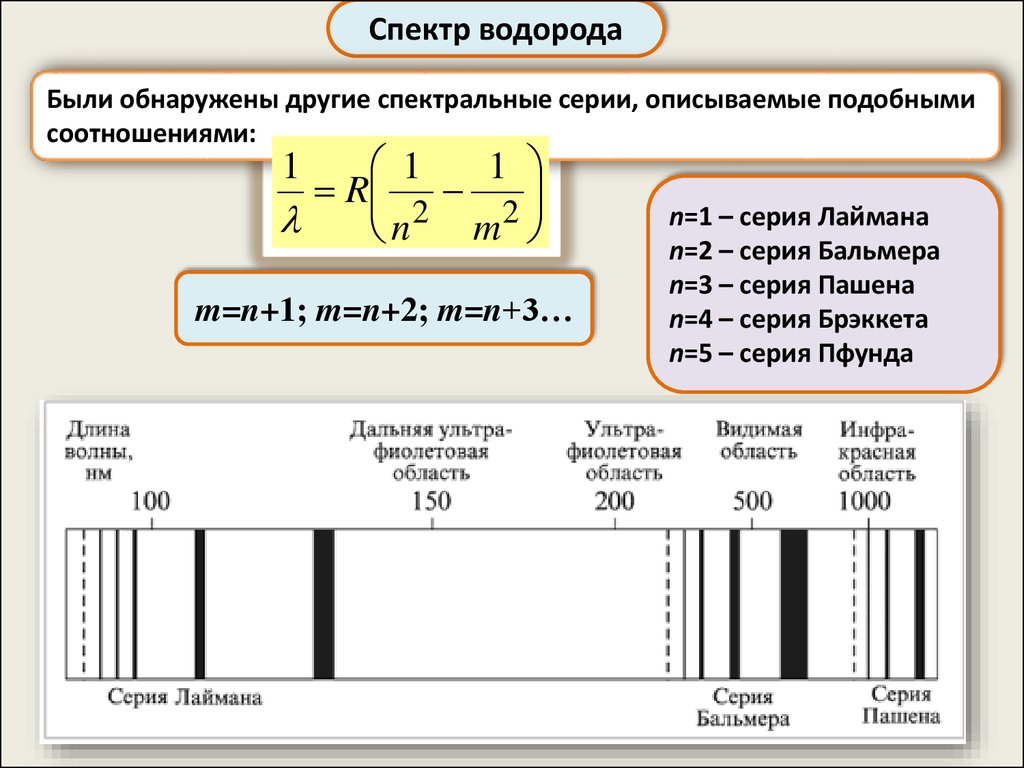
Спектр водорода
Были обнаружены другие спектральные серии, описываемые подобными
соотношениями:
1
1
R
n2 m2
1
m=n+1; m=n+2; m=n+3…
n=1 – серия Лаймана
n=2 – серия Бальмера
n=3 – серия Пашена
n=4 – серия Брэккета
n=5 – серия Пфунда

12.

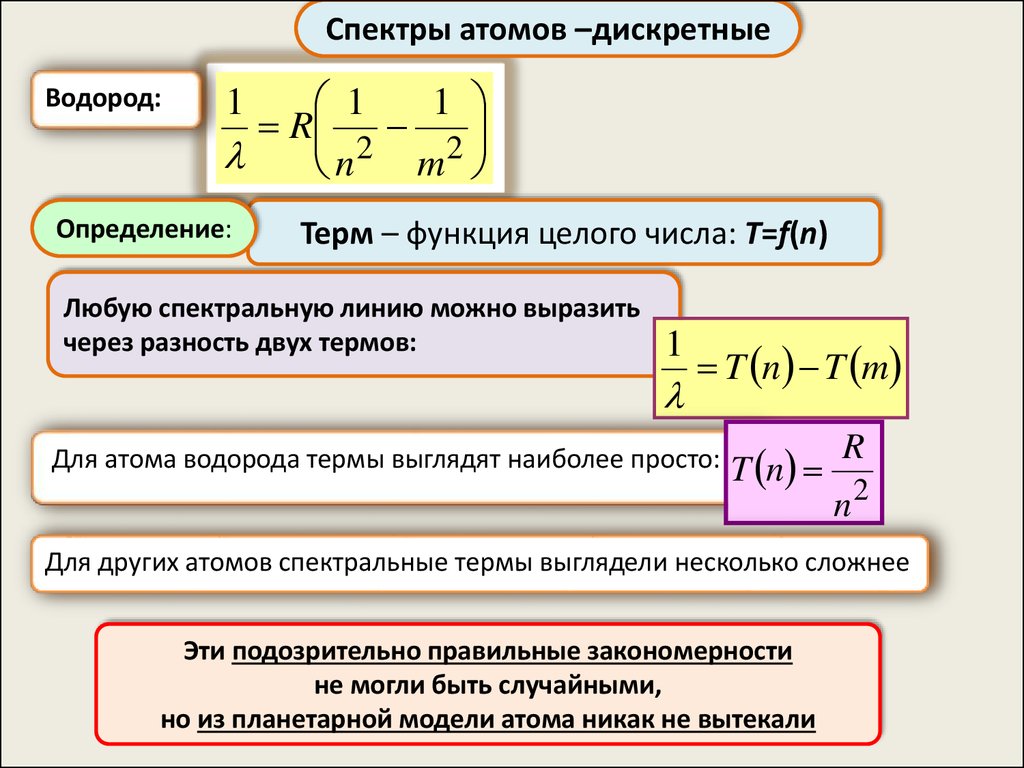
Спектры атомов –дискретные
Водород:
1
1
R
2
2
m
n
1
Определение:
Терм – функция целого числа: T=f(n)
Любую спектральную линию можно выразить
через разность двух термов:
1
T n T m
Для атома водорода термы выглядят наиболее просто:
T n
R
n2
Для других атомов спектральные термы выглядели несколько сложнее
Эти подозрительно правильные закономерности
не могли быть случайными,
но из планетарной модели атома никак не вытекали

13.

Постулаты Бора
Основаны на:
1. Экспериментальных закономерностях в атомных спектрах
2. Квантовом характере излучения и поглощения света
3. Ядерной модели атома

14.

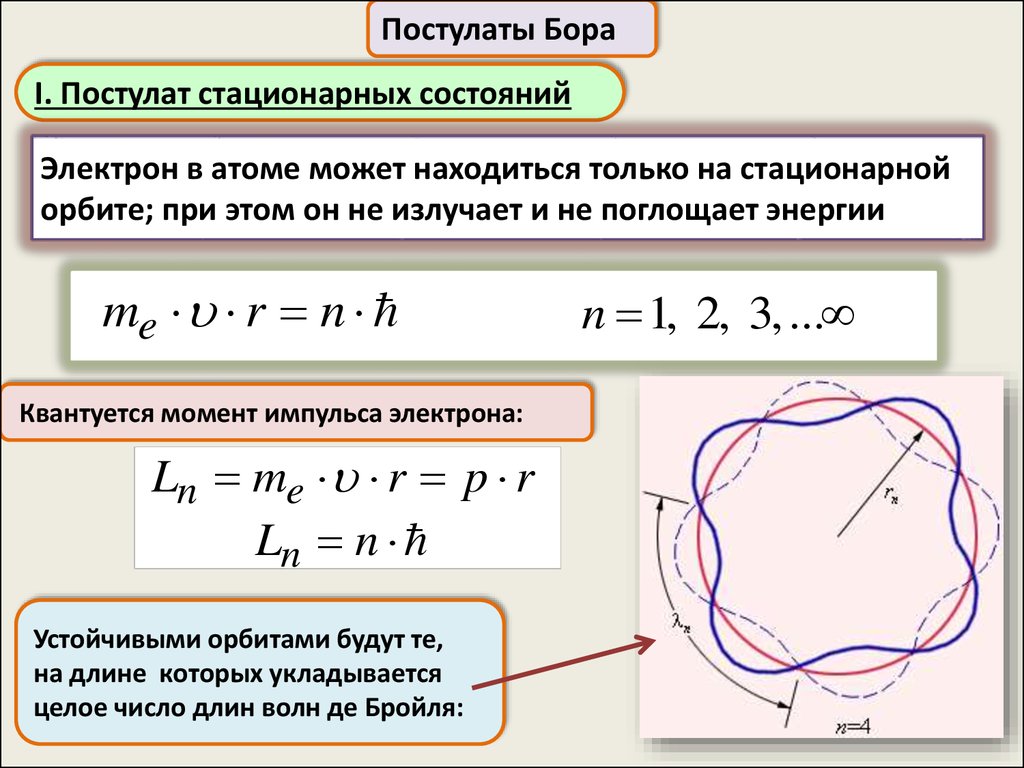
Постулаты Бора
I. Постулат стационарных состояний
Электрон в атоме может находиться только на стационарной
орбите; при этом он не излучает и не поглощает энергии
me r n
Квантуется момент импульса электрона:
Ln me r p r
Ln n
Устойчивыми орбитами будут те,
на длине которых укладывается
целое число длин волн де Бройля:
n 1, 2, 3, ...

15.

Постулаты Бора
II. Правило частот
Энергия излучается или поглощается атомом только при
переходе электрона между стационарными орбитами;
при этом квант энергии равен разности энергий стационарных
состояний, между которыми произошёл переход:
h Em En
m>n

16.

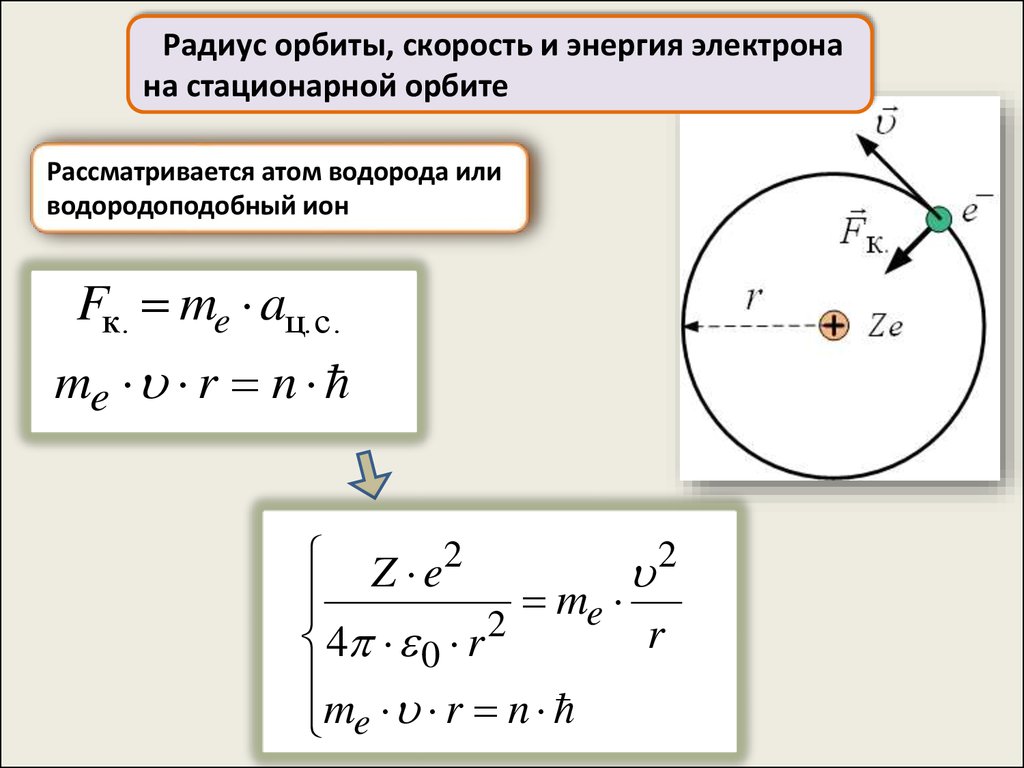
Радиус орбиты, скорость и энергия электрона
на стационарной орбите
Рассматривается атом водорода или
водородоподобный ион
Fк. me aц.с.
me r n
2
Z e2
me
2
r
4 0 r
me r n

17.

2
Z e2
me
2
r
4 0 r
me r n
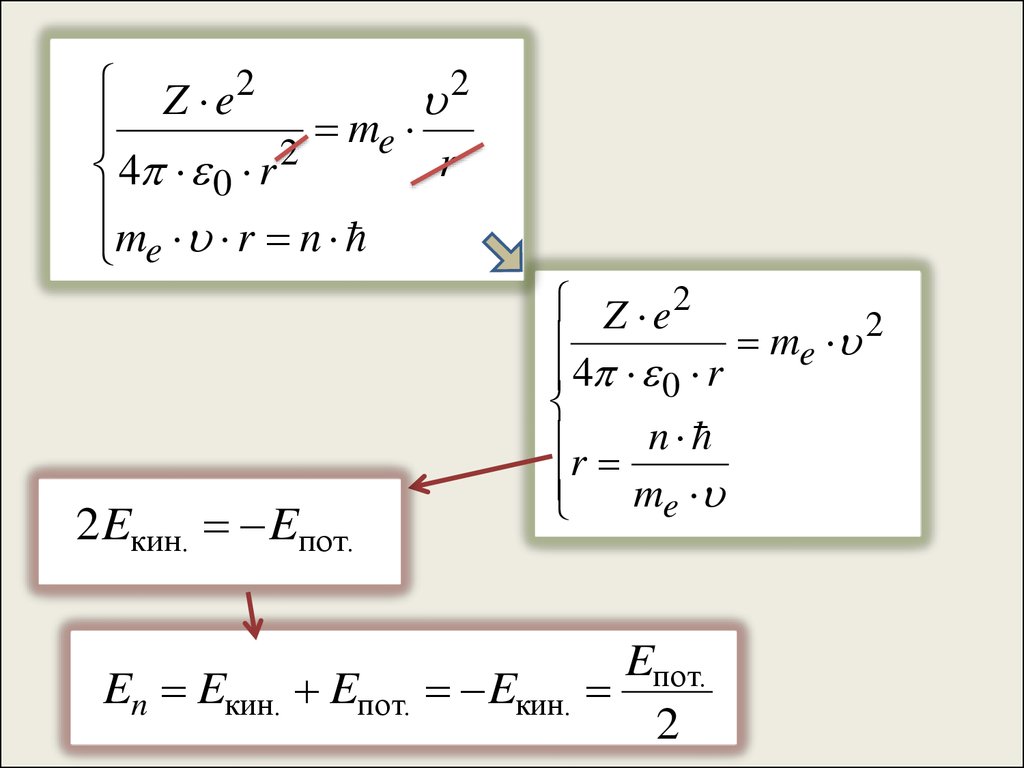
2 Eкин. Eпот.
Z e2
2
me
4 0 r
r n
me
Eпот.
En Eкин. Eпот. Eкин.
2

18.

Скорость электрона на стационарной орбите
Z e2
2
m
e
4 0 r
n h
r
me 2
2
Z e
me
n h
4 0
me 2
2
2
Z e
n
2 0 n h
2
Z
e
me
2
me
2 0 n h

19.

Радиус стационарной орбиты
Z e2
2
m
e
4 0 r
n
me r
2
2
Z e2
n2 h2
me
0 r
me2 r 2 2
2
Z e
n h
me
4 0 r
me r 2
Z e
0
2
n h
2
me r

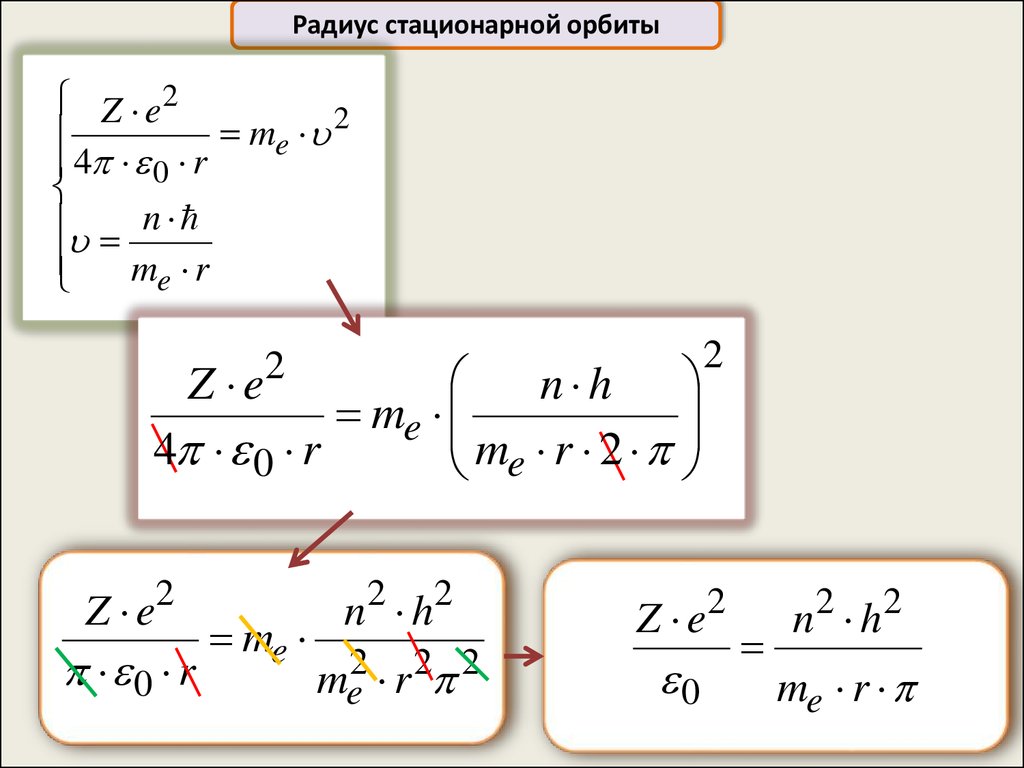
20.

Радиус стационарной орбиты
Z e2
0
n2 h2
me r
n h 0
rn
me Z e 2
2
2
Первая боровская орбита:
a0 r1
8.85 10 5.3 10
1 1.6 10 3.14
1 6.625 10
2
9.1 10 31
34 2
12
19 2
11
м 53 пм

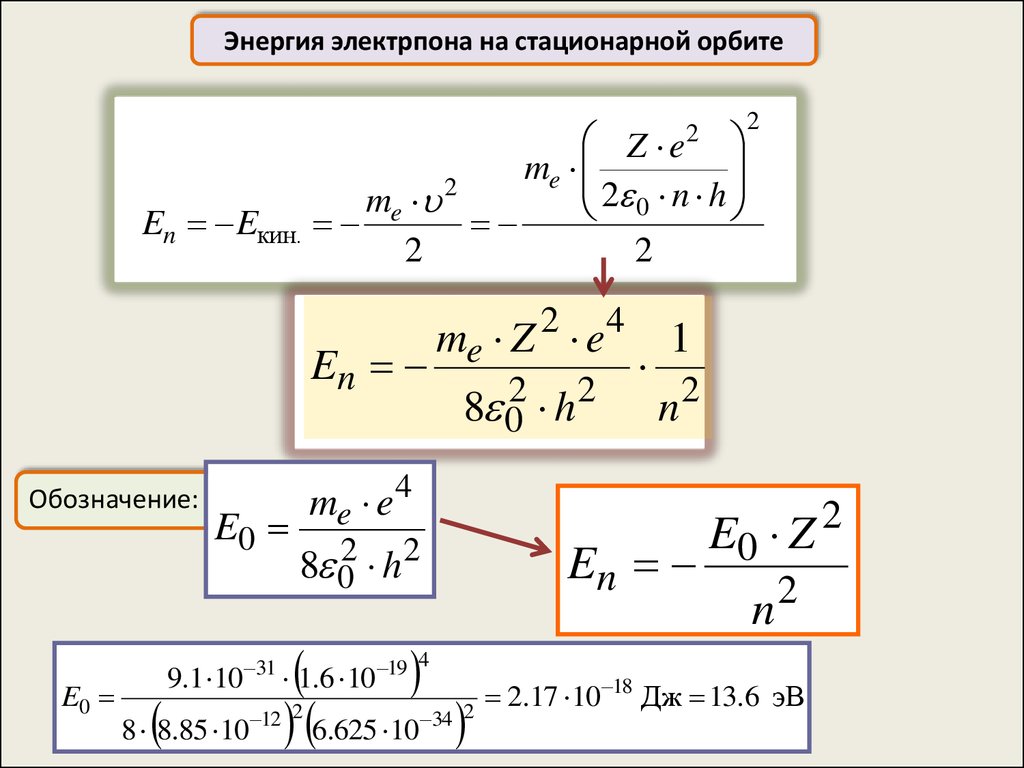
21.

Энергия электрпона на стационарной орбите
Z e
m
e
2 n h
me 2
0
En Eкин.
2
2
2
En
Обозначение:
E0
E0
8 02 h 2
me e 4
8 02 h 2
6.625 10
9.1 10 31 1.6 10 19
8 8.85 10 12
me Z 2 e 4
2
2
1
n2
En
E0 Z
n
2
4
34 2
2.17 10 18 Дж 13.6 эВ
2

22.

Схема уровней энергии атома водорода
En
me Z 2 e 4
8 02 h 2
En
E0 Z 2
n2
E0 13.6 эВ
1
n2

23.

II постулат Бора
h Em En
En
2
me Z e
4
2 2
8 0 h
1
n
2
4
me e 1
1
h Z
2 2
2
2
8 0 h n
m
2
4
me e 1
1
h Z
2 2
2
2
8 0 h n
m
c
2

24.

II постулат Бора. Спектр водорода
4
me e 1
1
h Z
2 2
2
2
8 0 h n
m
c
2
4
1
1
Z
2 3
2
2
8 0 h c n
m
1
2
Обозначение:
R
me e
4
8 02 h3c
me e
1
1
Z R
n 2 m2
1
2

25.

Спектр
1
1
Z R
n 2 m2
1
2
m=n+1; n+2; n+3…
n=1 – серия Лаймана
n=2 – серия Бальмера
n=3 – серия Пашена
n=4 – серия Брэккета
n=5 – серия Пфунда

26.

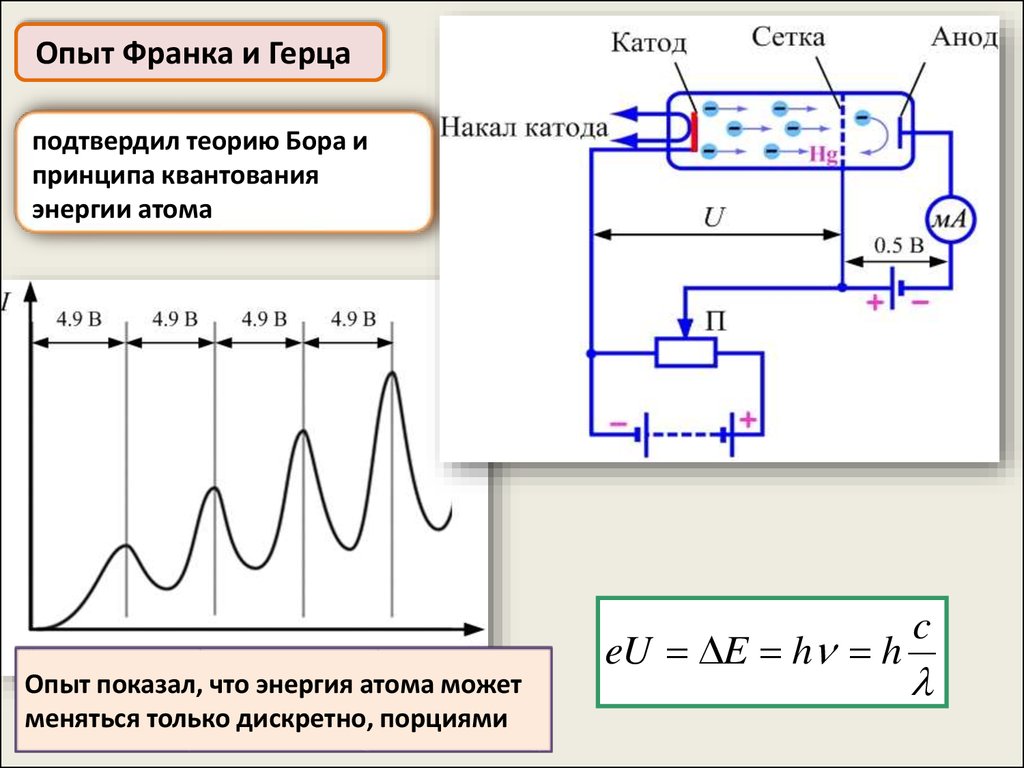
Опыт Франка и Герца
подтвердил теорию Бора и
принципа квантования
энергии атома
Опыт показал, что энергия атома может
меняться только дискретно, порциями
eU E h h
c

27.

Ограниченность теории Бора
Теория Бора работает только для одноэлектронных систем,
но не применима уже в случае простейшего двухэлектронного атома
– гелия
Причина такой ограниченности теории Бора в том, что она –
полуклассическая и использует второй закон Ньютона
Боровская теория атома водорода:
•даёт прекрасно согласующиеся с опытом результаты
в случае одноэлектронных систем
•проста настолько, что позволяет решить задачу
даже на уровне знаний школьника
•теория Бора была важным шагом на
пути построения квантовой механики
27

28.

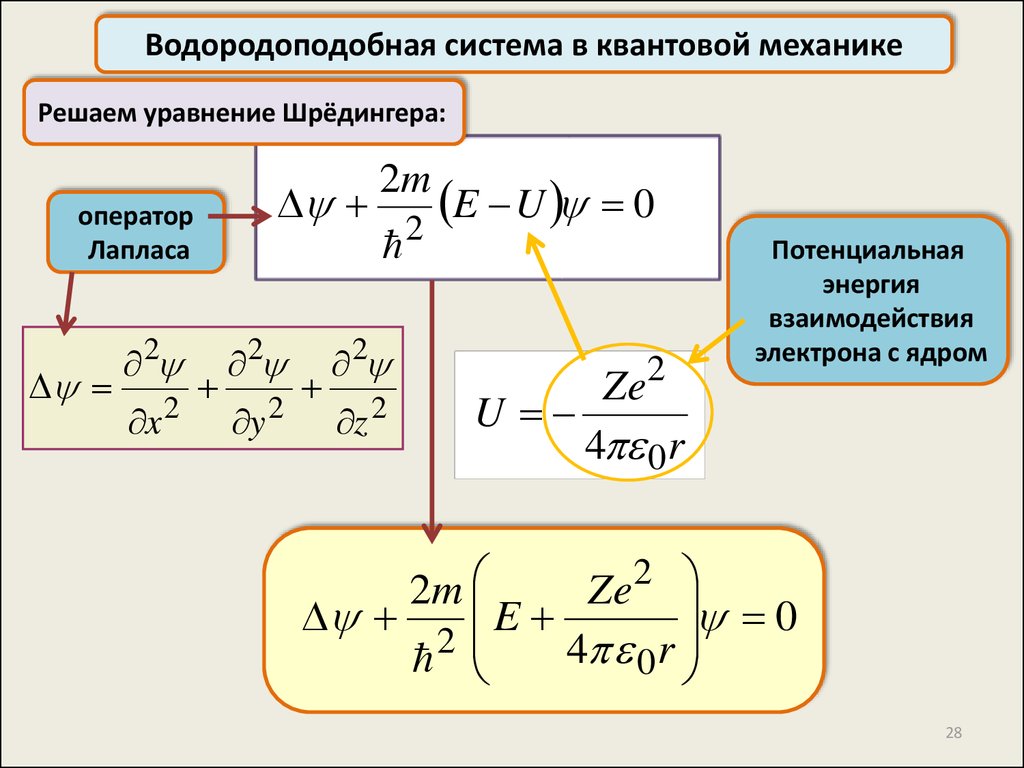
Водородоподобная система в квантовой механике
Решаем уравнение Шрёдингера:
оператор
Лапласа
2
x
2
2
y
2
2
z
E U
2
2m
2
0
2
Потенциальная
энергия
взаимодействия
электрона с ядром
Ze
U
4 0 r
2
2m
Ze
E
0
2
4 0 r
28

29.

Водородоподобная система в квантовой механике
2m
Ze2
E
0
2
4 0 r
Уравнение имеет однозначные, конечные
и непрерывные решения при:
1) любых положительных значениях Е;
2) дискретных отрицательных значениях
энергии, равных:
En
me Z 2 e 4
8 02 h 2
1
n2
Квантовая механика приводит к таким же значениям энергии
водородного атома, какие получались и в теории Бора
Однако в квантовой механике эти значения получаются логическим путём
при решении уравнения Шрёдингера без специальных дополнительных
предположений
29

30.

Квантовые числа
En
me Z 2 e 4
8 02 h 2
1
n2
– собственные значения энергии
Собственные функции:
ψn,l,ml(x,y,z) - зависят от трёх квантовых чисел:
n – главное квантовое число
n=1, 2, 3,…, ∞
l – орбитальное (азимутальное) квантовое число
l=0, 1, 2, …, (n–1)
ml – магнитное квантовое число
ml =0, ±1, ± 2, …, ± l

31.

n – главное квантовое число
n=1, 2, 3,…, ∞
определяет энергию водородоподобной системы
и размеры электронного облака
En
2
me Z e
2 2
8 0 h
4
1
n
2

32.

l – орбитальное (азимутальное) квантовое число
l=0, 1, 2, …, (n–1)
l=0 – s-состояние,
l=1 – p-состояние,
l=2 – d-состояние,
l=3 – f-состояние…
Всего n значений
l определяет форму электронного облака и величину
орбитального момента импульса электрона (механического
момента):
Ll l l 1
и связанного с ним магнитного момента:
e
pl
Ll
2me

33.

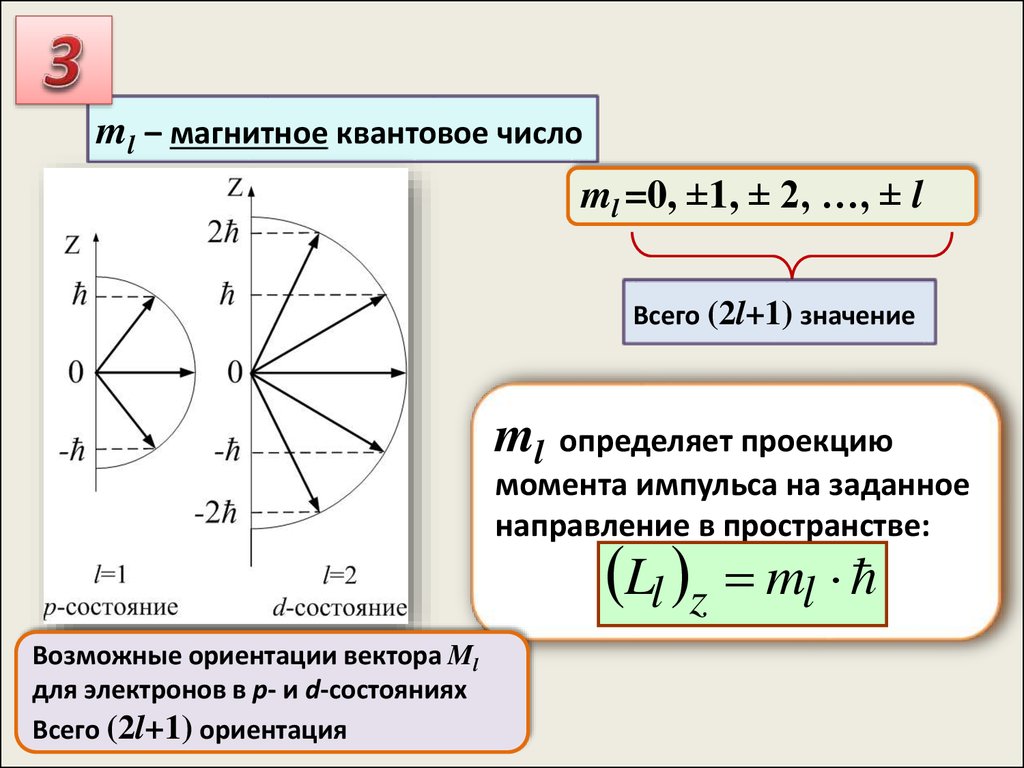
ml – магнитное квантовое число
ml =0, ±1, ± 2, …, ± l
Всего (2l+1) значение
ml определяет проекцию
момента импульса на заданное
направление в пространстве:
Ll z ml
Возможные ориентации вектора Ml
для электронов в p- и d-состояниях
Всего (2l+1) ориентация

34.

Квантовые числа
Кратность вырождения уровней
Каждому En, кроме E1, соответствует несколько волновых
функций ψnlm, отличающихся значениями квантовых чисел l
и ml
Это значит, что атом водорода, имея одну и ту же энергию,
может находиться в нескольких различных состояниях
Такие состояния называются вырожденными
Кратность вырождения энергетического уровня с номером n
можно рассчитать, исходя из возможных значений n:
n 1
2l 1 n
2
l 0
34

35.

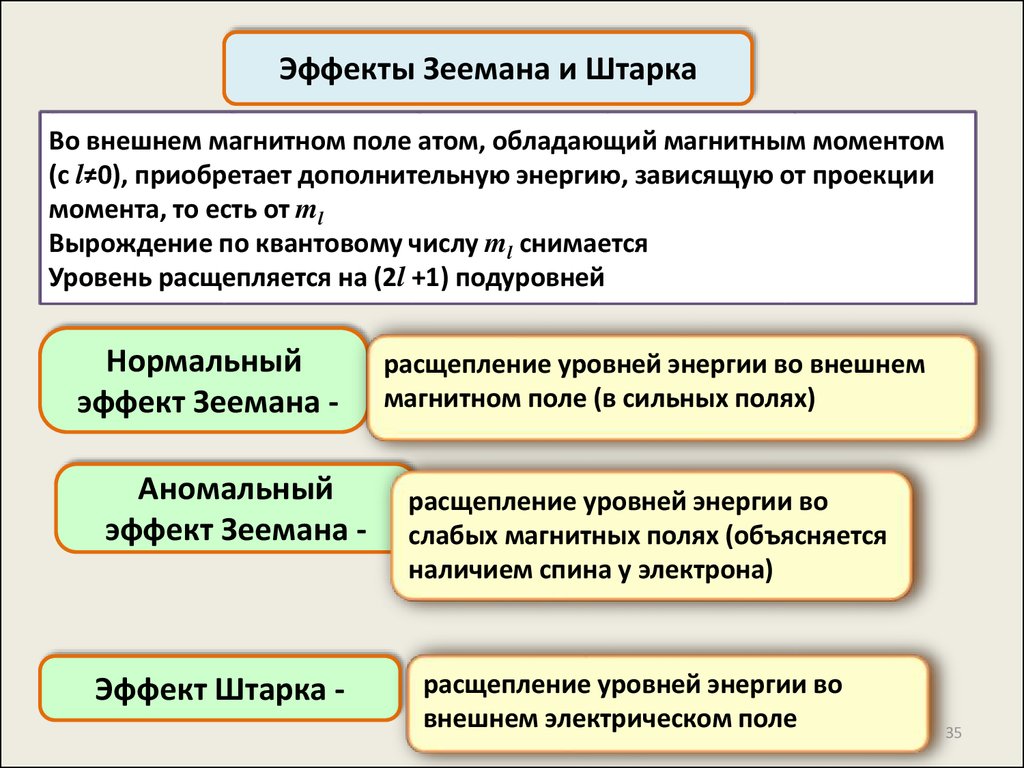
Эффекты Зеемана и Штарка
Во внешнем магнитном поле атом, обладающий магнитным моментом
(с l≠0), приобретает дополнительную энергию, зависящую от проекции
момента, то есть от ml
Вырождение по квантовому числу ml снимается
Уровень расщепляется на (2l +1) подуровней
Нормальный
эффект Зеемана Аномальный
эффект Зеемана -
Эффект Штарка -
расщепление уровней энергии во внешнем
магнитном поле (в сильных полях)
расщепление уровней энергии во
слабых магнитных полях (объясняется
наличием спина у электрона)
расщепление уровней энергии во
внешнем электрическом поле
35

36.

Эффекты Зеемана и Штарка
Спектры усложняются

37.

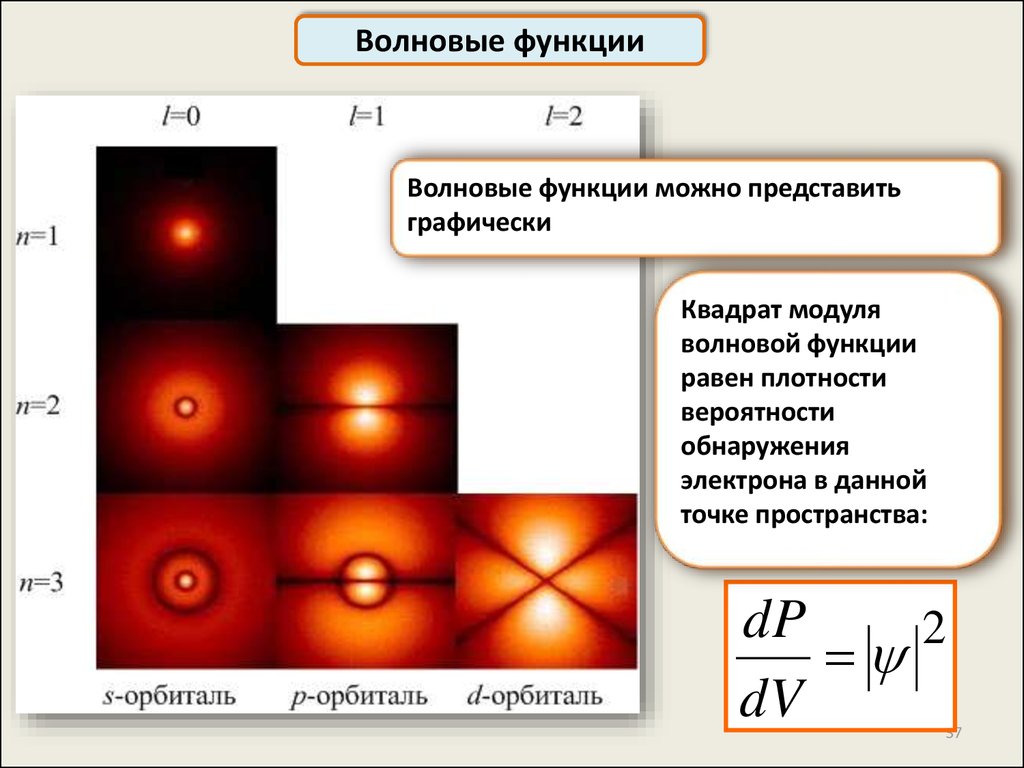
Волновые функции
Волновые функции можно представить
графически
Квадрат модуля
волновой функции
равен плотности
вероятности
обнаружения
электрона в данной
точке пространства:
dP
2
dV
37

38.

Волновые функции
dP
2
dV
38

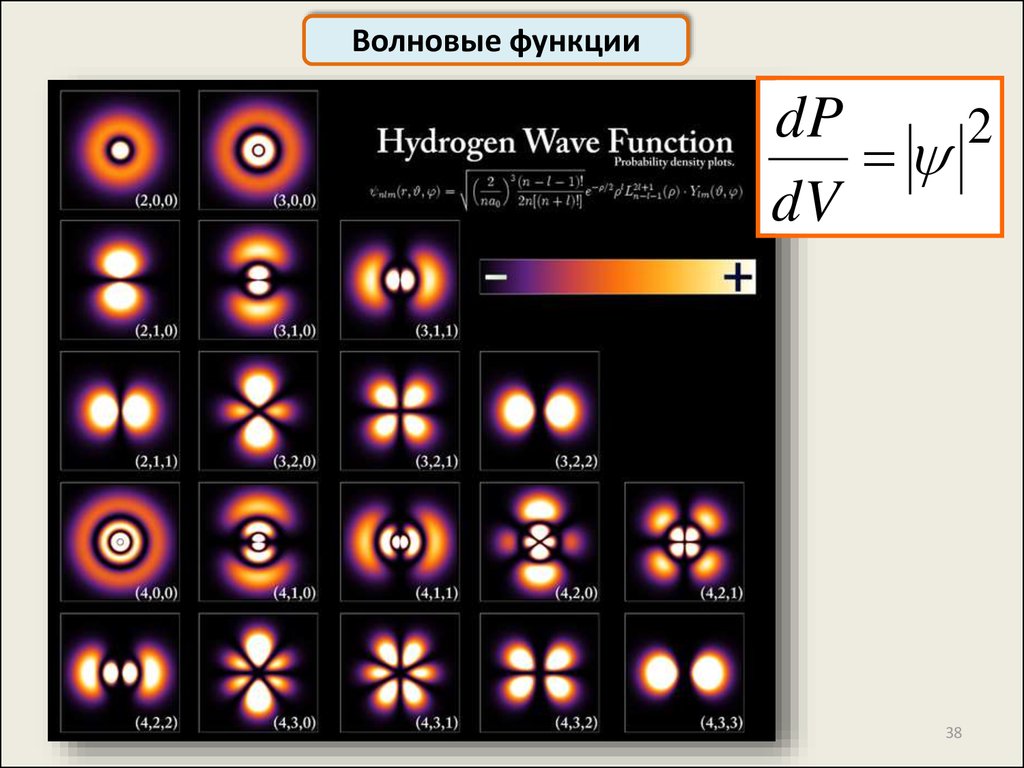
39.

Волновые функции
dP
2
dV
39

40.

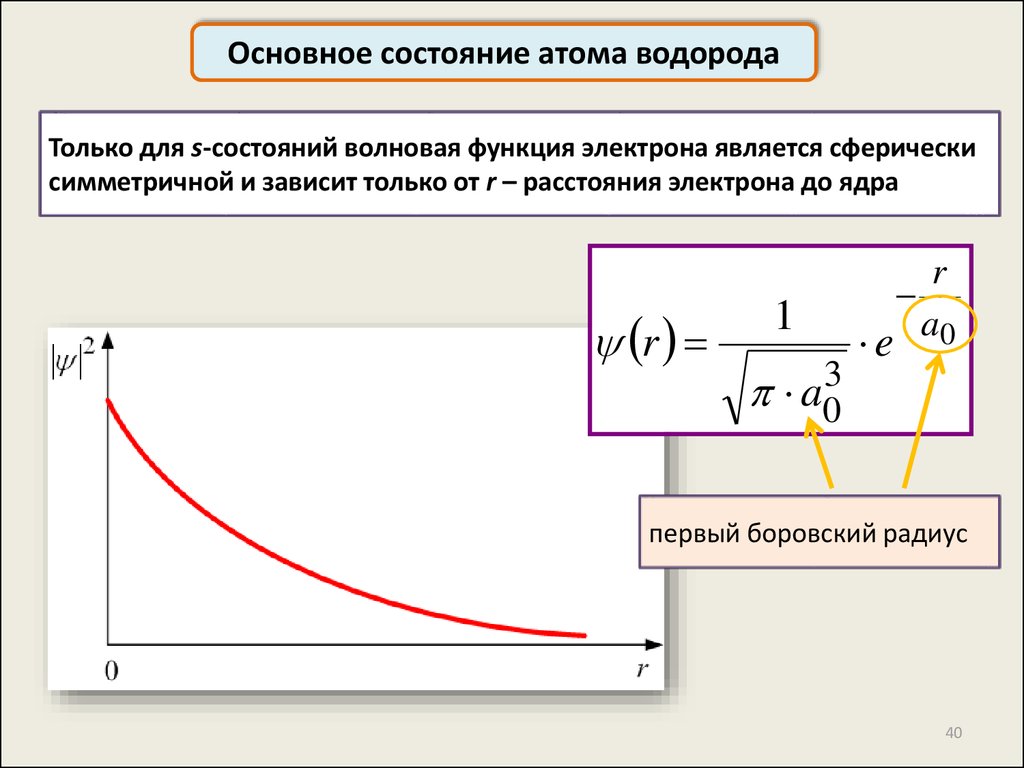
Основное состояние атома водорода
Только для s-состояний волновая функция электрона является сферически
симметричной и зависит только от r – расстояния электрона до ядра
r
1
3
a0
e
r
a0
первый боровский радиус
40

41.

Основное состояние атома водорода
Задача:
найти расстояния rmax от ядра атома, на которых с наибольшей
вероятностью может быть обнаружен электрон
Найдём вероятность того, что электрон находится на расстоянии r от ядра,
точнее – в интервале расстояний от r до r+dr, то есть в шаровом слое
объёмом
2
dV 4 r dr
dP
2
dV
2
r
2
dP dV 4 r dr
1
2
3
a0
e
1
a03
2r
a0
e
r
a0
4 r 2 dr

42.

Основное состояние атома водорода
2
2
dP dV 4 r dr
2
1
a03
e
2r
a0
4 r dr
2
Находим положение максимума функции f(r):
dP
1
2
2
f r
4 r
e
dr
a03
2r
a0
4 r 2
f 0
42

43.

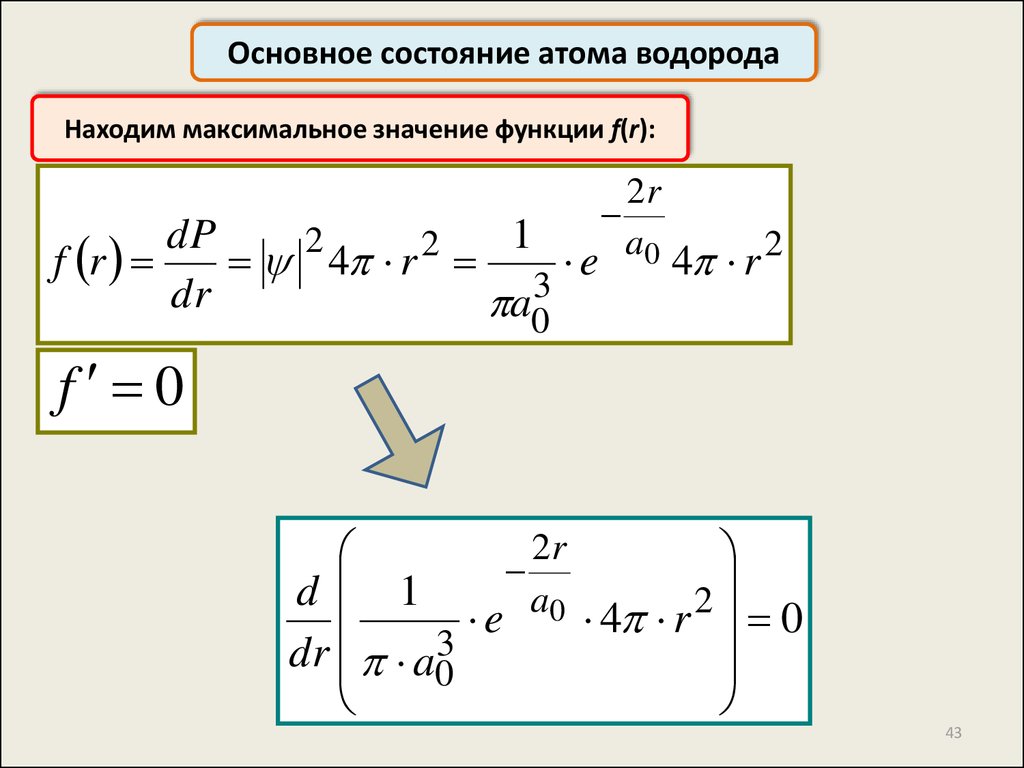
Основное состояние атома водорода
Находим максимальное значение функции f(r):
dP
1
2
2
f r
4 r
e
dr
a03
2r
a0
4 r
2
f 0
2r
d 1
a0
2
e
4 r 0
dr a03
43

44.

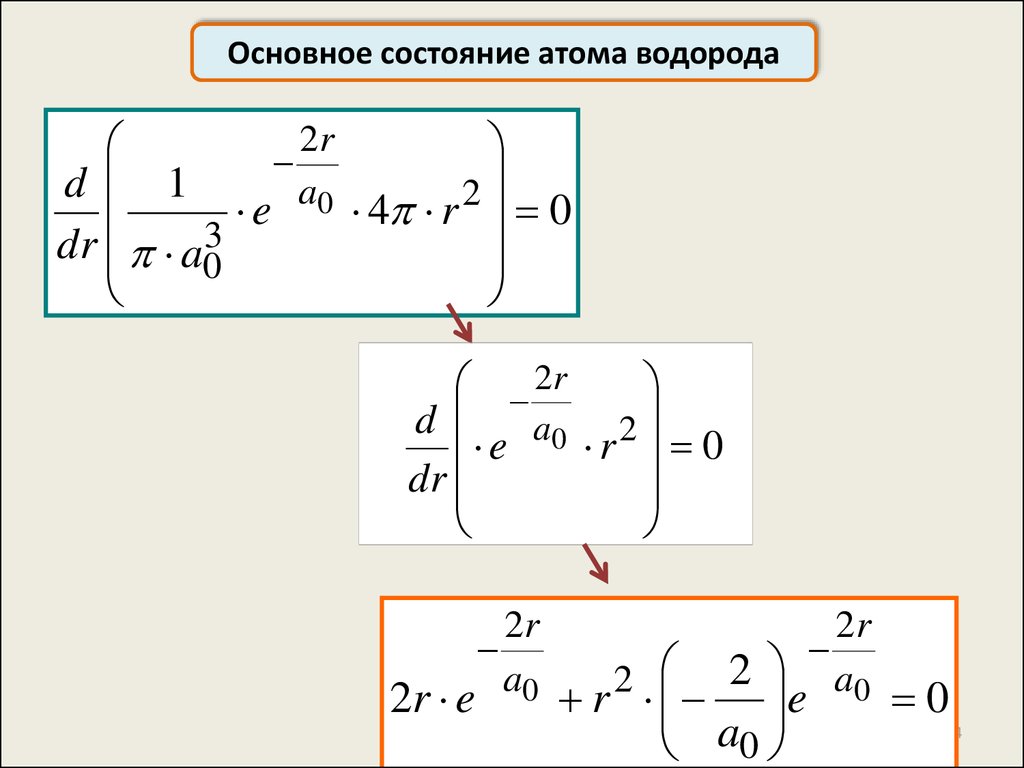
Основное состояние атома водорода
2r
d 1
a0
2
e
4 r 0
dr a03
2r
d
a0 2
r 0
e
dr
2r e
2r
a0
2
2r
2
a0
r e
a0
0
44

45.

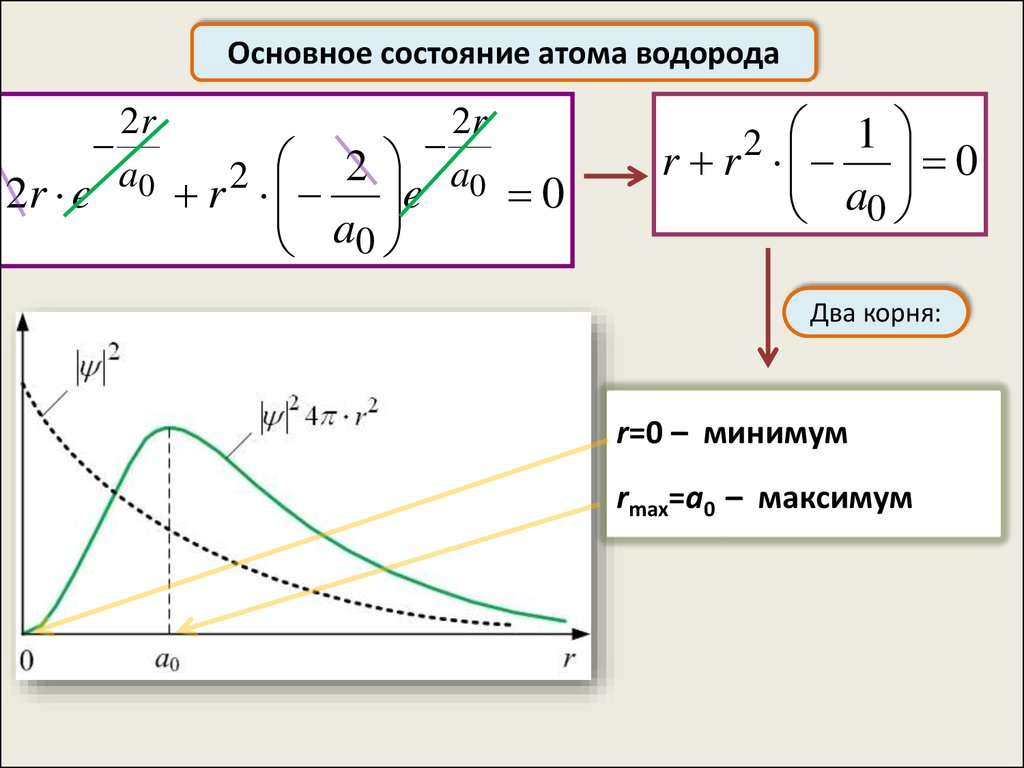
Основное состояние атома водорода
2r e
2r
a0
2
2r
2 a0
r e
a0
0
2
1
r r 0
a0
Два корня:
r=0 – минимум
rmax=а0 – максимум

46.

Основное состояние атома водорода
Боровские орбиты электрона
представляют собой
совокупность точек, в которых с
наибольшей вероятностью
может быть обнаружен
электрон
По теории Бора, вероятность обнаружить электрон в
состоянии с n=1 отлична от нуля только при r=а0
Согласно же квантовой механике, эта вероятность лишь
достигает максимума при r=а0, но она отлична от нуля во
всём пространстве
46

47.

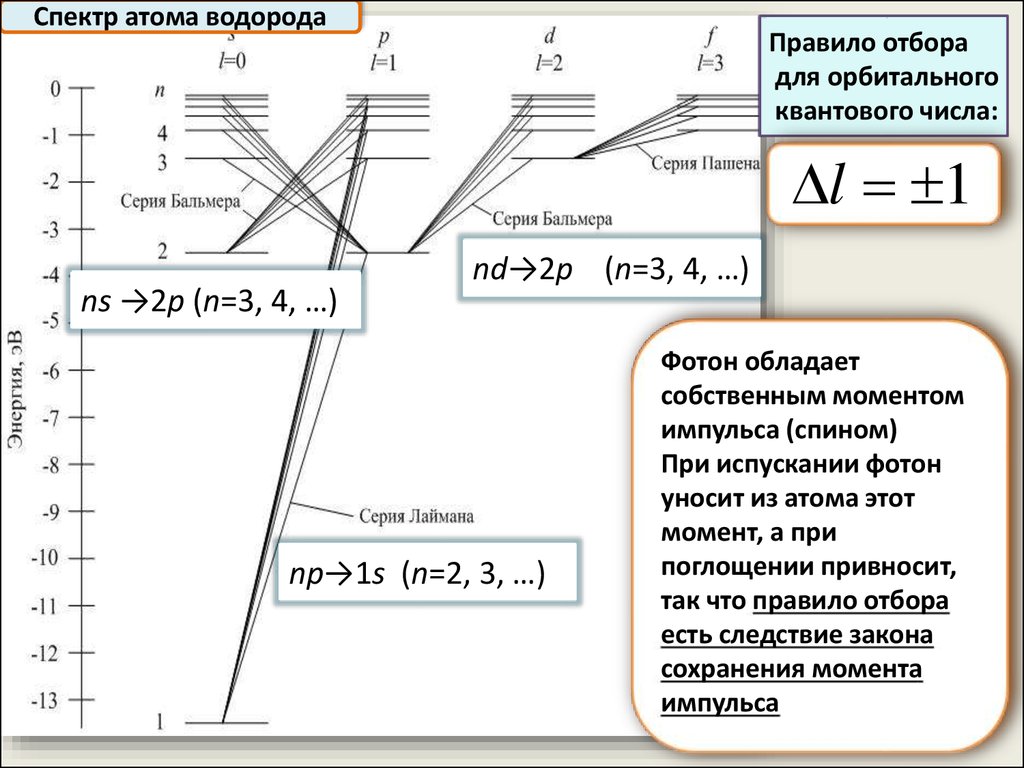
Спектр атома водорода
Правило отбора
для орбитального
квантового числа:
l 1
ns →2p (n=3, 4, …)
nd→2p (n=3, 4, …)
np→1s (n=2, 3, …)
Фотон обладает
собственным моментом
импульса (спином)
При испускании фотон
уносит из атома этот
момент, а при
поглощении привносит,
так что правило отбора
есть следствие закона
сохранения момента
импульса
47

48.

Спин электрона. Спиновое квантовое число
Электрон обладает собственным (спиновым) моментом
импульса Ls, не связанным с орбитальным движением
Спин – внутреннее свойство, присущее электрону, подобно
заряду или массе
Существование спина:
- доказано экспериментально
- вытекает из релятивистского уравнения
квантовой механики П. Дирака, соединившего теорию
относительности с квантовой механикой
Спин является свойством одновременно квантовым и
релятивистским
Спин есть у протонов, нейтронов (s=1/2), фотонов (s=1)….

49.

Спин электрона. Спиновое квантовое число
Спин электрона
1
s
2
1 3
Ls s s 1
3
2 2 2
Спин не обусловлен вращением электрона вокруг своей оси
С механическим моментом связан магнитный момент pm
Гиромагнитное отношение g:
pm
e
для шарика:
L 2me
для электрона:
s
e
Ls
me

50.

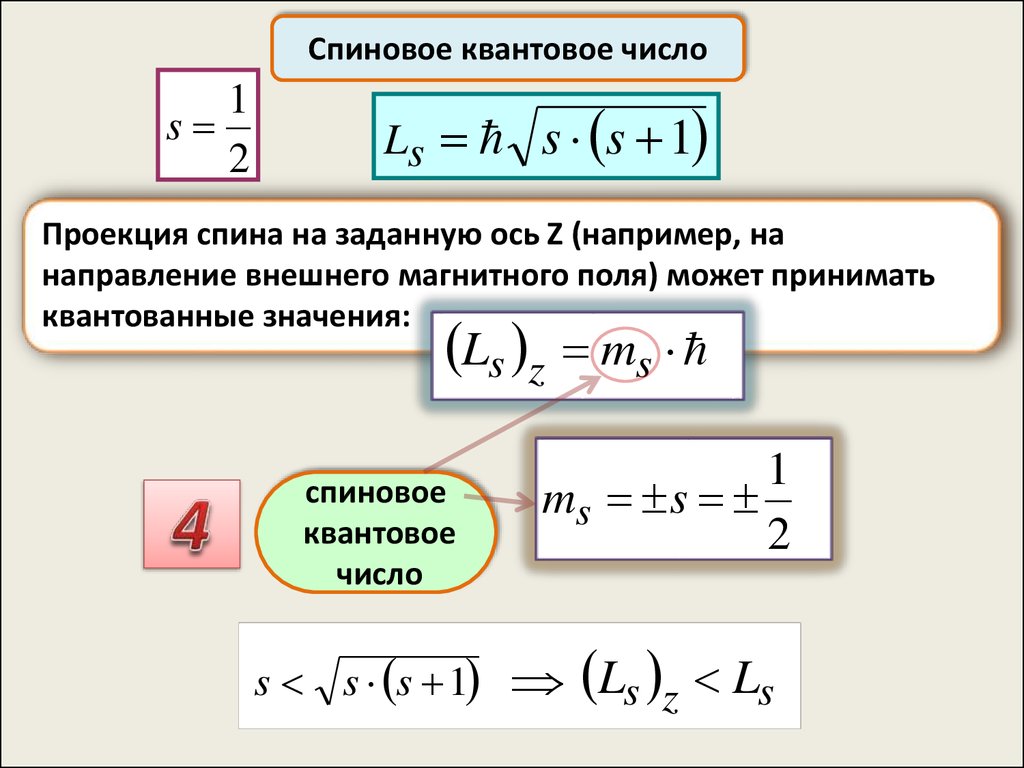
Спиновое квантовое число
1
s
2
Ls s s 1
Проекция спина на заданную
ось Z (например, на
направление внешнего магнитного поля) может принимать
квантованные значения:
Ls z ms
cпиновое
квантовое
число
1
ms s
2
s s s 1 Ls z Ls

51.

1 L s s 1
s
s
2
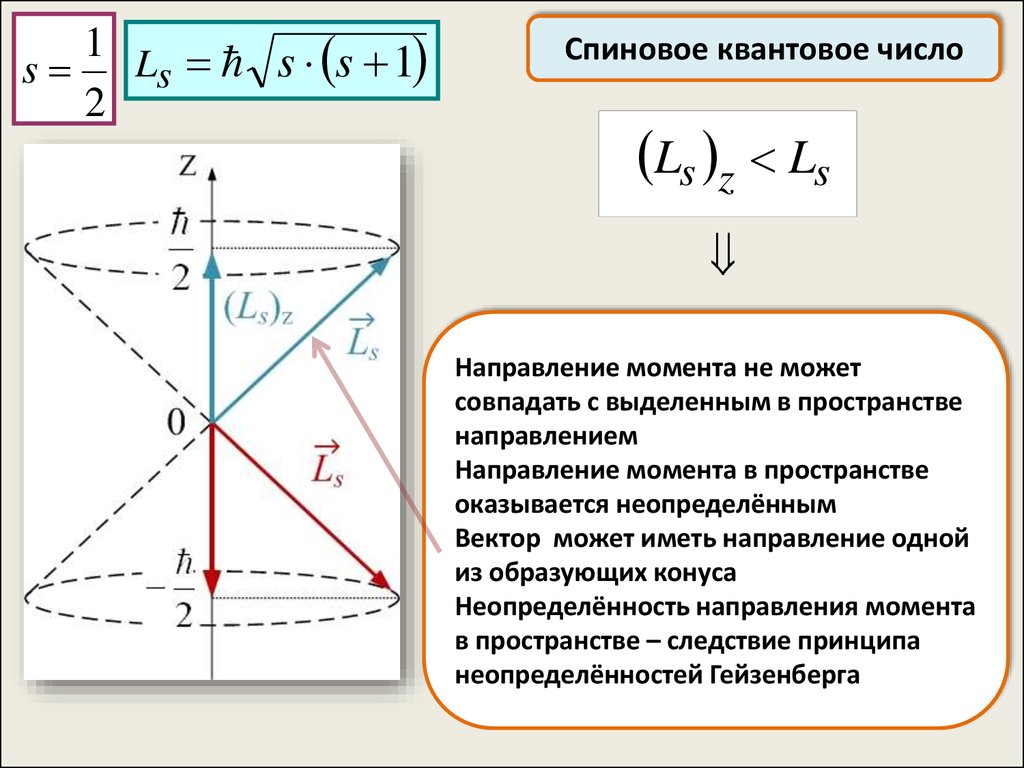
Спиновое квантовое число
Ls z Ls
Направление момента не может
совпадать с выделенным в пространстве
направлением
Направление момента в пространстве
оказывается неопределённым
Вектор может иметь направление одной
из образующих конуса
Неопределённость направления момента
в пространстве – следствие принципа
неопределённостей Гейзенберга

52.

Собственный магнитный момент электрона
1
s
2
Ls s s 1
e
e
e 3
s Ls
s s 1
B 3
me
me
me 2
магнетон Бора
Проекция спинового магнитного момента:
e
e
sz
Lsz
B
me
me 2

53.

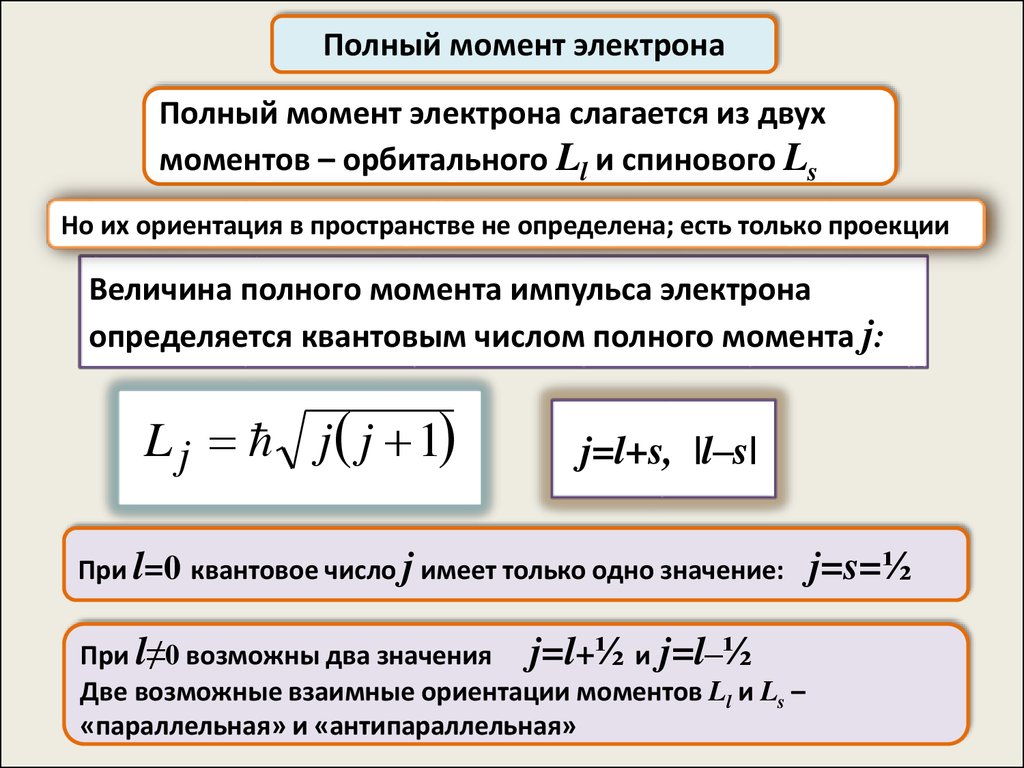
Полный момент электрона
Полный момент электрона слагается из двух
моментов – орбитального Ll и спинового Ls
Но их ориентация в пространстве не определена; есть только проекции
Величина полного момента импульса электрона
определяется квантовым числом полного момента j:
L j j j 1
j=l+s, |l–s|
При l=0 квантовое число j имеет только одно значение:
При l≠0 возможны два значения j=l+½ и j=l–½
Две возможные взаимные ориентации моментов Ll и Ls –
«параллельная» и «антипараллельная»
j=s=½

54.

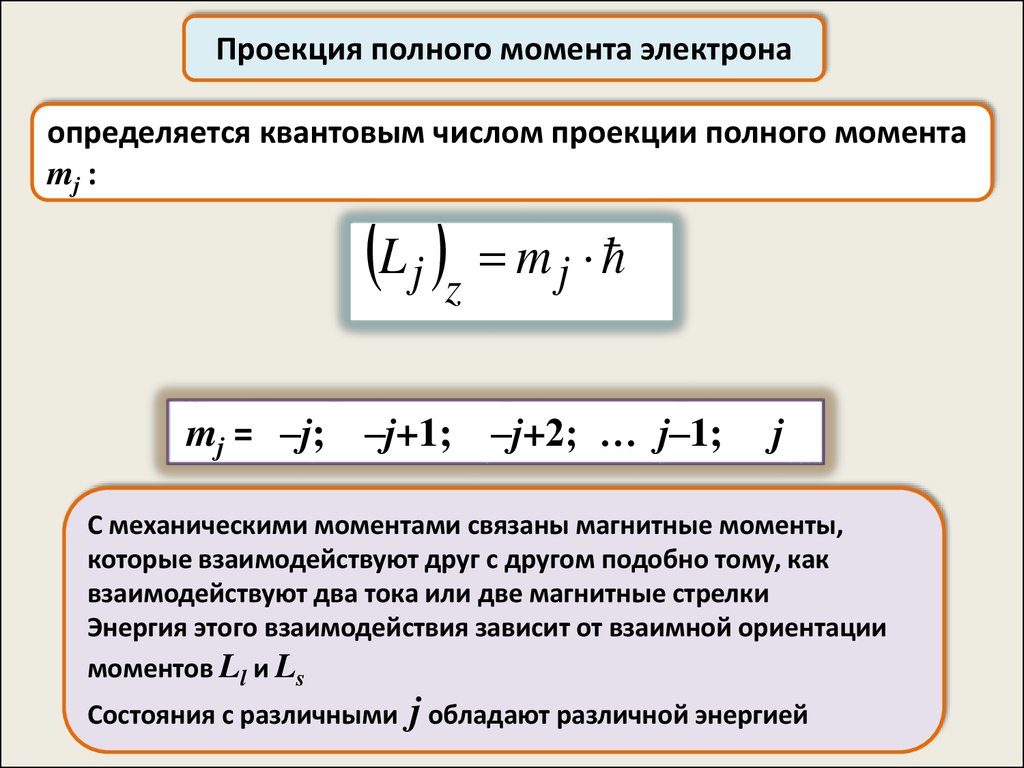
Проекция полного момента электрона
определяется квантовым числом проекции полного момента
mj :
L j z m j
mj = –j;
–j+1;
–j+2; … j–1;
j
С механическими моментами связаны магнитные моменты,
которые взаимодействуют друг с другом подобно тому, как
взаимодействуют два тока или две магнитные стрелки
Энергия этого взаимодействия зависит от взаимной ориентации
моментов Ll и Ls
Состояния с различными
j обладают различной энергией