Строение и свойства атомов. Лекция 8. Магнитный момент атома водорода

1. III. Строение и свойства атомов 8. Магнитный момент атома водорода

• 8.1. Магнитный момент атома как следствие орбитального
движения электрона. Гиромагнитное отношение.
Магнетон Бора.
• 8.2. Прецессия моментов во внешнем магнитном поле.
Опыт Штерна и Герлаха. Спин электрона и других
микрочастиц.
• 8.3. Спин-орбитальное взаимодействие. Полный момент
импульса электрона. Формула Дирака. Квантовые числа
n,l,j и mj.
• 8.4. Тонкая структура уровней энергии и спектральных
линий атома водорода. Лэмбовский сдвиг. Сверхтонкая
структура.

2.

8.1. Магнитный момент атома как следствие
орбитального движения электрона.
Гиромагнитное отношение. Магнетон Бора.
e
Pm I n n;
В простейшем случае круговой орбиты
r ;
2
Pm l l ;
e
l
;
2me

3.

8.1. Магнитный момент атома как следствие
орбитального движения электрона.
Гиромагнитное отношение. Магнетон Бора.
Pm l l ;
Pm l l 1 Pm0 l l 1 ;
e
Pm0
l -магнетон Бора
2me
Pm0 9,27 10
24
1
Дж Тл .
z
Pm l l z Pm0 m.
m - магнитное квантовое число, m 0, 1, 2,....

4.

8.2. Прецессия моментов во внешнем магнитном поле.
Опыт Штерна и Герлаха. Спин электрона и других
микрочастиц.
x
P
P
z
N
S
D
D
D
D
Ag
K
B
z B
Fz Pm
cos Pm B Pm
z
z
z
Pm l l z Pm0 m
m 0, 1, 2,....
Пучок атомов должен был бы расщепляться на нечетное число компонент.
Оказалось, что это не выполняется.
Для серебра пучок расщепляется на 2 компоненты.

5.

8.2. Прецессия моментов во внешнем магнитном поле.
Опыт Штерна и Герлаха. Спин электрона и других
микрочастиц.
• ВЫВОД. Наличие 3-х квантовых чисел n, l, m
недостаточно для описания квантовых состояний
электрона в атоме.
• ИДЕЯ. Паули сформулировал точку зрения,
согласно которой, «дублетная структура спектров
щелочных металлов возникает вследствие
характерной дублетности квантовых свойств
электрона, которую нельзя описать классически».
Паули предложил использовать для описания
состояний электрона в атоме не 3, а 4 квантовых
числа.

6.

8.2. Прецессия моментов во внешнем магнитном поле.
Опыт Штерна и Герлаха. Спин электрона и других
микрочастиц.
• Существенный шаг в развитии этой гипотезы сделали
голландские физики Юленбек и Гаудсмит, которые ввели
представление о вращении электрона вокруг собственной
оси. Это свойство называется спиновым.
• По общим законам квантовой механики спиновый момент
импульса (спин) выражается через спиновое квантовое
число s в соответствии с формулой:
s s s 1 , s 1 / 2.

7.

8.2. Прецессия моментов во внешнем магнитном поле.
Опыт Штерна и Герлаха. Спин электрона и других
микрочастиц.
s s s 1 , s 1 / 2.
•По общим законам квантовой механики проекция спинового момента
импульса выражается через квантовое число проекции спина в
соответствии с формулой:
s z ms , ms 1 / 2.

8.

8.2. Прецессия моментов во внешнем магнитном поле.
Опыт Штерна и Герлаха. Спин электрона и других
микрочастиц.
Магнитный момент электрона
Pms s s ,
Pms Pm0 3
e
s 2 l
,
me
- Магнитный момент электрона
z
Pms s s z 2 l ms Pm0 .

9.

•8.3. Спин-орбитальное взаимодействие. Полный
момент импульса электрона. Формула Дирака.
Квантовые числа n,l,j и mj.
При классическом рассмотрении:
0 2I
B
.
4 r
z
Esl Pms B Pm B ,
Pms Pm0 3 .
s
Pms Pm0 .
z

10.

•8.3. Спин-орбитальное взаимодействие. Полный
момент импульса электрона. Формула Дирака.
Квантовые числа n,l,j и mj.
• При квантовомеханическом рассмотрении:
Hˆ E ,
2
Hˆ Hˆ 0 Hˆ ,
2
k z e ˆ
ˆ
H0
, H Hˆ D Hˆ sl Hˆ p
2m
r
Ĥ D -поправка, определяющая дополнительную энергию взаимодействия
электрона с ядром в s-состояниях;
Ĥ -pпоправка к оператору кинетической энергии, возникающая из-за
изменения массы частицы при изменении ее скорости;
Ĥ sl -поправка, называемая оператором спин-орбитального взаимодействия.

11.

•8.3. Спин-орбитальное взаимодействие. Полный
момент импульса электрона. Формула Дирака.
Квантовые числа n,l,j и mj.
• При квантовомеханическом рассмотрении:
Hˆ Hˆ 0 Hˆ ,
Hˆ Hˆ D Hˆ sl Hˆ p .
E E0 E ,
E ED E p Esl .
E D -энергию взаимодействия электрона с ядром в s-состояниях;
E p -кинетической энергии, возникающая из-за изменения массы
частицы при изменении ее скорости;
E sl -энергия спин-орбитального взаимодействия.
,

12.

•8.3. Спин-орбитальное взаимодействие. Полный
момент импульса электрона. Формула Дирака.
Квантовые числа n,l,j и mj.
E p Esl En , j ,
hcR hcR 2 Z 4 1
3
En , j En En , j 2
,
3
n
n
j 1 4n
2
k e2
1
c
137
,
hcR Z
.
Esl E
E
1
1
3
n , j l
n , j l
n l( l 1 )
2
2
j?
2
4

13.

•8.3. Спин-орбитальное взаимодействие. Полный
момент импульса электрона. Формула Дирака.
Квантовые числа n,l,j и mj.
Векторная модель атома
j l s,
j
j
j l s.
l
j z m j ,
s
m j j, j.
j j 1 ,

14.

•8.4. Тонкая структура уровней энергии и
спектральных линий атома водорода.
Лэмбовский сдвиг. Сверхтонкая структура.
• Терм водородоподобного атома может быть представлен в
виде суммы:
T Tn Tn , j ,
RZ 2
Tn 2 ,
n
2 4
R Z
1
3
Tn , j
.
3
n
j 1 4n
2
Tn , j Tn
Для водорода Т1=27414,25 см-1, а ΔТn,j=0,366 см-1.

15.

•8.4. Тонкая структура уровней энергии и
спектральных линий атома водорода.
Лэмбовский сдвиг. Сверхтонкая структура.
• Вследствие спин-орбитального взаимодействия
спектральные термы смещаются и расщепляются,
возникает их тонкая структура.
• Результат: линии спектров имеют тонкую структуру.
n=2
j=3/2
j=1/2
Пример: образования тонкой структуры
Т1 и Т2 термов водорода.
n=1
j=1/2
T Tn Tn , j

16.

•8.4. Тонкая структура уровней энергии и
спектральных линий атома водорода.
Лэмбовский сдвиг. Сверхтонкая структура.
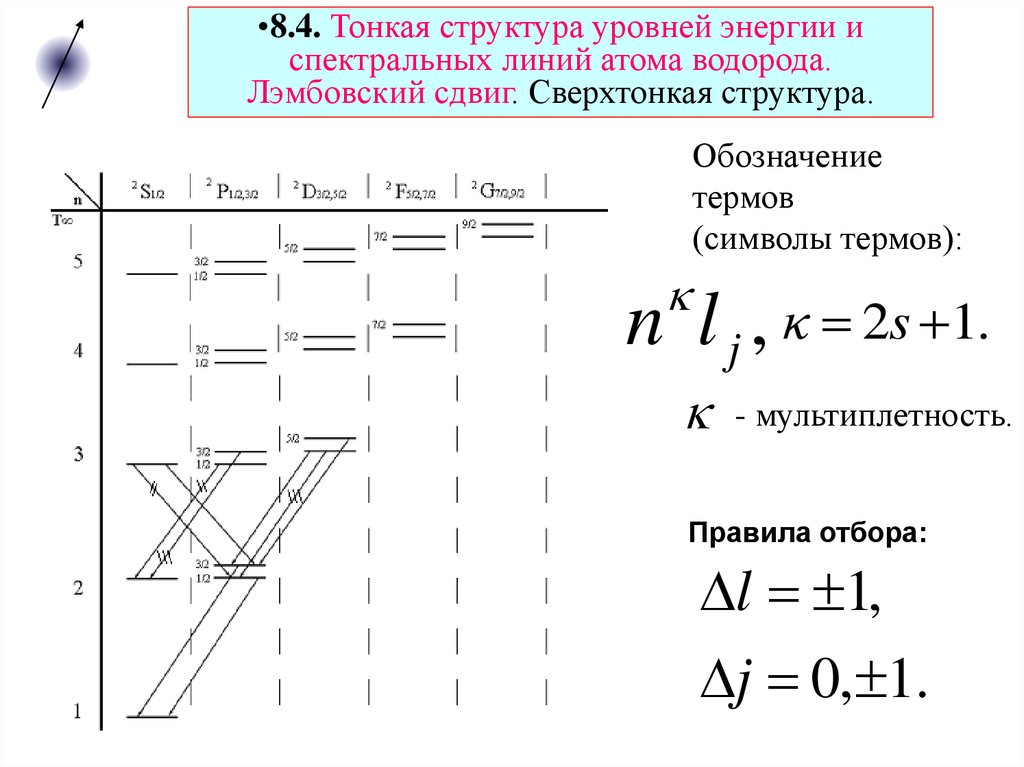
Обозначение
термов
(символы термов):
n l j , κ 2s 1.
- мультиплетность.
Правила отбора:
l 1,
j 0, 1.

17.

•8.4. Тонкая структура уровней энергии и
спектральных линий атома водорода.
Лэмбовский сдвиг. Сверхтонкая структура.
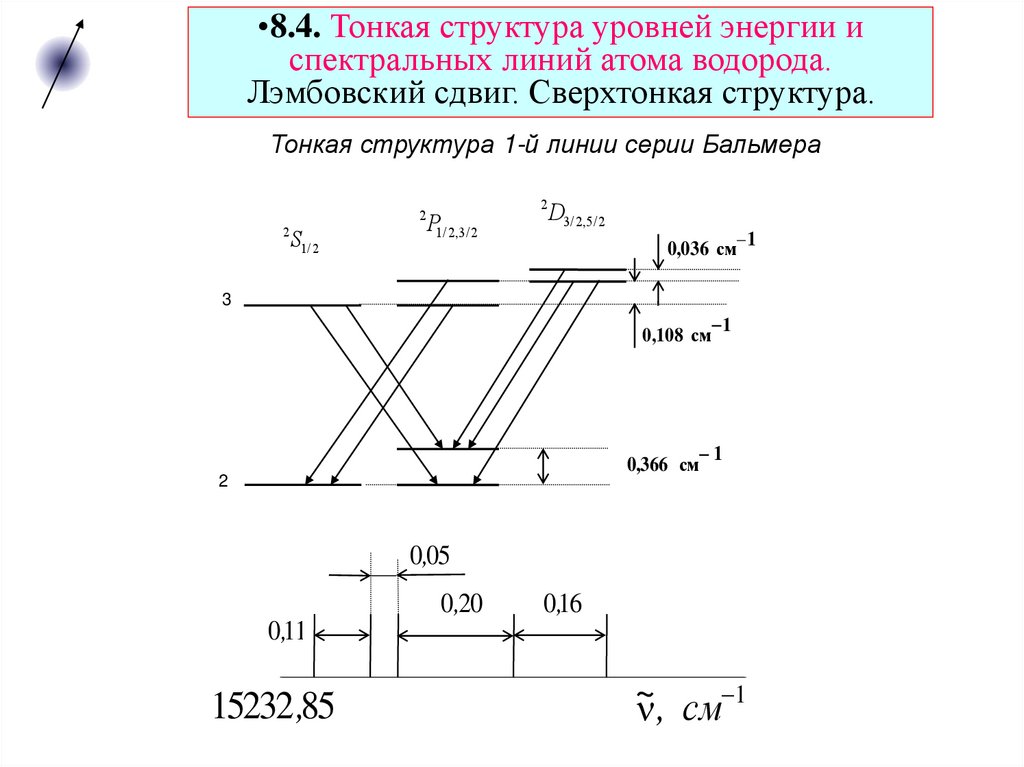
Тонкая структура 1-й линии серии Бальмера
2
2
S1/ 2
P1/ 2,3 / 2
2
D3/ 2,5 / 2
0,036 см 1
3
0,108 см
0,366 см
2
1
1
0,05
0,20
0,16
0,11
15232,85
~ , см 1