Многоэлектронные атомы

1. Многоэлектронные атомы

Неразличимость тождественных частиц
Фермионы и бозоны
Принцип запрета Паули

2. Неразличимость тождественных частиц

В классической механике
всегда можно, хотя бы в принципе, определить
индивидуальную траекторию каждой из многих
одинаковых частиц.
В квантовой механике
траектория «потеряна» с самого начала согласно
соотношениям неопределенностей.
Поэтому одинаковые частицы, которые имеют одинаковые
значения массы, электрического заряда, спина и т.д. и
находятся в общей области существования, оказываются
тождественными и принципиально
неразличимыми.

3.

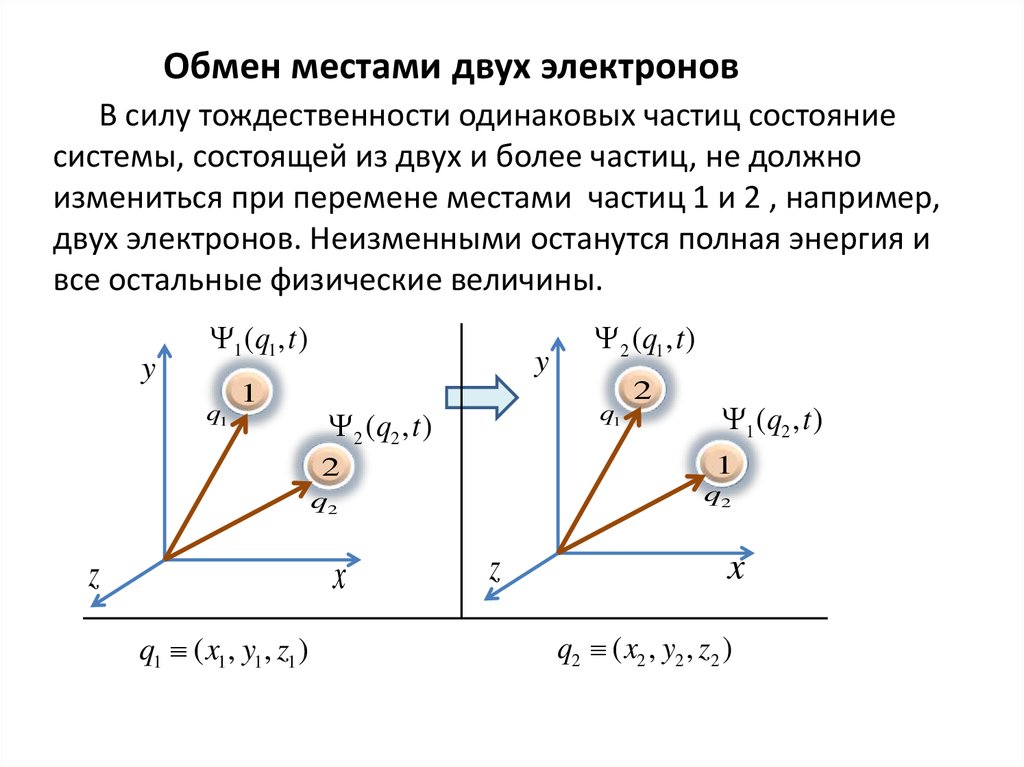
Обмен местами двух электронов
В силу тождественности одинаковых частиц состояние
системы, состоящей из двух и более частиц, не должно
измениться при перемене местами частиц 1 и 2 , например,
двух электронов. Неизменными останутся полная энергия и
все остальные физические величины.
y
1 (q1 , t )
q1
1
y
2 (q2 , t )
q1 ( x1 , y1 , z1 )
q1
2
1 (q2 , t )
2
1
q2
q2
x
z
2 (q1 , t )
z
x
q2 ( x2 , y2 , z2 )

4. Задача на поиск собственных значений оператора перестановки тождественных частиц местами

Введем оператор перестановки частиц местами Pˆ :
Pˆ (q1 , q2 , t ) p (q2 , q1 , t )
(1)
Поскольку обе волновые функции в (1) описывают одно и то же
квантовое состояние, то они являются решением уравнения Шредингера
Hˆ i
t
( Pˆ )
ˆ
ˆ
H ( P ) i
t
и могут различаться только постоянным множителем. Тогда уравнение
(1) можно переписать как
ˆ
P
(2)
Подействуем на левую и правую части уравнения (2) оператором
перестановки
ˆ ˆ 2
Pˆ ( Pˆ ) Pˆ ( ) или PP
Так как дважды применяемый оператор перестановки не меняет
волновую функцию , то получаем: 2 , 2 1,
1

5. Симметричные и антисимметричные состояния

Принцип тождественности
все возможные состояния
системы из одинаковых частиц делятся на два типа:
1. Симметричные состояния,
для которых S - функция системы одинаковых частиц
не меняет знака при перестановке частиц
местами:
S C 1 (q1, t ) 2 (q2 , t ) 1 (q2 , t ) 2 (q1, t )
Частицы, которые описываются симметричными S -функциями,
называются бозе-частицами или бозонами. Системы, состоящие из
таких частиц, подчиняются статистике Бозе-Эйнштейна, разработанной
индийским физиком Ш.Бозе для фотонов и развитой А.Эйнштейном для
идеального газа.

6.

2. Антисимметричные состояния,
для которых A - функция меняет знак при перестановке
частиц местами:
A A 1 (q1 , t ) 2 (q2 , t ) 1 (q2 , t ) 2 (q1, t )
Частицы, состояния которых описываются
антисимметричными A - функциями, называются
фермионами, они подчиняются статистике Ферми-Дирака,
развитой итальянским физиком Э.Ферми и английским
физиком П.Дираком.

7.

Бозоны и
фермионы
БОЗОНЫ: все частицы, имеющие нулевой и
«целочисленный спин» ( квантовое число s 0,1, 2, ):
фотоны, - мезоны и K - мезоны из семейства
элементарных частиц, участвующих в сильных
взаимодействиях и называемых адронами;
фононы в твердом теле (кванты колебаний
кристаллической решетки), и др.
ФЕРМИОНЫ:
все элементарные частицы, имеющие
«полуцелый спин» (квантовое число s 1 2,3 2, ):
электроны, протоны, нейтроны, нейтрино, …

8. Принцип запрета Паули для фермионов

Если взаимодействием между частицами можно
пренебречь, то состояние отдельной частицы в системе
описывается волновой функцией и набором квантовых
чисел, а состояние всей системы – произведением
волновых функций отдельных частиц.
Предположим, что в системе ферми-частиц, где возможен
обмен местами, две частицы находятся в одном и том же
стационарном состоянии , то есть 1 2 . Тогда волновая
функция A 0 , а это означает, что такое состояние
физически не может быть реализовано.
Принцип запрета В.Паули (1925 г. , немецкий физик):
В системе тождественных фермионов не может быть
двух частиц, находящихся в одном и том же квантовом
состоянии с одним и тем же набором кантовых чисел
n, l , m, ms .

9. Периодическая система элементов

2p
L-оболочка
Заполненные
состояния
2s
n=2
K-оболочка
1s2 и 2s2.
1s
H
He Li Be
B C
N
O
F
Ne
n=1
Схема заполнения электронами энергетических
состояний атомов от водорода(Z=1) до неона (Z=10).
Заполнение происходит, исходя из требования минимума
полной энергии атома с учетом принципа Паули.
Объясняется периодическая повторяемость химических
свойств атомов периодической системы элементов
Д.И.Менделеева

10.

E
7
3
Атом лития Li
3p
3s
2p
n=3
n=2
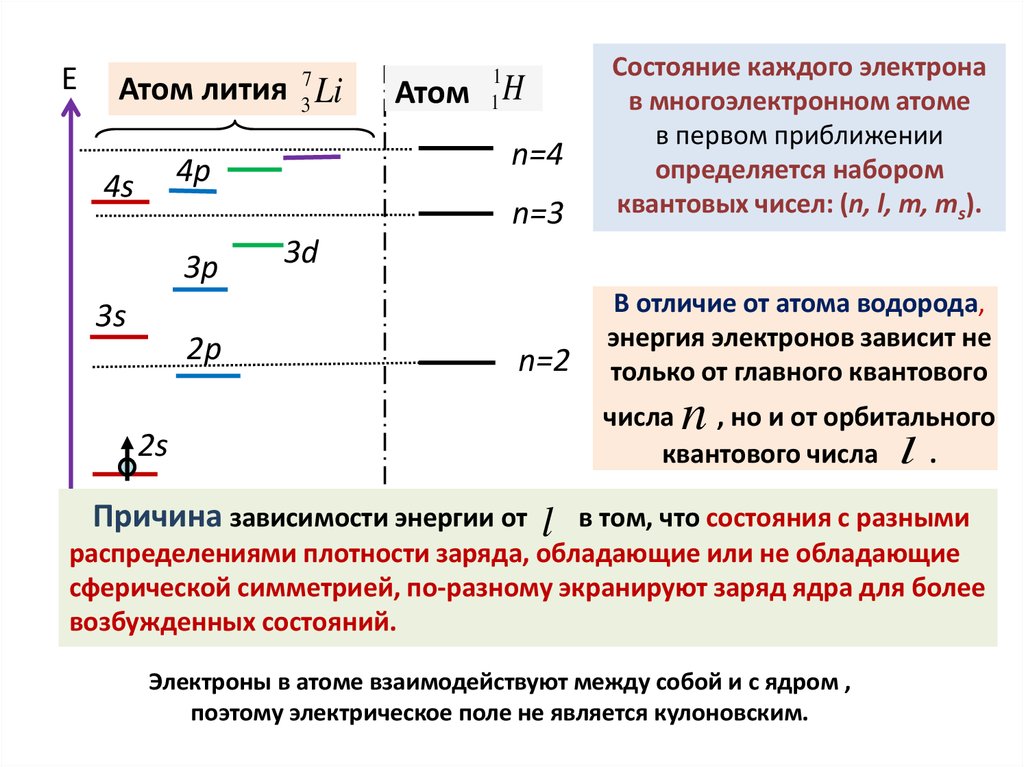
В отличие от атома водорода,
энергия электронов зависит не
только от главного квантового
Атом H
n=4
4p
4s
Состояние каждого электрона
в многоэлектронном атоме
в первом приближении
определяется набором
квантовых чисел: (n, l, m, ms).
1
1
3d
n
числа , но и от орбитального
квантового числа l .
2s
Причина зависимости энергии от
в том, что состояния с разными
распределениями плотности заряда, обладающие или не обладающие
сферической симметрией, по-разному экранируют заряд ядра для более
возбужденных состояний.
l
Электроны в атоме взаимодействуют между собой и с ядром ,
поэтому электрическое поле не является кулоновским.

11. Взаимодействие магнитных моментов в атоме.

В многоэлектронном атоме каждый из N электронов
обладает орбитальным L i и спиновым S i моментами
i и s ,i , которые
импульса и магнитными моментами
им соответствуют.
В результате взаимодействия магнитных
моментов отдельных электронов в атоме происходит
их сложение (по правилам квантовой механики) в
результирующий магнитный момент атома
,
которому соответствует полный механический
момент M J (суммарный момент импульса
многоэлектронного атома).
В легких и средних атомах встречается
LS - связь.

12. LS-связь в легких и средних атомах

1. В результате наиболее сильного взаимодействия орбитальных магнитных
моментов отдельных электронов образуются суммарный магнитный
орбитальный момент L и механический момент
всех электронов в атоме M L
L( L 1) ,
где L - орбитальное квантовое число атома (целое число либо ноль).
2. В результате менее сильного взаимодействия спиновых магнитных
моментов отдельных электронов образуется суммарный магнитный спиновый
момент S и суммарный спин
M
S (S 1) всех электронов в атоме,
S
где S- квантовое число суммарного спина. Если в атоме четное число
электронов, то квантовое число S является целым числом, либо равно нулю.
При нечетном числе электронов квантовое число S принимает полуцелые
значения.
3. Наиболее слабое спин-орбитальное взаимодействие между магнитными
моментами L и S приводит к образованию результирующего магнитного
момента J и механического момента всего атома
M
J ( J 1)
J
Квантовое число Jпринимает значения:
для заданной пары значений L и S .
J L S , L S 1, L S 2, , L S .

13. Обозначение квантовых состояний многоэлектронного атома

Энергия многоэлектронного атома зависит от всех квантовых
чисел n, L, S , J . Квантовое состояние атома символически
записывается в виде:
Символ:
(2 S 1)
" L" J
(" L ")
где под
понимается одна из следующих букв (S,P, …) в
схеме обозначений:
Квантовое число L : 0
1
2
3 ...
Буква : S
P
D
F ...

14.

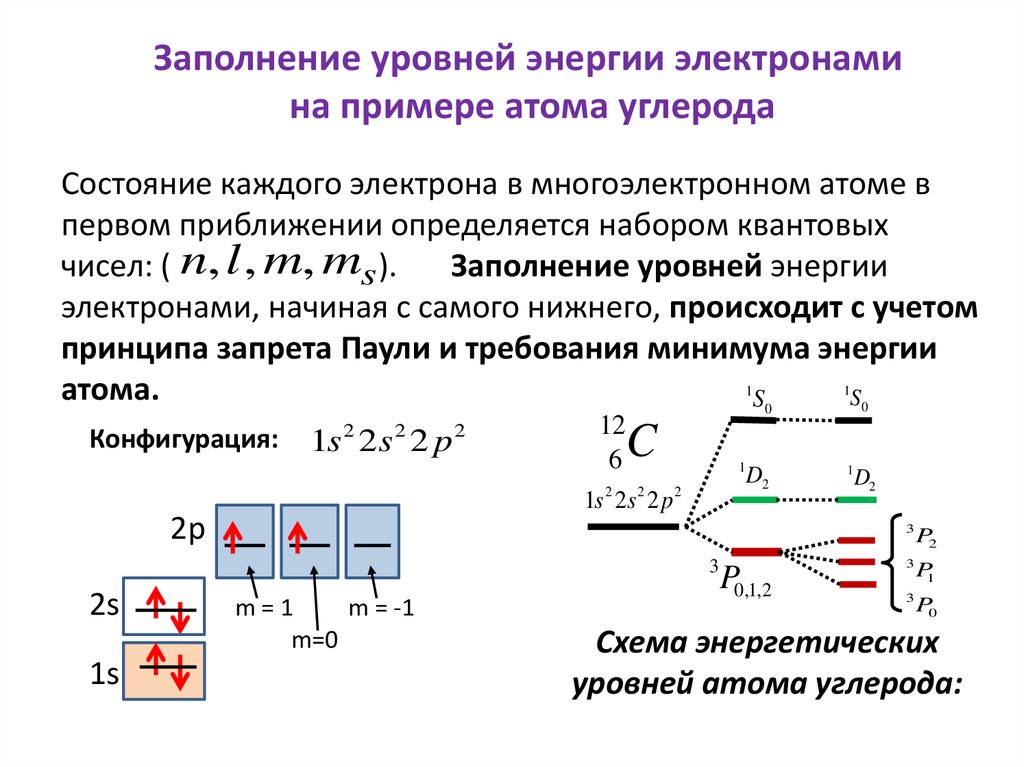
Заполнение уровней энергии электронами
на примере атома углерода
Состояние каждого электрона в многоэлектронном атоме в
первом приближении определяется набором квантовых
чисел: ( n, l , m, ms ).
Заполнение уровней энергии
электронами, начиная с самого нижнего, происходит с учетом
принципа запрета Паули и требования минимума энергии
1
атома.
S
S0
1
0
Конфигурация:
1s 2 2s 2 2 p 2
12
6
C
2
2
1s 2s 2 p
1
2
D2
2p
3
2s
1s
m=1
m = -1
m=0
P0,1,2
1
D2
3
P2
3
P1
3
P0
Схема энергетических
уровней атома углерода:

15. Правила отбора при оптических переходах

Правила отбора при оптических переходах атома.
Квантовая теория, исходя из закона сохранения моментов импульса,
обосновывает правила отбора для разрешенных оптических переходов
атома из одного квантового состояния в другое.
Переходы с излучением подчиняются следующим правилам
изменения квантовых чисел:
S 0, L 0, 1, J 0, 1, mJ 0, 1
Переход из состояния с ( J нач 0 ) в состояние с ( J кон 0 ) запрещен.
Примеры.
Разрешенные переходы:
Запрещенные
переходы:
2
2
D3 2 2 P1 2 ;
D3 2 S1 2 ;
2
2
2
D5 2 P1 2 ;
2
F7 2 2 D5 2
2
F5 2 P3 2
2

16.

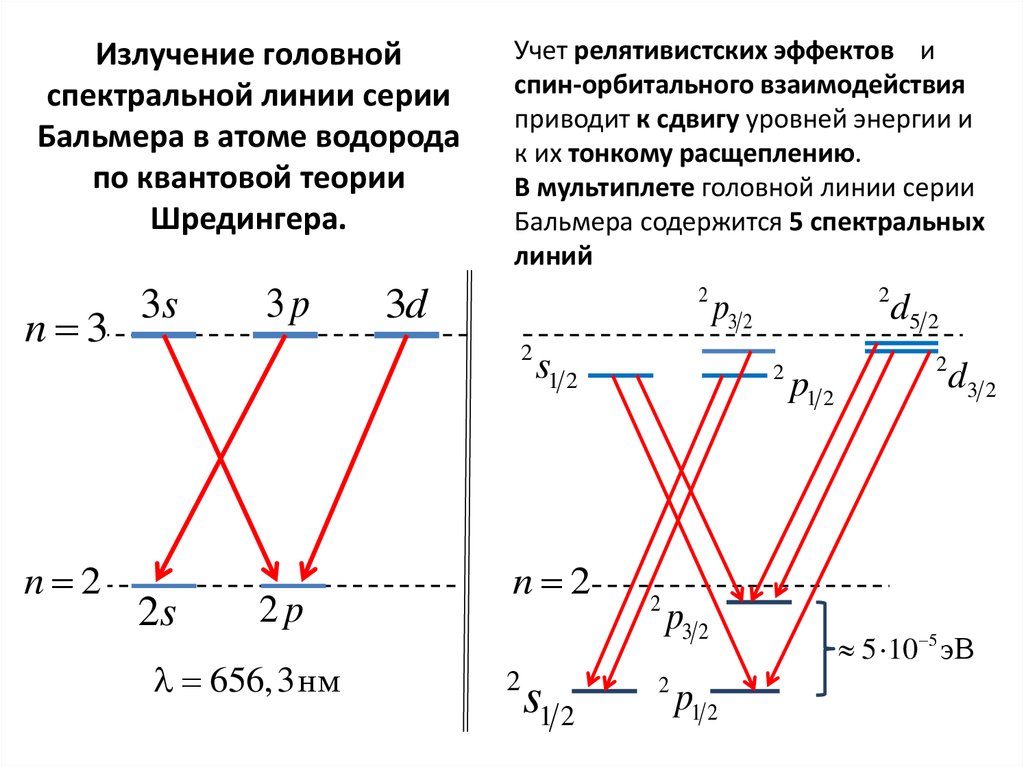
Излучение головной
спектральной линии серии
Бальмера в атоме водорода
по квантовой теории
Шредингера.
n 3
n 2
3s
3p
Учет релятивистских эффектов и
спин-орбитального взаимодействия
приводит к сдвигу уровней энергии и
к их тонкому расщеплению.
В мультиплете головной линии серии
Бальмера содержится 5 спектральных
линий
2
3d
2
2s
2p
656,3нм
s1 2
n 2
2
s1 2
2
p3 2
2
2
p3 2
2
p1 2
p1 2
d5 2
2
d3 2
5 10 5 эВ

17.

,
Проекция момента импульса атома на выделенное
направление в пространстве
Согласно пространственному квантованию
результирующего момента импульса M J число
проекций на выделенное направление в пространстве
(ось z) находится по формуле
M J , z mJ
где m J - квантовое число, которое принимает
следующие значения:
mJ J , J 1, , ( J 1), J

18. Магнитный момент многоэлектронного атома

Квантово-механический расчет приводит к следующему соотношению
между механическим моментом и результирующим магнитным
моментом всех электронов в атоме:
3 S ( S 1) L( L 1)
e
g
J
g M J ; J g Б J ( J 1) ;
2
2 J ( J 1)
2me
где множитель g называется
физик-теоретик).
L
MJ
L
S
MS
ML
J
g-фактором Ланде (А.Ланде – немецкий
J
e
ML
2me
ML
e
S 2
MS
2me
L( L 1)
MS
S 2 Б S (S 1)
S (S 1)

19. Эффект Зеемана (Расщепление спектральных линий излучения атома в магнитном поле на несколько компонент)

Проекция магнитного момента
выделенное направление
магнитного поля равна
J
на
z внешнего
mJ 3 2
2
Jz g Б mJ
Для заданного значения J существует
2J+1 различных ориентаций магнитного
момента атома по отношению к
направлению внешнего магнитного
поля.
Атом, помещенный во внешнее
магнитное поле B0 , приобретает
дополнительную энергию
U J J B0 Jz B0 g Б mJ B0
Атомный уровень энергии во внешнем
магнитном поле расщепляется на 2J+1
подуровня.
mJ 1 2
E2
P3 2
mJ 1 2
mJ 3 2
0
2
mJ 1 2
E1
S1 2
mJ 1 2
B 0
B 0
0
0
Расщепление уровней энергии атома в
магнитном поле и разрешенные
переходы между ними.

20.

Частоты спектральных линий в эффекте Зеемана
Расщепление спектральных линий излучения паров натрия, находящихся в
магнитном поле, впервые наблюдал нидерландский физик П.Зееман в 1896 г.
Верхний уровень энергии на рисунке во внешнем магнитном поле
расщепляется на 2J 1 4 подуровня с «расстоянием» между соседними
подуровнями EP g p Б B0 , где g p 4 3 .
Нижний уровень в магнитном поле расщепляется на два подуровня с
«расстоянием» между ними ES g s Б B0 , где g s 2 .
Для оптических переходов с верхних подуровней на нижние
частоты спектральных линий излучения можно найти по
формуле
Б B0
( p)
(s)
0 g p mJ g S mJ
Переходы с излучением подчиняются следующим правилам изменения
квантовых чисел:
S 0 ; L 0, 1 ; J 0, 1 ; mJ 0, 1 .
Исключением является переход из состояния с (J=0) в состояние с (J=0),
который запрещен.