Similar presentations:
Многоэлектронные атомы. Взаимодействие атомов с излучением
1. Многоэлектронные атомы. Взаимодействие атомов с излучением.
Государственный университет «Дубна»Факультет естественных и инженерных наук
Кафедра Ядерной физики
Специальный семинар по физике ядра и ядерным реакциям
В.В.Самарин
Многоэлектронные атомы.
Взаимодействие атомов с излучением.
Вопросы 12, 13,14.
2019
1
2. Вопросы
12. Многоэлектронный атом. Приближениесамосогласованного поля. Электронная
конфигурация. Терм. Тонкая структура
терма. Сложение моментов. Приближение
LS и jj-связей. Правила Хунда.
13. Нестационарная теория возмущений.
Золотое правило Ферми.
14. Вторичное квантование свободного
электромагнитного поля. Взаимодействие
атома с квантованным полем излучения.
2
3. Вопрос 12. Многоэлектронные атомы.
• Многоэлектронный атом.• Приближение самосогласованного поля.
• Электронная конфигурация. Терм. Тонкая
структура терма.
• Сложение моментов.
• Приближение LS связи.
• Приближение jj-связи.
3
4.
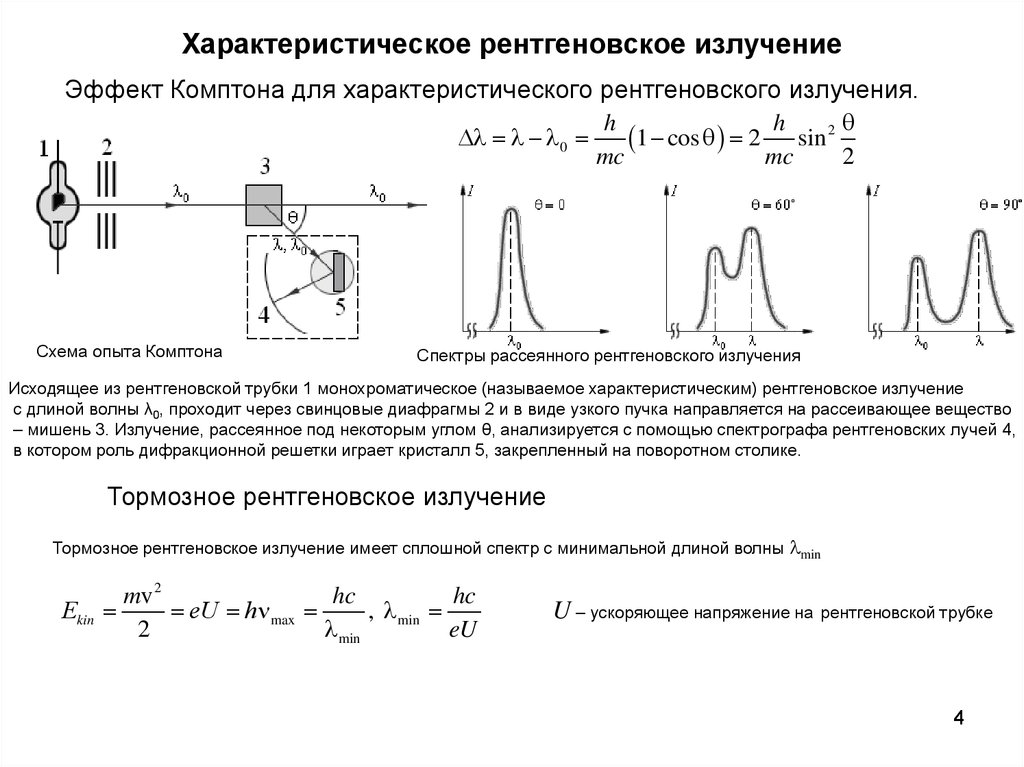
Характеристическое рентгеновское излучениеЭффект Комптона для характеристического рентгеновского излучения.
0
Схема опыта Комптона
h
h
1 cos 2 sin 2
mc
mc
2
Спектры рассеянного рентгеновского излучения
Исходящее из рентгеновской трубки 1 монохроматическое (называемое характеристическим) рентгеновское излучение
с длиной волны λ0, проходит через свинцовые диафрагмы 2 и в виде узкого пучка направляется на рассеивающее вещество
– мишень 3. Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских лучей 4,
в котором роль дифракционной решетки играет кристалл 5, закрепленный на поворотном столике.
Тормозное рентгеновское излучение
Тормозное рентгеновское излучение имеет сплошной спектр с минимальной длиной волны min
Еkin
mv 2
hc
hc
eU h max
, min
2
min
eU
U – ускоряющее напряжение на рентгеновской трубке
4
5. Характеристическое рентгеновское излучение
Закон Мозли для Ka-линий3
2
a R Z ,
4
hc 3
2
a h a
E0 Z ,
a 4
h a E2 E1 E0
En E0
Z
Z
22
2
2
Z
E0
,
2
1
2
, n 1(K),2(L).
n2
R постоянная Ридберга,
Е0=13.6 эВ
5
6. Фотоэффект на атоме (фотоионизация)
При атомном фотоэффекте фотон поглощается атомом, после чего атом испускает электрон содной из своих оболочек.
Схематичное изображение
атомного фотоэффекта (б) и
определение эффективного
сечения фотоэффекта σ (а).
Схематичный график эффективного
сечения фотоэффекта в зависимости
от энергии g-кванта
Сечение σ определяется как отношение числа рассеянных (в других
процессах – поглощенных) в единицу времени квантов к плотности
потока квантов (числу квантов, проходящих в единицу времени
через единицу площади).
Схематичный график
массового коэффициента
поглощения для серебра и меди
в зависимости от длины волны
рентгеновского излучения
Вероятность внутреннего фотоэффекта максимальна при энергиях Еg порядка нескольких десятков кэВ
(в частности, для характеристического рентгеновского излучения), а с возрастанием энергии гамма-кванта
уменьшается приблизительно обратно пропорционально Еg .
6
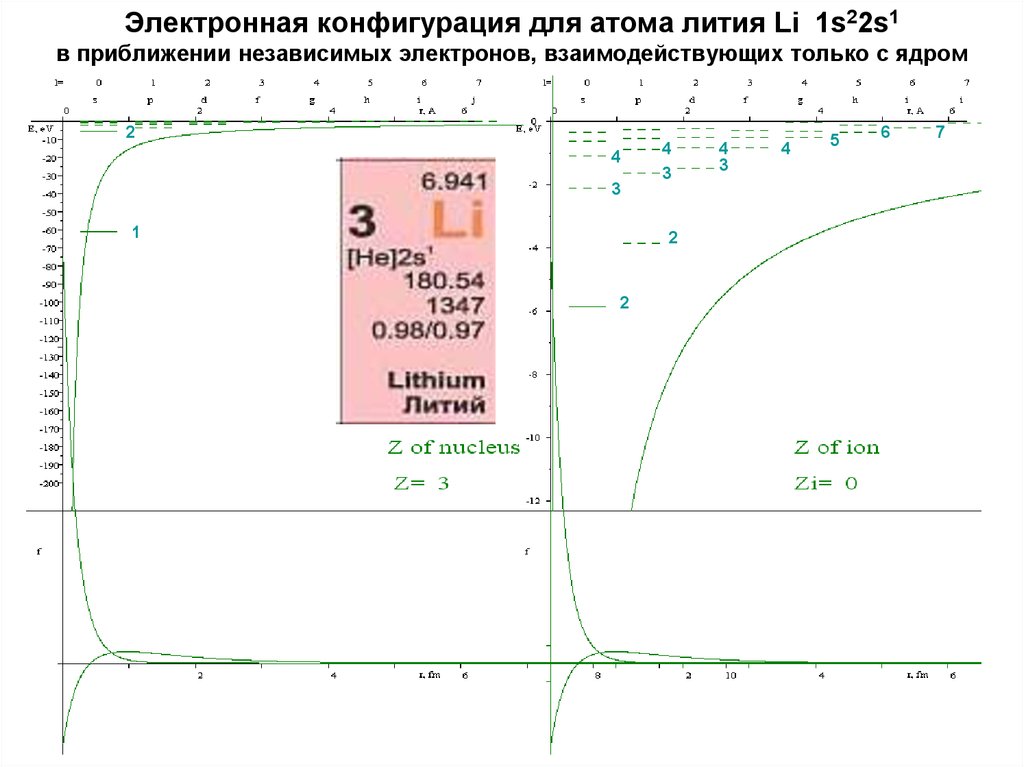
7. Электронная конфигурация для атомa лития Li 1s22s1 в приближении независимых электронов, взаимодействующих только с ядром
24
4
3
4
3
4
5
6
7
3
1
2
2
7
8. Приближение самосогласованного поля (ССП) − метод Хартри
Li+1s2
Na+ 1s22s22p6
K+ 1s22s22p63s23p6
8
См. файл атом_ССП.pdf
9. Приближение самосогласованного поля (ССП) − метод Хартри
9См. файл атом_ССП.pdf
10. Электронная конфигурация в приближении ССП для атома неона Ne 1s22s22p6
25
5
4
4
3
4
5
7
6
4
2
3
3
10
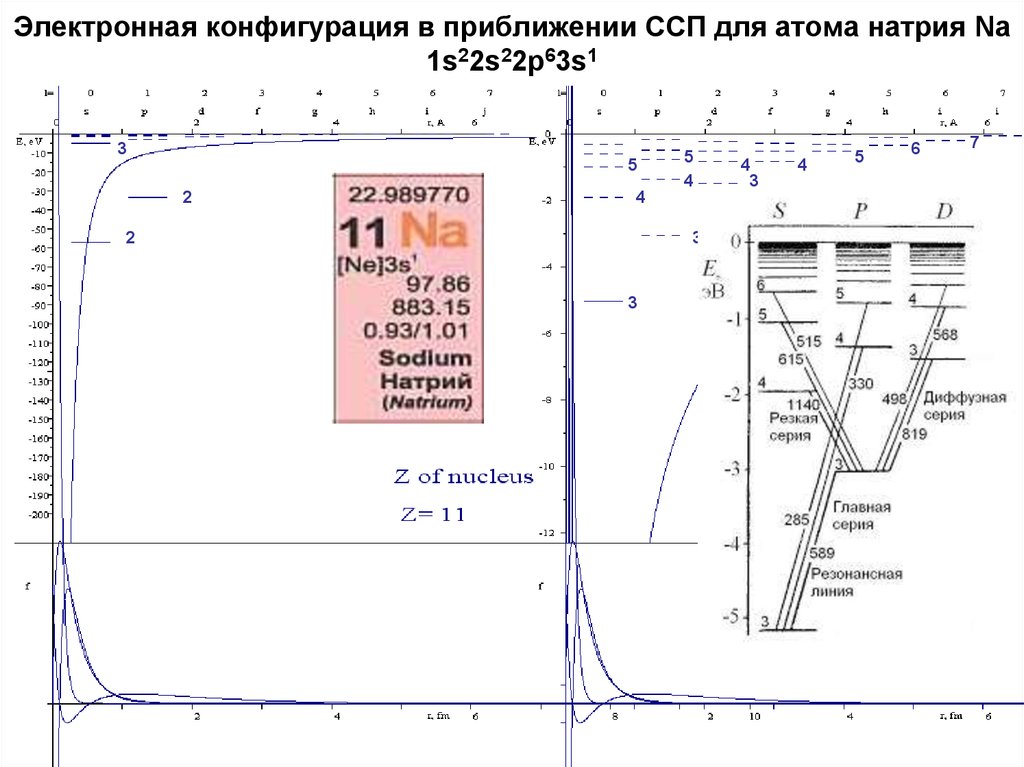
11. Электронная конфигурация в приближении ССП для атома натрия Na 1s22s22p63s1
35
2
5
4
4
3
4
5
7
6
4
2
3
3
11
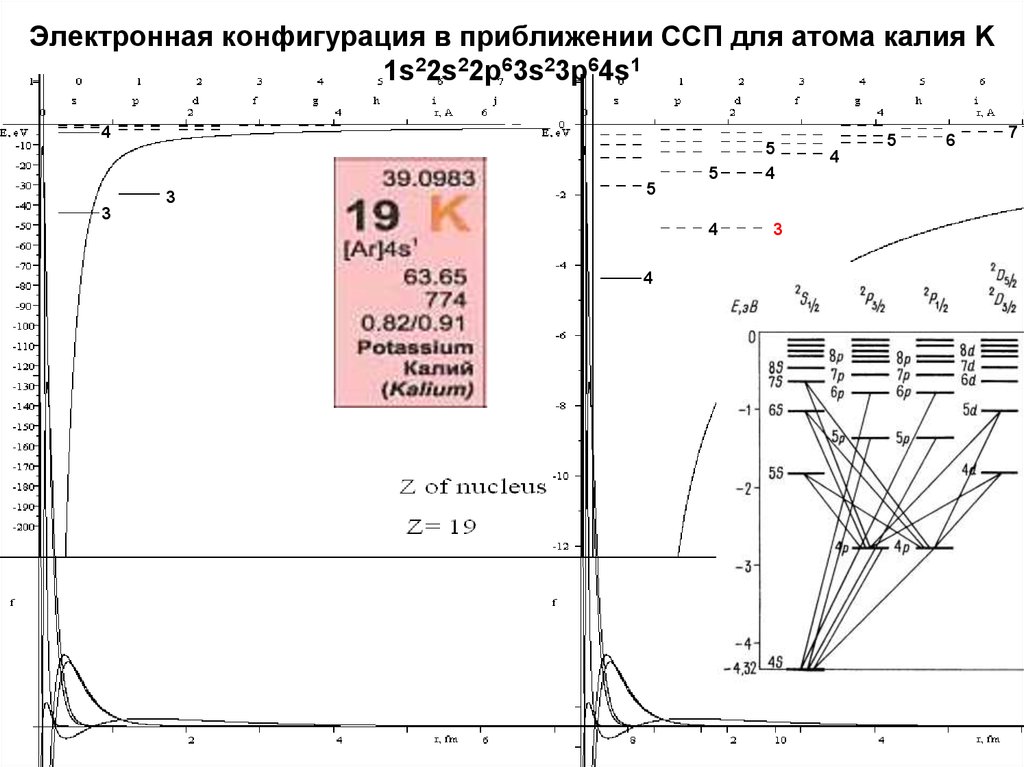
12. Электронная конфигурация в приближении ССП для атома калия K 1s22s22p63s23p64s1
45
3
5
4
5
6
4
5
3
4
3
4
12
7
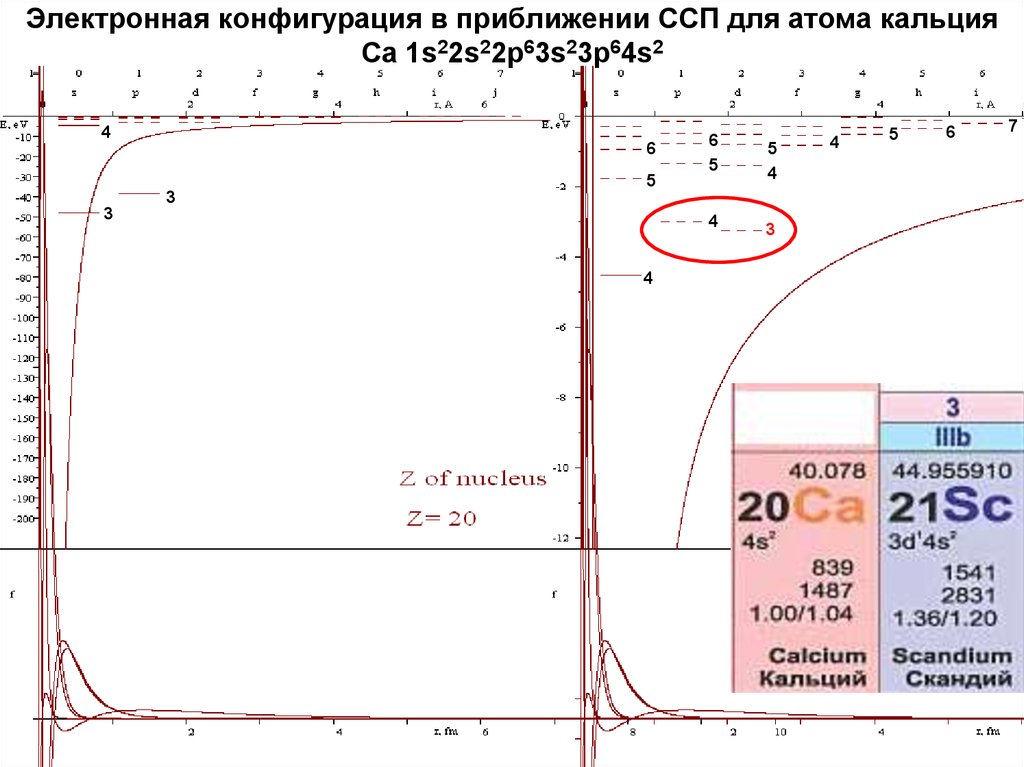
13. Электронная конфигурация в приближении ССП для атома кальция Ca 1s22s22p63s23p64s2
46
6
5
5
4
4
3
5
4
5
6
3
3
4
13
7
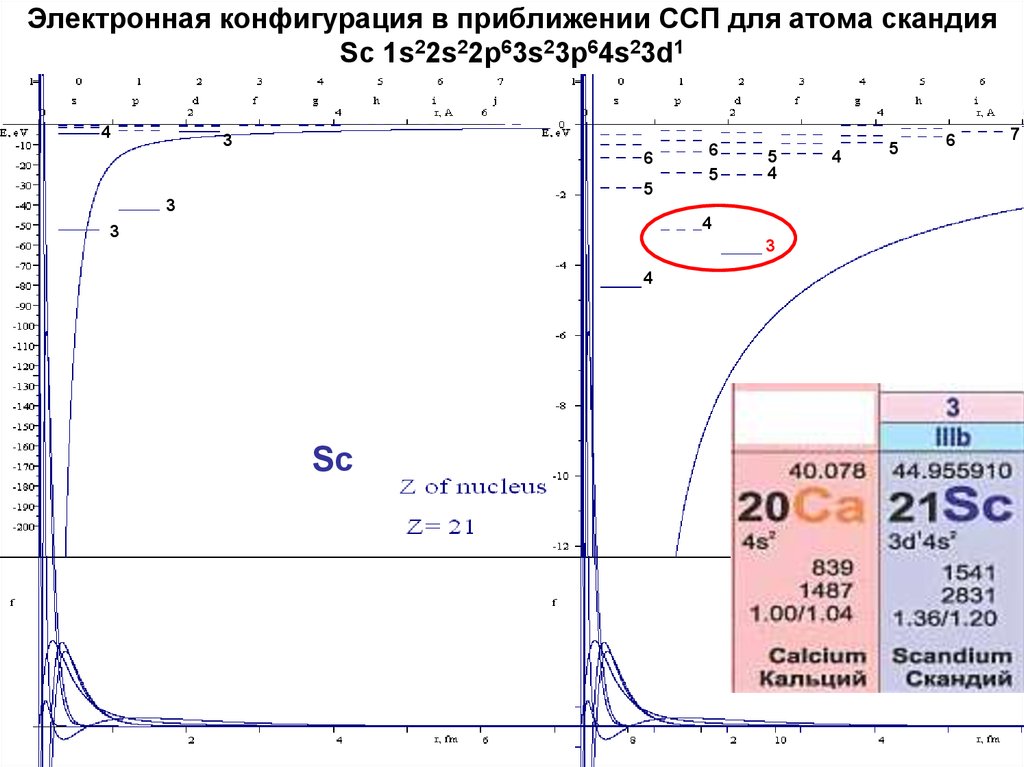
14. Электронная конфигурация в приближении ССП для атома скандия Sc 1s22s22p63s23p64s23d1
43
6
5
6
5
5
4
4
5
6
3
4
3
3
4
Sc
14
7
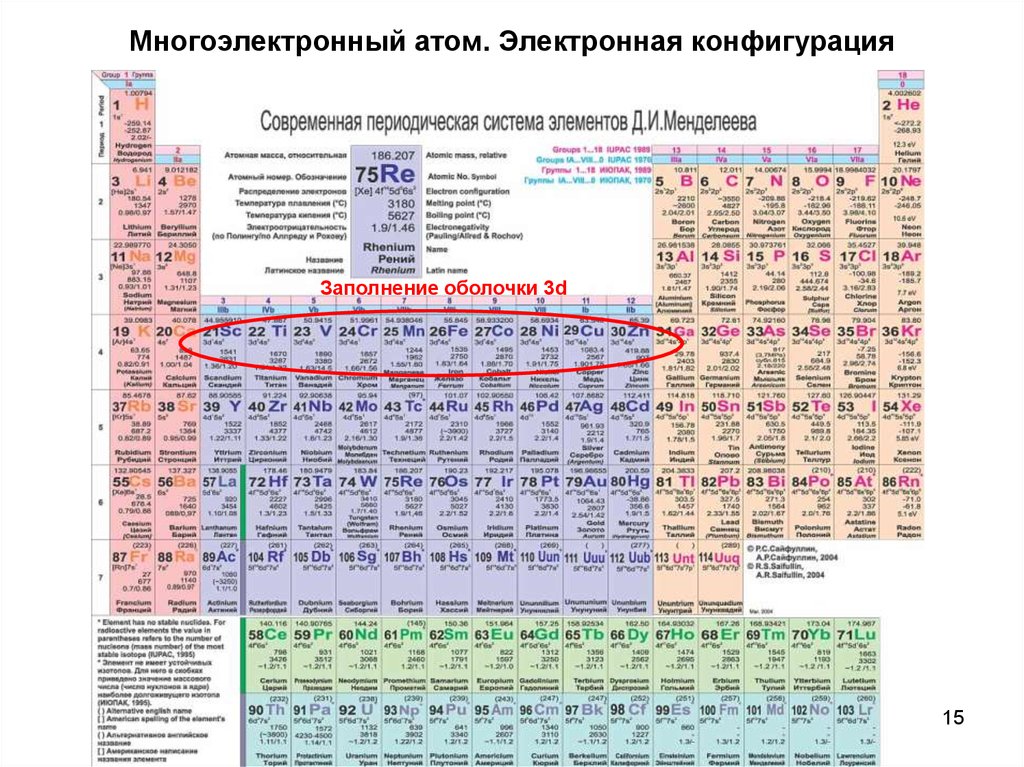
15. Многоэлектронный атом. Электронная конфигурация
Заполнение оболочки 3d15
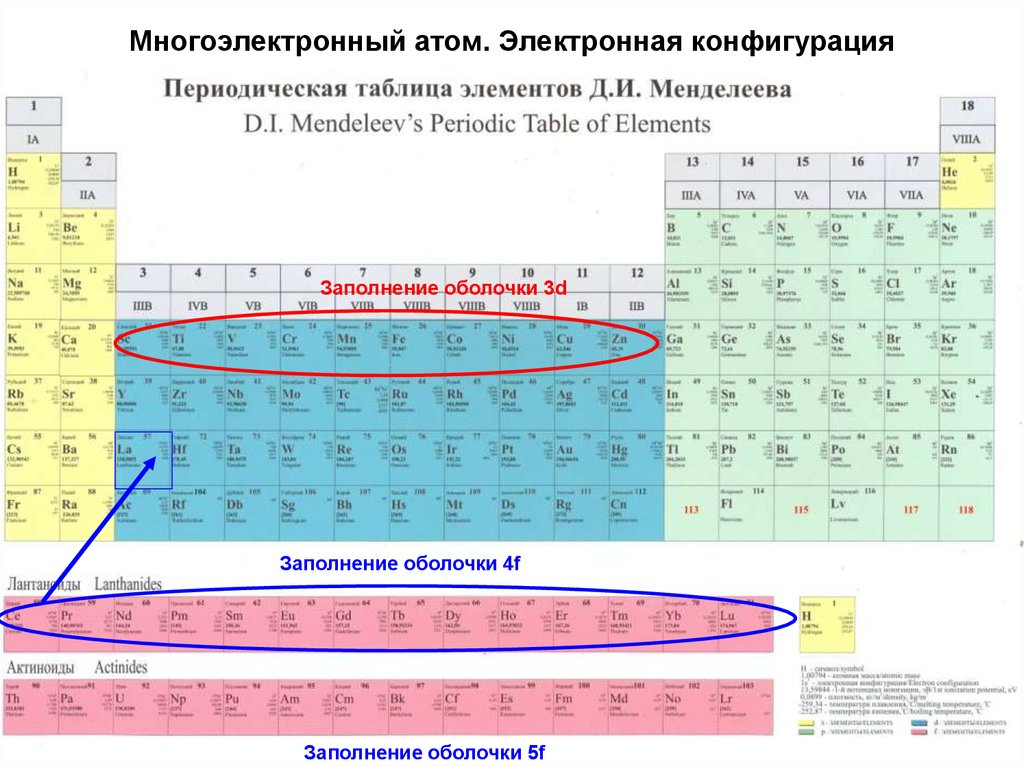
16. Многоэлектронный атом. Электронная конфигурация
Заполнение оболочки 3dЗаполнение оболочки 4f
16
Заполнение оболочки 5f
17. Обменное взаимодействие
Обменное взаимодействие учитывается впроцедуре ССП метода
Хартри-Фока и по
теории возмущений.
Простейший пример:
атом гелия с двумя электронами.
Основное состояние с
симметричной координатной волновой функцией:
терм 1S, конфигурация 1s2.
Возбужденные состояния
с конфигурацией 1s2s:
терм 3S с меньшей энергией
(ортогелий) с
антисимметричной волновой
функцией, спином S=1,
мультиплетностью 2S+1=3, L=0.
Tерм 1S с большей
энергией (парагелий) с
симметричной волновой
функцией, спином S=0,
мультиплетностью 2S+1=1, L=0.
Первое эмпирическое
правило Хунда:
Из термов, принадлежащих
данной электронной
конфигурации, наименьшей
энергией обладает терм с
наибольшим возможным
значением S и с наибольшим
возможным при таком S
значении L.
Для такого терма электроны в
среднем дальше друг 17
от друга
и энергия их отталкивания
меньше.
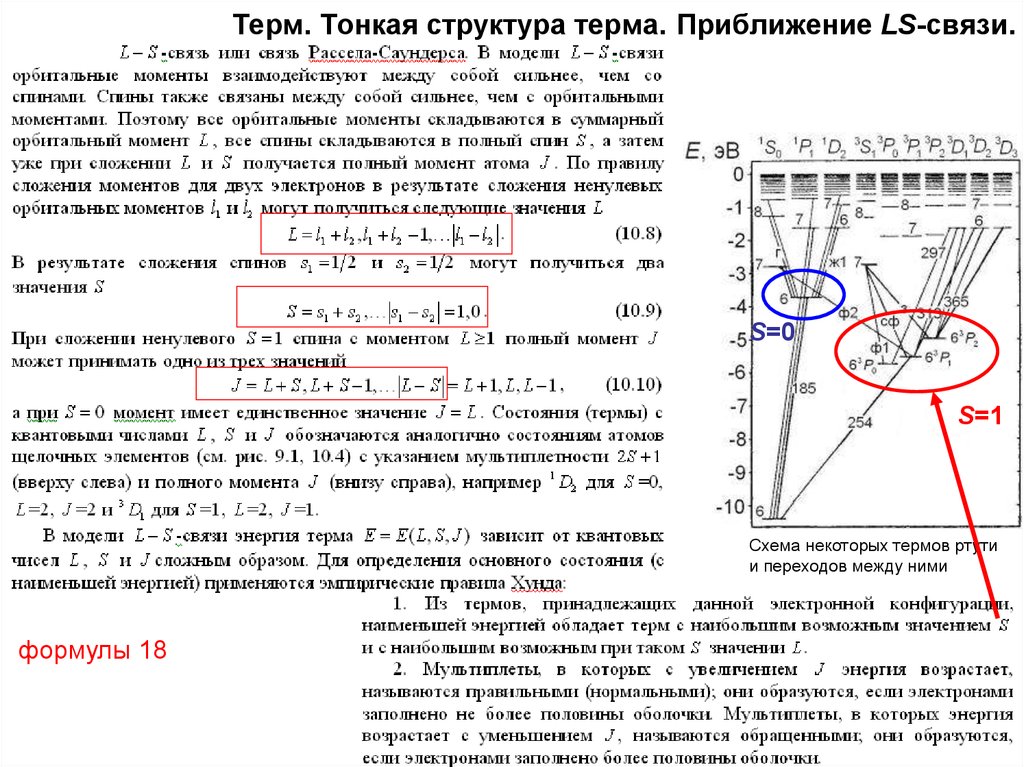
18. Терм. Тонкая структура терма. Приближение LS-связи.
S=0S=1
Схема некоторых термов ртути
и переходов между ними
формулы 18
18
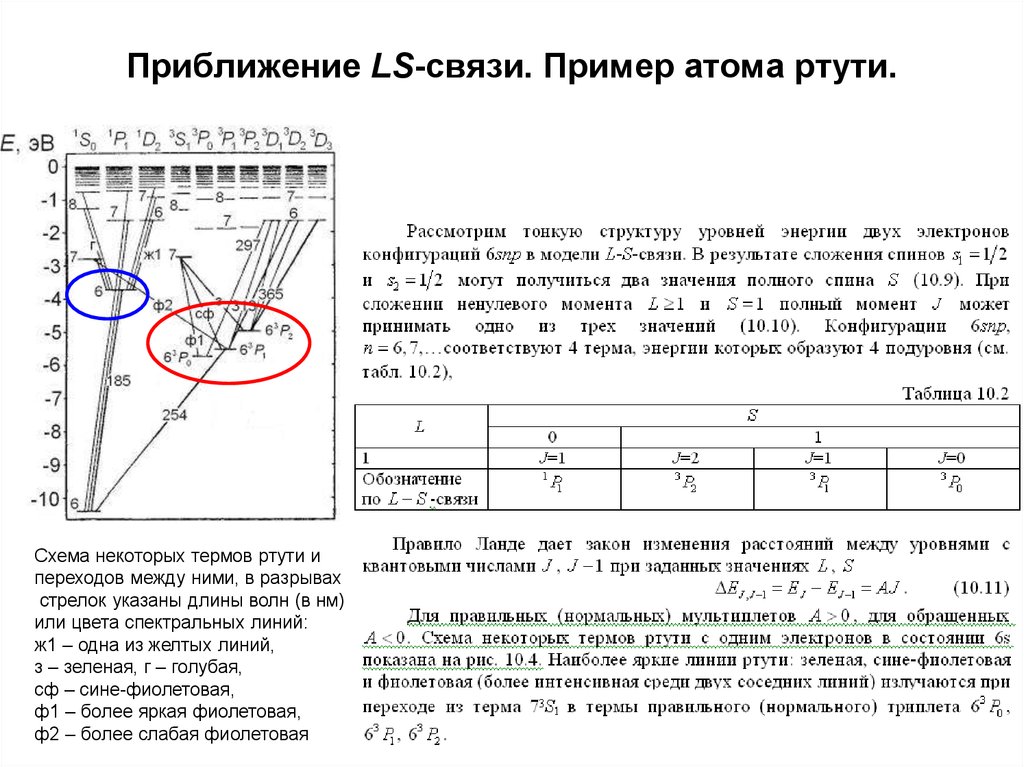
19. Приближение LS-связи. Пример атома ртути.
Схема некоторых термов ртути ипереходов между ними, в разрывах
стрелок указаны длины волн (в нм)
или цвета спектральных линий:
ж1 – одна из желтых линий,
з – зеленая, г – голубая,
сф – сине-фиолетовая,
ф1 – более яркая фиолетовая,
ф2 – более слабая фиолетовая
19
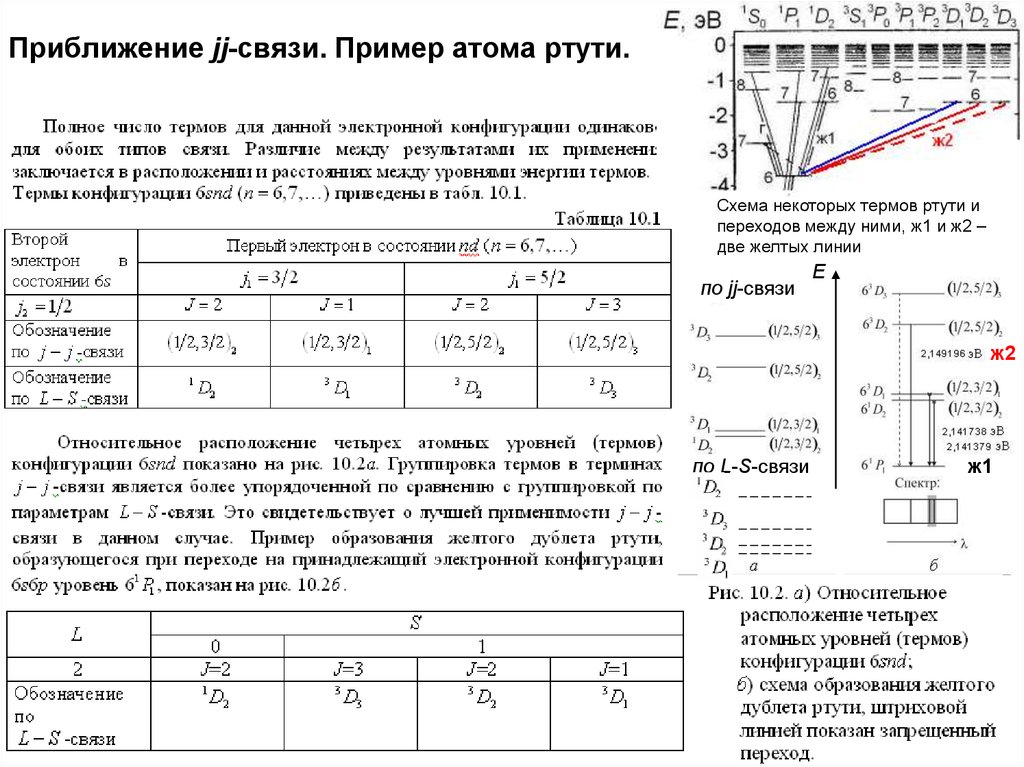
20. Приближение jj-связи.
2021. Приближение jj-связи. Пример атома ртути.
Схема некоторых термов ртути ипереходов между ними, ж1 и ж2 –
две желтых линии
по jj-связи
E
ж2
по L-S-связи
ж1
21
22. Вопрос 13.
• Нестационарная теория возмущений.• Золотое правило Ферми.
22
23. Нестационарная теория возмущений и переходы в дискретном спектре
При зависящем от времени возмущении приближенное вычисление волновой функции(t) выполняют c помощью разложения по волновым функциям стационарных состояний
невозмущенной системы
i
(0) ˆ (0)
i (0)
(0) (0)
(0)
(0)
Hˆ 0 Vˆ , Hˆ 0 (0)
E
,
i
H
,
(
t
)
exp
0 k
Ek t ,
k
k
k
k
k
k
t
t
Для j-го невозмущенного состояния, в котором система находилась при t – ,
(0)
(1)
(0)
ak (t ) (0)
k j ak (t ) k ,
k j
k
коэффициенты разложения в первом приближении равны
t
i
(0)
(1)
(1)
(1)
ak (t ) ak (t ) ak (t ) jk ak (t ), ak (t ) Vkj (t ) exp i mk t dt ,
mk
1
E
(0)
m
ˆ (0)
Ek(0) , Vmk (0)*
m V k dq
формулы 17
По истечении времени действия возмущения (или в пределе t ) коэффициенты akj
принимают постоянные значения akj( ), их квадраты модулей определяют вероятность
оказаться в k-м стационарном состоянии с энергией Ek(0)
Вероятность перехода из начального состояния i в конечное состояние f
Wi f
1
2
V f i (t ) exp i f it dt
2
В пределе, при достаточно медленном (адиабатическом)
изменении возмущения, модуль интеграла из-за быстроосциллирующего знакопеременного множителя (экспоненты)
очень мал, вероятность перехода стремится к нулю и 23
система остается в первоначальном состоянии.
24. Вывод формул нестационарной теории возмущений
При зависящем от времени возмущении приближенное вычисление волновой функции (t)выполняют c помощью разложения по волновым функциям стационарных состояний
невозмущенной системы
i
(0) ˆ (0)
1 (0)
(0) (0)
(0 )
(0)
Hˆ 0 Vˆ , Hˆ 0 (0)
E
,
i
H
,
(
t
)
exp
0 k
i Ek t ,
k
k
k
k
k
t
t k
ak (t ) (0)
k ,
k
i
(0)
k
k
i
(0) dak
ˆ ( 0)
ˆ (0)
i
k dt ak (t ) i t (0)
k ak (t ) H 0 k ak (t )V k ,
k
k
dak
ak (t )Vˆ (0)
k ,
dt
k
dam
1 (0)
ˆ (0)
ˆ (0)
Vmk (t )ak , Vmk (t ) (0)*
Em Ek(0) , Vmk (0)*
m V k dq Vmk exp i mk t , mk
m V k dq
dt
k
(0)
(0)
(1)
(0)
Для j-го невозмущенного состояния ak (t ) k j ak (t ) k ,
k
k j
коэффициенты разложения в первом приближении равны
ak
ak(0)
ak(1)
jk ak(1) ,
dak(1)
i
i
i
Vkn (t )an(0) Vkj (t ), ak(1) Vkj (t )dt Vkj exp i mk t dt
dt
n
24
25. Нестационарная теория возмущений и переходы в непрерывном спектре под действием постоянного возмущения
Волновая функция системы разлагается по невозмущенным волновым функциям дискретного спектра,нормированным на единицу, и по функциям непрерывного спектра, нормированным на -функцию,
k
(0)*
(0)*
(0)
(q) (0)
k ( q ) dq k k , ( q ) ( q ) dq ,
(0)
ak (t ) (0)
k a (t ) d
k
при действии постоянного (не зависящего от времени) возмущения V
коэффициенты разложения в первом приближении равны
t
1 exp i f i t
i
1
(1)
(0)
ˆ (0)
a f (t ) V f i exp i f i t dt V f i
, fi E (0)
, V f i (0)*
f Ei
f V i dq,
f i
0
2
a (1)
f (t )
2
Vf i t
sin 2 f i t 2
2
t f i 2
2
1
2
2
V f i f i 2 t
2
2
(0)
V f i E (0)
t , t .
f Ei
Вероятность перехода в единицу времени (скорость перехода) из начального невозмущенного состояния i
в конечное состояние f, в котором величины имеют значения в интервале d f под действием
постоянного (не зависящего от времени) возмущения V:
dw Pf i
2
2
(0)
V f i E (0)
d f Эта вероятность отлична от нуля лишь для переходов в состояния
f Ei
с энергией Ef = Ei в согласии с законом сохранения энергии.
Дельта-функция устраняется при интегрировании по конечному интервалу
состояний. Для невырожденных состояний непрерывного спектра d f = dEf
w Pf i dE f
.
2
Vf i
Для плотности состояний r(Ef) (числа конечных состояний данного типа, приходящихся на единичный
интервал энергий Ef) d f = r(Ef) dEf:
w Pf i Pf i r( E f )dE f
2
2
V f i r( E f )
Эту формулу Ферми назвал золотым правилом из-за
25
ее исключительной важности и пользы.
формулы 17
2
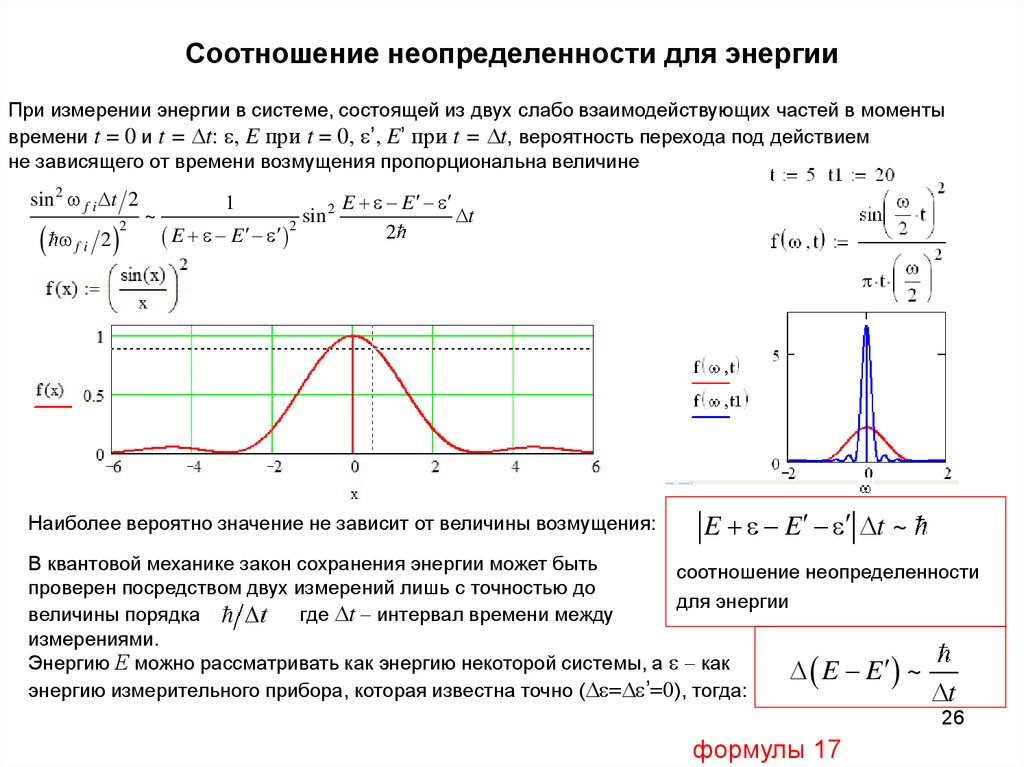
26. Соотношение неопределенности для энергии
При измерении энергии в системе, состоящей из двух слабо взаимодействующих частей в моментывремени t = 0 и t = t: , E при t = 0, ’, E’ при t = t, вероятность перехода под действием
не зависящего от времени возмущения пропорциональна величине
sin 2 f i t 2
f i 2
2
~
1
E E
sin 2
2
E E
t
2
Наиболее вероятно значение не зависит от величины возмущения:
E E t ~
В квантовой механике закон сохранения энергии может быть
соотношение неопределенности
проверен посредством двух измерений лишь с точностью до
для энергии
величины порядка
где t интервал времени между
измерениями.
Энергию Е можно рассматривать как энергию некоторой системы, а как
E E ~
энергию измерительного прибора, которая известна точно ( ’ 0), тогда:
t
26
формулы 17
27. Нестационарная теория возмущений и переходы в непрерывном спектре под действием периодического возмущения
Волновая функция системы разлагается по невозмущенным волновым функциям дискретного спектра,нормированным на единицу, и по функциям непрерывного спектра, нормированным на -функцию,
k
(0)*
(0)*
(0)
(q) (0)
k ( q ) dq k k , ( q ) ( q ) dq ,
(0)
ak (t ) (0)
k a (t ) d ,
Vˆ (t ) Uˆ exp i t
k
при действии периодически зависящего от времени между моментами включения и
выключения возмущения V коэффициенты разложения в первом приближении равны
t
1 exp i ( f i )t
i ( )
(1)
ˆ ( ) (0) dq,
a f (t ) U f i exp i ( f i )t dt U (f i)
, U (f i) (0)*
i
f U
( f i )
0
2
a (1)
(
t
)
f
2
U (f i)
sin 2 ( f i )t 2
2
( f i ) 2
2
2
2
(0)
U (f i) E (0)
f Ei t , t .
Вероятность перехода в единицу времени (скорость перехода) из начального невозмущенного состояния i
в конечное состояние f, в котором величины имеют значения в интервале d f под действием
постоянного (не зависящего от времени) возмущения V
dw
2
2
(0)
V f i E (0)
f Ei d f
Эта вероятность отлична от нуля лишь для переходов в состояния с энергией Ef=Ei
в согласии с
законом сохранения энергии. При возмущении ~exp(i t) система теряет энергию (например, испускает
фотон), а при возмущении ~exp(–i t) увеличивает энергию (например, поглощает фотон).
27
28. Квазистационарные состояния
Энергия способной к распаду системы может быть определена лишь с точностью до величиныпорядка
, где t = t продолжительность жизни этого состояния системы, т.е. величина,
обратная вероятности w распада в единицу времени
t 1 w
Если Е0 начальная энергия системы, Е и энергии частей, на которые распалась система, то
E0 E ~
t
Энергия способной к распаду системы может быть определена лишь с точностью до величины порядка
t . Система, способная к распаду, не обладает строго дискретным спектром энергий, поскольку
частица, уходящая на бесконечность имеет непрерывный спектр энергий (ее движение инфинитно).
Если вероятность распада мала, например в случае потенциального барьера с малой проницаемостью,
то состояние системы называется квазистационарным с квазидискретным спектром из ряда размытых
уровней, ширины G, которых определяются их продолжительностью жизни и малы по сравнению с
расстояниями между уровнями
G=
t
w
28
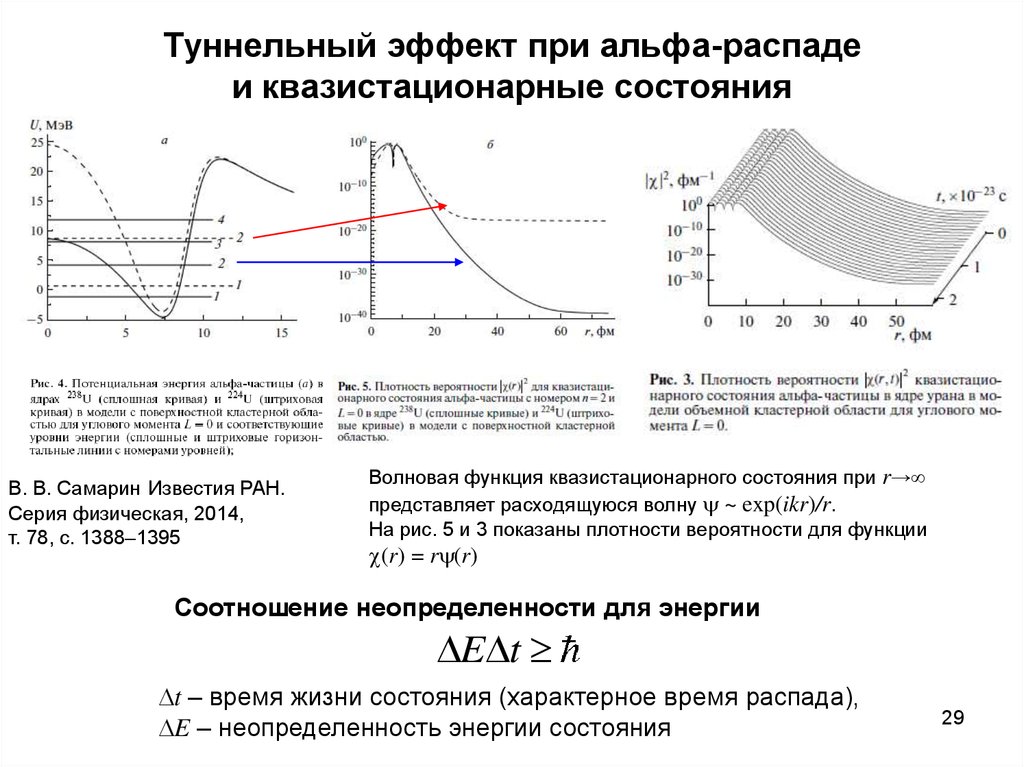
29. Туннельный эффект при альфа-распаде и квазистационарные состояния
В. В. Самарин Известия РАН.Серия физическая, 2014,
т. 78, с. 1388–1395
Волновая функция квазистационарного состояния при r→
представляет расходящуюся волну ~ exp(ikr)/r.
На рис. 5 и 3 показаны плотности вероятности для функции
c(r) = r (r)
Соотношение неопределенности для энергии
E t
t – время жизни состояния (характерное время распада),
E – неопределенность энергии состояния
29
30. Вопрос 14.
Вторичное квантование свободного
электромагнитного поля.
Взаимодействие атома с
квантованным полем излучения.
30
31. Обобщенные координаты и функция Гамильтона для свободного электромагнитного поля
Свободное электромагнитное поле описывают векторным потенциалом A в калибровке, в которойскалярный потенциал равен нулю. Поле в большом объеме пространства (например, кубе = L3)
можно разложить на бегущие плоские волны (в системе единиц, где скорость света равна 1)
A
k
2
ck exp ikr c*k exp ikr , ck k 0, ck ~ exp i t , k
L
Суммирование производится по дискретному набору значений компонент волнового вектора,
таких, что exp(ikxL)=1, exp(ikyL)=1, exp(ikzL)=1 и один вектор приходится на объем ( k)3
в пространстве волновых векторов
3
3
k x nx k , k y n y k , k z nz k , nx , n y , nz 0, 1, 2,
k
dk x dk y dk z
k
3
, k
2 2 ,
2
3
, k 3
L
L
dk x dk y dk z
2
3
Канонические переменные поля (обобщенные координаты Q и обобщенные импульсы P ) и функция
Гамильтона (энергия поля) даются формулами:
Qk
1
i
1
1
ck c*k , Pk Qk
ck c*k , H Pk2 2Qk2 Pk2 2Qk2
2 k
2 k
2
2
где = 1,2 компоненты векторов в плоскости, перпендикулярной волновому вектору (2 поляризации).
Функция Гамильтона распадается на сумму независимых членов, каждый из которых соответствует
бегущей волне с определенным волновым вектором и поляризацией и имеет вид функции
Гамильтона одномерного гармонического осциллятора. Для перехода к квантовому описанию
31
канонические переменные заменяются на операторы.
32. Квантование свободного электромагнитного поля
Гамильтониан поля получается заменой канонических переменных (обобщенных координат Q иобобщенных импульсов P ) соответствующими операторами. Собственные значения гамильтониана
находятся аналогично энергиям линейных осцилляторов (в системе единиц, где скорость света и
постоянная Планка равны 1) .
1
1
Hˆ Hˆ k , Hˆ k Pˆk2 2Qˆ k2 , E N k
2
2
k
k
Линейные комбинации операторов обобщенных координат Q и обобщенных импульсов P,
соответствующие коэффициентам с в разложении векторного потенциала А имеют более глубокий смысл
1
1
cˆk
Qˆ k iPˆk , cˆk
Qˆ k iPˆk , cˆk cˆk cˆk cˆk 1,
2
2
N k 1| cˆk | N k N k | cˆk | N k 1 N k
ˆ
A
k
единственные отличные от нуля матричные элементы
2
cˆ k e ( ) exp ikr cˆ +k e ( )* exp ikr .
е( ) – единичные вектора поляризации осцилляторов
В этом шредингеровском представлении операторы не содержат явной зависимости от времени,
временнáя эволюция системы описывается временнóй эволюцией волновой функции. В гейзенберговском
представлении явная зависимость от времени перенесена с волновой функции на операторы.
В релятивистской квантовой теории равноправная зависимость операторов от координаты и времени
позволяет более явно выявить релятивистскую пространственно-временную инвариантность теории.
В гейзенберговском представлении для операторов А в каждом члене суммы добавляется множитель
exp(–i t) (или ему сопряженный), соответствующий временнóй зависимости “стационарных состояний
осцилляторов поля”
ˆ
A r, t cˆ k Ak + cˆ +k A*k , A k = e ( )
k
2
exp i t kr
32
33. Линейный квантовый гармонический осциллятор (матричный метод)
ivˆ
m
1
ˆ ˆ U
Hvˆ ˆ vH
m
33
34. Описание эволюции квантово-механических систем. Уравнения Гейзенберга и Шредингера.
Изменение со временем волновой функции в представлении Шредингераi
ˆ
i ˆ
1 ˆˆ 2
H , (t ) 1
Ht
HHt
2
t
1!
2!
i ˆ
(0) exp Ht (t 0).
Изменение со временем плотности вероятности в представлении Шредингера
*
1
1
*
*
* Hˆ Hˆ * ,
t
t
t
i
i
i ˆ
(0)
exp
H
Ht (t )
Волновая функция в представлении Гейзенберга (Н) не зависит от времени
Операторы в представлении Гейзенберга зависят от времени t: fˆ exp i Ht
ˆ fˆ exp i Ht
ˆ , Hˆ Hˆ
H
H
Средние значения физических величин в представлениях Шредингера
и Гейзенберга (Н)
f * (t ) fˆ (t )dq
*
ˆ
i ˆ
i ˆ
i ˆ ˆ
i ˆ
*
* ˆ
f exp Ht
(0)
f
exp
Ht
(0)
dq
exp
Ht
f
exp
H
Ht H dq H f H H dq
Изменение со временем средних значений физических величин в представлениях Шредингера и
Гейзенберга (Н)
fˆH i
*
* ˆ
* d ˆ
*
ˆ
ˆ
ˆ
ˆ
ˆ
f (t ) f (t )dq H f H H dq H
f H H dq H
Hf H f H H H dq
t
t
t
t
dt
Уравнения для операторов в представлении Гейзенберга
fˆH i ˆ ˆ
d ˆ
fH
Hf H fˆH Hˆ
dt
t
34
35. Вторичное квантование свободного электромагнитного поля
Энергию E электромагнитного поля можно записать вычеркнув энергию нулевых колебаний(слагаемое ½), вместе с импульсом поля P они даются формулами (в обычных единицах).
E N k , P N k k
k
k
Эти формулы служат обоснованием понятия о фотонах. Свободное электромагнитное поле можно
рассматривать как совокупность частиц, каждая из которых имеет энергию
и импульс
Соотношение между импульсом и энергией – такое же как в релятивистской механике для частиц с
нулевой массой покоя, движущихся со скоростью света. Числа Nk имеют смысл чисел фотонов с
заданными импульсами и поляризациями. Свойство поляризации фотона аналогично понятию спина у
других частиц. В методе вторичного квантования роль независимых переменных играют числа
заполнения (в данном случае – числа Nk ), а операторы действуют на функции этих чисел. При этом
основную роль играют операторы “уничтожения” (с) и “рождения” (с+) фотонов, соответственно
уменьшающие и увеличивающие на единицу числа заполнения.
.
N k 1| cˆk | N k N k | cˆk | N k 1 N k , cˆk cˆk cˆk cˆk 1,
ˆ
A r, t cˆ k A k + cˆ k+ A*k , A k = e ( )
k
правила коммутации для бозонов
2
exp i t kr
Плоские волны коэффициенты перед операторами уничтожения фотонов можно трактовать как
волновые функции фотонов с определенными импульсами и поляризациями, нормированные на
“один фотон в объеме ”. Но волновую функцию фотона нельзя рассматривать как амплитуду его
пространственной локализации. О координатах фотона имеет смысл говорить, когда характеристические
размеры задачи велики по сравнению с длиной волны (“классический” предельный случай геометрической
оптики). В квантовом случае, когда длна волны не может рассматриваться как малая, понятие
35
координат фотона становится беспредметным.
36. Момент и четность фотона
Поскольку роль волновой функции играет вектор А (с тремя компонентами, при поворотах системыкоординат, преобразующиеся по определенному закону) фотону можно приписать спин s = 1 (2s+1=3).
Полный момент фотона складывается из спина (собственного момента) фотона и орбитального момента,
связанного с координатной зависимостью волновых функций. Состояниям с орбитальным моментом l
соответствуют волновые функции, выражающиеся через сферические гармоники порядка l.
Полный момент может пробегать лишь целочисленные значения: 1, 2, 3,…
Состояние фотона может характеризоваться также его четностью, связанной с поведением волновой
функции при инверсии системы координат. Состояние называют четным, если векторная волновая
функция А(r) не меняет знак при инверсии, и нечетным, если она меняет знак. Принята определенная
терминология для различных состояний фотона с определенными моментами и четностями:
фотон в состоянии с моментом j и четностью ( 1)j называется электрическим 2j –польным
(или Ej-фотоном), а при четности ( 1)j+1 магнитным 2j –польным (или Мj-фотоном),
Фотон с определенным направлением волнового вектора может иметь определенное значение проекции
момента на это направление спиральности. Спиральность совпадает с проекцией спина частицы на
направление ее движения. Для фотона возможны лишь значения ±1.
36
37. Оператор электромагнитного взаимодействия
iУравнение Дирака
1) для свободного
движения электрона:
capˆ mc 2 , i
ˆ , , 1 , c 3 ,
t
t
c
2
4
0
I
0
0 1
0 i
1 0
,
3
.
0
0
1
ˆ capˆ mc 2 , a
,
, 1
, 2
0
0
I
1
0
i
2) для электрона в
ˆ pˆ q A, ˆ capˆ mc 2 ˆ ca pˆ q A mc 2 capˆ mc 2 qaA,
p
электромагнитном поле с
c
c
калибровкой, в которой
оператор взаимодействия с заданным электромагнитным полем
Vˆ qaA
скалярный потенциал
оператор взаимодействия с изменяющимся электромагнитным
ˆ
F = 0:
Vˆ qaA
полем
ˆ
A r, t cˆ n An r, t + cˆ n+ A*n r, t
n
Здесь n – индекс состояния фотона. Для излучения или поглощения фотонов с определенными
волновыми векторами и поляризациями, то волновые функции A – плоские волны. Если излучаются
(поглощаются) фотоны с определенными значениями момента, то А – сферические волны.
Взаимодействие электронов с полем электромагнитного излучения может, как правило, рассматриваться
с помощью теории возмущений. Слабость электромагнитного взаимодействия выражается в малости
“константы связи” – постоянной тонкой структуры a = 1/137.
В первом приближении теории возмущений вероятности процессов определяются квадратом модуля
|Vij|2 матричного элемента оператора возмущения между начальным (i) и конечным (j) состояниями
системы зарядов и поля. Каждый из операторов “уничтожения” (с) и “рождения” (с+) фотонов имеет
отличные от нуля матричные элементы лишь для уменьшения или увеличения соответствующего числа
заполнения на 1. Поэтому и оператор A имеет матричные элементы лишь для переходов с однократным
37
поглощением или излучением фотона.
38. Оператор электромагнитного взаимодействия
Оператор взаимодействия сизменяющимся электромагнитным
полем
Матричные элементы
1) для испускания фотона
2) для поглощения фотона
ˆ
A r, t cˆ n An r, t + cˆ n+ A*n r, t
n
V f i (t ) q *f a i A*n dV , jf i (r ) *f a i
ток перехода
V f i (t ) q *f a i A n dV
Здесь i и f – волновые функции начального и конечного состояний излучателя (электрона). Один
электрон и может излучать лишь при движении во внешнем поле. Свободный, движущийся с
постоянной скоростью электрон не излучает.
Приведенные выше матричные элементы зависят от времени. Для перехода к независящим от времени
матричным элементам выделяют в волновых функциях множители, зависящие от времени.
V f i (t ) V f i exp i Ei E f t ,
2
dw 2 V f i Ei E f d ,
d dk x dk y dk z 2 d d
2
dw 2 V f i Ei E f
2 d d
1
+ для поглощения фотона, для испускания фотона
В первом приближении нестационарной теории возмущений
вероятность перехода i f с испусканием фотона.
Для фотонов с определенными значениями волнового вектора.
С учетом нормировки на 1 фотон в объеме .
Дельта-функция выражает закон сохранения энергии,
интегрирование по d устраняет ее и приводит к
2
выражению для вероятности испускания фотона в
2 *
dw 2 V f i 2 d , V f i q
e j f i (k ),
телесном угле d .
4
38
j f i (k ) j f i (r ) exp ikr dV ток перехода в импульсном представлении
2 3
39. Взаимодействие атома с квантованным полем излучения
Основные процессы:1. Спонтанное и вынужденное испускание фотона:
Соотношение между вероятностью испускания wrad и вероятностью поглощения wcup фотона
при переходах между заданной парой уровней излучающей системы (например, атома)
wrad Nn 1
wcap
Nn
2. Дипольное излучение: интенсивность излучения I определяется матричным элементом
2
2
4 4
4 4
I w 3 d f i , d qr , I n 3 d n , d(t ) d n exp in 0t
3c
3c
n
аналогично классической формуле для интенсивности излучения In c частотой = nw0 системой
частиц, движущихся периодически с частотой 0. Согласно принципу соответствия Бора компонентам
дипольного момента
Фурье классических величин отвечают квантовые матричные элементы в квазиклассическом случае,
(но для интенсивности дипольного излучения I и в общем квантовом случае).
Электрическое дипольное излучение фотона с моментом 1 и отрицательной четностью играет наиболее
важную роль в оптических спектрах атомов и для приводит к приближенным правилам отбора при
L-S-связи: Sf = Si, Lf = Li + 1, Li – 1,
3. Рассеяние света
4.
Рассеяние фотона атомом представляет собой поглощение начального фотона (с волновым вектором
k) с одновременным испусканием другого фотона k’. При этом атом может остаться либо на
начальном, либо на каком-то другом уровне энергии. В первом случае частота фотона не меняется,
такое рассеяние называют релеевским или несмещенным. Во втором частота фотона меняется на
величину ’ – = Ei – Ef, где Ei, Ef – начальная и конечная энергии атома (молекулы), такое рассеяние
называют комбинационным или смещенным.
G
d
dW i
Естественная ширина спектральных линий:
2 E E 2 G 2 4
i
f
i
Естественная форма спектральной линии – распределение
39
фотонов по частотам, G/
– вероятность (в 1с) всех возможных процессов “распада” данного состояния.
40. Спонтанное и вынужденное испускание фотона (подробности)
Матричный элемент оператора рождения фотонаМатричный элемент оператора электромагнитного
взаимодействия
1) для испускания фотона при условии, что в
начальном состоянии фотонов нет (Nn=0)
2) для испускания фотона при условии, что в
начальном состоянии уже имеется Nn фотонов
Матричный элемент оператора уничтожения фотона
Матричный элемент оператора электромагнитного
взаимодействия
1) для поглощения одного имеющегося фотона
2) для поглощения одного фотона из Nn имеющихся.
N n 1 | cn | N n N n 1
V f i (t ) q *f a i A*n dV
V f i (t ) q N n 1 *f a i A*n dV
вынужденное (индуцированное) излучение
N n 1 | cn | N n N n
V f i (t ) q *f a i A n dV
V f i (t ) q N n *f a i A n dV
Соотношение между вероятностью испускания wrad и вероятностью поглощения wcup фотона при
переходах между заданной парой уровней излучающей системы (например, атома)
wrad Nn 1
wcap
Nn
было впервые установлено в 1916 г.
Эйнштейном, предсказавшим
явление вынужденного испускания.
Оно лежит в основе принципа
действия лазера.
40
41. Дипольное излучение в заданном направлении (подробности)
dw2 2
2 *
вероятность испускания фотона в телесном угле d
V
d
,
V
q
e j f i (k ),
f
i
f
i
2
4
В случае длины волны фотона 2 /k много большей по сравнению с размерами излучающей системы а
exp ikr 1
Пример: длины волн видимого света от 400 до 700 нм, размер атома порядка 0.1 нм.
Импульсом фотона можно пренебречь по сравнению с импульсами частиц системы.
j f i v f i r f i i E f Ei r f i i d f i ,
q
Это приближение соответствует дипольному приближению
в классической теории излучения.
Замена матричного элемента тока перехода на нерелятивистское
выражение – матричный элемент оператора скорости по отношению
к шредингеровским (нерелятивистским) волновым функциям.
j f i (k ) j f i (r ) exp ikr dV j f i (r )dV j f i (0)
d qr
Дипольный момент электрона (в его орбитальном движении)
2
Вероятность дипольного излучения (вектор поляризации e должен
2 *
3 *
V f i q
e d f i , dw
e d f i d ,
быть перпендикулярен волновому вектору k.
2
2
Полная вероятность испускания получается интегрированием по всем направлениям
2
2
1
*
e df i df i
dfi
испускания фотона и суммированием по двум возможным независимым поляризациям.
x
3
Для линейной поляризации, интегрирование по d сводится к умножению на 4 , а
4 3
w
dfi
3
4 3
w
dfi
3 c3
2
2
2
4 4
I w 3 df i
3c
ˆ
ˆ
ˆ
Vˆ Ed, E A t
суммирование по поляризациям – к умножению на 2.
Полная вероятность испускания фотона в системе единиц, где с = 1,
1
Полная вероятность испускания фотона в обычной системе единиц.
Интенсивность излучения
Приближенный оператор взаимодействия и оператор напряженности электрического
поля для излучения любой нерелятивистской системой частиц.
41
42. Мультипольное излучение фотонов с определенным моментом (подробности)
Вследствие закона сохранения момента начальный момент излучающей системы Ji должен совпадать ссуммарным моментом конечной системы Jf и фотона j. Согласно квантовомеханическому правилу
сложения моментов
Jf = Ji + j, Ji + j – 1, …| Ji – 1|, j = 1, 2,…
Начальная четность системы Pi должна совпадать с общей четностью конечной системы Pf и фотона Pg:
Pi = Pf Pg. Поскольку все четности могут равняться только ±1, то PiPf = Pg.
При любом значении j испускание одиночного фотона при переходе системы между двумя состояниями с
J = 0 (переходы 0 0) запрещено правилом сложения моментов. При этом в более высоких приближениях
теории возмущений возможно с существенно меньшей вероятностью одновременное испускание двух
фотонов с антипараллельными моментами.
Дипольное приближение отвечает испусканию фотона в состоянии 1– (фотон Е1), при этом разрешены
переходы между состояниями с противоположными четностями и со следующими возможными
изменениями полного момента J:
Испускание фотона 1+ (фотон M1) называют
J J + 1, J, J – 1 при (J 1), 0 1, ½ 3/2, ½
магнитным дипольным излучением, фотона 2– –
электрическим квадрупольным излучением и т.д.
В оптических спектрах атомов электрическое дипольное излучение – Е1-переходы наиболее важны, их
вероятности (если они допускаются правилами отбора) значительно превосходят вероятности
мульпольных переходов более высоких рангов.
Приближенные правила отбора для состояний, построенных по типу L-S-связи (при слабом спинорбитальном взаимодействии, нарушающим раздельное сохранение орбитального момента и спина:
Sf = Si, Lf = Li + 1, Li, Li – 1. Зависимость координатной волновой функции частицы от углов в
центральном поле задается сферической функцией YLM, при инверсии она умножается на (–1)L. Поэтому
все состояния с четным L четны, а с нечетным L нечетны. При испускании фотона в состоянии 1–
из закона сохранения четности следуют правила отбора
Lf = Li + 1, Li – 1.
42
43. Четность состояний в центральном поле и правила отбора для дипольного излучения
формулы 1843
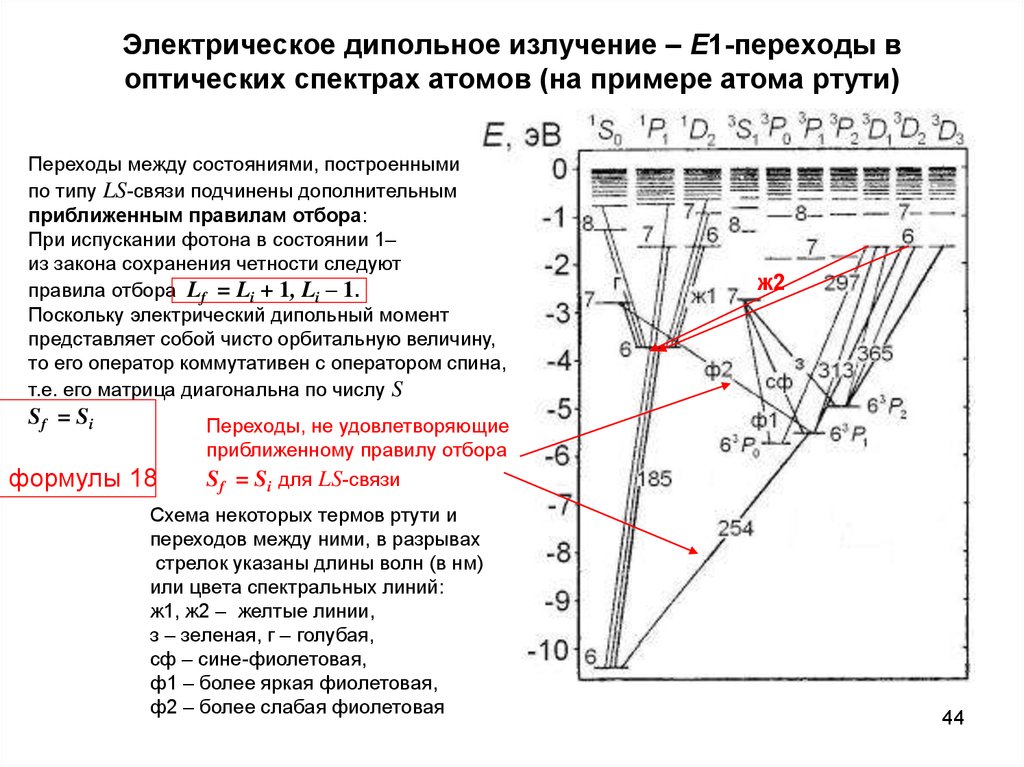
44. Электрическое дипольное излучение – Е1-переходы в оптических спектрах атомов (на примере атома ртути)
Переходы между состояниями, построеннымипо типу LS-связи подчинены дополнительным
приближенным правилам отбора:
При испускании фотона в состоянии 1–
из закона сохранения четности следуют
правила отбора Lf = Li + 1, Li – 1.
Поскольку электрический дипольный момент
представляет собой чисто орбитальную величину,
то его оператор коммутативен с оператором спина,
т.е. его матрица диагональна по числу S
Sf = Si
формулы 18
ж2
Переходы, не удовлетворяющие
приближенному правилу отбора
Sf = Si для LS-связи
Схема некоторых термов ртути и
переходов между ними, в разрывах
стрелок указаны длины волн (в нм)
или цвета спектральных линий:
ж1, ж2 – желтые линии,
з – зеленая, г – голубая,
сф – сине-фиолетовая,
ф1 – более яркая фиолетовая,
ф2 – более слабая фиолетовая
44
45. Рассеяние света
в системе единиц, где с = 1,1
Рассеяние фотона атомом (молекулой) представляет собой поглощение начального фотона (с волновым
вектором k) с одновременным испусканием другого фотона k’. При этом атом может остаться либо на
начальном, либо на каком-то другом уровне энергии. В первом случае частота фотона не меняется,
такое рассеяние называют релеевским или несмещенным. Во втором частота фотона меняется на
величину ’ – = Ei – Ef, где Ei, Ef – начальная и конечная энергии атома (молекулы), такое рассеяние
называют комбинационным или смещенным. Эффект рассеяния проявляется лишь во втором приближении
теории возмущений. Его рассматривают как происходящее через промежуточные состояния двух типов:
1) Фотон k поглощается, атом переходит с начального уровня Ei на один из других своих возможных
уровней En, при последующем переходе в конечное состояние испускается фотон k’.
2) Испускается фотон k’, атом переходит в состояние En, при переходе в конечное состояние поглощается
фотон k.
Такому описанию не следует придавать буквального смысла.
В первом порядке нестационарной теории возмущений матричный элемент Vfi и поправка к волновой
функции равны нулю.
V f kVk i 1 exp i f i t
k промежуточные состояния, далее обычные
Во втором порядке: (2)
a f i (t )
единицы
k
k
i
f
i
сечения матричный элемент V заменяется на сумму
В формулах первого порядка для
fi
V f kVk i
V f nVni
V f nVni
(1) (2) , i Ei , (1)n En , (2)
n En
ki
k
n i
n
i
n
Vni и Vfn матричные элементы переходов с поглощением, а V’ni и V’fn с испусканием фотона; из
суммирования по n исключается начальное состояние атома (молекулы).
Сечение рассеяния d и амплитуда рассеяния Afi равны:
d Af i
2
*
d f n e * d n i e
d
e
d
e
f
n
n
i
3
d , Af i
2 2
n f
c
n
ni
,
n i En Ei , n f En E f
45
46. Рассеяние света
Рассеяние фотона атомом (молекулой) представляет собой поглощение начального фотона (с волновымвектором k) с одновременным испусканием другого фотона k’. При этом атом может остаться либо на
начальном, либо на каком-то другом уровне энергии. В первом случае частота фотона не меняется,
такое рассеяние называют релеевским или несмещенным. Во втором частота фотона меняется на
величину ’ – = Ei – Ef, где Ei, Ef – начальная и конечная энергии атома (молекулы), такое рассеяние
называют комбинационным или смещенным.
Сечение рассеяния d и амплитуда рассеяния Afi равны:
d Af i
2
d f n e * d n i e
d f n e d n i e *
3
d , Af i
2 2
n i
n f
c
n
,
n i En Ei , n f En E f
Амплитуда рассеяния отлична от нуля только для переходов между состояниями одинаковой четности.
При 0 амплитуда рассеяния стремится к конечному пределу. Сечение несмещенного рассеяния
( ’ = ) при малых оказывается пропорциональным 4.
При рассмотрении рассеяния света совокупностью N одинаковых атомов в объеме, размеры которого
малы по сравнению с длиной волны, амплитуда рассеяния равна сумме амплитуд рассеяния на
каждом из атомов. Волновые функции атомов определены с точностью до фазовых множителей,
сечение рассеяния должно быть усреднено по ним независимо. Для смещенного рассеяния при
усреднении по фазам атомов останутся лишь квадраты модулей каждого слагаемого. Полное сечение
рассеяния N атомами получится умножением на N сечения рассеяния на отдельном атоме
складываются сечения рассеяния, а не его амплитуды. Такое рассеяние называют некогерентным.
Если начальное и конечное состояния атома совпадают, то амплитуда рассеяния будет отличаться от
амплитуды рассеяния на отдельном атоме множителем N, сечение рассеяния соответственно
множителем N2. Такое рассеяние называют когерентным.
46
47. Литература
1.2.
3.
4.
5.
6.
Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической
физики. Т. 2. Квантовая механика. − М. Наука. 1971.
Ландау Л.Д. Лифшиц Е.М. Курс теоретической физики. Т. 3.
Квантовая механика. Нерелятивистская теория − М. Наука.
1971.
Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Квантовая
электродинамика. Ландау Л.Д. Лифшиц Е.М. Курс
теоретической физики. Т. 4. − М. Наука. 1971.
Сивухин, Д. В. Общий курс физики. В 5 Т. Т 5: Атомная и
ядерная физика: учеб. пособие– М.: Физматлит, 2002
Робертсон, Б. Современная физика в прикладных науках / Б.
Робертсон. – М.: Мир, 1985. 272 с.
Хабердитцл, В. Строение материи и химическая связь. /В.
Хабердитцл. – М.: Мир, 1974. – 296 с.
47

































 physics
physics








