Similar presentations:
Физика конденсированного состояния. Движение электронов в атоме
1. Физика конденсированного состояния
Электронный учебно-методическийкомплекс
Физика конденсированного
состояния
Презентации к лекционному курсу
МОСКВА
2012
НИУ «МЭИ»
2. Движение электронов в атоме
Все окружающие нас тела состоят изэлементарных частиц (атомов) или из
групп определенным образом
объединенных атомов (молекул). Любая
молекула состоит из совокупности
электронов и атомных ядер, движение и
взаимное расположение которых
определяют значение внутренней энергии
молекулы
3.
Эрне́ст Ре́зерфорд(англ. Ernest Rutherford)
30.08.1871, Спринг Грув 19.10.1937, Кембридж) –
британский физик
новозеландского
происхождения.
Известен как «отец» ядерной
физики, создал планетарную
модель атома.
Лауреат Нобелевской премии
по химии 1908 года.
4.
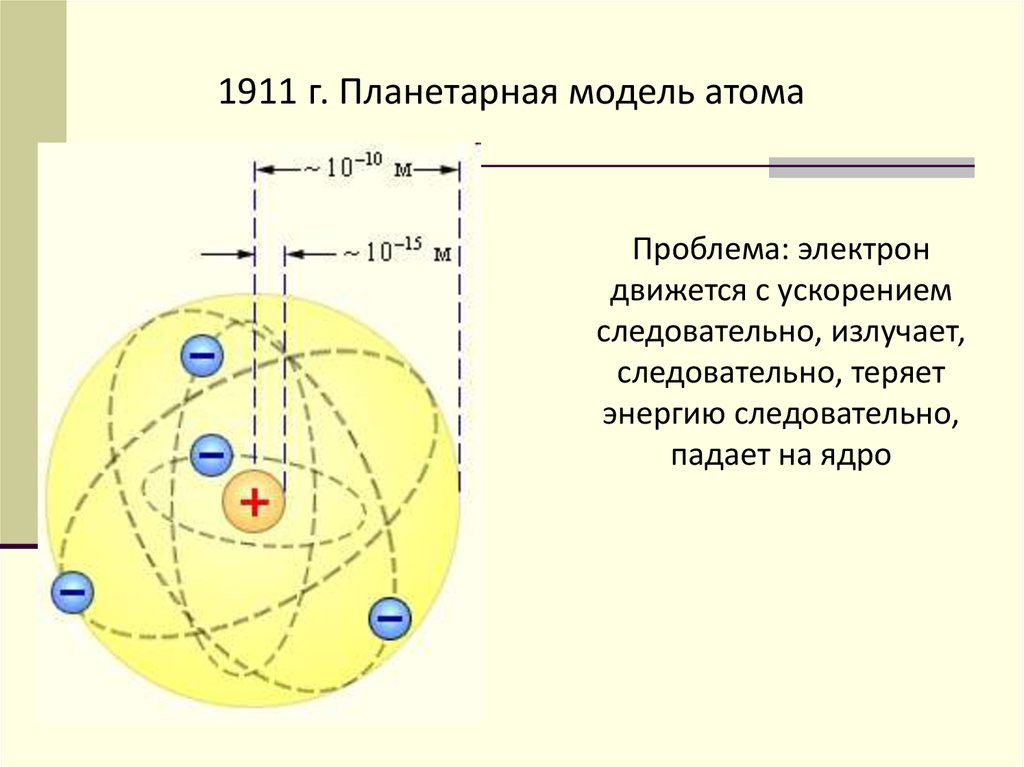
1911 г. Планетарная модель атомаПроблема: электрон
движется с ускорением
следовательно, излучает,
следовательно, теряет
энергию следовательно,
падает на ядро
5.
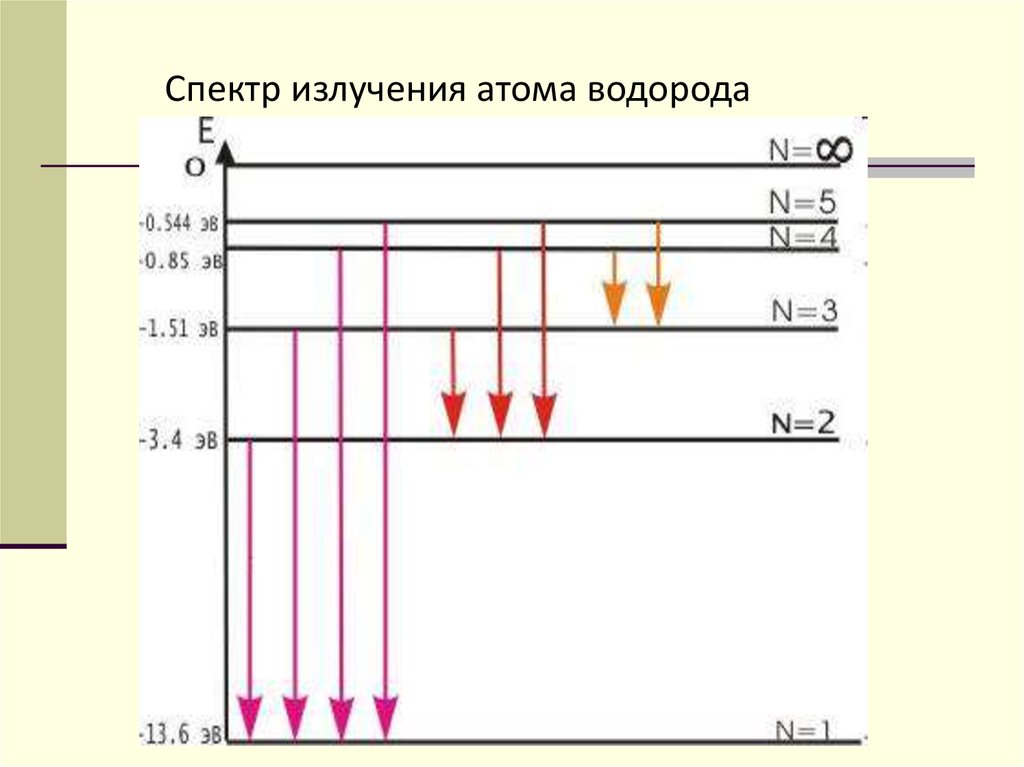
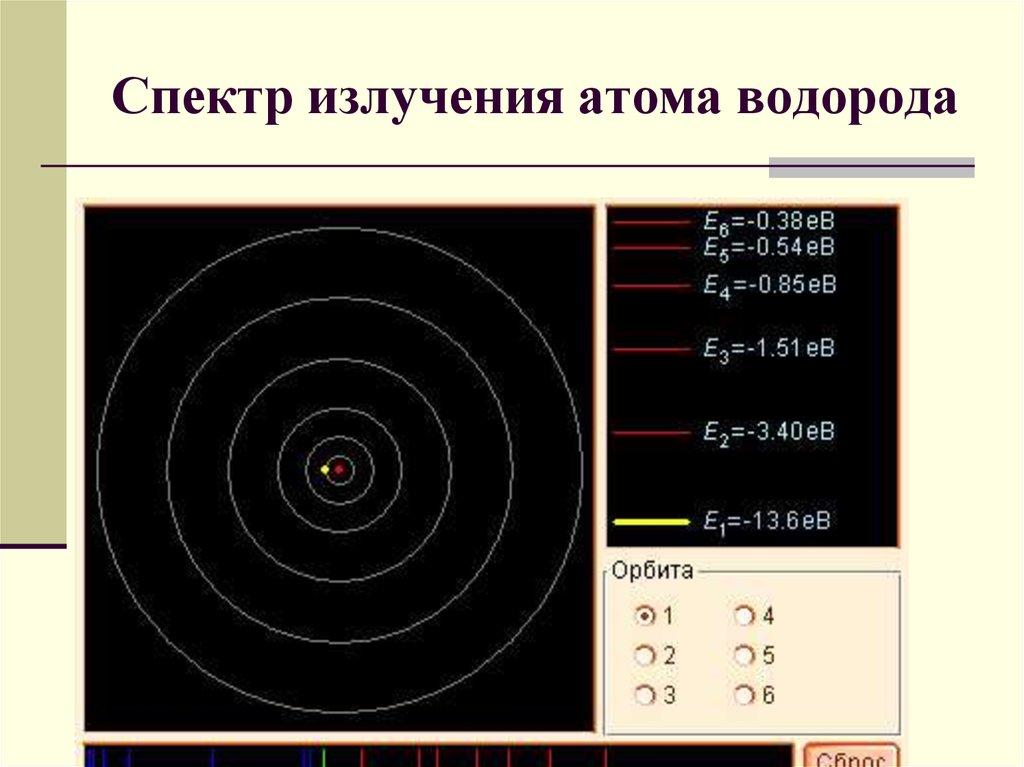
Спектр излучения атома водорода6.
Каждый атом или молекула может находиться в томили другом энергетическом состоянии. Иначе говоря, их
внутренняя энергия квантована. Целью теории Бора
было объяснить дискретные уровни энергии в атоме,
иными словами, произвести квантование движения в
атоме.
Для описания электронной системы, будь то атом,
молекула или кристалл необходимо знать все её
возможные квантовые состояния, характеризуемые
энергетическим спектром системы (кристалла, атома).
Если электронная система находится в равновесии и не
подвергается никаким внешним воздействием, то
находящиеся в ней электроны должны занимать
состояния с минимальной энергией.
7.
Взаимодействие частиц в квантовоймеханике характеризуют потенциальной
энергией, формула которой заимствуется
из классической механики. Например,
потенциальная энергия заряженной
частицы (например, электрона с зарядом
минус q) в электрическом поле другой
заряженной частицы (например, ядра
атома водорода c зарядом плюс q)
выражается формулой
2
q
E ï U (r ) q
4 0 r
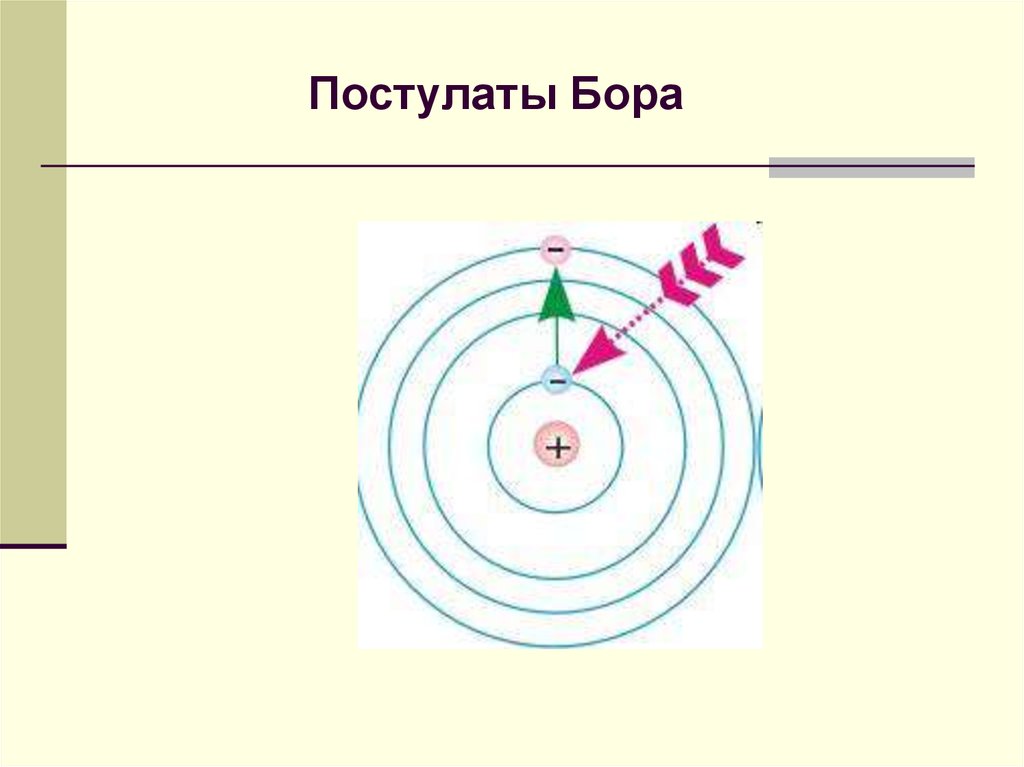
8. Постулаты Бора
Нильс Хе́нрик Дави́д Бор(дат. Niels Henrik David Bohr;
7.10 1885, Копенгаген ‒ 18.11 1962,
Копенгаген) ‒ датский физик-теоретик.
Лауреат Нобелевской премии по
физике (1922).
Был членом более чем 20 академий
наук мира, в том числе
иностранным почётным членом АН
СССР
9. Постулаты Бора
1. Электрон в атоме может двигаться только поопределенным стационарным орбитам, каждой из
которых можно приписать определенный номер n=1, 2, 3...
Такое движение соответствует стационарному состоянию
атома с неизменной полной энергией En . Это означает,
что движущийся по стационарной замкнутой орбите
электрон, вопреки законам классической
электродинамики, не излучает энергии. Стационарное
состояние характеризуется определенной энергией и
распределением электронной плотности. Совокупность
энергий стационарных состояний образует энергетический
спектр электрона в атоме
10.
Постулаты Бора11.
Постулаты Бора2. Разрешенными стационарными орбитами
являются только те, для которых угловой
момент импульса L электрона равен целому
кратному величины постоянной Планка .
Поэтому для n-ой стационарной орбиты
выполняется условие квантования
L n , n 1,2.3...
h 2 = 1,054·10-34 Дж с – приведенная
постоянная Планка или постоянная Дирака.
12. Постулаты Бора
3. Излучение или поглощение квантаизлучения происходит при переходе атома
из одного стационарного состояния в
другое. При этом частота излучения атома
определяется разностью энергий атома в
двух стационарных состояниях, так что
nk Ek En , k n
13. Постулаты Бора
Распределение электронной плотностипоказывает, в каких областях вокруг атома
электрон пребывает преимущественно, то
есть с вероятностью, близкой к 1.
Излучение или поглощение энергии
атомом происходит при переходе его из
одного стационарного состояния в другое.
14. Квантование энергии атома
Запишем условие вращения электронамассы m0 по круговой орбите радиуса r под
действием кулоновской силы со стороны
ядра и формулу Бора квантования
m
момента импульса электрона:
0
m0 2
1 q2
2
4 0 r
r
m r n
0
15. Квантование энергии атома
Решая эту систему уравнений, находимдля радиусов стационарных орбит
электрона в атоме водорода следующее
выражение
4 n 2 0 2
rn
m0 q 2
16. Квантование энергии атома
Вводя в качестве универсальнойконстанты теории боровский радиус
4 0 2
а
m0 q 2
=0,529∙10-10 м
как радиус первой стационарной орбиты
электрона в атоме водорода, запишем
формулу в виде
rn а n
2
17. Квантование энергии атома
Для скорости электрона на n-ойстационарной орбите получаем значение
q2
n
4 0 n
1
Полная энергия электрона, движущегося
по n -ой стационарной орбите,
складывается из его кинетической энергии
m0 2
m0
q2
Ek
2 2
2 2
2
32 0 n
18. Квантование энергии атома
и потенциальной энергии кулоновскоговзаимодействия электрона с ядром
q2
m0
q2
U
2 2
2
2 2
4 0 rn
16 0 n
m0 q 2
1
13,6
Е Ek U
2 2 эВ
2 2 2
32 0 n
n
19. Квантование энергии атома
Полная энергия электрона в атомеоказалась отрицательной, так как
отрицательна потенциальная
электростатическая энергия
взаимодействия электрона с ядром. С
ростом номера орбиты полная энергия
электрона в атоме возрастает. При этом
номер орбиты является квантовым
числом в такой теории
20. Квантование энергии атома
Для описания атома используютквантовые числа – энергетические
параметры, определяющие состояние
электрона и тип атомной орбитали, на
которой он находится
21.
Главное квантовое число n может принимать любыецелые положительные значения от 1 до ∞. Оно
определяет величину энергии
Z q m0
1
En
13
,
6
2
2
2
2
8 0 h n
n
2
4
эВ (1)
n 0 h
Rn
2
m0 Z q
2
2
Здесь Z – порядковый номер элемента в таблице
Д.И. Менделеева.
22.
С увеличением n расстояние междуэнергетическими уровнями и энергия связи электронов
с ядрами уменьшается, значение энергетического
зазора между уровнями падает.
Согласно (1), энергия электрона, находящегося в
связанном состоянии (например, энергия электрона
атома любого вещества), может принимать лишь
некоторые дискретные значения, а все остальные
значения невозможны или, как принято говорить,
запрещены.
23. Спектр излучения атома водорода
24. Орбитальное квантовое число l
определяет форму орбитали. Значениеорбитального числа l=(n-1)=0,1,2,3...(n-1).
Также вводят буквенные обозначения: 0-s,
1-p, 2-d, 3-f.
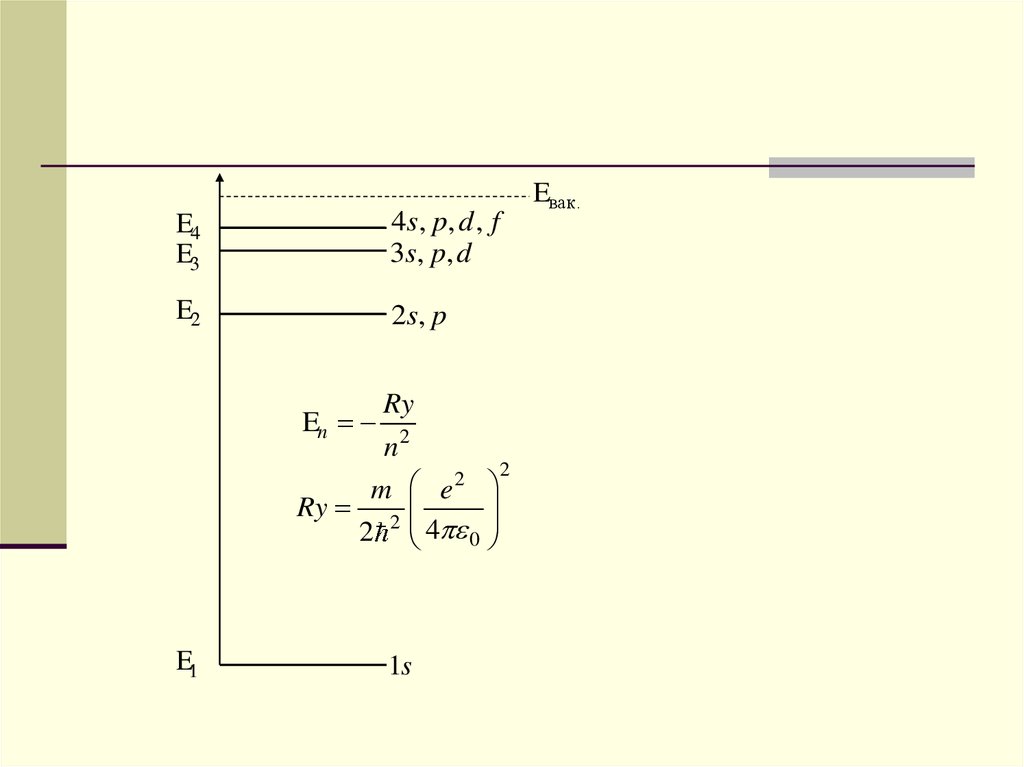
25.
E4E3
4 s , p, d , f
3s, p, d
E2
2 s, p
En
Ry
n2
2 2
m
e
Ry 2
4
2
0
E1
1s
Eвак.
26. Число орбиталей на энергетических подуровнях
Орбитали с l = 0 называются s-орбиталями,
l = 1 – р-орбиталями (3 типа,
отличающихся магнитным квантовым
числом m),
l = 2 – d-орбиталями (5 типов),
l = 3 – f-орбиталями (7 типов)
27.
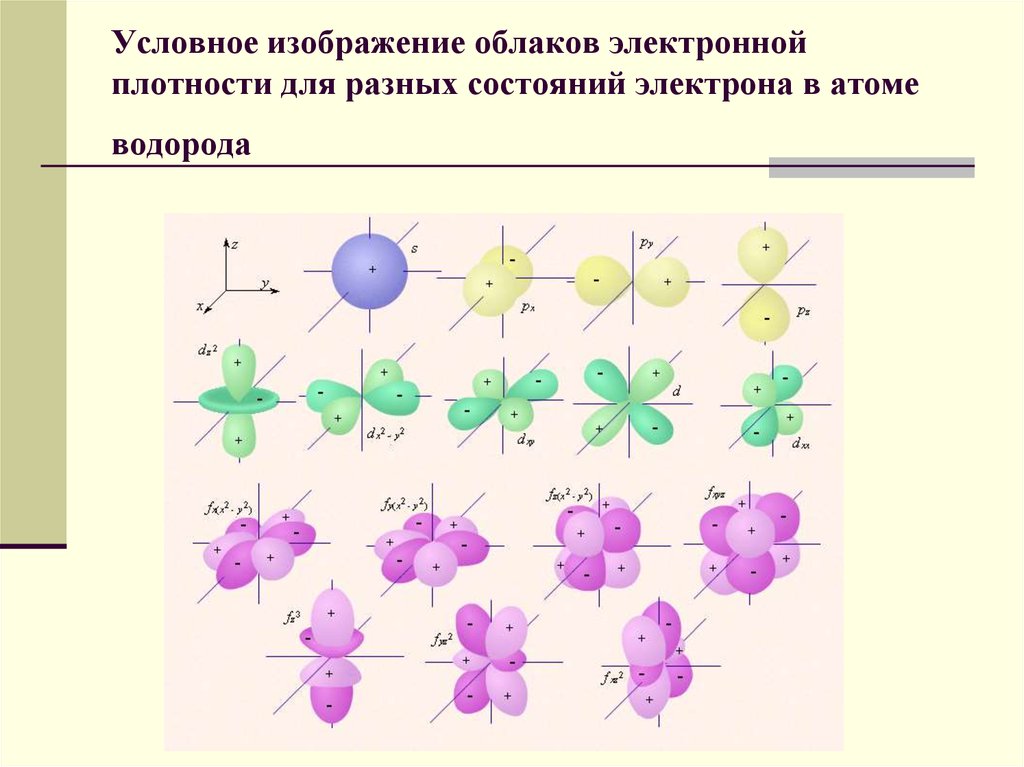
Каждому уровню энергии соответствуетстоячая электронная волна, электрон
колеблется вокруг и возле атомов и
образует как бы облако электронной
плотности. Плотность этого облака
показывает вероятность обнаружения
электрона в той или иной области
пространства или долю времени, которую
электрон проводит в той или иной области.
28. Условное изображение облаков электронной плотности для разных состояний электрона в атоме водорода
29. Магнитное квантовое число
характеризует величину магнитного поля,создаваемого при вращении электрона
вокруг ядра. Поэтому значение магнитного
квантового числа m связано со значением
орбитального квантового числа и
изменяется от –l до + l, а всего число
может принимать (2l+1) значение, включая
нулевое.
Например, для l = 2: m = -2, -1, 0, 1, 2.
30. Магнитное квантовое число
характеризует величину магнитного поля,создаваемого при вращении электрона
вокруг ядра. Поэтому значение магнитного
квантового числа m связано со значением
орбитального квантового числа и
изменяется от –l до + l, а всего число
может принимать (2l+1) значение, включая
нулевое.
Например, для l = 2: m = -2, -1, 0, 1, 2.
31. Спиновое квантовое число s
Спиновое квантовое число sЭлектрон помимо координат и импульса
характеризуется вектором спина, спин,
подобно заряду, – внутренняя
характеристика электрона, в классической
теории аналогичного понятия быть не
может. Спиновое число s =+½.
Внутренний момент импульса, связанный с
этим вращением, назвали спином (от англ.
spin – вращение), а момент, связанный с
вращением вокруг ядра – орбитальным
моментом.
32.
Слева направо:Джордж Уленбек,
Хендрик Крамерс и
Сэмюэл Гаудсмит
В том же 1925 г. голландец
Ральф Кронинг и независимо
Джордж Уленбек и Самюэль
Гаудсмит предположили, что
электрон вращается вокруг
собственной оси.
33.
Спин – это одно из проявлений принципатождественности частиц, который
применительно к электронам звучит так:
все электроны Вселенной неразличимы.
Электроны, как и фотоны,
можно изучать лишь в совокупности.
34. Заполнение электронных состояний в атоме кремния
3sp2p
2s
1s




























 physics
physics








