Similar presentations:
Уравнение Шредингера
1. Уравнение Шредингера
Лекция 7Уравнение Шредингера
2. §§ Волновая функция (ВФ)
Состояние частицы описывается волной2
( x, t ) A cos
x t
2
A exp i
x t к.с.
A – амплитуда волны
ω – частота
λ – длина волны
x – координата (не координата частицы)
02
3. §§ Уравнение Шредингера
Для частицы:E
,
2
P
i
( x, t ) A exp Px Et
Связь энергии и импульса
2
P
P 2mE E
2m
Найдем E и P2 из волновой функции
2
03
4.
iE i
E (1)
t
t
2
2
2
P
2
2
P
2
2
2
x
x
2
2 2
P
т.к. E
, то
E
(2)
2
2m
2m x
i
2
2m x
2
2
одномерное
уравнение
Шредингера
t
для свободной частицы
04
5.
Пустьi
i
( x, t ) exp Et A exp Px
( x)
Тогда получаем УШ для стационарных
состояний свободной частицы
( x)
E
(
x
)
0
2
2m x
2
2
05
6. §§ Частица в силовом поле
Пусть U(x) – потенциальная энергиячастицы в стационарном СП, тогда
Eполн E U ( x) E Eполн U ( x)
Получаем
( x)
E
U
(
x
)
(
x
)
0
полн
2
2m x
2
2
– УШ для стационарных состояний
06
7.
Т.к.*
2
– интенсивность, то
dp ( x) *( x)dx
– вероятность обнаружения частицы в
интервале [x, x+dx].
Необходимо ввести нормировку.
Во всем пространстве
dp
( x) dx 1
2
07
8.
Пример: дифракция электроновПеремещая детектор можно построить
график плотности вероятности
обнаружения электронов |ψ|2
Саму волновую функцию на опыте
получить не удается
08
9.
Пример 2: интерференция электронов09
10. §§ Свойства УШ и решения
Явления, в которых постояннаясущественную роль, называют
квантовыми.
h играет
УШ – основной закон квантовой
механики, учитывающий
корпускулярно-волновой дуализм.
Область применимости: энергия мала
по сравнению с энергией покоя частицы.
Рассмотрим его решение – волновую
функцию частицы в случае U(x) = const.
10
11.
1)E>U
2
2m
2
0,
E
U
2
2
x
( x) A1 sin x A2 cos x
A sin( x ) A cos( x )
2)
E<U
2
2m
2
0,
U
E
2
2
x
( x) A1 exp( x) A2 exp( x)
11
12.
Вид потенциальной функции U(x)определяет характер движения частицы.
Если U(x) – сложная функция или
содержит несколько областей,
то на решение (т.е. на ψ(x))
накладывают следующие условия:
1) ( x ),
– конечная, однозначная и
x
непрерывная для всех x
2)
* dx 1 – условие нормировки
(ее квадрат – интегрируем)
12
13.
Решение уравнения Шредингера,удовлетворяющее этим условиям,
существует только при определенных
значениях E = {E1, E2, … , EN, …},
которые называются
собственными значениями,
а функции ψ = {ψ1, ψ2, …, ψN,…}
при этих значениях называются
собственными функциями
13
14. §§ Потенциальные барьеры
Рассмотрим частицу с энергией E,которая проходит через границу
c двумя значениями потенциала U:
барьер типа
«ступенька»
0, x 0 (область I)
U ( x)
U 0 , x 0 (область II)
14
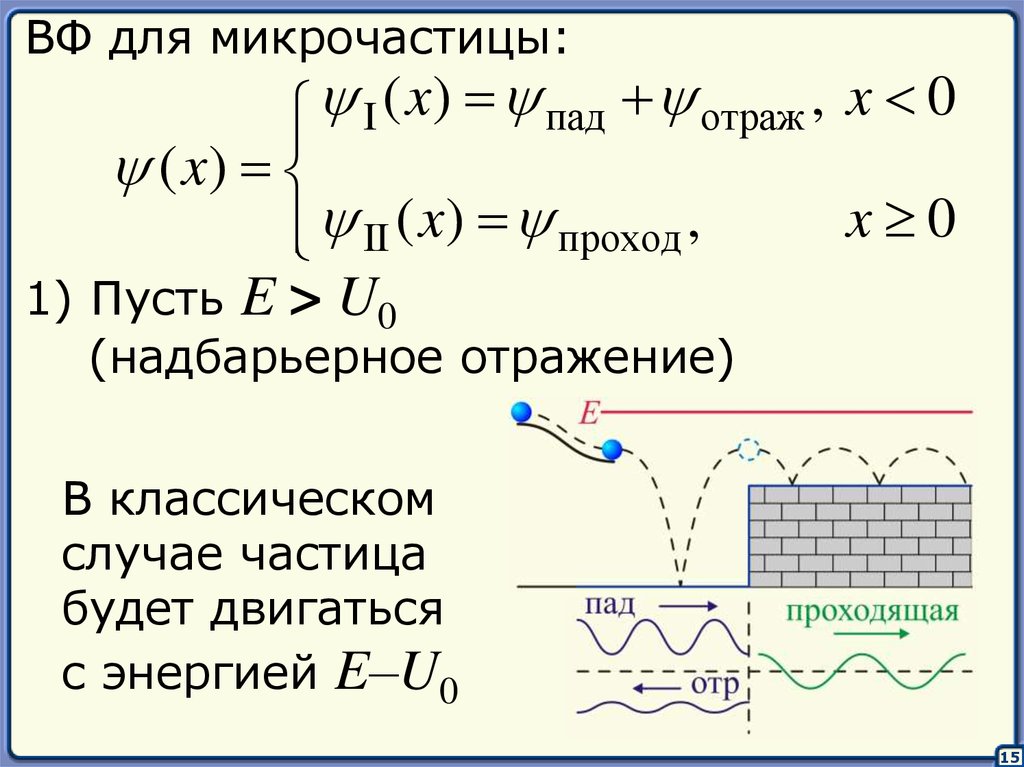
15.
ВФ для микрочастицы:I ( x) пад отраж , x 0
( x)
x 0
II ( x) проход ,
1) Пусть E > U0
(надбарьерное отражение)
В классическом
случае частица
будет двигаться
с энергией E–U0
15
16.
пад ( x) A0 sin( I x 0 )отр ( x) Aотр sin( I x 0 )
прох ( x) Aпрох sin( II x 0 )
Амплитуды проходящей и отраженной
волны находятся из условий
непрерывности и однозначности ВФ:
I (0) II (0)
d I
dx
x 0
d II
dx
x 0
16
17.
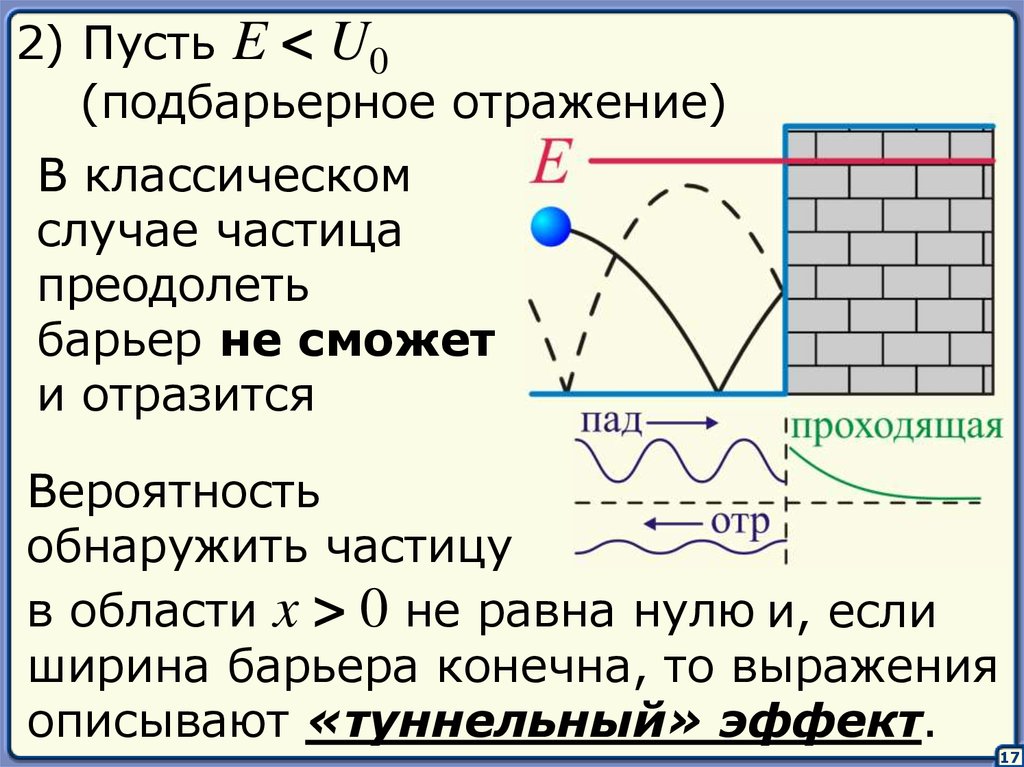
2) Пусть E < U0(подбарьерное отражение)
В классическом
случае частица
преодолеть
барьер не сможет
и отразится
Вероятность
обнаружить частицу
в области x > 0 не равна нулю и, если
ширина барьера конечна, то выражения
описывают «туннельный» эффект.
17
18. §§ Потенциальная яма
Часто движение частицы происходит вконечном объеме (тело, атом, ядро)
U(x) – зависимость потенциальной
энергии, которая известна с точностью
до произвольной постоянной
В большинстве случаев вид реальной
U(x) либо очень сложен, либо неизвестен
Пусть U(x) описывает потенциальную
яму прямоугольной формы.
18
19.
L 20
L 2
0
0
U 0
свободная
частица
частица
в яме
U 0
Пусть U 0 – случай бесконечно
глубокой потенциальной ямы
( x), x [0, L]
( x) I I
( x) 0, x L
III
III
I
II
0
(
x
)
0,
x
0
I
L
19
20.
II ( x) A sin( x ), где2mE
2
(0) 0
граничные условия:
( L) 0
sin 0
0
sin( L ) 0
L n
n 1,2,... (n ≠ 0)
т.е. решение задачи возможно только
при определенных значениях n.
20
21.
собственные значения энергииL
2mE
2
n En
2
2
2
2m L
n
2
Собственные функции
n x
n ( x) A sin
L
должны удовлетворять условию
нормировки:
L
A
(
x
)
dx
1
0
2
2
L
21
22.
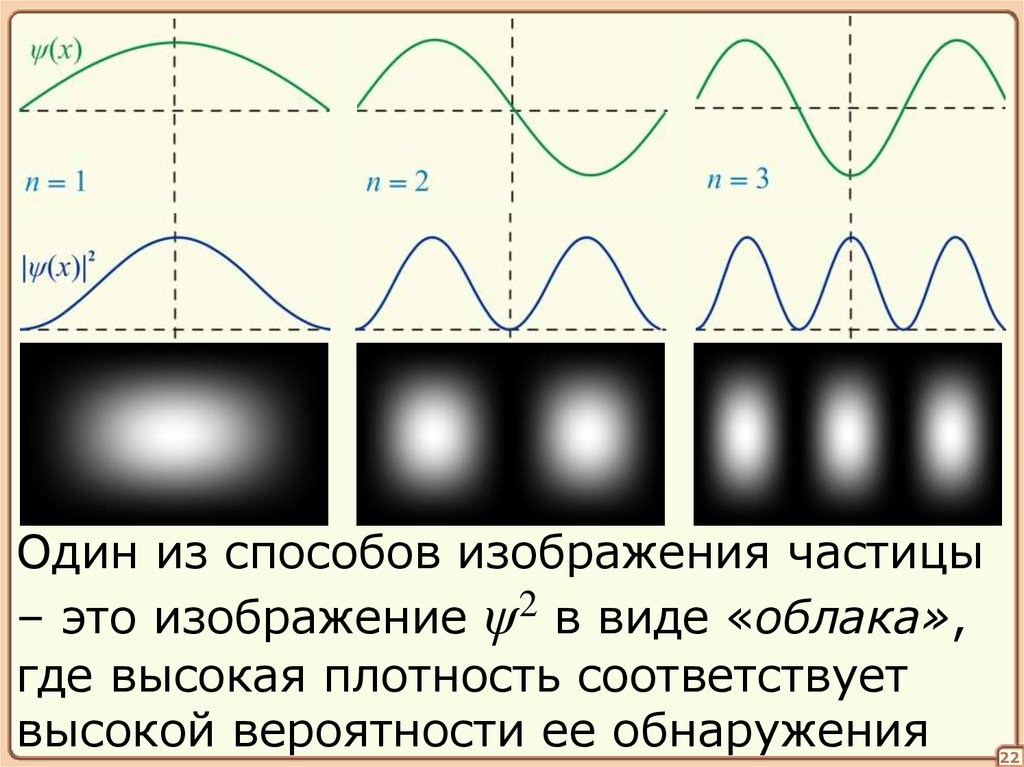
Один из способов изображения частицы– это изображение ψ2 в виде «облака»,
где высокая плотность соответствует
высокой вероятности ее обнаружения
22
23.
Выводы:1) у связанной частицы не может быть
состояния с E = 0.
2) движение частицы в яме возможно
только при определенных E
Спектр
E – дискретный и En ~ n2.
3) вид функции ψ(x) несовместим с
классическим понятием траектории,
когда все положения равновероятны
23
24. §§ Атом водорода
Рассмотрим атом с порядковым номеромZ, который имеет 1 электрон (H,He+,Li++)
Потенциал электрического поля:
Ze
U (r ) k
r
2
24
25.
уравнения Шредингера:2 2 2
2 2 2
2m x
y
z
2
Eполн U 0
Спектр собственных значений энергии
4
2
mee Z
En 2 2
2
n
Собственные функции электрона:
nlm nlm (r , , )
УШ решают в сферической СК
25
26.
r 00 2
0
Квантовые числа
n = 1, 2, 3, … – главное (r)
l = 0, 1, 2, …n–1 – азимутальное
(орбитальное, θ)
m = –l,…, –1, 0, 1, …, l – магнитное (φ)
26
27.
Каждому значению En соответствуетнесколько волновых функций с разными
l и m, т.е. электрон может находиться в
нескольких состояниях с одной энергией.
Такие состояния называются
вырожденными, а число таких
состояний называется кратностью
вырождения.
Для уровня
En кратность вырождения
составляет n2 (2n2 – если учитывать спин)
27
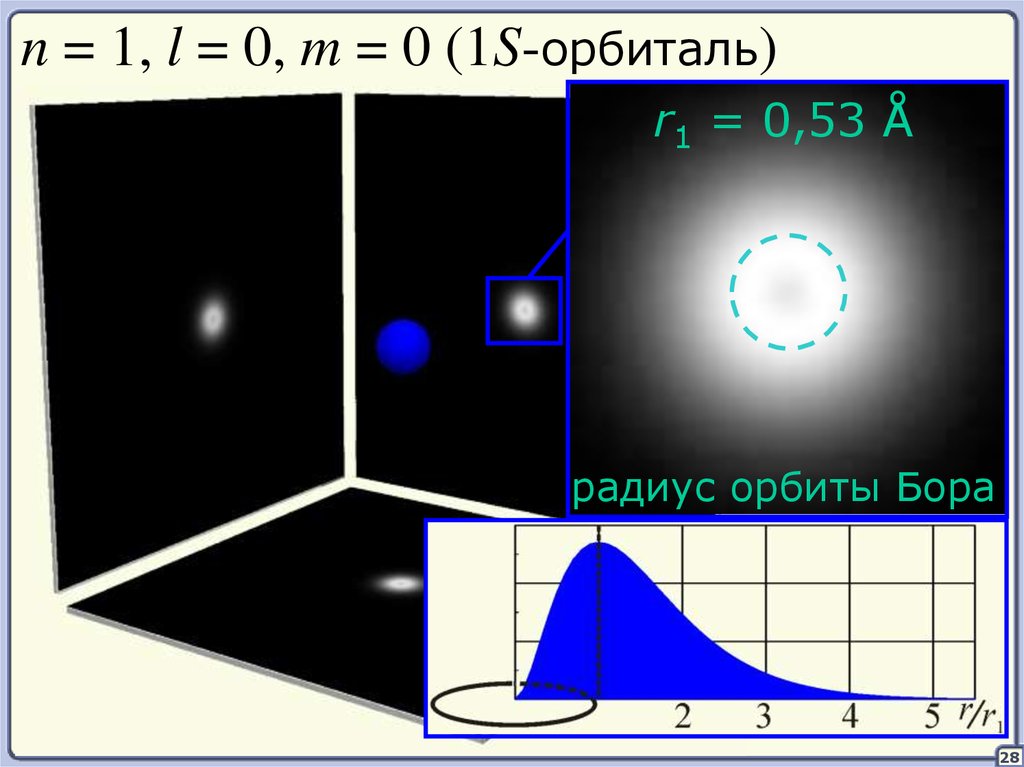
28.
n = 1, l = 0, m = 0 (1S-орбиталь)r1 = 0,53 Å
радиус орбиты Бора
28
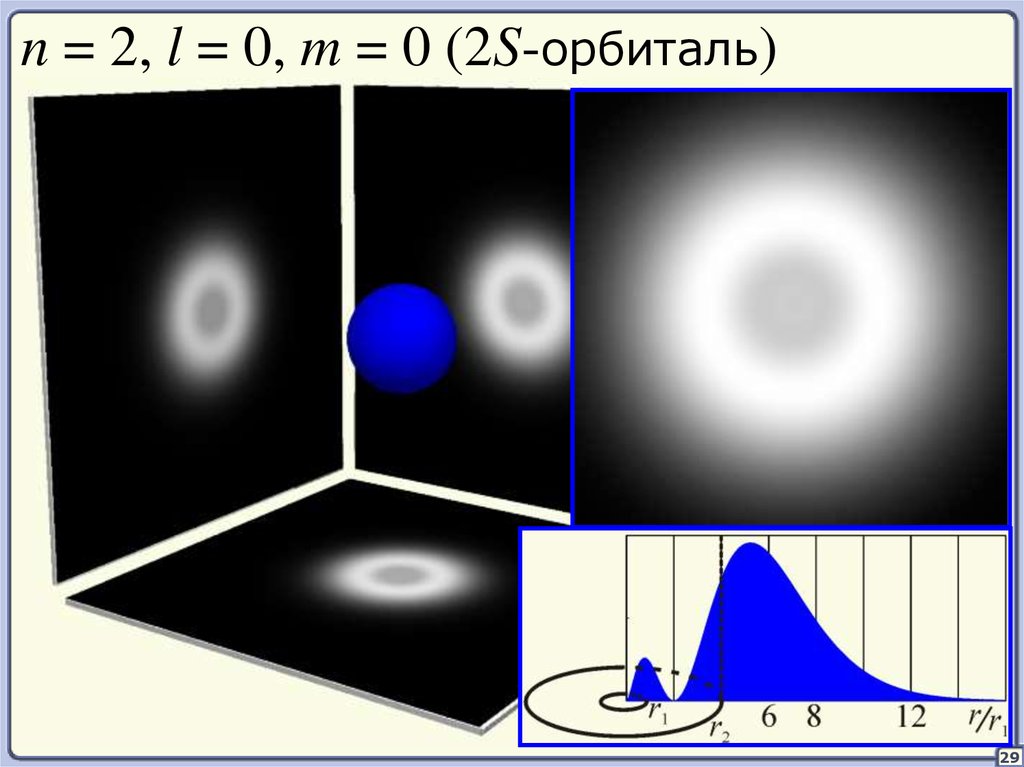
29.
n = 2, l = 0, m = 0 (2S-орбиталь)29
30.
n = 2, l = 1, m = 0(2P-орбиталь)
n = 2, l = 1, m = ±1
(2P-орбиталь)
30
31.
Электронное облако для S-состоянияимеет шаровую симметрию
с характерным радиусом 0,5(S1)–5Å(S3).
31
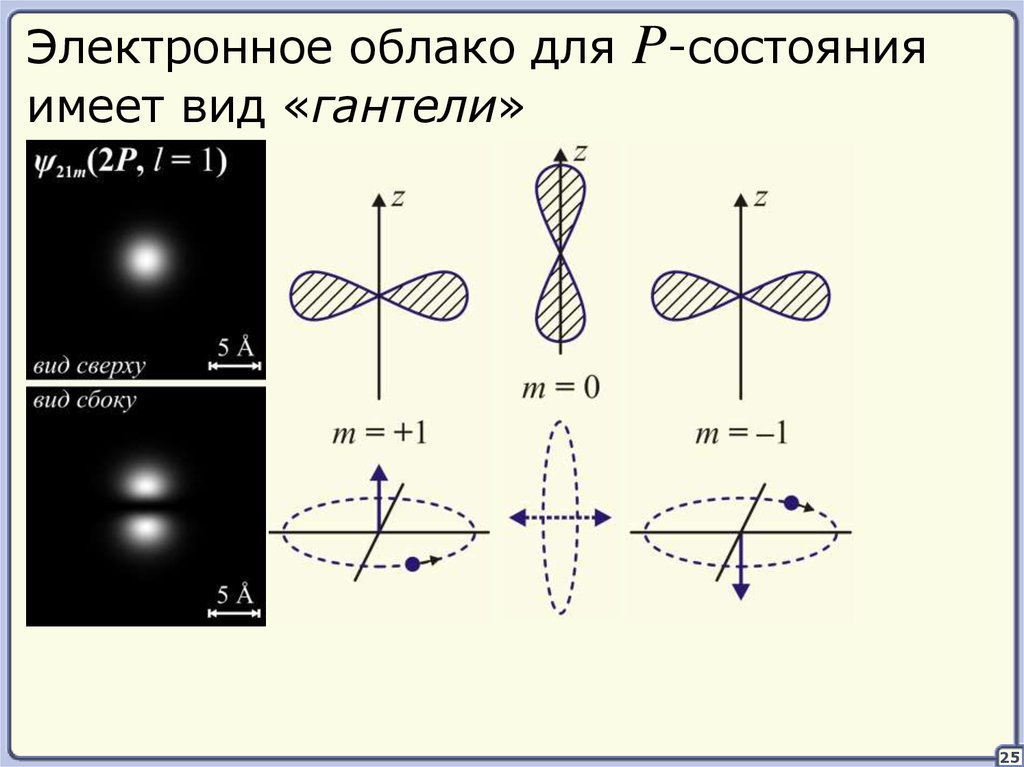
32.
Электронное облако дляимеет вид «гантели»
P-состояния
25
33. §§ Правило отбора
Фотон изменяетмомент атома,
т.к. обладает
спином S = ±1
Переходы электрона между уровнями
возможны только с Δl = ±1.
При других переходах атом не излучает
энергию или они невозможны.
33
34. §§ Многоэлектронные атомы
Атом с порядковым номером Z содержитZ электронов, которые двигаются в поле
ядра и других электронов.
Состояние электрона определяют
три квантовых числа:
n – главное квантовое число (1, 2,
l – орбитальное квантовое число
...)
l = 0(s), l = 1(p), l = 2(d), l = 3( f )
m = ml – орбитальное магнитное
квантовое число
34
35.
К тройке добавим еще одно квантовоечисло. Электрон обладает спином
– внутренним (собственным) моментом
количества движения.
ms = ±½ – спиновое квантовое число
1
– собственный механический
S
2
момент электрона
Наличие у электрона спина объясняет
тонкую структуру спектров, расщепление
линий в магнитных полях и порядок
заполнения электронных оболочек в атомах
35
36.
Принцип (запрета) ПаулиВ квантовой системе (атоме)
не может быть двух электронов,
обладающих одинаковой
совокупностью четырех
квантовых чисел n, l, ml, ms.
Иными словами,
в одном и том же состоянии не могут
одновременно находиться 2 электрона
Совокупность электронов с одинаковым
n образуют слой, с одинаковыми n и l
– образуют оболочку.
36
37.
Пример: электронная конфигурацияосновного состояния атома 11Na (Z = 11)
10Ne
– неон, инертный газ, атом
с завершенным слоем
2 2s2 2p6 3s1 = (Ne)10 3s1
Na
=
1s
11
10 3s23p5
Cl
=
(Ne)
17
37
38. §§ Энергетические зоны
Теория конденсированного веществастроится на основе квантовой механики
Описание системы взаимодействующих
электронов и ядер связано с расчетными
и математическими трудностями.
Сейчас есть возможность проводить
такие расчеты из первых принципов
Рассмотрим радикально упрощенную
одномерную модель.
38
39.
Пусть атомы находятся далеко друг отдруга.
a – межъядерное расстояние
Тогда каждый из них – электрически
нейтрален и обладает собственной
системой энергетических уровней.
39
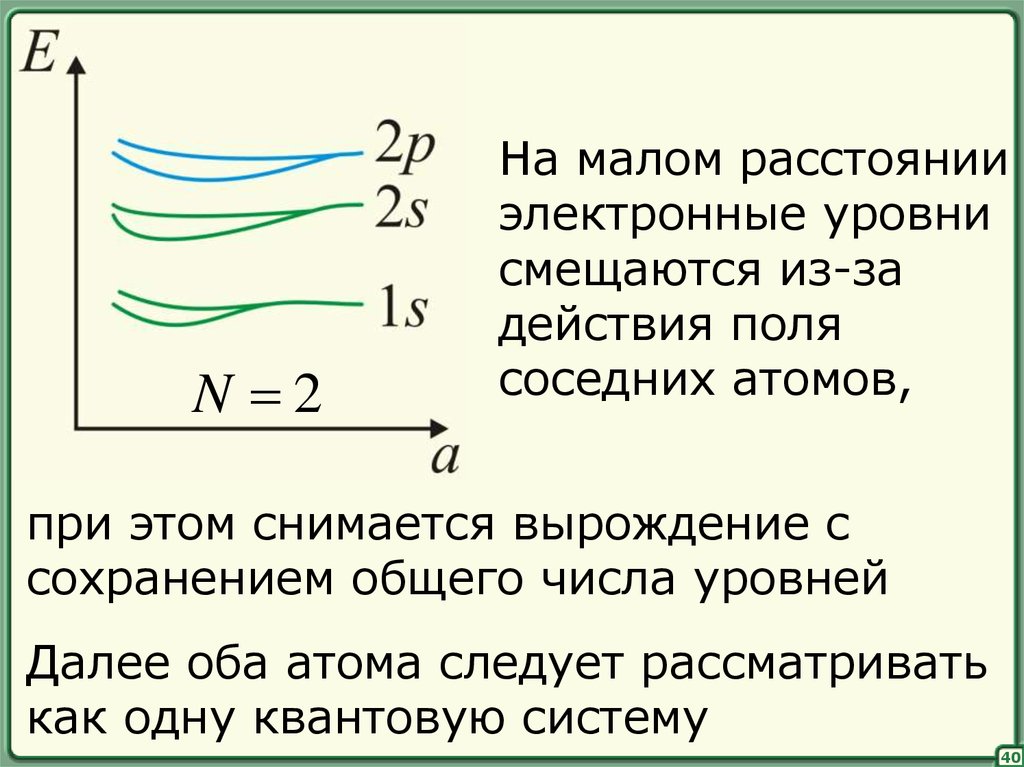
40.
N 2На малом расстоянии
электронные уровни
смещаются из-за
действия поля
соседних атомов,
при этом снимается вырождение с
сохранением общего числа уровней
Далее оба атома следует рассматривать
как одну квантовую систему
40
41.
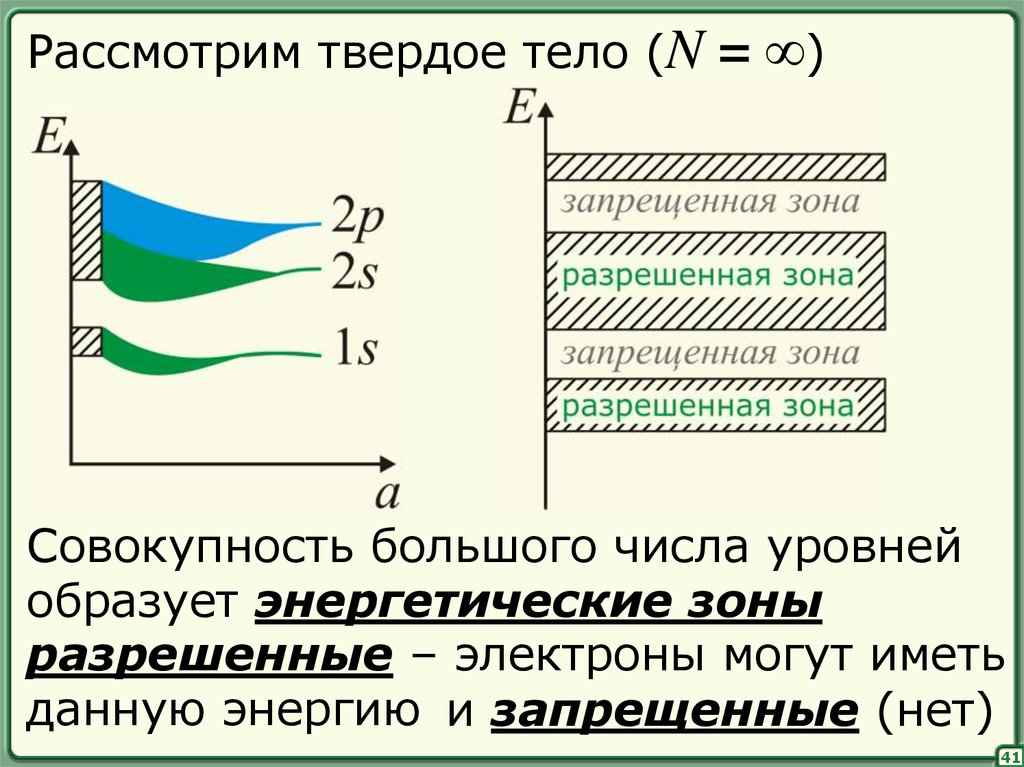
Рассмотрим твердое тело (N= ∞)
Совокупность большого числа уровней
образует энергетические зоны
разрешенные – электроны могут иметь
данную энергию и запрещенные (нет)
41
42.
При заполнении разрешенных зонпринцип запрета остается справедливым
При T = 0 заполняются сначала уровни
с минимальной энергией.
свободная зона
ΔE – ширина запрещенной зоны
заполненные зоны
42
43.
Электроны полностью заполненныхэнергетических зон не участвуют в
процессах переноса
При ΔE ≥ 5 эВ на рисунке – зонная
структура диэлектрика
При ΔE = 0,1 – 3 эВ получаем зонную
структуру полупроводника,
в которой даже небольшое повышение
температуры приводит к переходу
электронов в свободную зону
и сопротивление п/п уменьшается по
экспоненциальному закону
43
44.
Проводник – одна или две зонызаполнены частично (10–90 %).
Электроны таких зон участвуют
в процессах переноса
(электро- и теплопроводность)
Энергетическая структура реального
кристалла зависит от свойств отдельных
атомов и их взаимного расположения
Возможны также и перекрытия зон
в некоторых направлениях
44
45. §§ Вынужденное излучение
При термодинамическом равновесиичисло частиц на верхнем уровне
значительно меньше, чем на нижнем.
Вероятность заселения уровня
определяется законом Больцмана
Ei
Pi const exp
k BT
Атомы могут взаимодействовать со
светом, поглощая или испуская фотоны.
45
46.
Если атом переходит с уровня Em науровень En, то произойдет излучение
кванта с энергией
h Em En
Вероятность перехода атома
P = Pсп + Pвын
Pсп– вероятность спонтанного излучения
Pвын– вероятность вынужденного
излучения, линейно зависящая от
плотности поля на данной частоте
46
47.
Если система находится в состоянииравновесия, то она будет поглощать
проходящее через нее излучение
При работе генераторов и усилителей
создают инверсию заселенностей.
С помощью накачки переводят как
можно большее число частиц в
возбужденное состояние.
В этом случае
среда усиливает
проходящий поток.
47
48.
Схема лазера(оптического квантового генератора)
Многократно отразившись от зеркал
резонатора из лазера выходит свет,
обладающий высокой когерентностью
и монохроматичностью.
48
49. §§ Типы лазеров
Лазеры классифицируют по агрегатномусостоянию рабочего тела:
1) твердотельные
2) газовые
3) жидкостные
В твердотельных рабочим ансамблем
являются примесные атомы, введенные
в основную матрицу твердого тела.
49
50.
Примеры:рубиновый лазер – корунд (Al2O3),
кристалл, примесь – Cr (хром)
неодимовый лазер – стекло,
аморфное тело, примесь – Nd (неодим)
Накачка у таких лазеров осуществляется
с помощью газоразрядной лампы
(оптическая накачка).
КПД – доли %, поэтому такие лазеры
требуют интенсивного охлаждения.
50
51.
Газовые лазеры:1) атомарные – лазеры на инертных
газах (He, Ne, Ar, Kr, He-Ne)
2) ионные
Энергетические уровни ионов
лежат выше, чем у атомов
и имеют более высокую
вероятность перехода.
3) молекулярные
используют вращательные и
колебательные уровни молекул
КПД выше, чем у 1) и 2)
51
52.
Жидкостные лазеры имеют в качестверабочего тела неорганическую жидкость
или раствор органических красителей
Используется оптическая накачка
Полупроводниковые лазеры
в качестве рабочего тела используют
кристалл полупроводника.
Если п/п – однородный, то инверсия
заселенности достигается оптической
накачкой или бомбандировкой
электронным пучком.
52
53.
Если п/п – неоднородный, то инверсиюосуществляют инжекцией носителей
тока под действием приложенной
разности потенциалов.
Химические лазеры
Инверсия заселенности возникает
при химической реакции, которая
проходит при фотодиссоциации
молекул или электрическом разряде
53










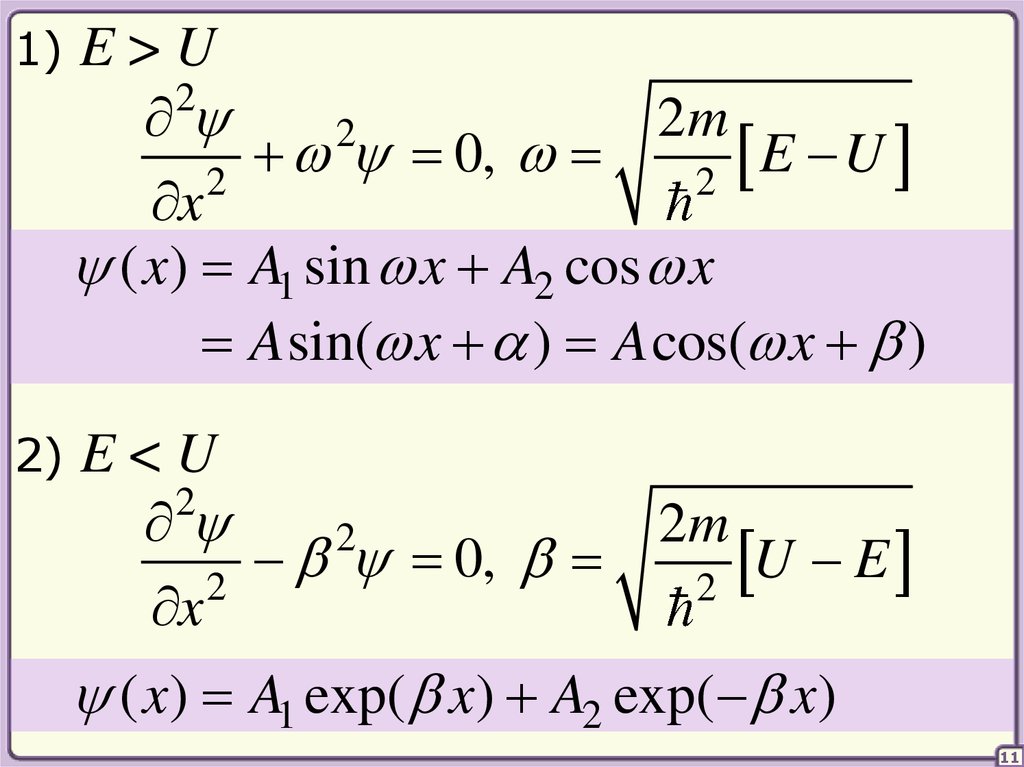


































 physics
physics








