Уравнения Шредингера. Движение свободной частицы

1.

2
U ( x, y, z,t ) i
2m
t
i – мнимая единица
( i - 1)
2
2
2
2 2 2
x y z
( x, y, z,t )
U ( x, y, z,t)
оператор Лапласа
- волновая функция частицы
- силовая функция
(характеризует силовое поле, в котором движется частица)

2.

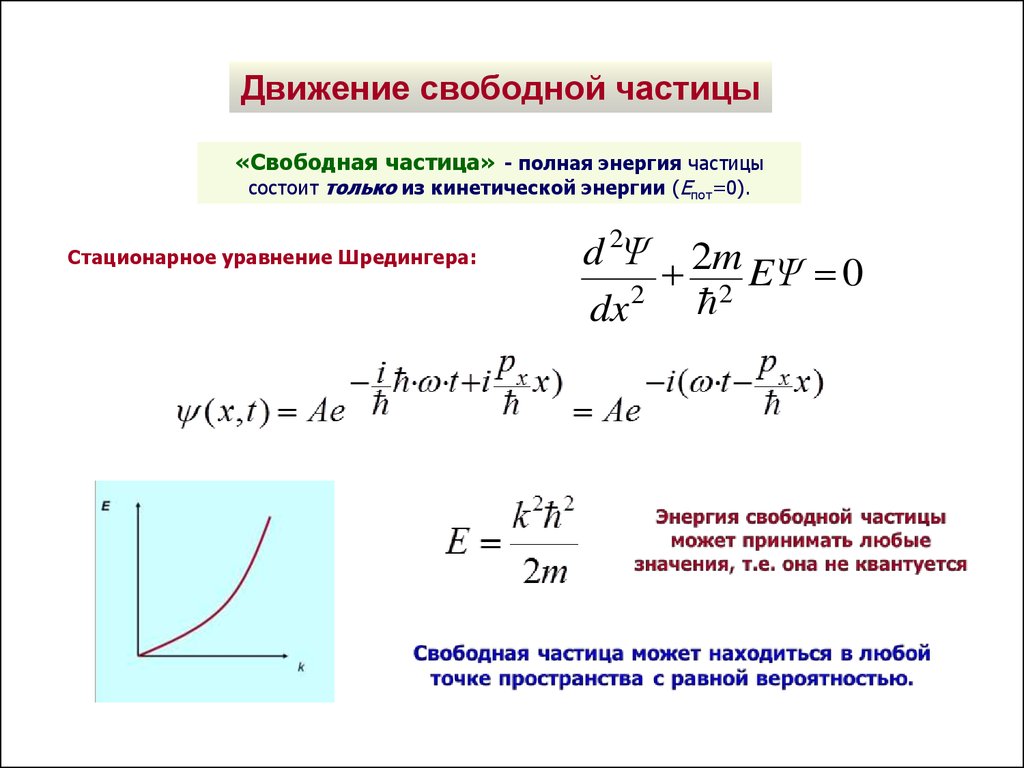
Движение свободной частицы
«Свободная частица» - полная энергия частицы
состоит только из кинетической энергии (Епот=0).
Стационарное уравнение Шредингера:
d 2Ψ 2m
2 EΨ 0
2
dx

3.

Частица в одномерной потенциальной яме бесконечной глубины
Потенциальной яма - область пространства,
где потенциальная энергия U частицы
меньше некоторого значения Umax .
При U=U(x) и Umax=∞ - одномерная потенциальная
яма бесконечной глубины.
Одномерное движение в потенциальной яме вдоль оси Х.
Из ямы частица выйти не может.
U =∞ при х < 0 и х > а - вне потенциального ямы
U = 0 при 0 ≤x ≤ а - внутри потенциального ямы
Граничные условия:
1. Яма бесконечно глубокая, выйти из неё частица не может, => вероятность
обнаружить частицу вне ямы равна нулю → Ψ = 0 вне ямы.
2. Из непрерывности Ψ-функции и условия 1 → на границах ямы с бесконечно
высокими стенками Ψ обращается в нуль, т. е. Ψ(0) =Ψ(а) = 0.

4.

Стационарное уравнение Шредингера для одномерного случая
d 2 2m (E U ) 0
dx 2 2
В областях I, II и III разные решения уравнения:
1. В I и III частица быть не может по условию задачи и Ψ = 0.
2. В области II U(x) = 0 и уравнение Шредингера
принимает вид:
2mE
k 2
2
→
d 2 2m E 0
dx2 2
d 2 k 2 0
dx2
(1)

5.

Найдем решение уравнения в виде
k и α найдем из граничных условий:
при
Ψ(x) =A sin (kx + α)
х=0 Ψ=0= Аsin α =>
α=0
при х=a Ψ(х=a)=0= Аsin ka => sin ka=0 и ka=±nπ, где n=1, 2, …
=> k= ± nπ/a
→
(2)
n
E
2ma2
2
2 2
n
2mE
2
k 2 2
a
2
(3)
→ энергия микрочастицы в потенциальной яме
принимает дискретный ряд значений (квантуется)
Результат имеет общее
значение: при движении
микрочастицы в ограниченной области пространства ее
энергия может принимать только дискретный ряд значений.

6.

n 2 2
E
2ma2
Частица не может иметь Е = 0 (n≠ 0).
→
Наименьшая энергия частицы в яме при n=1.
При Т=0 К Е≠ 0 (противоречит классической физике).
Внутри потенциального ящика :
( x) Аsin na x
Для нахождения А воспользуемся
условием нормировки Ψ:
среднее значение
2 n
sin
a
0
a
=>
Внутри потенциального ящика
(4)
2
2 sin 2 n x dx 1
dx
A
a
a
a
0
0
sin 2 n x 1/2
a
A 2
a
( x) a2 sin na x
x dx а/2
(5)

7.

Какую информацию дает
( x) a2 sin na x
?
Из рис.: n=1 (при Е1) макс. вероятность нахождения частицы в середине ящика.
При Е2 вероятность нахождения частицы в середине ящика равна нулю,
максимальная - в точках ¼ а и ¾ а.

8.

Контрольные вопросы:
??
1. Частица в прямоугольной потенциальной яме, шириной l
находится во втором возбужденном состоянии. Плотность
вероятности нахождения частицы максимальна в точке
интервала (0< x <l) …
l
l
3l
l
1. х =
2. х =
3. х = 4
4. х = 8
8
2
2. На рисунке изображена плотность вероятности обнаружения
микрочастицы на различных расстояниях от ,,стенок” ямы.
Вероятность её обнаружения на участке l /4< х < l …
2
1. 3/4
2. ½
3. 1/4
4. 0
φ
0
l /2
l х

9.

Различие в поведении
микрочастицы, подчиняющейся
квантовым законам, и
классической макрочастицы:
Макрочастица с энергией Е : вероятность нахождения
в пределах ямы везде одинакова |Ψ(x)|2 =const .
Микрочастица: |Ψ(x)|2 ≠const.
С ростом уровня энергии: число максимумов |Ψ|2 растет, максимумы сближаются.
При n→∞ максимумы сливаются в прямую линию, как у макрочастицы.
Расстояние между любыми уровнями энергии
En En 1 En
При 2n >>1
2
n 1
2ma
2n+1≈2n и
2
2
2
n
(2n 1)
2
2ma
2
En 2 n
ma
(6)
При увеличении а расстояние между соседними уровнями уменьшается и
при а→∞ (частица в свободном пространстве) ΔΕ=0 →
энергия частицы может принимать любые значения и не квантуется.

10.

Выводы о поведении микрочастицы в одномерной потенциальной
яме бесконечной глубины (с бесконечно высокими стенками):
1. Энергия микрочастицы в потенциальной яме дискретна.
2. Энергия не равна нулю даже на наименьшем энергетическом
уровне при n = 1.
3. Вероятность пребывания частицы в различных точках ямы в
состояниях с разной энергией разная.
4. Квантование энергии Еn и вероятности состояний |Ψ|2 сильнее
проявляются при малой массе частицы и малых размерах
ямы.
n 2 2
E
2ma2
Модель частицы в бесконечной глубокой потенциальной яме описывает
поведение электронов в металле, протонов в ядре: микрочастица не может
выйти за границы некоторой области, внутри области частица свободна.

11.

Прохождение частицы через потенциальный
барьер конечной ширины
Микрочастица в поле, в котором U(x) имеет вид:
U(х) =
0 при х < 0
U0 при 0 ≤ х ≤ а
0 при х >а
(область I)
(область II)
(область III)
Пусть микрочастица движется вдоль оси Х. Если Е>U0,
частица проходит над барьером и попадает из I в Ш.
Одинаково
механике.
в классической и квантовой
Если Е<U0, согласно классической механике,
частица не может пройти из I в III.
Результат, даваемый квантовой
механикой ?

12.

Уравнение Шредингера для каждой из областей :
2
d Ψ13 2m
2 EΨ13 0
2
dx
d 2Ψ 2 2m
2 EΨ 2 0
2
dx
для областей I и III
для области II
Из решения уравнений следует:
1. В области I будет
плоская волна, распространяющаяся в направлении оси Х
(соответствует частице, движущейся к барьеру), и волна, отраженная от барьера,
(соответствует частице, движущейся от барьера).
2. В области II даже при Е<U0 Ψ2 ≠0.
3. В III (если барьер не очень широк) будет волна, прошедшая сквозь барьер (слеванаправо), имеющая частоту, что в I, но меньшую амплитуду.

13.

Качественный вид функций Ψ1(x), Ψ2(x), Ψ3(x) в различных областях
В области II Ψ имеет вид
затухающей экспоненты.
При конечной ширине барьера на
2-границе Ψ2(а)≠0. => Есть
вероятность (≠0) оказаться в
III.
В I и Ш λ1=λ3 (ν1= ν3), Е не меняется, меняется амплитуда ψ-функции.
Вероятность найти частицу в Ш меньше, чем в II, т.к. у частицы существует вероятность
отразиться от границы х=а, есть и вероятность ~ |Ψ|2, пройти границу а и оказаться в Ш.
ВЫВОД: квантовая частица имеет отличную от нуля вероятность
прохождения через потенциальный барьер конечной ширины и в том
случае, когда ее энергия меньше высоты барьера (Е<U0).
Вероятность тем больше, чем меньше ширина барьера.

14.

Эффект прохождения частицы через потенциальный барьер - туннельный эффект.
«Коэффициент прозрачности потенциального барьера» отношение плотности потока прошедших частиц (интенсивности Iпрох)
к плотности потока падающих частиц (Iпад):
D – прозрачность потенциального барьера
D
I прох
I пад
определяет вероятность прохождения
частицы через потенциальный барьер.
I~А2
Прямоугольный потенциальный
барьер высотой U0 и шириной а:
D
A3
2
A1
2
D D0 exp( 2a 2m(U0 E)
D0 – постоянный множитель, близкий к единице

15.

Туннельный эффект играет заметную роль, если D не слишком мал (линейные
размеры потенциального барьера соизмеримы с атомными размерами).
Туннельное прохождение через потенциальный барьер лежит в основе
явлений ФТТ (явления в контактном слое на границе двух полупроводников),
атомной и ядерной физики (α-распад, протекание термоядерных реакций).

16.

Гармонический осциллятор в квантовой механике
«Гармонический осциллятор» - тело, совершающее малые
колебания около положения равновесия по гармоническому закону.
Пример:
пружинный маятник
d 2x k x 0
dt 2 m
k
0 m
x x0 cos( 0t )
- циклическая частота собственных
колебаний осциллятора
2 x2
m
U
1 kx02 cos2 ( 0t ) 0
2 2
2
2 sin 2 ( t )
2
kx
mv
0
0
kx2
T
2
2
(1)

17.

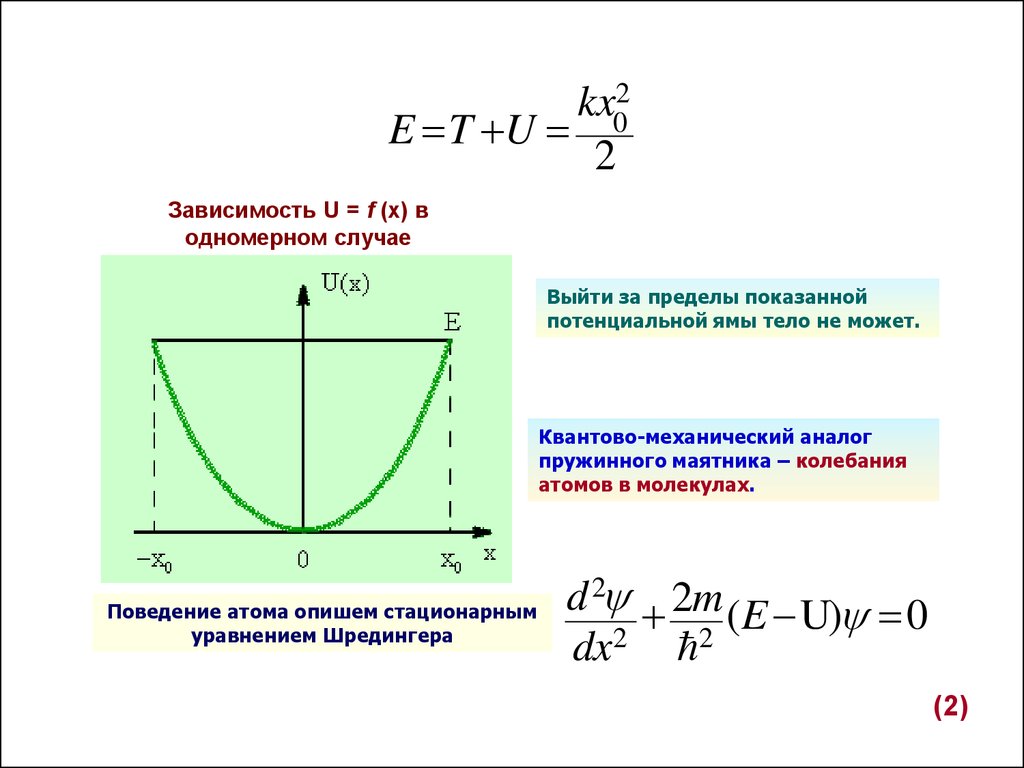
kx02
E T U
2
Зависимость U = f (х) в
одномерном случае
Выйти за пределы показанной
потенциальной ямы тело не может.
Квантово-механический аналог
пружинного маятника – колебания
атомов в молекулах.
Поведение атома опишем стационарным
уравнением Шредингера
d 2 2m (E U) 0
dx2 2
(2)

18.

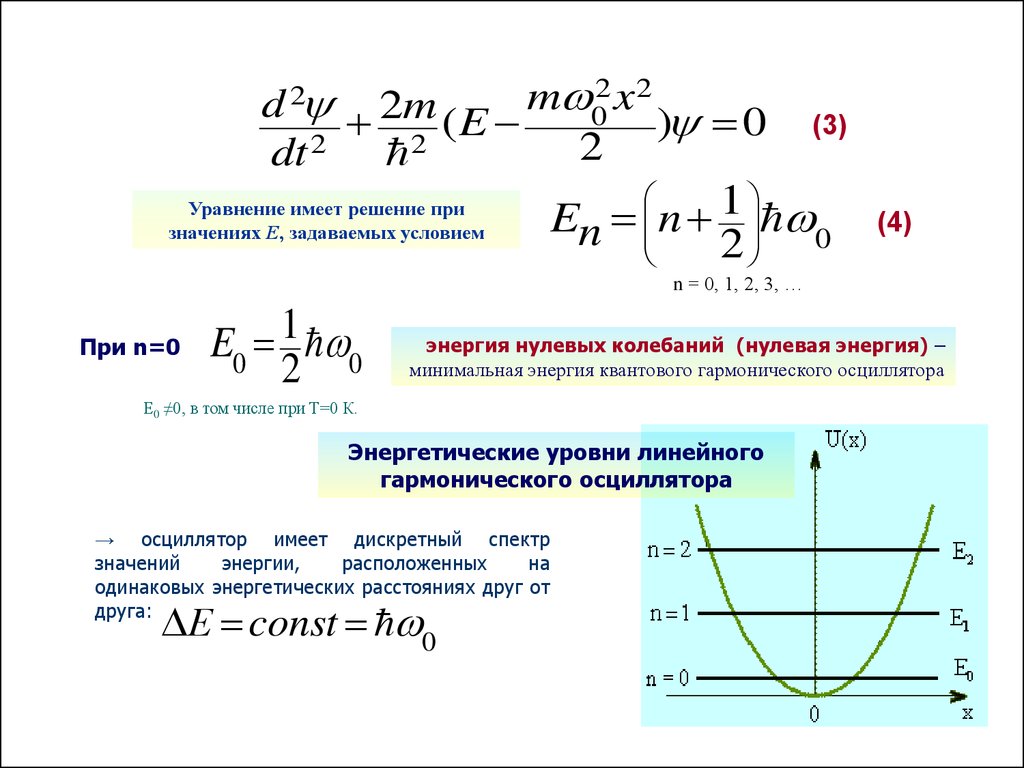
d 2 2m ( E m 02 x2 ) 0 (3)
2
dt 2 2
1
Уравнение имеет решение при
En n 0
значениях Е, задаваемых условием
2
(4)
n = 0, 1, 2, 3, …
При n=0
E0 1 0
2
энергия нулевых колебаний (нулевая энергия) –
минимальная энергия квантового гармонического осциллятора
Е0 ≠0, в том числе при Т=0 К.
Энергетические уровни линейного
гармонического осциллятора
→ осциллятор имеет дискретный спектр
значений
энергии,
расположенных
на
одинаковых энергетических расстояниях друг от
друга:
Ε const 0

19.

Изучение рассеяния света кристаллами (на колеблющихся атомах,
молекулах и ионах, расположенных в узлах кристаллической решетки)
при T ≈ 0 К подтверждает существование нулевого уровня.
Плотности вероятности |Ψ|2 разных уровней n отличаются.
Вероятность W нахождения гармонического осциллятора в яме
n=1
Wсl – классическая, Wkw- квантовая
С ростом n кривая распределения вероятностей
становится похожей на классическую кривую.
n=10
Wkw ( x)dx n ( x) dx
2

20.

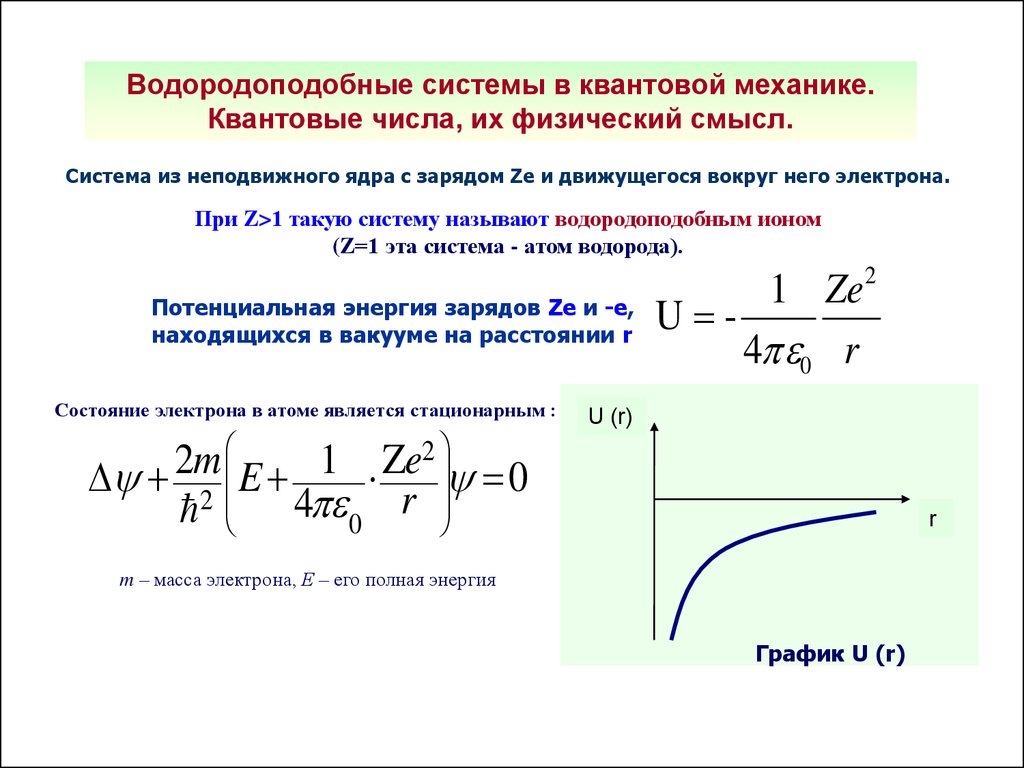
Водородоподобные системы в квантовой механике.
Квантовые числа, их физический смысл.
Система из неподвижного ядра с зарядом Ze и движущегося вокруг него электрона.
При Z>1 такую систему называют водородоподобным ионом
(Z=1 эта система - атом водорода).
Потенциальная энергия зарядов Ze и -e,
находящихся в вакууме на расстоянии r
Состояние электрона в атоме является стационарным :
2
2
m
1
Z
e
2 E
0
4 0 r
1 Ze
U 4 0 r
2
U (r)
r
m – масса электрона, Е – его полная энергия
График U (r)

21.

2 2 2
Для трехмерного случая
2 y 2 z 2
x
(электрон может менять свое положение относительно ядра произвольным образом)
mядра>>mе → ядро двигается медленнее электрона ↔ ядро неподвижно
Кулоновское поле центрально-симметричное → движение электрона
рассматривают в сферической системе координат.
Точка А в сферической системе имеет
координаты r, φ, θ, связанные с х, у, z :
x = r·sinθ·cosφ
y = r·sinθ·sinφ
z = r·cosθ
Ψ=f (r, φ, θ)
Оператор Лапласа в сферических координатах :
2
2
1
1
1
2 r
2
sin 2 2
r sin 2
r r r r sin

22.

В сферических координатах:
2 2m E 1 Ze 2 0
1 r 2 1
sin
1
r 2 sin 2 2 2
4 0 r
r 2 r r r 2 sin
(1)
Метод разделения переменных:
Ψ(r, θ, φ) = R(r) ·Ф(θ, φ)
R(r) - функция радиального распределения;
Ф(θ,φ) - функция углового распределения.
решение при любых Е > 0 (свободный электрон) и при Е < 0
(электрон в атоме), удовлетворяющих условию:
1
En
4
0
2
mZ 2e4 1
2 2 n2
n = 1, 2, 3, …
главное
квантовое
число
(2)
Вывод: существуют стационарные состояния атомов, характеризуемые определенной энергией.

23.

Уровни возможных значений полной энергии атома
Е, U
Е>0
r
Е3
U (r)
Е2
Е1
С ↑ n расстояние между электроном и ядром ↑, Е и Екин → 0.
Е<0 движение электрона является связанным.

24.

В R( r ) и Ф(θ, φ) входят целочисленные параметры, обозначаемые l и m .
l = 0, 1, 2, …, (n-1)
m= 0, ±1, ±2, …, ±l
l
орбитальное (азимутальное) квантовое число
магнитное квантовое число
определяет момент импульса электрона
(орбитальный момент импульса):
m определяет проекцию момента импульса электрона на
направление Z внешнего магнитного поля:
L Le ( 1)
Lz m
ВЫВОД:
Модуль Lе электрона в атоме и его
ориентации в пространстве квантуются.
Возможная ориентация вектора Lе
для d-состояния
(l = 2, m = 0,±1, ±2)

25.

Из уравнения Шредингера → состояние электрона в атоме
характеризуют квантовые числа n, l, m
Решение уравнения :
Ψ-функция содержит квантовые числа.
Число равно числу степеней свободы частицы.
→в случае одномерной потенциальной ямы появляется одно n
Если заданы n и l, то возможны (2l+1) состояние.
Если задано n, то число состояний :
1 2n 2 1n n2
(
2
1
)
2
0
n 1
(3)

26.

Энергетические уровни. Спектр излучения.
Энергия электрона зависит только от n :
1
En
4
0
2
mZ 2e4 1
2 2 n2
Одному n может соответствовать несколько l и m.
→ Электрон в атоме может иметь одно значение энергии,
находясь в различных состояниях.
Состояния с одинаковой энергий называют вырожденными.
Кратность вырождения энергетического
уровня - число состояний с одинаковой энергией .
Число состояний, соответствующих данному значению n равно n2
n 1
(2 1)
0
1 2n 2 1n n2
2
Состояния с различными l различаются величиной Lе.

27.

Обозначения состояний электрона с различными значениями l
(в атомной физике)
ℓ
=
0
1
2
3 …
состояние
s
p
d
f …
Возможные состояния электрона в атоме «Н» (водородоподобном ионе)
n
ℓ
m
Состояние
Кратность
вырождения
1
0
0
1s
1
2
0
1
0
-1, 0, +1
2s
2p
4
3
0
1
2
0
-1, 0, +1
-2, -1, 0, +1, +2
3s
3p
3d
9

28.

Схема энергетических уровней электрона в атоме «Н»
Энергия электрона в атоме «Н» зависит от n, не зависит от l и m.
Состояние 1s – основное состояние электрона в атоме «Н».
Атом имеет минимальную энергию.

29.

Контрольные вопросы:
??
1. Электрон в атоме находится в f-состоянии.
Орбитальный момент импульса Lе электрона
равен …
1.
3
2.
2 3
3.
3
4.
3
2
2. Электрон в атоме водорода находится в рсостоянии. Возможные проекции орбитального
момента импульса электрона на направление
магнитного поля равны … .
1. 0, ±2, ±½
2. 0, ±1, ±2
3. 0, ±1, ±½
4. 0, ±1