Similar presentations:
Применение уравнения Шредингера. (Лекция 6)
1.
Кафедра физикиЛЕКЦИЯ 6
ПЛАН ЛЕКЦИИ
1. Движение свободной частицы.
2. Частица в одномерной глубокой потенциальной яме.
3. Прохождение частицы через потенциальный барьер.
Туннельный эффект.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
1
2.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Рассмотрим некоторые простейшие стационарные задачи
квантовой механики, связанные с решением уравнения
Шредингера в разных потенциальных полях.
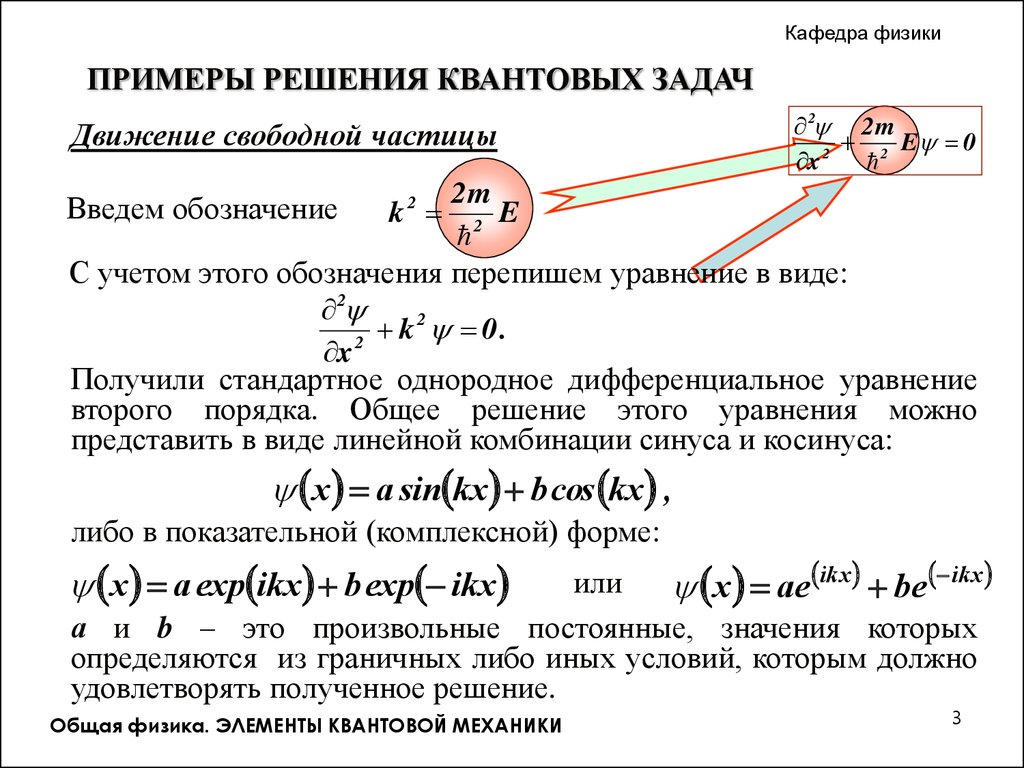
Движение свободной частицы
Свободная частица – это частица, движущаяся в отсутствие
внешних полей.
Рассмотрим одномерный случай. Пусть частица движется вдоль
оси x.
На свободную частицу силы не действуют, потенциальная энергия
частицы U x const и ее можно принять равной нулю.
Тогда полная энергия совпадает с ее кинетической энергией.
Вид уравнения Шредингера:
2m
2 E U 0
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
2 2 m
2 E 0
2
x
2
3.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Движение свободной частицы
2 2 m
E 0
x 2 2
2m
E
2
С учетом этого обозначения перепишем уравнение в виде:
2
2
k
0.
2
x
Получили стандартное однородное дифференциальное уравнение
второго порядка. Общее решение этого уравнения можно
представить в виде линейной комбинации синуса и косинуса:
Введем обозначение
k2
x a sin kx b cos kx ,
либо в показательной (комплексной) форме:
x a exp ikx b exp ikx
или
x ae ikx be ikx
а и b – это произвольные постоянные, значения которых
определяются из граничных либо иных условий, которым должно
удовлетворять полученное решение.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
3
4.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
2
2
Движение свободной частицы
k
0.
2
x
Вспомним, что представление решения в комплексной форме
позволяет заменить при некоторых математических операциях
громоздкие тригонометрические преобразования более простыми
действиями над комплексными величинами.
В рассматриваемой задаче для свободной частицы записанное
уравнение известно нам из теории гармонических колебаний.
Решение уравнения гармонических
x a sin kx
колебаний имеет вид:
Решение удовлетворяет стандартным ограничительным условиям
для пси – функции при любых значениях k и х: конечность,
однозначность, непрерывность.
Вывод: частица может иметь любые
2 2
E
k 2m
возможные значения энергии:
Итак, свободная частица имеет непрерывный спектр энергии.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
4
5.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Найдем собственные значения энергии и соответствующие им
собственные функции для частицы, находящейся в бесконечно
глубокой одномерной потенциальной яме.
Потенциальной ямой называется такая область пространства, в
которой потенциальная энергия частицы достигает локального
минимума.
U
U=
Предположим, что частица
двигаться только вдоль оси х
U=
может
Пусть
движение
ограничено
непроницаемыми
для
частицы
отвесными стенками: х = 0 и х = l.
0
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
5
6.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Потенциальная энергия имеет следующий вид: она равна нулю при
0 ≤ х ≤ l и обращается в бесконечность при х 0 и х l.
Уравнение Шредингера для заданных условий запишем в виде:
2 2m
2 E U 0
2
x
За пределы потенциальной
частица попасть не может.
U
U=
U=
ямы
Поэтому вероятность обнаружения
частицы вне ямы равна нулю.
0
l
x Соответственно и функция
пределами ямы равна нулю.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
за
6
7.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Функция должна быть непрерывной,
2
2m
следовательно, она должна быть равна
2 E U 0
2
x
нулю и на границах ямы.
Запишем это так: 0 l 0
Этому условию должны удовлетворять
решения уравнения Шредингера.
U
U=
В области х 0 и х l уравнение
Шредингера имеет вид:
U=
2 2 m
2 E 0 ,
2
x
0
l
x
поскольку в этой области U = 0.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
7
8.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Как и в предыдущей задаче, введем
2
2m
обозначение
2m
E
U
0
2
2
2
x
k
2 2 m
2 E 0 ,
2
x
E
С учетом этого обозначения перепишем
последнее уравнение в виде:
2
2
k
0
2
x
U
U=
2
Это уравнение колебаний. Решение
имеет вид:
U=
x a sin kx
Определим значения констант k и ,
воспользовавшись записанными ранее
граничными условиями
0
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
0 l 0
8
9.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Из условия 0 0 получим:
2 2 m
2 E U 0
2
x
0 a sin 0
2 2 m
Отсюда следует, что должна быть равна нулю.
E
0
,
x 2 2
Используем второе граничное условие - l 0:
2
2
l a sin kl 0
k
0
2
x
Это соотношение выполняется только в том
случае, если
(n = 1, 2, 3. …).
kl n
U
U= U=
Вспомним введенное
ранее обозначение
0
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
k2
2m
E
2
9
10.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
2 2
n
Поскольку k 2 , запишем выражение для
l2
2
k 2 0
2
x
энергии в виде:
U
U= U=
0
E
l
Таким
2 2
2 ml
2
n
,
2
образом,
(n = 1, 2, 3. …).
стационарное
уравнение
x Шредингера, описывающее движение частицы
в потенциальной яме с бесконечно высокими стенками,
удовлетворяется только при собственных значениях энергии,
зависящих от целого числа n.
Следовательно, энергия
En
частицы принимает
определенные дискретные значения, т.е. квантуется.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
лишь
10
11.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
E
2 2
2
n
2
Иначе, спектр энергии оказался дискретным.
2 ml
Квантованные значения энергии En называются уровнями энергии, а
число n, определяющее энергетические уровни частицы, называется
главным квантовым числом.
В природе есть универсальный принцип:
n=4
E4 всякий объект стремится к состоянию с
минимальной энергией.
n=3
n=2
n=1
E3
E2
E1
Это характерно и для микрочастиц: из
возможных стационарных состояний для
микрочастицы наиболее предпочтительным
является состояние с минимальной энергией.
Это состояние наиболее устойчиво.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
11
12.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
состояние с минимальной энергией
2 2 2 Стационарное
называется основным состоянием (основным
E
n
2
2 ml
уровнем). Все остальные стационарные состояния
(уровни) называются возбужденными.
n=4
n=3
n=2
n=1
E4
E3
E2
E1
Из выражения для энергии видно, что
степень дискретности энергии сильно
зависит от ширины потенциальной ямы l и
массы частицы m.
Оценим расстояния между соседними
уровнями для различных значений m и l .
Разность энергий двух соседних уровней
равна:
En En 1 En
2 2
2ml
n 1
2
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
2
2 2
2ml
2
n
2
2 2
2ml
2
2n 1
12
13.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
2 2
Примерно
можно
записать:
2 2
En
n
2
2
ml
E
n
2
2 ml
Если взять m порядка массы молекулы
( 10-27 г), а l порядка 10 см (молекулы газа
-32 ·n эрг.
n=4
в
сосуде),
получается
порядка
10
E
4
n=3
n=2
n=1
E3
E2
E1
Столь густо расположенные энергетические
уровни будут практически восприниматься
как сплошной спектр энергии.
Поэтому, несмотря на то, что энергия
квантована, на характер движения молекул
это влиять не будет.
Близкий результат получится, если взять m порядка массы электрона
при тех же размерах ямы (свободные электроны в металле).
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
13
14.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
E
2 2
2 ml
En
2
n
2
2 2
ml
n=4
n=3
n=2
n=1
2
Однако совсем иной результат получается для
электрона, если область, в пределах которой он
движется, будет порядка атомных размеров
( 10-10 м).
n
E4
E3
В этом случае E n получается порядка 102 ·n эВ,
так что дискретность энергетических уровней
будет заметной.
E2
E1
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
14
15.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Определим собственные значения функции x , подставив в
уравнение x a sin kx значение k из условия kl n :
n x a sin n x / l
Коэффициент a определим из условия нормировки ( 2 dV 1 ),
которое запишем следующим образом:
V
n x
a sin
dx 1
l
0
l
2
2
(Задача одномерная, поэтому в условии
нормировки интеграл по объему заменили
на интеграл по координате х).
a 2l
1.
Результат интегрирования:
2
Отсюда a 2 l .
Собственные значения функции x теперь могут быть определены
из выражения:
2
n
n x
sin
x
(n = 1, 2, 3, …)
l
l
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
15
16.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Графики собственных функций изображены на рисунке а).
2
На рисунке б) показана плотность вероятности n x обнаружения
частицы на различных расстояниях от стенок ямы.
n x
n x
2
n=4
n=4
n=3
а)
n=3
б)
n=2
n=2
n=1
0
n=1
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
0
l
x
16
17.
Кафедра физикиПРИМЕРЫ РЕШЕНИЯ КВАНТОВЫХ ЗАДАЧ
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
n x
n x
2
n=4
n=4
n=3
а)
n=3
б)
n=2
n=2
n=1
0
n=1
l
x
0
l
x
Из графиков, например, следует, что в состоянии с n = 2 частица не
может быть обнаружена в середине ямы и вместе с тем одинаково
часто бывает как в левой, так и в правой половинах ямы.
Такое представление частицы, конечно же, несовместимо с
представлением о траекториях.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
17
















 physics
physics








