Similar presentations:
Основы квантовой механики (Лекция 6)
1. Омский государственный технический университет Кафедра физики
Калистратова Л.Ф.Электронные лекции по разделам оптики,
квантовой механики, атомной и ядерной физики
9 лекций
(18 аудиторных часов)
2. Лекция 6. Основы квантовой механики
План лекции6.1. Уравнение Шредингера.
6.2. Волновая функция и её свойства.
6.3. Движение свободной частицы.
6.4. Микрочастица в одномерной потенциальной яме.
6.5. Туннельный эффект.
3. 6.1. Уравнение Шредингера
Уравнение Шредингера:- основное уравнение квантовой механики,
- описывает поведение микрочастицы в силовом
поле,
- сочетает в себе как волновые, так и
корпускулярные свойства микрочастиц,
- является законом природы,
- его нельзя строго вывести из каких-либо известных
ранее соотношений (как и уравнения Ньютона в
классической механике).
Справедливость уравнения Шредингера (записано в
1926 году) доказывается тем, что все вытекающие из
него следствия точно согласуются с опытными
фактами.
4.
1. Масса микрочастицы - m: определяет еёкорпускулярные свойства.
2. Потенциальная энергия U(х, у, z, t): определяет
взаимодействие частицы с силовым полем.
В общем случае она зависит от координат
микрочастицы и от времени.
3. «Пси»-функция (х, у, z, t): определяет
волновые свойства микрочастицы.
- является также функцией координат и времени.
Вид - функции определяется потенциальной
энергией , то есть, характером тех сил, которые
действуют на частицу.
5.
Нестационарными называются состояниямикрочастицы, в которых потенциальная энергия
зависит и от координат и от времени:
U U( x, у, z, t )
Уравнение Шредингера для нестационарных
состояний записывается как
U i
2m
t
2
Здесь
2 2 2 - оператор Лапласа.
x
y
z
2
2
2
6.
Стационарными называются состояниямикрочастицы, в которых её потенциальная
энергия не зависит от времени и является
функцией только координат:
U U( x, у, z)
Уравнение Шредингера для стационарных
состояний (без вывода):
2m
2 E U 0
Е – полная энергия микрочастицы.
7.
Уравнение Шредингшера позволяет найти ответ наследующие вопросы.
1. Каков энергетический спектр микрочастицы:
дискретный или непрерывный?
Е1, Е2,…,Еn
2. Каков вид волновых функций?
1 , 2
, …,
n
3. В какой точке силового поля локализована
микрочастица?
1
2
, 2
2
, …, n
2
8. 6.2. Волновая функция и её свойства
Особенностью квантово-механического описанияповедения микрочастиц является
вероятностный подход .
Вероятностной является причинно – следственная
связь между событиями микрочастицы.
При этом изменяется не сама вероятность поведения
микрочастицы, а величина, названная амплитудой
вероятности или «пси»-функцией.
x, y, z, t
Волновая функция описывает волновые свойства
частиц.
9.
Свойства волновой функцииПравильную интерпретацию физического смысла
волновой функции дал М. Борн в 1926 г.
1. Физический смысл имеет не сама волновая
функция, а квадрат ее модуля: квадрат модуля
волновой функции равен плотности вероятности
нахождения частицы в соответствующем объёме
пространства.
dP
dV
2
2. Вероятность Р нахождения микрочастицы в
заданном объёме V равна единице:
P dP 1
10.
3. Условие нормировки волновой функции:2
dV 1
V
4. Волновая функция должна быть:
- непрерывной, поскольку описывает
последовательное изменение поведения
микрочастицы в некотором заданном пространстве;
- однозначной и конечной, т.е. давать один ответ на
поставленный вопрос о месте нахождения
микрочастицы;
- интегрируемой и дифференцируемой по
координатам и времени.
11.
5. Первые и вторые производные от волновойфункции должны быть также непрерывными.
Из уравнения Шредингера и из условий, налагаемых на
волновую функцию, непосредственно вытекают
правила квантования.
Решения уравнения Шредингера существуют не при
любых, а только при некоторых значениях величин,
получивших название собственных значений.
Собственные значения полной энергии образуют
дискретный энергетический спектр микрочастицы:
E1 , E 2 , E 3 ...
12.
Собственным значениям энергии микрочастицысоответствуют собственные волновые функции.
1 , 2 , 3 ...
Далее можно найти вероятность нахождения
частицы в различных точках пространства:
1 , 2 ,..., n
2
2
2
Нахождения собственных значений всех величин
представляет весьма трудную математическую
задачу.
13. 6.3. Движение свободной частицы
Свободная частица движется вдоль оси Х в свободномпространстве при отсутствии внешних силовых
полей.
В этих условиях потенциальная энергия частицы
равна нулю (U = 0).
Тогда полная энергия частицы (Е=ЕК+U) равна её
кинетической энергии:
2
p
E
2m
14.
Уравнение Шредингера в одномерном случаедвижения имеет вид:
2
d 2m
E
0
2
2
dx
Это уравнение похоже на дифференциальное
уравнение гармонических колебаний,
2
d x
2
x 0
2
dt
решением которого является выражение:
x x O sin( t )
15.
По аналогии обозначим величину2mE
2
2
Тогда решением уравнения Шредингера является
выражение:
( x ) O sin( t )
Эта функция представляет собой плоскую
монохроматическую волну де Бройля.
16.
Область локализации частицы определяет квадратмодуля волновой функции.
O sin ( x )
2
2
1
sin x
2
2
2
Поскольку
, то
O
2
2
2
Получили, что все положения частицы в
пространстве (вдоль оси Х) равновероятны.
.
17.
Определим значения полной энергии и импульсачастицы:
E
2m
2
2
p
Поскольку частота волновой функции может
принимать любые положительные значения, то
импульс р и энергия Е частицы принимают
любые значения.
Энергетический спектр свободной частицы является
непрерывным.
18.
Зависимость полной энергии от импульса(равнозначно от частоты)
Е
2 2
E
2m
p2
E
2m
р
Непрерывный энергетический спектр
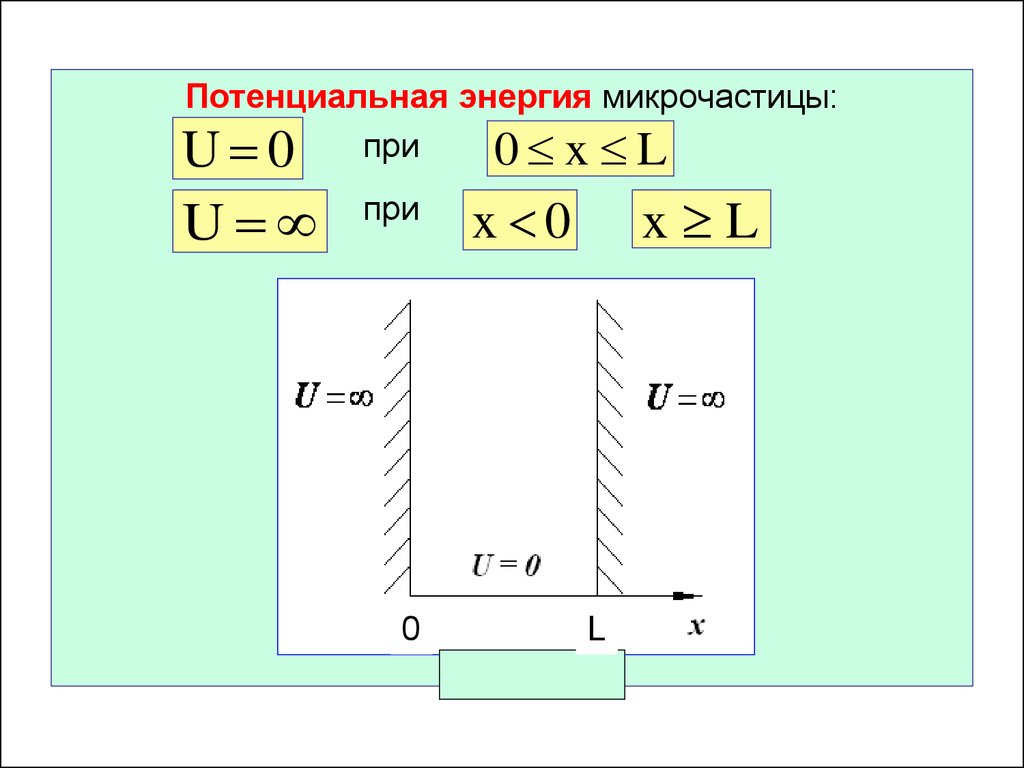
19. 6.4. Частица в одномерной потенциальной яме
Потенциальной ямой называется областьпространства, в которой частица будет
находиться, имея заданное значение полной
энергии Е.
Исследуем поведение микрочастицы в бесконечно
глубокой одномерной потенциальной яме.
Взаимодействие частицы с силовым полем определяет
потенциальная энергия U (x,у,z, t).
20.
Рассмотрим частицу массой m в таком силовом поле, вкотором потенциальная энергия U:
- зависит только от одной координаты (одномерный
случай движения);
- не зависит от времени (стационарные состояния
частицы).
В данном случае частица может двигаться только вдоль
оси х .
Пусть движение ограничено непроницаемыми для
частицы стенками:
x=0 и x=L .
L – ширина потенциальной ямы.
21.
Потенциальная энергия микрочастицы:U 0 при 0 x L
U
при
0
x L
x 0
L
22.
Уравнение Шредингера для стационарных состоянийбудет иметь вид:
d 2m
E
U
0
2
2
dx
2
За пределы потенциальной ямы частица попасть не
может, поэтому вероятность обнаружить эту
частицу за пределами ямы равна нулю.
Тогда и волновая функция за пределами ямы
равна нулю.
23.
Граничные условия:- определяют те условия, которым должны
удовлетворять решения уравнения Шредингера,
имеющие физический смысл.
- они вытекают из условия непрерывности
волновой функции .
должна быть равна нулю не только за
пределами ямы, но и на границах ямы.
24.
Граничные условия для волновой функциимикрочастицы, находящейся в потенциальной
одномерной яме:
( 0) 0
(L) 0
В области между 0
и L потенциальная энергия
U = 0, но волновая функция
0
.
25.
Уравнение Шредингера примет вид:d 2 2m
2 E 0
2
dx
Введём обозначение
2mE
2
2
и перепишем уравнение Шредингера.
d
2
0
2
dx
2
Этот вид уравнения хорошо известен в теории
колебаний как дифференциальное уравнение для
собственных колебаний осциллятора.
26.
Его решением является выражение для волновойфункции:
.
(x) O sin x
Применим к этому выражению граничные условия.
1. Из первого условия (0) 0 получаем:
(0) O sin 0
.
sin 0
Отсюда следует, что постоянная величина
0
.
27.
2. Из второго условия( L) 0
следует:
(L) O sin L 0
Это возможно только, если
L n
параметр n = 1, 2, 3, …
Значение n = 0 отпадает, поскольку при этом
частица в потенциальной яме не находится, что
противоречит условию задачи.
28.
Решения уравнения Шредингера будут иметьфизический смысл не при всех значениях энергии , а
лишь при значениях, удовлетворяющих соотношению:
2m
2
En 2 n
2
L
2
Таким образом, мы получили собственные значения
полной энергии в виде дискретного ряда:
2
En
n
2
2mL
2
2
(n = 1, 2, 3, …)
29.
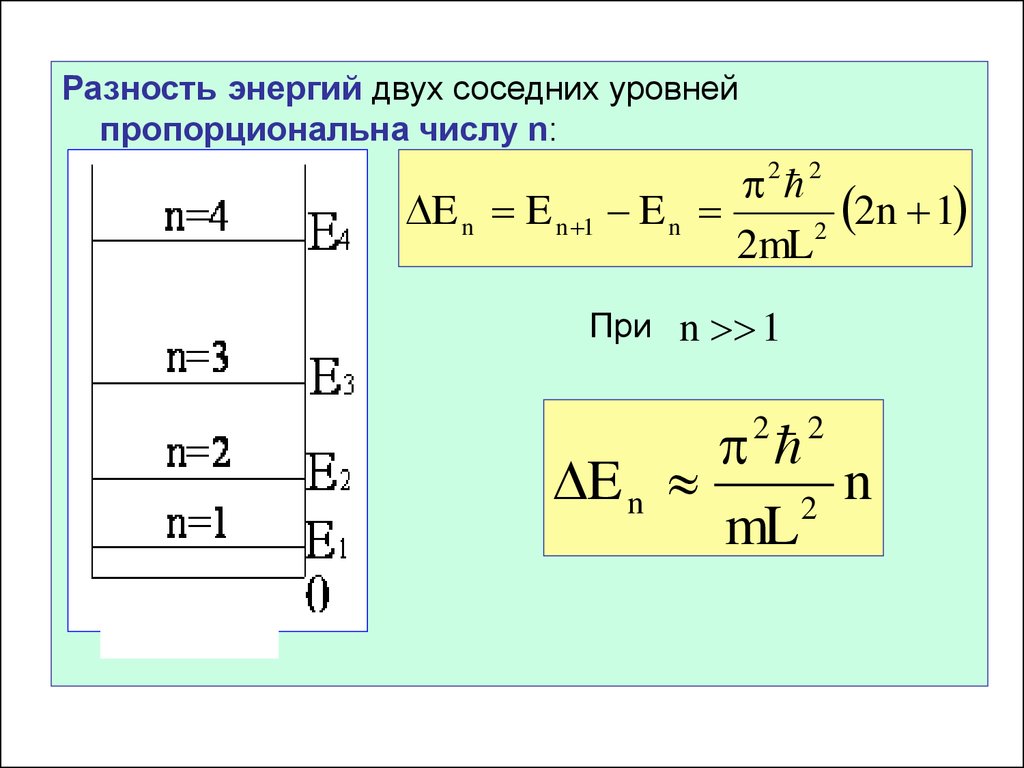
Особенности энергетического спектра1. Полная энергия частицы положительная ( E 0 ).
2. Полная энергия квантуется: принимает дискретный
набор значений, причём
E n n E1
E n n 2 E1
2
Энергия первого (основного) состояния: E 1
2
2mL
2
2
3. Энергетический спектр является расходящимся,
поскольку расстояния между уровнями
увеличиваются.
30.
Разность энергий двух соседних уровнейпропорциональна числу n:
2 2
2n 1
E n E n 1 E n
2
2mL
При
n 1
E n
n
2
mL
2
2
31.
Произведем оценку расстояний между соседнимиуровнями для различных значений массы частицы m
и ширины ямы L.
26
Пример 1. Рассмотрим молекулу ( m ~ 10 кг ) в сосуде
(
): ~ 0,1м
L
3,142 (1,05 10 34 ) 2
39
20
E n
n
10
n
Дж
10
n эВ.
26
2
10 0,1
Столь густо расположенные энергетические уровни
будут практически восприниматься как сплошной
спектр энергии.
Квантование энергии в этом случае в принципе имеет
место, но на характере движения молекул это не
сказывается.
32.
Пример 2. Свободные электроны ( m ~ 10 30 кг ) вметалле ( L ~ 0,1м ).
En ~ n 10
35
Дж n 10
16
эВ
В этом случае квантованием энергии также можно
пренебречь.
Пример 3. Электрон в атоме (L = 0,1 нм).
34 2
3,14 (1,05 10 )
17
2
E n
n
10
Дж
n
10
эВ
30
10 2
10 (10 )
2
Дискретность энергетических уровней будет
проявляться весьма заметно.
33.
Перейдём к рассмотрению собственных значенийволновых функций:
, где
n
n O sin x
Тогда
L
n x
( x ) O sin
L
O
Для нахождения амплитуды волновой функции
воспользуемся условием нормировки, в котором
пределы интегрирования будут от 0 до L (частица
существует только внутри ямы).
34.
dx 12
0
n x
O sin
dx 1
L
0
L
L
2
O
2
Амплитуда волновой функции
2
L
1
2
O
2
L
.
Окончательно волновые функции запишутся как
2
n x
n
sin
L
L
n = 1, 2. 3,…
35.
Поскольку для энергии микрочастицыимеем следующие выражения:
то импульс частицы будет равен:
С учётом
n
L
2
p
E
2m
2 2
E
2m
p h
получим выражение для
длины волны де Бройля:
h 2L
Б
p
n
.
36.
Область локализации частицы в потенциальной ямеопределяется через квадрат модуля волновой
функции:
n
2
2
2 n x
sin
L
L
.
Частица вероятнее всего находится в той точке ямы,
для которой наблюдается наибольшее значение
вероятности, определяемое как
x
P
O
2 2 n x
sin
L
L
37.
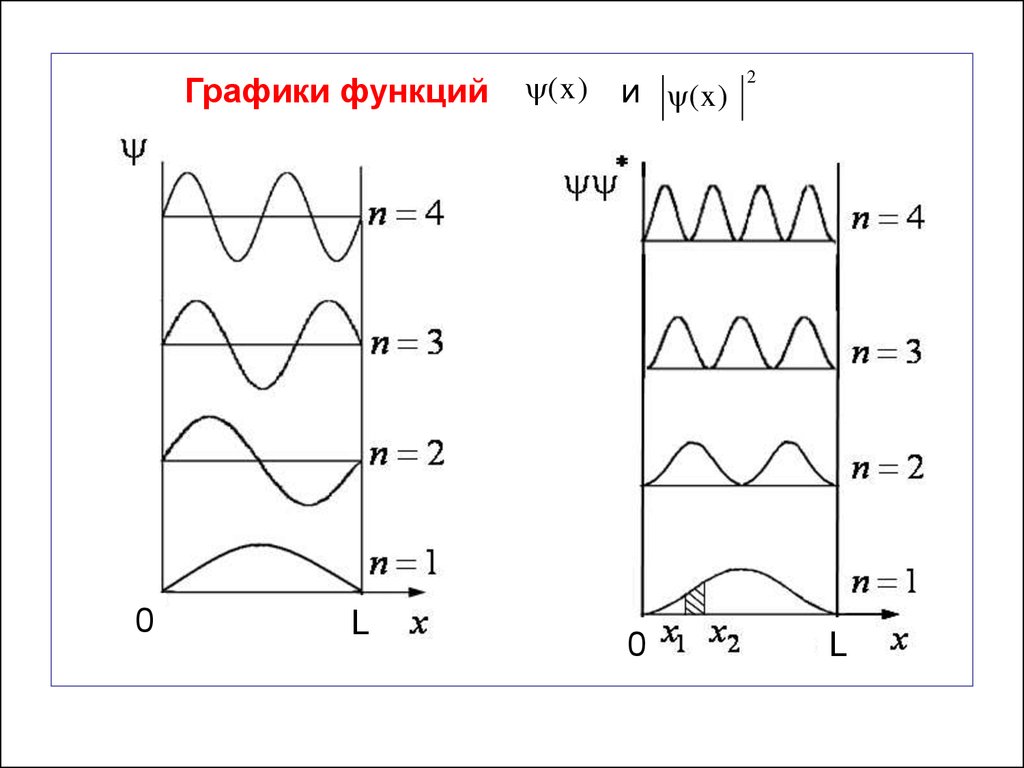
Графики функций0
L
(x)
и ( x )
0
2
L
38.
Если необходимо найти вероятность обнаружениячастицы в некоторой области ямы между точками с
координатами х1 и х2, то согласно смыслу волновой
функции необходимо вычислить интеграл вида:
.
x2
P ( x ) dx
2
x1
При этом искомая вероятность Р на рисунке будет
изображаться заштрихованной площадью между
точками х1 и х2.
39.
Выводы:1. При n = 1 (основное состояние). Микрочастица
- имеет энергию Е1;
2 2
E1
2mL2
- имеет длину волны де Бройля
2L
Б
2L
n
- на ширине ямы укладывается половина длины
волны де Бройля частицы;
- вероятнее всего будет находиться в середине ямы с
координатой х = L/2.
40.
2. При n = 2 (первое возбуждённое состояние).Микрочастица
- имеет энергию Е2
E2 4E1
;
- имеет длину волны де Бройля
2L
Б
L
n
- на ширине ямы укладывается целая длина волны
де Бройля;
- частица с одинаковой вероятностью может
находиться в двух точках потенциальной ямы с
координатами х1 = L/4 и х2 = 3L/4.
41.
3. Если частицу возбудить до высоких энергий(
), то она может находиться в любой точке
ямы.
В этих условиях частица может покинуть пределы
ямы и перейти в область потенциального барьера.
n
Вероятность обнаружения частицы за пределами
потенциальной ямы оказывается хотя и очень малой,
но отличной от нуля.
Это совершенно невозможно с точки зрения
классической теории.
В квантовой же механике подобные явления возможны
благодаря так называемому туннельному эффекту.
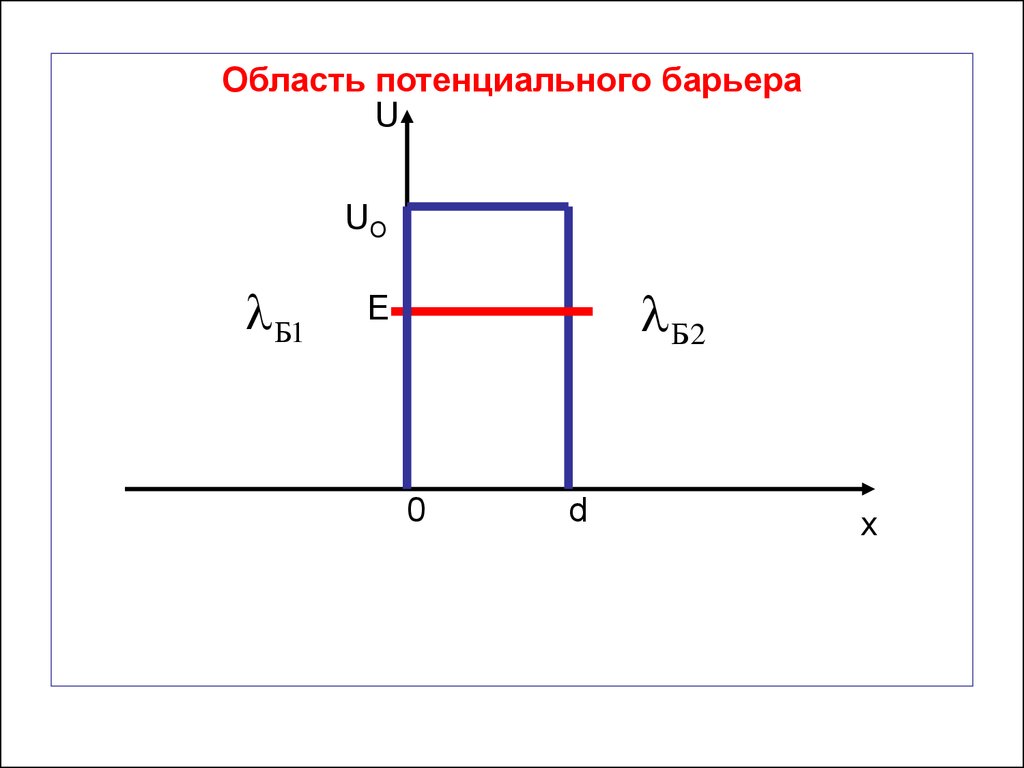
42. 6.5. Туннельный эффект
Потенциальным барьером называется областьпространства, в которой частица не может
находиться , имея данную энергию Е.
Туннельный эффект:
- явление прохождения частиц через
потенциальный барьер;
– явление чисто квантовое, не имеющее аналога в
классической физике.
43.
Одномерный потенциальный барьер спрямоугольными стенками
U(x)
Uo
E
I
II
0
III
ed
x
44.
Пусть частица, движущаяся слева направо, встречаетна своем пути потенциальный барьер:
- высотой U0 ;
- шириной d.
По классическим представлениям поведение
частицы имеет следующий характер:
- если энергия частицы больше высоты барьера
(Е > U0), то она беспрепятственно проходит над
барьером;
- на участке 0 ≤ х ≤ d лишь уменьшается скорость
частицы, но затем, при х > d снова принимает
первоначальное значение;
45.
- если же Е < U0 , то частица отражается от барьераи летит в обратную сторону.
Классическая частица сквозь барьер проникнуть
не может.
В области потенциального барьера полная энергия
частицы меньше потенциальной энергии:
Е < U0.
Как известно, полная энергия равна сумме
кинетической и потенциальной энергий: Е = ЕК +U.
46.
Тогда кинетическая энергия классической частицы вобласти потенциального барьера должна быть
отрицательной:
ЕК < 0.
Этого не может быть с точки зрения классической
физики.
Совершенно иначе выглядит поведение частицы
согласно квантовой механике.
Во - первых, даже при Е > U0 имеется отличная от
нуля вероятность того, что частица отразится от
барьера и полетит в обратную сторону.
47.
Во - вторых, при Е < U0 имеется отличная от нулявероятность того, что частица проникнет «сквозь»
барьер и окажется в области, где х > d.
Такое совершенно невозможное с классической точки
зрения поведение микрочастиц вытекает
непосредственно из уравнения Шредингера.
Рассмотрим задачу для случая, когда полная энергия
микрочастицы меньше высоты потенциального
барьера:
Е < U0
48.
В этом случае уравнение Шредингера имеет вид:d 2m
2 E 0
2
dx
2
d 2m
2 E U 0 0
2
dx
для областей I и III
2
причем
E U0 0
для области II,
49.
Решение данной задачи является сложным, поэтомуограничимся основными выводами.
Что происходит с микрочастицей в области
потенциального барьера - неизвестно.
Достоверно известно лишь то, что частица была перед
барьером, имея длину волны де Бройля Б1 , и
стала находиться в области за потенциальным
барьером, изменив свои волновые свойства и
обладая длиной волны де Бройля Б 2 .
50.
Область потенциального барьераU
UO
Б1
Б2
E
0
d
x
51.
На отрезке x d неопределённость импульса pсоставляет величину
.
p
d
Связанная с этим разбросом неопределённость
2
кинетической энергии
p
E
2m
может оказаться достаточной для того, чтобы полная
энергия частицы Е оказалась больше потенциальной
энергии UO .
Частица в этих условиях преодолевает область
потенциального барьера.
52.
Поскольку в области потенциального барьера дляквантовой частицы «работает» соотношение
неопределённостей, то координата и импульс
частицы не могут иметь определенных значений.
Это означает, что не могут быть одновременно точно
определены кинетическая ЕК и потенциальная U
энергии.
Кинетическая энергия зависит от импульса, а
потенциальная от координат.
53.
Таким образом, хотя полная энергия частицы имеетопределенное значение Е, она не может быть
представлена в виде суммы точно определенных
энергий ЕК и U.
Ясно, что в этом случае заключение об
отрицательности кинетической энергии ЕК «внутри
туннеля» становится бессмысленным.
54.
Вероятность прохождения частицы через барьерназвана коэффициентом прозрачности D.
D DO e
2d
2 m U0 E
Вероятность прохождения частицы через
потенциальный барьер сильно зависит от:
- ширины барьера d,
- величины U 0 E .
Коэффициент прозрачности сильно уменьшается
при увеличении массы частицы m.
55.
Если при какой-то ширине барьера коэффициентпрочности D = 0,01, то при увеличении ширины
барьера в 2 раза величина D = 0,012, коэффициент
прозрачности уменьшается в 100 раз.
Тот же эффект вызвало бы вырастание в 4 раза
величины U 0 E .
При преодолении потенциального барьера частица как
бы проходит через «туннель» в этом барьере, в
связи с чем рассмотренное нами явление называют
туннельным эффектом.
56.
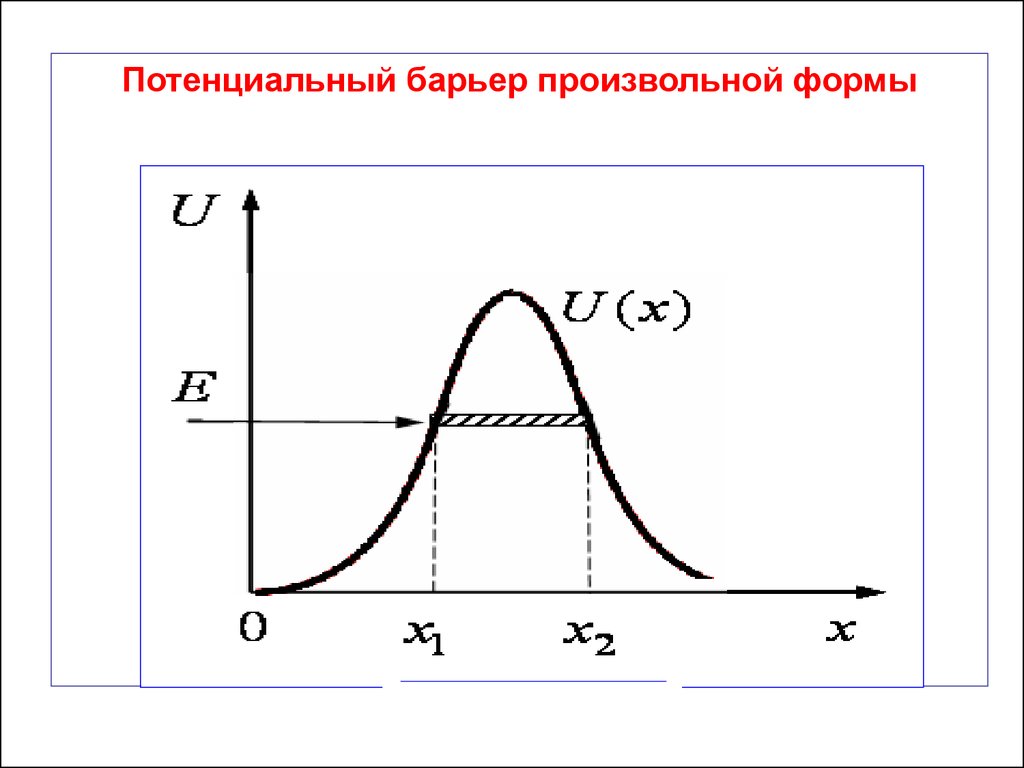
Потенциальный барьер произвольной формы57.
Коэффициент прозрачности для потенциальногобарьера произвольной формы имет вид:
D e
где
2
x2
x1
U U x .
2 m U 0 E dx
58.
Примером проявления туннельного эффектамогут служить следующие явления природы:
- радиоактивность;
- холодная эмиссия электронов из металла;
- ионизация атома в поле сильной
электромагнитной волны;
- ионизация атома в сильном электрическом поле.





















































 physics
physics








