Свободные затухающие колебания

1. 5.2 Свободные затухающие колебания

-это колебания, происходящие под действием внутренних
сил системы; при этом амплитуда колебаний со временем
уменьшается из-за потерь энергии реальной колебательной
системой.
-В механических системах колебания затухают из-за
взаимного трения частей системы или сопротивления среды;
в колебательном контуре – из-за выделения джоулева тепла
или излучения электромагнитной энергии.

2.

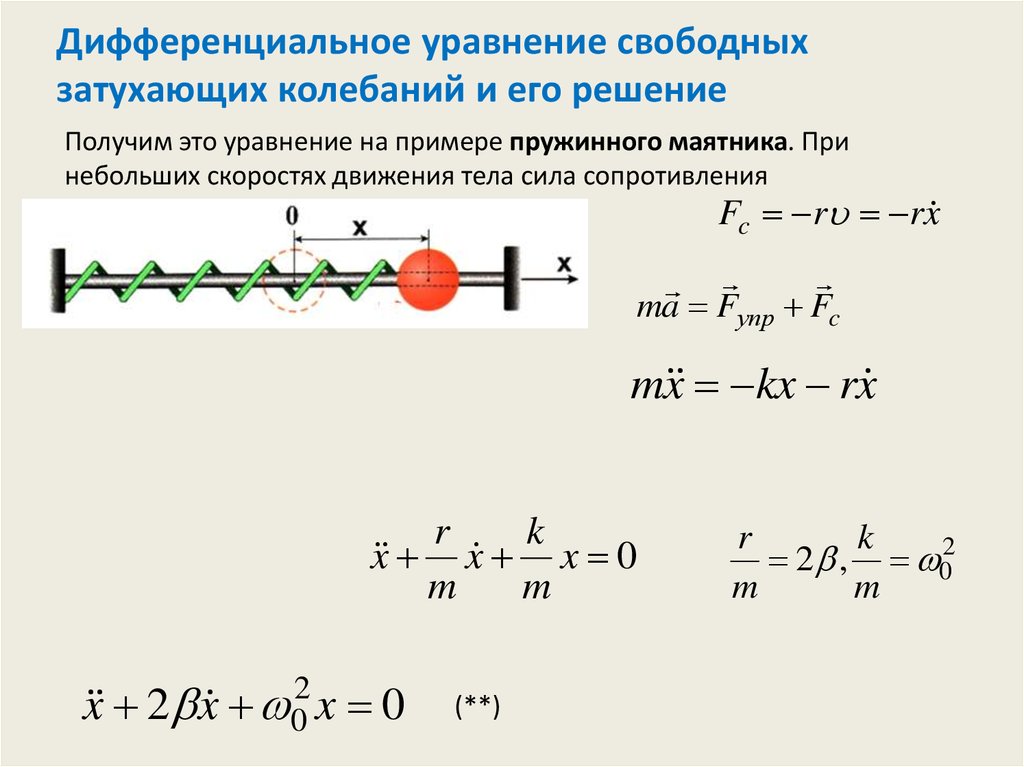
Дифференциальное уравнение свободных
затухающих колебаний и его решение
Получим это уравнение на примере пружинного маятника. При
небольших скоростях движения тела сила сопротивления
Fc r rx
ma Fупр Fc
m x kx rx
r
k
x x x 0
m
m
x 2 x 02 x 0
(**)
r
k
2 , 02
m
m

3.

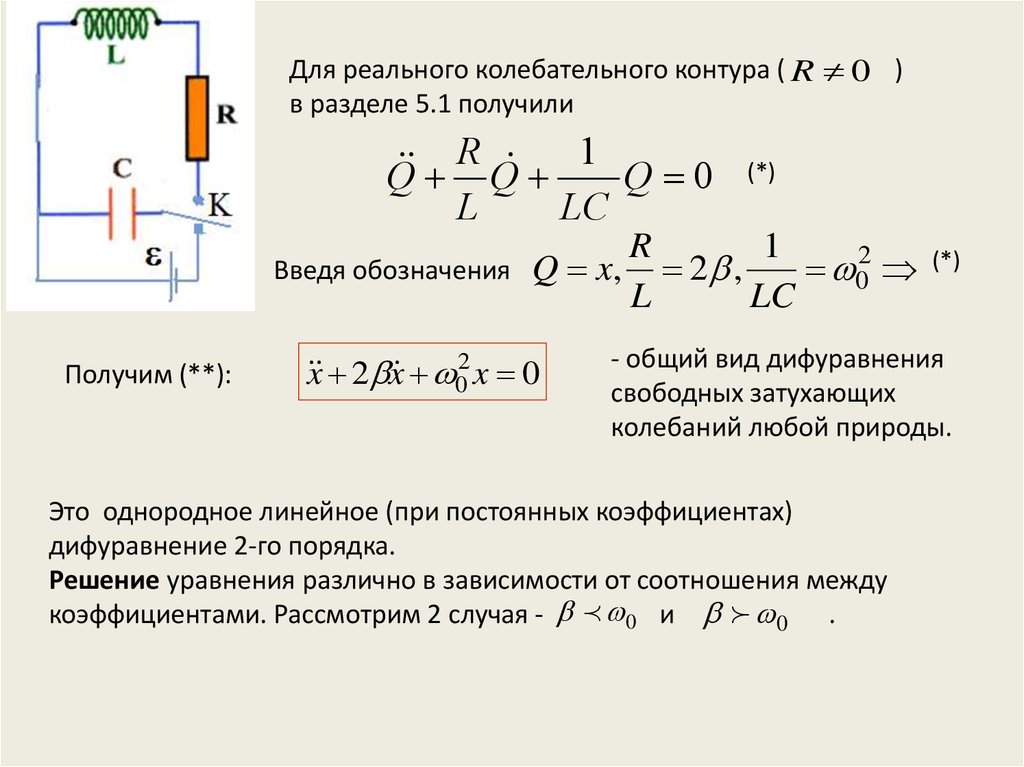
Для реального колебательного контура ( R 0 )
в разделе 5.1 получили
R
1
Q Q
Q 0
L
LC
Введя обозначения
Получим (**):
(*)
R
1
Q x, 2 ,
02
L
LC
x 2 x 02 x 0
(*)
- общий вид дифуравнения
свободных затухающих
колебаний любой природы.
Это однородное линейное (при постоянных коэффициентах)
дифуравнение 2-го порядка.
Решение уравнения различно в зависимости от соотношения между
коэффициентами. Рассмотрим 2 случая - 0 и 0 .

4.

1) При небольшом затухании 0
x (t ) A0e t cos( t 0 )
, где начальная амплитуда и начальная фаза A0 , o определяются из
начальных условий: x(0), x (0) .
Частота колебаний
02 2
Период колебаний
T
2
02 2
Амплитуда
A(t ) A0 e
С ростом затухания период колебаний растет.
t
0, 0, T .

5.

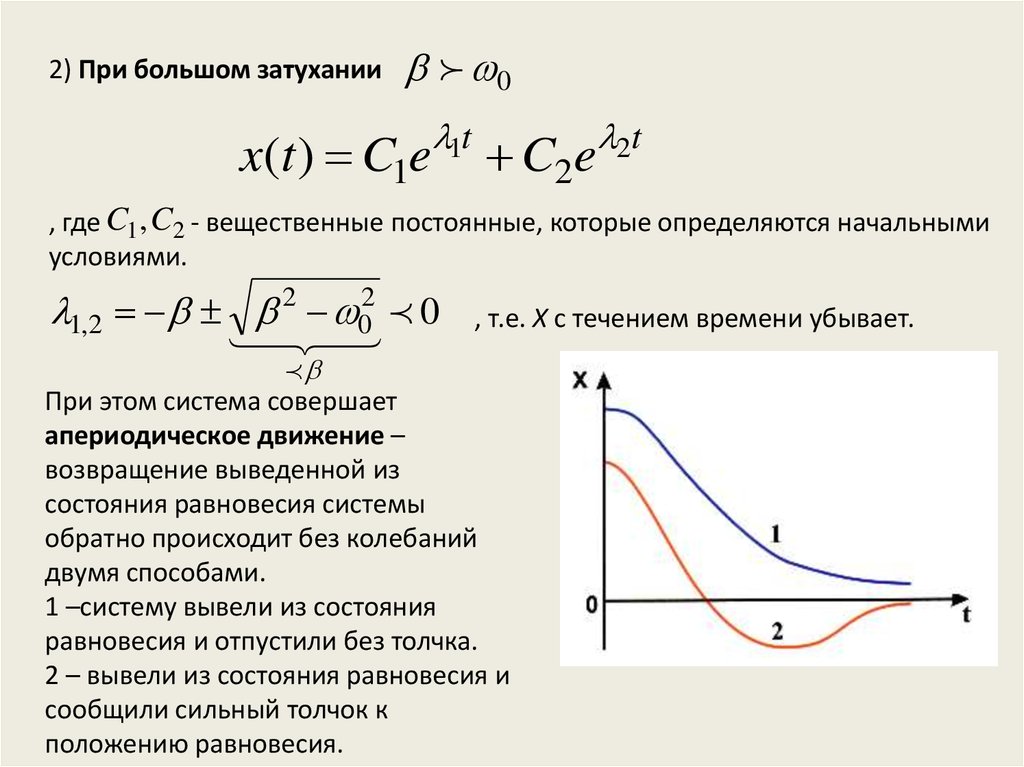
2) При большом затухании
0
x(t ) C1e
1t
C2e
2t
, где C1 ,C2 - вещественные постоянные, которые определяются начальными
условиями.
1,2 2 02 0 , т.е. X с течением времени убывает.
При этом система совершает
апериодическое движение –
возвращение выведенной из
состояния равновесия системы
обратно происходит без колебаний
двумя способами.
1 –систему вывели из состояния
равновесия и отпустили без толчка.
2 – вывели из состояния равновесия и
сообщили сильный толчок к
положению равновесия.

6.

Условие, при котором затухающие колебания переходят в апериодический
процесс:
0
Для колебательного контура:
Rкр
1
L
, Rкр 2
2L
C
LC
-критическое сопротивление, при котором прекращаются колебания в контуре.
В механической системе с диссипативными силами:
rкр
k
, rкр 2 km
2m
m

7.

Общие характеристики колебательной системы с затуханием
1. Коэффициент затухания β . Время релаксации τ.
Рассмотрим промежуток времени
1
Отношение двух амплитуд, отстоящих друг от друга на этот промежуток
времени
A(t ) A0e ( t )
1
e
t
A(t )
e
A0e
A(t )
A(t )
e
Коэффициент затухания обратен по величине промежутку времени, за
который амплитуда уменьшается в e раз.
Промежуток времени, за который амплитуда колебаний уменьшается в е
раз, называется временем релаксации колебаний.

8.

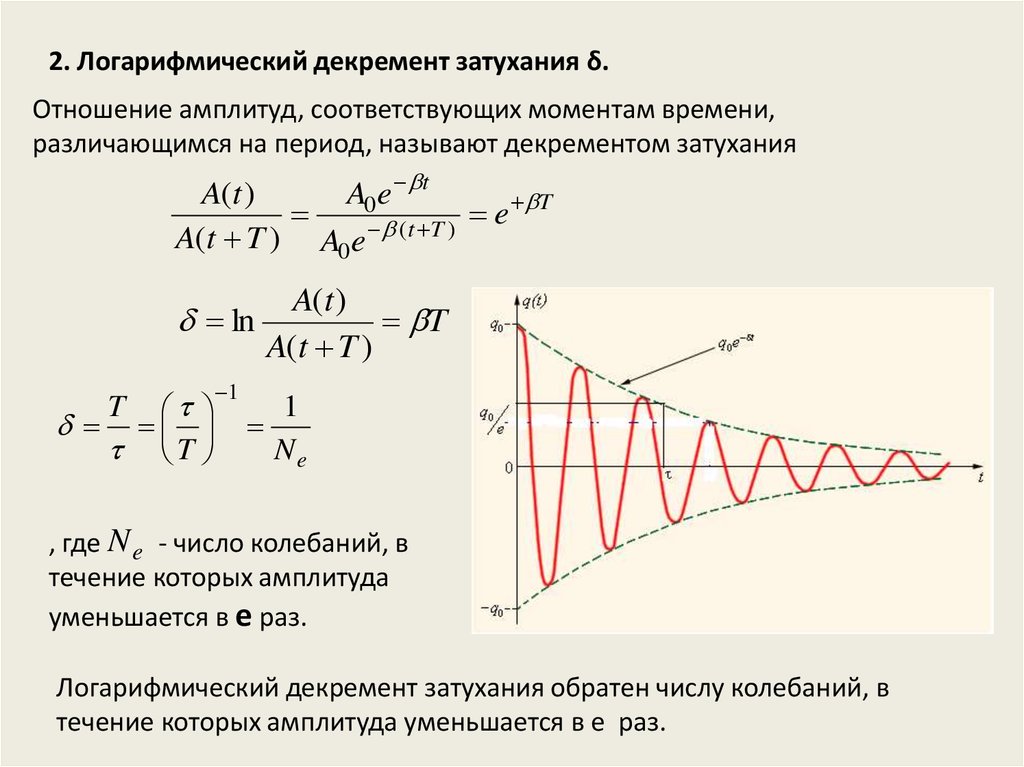
2. Логарифмический декремент затухания δ.
Отношение амплитуд, соответствующих моментам времени,
различающимся на период, называют декрементом затухания
A(t )
A0e t
T
e
A(t T ) A0e ( t T )
A(t )
ln
T
A(t T )
T
T
1
1
Ne
, где N e - число колебаний, в
течение которых амплитуда
уменьшается в е раз.
Логарифмический декремент затухания обратен числу колебаний, в
течение которых амплитуда уменьшается в е раз.

9.

3. Добротность колебательной системы Q.
Добротность характеризует потери энергии в колебательной системе
Q 2
E (t )
E (t ) E (t T )
(1)
Она равна произведению 2 на отношение энергии, запасенной в
системе в произвольный момент времени, к убыли этой энергии за один
период колебаний.
Рассмотрим колебательный контур с малым затуханием.
Q (t ) Q0e t cos( t 0 )
Когда вся энергия сосредоточена в конденсаторе, полная энергия колебаний
Q 2 Q02e 2 t
E (t )
2C
2C
Q02e 2 (t T )
E (t T )
2C
E (t T )
e 2 T
E (t )
(1)

10.

Q 2
1
2
E (t T ) 1 e 2 T
1
E (t )
При малом затухании колебаний
T
2
02
2
0
(2)
:
2
2
0
1
1
1
e x
x 1
1 x
(2)
2
2
Q
N e
2 T
1 (1 2 T ) T
1 e
Q N e
Добротность системы с малым затуханием пропорциональна числу
колебаний, в течение которых амплитуда уменьшается в е раз.

11.

5.3 Вынужденные колебания
-Происходят под действием внешней, периодически меняющейся со
временем силы. Чтобы в реальной колебательной системе получить
незатухающие колебания, надо компенсировать потери энергии.
В колебательном контуре, например, такая компенсация осуществляется
с помощью источника переменного тока.
Дифференциальное уравнение вынужденных колебаний
и его решение
Получим это уравнение на примере колебательного контура,
подключенного к переменной ЭДС.
(t ) s U C U R
dI
Q 1
(t ) L IR
dt
C L
d 2Q R dQ 1
(t )
Q
2
L dt LC
L
dt

12.

(t )
L
f (t ) - некая периодическая функция времени. Пусть, например,
она меняется по гармоническому закону:
f (t )
0
L
cos t f 0 cos t
Общий вид дифференциального уравнения вынужденных
колебаний любой природы:
x 2 x 02 x f (t )
Если вынуждающая сила изменяется по гармоническому закону с частотой Ω
уравнение имеет вид
x 2 x 02 x f 0 cos t (1)
(1) – линейное (при постоянных коэффициентах) неоднородное
уравнение 2-го порядка. Общее решение такого уравнения есть сумма
общего решения однородного уравнения + любое частное решение
неоднородного уравнения:
x (t ) xод (t ) xн (t )

13.

Рассмотрим случай не очень быстрого затухания собственных колебаний,
когда 0
Тогда xод (t ) A0 e t cos( t 0 ) ,
а xн (t ) соответствует незатухающим колебаниям с частотой
вынуждающей силы:
xн (t ) A cos( t ),
(2)
Где А – амплитуда, - величина отставания по фазе вынужденного
колебания от вынуждающей силы.
После приложения периодически действующей силы к колебательной
системе вначале возникает переходный процесс: со временем
собственные колебания в системе затухают и остаются только колебания
вида (2):
x (t ) t t A cos( t )
1
(3)

14.

x (t ) t t A cos( t )
(3)
1
Определим А и
, потребовав, чтобы x(t) удовлетворял (1).
dx
A sin( t ) A cos( t )
dt
2
(4)
d 2x
2
2
A
cos(
t
)
A
cos( t )
2
dt
(5)
(3), (4), (5)⇨ (1):
A cos( t ) 2 A cos( t
2
f 0 cos t.
2
) A 02 cos( t )
Последнее уравнение должно выполняться в любой момент времени. Для t=0:
A 2 cos( ) 2 A cos( ) A 02 cos( ) f 0
2
Т.к. cos( ) cos( ) , то

15.

A( o2
) cos( ) 2 A cos( ) f 0
2
2
A( o2 2 ) cos 2 A sin f 0
(6)
Далее используем метод векторных диаграмм. Рассмотрим векторное
уравнение
f 0 A( 02 2 ) 2 A
Выражение (6) – проекция на ось OX векторного уравнения (см. рис.)
а)
0
б) 0

16.

f 02 A2 ( 02 2 ) 4 2 2
Из прямоугольного треугольника
A
f0
( 02
) 4
2 2
2
tg 2
0 2
2
2
(7)
(8)
Т.о. А и зависят от соотношения 0 и , хотя вынужденные
колебания происходят при частоте вынуждающей силы.
Если нет затухания, т.е. 0 , то 0 - нет отставания по фазе
колеблющейся величины X от вынуждающей силы.

17. Резонанс

f0
A
Амплитуда вынужденных колебаний
2
2 2
2 2
(
)
4
определяется выражением
0
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной
системы частоте амплитуда достигает максимального значения. Это явление называется резонансом, а соответствующая частота - резонансной.
Рассмотрим две ситуации.
а) 0 , const , меняется .
Резонансную частоту р определим из условия максимального значения
амплитуды или минимального значения для подкоренного выражения
в знаменателе. Продифференцировав это выражение по и приравняв
нулю, получим условие, определяющее резонансную частоту:

18.

d
( 02 2 )2 4 2 2 0
d
2
2( 0
)( 2 ) 8 0
2
2
02 2 2 2
р 02 2 2
Amax
Amax
- частота вынуждающей силы, при которой
амплитуда вынужденных колебаний
максимальна.
f0
( 02 р ) 4 2 р
2 2
f0
2
02 2 2
02
2
f0
2
2
f0
4 4 4 2 ( 02 2 2 )

19.

A
f0
( 02 2 )2 4 2 2
р
02
2
Исследуем зависимость
2
Amax
f0
2 02 2
A( ) :
1)
0 : A A0
f0
02
- статическое
смещение системы из положения
равновесия под действием постоянной
силы f 0 .
2) : A 0.
3) Изменяем :
0, р 0, Amax
0, , р , Amax .

20.

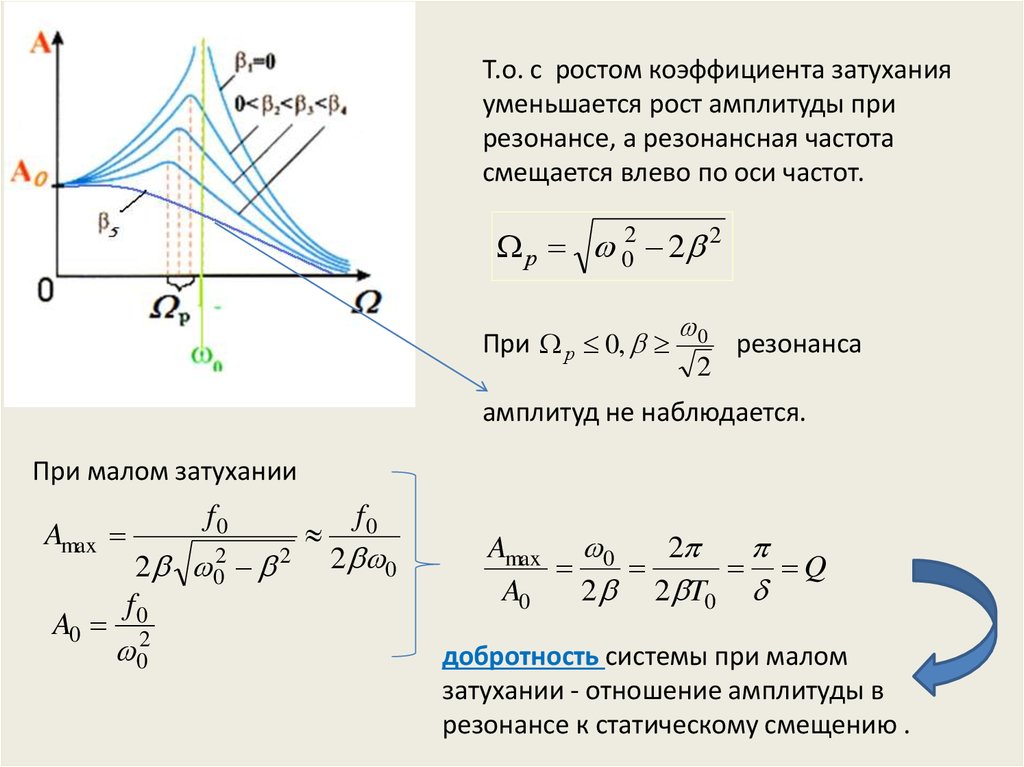
Т.о. c ростом коэффициента затухания
уменьшается рост амплитуды при
резонансе, а резонансная частота
смещается влево по оси частот.
р 02 2 2
При р 0,
0
2
резонанса
амплитуд не наблюдается.
При малом затухании
Amax
A0
f0
2
f0
02
02
2
f0
2 0
Amax 0
2
Q
A0
2 2 T0
добротность системы при малом
затухании - отношение амплитуды в
резонансе к статическому смещению .

21.

2
tg 2
0 2
(8)
Изобразим фазовые резонансные кривые ( )
0 : tg 0, 0
0 : tg ,
2
: tg 0,
б) , const, меняется 0 . (Например, настройка радиоприемника на
частоту передающей станции).

22.

Различают несколько видов резонанса.
Рассмотренный вид называется резонансом смещений (в колебательном
контуре это резонанс напряжения на обкладках конденсатора).
Другой вид резонанса – резонанс скоростей- возрастание амплитуды
скорости вынужденных колебаний ( в колебательном контуре это
соответствует резонансу тока).