Затухающие колебания

1. 18. Затухающие колебания

2.

Во всякой реальной колебательной системе
имеются
силы
сопротивления,
действие
которых приводит к уменьшению энергии
системы. В этом случае могут возникнуть
затухающие колебания.

3.

Рассмотрим колебательную систему в которой
помимо возвращающей силы имеются силы
сопротивления.
Запишем
второй
закон
Ньютона для тела массой m.
Fупр Fсопр ma
Возвращающая сила является квазиупругой
Fупр kx
Сила сопротивления пропорциональна скорости
(b – коэффициент сопротивления)
Fñî ï ð b

4.

В проекциях уравнение принимает вид:
kx b ma
kx bx mx
mx bx kx 0
b
k
x x x 0
m
m
Коэффициент затухания
Квадрат собственной
циклической частоты
b
2m
k
2
0
m

5.

Получили дифференциальное уравнение затухающих
колебаний:
x
2
2 x 0 x
0

6.

Для решения однородного ДУ 2-го порядка запишем
характеристическое уравнение и найдем его корни
(сведения из математики):
mx bx kx 0

7.

b
k
a a 0
m
m
2
2
k
b
D 4
m
m
2
b
k
b
4
m
m
m
a1,2
2
2
2
b
k b
b
k b
a1,2
1
i
2m
m
2
m
2
m
m
2
m
a1,2 i ,
i 1

8.

Решением ДУ является функция вида:
x A0e
t
cos t sin t
0
0
b
2m
2
k b
2
2
0
m 2m
где А0 и 0 – начальные амплитуда и начальная фаза
соответственно.

9.

Следовательно, решением ДУ является функция,
описывающая зависимость координаты тела при
затухающих колебаниях:
x A0e
t
cos t 0
где А0 и 0 – начальные амплитуда и начальная фаза
соответственно.
Функция удовлетворяет условию:
x(t ) t 0

10.

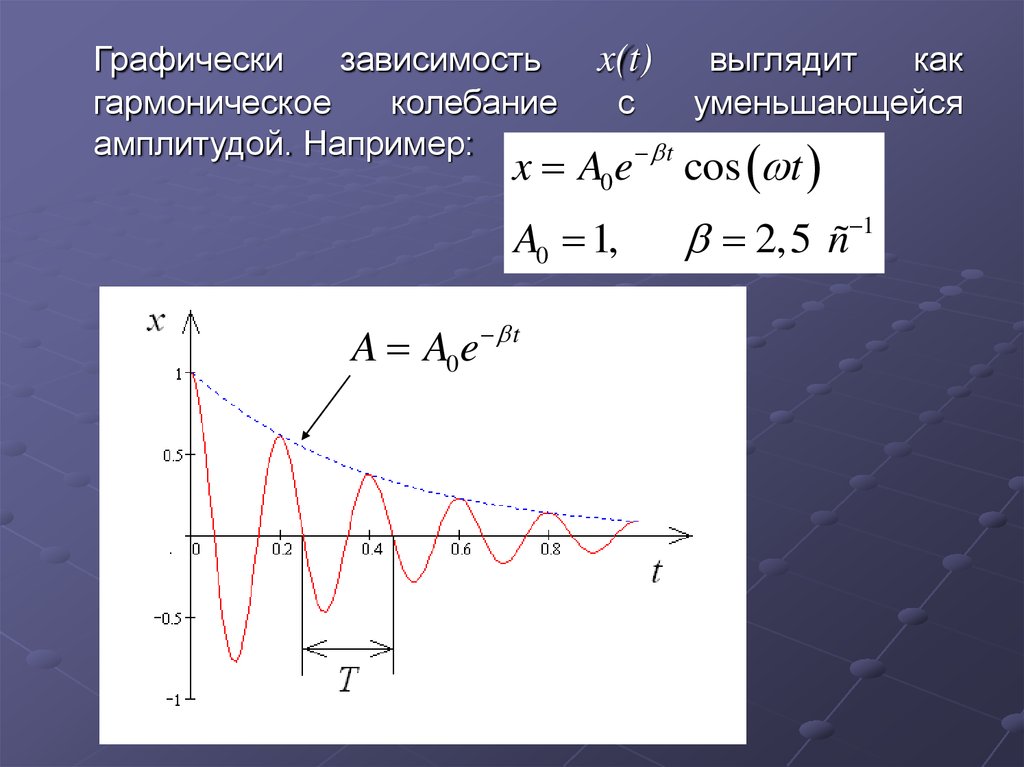
Графически
зависимость
гармоническое
колебание
амплитудой. Например:
x(t)
с
выглядит
как
уменьшающейся
x A0 e t cos t
A0 1,
A A0e t
2,5 ñ 1

11.

Циклическая
частота
затухающих
колебаний
уменьшается по сравнению с собственной частотой
колебаний системы:
2
k b
2
2
0
m 2m
Период колебаний увеличивается по сравнению с
собственным периодом T0 :
T
2
2
0
2
T0
T0
2
0

12.

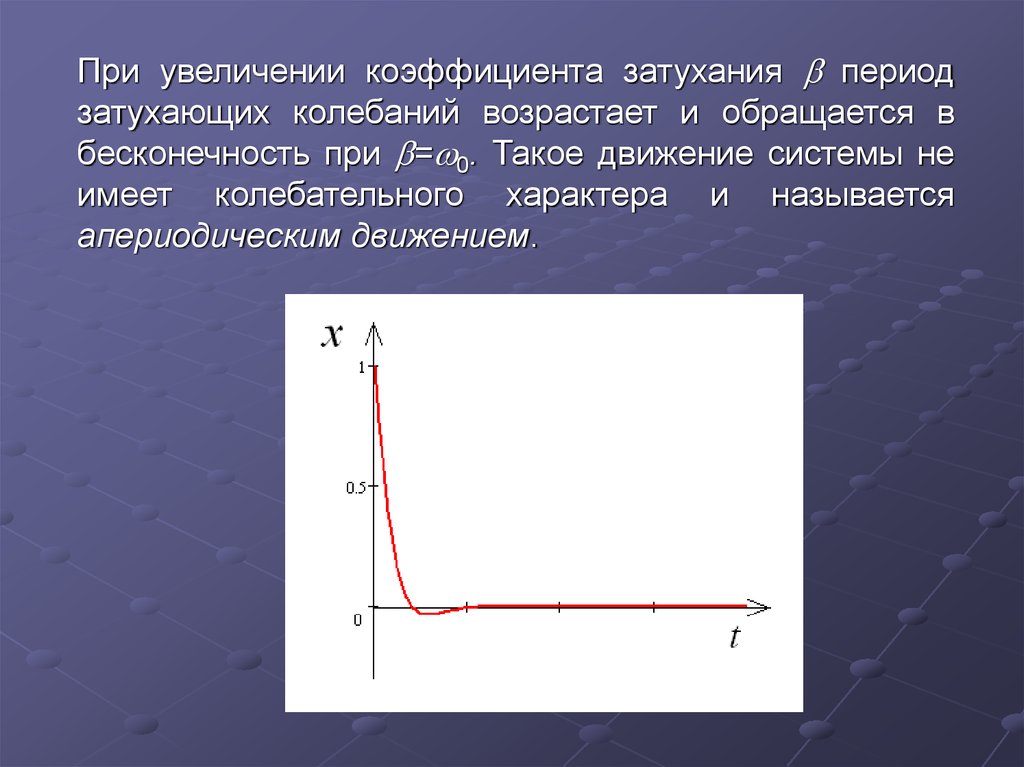
При увеличении коэффициента затухания период
затухающих колебаний возрастает и обращается в
бесконечность при = 0. Такое движение системы не
имеет колебательного характера и называется
апериодическим движением.

13.

Практическое применение апериодического движения:
1. Плавное закрытие дверей;
2. Амортизаторы автомобилей;
3. Успокоение
колебаний
стрелочных
приборов
(воздушные, электромагнитные демпферы).

14.

Амплитуда колебания со временем уменьшается по
экспоненциальному закону:
t
А A0 e
Промежуток времени, в течение которого амплитуда
колебаний уменьшается в е раз, называется временем
релаксации:
1

15. Однако время релаксации можно определить и другим способом. Найдем производную функции A(t) в начальный момент времени.

А A0 e t A0 e t
А 0 A0
A0
Время релаксации можно определить по касательной в
в начальной точке. Пример: моделирование процессов
релаксации (радиоактивный распад).

16.

Для
количественной
характеристики
быстроты
убывания
амплитуды
затухающих
колебаний
пользуются понятиями декремента (отношение
амплитуд через период) и логарифмического
декремента затухания:
A(t )
T
e
A(t T )
A(t )
T
1
ln
T
A(t T )
Ne
Ne – число колебаний за время, равное времени
релаксации.

17.

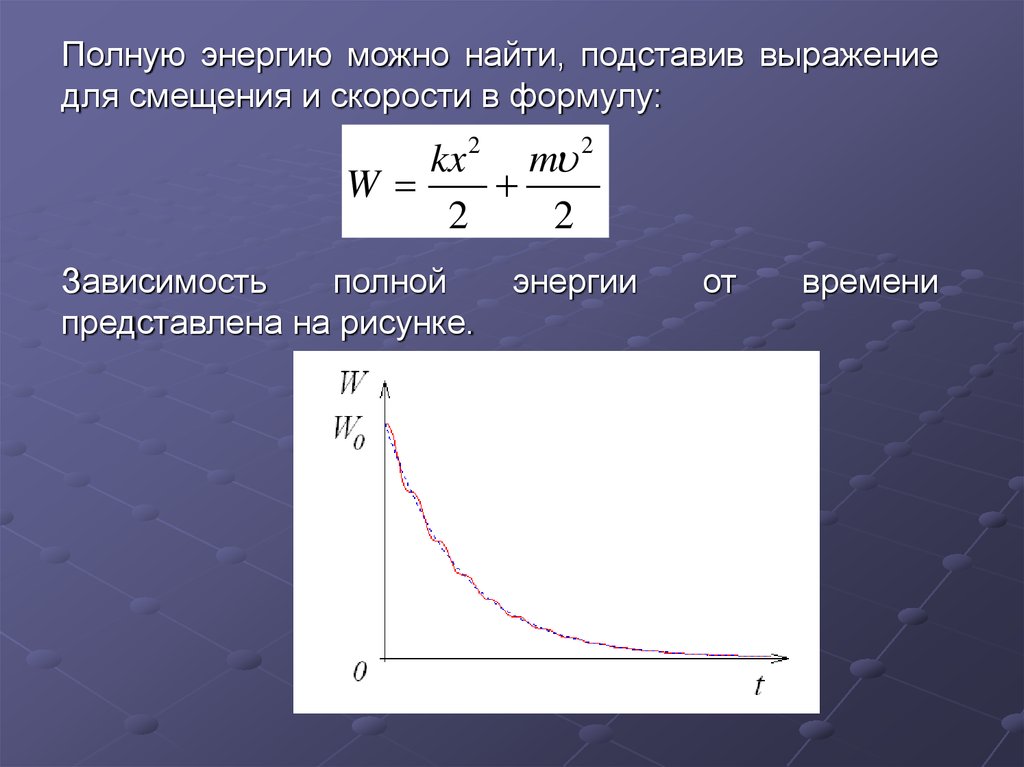
Полную энергию можно найти, подставив выражение
для смещения и скорости в формулу:
kx 2 m 2
W
2
2
Зависимость
полной
представлена на рисунке.
энергии
от
времени

18.

При малом затухании ( << ) выражение для полной
энергия колебательной системы принимает вид:
W W0 e
2 t
Полная
энергия
колебательной
системы
уменьшается со временем по экспоненциальному
закону.

19.

Добротностью
Q
колебательной
системы
называется
безразмерная
величина,
равная
произведению 2 на отношение энергии системы в
произвольный момент времени к убыли этой
энергии за период:
W (t )
Q 2
W (t ) W (t T )
e 2 t
2
2 2 t 2 t T
2 T
1
e
e
e

20.

При малом затухании:
2
Q
Ne
1 1 2 T T
Добротность пропорциональная числу колебаний за
время релаксации Ne.

21.

В ряде случаев удобно изучать колебательные
процессы в системе координат (x, v). Плоскость таких
координат называют фазовой плоскостью, - а кривая
– фазовой траекторией.
Например, фазовым портретом
колебания является эллипс.
гармонического

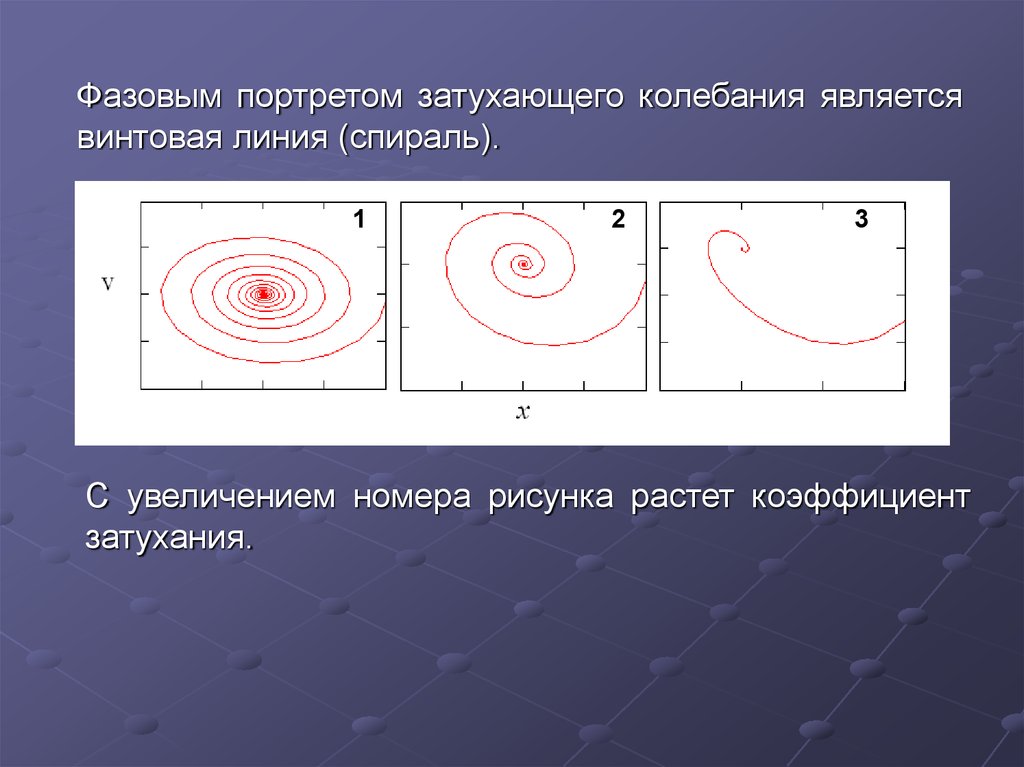
22.

Фазовым портретом затухающего колебания является
винтовая линия (спираль).
1
2
3
С увеличением номера рисунка растет коэффициент
затухания.

23. 19. Вынужденные колебания. Резонанс

24.

Вынужденными
колебаниями
называются
незатухающие
колебания
системы,
которые
вызываются действием на нее внешних сил,
периодически изменяющихся во времени.
Примеры вынужденных колебаний: колебания
мембраны телефона, колебания силы тока в
электрической сети, колебания гребных винтов,
валов турбин под действием периодически
изменяющихся внешних сил.

25.

В качестве модели рассмотрим тело, совершающее
колебания
под
действием
возвращающей
квазиупругой силы, силы сопротивления и внешней
периодической силы. Второй закон Ньютона
принимает вид:
Fупр Fсопр F ma
kx b Fo cos t ma

26.

Преобразуя,
получаем
дифференциальное
уравнение вынужденных колебаний (1):
mx bx kx Fo cos t
(1)
F0
x 2 x x
cos t ,
m
b
k
2
, 0 .
2m
m
2
0
и 0 – коэффициент затухания и циклическая
частота свободных незатухающих колебаний.

27.

Решение дифференциального уравнения вынужденных
колебаний равно сумме двух решений: общего и
частного:
x(t ) xo (t ) xч (t )
Общее решение – уравнение затухающего колебания,
частное – установившееся колебание, описываемое
уравнением:
(2)
x A cos( t )
где А – амплитуда вынужденных колебаний смещения,
– разность фаз между колебаниями смещения и
силы.

28.

Подставим решение (2) в уравнение (1) и определим
амплитуду и фазу между силой и смещением:
m 2 A cos( t ) bA sin t
kA cos( t ) F0 cos t
m 2 A cos( t ) cos( ) sin( t ) sin( )
bA sin t cos cos t sin
kA cos( t ) cos( ) sin( t ) sin( ) F0 cos t

29.

при косинусе
m 2 A cos( ) bA sin kA cos( ) F0 (3)
при синусе
m A sin( ) bA cos kA sin( ) 0
2
(4)

30.

Решая совместно (3) и (4), находим амплитуду А
установившихся вынужденных колебаний и сдвиг
фаз межу колебаниями силы и смещения:
А
m
02
F0
2 2
4 2 2

31.

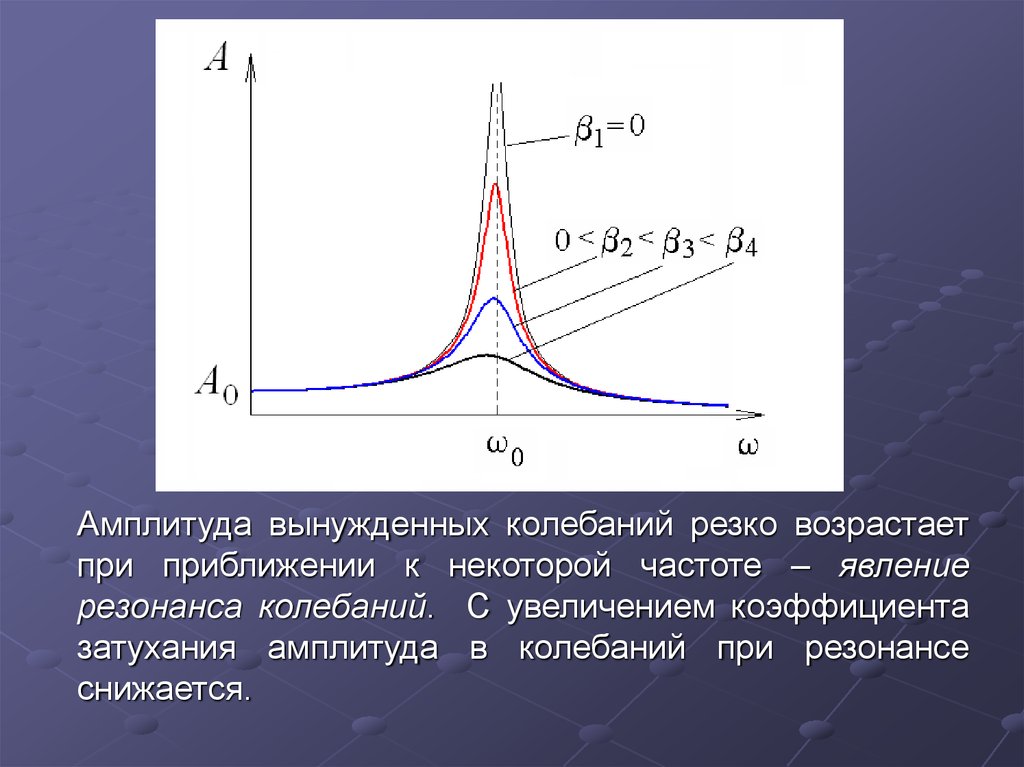
Амплитуда вынужденных колебаний резко возрастает
при приближении к некоторой частоте – явление
резонанса колебаний. С увеличением коэффициента
затухания амплитуда в колебаний при резонансе
снижается.

32.

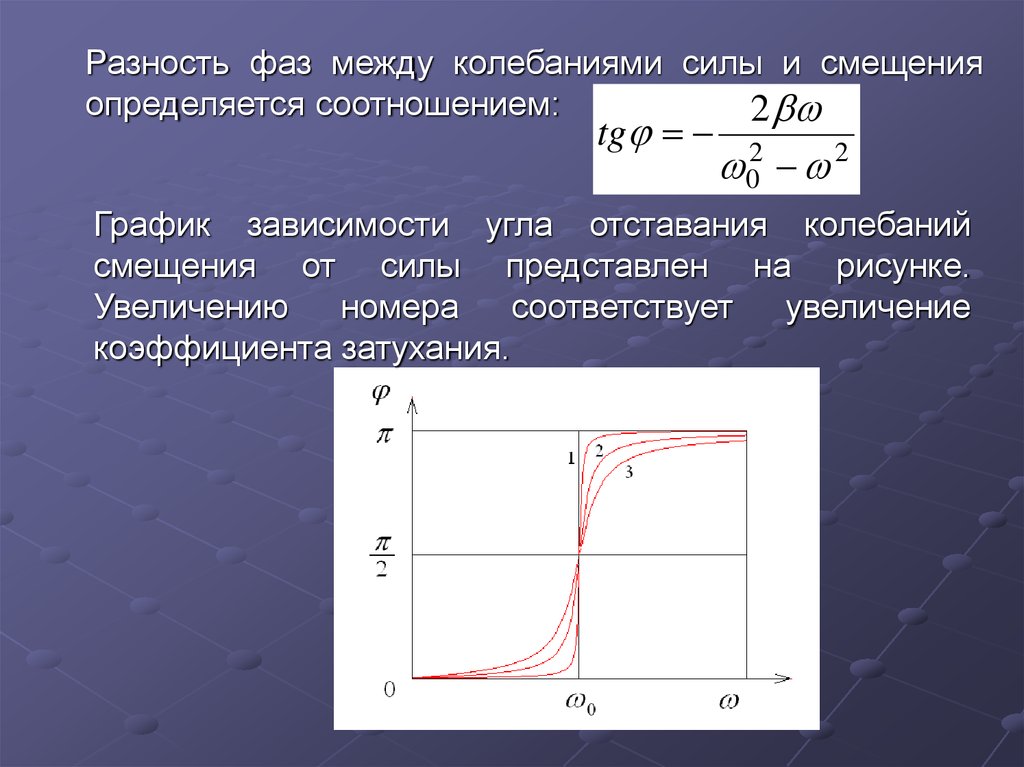
Разность фаз между колебаниями силы и смещения
определяется соотношением:
2
tg
02 2
График зависимости угла отставания колебаний
смещения от силы представлен на рисунке.
Увеличению
номера
соответствует
увеличение
коэффициента затухания.

33.

В области малых частот амплитуда вынужденных
колебаний почти постоянна, а сдвиг фаз равен нулю:
F0
A
m 02
0
F0
x t
cos( t )
2
m 0
В области малых частот колебания системы
практически без искажения следуют за силой. Это
важно с точки зрения измерительной техники.

34.

Для нахождения резонансной частоты для амплитуды
колебаний необходимо найти максимум функции А( ),
т.е. приравнять к нулю производную по частоте:
F0
m 2 2 2 4 2 2
0
0
В результате, резонансная частота равна:
ð 02 2 2

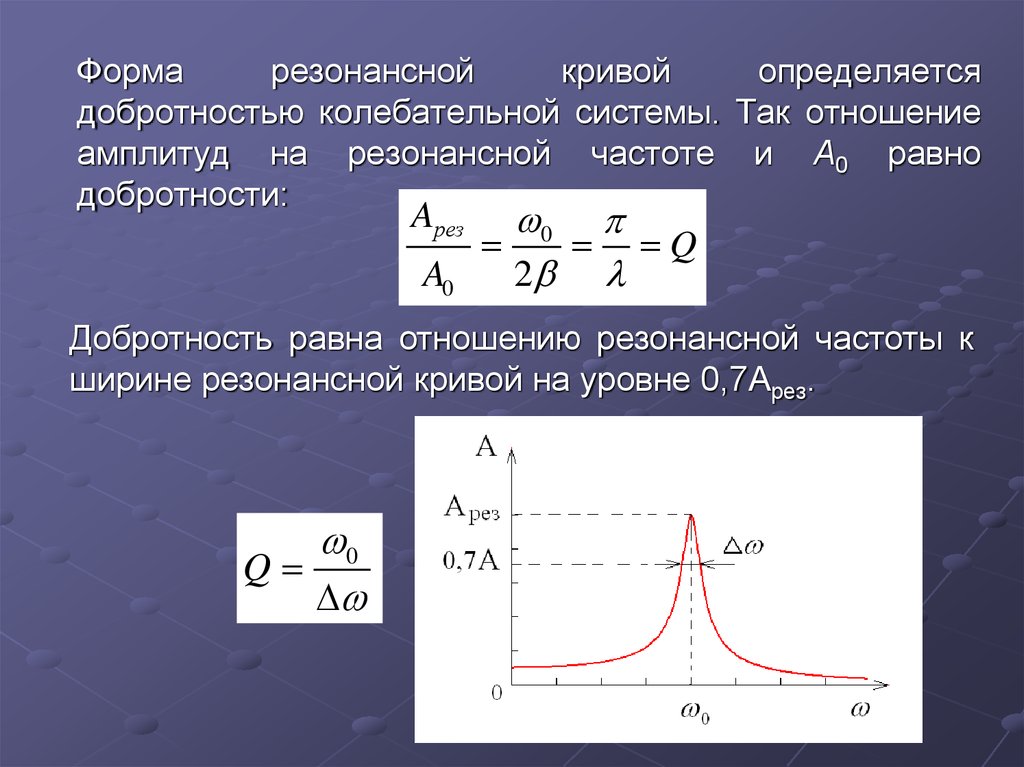
35. Форма резонансной кривой определяется добротностью колебательной системы. Так отношение амплитуд на резонансной частоте и A0 равно доброт

Форма
резонансной
кривой
определяется
добротностью колебательной системы. Так отношение
амплитуд на резонансной частоте и A0 равно
добротности:
0
Q
A0
2
Aрез
Добротность равна отношению резонансной частоты к
ширине резонансной кривой на уровне 0,7Aрез.
0
Q

36.

Резонансная частота для амплитуды
находится аналогичным образом:
0 A
F0
m 2 2 2 4 2 2
0
скор
0
р
0
скорости

37.

Для анализа частотной зависимости амплитуды
ускорения необходимо исследовать функцию:
a0 2 A
2 F0
m 2 2 2 4 2 2
0
Резонансная
частота
для
определяется соотношением
руск
0
амплитуды
02
02 2 2
ускорения

38.

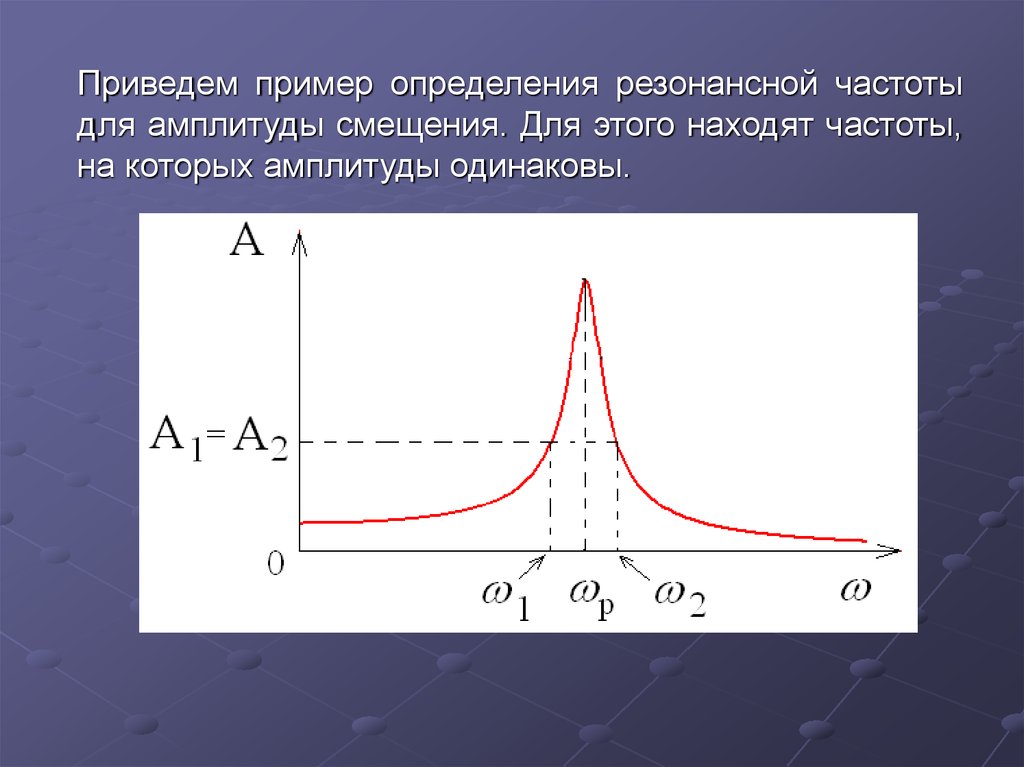
Приведем пример определения резонансной частоты
для амплитуды смещения. Для этого находят частоты,
на которых амплитуды одинаковы.

39.

Вычисляют резонансную частоту.
A1 1 A2 2
F0
m
2
0
2
1
2
4
2
2
1
ð 2 , ð
2
0
F0
2
m
22 12
2
2
0
2
2
2
4 2 22

40. Явление резонанса необходимо учитывать при конструировании машин и сооружений. Резонансная частота не должна быть близка к внешней часто

Явление резонанса необходимо учитывать при
конструировании машин и сооружений. Резонансная
частота не должна быть близка к внешней частоте.
Явление
резонанса
используется
радиотехнике, в науке и технике.
в
акустике,

41.

Параметрические колебания
Возбудить незатухающие колебания можно и другим
способом – периодическим изменением в такт с
колебаниями системы одного из параметров системы.
Например,
с
помощью
периодического
изменения
длины маятника. Подобные колебания называются
параметрическими.

42. В момент прохождения маятником равновесия, под действием силы уменьшается длина маятника. В результате угол отклонения увеличивается. Так

В момент прохождения маятником равновесия, под действием
силы уменьшается длина маятника. В результате угол отклонения
увеличивается. Таким образом, под действием внешнего
воздействия (изменения длины маятника) поддерживаются
незатухающие колебания.
m 12
mgl 1 cos
2
1 2 gl 1 cos
m 1l m 2 l l
2 1
l
l l
2 2 g l l 1 cos
l
l l
3
2

43.

Автоколебания
Восполнять убыль энергии можно за счет поступлений энергии из
вне в определенные моменты времени (согласованно). Можно
сделать так, чтобы колеблющая система сама управляла внешним
воздействием, обеспечивая согласованность сообщаемых ей
толчков
со
своим
движением.
Такая
система
называется
автоколебательной, а совершаемые незатухающие колебания –
автоколебаниями.
Примеры: колебания маятника в часах, ламповый генератор.