Similar presentations:
Матрицы
1. Алгебра и геометрия
1 семестр 20132. Разделы курса
1. Матрицы, определители, системылинейных уравнений.
2. Векторная алгебра.
3. Аналитическая геометрия.
Шмагунов Олег Александрович
3. 1. Матрицы и действия на ними
1.1. Матрицы.МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНАЯ ИЛИ
КВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ.
ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ ЕЁ ЭЛЕМЕНТАМИ
a11
a21
A
...
a
n1
Второй столбец
a12
a22
...
...
...
...
a1m
Вторая строка
a2m
...
an2 ... anm
ai i - я строка
a j j - й столбец
A m n матрица
aij элемент матрицы
4.
Виды матриц :m n квадратная;
m n прямоуголь ная
m 1 вектор - столбец;
n 1 вектор - строка
побочная диагональ
Главная диагональ
a11
a21
A
...
a
n1
1
0
1
0
a
0
A
...
A
...
0
e
0
k
0
a
02
1
0
...
a12
a22
...
...
...
...
a1m
a2m
Виды квадратных матриц :
...
an2 ... anm
aij 0, при 1 i,j n нулевая матрица
aij 0, при 1 i,j n, i j
единичная матрица
e a k1, при 1 i n
ii
03 0
aij a ji , при 1 i,j n симметричная
...
...
...
...
0
... ... ...
...
...
...
30 ... g f
00 ...
0
1
... 0f 1
aij 0, при i j треугольн ая
5.
a11a21
A
...
a
n1
1.2. Действия с матрицами.
a12 ... a1m
a22 ... a2m
aij
...
an2 ... anm
...
...
i 1,n
j 1,m
a) умножение матрицы на число :
б) сложение матриц :
Матрицы разного размера
складывать нельзя
Вычитание — это тоже сложение
A a
ij i 1,n
j 1,m
A a
, B b
ij i 1,n
ij i 1,n
j 1,m
j 1,m
C A B a b
ij i 1,n
ij
j 1,m
6.
Лирическое отступление…скалярное произведение векторов
a1, a2 ,..., an b1,b2 ,...,bn a1b1 a2b2 ..anbn
в) умножение матриц :
A a
, B b
ij i 1,n
ij i 1,m
j 1,m
j 1,k
i-я строка А
j j-й столбец В
C AB a b
i
i 1,n
j 1,m
A n m
AB n k
B m k
C c
ij i 1,n
j 1,k
г) транспонир ование матриц :
A a
,
ij i 1,n
j 1,m
AT a
ji j 1,m
i 1,n
7.
Примеры3 1 2 15
a ) 5 4 2 0 20
5 6 1
25
5 10
10 0
30 5
3 1 2 8 5 5 3 8 1 5 2 5 11 6 7
á)
4
7
2
3
0
14
4
2
0
7
3
14
11
5
14
3 1 2 8 3 8 1 7 2 2 21
в)
4 2 0 7 4 8 2 7 0 2 46
5 6 1 2 5 8 6 7 1 2 4
3 1
3 3
3 1
7
11 11
T
2 5 3 0 2 7 5 0 3 4 2
11 6 7
6
5
4
1 1 г ) 11 5 14
7 14
1 3
3 1
скалярное произведение векторов " по - матричному"
8.
1.3. Свойства операций над матрицами.линейная комбинация :
A B
A a
, B b
, 0 0 i 1,n
ij
ij
i 1,n
i 1,n
j 1,m
j 1,m
j 1,m
свойства линейных операций :
1) коммутативноcть сложения :
2) ассоциатив ноcть сложения :
3) существование нуля :
A B B A
A B C A B C
A 0 0 A A
Доказать самостоятельно, используя определения действий (операций)
9.
свойства умножения :3) существование нуля :
1
0
E
...
0
0 ... 0
1 ... 0
единичная матрица
... ... ...
0 ... 1
A 0 0 A 0
AB BA
AE EA A
4) НЕкоммутат ивноcть умножения :
5) существование единицы :
E выбираем подходящего размера
6) ассоциатив ность :
A BC AB C ABC
А, В, С подходящего размера
7) дистрибут ивность :
A B C AC BC справа
A B C AB AC слева
10.
свойства транспонир ования :8) инволютивность :
A
T T
A
Обратная самой себе операция называется инволютивной
9) линейность :
AB
T
10)
11)
A B A B
T
T
A A
T
T
T
B A
T
T
A A A симметричная
T
11.
Докажем что-нибудь…5) существование единицы :
A n m E n n
AE EA A
A n m E m m
Требуется доказать, что ij-й элемент произведения AE
такой же, как и ij-й элемент A
a11
a21
AE
...
a
n1
a12
a22
a1m 1
a2m 0
*
...... * *
0 ... 0 aa
11
11 a12
...
1 ... 0 * *
*
...... * *
... ... ... ... ... ... ... ...... ... ...... ......
an2 ... anm 0 0 ... 1 * * * ...... * *
...
(a11a12 ....a1m ) (10 0... 0) a11 1 a12 0 .... a1m 0 a11
(a11a12 ....a1m ) (010 0... 0) a11 0 a12 1 .... a1m 0 a12
j
ai e j ai1 ai 2 ....aim (0...010....0)T
AE aij i 1,n A
m
ai1 0 ai 2 0 ...ai ( j 1) 0 aij 1 ai ( j 1) 0 ...aim 0 aij
j 1,m
12.
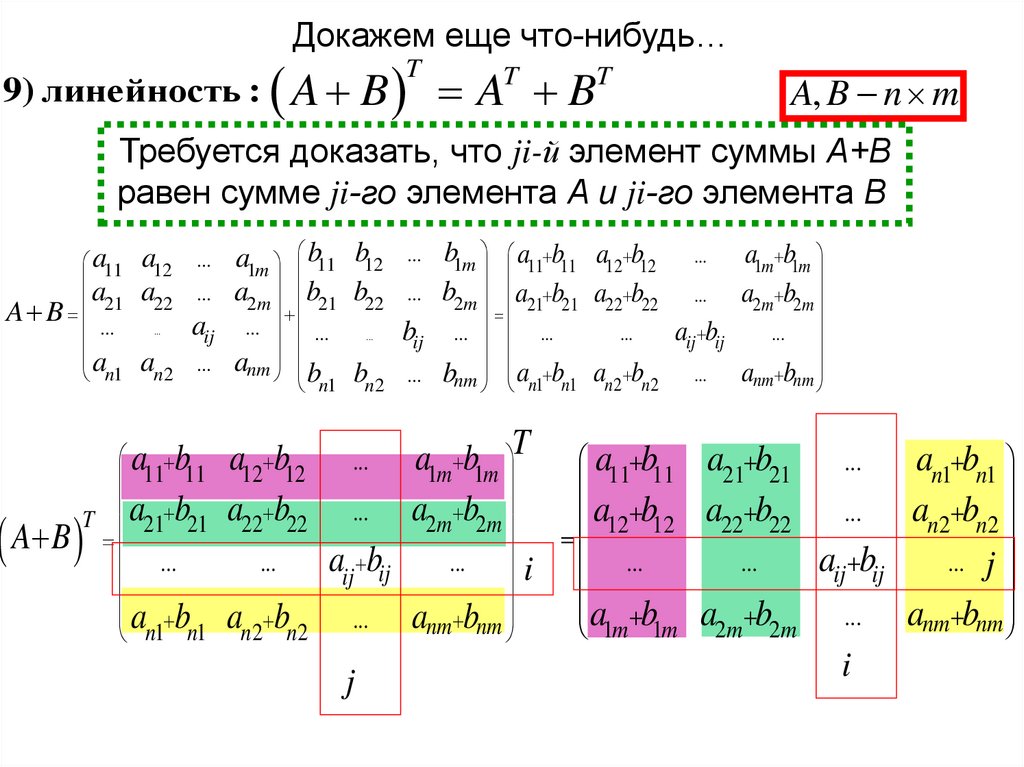
Докажем еще что-нибудь…9) линейность :
T
T
A
B
A
B
T
A, B n m
Требуется доказать, что ji-й элемент суммы A+B
равен сумме ji-го элемента A и ji-го элемента В
a11
a21
A B ...
a
n1
a12
a22
...
...
...
aij
an2
...
a b
11 11
T a21 b21
...
a b
n1 n1
A B
a1m b11 b12
a2m b21 b22
... ...
anm b
n1
...
...
...
bij
bn2
...
a12 b12
a22 b22
...
...
aij bij
an2 bn2
...
...
j
b1m a11 b11 a12 b12
b2m a21 b21 a22 b22
...
bnm
...
a b
n1 n1
a1m b1m T
a2m b2m
anm bnm
...
i
...
...
...
aij bij
an2 bn2
...
a b
11 11
a b
12 12
...
a b
1m 1m
a1m b1m
a2m b2m
anm bnm
...
a21 b21
a22 b22
...
...
aij bij
a2m b2m
...
...
i
an1 bn1
an2 bn2
anm bnm
...
j
13.
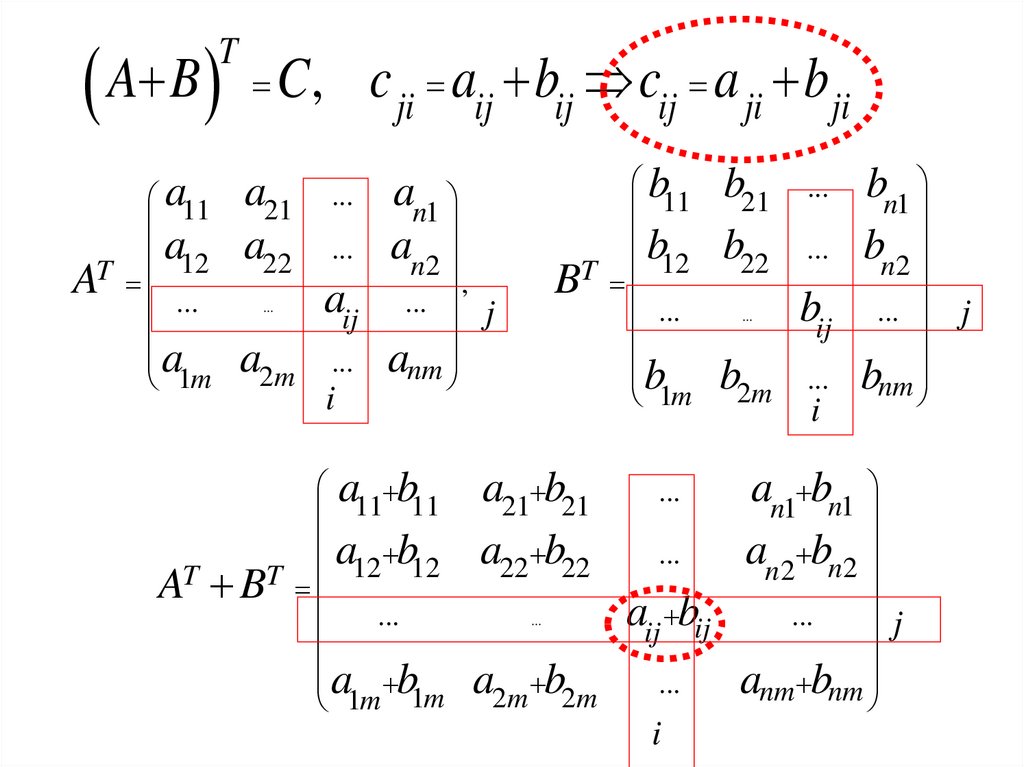
A BT
a11
a12
AT ...
a
1m
c ji aij bij cij a ji b ji
C,
a21
a22
...
...
...
aij
a2m
...
i
b
11
b
BT 12
...
b
1m
an1
an2
,
... j
anm
a b
11 11
a b
AT BT 12 12
...
a b
1m 1m
a21 b21
a22 b22
...
...
...
aij bij
a2m b2m
...
i
b21
b22
...
...
...
bij
b2m
...
i
bn1
bn2
...
bnm
an1 bn1
an2 bn2
j
anm bnm
...
j
14.
1.4. Обратная матрица.Обратная (по умножению) матрица — это
матрица, произведение с которой равно единице:
Бывает еще обратная по сложению:
1
1
A A A A E
A A A A 0
свойства обратимост и :
1) Обратная бывает у квадратных, и то не у всех.
2) Обратная к обратной равна исходной.
3) Обратная к транспонированной
равна транспонированной обратной.
1
A, A n n
A A
A A
1 1
T
1
1 T
4) Обратная произведения равна произведению обратных
1
в обратном порядке.
AB
5) Обратная к умноженной на число равна
обратной, разделенной на это число
1
B A
1
1
A
A
1
1
15.
Пример на умножение….3 1 2 8 1 3 8 1 7 2 2 3 1 1 2 2 3 21 5
4 2 0 7 2 4 8 2 7 0 2
4
1
2
2
0
3
46
8
5 6 1 2 3 5 8 6 7 1 2 5 1 6 2 1 3 4 4
1 x 1 z 1
Найдем обратную матрицу….
1 y 1 t 0
1
1 1 x y 1 0
1 1
2 3 ? 2 3 z t 0 1
2 x 3 z 0
2 y 3 t 1
x z 1
1,5 z z 1 z 0,4
y t
y t
0,2
1 0,6
A
x
1,5
z
x 1,5 z
0,4
0,2
2 ( t ) 3 t 1 t 0,2
2 y 3 t 1
Выполним проверку….
1 1 0,6 0,2 0,6 0,4 0,2 0,2
2 3 0,4 0,2 1,2 1,2 0,4 0,6 E
16.
Более сложный пример на нахождение обратной матрицы2 7 3 x1 y1 z1 1 0 0
2 7 3
3 9 4 x y z 0 1 0
3 9 4 ?
2
2
2
1 5 3 x y z 0 0 1
1 5 3
3
3
3
2 x1 7 x2 3 x3 1
2 x1 7 x2 3 x3 1
2 y 7 y 3 y 0
2 y 7 y 3 y 0
2
3
2
3
1
1
2 z1 7 z2 3 z3 0
2 z1 7 z2 3 z3 0
3 x1 9 x2 4 x3 0
3 x1 9 x2 4 x3 0
3 y1 9 y2 4 y3 1
3 y1 9 y2 4 y3 1
3z 9 z 4 z 0
3z 9 z 4 z 0
2
3
2
3
1
1
x1 5 x2 3 x3
1x1 5 x2 3 x3 0
y 5 y 3 y
1y 5 y 3 y 0
2
3
2
3
1
1
z1 1 5 z2 3 z3
1z1 5 z2 3 z3 1
1
17.
Подставляем и упрощаем:10 x2 6 x3 7 x2 3 x3 1
10 y 6 y 7 y 3 y 0
2
3
2
3
2 10 z2 6 z3 7 z2 3 z3 0
15 x2 9 x3 9 x2 4 x3 0
15 y2 9 y3 9 y2 4 y3 1
3 15 z 9 z 9 z 4 z 0
2
3
2
3
x1 5 x2 3 x3
y 5 y 3 y
2
3
1
z1 1 5 z2 3 z3
3 x2 3 x3 1
3 y 3 y 0
3
2
3 z 2 3 z 3 2
6 x2 5 x3 0
6 y2 5 y3 1
6 z 5 z 3
3
2
x1 5 x2 3 x3
y 5 y 3 y
3
2
1
z1 1 5 z2 3 z3
18.
Перегруппируемуравнения…
3 x2 3 x3 1
3 y 3 y 0
2
3
3 z2 3 z3 2
6 x2 5 x3 0
6 y2 5 y3 1
6 z 5 z 3
2
3
x1 5 x2 3 x3
y 5 y 3 y
2
3
1
z1 1 5 z2 3 z3
и система
разобьётся
на четыре:
Решаем их по отдельности:
3x2 3x3 1
6 x2 5 x3 0
3 y2 3 y3 0
6 y2 5 y3 1
3z2 3z3 2
6 z2 5 z3 3
x1 5 x2 3 x3
y1 5 y2 3 y3
z 1 5 z 3z
2
3
1
x2 5 3
x3 2
z2 1 3
z3 1
y2 1
y3 1
x1 7 3
y1 2
z 1 3
1
И получаем:
1
2 7 3
3 9 4
1 5 3
7 3 2 1 3
5 3 1 1 3
2
1
1
19.
ЛитератураТеория:
1. Зеленцов Б.П. Алгебра и геометрия. Учебное пособие,
Новосибирск, 2009.
2. Письменный Д. Конспект лекций по высшей математике. (Есть в
библиотеке.)
Задачники:
1. Зеленцов Б.П. Линейная и векторная алгебра. Новосибирск,
2005.
2. Рычков, Захарова. Основы линейной алгебры и аналитической
геометрии. (Есть на сайте и в библиотеке.)

















 mathematics
mathematics








