Матрицы. Основные понятия

1.

Матрицы.
Основные понятия.
Матрицей А размера n m называется совокупность nm
чисел, расположенных в виде таблицы, состоящей из n строк и m
столбцов:
a11 a12 … a1m
a21 a22 … a2m
Аn m=
.……………
an1 an2… anm
.
Краткие обозначения матриц имеют вид:
A = (aij), (i = 1, 2,…, n; j = 1, 2,…, m).
Числа aij, составляющие данную матрицу, называются ее
элементами; элемент матрицы aij – число, расположенное в i – ой
строке и j – ом столбце.
Квадратная матрица – матрица с одинаковым числом
строк и столбцов (n = m).
Совокупность
элементов
квадратной
матрицы,
расположенных на отрезке, соединяющем левый верхний угол с
правым нижним, называется главной диагональю, а на отрезке,
соединяющем правый верхний угол с левым нижним, - побочной
диагональю матрицы.
Две матрицы, имеющие одинаковое количество (n) строк и
одинаковое количество (m) столбцов, называются матрицами
одинакового размера [n m ].

2.

2. Частные типы матриц
Диагональная матрица – квадратная матрица, у которой
отличны от нуля лишь элементы главной диагонали:
d1 0 … 0
0 d2 … 0
D = diag(d1, d2,…, dn) = …………...
0 0
… dn
.
Единичная матрица – диагональная матрица, у которой все
элементы главной диагонали равны единице:
1 0 … 0
0 1 … 0
E = …………...
0 0
…1
n n.

3.

Квадратная матрица называется треугольной, если все
элементы, стоящие выше (или ниже) главной диагонали, равны
нулю. При этом матрица:
a11 a12 … a1n
0
a22 … a2n
A = ………….….
0
0
…
ann
называется верхней треугольной, а матрица:
B =
b11 0 … 0
b21 b22 … 0
………….….
bn1 bn2 … bnn
называется нижней треугольной.
Нулевая матрица – матрица, все элементы которой равны
нулю:
0 0
… 0
0 0 …
0
O =
…………...
0
0
… 0
n m.

4.

Матрица – строка (вектор - строка) – матрица размера
1 m:
A = ( a1 a2 … am ).
Матрица – столбец (вектор – столбец, n – мерный
вектор) – матрица размера n 1:
b1
b2
B =
.
.
.
bn .
Симметрическая матрица – квадратная матрица, элементы
которой, симметричные относительно главной диагонали (a11,
a22,…, ann) равны между собой, то есть:
aij = aji, i, j = 1, 2, …, n.

5.

3. Операции над матрицами
Две матрицы A и B равны между собой, если их размерности
совпадают и равны их элементы, стоящие на одинаковых местах:
A = B aij = bij, i = 1, 2,…, n; j = 1, 2,…, m.
Перечислим линейные операции над матрицами.
1) Сложение матриц.
Суммой двух матриц A = (aij) и B = (bij) одинаковой
размерности называется матрица C = (cij) той же размерности,
каждый элемент которой равен сумме элементов матриц A и B:
cij = aij + bij.
Пример
Найти сумму матриц:
1 –8
3 0
A = -2
5 4
1
B =
4 -7 0 -6 ,
3 1
2
0
4 -9 1 -1
2 7 -3 –1 .
Решение
Суммой матриц A и B по определению является матрица C:
1 + 3 -8 + 1
3 + 2
0 + 0
4 –7 5
0
C = -2 + 4
5 - 9
4 + 1
1 - 1
= 2 -4 5
0
4 + 2 -7 + 7
0 - 3
-6 - 1
6
0 -3 –7 .
Ответ: С =
4 -7 5 0
2 -4 5
0
6
0 -3 -7
.

6.

2) Умножение матрицы на число.
Произведением матрицы A на действительное число
называется
матрица
той
же
размерности,
полученная
из
умножением всех ее элементов на число :
(aij)m,n = (aij )m,n.
Пример
Пусть даны матрица A и число :
A =
0 –7 5 1
-2 1 0
2
4
0 -3 8
= 4.
,
Найти A.
Решение
Произведением матрицы A на число по определению является
матрица С:
0 –28 20
4
C = 4A =
-8
4
0
8
16 0 -12
32 .
0 –28 20
4
Ответ: C = -8
4
0
8
16
0 -12
32 .
A

7.

Свойства линейных операций
Пусть A, B, C, O – матрицы одинаковой размерности,
, R, тогда:
1. A + B = B + A.
2. (A + B) + C = A + (B + C).
3. A + O = A.
4. A + (-1) A = O.
5. (A +B) = A + B.
6. ( + )A = A + A.
7. ( )A = ( A) = ( A).
8. 1 A = A.

8.

4. Умножение матриц
Произведением матрицы (вектора) – строки размера 1 m
на матрицу (вектор) – столбец размера n 1 называется число,
равное сумме произведений элементов A и B с одинаковыми
номерами:
b1
b2
n
A B = ( a1 a2 … am )
.
= a1b1 + a2b2 +…+ anbn = aibi.
i 1
.
.
bn
Произведением матрицы A размера n m на матрицу B
размера m p называется матрица C размера n p, каждый элемент
которой cij равен сумме произведений i- го вектора – строки
матрицы A на j – ый вектор – столбец матрицы B:
С = АВ,
n
где
cij = aisbsj.
s 1

9.

Произведение матриц AB существует (определено), если
число столбцов матрицы A равно числу строк матрицы B, то есть
матрицы A и B согласованы по операции умножения.
Пример
Найти произведение матриц A B и B A, если:
1 2 -2
2
A =
В = -1
0 3
1 ,
5
.
Решение
Найдем произведение AB, для этого выясним его определенность:
A2 3 B3 1 = C2 1.
Получим:
1 2 -2
2
2 – 2 - 10
-10
C =
-1
=
=
0 3
1
5
0 – 3 + 5
2
.
Найдем
произведение
B A,
для
этого
выясним
его
определенность, B3 1 A2 3. Значит, результат не имеет смысла, так
как число столбцов матрицы B не совпадает с числом строк
матрицы A.
-10
Ответ: АВ =
2
.

10.

Свойства операции умножения матриц
Для матриц A, B, C, O, E согласованных размерностей
выполняются следующие свойства:
1. AB BA.
2. A(B + C) = AB + AC.
3. (A + B)C = AC + BC.
4. (AB)C = A(BC).
5. AO = O.
6. OB = O.
7. AE = A.
8. EB = B.

11.

Степени матриц
Пусть A - квадратная матрица, тогда:
An = A A … A,
n cомножителей
A0 = E,
если A невырожденная матрица.
ApAq = Ap+q;
(Ap)q = Apq.

12.

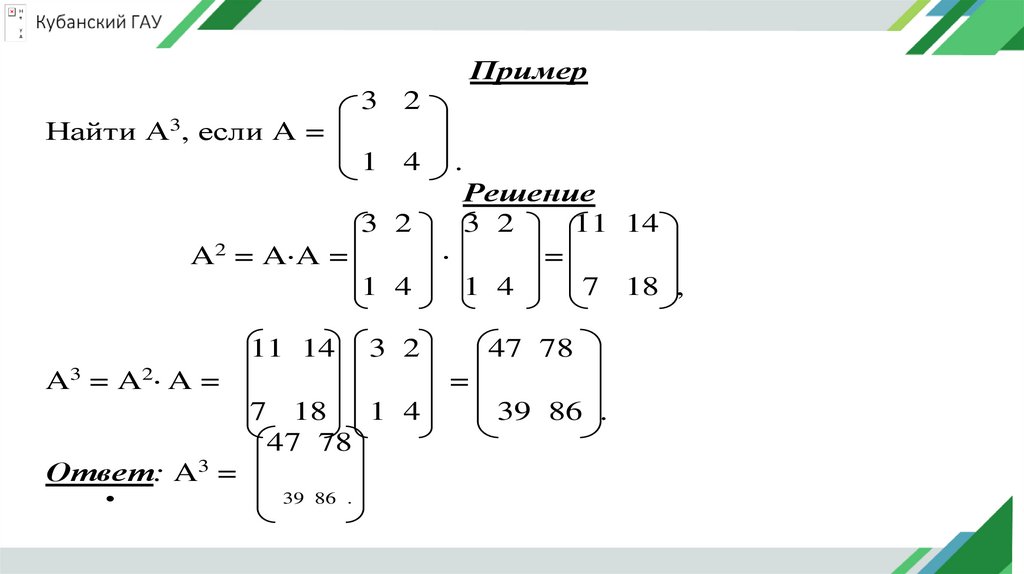
Пример
3 2
Найти A3, если A =
1 4
3 2
A2 = A A =
1 4
11 14
3 2
A3 = A2 A =
47 78
=
7 18
1 4
47 78
Ответ: A3 =
.
Решение
3 2
11 14
=
1 4
7 18 ,
39 86 .
39 86 .

13.

5. Транспонирование матриц
Транспонирование – операция преобразования матрицы A
размера n m в матрицу AT размера m n, заключающаяся в замене
строк A ее столбцами при сохранении их нумерации:
A = ( aij ) AT = (aji), i = 1,.., n, j = 1,…,m.
a11 a12 … a1m
a11 a21 … an1
a21 a22 … a2m
a12 a22 … an2
A = ……………. AT = ……………..
an1 an2 … anm n m
a1m a2m … anm
m n.

14.

Свойства операции транспонирования
1. ( A)T = AT, R.
2. (A + B)T = AT + BT.
3. (AT)T = A.
4. (AB)T = BTAT.
5. Если A – симметрическая матрица, то
A = AT .
6. Для любой матрицы A матрицы (ATA) и (AAT)
симметрические.
7. Если x – n - мерный вектор размера n 1, то
xTx = x12 + x22 + … + xn2,
x1
x2
.
где x = .
.
xn .
всегда

15.

Обратная матрица
Матрица A называется невырожденной (неособенной,
обратимой), если A 0.
Любая невырожденная матрица имеет обратную.
-1
Квадратная матрица A называется обратной для
квадратной матрицы A, если:
-1
-1
A A = AA = E.

16.

1.
2.
3.
4.
5.
Свойства обратной матрицы
(AB)-1 = B-1A-1, если существуют A-1, B-1.
(A-1)-1 = A.
(AT)-1 = (A-1)T.
E-1 = E.
det(A-1) = 1 .
6. Если D =
det A
d1 0 … 0
1
d1
0 d2 … 0
, то D-1= 0
.…………
0 0 … dn
0
…0
1
d2
… 0
……………..
0
0
...

17.

Алгоритм вычисления обратной матрицы
a11 a12 … a1n
Если
a21 a22 … a2n , то для нахождения A-1 требуется:
…………….
an1 an2 … ann
1. Вычислить A (если A 0, то A-1 существует).
2. Вычислить алгебраические дополнения Aij для всех элементов
aij матрицы A и сформировать матрицу алгебраических
~
дополнений A
:
A11 A12 … A1n
A=
~
A
=
A21 A22 … A2n
………………
An1 An2 … Ann .

18.

~
3.Транспонировать A
и сформировать присоединенную (союзную)
~ T
матрицу A
:
A11 A21 … An1
~
A T=
A12 A22 … An2
………………
A1n A2n … Ann
4. Вычислить A-1:
A-1 =
1 ~ T
A
.
A
5. Проверить правильность вычислений:
A-1A = E,
AA-1 = E.
.

19.

Пример
3 2
2
Дана матрица A =
1 3
1
5 3
4
Найти обратную матрицу.
.
Решение
1. Вычислим A по правилу Саррюса:
3 2
2
A = 1 3
1
= 36 + 10 + 6 – 30 – 8 – 9 = 5.
5 3
4
Так как A 0, то A-1 существует.
2.
Вычислим
алгебраические
дополнения
определителя:
A11 =
3
1 = 12 – 3 = 9,
3
4
A21 = - 2
2
= -8 + 6 = -2,
3
4
A31 =
2
2
= 2 - 6 = -4,
3
1
A12 = - 1
1
= -4 + 5 = 1,
5
4
A22 =
3
2
= 12 - 10 = 2,
5
4
элементов
этого

20.

A32 = - 3 2 = -3 + 2 = -1,
1 1
A13 = 1 3 = 3 - 15 = -12,
5 3
A23 = - 3 2 = -9 + 10 = 1,
5 3
A33 = 3 2 = 9 - 2 = 7.
1 3
Составим матрицу алгебраических дополнений:
9 1 -12
~
A = -2 2 1
-4 -1 7 .
~T
3. Составим присоединенную матрицу A
:
9 -2 -4
~
AT =
1 2 -1
-12 1 7 .

21.

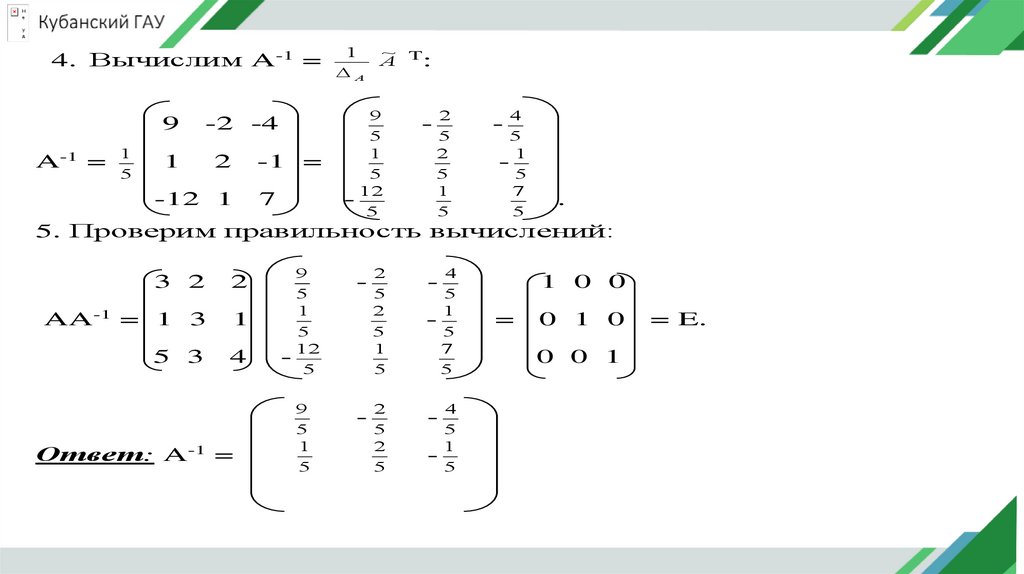
4. Вычислим A-1 =
A-1 =
1
5
9
-2 -4
1
2
-1 =
-12 1
7
1
A
~
A T:
9
5
1
5
- 12
5
-2
5
2
5
1
5
-4
5
-1
5
7
5
.
5. Проверим правильность вычислений:
3 2
2
AA-1 = 1 3
1
5 3
4
Ответ: A-1 =
9
5
1
5
- 12
5
-2
5
2
5
1
5
5
-1
5
7
5
9
5
1
5
-2
-4
5
2
5
-4
5
-1
5
1 0 0
=
0 1 0
0 0 1
= E.

22.

Ранг матрицы
Ранг матрицы (rgA, rankA) – максимальное число линейно
независимых в ней строк (столбцов).
Максимальное число линейно независимых строк и столбцов
во всякой матрице одинаково.
Две матрицы A и B эквивалентны (A B), если равны их
ранги (rgA = rgB).
Эквивалентные преобразования матрицы – преобразования, не
изменяющие ее ранга, а именно:
1. Перестановка строк (столбцов).
2. Умножение какой либо строки или столбца на число 0.
3. Прибавление к какой – либо строке (столбцу) линейной
комбинации других строк (столбцов).
В матрице A размера n m минор r порядка r
(r
min {n, m}) называется базисным минором, а его строки и
столбцы базисными, если r 0, а все остальные миноры порядка
r + 1 равны нулю или не существуют.
Ранг матрицы равен порядку ее базисного минора.
Любая
строка
(столбец)
матрицы
являются
линейной
комбинацией ее базисных строк (столбцов).

23.

Нахождение rgA с помощью эквивалентных преобразований
приведением к "трапецеидальному" виду
a11 a12 … a1m
A = a21 a22 … a2m
………………
an1 an2 … anm
эквивалентные
преобразования
d11 d12 … d1r d1m
0 d22 … d2r d2m
…………………...
0 0 … drr …drm
0 0 … 0 … 0
…………………..
0 0 … 0 … 0
rgA = r ( r 0, все r+1 = 0 или не существуют).

24.

Некоторые свойства рангов матриц
1. rg(AB) min{rgA, rgB}.
2. rgA = rgAT = rg(ATA) = rg(AAT).
3. Если A – произвольная матрица, P и Q – любые согласованные
с A по умножению квадратные невырожденные матрицы, то:
rg(PAQ) = rgA.

25.

Рангом матрицы называется наивысший порядок отличных
от нуля миноров этой матрицы
Канонической матрицей называется матрица, у которой в
начале главной диагонали стоят подряд несколько единиц (число
которых может равняться нулю), а все остальные элементы равны
нулю.
При помощи элементарных преобразований строк и столбцов
любую матрицу можно привести к канонической. Ранг
канонической матрицы равен числу единиц на ее главной
диагонали.

26.

Правило вычисления ранга матрицы методом
окаймляющих миноров
Ищем минор первого порядка или сразу минор второго
порядка, отличный от нуля. Затем вычисляем окаймляющие его
миноры следующего порядка, пока не найдем среди них отличного
от нуля.
Если уже найден отличный от нуля минор r – го порядка r,
то вычисляем миноры (r + 1)- го порядка, окаймляющие минор r.
Если все они равны нулю или таких миноров вообще нет (в
случае, когда матрица содержит rстолбцов или r строк), то ранг
матрицы равен r. В противном случае продолжаем этот процесс.

27.

Пример
Вычислить методом окаймляющих миноров ранг
1 2 1 4
матрицы: A = 0 1 -1 3
2 5 1 11 .
Решение
1
2
Так как минор 2 –го порядка
= 1 0,
0
1
а оба окаймляющие его миноры третьего порядка равны нулю:
1 2 1
1 2 4
0 1 –1 = 0,
0 1 3
= 0,
2 5 1
2 5 11
то rangA = 2.
Ответ: rang А = 2.

28.

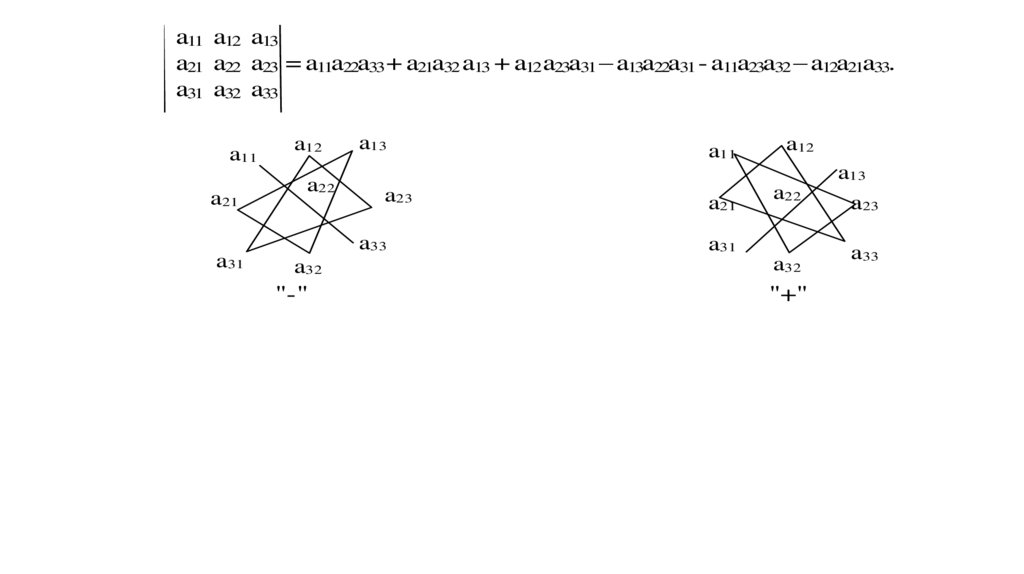
a11 a12 a13
a21 a22 a23 = a11a22a33 + a21a32 a13 + a12 a23a31 – a13a22a31 - a11a23a32 – a12a21a33.
a31 a32 a33
a11
a21
a31
a12
a22
a13
a11
a12
a13
a23
a33
a21
a22
a31
a32
a32
"-"
"+"
a23
a33

29.

Вычислить определитель четвертого порядка:
1 2 4 7
0 3 0 2
2 4 3 2
6 3 1 1 .
Решение
Данный определитель можно разложить по любой строке или
столбцу (см. свойства определителей). Однако объем вычислений
можно уменьшить, если выбрать такую строку или столбец, где
больше элементов, равных нулю. В нашем случае такой строкой
является вторая и разложение определителя по ней имеет вид:
1 2 4 7
1 4 7
124
0 3 0 2 =0А21+3А22+0А23+2А 24 =3(-1)4 2 3 2 + 2(-1)6 2 4 3 =
2 4 3 2
6 1 1
631
6 3 1 1
= 3(3 + 14 + 48 – 126 – 2 - 8) + 2(4 + 24 + 36 – 48 – 9 - 4) = -207.
Ответ: -207.

30.

Решить методом Гаусса систему уравнений:
2x1 + x2 - 5x3 + x4 = 8,
x1 - 3x2 - 6x4 = 9,
2x2 – x3 + 2x4 = -5,
x1 + 4x2 - 7x3 + 6x4 = 0.
Решение
Выпишем расширенную матрицу этой системы:
2 1 -5 1
8
1 -3
0 -6
9
0 2 -1 2
-5
1 4 -7 6
0
и произведем следующие элементарные преобразования над ее
строками:
1). Разделим элементы первой строки на 2, а затем из второй и
четвертой строк вычтем первую:
1
5
1
1
5
1
1
4
1
4
2
2
2
1 -3
0
-6
9
0
1
-1
-7
2
6
5
0
2
4
~
0
0
0
2
7
2
2
5
2
2
13
2
2
-1
9
-
2
7
2
2
11
2
5
-5
-4
.

31.

2). Разделим элементы второй строки на - 7 , а затем из третьей и
2
четвертой строк вычтем вторую, умноженную соответственно на
2 и 7 :
2
~
1
1
2
0
1
0
0
- 5
2
- 5
7
1
2
13
7
2
-1
2
7
2
- 9
2
11
2
1
1
2
0
1
5
0
0
-4
0
0
4
- 10
7
~
- 5
2
5
7
3
7
-2
3). Разделим элементы третьей строки на
1
2
13
7
12
7
- 10
1
1
3
7
4
~
7
15
7
.
, а затем прибавим к
четвертой строке элементы третьей, умноженной на 2:
1
1
1
1
1
- 5
4
1
- 5
4
2
~
0
2
- 5
7
1
2
13
7
2
- 10
7
~
0
1
2
- 5
7
2
13
7
- 10
7
0
0
1
-4
-5
0
0
1
-4
-5
0
0
- 2
-1
1
0
0
0
-9
-9
.
4). Разделим элементы четвертой строки на –9. В результате всех
этих преобразований данная система приводится к треугольному
виду:
1
5
1
x1 +
x2 –
x3 +
x4 = 4,
x2 –
2
5
x3
7
+
2
13
x4
7
=
2
10
,
7
x3 - 4 x4 = -5,
x4 = 1.
Система
имеет
единственное
решение.
Из
последнего
уравнения
имеем
x4
=
1.
Подставляем
это
значение
x4
в
предыдущее уравнение и находим из него x3 = -1. Далее из второго
и первого уравнений находим x2 = -4 и x1 = 3.
Ответ: x1 = 3, x2 = -4, x3 = -1, x4 = 1.

32.

Решить по формулам Крамера систему уравнений:
x1 – x2 + x3 = 5,
2x1 + x2 + x3 = 6,
x1 + x2 + 2x3 = 4.
Решение
Определитель этой системы имеет вид:
1 –1 1
=
2
1 1 = 5 0.
1
1 2
Вычислим определители j, получающиеся из определителя
системы
путем
замены
в
нем
столбца,
состоящего
из
коэффициентов при xj, столбцом из свободных членов:
5 -1 1
0 -1 0
1 = 6 1 1 = 11 1 2 = 15,
4 1 2
9 1 3
1 5 1
1
0 0
2 = 2 6 1 = 2 -4 -1
= -5,
1 4 2
1 -1 1
1 -1 5
0 -1 0
3 = 2 1 6 = 3 1 11
= 5.
1 1 4
2 1 9
15
5
5
Отсюда x1 =
= 3, x2 = = -1, x3 =
= 1.
5
5
Ответ: x1 = 3, x2 = -1, x3 = 1.
5

33.

Решить матричным способом систему уравнений:
x1 – x2 + x3 = 6,
2x1 + x2 + x3 = 3,
x1 + x2 + 2x3 = 5.
Решение
1 -1
1
x1
6
Положим A = 2
1
1
X = x2
F = 3
1
1
2 ,
x3 ,
5
.
Тогда
данная
система уравнений
запишется
уравнением:
AX = F.
Так как определитель матрицы A имеет вид:
1
-1
1
detA = = 2
1
1
= 5 0,
1
1
2
то матрица A не вырождена и имеет обратную:
1
3 -2
1
А-1 =
-3
1
1
матричным
5
1
-2
3
.
Для получения решения X мы должны умножить вектор столбец F слева на матрицу A-1:
1
3
x1
- 2
6
1
x2
x3
=
5
- 3
5
5
1
5
1
5
- 2
5
5
1
5
3
5
3
= -2
5
3
Ответ: x1 = 1, x2 = -2, x3 = 3.
.

34.

Пример
Векторы
заданы
в
ортонормированном
базисе
k
j ,
i ,
координатами а
= (2, -1, 8), е 1= (1, 2, 3), е 2 = (1, -1, -2),
е 3 = (1, -6, 0). Убедиться, что тройка е 1 , е 2 , е 3 образует базис, и
найти координаты вектора а в этом базисе.
Решение
Если определитель, составленный из координат векторов е 1 , е 2 ,
е 3 не равен нулю, то векторы е 1 , е 2 , е 3 линейно независимы, и,
значит, образуют базис. Убеждаемся, что:
1
2 3
=
1 -1 -2 = -31 0.
1 -6 0
Таким образом, тройка е 1 , е 2 , е 3 – базис.
Обозначим координаты вектора а в базисе е 1 , е 2 , е 3 через
x, y, z. Тогда получим:
а = (x, y, z) = x е 1 + y е 2 + z е 3.
Так как по условию:
j + 8 k , е 1 = i +2 j +3 k , е 2 = i - j -2 k , е 3 = i - 6 j ,
а = 2i то система для нахождения неизвестных имеет вид:
x + y + z = 2,
2x – y – 6z = -1,
3x – 2y = 8.
Решая ее любым из изученных методов, получим:
x = 2, y = -1, z = 1.
Следовательно, имеем:
а = 2 е 1 - е 2 + е 3 = (2, -1, 1).
Ответ: а = 2 е 1 - е 2 + е 3 = (2, -1, 1).

35.

Пример
3 2 2
Дана матрица A = 1 3 1
5 3 4 .
Найти обратную матрицу.
Решение
1. Вычислим A по правилу Саррюса:
3 2 2
A = 1 3 1 = 36 + 10 + 6 – 30 – 8 – 9 = 5.
5 3 4
Так как A 0, то A-1 существует.
2.
Вычислим
алгебраические
дополнения
определителя:
A11 =
3 1 = 12 – 3 = 9,
3 4
A21 = - 2 2 = -8 + 6 = -2,
3 4
A31 =
2 2 = 2 - 6 = -4,
3 1
A12 = - 1 1 = -4 + 5 = 1,
5 4
A22 =
3 2 = 12 - 10 = 2,
5 4
элементов
этого

36.

A32 = - 3 2 = -3 + 2 = -1,
1 1
A13 = 1 3 = 3 - 15 = -12,
5 3
A23 = - 3 2 = -9 + 10 = 1,
5 3
A33 = 3 2 = 9 - 2 = 7.
1 3
Составим матрицу алгебраических дополнений:
9 1 -12
~
A = -2 2 1
-4 -1 7 .
3. Составим присоединенную матрицу A~ T:
9 -2 -4
~
AT =
1 2 -1
-12 1 7 .

37.

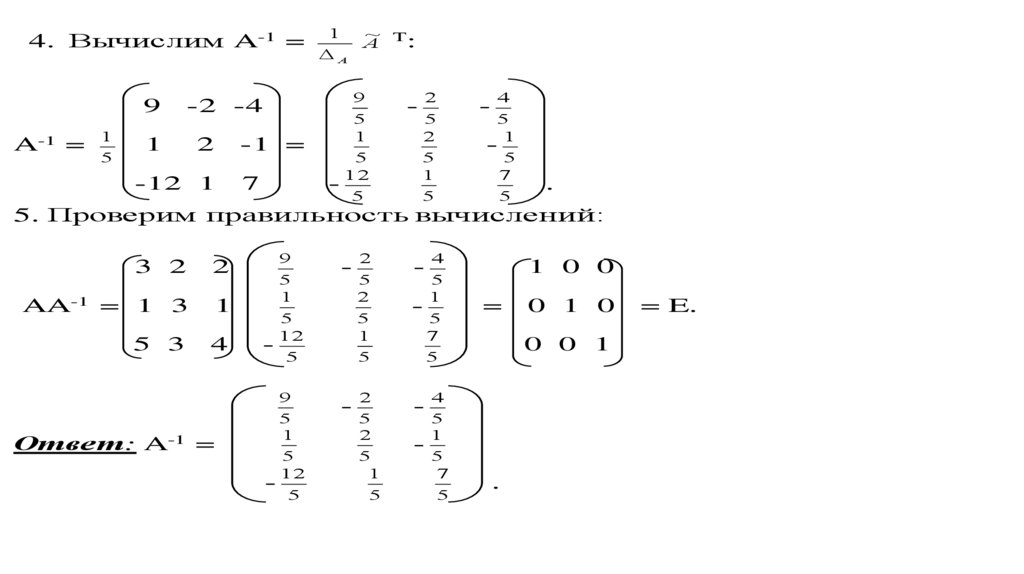
4. Вычислим A-1 =
A-1 =
1
5
9
-2 -4
1
2
-12 1
-1 =
7
1
A
~
A T:
9
5
1
5
- 12
5
-2
-2
-4
5
2
5
1
5
-4
5
-1
5
7
5
.
5. Проверим правильность вычислений:
3 2
2
AA-1 = 1 3
1
5 3
4
Ответ: A-1 =
9
5
1
5
12
5
9
5
1
5
12
5
5
2
5
1
5
-
2
5
2
5
1
5
5
-1
5
7
5
4
5
1
5
7
5
1 0 0
=
0 1 0
0 0 1
-
.
= E.