Similar presentations:
Матрица. Сложение и умножение матриц
1. Матрицы.
Сложение и умножениематриц.
2.
Матрица.Прямоугольная таблица чисел называется
матрицей. Если в указанной таблице m
строк и n столбцов, то ее в общем виде
можно записать так:
a11
a21
A
...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
3.
A aij mn .или
Числа
aij i 1, m;
j 1, n
называются элементами матрицы
А.
4.
Главная диагональДля квадратной матрицы
a
ij nn
совокупность чисел
a11, a22 ,....., ann
называется ее главной диагональю.
5.
Равные матрицы.Две матрицы считаются равными,
если они имеют одинаковые размеры и их
соответственные элементы равны между
собой:
A aij mn B bij kl m k; n 1;
aij bij , i 1, m;
j 1, n.
6.
Сложение матриц.Если две матрицы имеют одинаковые
размеры, то их можно сложить,
складывая соответственные элементы.
Так, если
a11
a21
A
...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
и
7.
b11 b12b21 b22
B
... ....
b
m1 bm 2
... b1n
... b2 n
,
... ...
... bmn
a11 b11 a12 b12
a21 b21 a22 b22
A B
...
...
a b
m1 m1 am 2 bm 2
то
a1n b1n
... a2 n b2 n
,
...
...
... amn bmn
...
8.
или(aij ) mn (bij ) mn (aij bij ) mn .
9.
Умножение матрицы на числоВсякую матрицу можно умножить на любое
число согласно следующему определению:
aij mn aij mn
10.
Пример 1. Даны матрицы А и В0 2 1
1 2 1
, B
A
3
7
5
3
0
1
Найти матрицу
2 A 3B
11.
Решение1 2 1
0 2 1
3
2
3 0 1
3 7 5
12.
2 4 2 0 6 36 0 2 9 21 15
2 2 5
.
3 21 17
13.
Свойства.Легко видеть, что операции сложения и
умножения матрицы на число
удовлетворяют следующим свойствам:
1.свойство коммуникативности
A B B A
14.
2. Свойство ассоциативностиA ( B C ) ( A B) C
3.
( A B) A B
15.
4.5.
( ) A A A
( A) ( ) A
16.
Нулевая матрицаМатрица, все элементы которой равны нулю,
называется нулевой. Ее будем обозначать
буквой О.
0
0
O
...
0
0 ... 0
0 ... 0
... ... ...
0 ... 0
17.
Умножение матрицПусть у нас имеются две матрицы
A aij mk
B bij kn
18.
Здесь число столбцов первой матрицы равночислу строк второй. Тогда произведение
матрицы А на матрицу В определяется
следующим образом:
a11
a21
...
a
m1
a12
a22
...
am 2
... a1k
... a2 k
... ...
... amk
b11 b12
b21 b22
... ...
b
k1 bk 2
... b1n
... b2 n
... ...
... bkn
19.
c11 c12c21 c22
... ...
c
m1 cm 2
... c1n
... c2 n
... ...
... cmn
где
cij ai1b1 j ai 2b2 j ... aik bkj
20.
Оператор суммированияЕсли воспользоваться оператором
суммирования
n
a
i 1
i
a1 a2 ... an ,
то
k
cij aisbsj
s 1
21.
Произведение матрицПроизведение матриц А и В записывается так:
C AB
22.
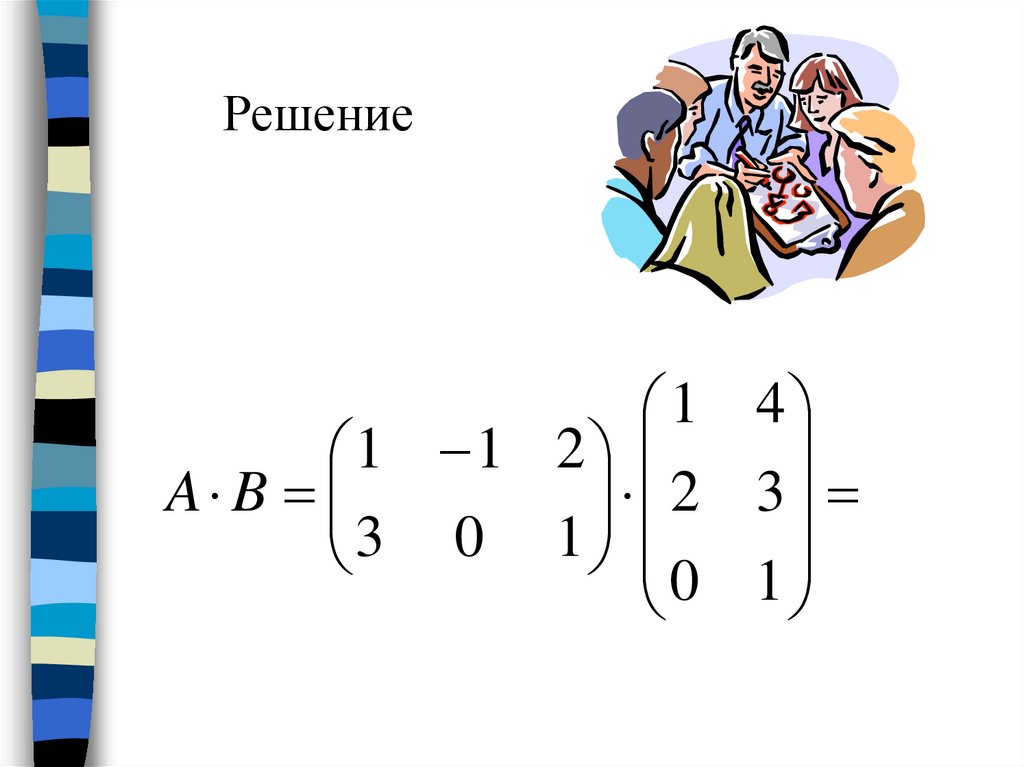
Пример 1Умножить матрицу
1 1 2
A
3 0 1
на матрицу
1 4
B 2 3
0 1
23.
Решение1 4
1 1 2
2 3
A B
3 0 1 0 1
24.
1 1 1 2 2 0 1 4 1 3 2 13 4 0 3 1 1
3 1 0 2 1 0
1 3
3 13
25.
Транспонирование матрицПусть у нас имеется матрица
A aij m n
.
Если каждую строку этой матрицы
заменить ее столбцом с тем же номером,
то получим новую матрицу размера
, которая называется
n m
транспонированной к данной и
обозначается
T :
A
26.
a11a
12
T
A
....
a
1n
a21 .... am1
a22 .... am 2
.... .... ....
a2 n .... amn
27.
Определители второго и третьегопорядков
По определенному правилу каждой
квадратной матрице А ставится
определенное число, которое называется
ее определителем и обозначается A
Рассмотрим определители порядков
1, 2, 3.
28.
Если порядок матрицы А равен единице,то
A a11
Для квадратной матрицы второго порядка
a11 a12
A
a
a
21
22
A
a11
a12
a21 a22
a11a22 a12a21
29.
Опираясь на это определение определителявторого порядка дадим определение
определителя третьего порядка.
Если
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
, то
30.
a11a12
a13
A a21 a22
a31
a11
a32
a22 a23
a32 a33
a31
a23
a33
a21
a12
a13
a22
a23
a12
a13
a32 a33
31.
a11a12
a13
a21 a22
a23 a11a22a33 a21a32 a13
a31
a33
a32
a31a12a23 a11a32a23 a21a12a33
a31a22a13.
32.
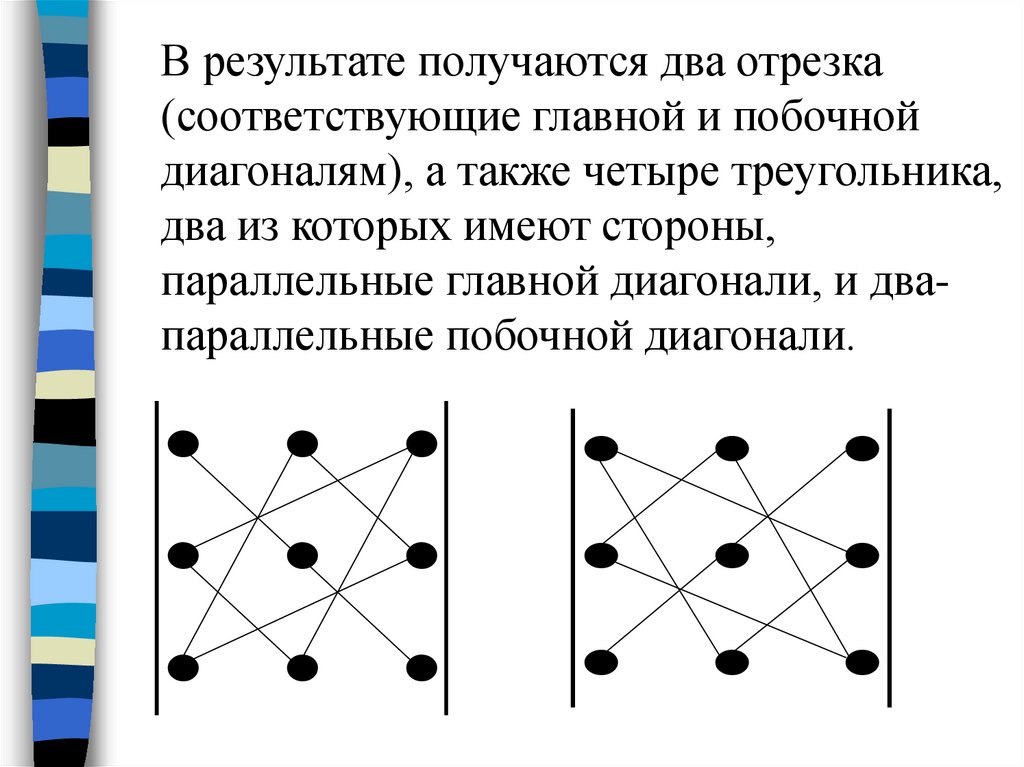
Для запоминания правила вычисленияопределителя третьего порядка
используется правило треугольников или
правило Саррюса.
Оно состоит в изображении (явном или
мысленном) элементов матрицы точками.
Точки, соответствующие произведениям,
которые входят в определитель,
соединяются отрезками.
33.
В результате получаются два отрезка(соответствующие главной и побочной
диагоналям), а также четыре треугольника,
два из которых имеют стороны,
параллельные главной диагонали, и двапараллельные побочной диагонали.
34.
Главной диагонали и тем двумтреугольникам, основания которых
параллельны главной диагонали,
соответствуют произведения со знаком
«+», а побочной диагонали соответствуют
произведения со знаком «-».
Пример 1. Вычислить определитель
2
1 3
1
5 2
1 4 2
35.
Решение:2 5 2 1 4 3
1 2 1 1 5 3
1 1 2 4 2 2 20 12 2
15 2 16 27
36.
Обратная матрицаПусть у нас имеется квадратная матрица
A aij n n.
Матрица
B bij n n
обратной к матрице
называется
А, если
BA AB E ij n n ,
37.
где1, при i j,
ij
0, при i j.
ij
называется символом Кронекера.
38.
Квадратная матрица называетсяневырожденной, если ее определитель
не равен нулю. В противном случае
матрица называется вырожденной.
Пример:
Найти матрицу, обратную к
матрице
1 0 1
A 2 3 2
1 1 2
39.
Решение.Сначала проверим, является ли
определитель матрицы А отличным от
нуля:
1
A 2
0 1
3
1 1
2 6 2 3 2 1 0.
2
40.
Отсюда вытекает, что матрица Аневырожденная и у нее есть обратная:
A11
1
1
A A12
A13
A
A21
A22
A23
A31
A32
A33
41.
В нашем случае:A11 1
1 1
A12 1
1 2
3 2
1 2
2
2
1 2
4;
6
42.
2A13 1
1 3
A21 1
1 1
2 1
A22 1
1 3
3
0 1
1
2
1
1
1
2
5;
1;
1;
43.
A23 11
2 3
0
1 1
1;
A31 1
0 1
A32 1
1 1
3 1
3 2
3
2
2
2
3;
4;
44.
A33 13 3
1 0
2 3
3.
Отсюда
4 1 3
1
A 6 1 4 .
5 1 3
45.
Ранг матрицыПусть у нас имеется матрица
содержащая
a11
a21
...
a
m1
A aij n n
m строк и n столбцов:
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
46.
Выделим в этой матрице k строк k столбцовk m,
k n
элементов, стоящих на
пересечении выделенных строк и столбцов,
составим определитель k-го порядка. Все
такие определители называются минорами
нашей матрицы. Элементы матрицы- это
миноры первого порядка.
Определение: Рангом матрицы
называется наивысший порядок отличных
от нуля миноров этой матрицы.
47.
Пример. Найти ранг матрицы3 2 1 2
A 2 0 1 1
0 4 5 1
У этой матрицы 12 миноров первого
порядка, 18 миноров второго порядка:
3 2 3 1 3 2 2 1
,
,
,
,
2 0 2 1 2 1 0 1
48.
2 2 1 2 3 2 3 1,
,
,
,
0 1 1 2 0 4 0 5
3 2 2 1 2 2 1 2
,
,
,
,
0 1 4 5 4 1 5 1
49.
2 0 2 1 2 1 0 1,
,
,
,
0 4 0 5 0 1 4 5
0 1 1 1
,
,
4 1 5 1
50.
и наконец 4 минора третьего порядка:3 2
1 3
1
2
2 0 1, 2 1 1 ,
0 4
5 0
5
1
3 2 2 2
1
2
2 0 1 , 0 1 1 .
0 4 1 4
5
1
51.
Нетрудно проверить, что все минорытретьего порядка матрицы А равны нулю,
а миноры второго порядка во всяком
случае не все равны нулю. Поэтому ранг
матрицы А равен 2
r A 2
52.
При вычислении ранга матрицысущественную роль играют элементарные
преобразования матрицы:
1) умножение элементов любой
строки (столбца) матрицы на число
0;
2) прибавление к строке (столбцу) другой
строки (столбца), умноженной на
некоторое число;
3) перестановка двух строк (столбцов)
матрицы.
53.
При элементарных преобразованияхранг матрицы не изменяется. С помощью
элементарных преобразований любую
матрицу можно привести к виду
1 0 0 ... 0 0 ... 0
0 1 0 ... 0 0 ... 0
0 0 0 ... 0 0 ... 0
54.
где на «главной диагонали» стоит rединиц, а все остальные элементы матрицы
равны нулю. Ранг такой матрицы, а значит,
и исходной матрицы, равен r.
Если ранг матрицы А равен рангу
матрицы В, то матрицы А и В называются
эквивалентными. В этом случае пишут
A ~ B.
55.
Системы линейных уравненийОсновные понятия и определения
Системой линейных алгебраических
уравнений с n переменными х1, х2, …, хn
называется система вида
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
..........
..........
..........
..........
....
am1 x1 am 2 x2 ... amn xn bm .
56.
Здесь числаaij i 1, m;
j 1, n
называются коэффициентами системы,
а числа b1, b2, …,bm-ее свободными
членами.
Если b1= b2=…=bm=0, то система
называется однородной;
Если хотя бы одно из bi i 1, m
от нуля, то система называется
неоднородной
отлично
57.
Решением системы называется всякаяупорядоченная совокупность n чисел
(с1, с2, …, сn), которая при подстановке
в каждое уравнение системы вместо
соответствующих переменных превращает
каждое уравнение в тождество.
Система называется совместной,
если у нее есть хотя бы одно решение, и
несовместной в противном случае.
58.
Совместные системы делятся наопределенные и неопределенные.
Система, которая имеет только одно
решение, называется определенной.
Если система имеет больше одного
решения, то она называется
неопределенной.
59.
Систему удобно записать в матричнойформе, для чего введем необходимые
понятия. Матрица
a11
a21
A
...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
,
... ...
... amn
элементы которой являются
коэффициентами системы, назовем
матрицей системы.
60.
Введем еще две матрицы, каждая изкоторых состоит из одного столбца
(матрицы-столбца):
x1
x2
X ,
...
x
n
b1
b2
B .
...
b
m
Это матрица-столбец переменных и
матрица-столбец свободных членов.
61.
У матрицы А n столбцов, а у матрицы X nстрок, поэтому А можно умножить на X.
a11 x1 a12 x2 ... a1n xn
a21 x1 a22 x2 ... a2 n xn
AX
.
.....................................
a x a x ... a x
mn n
m1 1 m 2 2
62.
Как показывают равенства, каждыйэлемент матрицы столбца АХ есть
соответствующий элемент матрицы В.
Отсюда в соответствии с определением
равенства матриц, получаем матричную
запись системы:
AX B.
63.
Введем в рассмотрение матрицы-столбцыa11
a12
a1n
a21
a22
a2 n
P1 , P2
,...,
P
,
n
...
...
...
a
a
a
m1
m2
mn
тогда система уравнений может быть
записана так:
x1P1 x2 P2 ... xn Pn B
64.
Две системы линейных алгебраическихуравнений называются эквивалентными
(равносильными), если всякое решение
одной из них является решением второй,
и наоборот.
Элементарными преобразованиями
системы линейных уравнений называют
следующие действия:
65.
1) умножение на число, отличное от нуляодного из уравнений системы;
2)
прибавление к одному уравнению
системы другого ее уравнения,
умноженного на произвольное число,
при этом сохраняются остальные
уравнения системы в том числе и то,
которое прибавлялось;
3) перестановка местами двух уравнений
системы.
66.
Формула КрамераПусть дана система n линейных
алгебраических уравнений с
n-переменными (неизвестными):
a11 x1 a12 x2 ... aij x j ... a1n xn b1
a x a x ... a x ... a x b
21 1 22 2
2j j
2n n
2
..........
..........
..........
..........
..........
..........
.
an1 x1 an 2 x2 ... anj x j ... ann xn bn .
67.
Если определительсистемы
матрицы
A aij n n
отличен от нуля и система совместна,
то она и определенная.
Если система имеет решение, то оно
единственно и может быть найдено
по формулам, которые называются
формулами Крамера.
68.
Пример. Решить систему линейныхуравнений
2 x1 x2 3 x3 x4 0
x2 2 x4 2
x
x
2
x
x
1
1
2
3
4
x1 2 x1 x3 3 x4 1
69.
Решение. Вычислим определительсистемы следующим образом. Из первой
строки вычтем удвоенную третью строку,
из третьей-четвертую, тогда получим
2
1
3
1
0
1
0
2
1 1 2
1
1
3
2
1
70.
2 2 1 2 3 4 1 20
1
0
2
1 1
1 2
2 1
1 3
1
2
1
3
0
3
1
1
0
1
0
2
0 3 3 2
1
2
1
3
a41 A41
71.
31 1
5
1
1
0
2 1 0 2
3 3 2
3 6 18 2 7.
3 1
3 3
1
2
72.
Определитель0, следовательно,
правило Крамера применимо к системе.
Составим и вычислим определители
1 , 2 , 3 , 4 .
1
0
1
3
1
2
1
0
2
1 1 2
1
1
3
2
1
23,
73.
23
2
0
3
1
0
2
0
2
1 1 2
1
1
1
1
3
2
1
0
1
0
1
2
2
1 1 1
1
1
3
2
1
2,
12,
74.
42
1
3
0
0
1
0
2
1 1 2 1
1
2
1
8.
1
Отсюда искомое решение данной системы
1 23
x1
;
7
3 12
x3
;
7
2
2
x2
;
7
4
8
x4
.
7







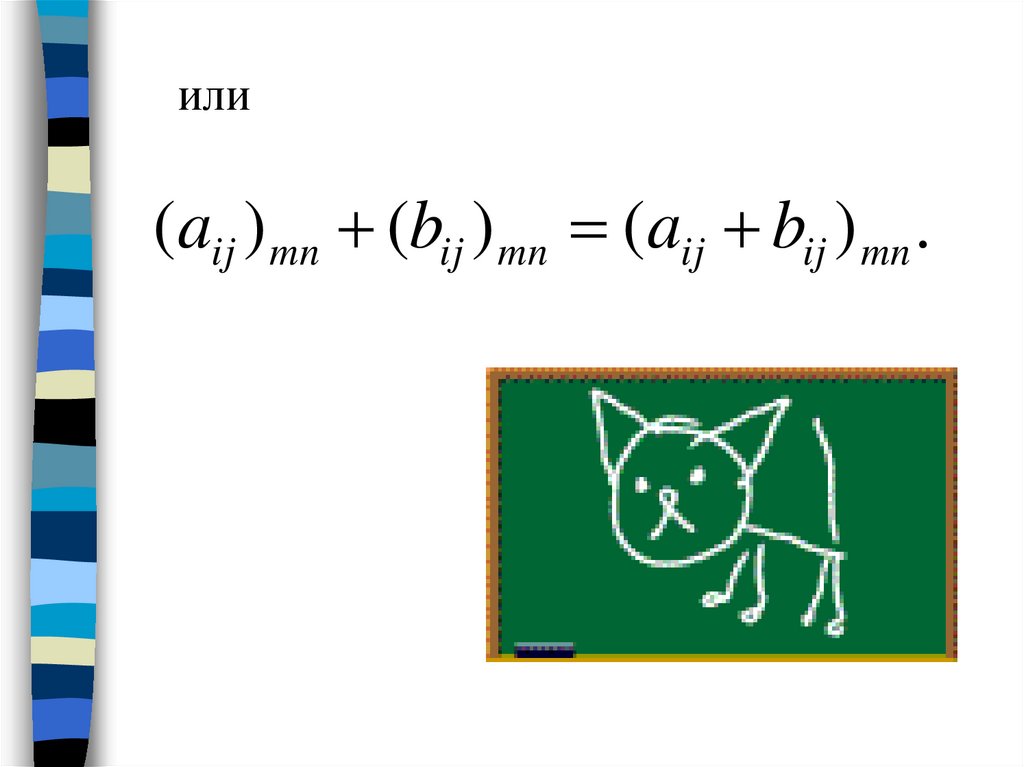



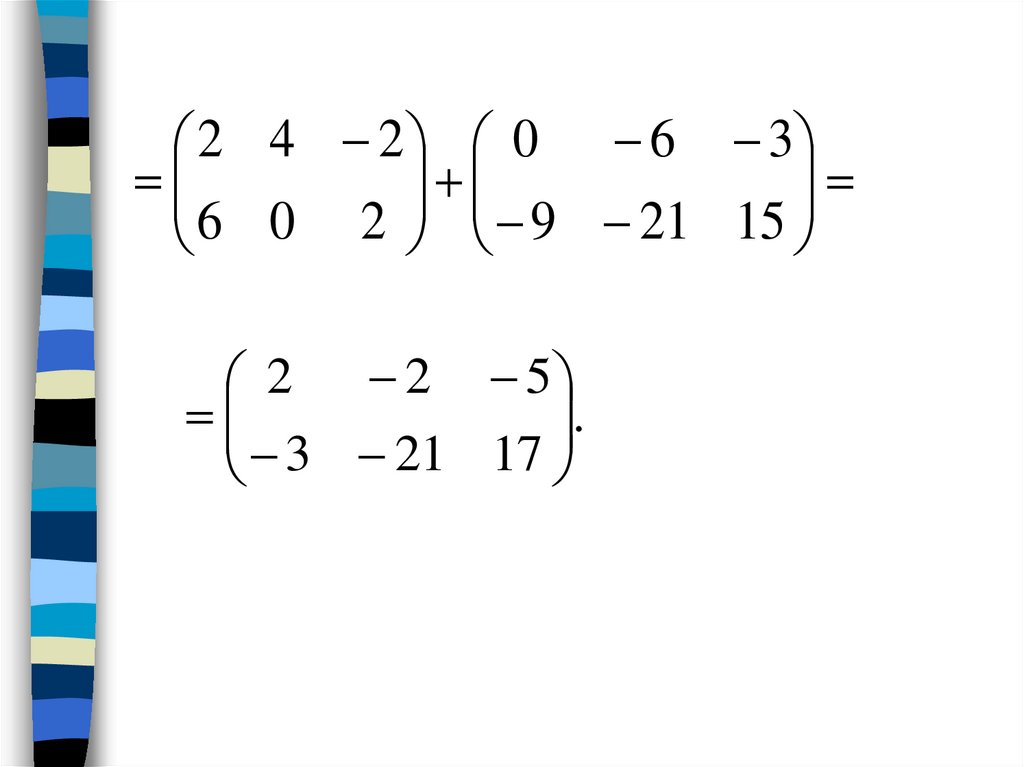

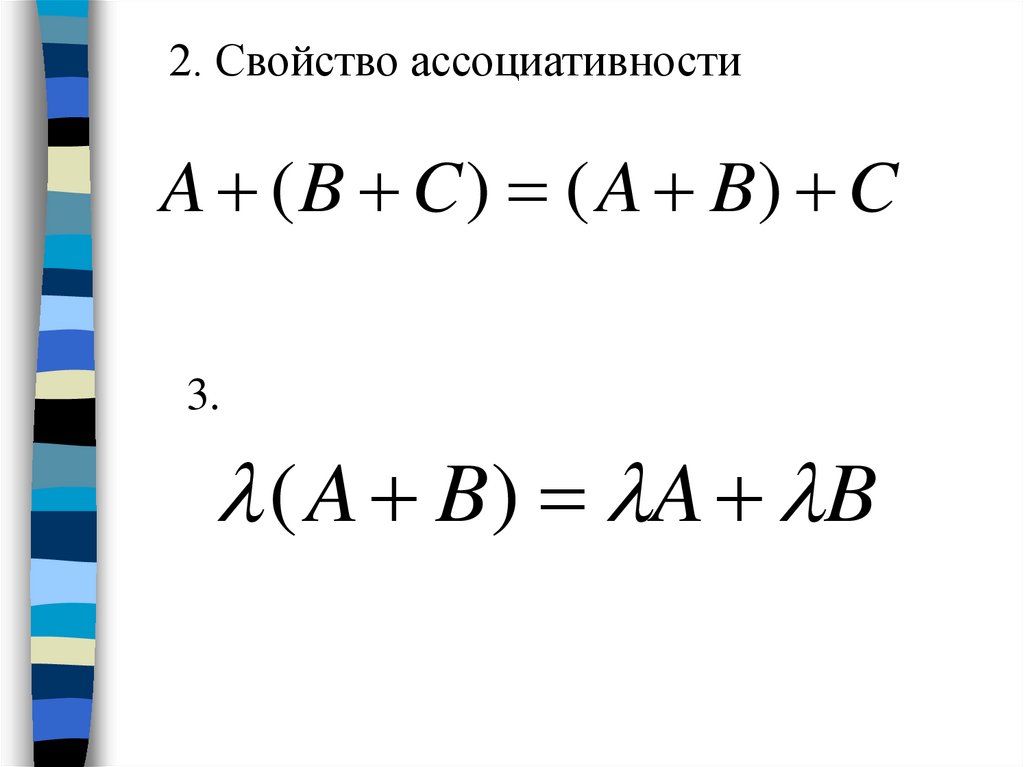














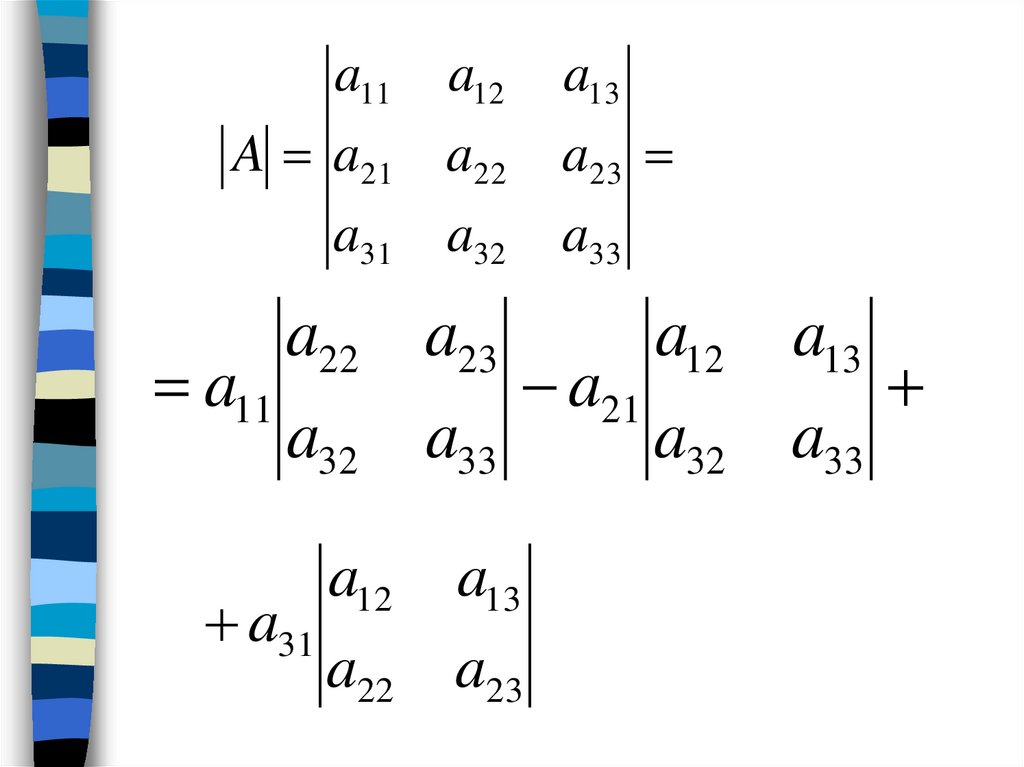



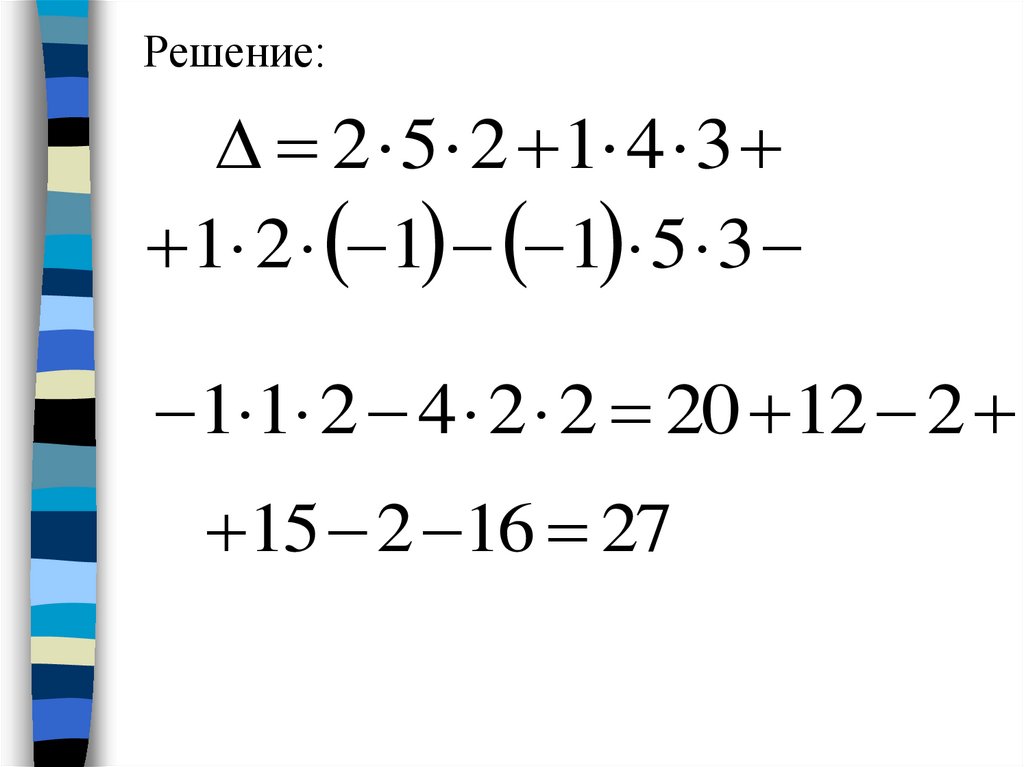





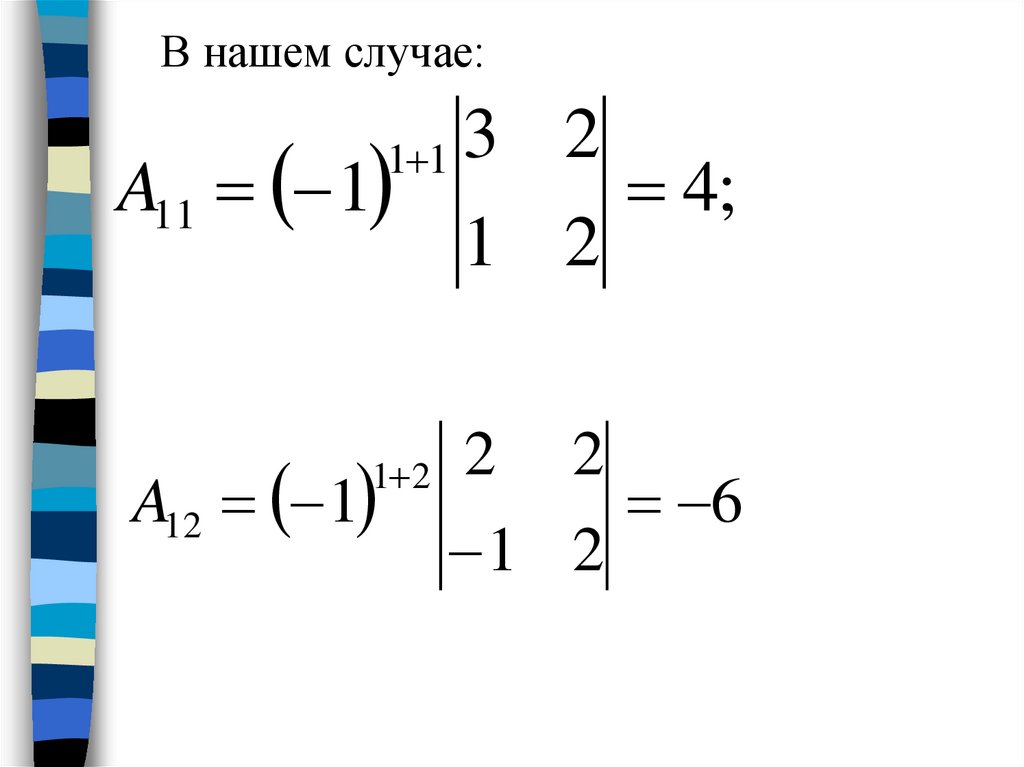

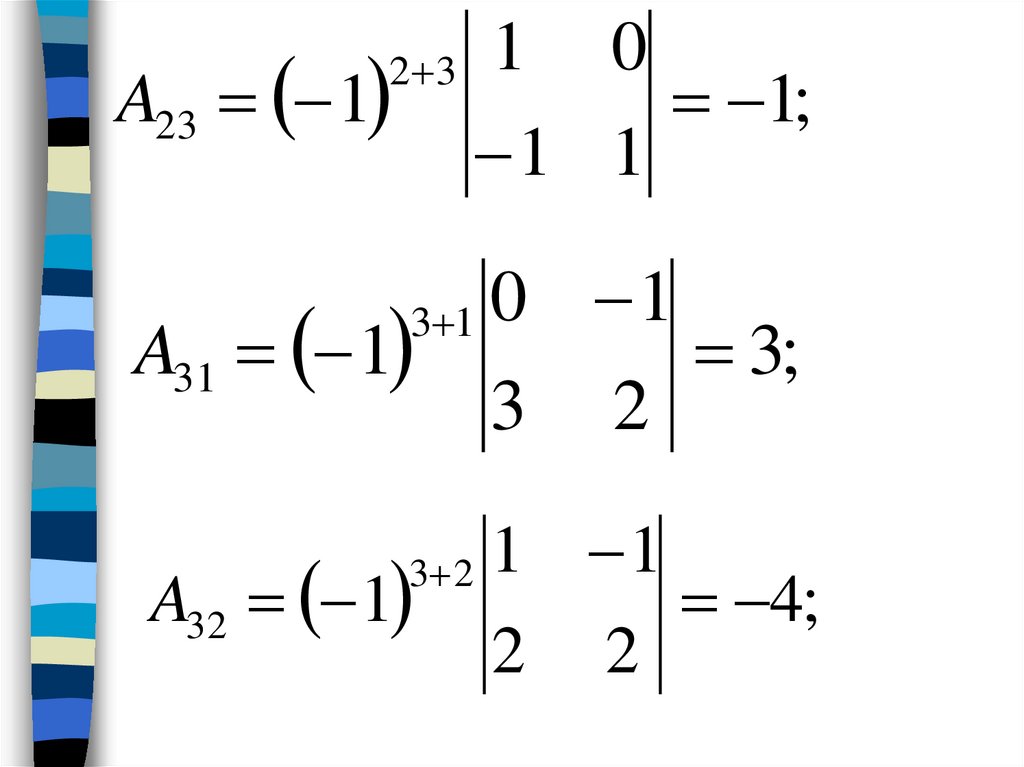


























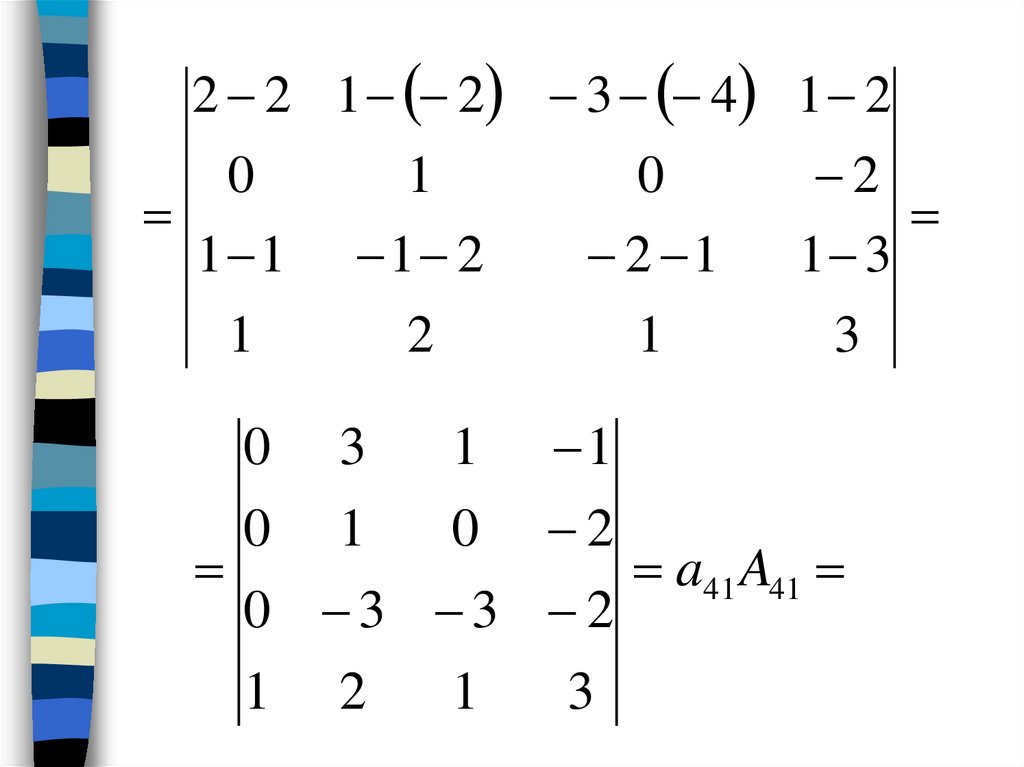





 mathematics
mathematics








