Similar presentations:
Определители, матрицы и действия над матрицами
1. Определители
2.
• Рассмотрим таблицуa11
a
21
a12
a 22
3.
Числаa11 , a12 , a21 , a22
– это
элементы таблицы.
aij
i номер строки;
j номер столбца
4.
• Число строк – порядок таблицы.• Главная диагональ – диагональ
идущая с левого верхнего угла в
правый нижний.
• Побочная диагональ – диагональ
идущая с верхнего правого угла в
левый нижний.
5.
a11a
21
побочная
a12
a 22
главная
6.
• Числоa11 a22 a21 a12
называется определителем 2-го
порядка .
7.
a11a21
a12
a11 a22 a21 a12
a22
8. Определители третьего порядка
9.
• Рассмотрим таблицуa11
a21
a
31
a12
a22
a32
a13
a23
a33
10.
• Числоa11a22 a33 a12 a 23a31 a13a21a32
a13a22 a31 a11a23a32 a12 a21a33
называется определителем третьего
порядка
11.
a11 a12 a13a21 a22 a23 a11a22a33 a12a23a31 a13a21a32
a31 a32 a33
a13a22a31 a11a23a32 a12a21a33
12. Методы вычисления определителей третьего порядка
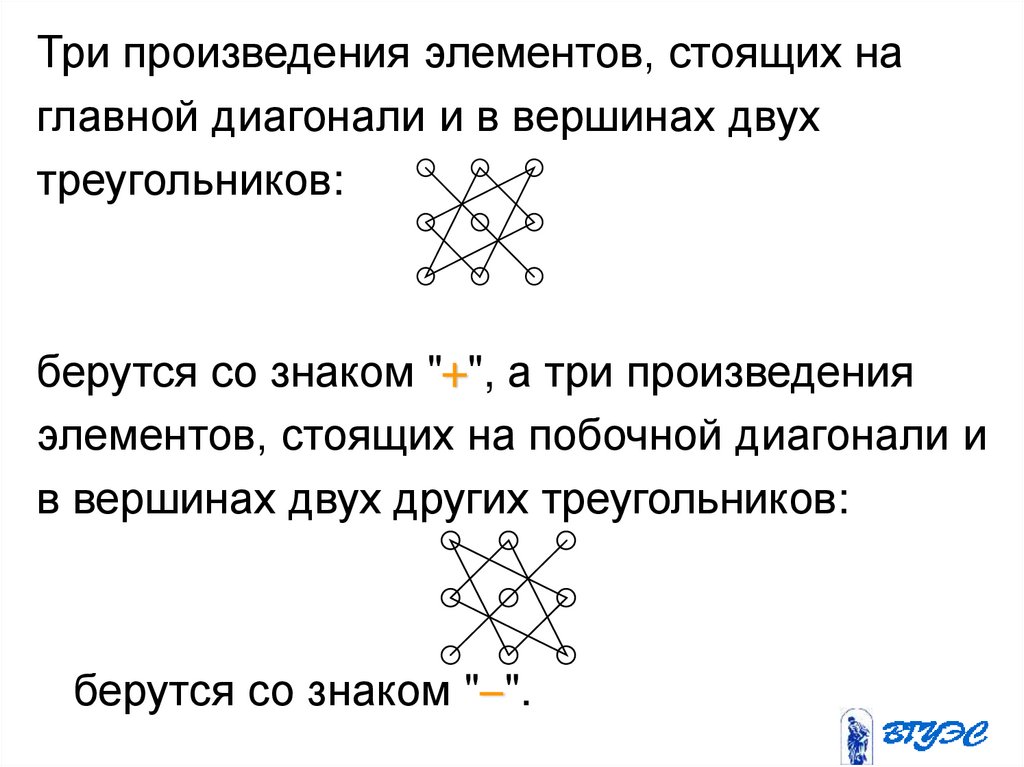
13. Правило треугольника
14.
Три произведения элементов, стоящих наглавной диагонали и в вершинах двух
треугольников:
берутся со знаком " ", а три произведения
элементов, стоящих на побочной диагонали и
в вершинах двух других треугольников:
берутся со знаком " ".
15. Разложение по элементам какой-либо строки(столбца)
16. Минор
17.
Опр. Минором элемента определителя3-го порядка называется определитель
2-го порядка, получающийся из данного
определителя вычёркиванием строки и
столбца, в которых расположен элемент.
18. Обозначение минора
Минор элемента , стоящего напересечении i-й строки и j-го
столбца определителя,
обозначают
M ij
19. Алгебраическое дополнение
20.
Опр. Алгебраическим дополнениемэлемента определителя
3-го
порядка называется минор
этого элемента, умноженный на
(-1) в степени k , где
k i j.
21.
Aij 1 M ijk
Aij 1 M ij
i j
22. Теорема разложения
Определитель 3-го порядка равенсумме произведений элементов
какой-либо строки (столбца)
определителя на их
алгебраические дополнения.
23.
Таким образом,разложений:
имеет
место
шесть
a11 A11 a12 A12 a13 A13 ,
a 21 A21 a 22 A22 a 23 A23 ,
a 31 A31 a 32 A32 a 33 A33 ,
a11 A11 a 21 A21 a 31 A31 ,
a12 A12 a 22 A22 a 32 A32 ,
a13 A13 a 23 A23 a 33 A33 .
24. Свойства определителей
1.Определитель не меняет своегозначения при замене каждой строки
соответствующим столбцом.
2.Определитель изменит знак ,если
поменять местами любые две
строки или столбца.
25.
3.Общий множитель элементовкакого-либо строки (столбца) определителя
можно выносить за знак определителя.
4.Определитель равен нулю, если он
имеет два одинаковых столбца или две
одинаковые строки.
5.Определитель равен нулю, если элементы
какой-либо строки (столбца) все равны нулю.
26.
6. Значение определителяне
изменится, если к элементам строки
или столбца прибавить соответствующие
элементы другой строки или столбца,
умноженные на одно число.
27. Определители высших порядков
28.
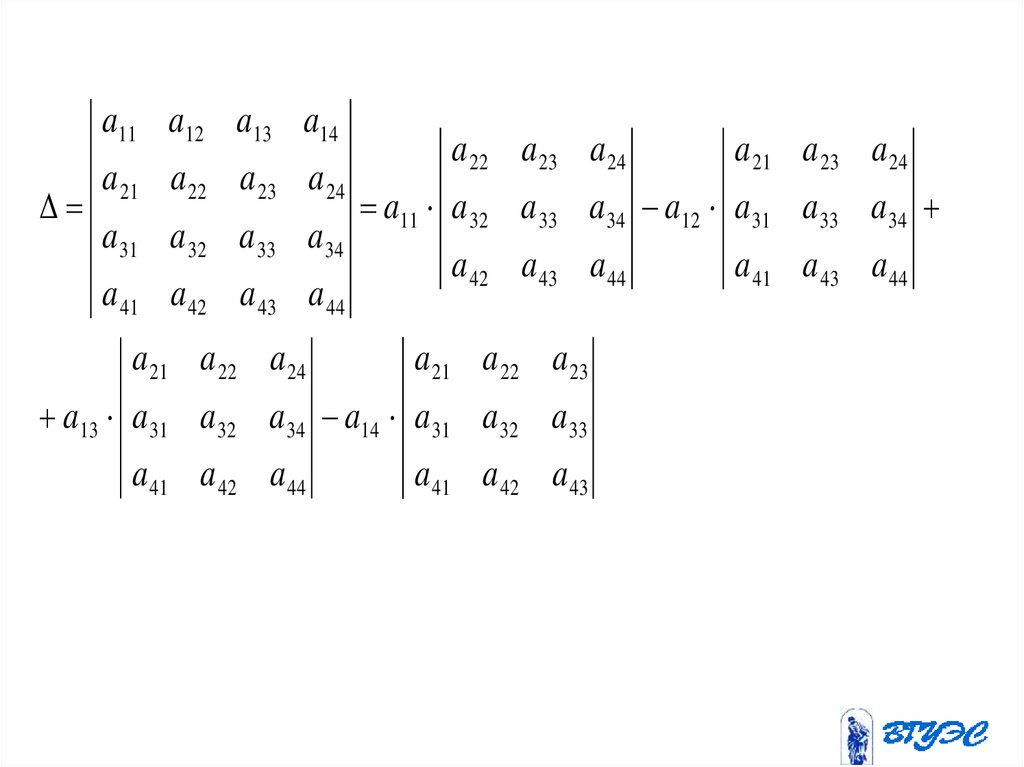
a11 a12 a13 a14a 21 a 22 a 23 a 24
a 31 a 32 a 33 a 34
a 41 a 42 a 43 a 44
a 21 a 22 a 24
a 22 a 23 a 24
a11 a 32 a 33 a 34 a12 a 31 a 33 a 34
a 42 a 43 a 44
a 21 a 22 a 23
a13 a 31 a 32 a 34 a14 a 31 a 32 a 33
a 41 a 42 a 44
a 21 a 23 a 24
a 41 a 42 a 43
a 41 a 43 a 44
29.
• С помощью свойства 6 добиваютсятого, чтобы в некоторой строке или в
некотором столбце все элементы,
кроме одного, были равны нулю.
• Затем раскладывают определитель
по элементам этой строки или столбца.
30.
23
1
1
1
2
0
2
0
1
1
1
2
0
3
3
31.
23
1
1
1
2
0
2
0
1
1
1
2
0
3 (-1)
+
3
32.
23
1
0
1
2
0
2
0
1
1
0
2
0
3
0
33.
2 0 24 2
2 1 3 1 0
1 1 3
34.
2 0 22 3 1 0 (-1)
+
1 1 3
35.
2 0 22 2
2 2
2 3 1 0 2 1 1
4 3
4 0 3
2 6 8 28
36.
3 1 2 15 1 2 1
9 1 1
3
3 0
6 1
5 2
3 2
1
2
4
3
1
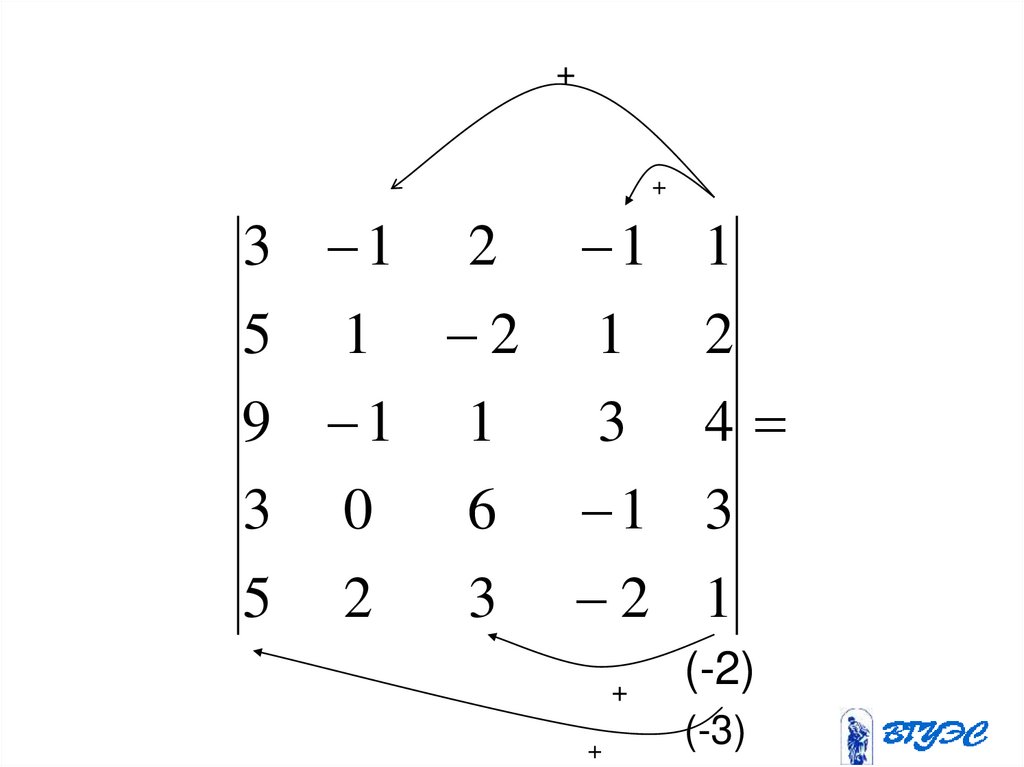
37.
++
3 1 2 1
5 1 2 1
9 1 1
3
3 0
6 1
5 2
3 2
+
+
1
2
4
3
1
(-2)
(-3)
38.
01
3
6
2
0 0
0
3 6 3
3 7 7
3 0
2
3 1 1
1
2
4
3
1
39.
13
1 5
1 1
6
2
1
3
3
6
2
3 6 3
3 7 7
3 0
2
3 1 1
1 6 3 (-1)
+
1 7 7
1 0
2
1 1 1
+
+
40.
12
3
5
3
1 6 3
0 1 4
0 6 1
0 7 4
2 1 4 (-5) 3
+
1 2
3 1 1 5 6 1 2 +
3
7 4 2
41.
2 1 422
1
1 1 1 17
3 0 17 22 3 2 1
4
4 11 4
0 11 4
1
1860
6 68 242
465
4
4
42. Метод приведения к треугольному виду
Метод приведения к треугольномувиду заключается в таком
преобразовании данного определителя,
когда все элементы его, лежащие над
(под) главной диагональю, становятся
равными нулю.
43.
a11a21
a31
a41
0
a22
a32
a42
0
0
a33
a43
0
0
a11 a22 a33 a44
0
a44
44.
а110
0
0
а12
а 22
0
0
а13
а 23
а33
0
а14
а 24
а11 а 22 а33 а 44
а34
а 44
45. Матрицы
46.
Матрицей называется прямоугольнаятаблица чисел .
Если матрица содержит
m строк и n
столбцов, то говорят, что матрица имеет
размерность m n .
m - порядок матрицы
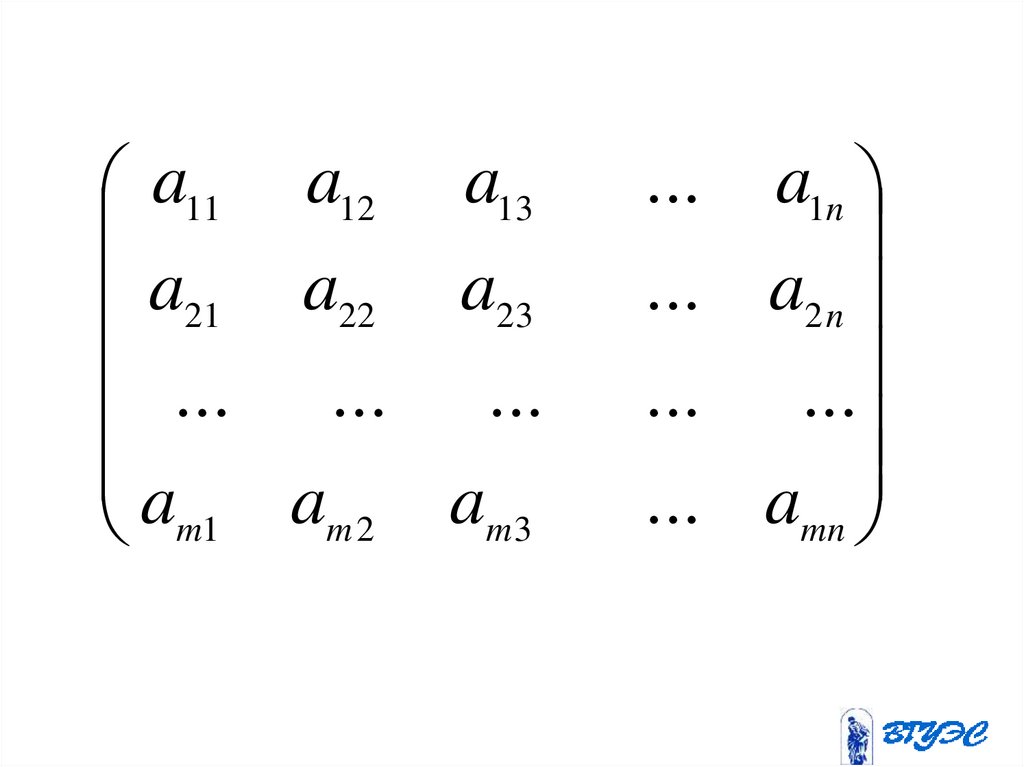
47.
a11 a12 a13a21 a22 a23
... ... ...
am1 am 2 am 3
... a1n
... a2 n
... ...
... amn
48.
• Обозначение матрицА aij m n
49.
Матрица размера m m называетсяквадратной.
Матрица , имеющая только одну строку
называется матрицей-строкой.
Матрица, имеющая только один
столбец называется
матрицей-столбцом .
50.
Две матрицы считаются равными,если равны их размеры и равны
элементы, стоящие на одинаковых
местах.
Квадратная матрица называется
невырожденной (неособенной), если
её определитель отличен от нуля, и
вырожденной (особенной) , если
определитель её равен нулю.
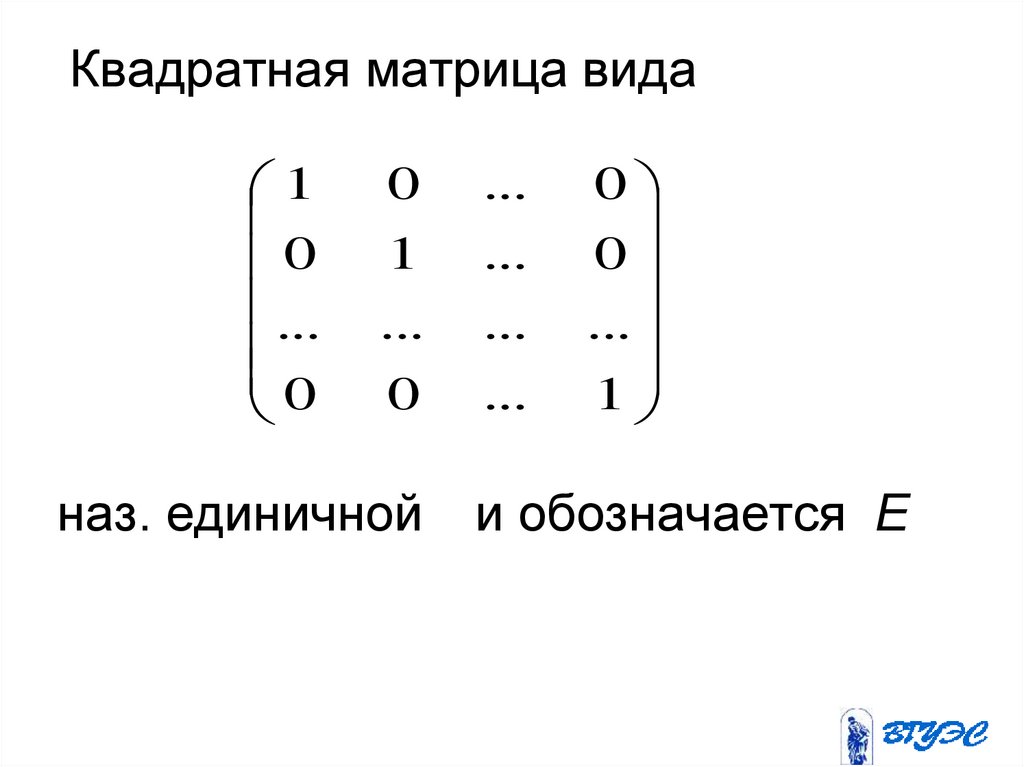
51.
Квадратная матрица вида1
0
...
0
0
1
...
0
наз. единичной
...
...
...
...
0
0
...
1
и обозначается Е
52.
• Матрица, все элементы которойравны нулю, наз. нулевой.
• Определитель, составленный из
элементов квадратной матрицы,
наз. определителем матрицы.
Очевидно
Е 1
53.
• Матрицаa11
T
A a12
a
13
a21
a22
a23
a31
a32
a33
наз. транспонированной по отношению к
матрице
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
54. Действия над матрицами.
Суммой двух матриц одинаковойразмерности А и В называется
матрица С той же размерности,
элементы которой равны суммам
элементов матриц A и B с
одинаковыми индексами.
55.
Произведением матрицына
число называется матрица ,
получающаяся из матрицы A
умножением всех её элементов
на .
56.
Разностью двухматриц А и В
одинаковой
размерности
называется матрица С=A+(-B).
57.
Произведением матрицы A (aij )размера m n на матрицу B (bij )
размера n k
называется матрица C (cij )
размера
m k , элемент cij которой , стоящий в
i-ой строке и j-ом столбце, равен
сумме произведений элементов i-ой
строки матрицы A и соответствующих
элементов j-го столбца матрицы B.
58. Свойства операций над матрицами
59.
1.A+B=B+A2.(A+B)+C=A+(B+C)
3.k(A+B)=kA+kВ
4. АВ≠ВА
60.
5. (AB)C=A(BC)6. A(B+C)=AB+AC
7. A+O=A
8. AE=EA=A
61.
• Если A и B две квадратныематрицы одного порядка, то
A B A B
62.
Обратная матрица63.
AПусть
- квадратная матрица.
Обратной для неё матрицей наз.
квадратная матрица того же порядка,
1
обозначаемая A
и
удовлетворяющая условию
A A A A E
1
1
64.
• Для того, чтобы квадратнаяматрица A имела обратную
матрицу, необходимо и достаточно,
чтобы матрица A была
невырожденной.
65.
А11 А21 А31А11 А21 А31
А
А
А
1
1
12
22
32
А
А12 А22 А32
А13 А23 А33
А13 А23 А33
66. Р а н г м а т р и ц ы
Рангматрицы
Рангом матрицы называется наивысший
из порядков отличных от нуля миноров
матрицы.
Ранг матрицы A обозначается:
r A
или
rang A .
67. Теорема о ранге матрицы
Ранг матрицы равенмаксимальному числу линейно –
независимых строк матрицы.
68. Элементарные преобразования матрицы.
cijЭлементарные
преобразования матрицы.
1.Умножение всех элементов строк
на одно и то же число не равное 0.
2. Перестановка строк местами.
3. Прибавление к элементам одной
строки соответствующих
элементов другой строки,
умноженных на одно и тоже число.
69.
4.Отбрасываниеодной из
одинаковых строк.
двух
5.Отбрасывание нулевой строки
70.
Теорема: Элементарныепреобразования не меняют ранг
матрицы.
Матрицы, полученные с помощью
элементарных преобразований
наз. эквивалентными (~).
71.
2 1 3 5A 1 3 1 2 ~
1 10 6 1
72.
(-1)(-2)
1
3
1
2
+
+
2 1 3 5
~
1 10 6 1
73.
1 3 1 21
0 7 5
0 7 5 1
+
~
74.
1 3 1 20 7 5 1
0 0
0
0
r ( A) 2
75.
2 3 5 3 2 3 5+
A 3 4 3 1 3 (-2)
5 6 1 4 4 (-2)
76.
2 3 5 3 20 (-3) ~
~ 0 1 9 7
+
0 3 27 23 2
77.
2 3 5 3 20 1 9 7 0
0 0 0 2 2
r ( A) 3
78. Системы линейных алгебраических уравнений (СЛАУ)
79.
a11x1 a12 x2 a13 x3 ... a1n xn b1a x a x a x ... a x b
21 1 22 2
23 3
2n n
2
..........
..........
..........
..........
..........
.....
am1 x1 am 2 x2 am 3 x3 ... amn xn bm
80.
• Здесьx1 , x2 ,..., xn - неизвестные;
aij - коэффициенты при неизвестных,
где
i - номер уравнения,
j - номер неизвестного;
bi - свободные члены (правые части).
81.
• Система наз. неоднородной, еслине все bi равны нулю.
Система наз. однородной, если все
bi равны нулю.
82.
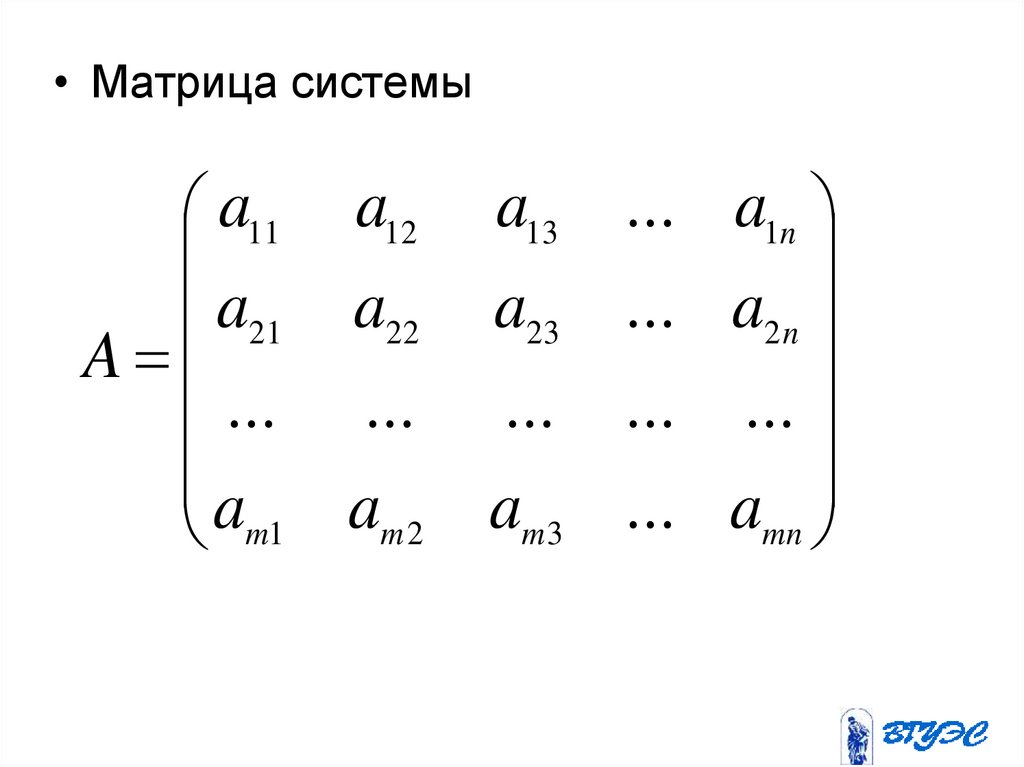
• Матрица системыa11 a12 a13
a21 a22 a23
A
... ... ...
am1 am 2 am 3
... a1n
... a2 n
... ...
... amn
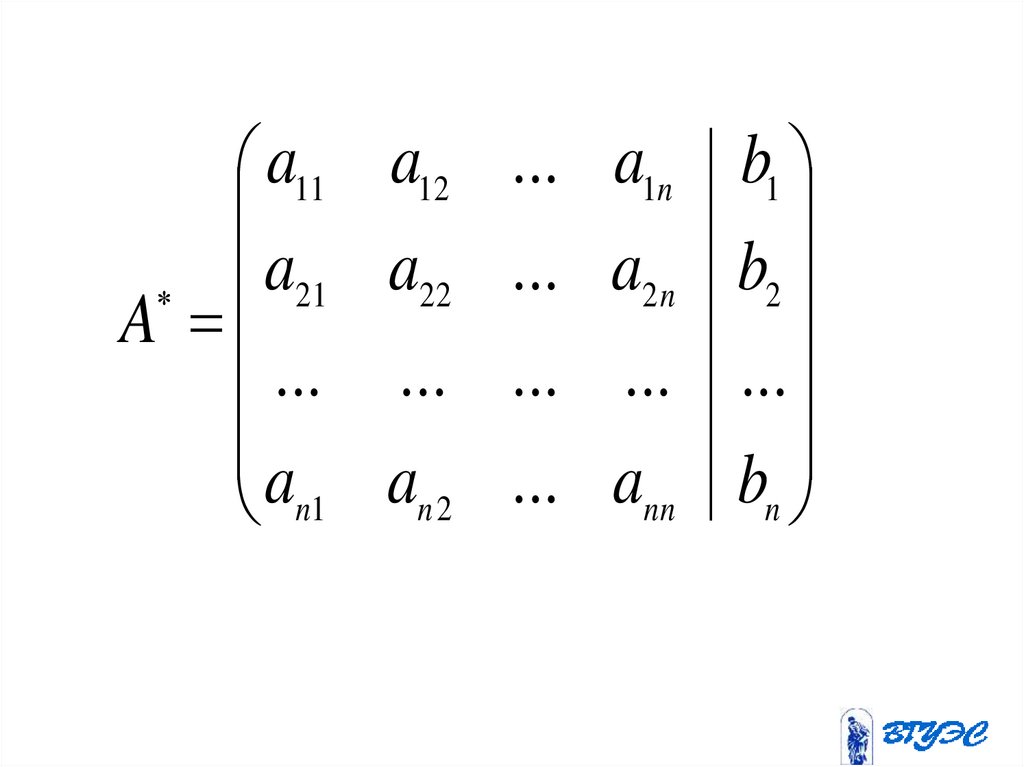
83. Расширенная матрица
a11 a12a21 a22
A
... ...
am1 am 2
...
...
...
...
a1n
a2 n
...
amn
b1
b2
...
bm
84.
Решением системы будем называтьупорядоченный набор чисел
x1 , x2 ,..., xn
обращающий каждое уравнение
системы в верное равенство.
85.
Решить систему — значит найтивсе ее решения или доказать, что ни
одного решения нет.
Система, имеющая хотя бы одно
решение, называется совместной.
Если система имеет только одно
решение, то она называется
определенной.
86.
Если система не имеет решений, тоона называется несовместной.
Система, имеющая более чем одно
решение, называется неопределенной
(совместной и неопределенной).
Если число уравнений системы
совпадает с числом неизвестных , то
система называется квадратной.
87.
Две системы, множества решенийкоторых совпадают, называются
эквивалентными или равносильными.
Преобразование, применение которого
превращает систему в новую
систему, эквивалентную исходной,
называется эквивалентным или
равносильным преобразованием.
88. Метод Гаусса
89.
Рассмотрим квадратную систему:x1 x2 3x3 2 x4 11;
4 x 6 x x
1;
1
2
3
3
x
2
x
2
x
x
3
;
1
2
3
4
5 x1 x2 2 x3 x4 2.
90.
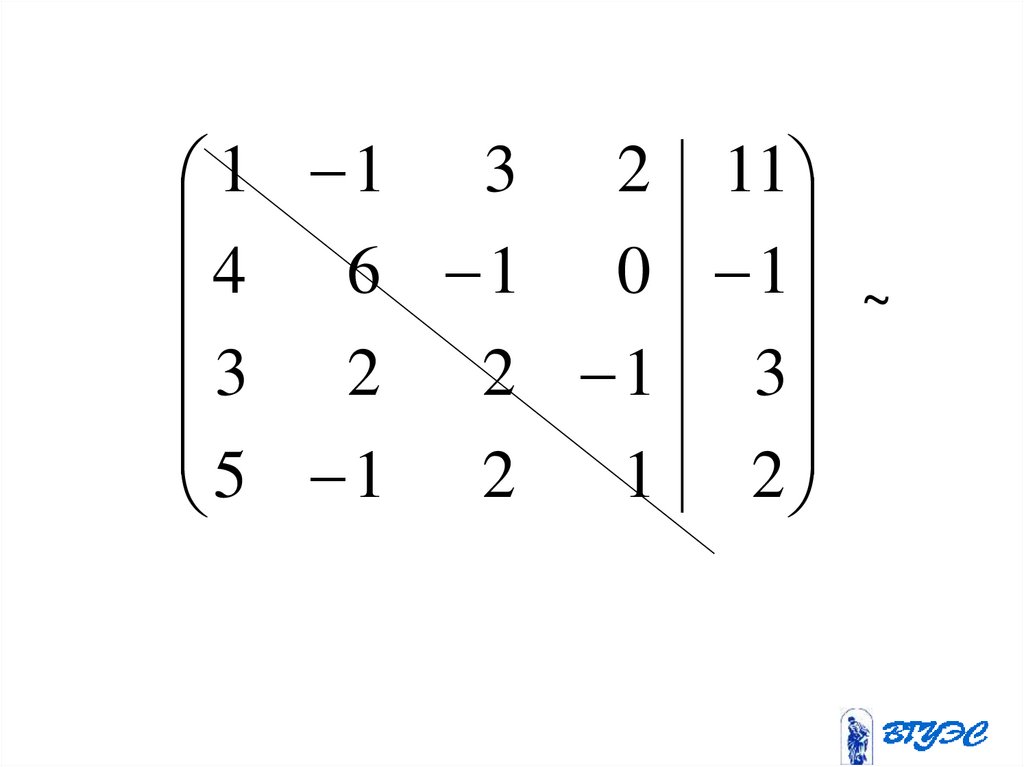
1 1 3 2 114 6 1 0 1 ~
3 2 2 1 3
1 2
5 1 2
91.
1 1 3 2 114 6 1 0 1 ~
3 2 2 1 3
1 2
5 1 2
92.
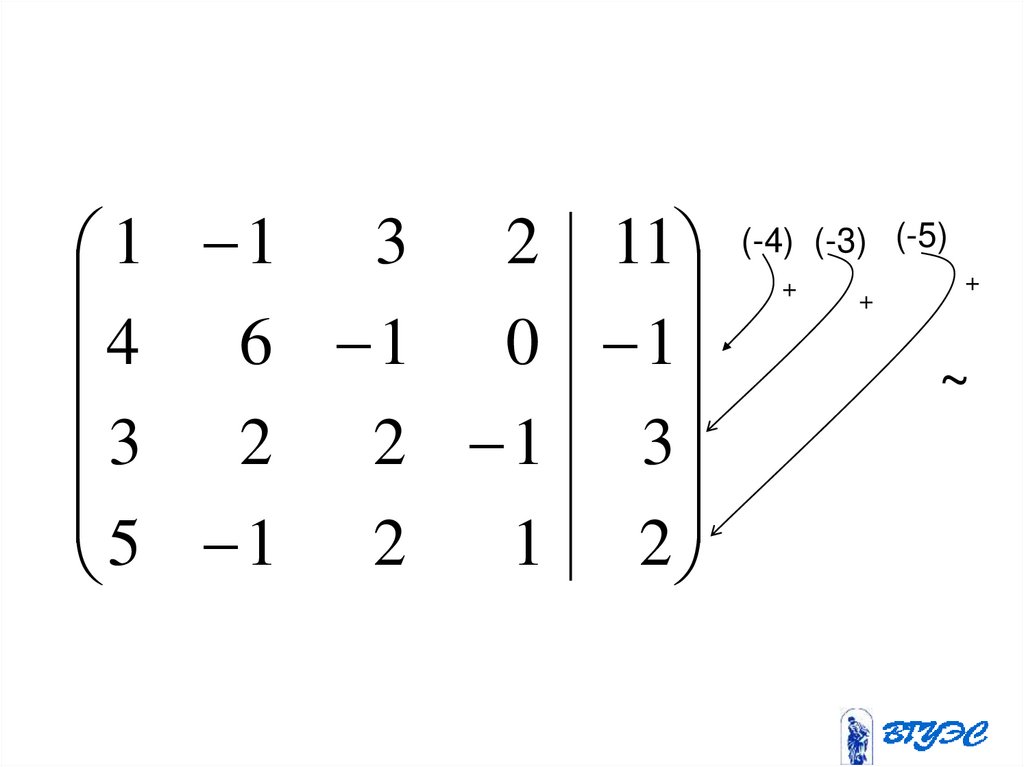
(-5)(-4)
(-3)
1
1
3
2
11
4 6 1 0 1
~
3 2 2 1 3
1 2
5 1 2
+
+
+
93.
10
0
0
3
1
10 13
5 7
4 13
11
2
8 45 2
+
+
(-2)
7 30
9 53 (-5)
94.
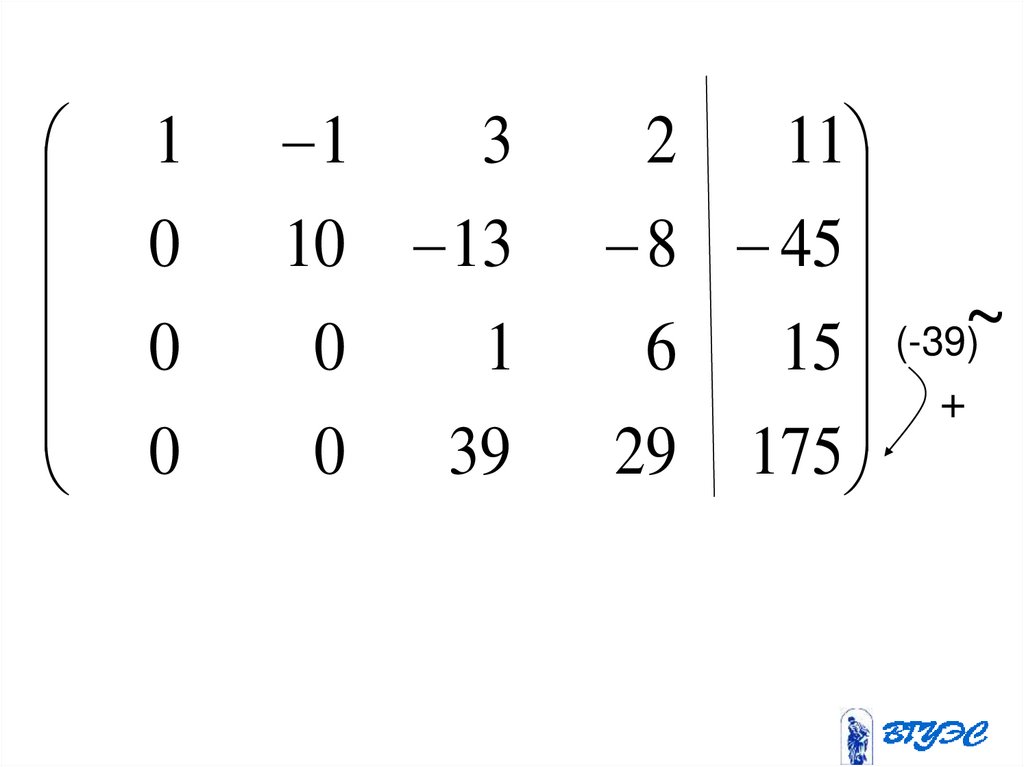
10
0
0
1
3
10 13
0
1
0 39
2
11
8 45
~
(-39)
6 15
+
29 175
95.
10
0
0
1
10
0
0
3
2
11
13
8 45
1
6
15
0 205 410
96.
Полученная матрица соответствует системе:x1 x2 3x3 2 x4 11;
10 x2 13 x3 8 x4 45;
x
6
x
15
;
3
4
205 x4 410 .
97.
x1 11 x2 3 x3 2 x4 11 1 3 3 2 211 1 9 4 1;
10 x2 45 13 x3 8 x4 45 13 3 8 2
45 39 16 10; х2 1;
x3 15 6 x4 15 6 2 15 12 3;
x4 2.
98.
6 x1 9 x2 3x3 2 x4 42 x1 3x2 5 x3 4 x4 2
4 x 6 x 4 x 3 x 3
1
2
3
4
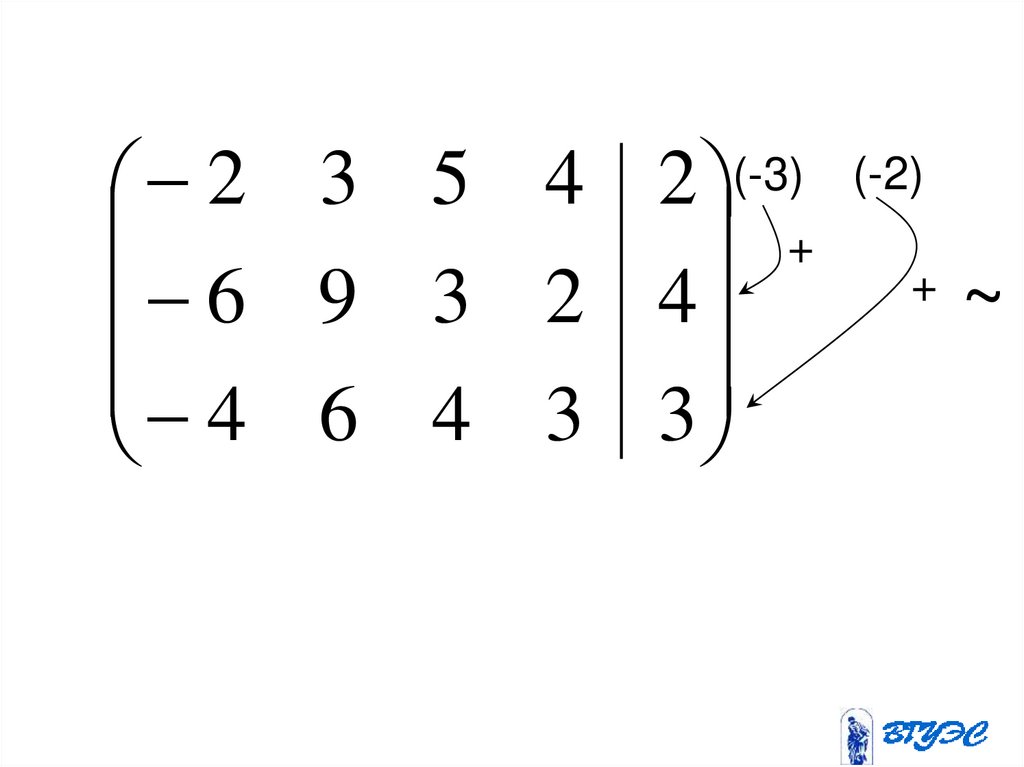
99.
6 9 3 2 42 3 5 4 2 ~
4 6 4 3 3
100.
(-2)(-3)
2
3
5
4
2
+ +
~
6 9 3 2 4
4 6 4 3 3
101.
54
2
2 3
0 0 12 10 2 ~
0 0 6 5 1
102.
54
2
2 3
0 0 6 5 1 (-2) ~
0 0 12 10 2 +
103.
42
2 3 5
0 0 6 5 1 ~
0 0 0
0
0
104.
2 30
0
5
4 2
6 5 1
105.
• Рассмотрим минор2 5
12 0
0 6
назовем его базисным. Тогда
x1 , x3 базисные переменные.
106.
2 x1 3 x2 5 x3 4 x4 26 x3 5 x4 1
107.
5 x4 1x3
;
6
5
1
x3 x4 ;
6
6
108.
2 x1 2 3x2 5 x3 4 x4 ;2 3x2 5 x3 4 x4
x1
;
2
3
5
x1 1 x2 x3 2 x4
2
2
3
5 5
1
1 x2 x4 2 x4
2
2 6
6
3
25
5
7 3
1
1 x2 x4 2 x4 x2 x4 ;
2
12
12
12 2
12
109.
31
7
x1 x2 x4 ;
2
12
12
5
1
x3 x4 ;
6
6
110.
31
7
x1 C2 C4 ;
2
12
12
x2 C2 ;
5
1
x3 C4 ;
6
6
x4 C4 .
111. Метод Жордана-Гаусса
112.
a11x1 a12 x2 a13 x3 ... a1n xn b1a x a x a x ... a x b
21 1 22 2
23 3
2n n
2
..........
..........
..........
..........
..........
.....
an1 x1 an 2 x2 an 3 x3 ... ann xn bn
113.
a11 a12a
a
21
22
A
... ...
an1 an 2
...
...
...
...
a1n
a2 n
...
ann
b1
b2
...
bn
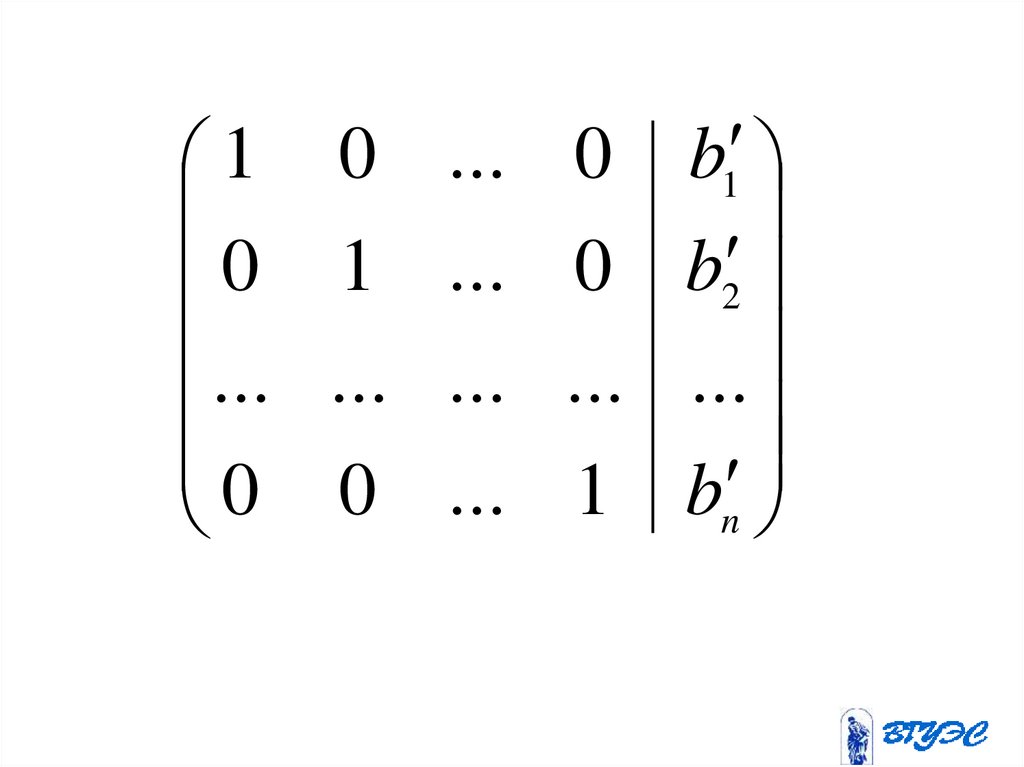
114.
10
...
0
0
1
...
0
...
...
...
...
0
0
...
1
b1
b2
...
bn
115.
x1 2 x2 4 x3 315 x1 x2 2 x3 29
3x x x 10
2
3
1
116.
1 2 4 315 1 2 29
3 1 1 10
117.
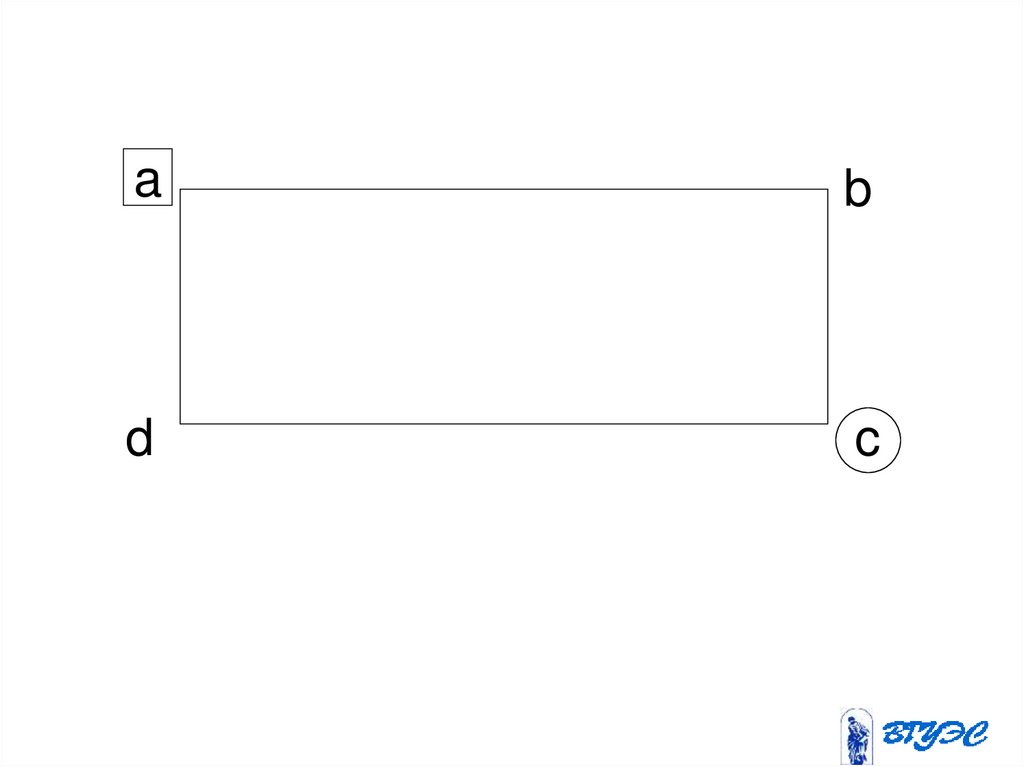
ab
d
c
118.
a с b dс
a
119.
столбецразрешающий
1 2 4 31
5 1 2 29
3 1 1 10
разрешающая
строка
~
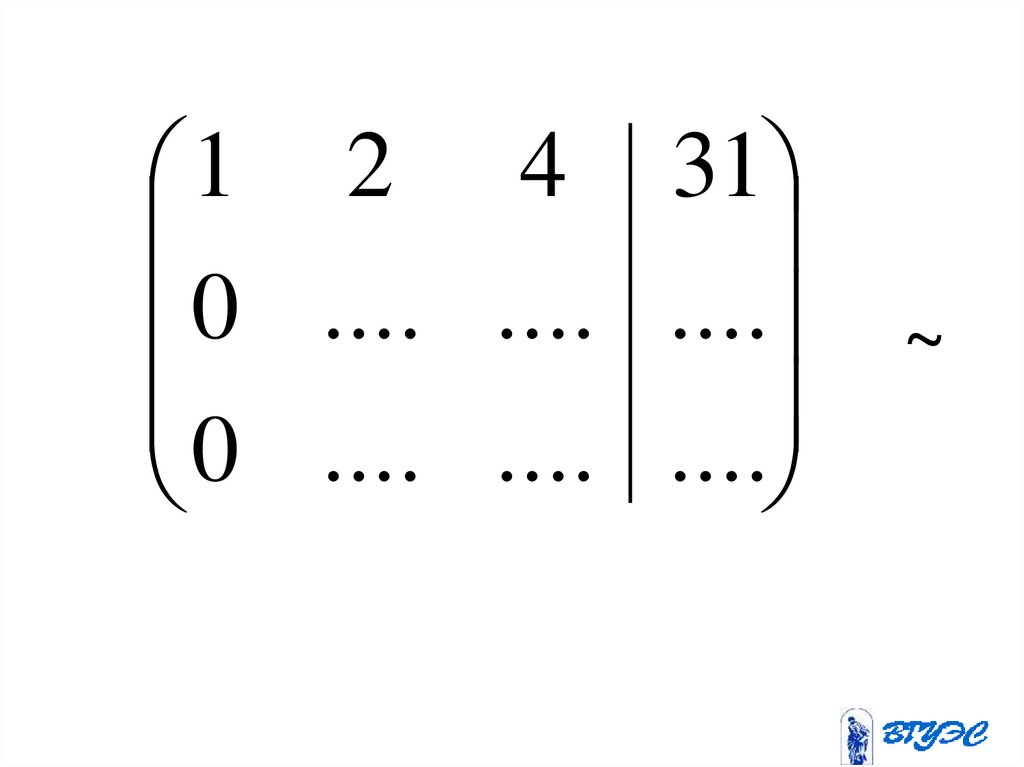
120.
1 2 4 310 .... .... ....
0 .... .... ....
~
121.
431
1 2
0 9 18 126
0 7 11 83
~
122.
431
1 2
1
0 9 18 126 ~
9
0 7 11 83
123.
431
1 2
2
14
0 1
0 7 11 83
~
124.
1 0 ... ...~
0
1
2
14
0 0 ... ...
125.
1 0 0 30 1 2 14
1
0 0 3 15
3
~
126.
1 0 0 30 1 2 14
0 0 1 5
~
127.
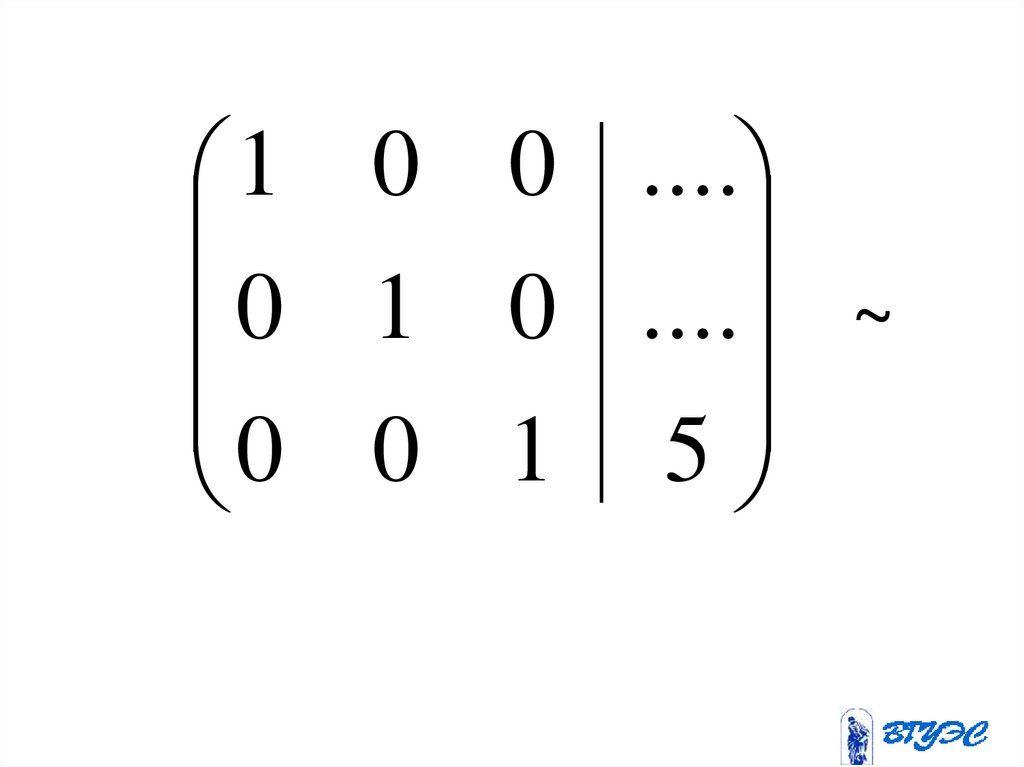
1 0 0 ....0 1 0 .... ~
0 0 1 5
128.
1 0 0 30 1 0 4
0 0 1 5
129.
x1 3x
4
2
x 5
3
130.
6 x1 9 x2 3x3 2 x4 42 x1 3x2 5 x3 4 x4 2
4 x 6 x 4 x 3 x 3
1
2
3
4
131.
6 9 3 2 42 3 5 4 2
4 6 4 3 3
~
132.
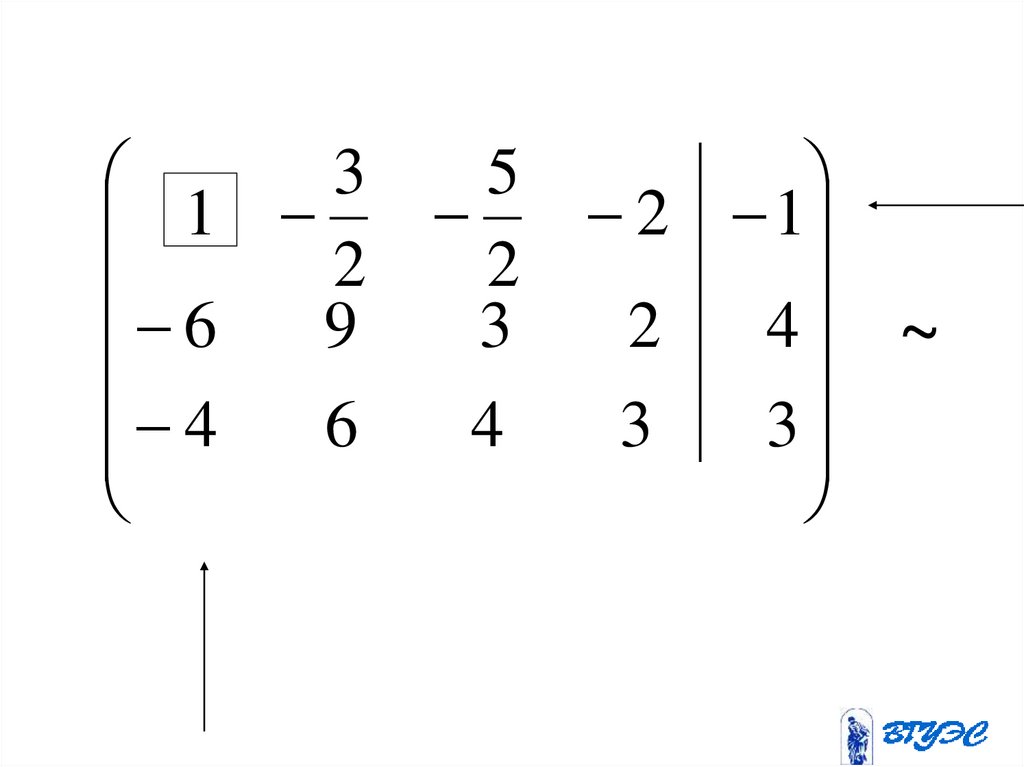
2 3 5 4 26 9 3 2 4
4 6 4 3 3
1
2
~
133.
31
2
9
6
4
6
5
2
3
4
2 1
2
4 ~
3
3
134.
31
2
0
0
0
0
5
2 1
2
12 10 2 ~
6 5 1
135.
31
2
0
0
0
0
5
2 1
2
1 ~
6 5 1 6
12 10 2
136.
35
2 1
1
2
2
5
1
0
0
1
6
6
0
0 12 10 2
~
137.
31
2
0
0
0
0
1
0
12
5
1
6
0 0
7
12
1
6
0
138.
31
7
x
x
x
1 2 2 12 4
12
5
1
x
x
3
4
6
6
139.
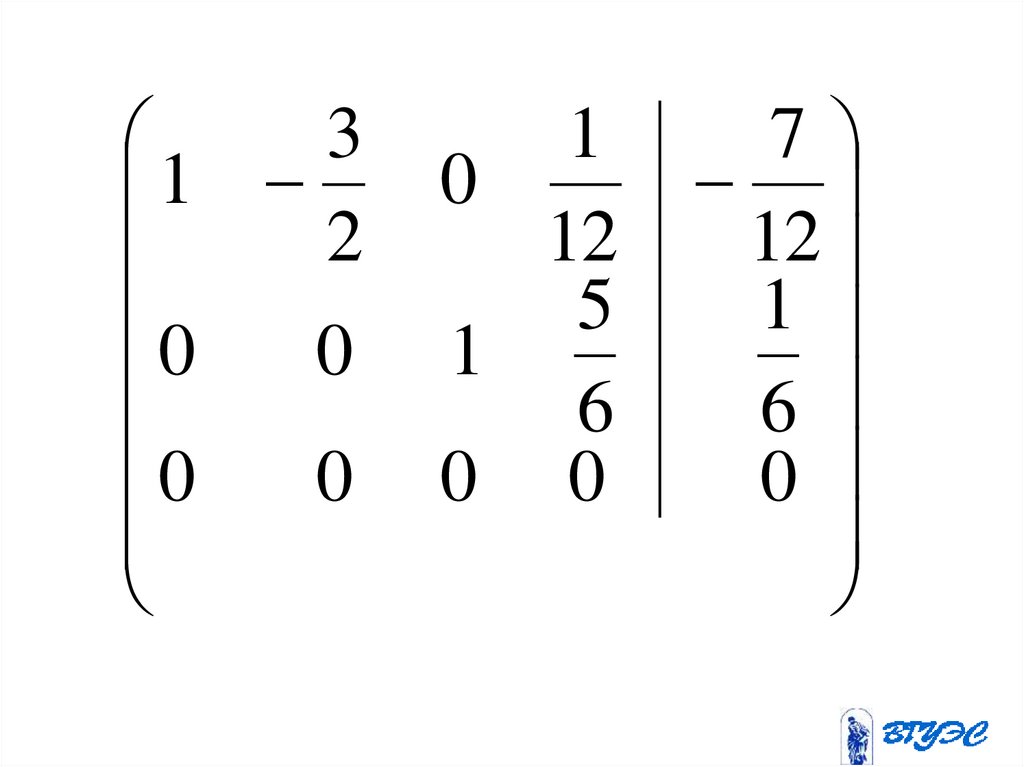
31
7
x1 x2 x4 ;
2
12
12
5
1
x3 x4 .
6
6
140.
31
7
x1 C2 C4 ;
2
12
12
x2 C2 ;
5
1
x3 C4 ;
6
6
x4 C4 .
141. Матричный метод
142.
• С помощью этого метода можнорешать квадратные системы
линейных уравнений
143.
a11x1 a12 x2 a13 x3 ... a1n xn b1a x a x a x ... a x b
21 1 22 2
23 3
2n n
2
..........
..........
..........
..........
..........
.....
an1 x1 an 2 x2 an 3 x3 ... ann xn bn
144.
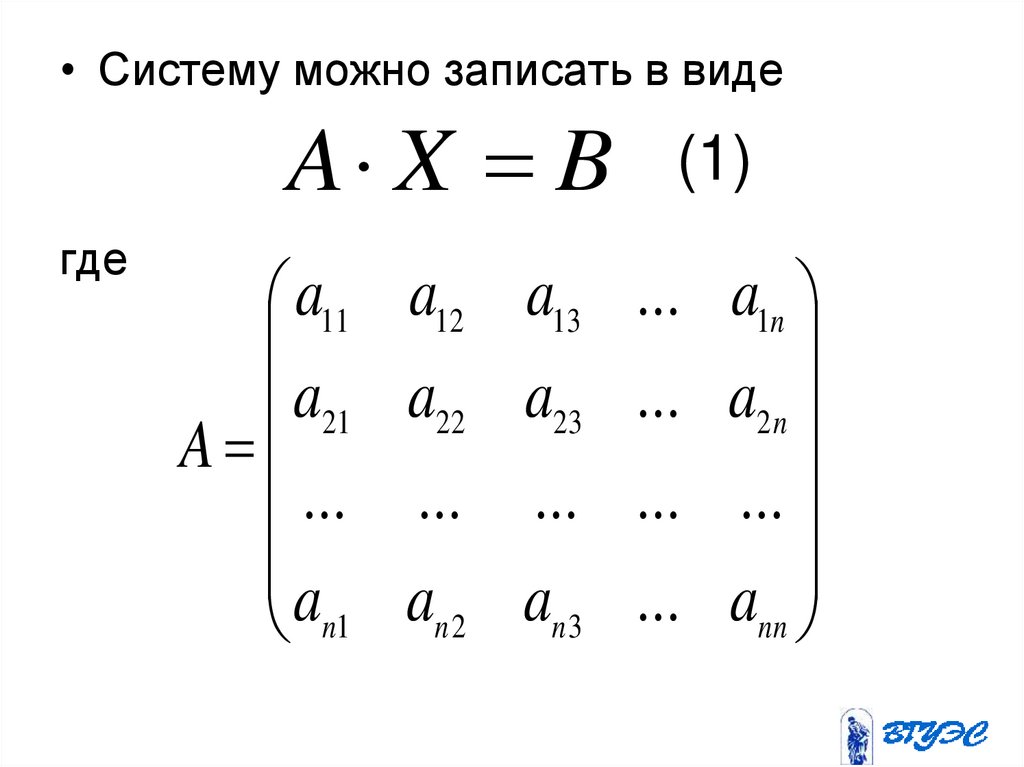
• Систему можно записать в видеA X B (1)
где
a11
a21
A
...
an1
a12 a13
a22 a23
... ...
an 2 an 3
...
...
...
...
a1n
a2 n
...
ann
145.
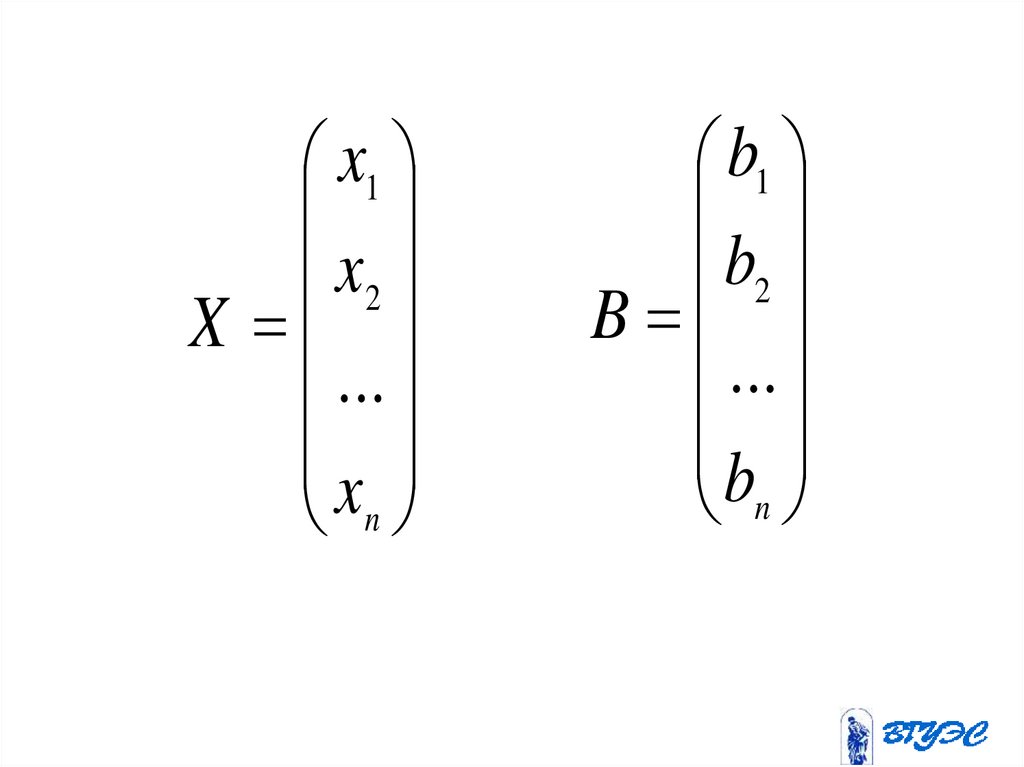
x1x2
X
...
xn
b1
b2
B
...
bn
146.
• Если матрицаA невырожденная, то
можно выполнить преобразования
A A X A B
1
1
X A B
1
(2)
147.
x 2 y z 22 x y 3 z 9
5 x 2 y 2 z 3
1 2 1
x
2
A 2 1 3 , X y , B 9
5 2 2
z
3
148.
X A B1
149.
А111
1
А А12
А
13
А21
А22
А23
А31
А32
А33
150.
1 2 12 1 3 2 4 30 5 6 8 25
5 2 2
151.
1 3A11
2 6 4
2 2
2 3
A12
( 4 15) 19
5 2
2 1
A13
4 5 9
5 2
152.
2 1A21
( 4 2) 2
2 2
1 1
A22
2 5 3
5 2
1 2
A23
(2 10) 8
5 2
153.
2 16 1 5
A31
1 3
1 1
(3 2) 5
A32
2 3
1 2
1 4 5
A33
2 1
154.
4 2 51
1
A 19 3 5
25
5
8
9
155.
x4 2 5 2
1
X y 19 3 5 9
25
z
9 8 5 3
4 2 2 9 5 3
1
19 2 3 9 ( 5) 3
25
9 2 8 9 ( 5) 3
156.
8 18 1525 1
1
1
38 27 15 50 2
25
25
18 72 15
75 3
157.
x 1y 2
z 3
158. Метод Крамера
159.
• Если определитель системы nлинейных уравнений с n
неизвестными отличен от нуля, то
эта система является определенной
и её единственное решение
находится по формулам
160.
ixi
i 1,2,...., n
161.
a11a21
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
162.
Здесьi
– определитель,
получающийся из определителя
заменой i-го столбца столбцом
свободных членов.
163.
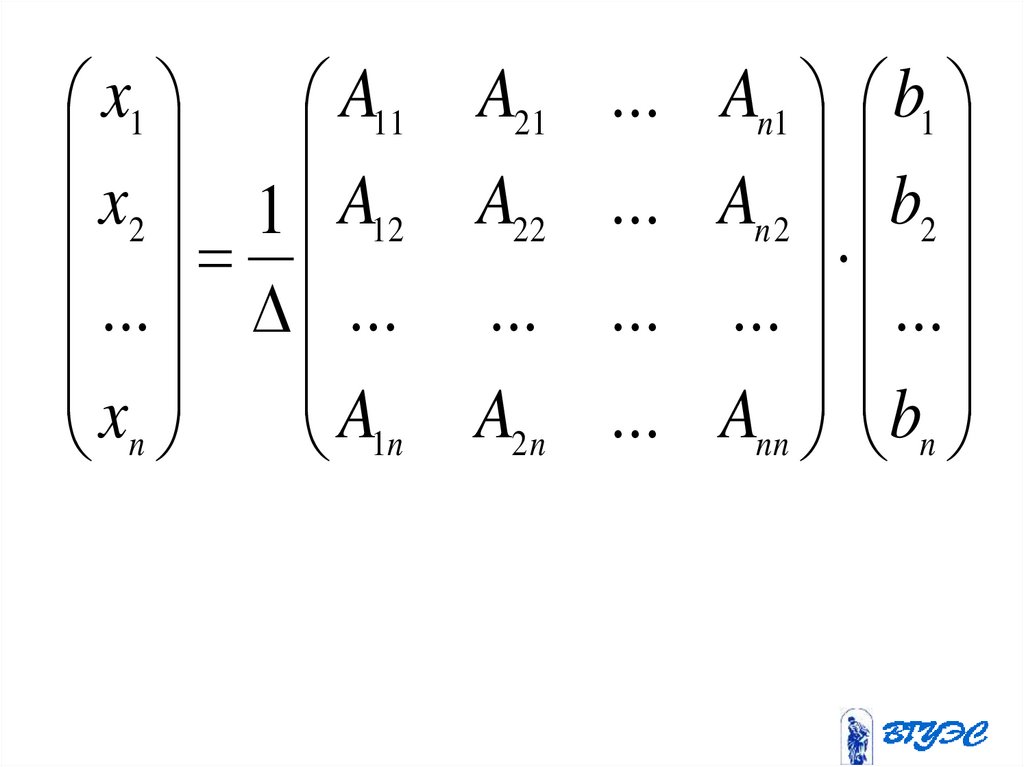
x1A11 A21
x2 1 A12 A22
... ... ...
x
A
A
n
1n
2n
...
...
...
...
An1 b1
An 2 b2
...
...
Ann bn
164.
A11 b1 A21 b2 ... An1 bnx1
b1
b2
...
bn
a12
a22
...
an 2
... a1n
... a2 n
A11 b1 A21 b2 ... An1 bn
... ...
... ann
165.
1x1
166.
x 2 y z 22 x y 3 z 9
5 x 2 y 2 z 3
167.
xx
;
y
y
;
z
z
168.
1 2 12 1 3
5 2 2
2 4 30 5 6 8 25
169.
2 2 1x 9 1 3
3 2 2
4 18 18 3 12 36 25
170.
1 2 1y 2 9 3
5 3 2
18 30 6 45 9 8 50
171.
1 2 2z 2 1 9
5 2 3
3 8 90 10 12 18 75
172.
25x
1;
25
50
y
2;
25
75
z
3.
25
173.
• Если 0 и по крайне мере один изопределителей i 0, то система не
имеет решения.
• Если 0 и i 0 , система либо
не имеет решения, либо имеет
бесконечно много решений.
174.
x y 2z 22 x 2 y 4 z 4
3x 3 y 6 z 3
175.
1 1 21 1 2
2 2 4 2 1 1 2 0
3 3 6
3 3 6
2 1 2
2 1 2
x 4 2 4 2 2 1 2 0
3 3 6
3 3 2
176.
1 2 21 2 2
y 2 4 4 2 1 2 2 0
3 3 6
3 3 6
1 1 2
1 1 2
z 2 2 4 2 1 1 2 0
3 3 3
3 3 3
177.
• Система не имеет решения, т.к.первое и третье уравнения
противоречивы
178.
2 x 3 y z 34 x 6 y 2 z 6
3x y 2 z 1
179.
2 3 12 3 1
4 6 2 2 2 3 1 0
3 1 2
3 1 2
3
3 1
x 6
6 2 0
1 1 2
180.
2 3 12 3 1
y 4 6 2 2 2 3 1 0
3 1 2
3 1 2
2 3
3
z 4 6
6 0
3 1 1
181.
• Второе уравнение получаетсяумножением первого на два. Данная система
равносильна системе
2 x 3 y z 3
3
x
y
2
z
1
Система имеет бесчисленное множество
решений.
182.
2 32 9 11
3 1
183.
y 3x 2 z 12 x 3 3 x 2 z 1 z 3
2x 9x 6z 3 z 3
11x 5 z 0
5
x z
11
15
y z 2z 1
11
7
y 1 z
11
184.
5x z
11
7
y 1 z
11
z z
185. Т е о р е м а К р о н е к е р а - К а п е л л и
ТеоремаКронекера-Капелли
m
Для того чтобы система
неоднородных линейных уравнений
с
неизвестными была совместной,
необходимо и достаточно, чтобы
n
r A r A
186.
• Замечание. Пусть система совместна иr A r A k
- k n если число уравнений равно
числу неизвестных, причем 0 , то
система имеет единственное решение;
-
k n если число уравнений меньше
числа неизвестных, то система имеет
множество решение.
187.
1 5 4 3 1*
A 2 1 2 1 0
5 3 8 1 1
(-2) (-5)
~
188.
54
3
1
1
(-2)
0
11
6
7
2
~
0 22 12 14 4
189.
43
1
1 5
0 11 6 7 2
0 0
0
0
0
r ( A) r ( A ) 2 4
*
190.
1 142
x1 x3 x4 ;
11 11
11
2 6
7
x 2 x3 x 4 .
11 11
11
191. Однородные системы
a11x1 a12 x2 ... a1n xn 0,a x a x ... a x 0,
21 1
22 2
2n n
..........
..........
..........
..........
.....
am1 x1 am 2 x2 ... amn xn 0.
192. Теорема о совместности однородной системы
Для того чтобы однородная системалинейных уравнений имела решение,
необходимо и достаточно, чтобы ранг
матрицы этой системы был меньше числа
неизвестных n.






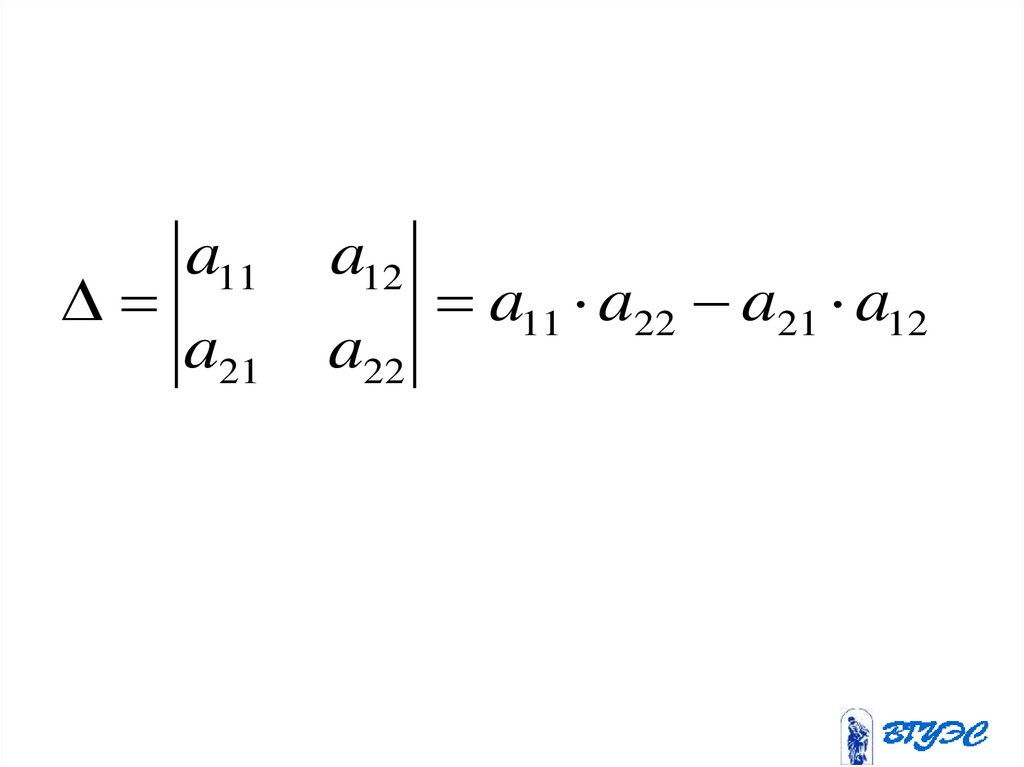












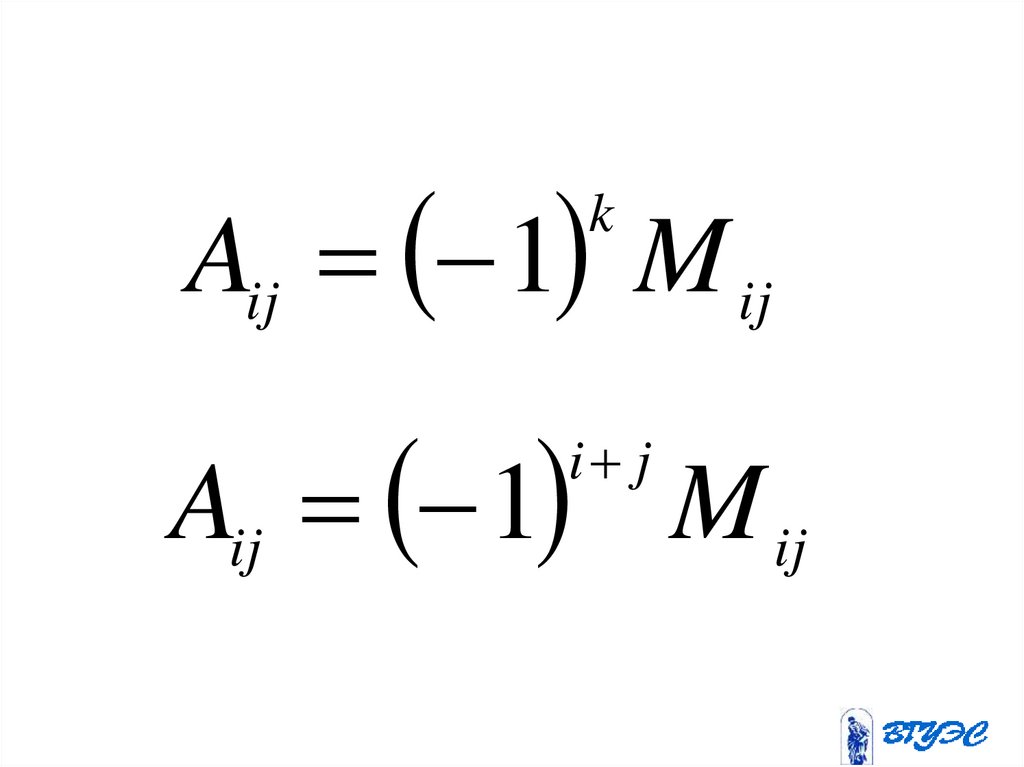







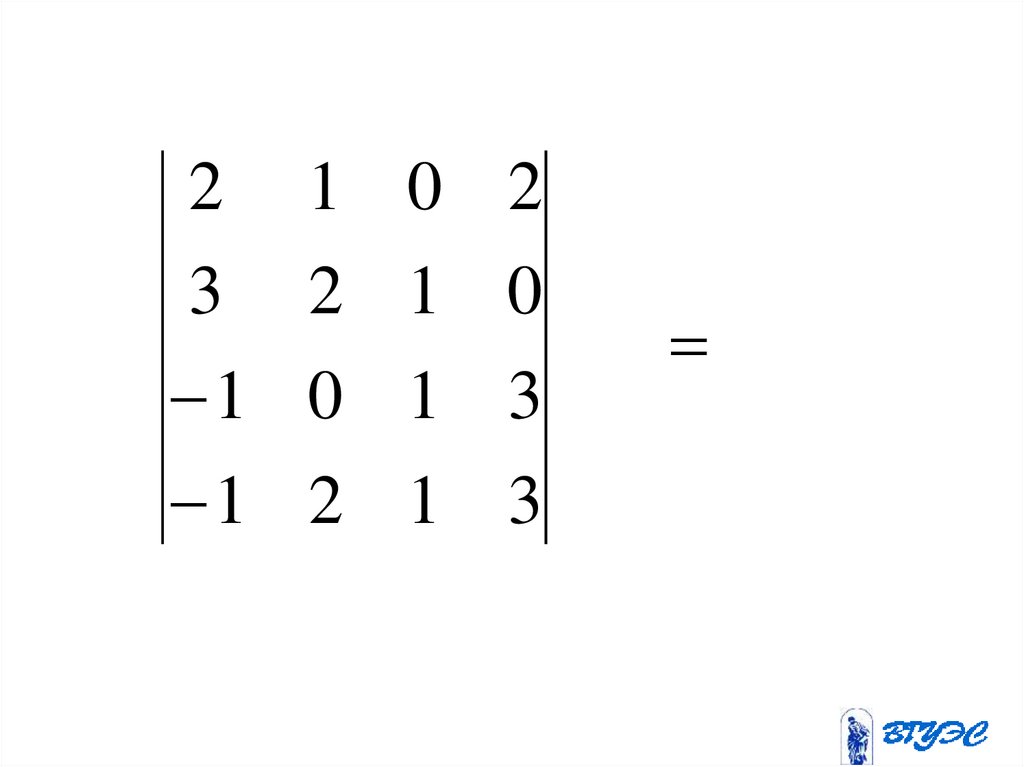


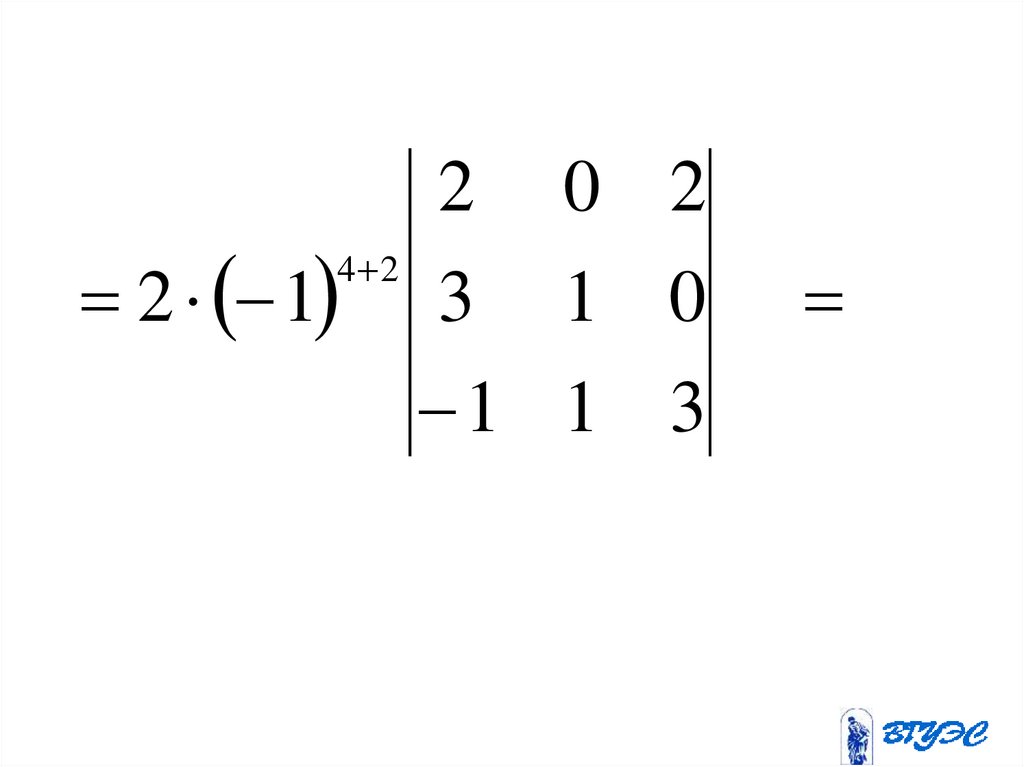
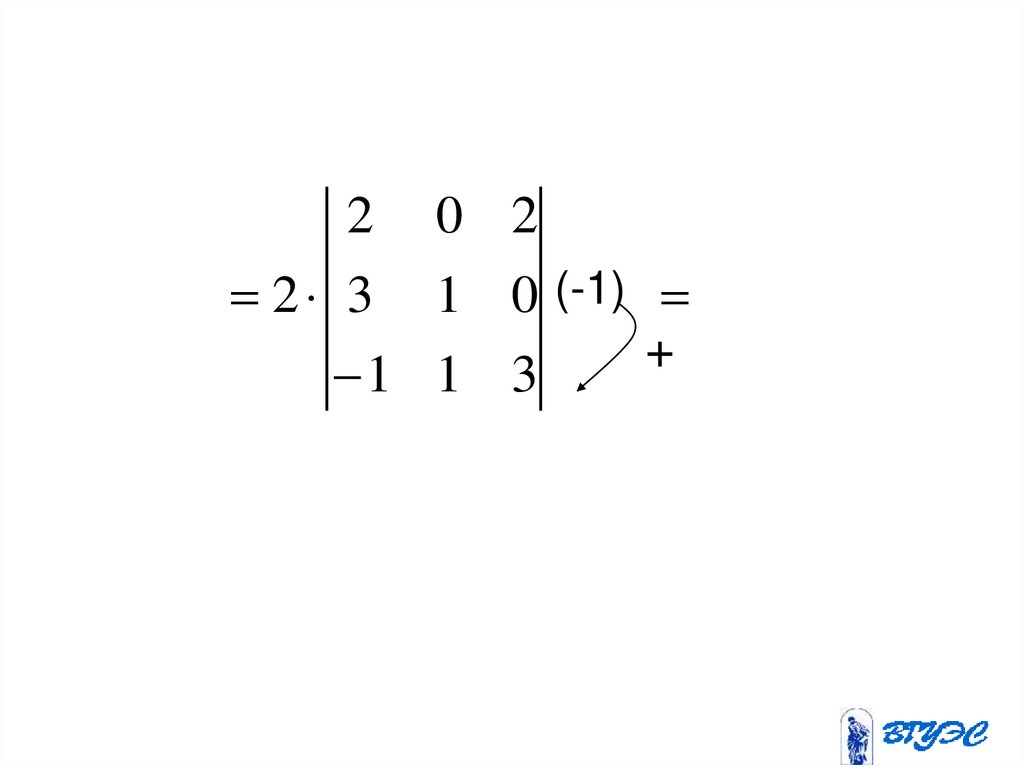




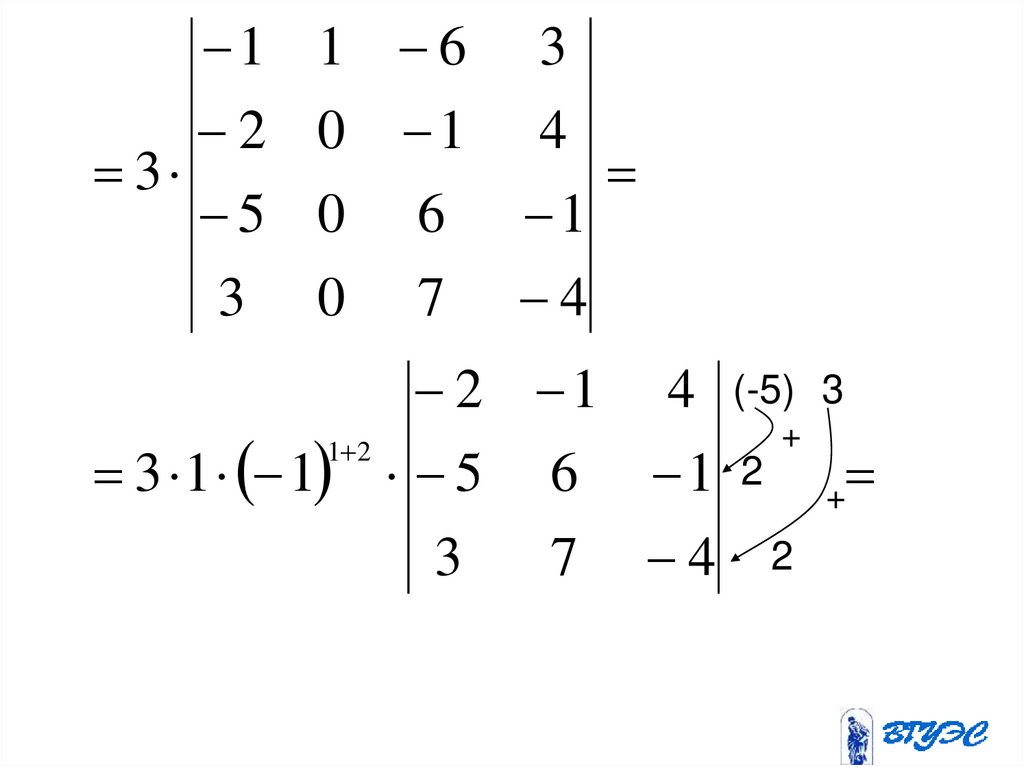
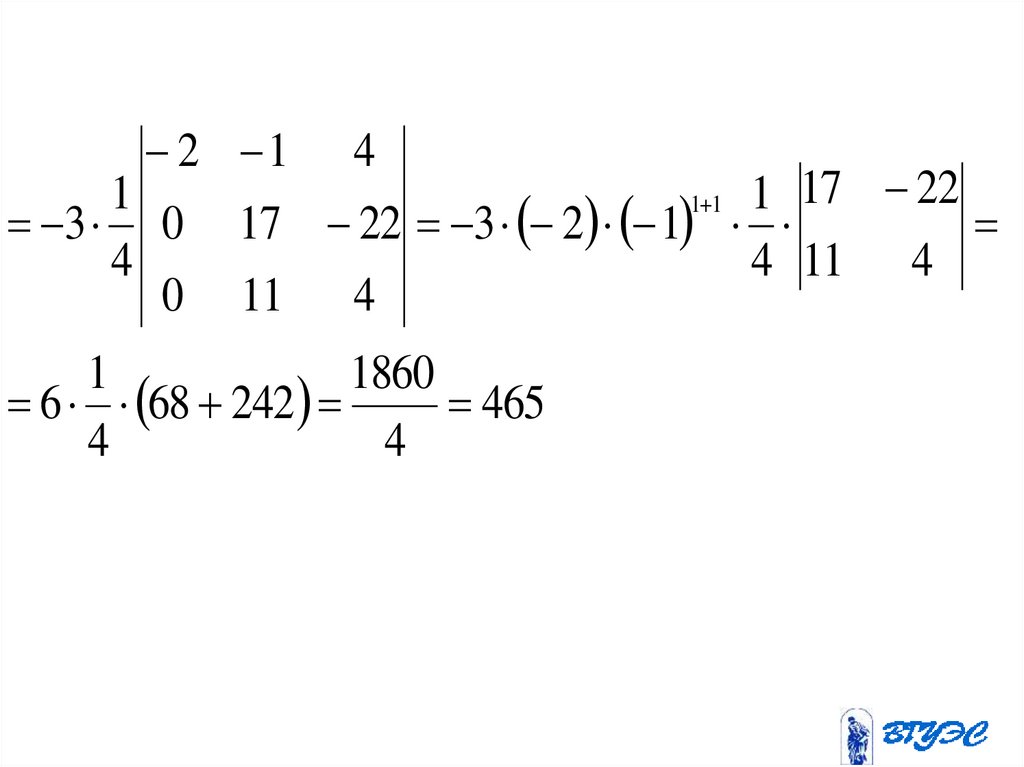



























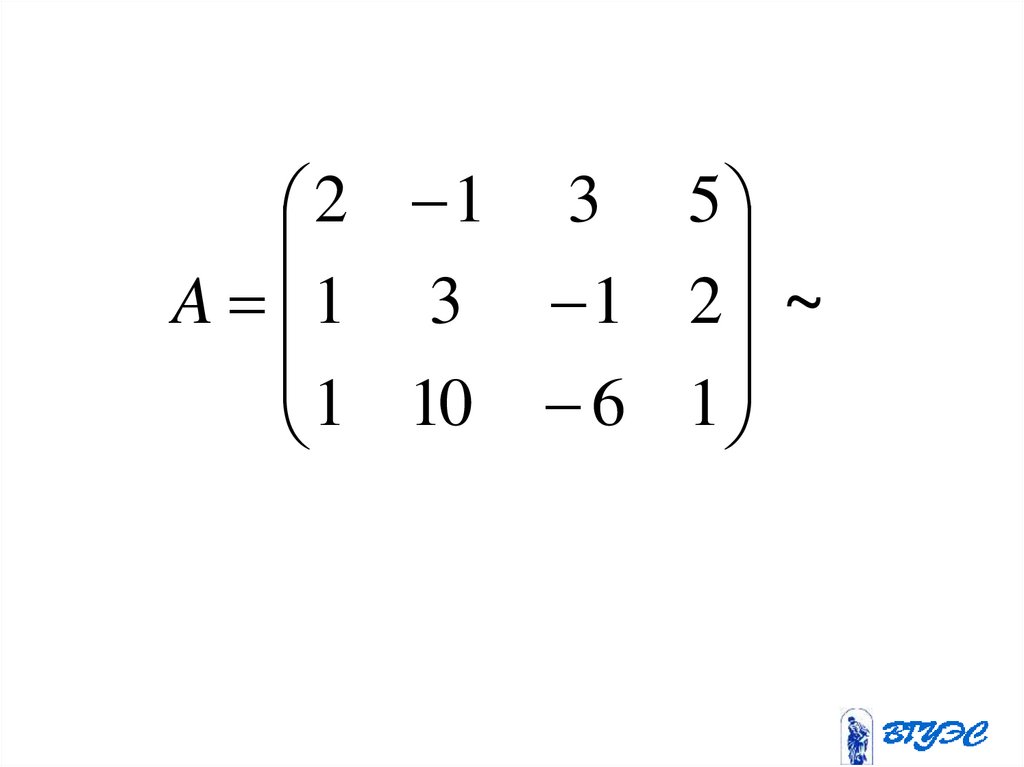



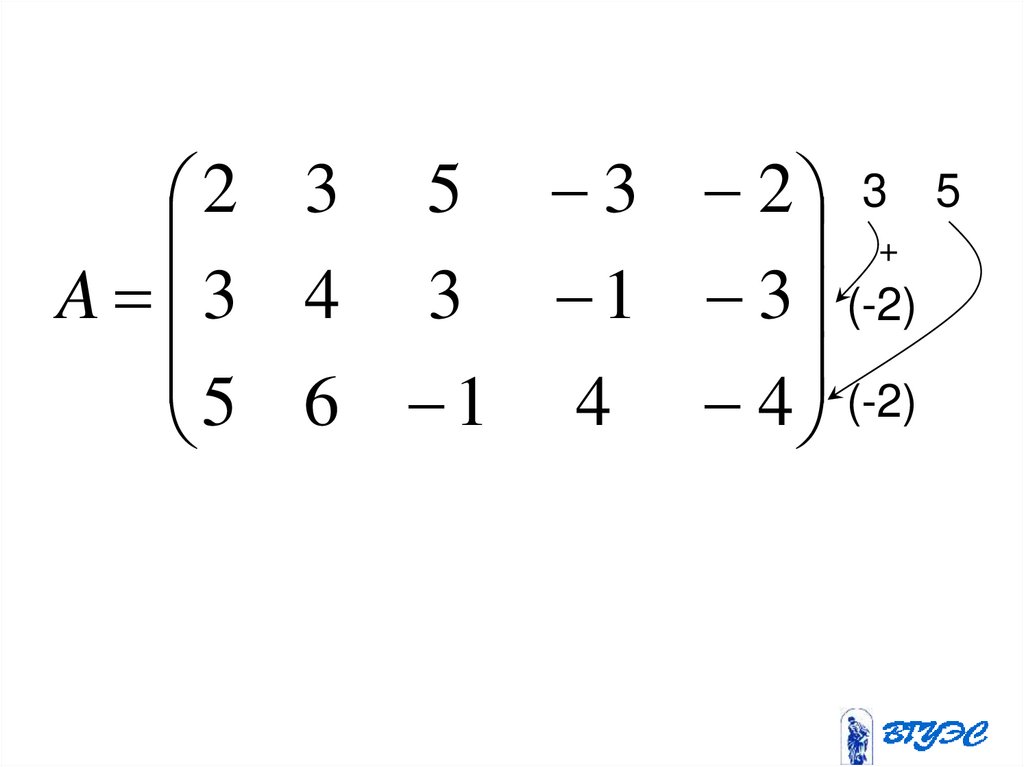

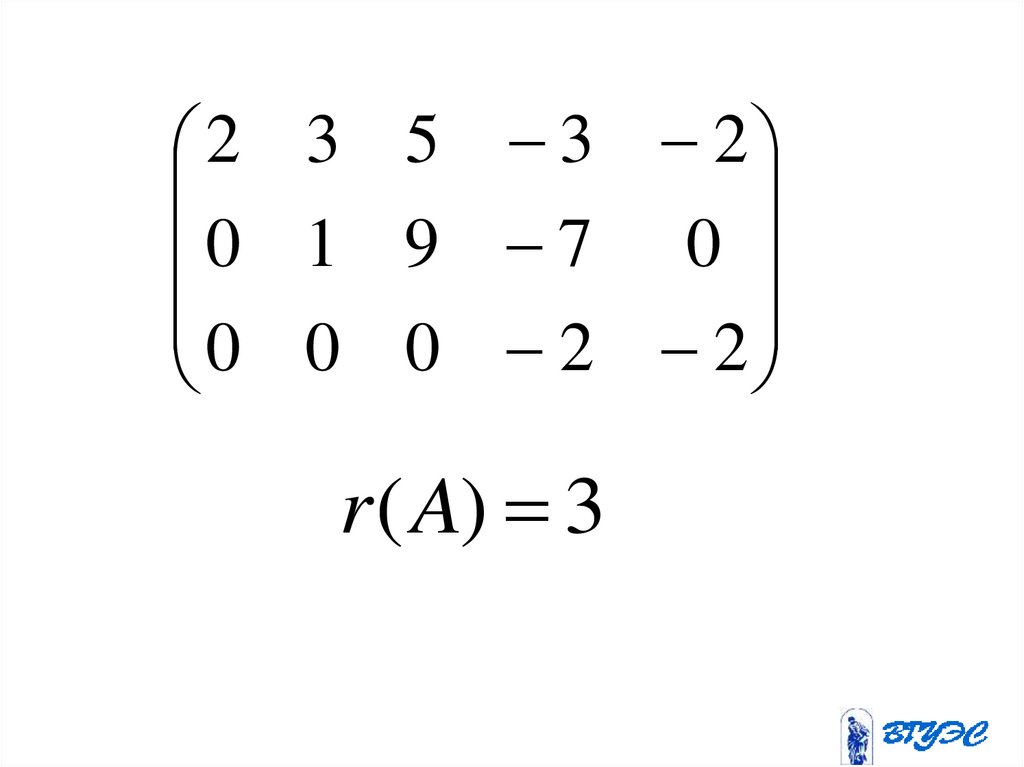

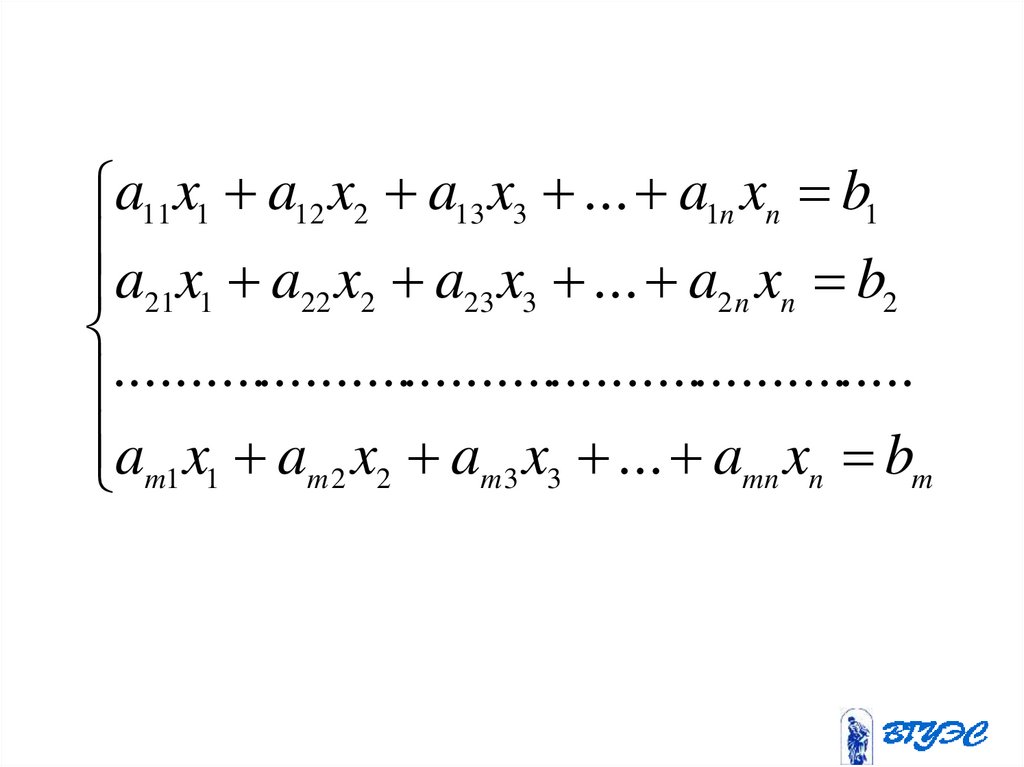














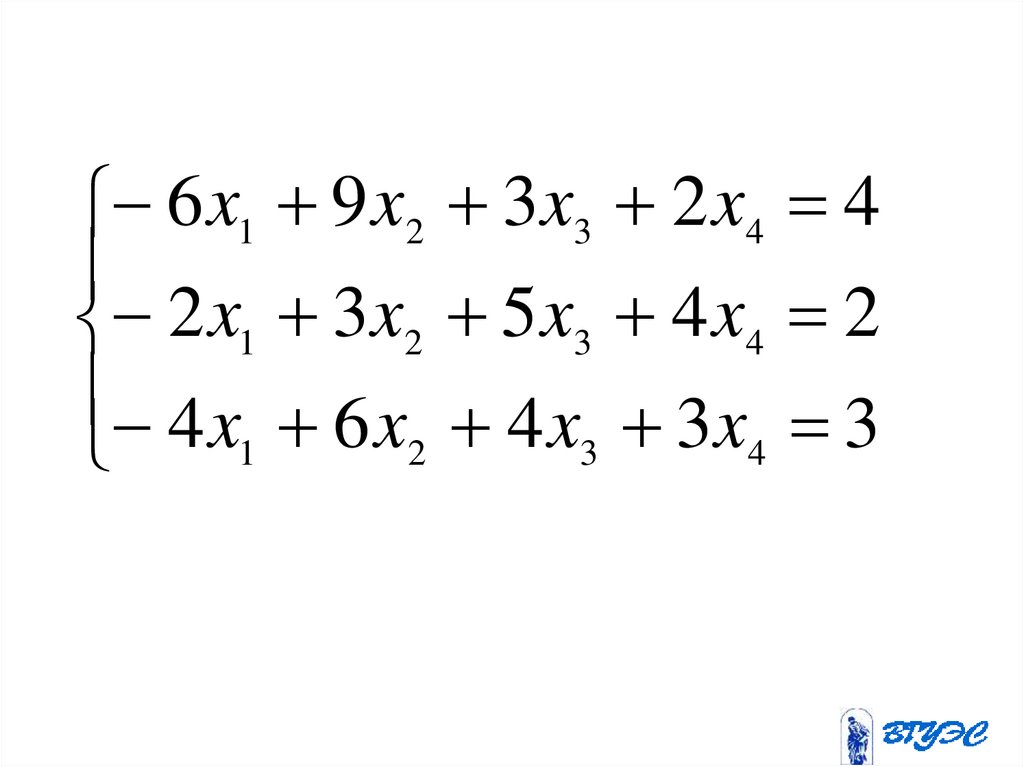






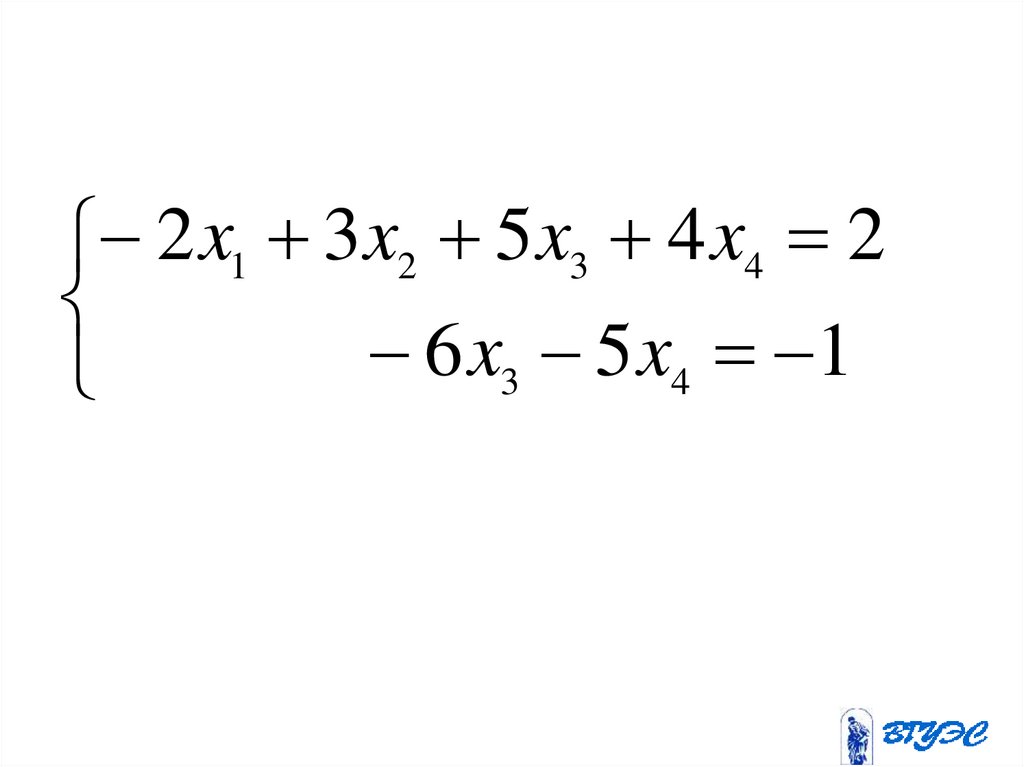
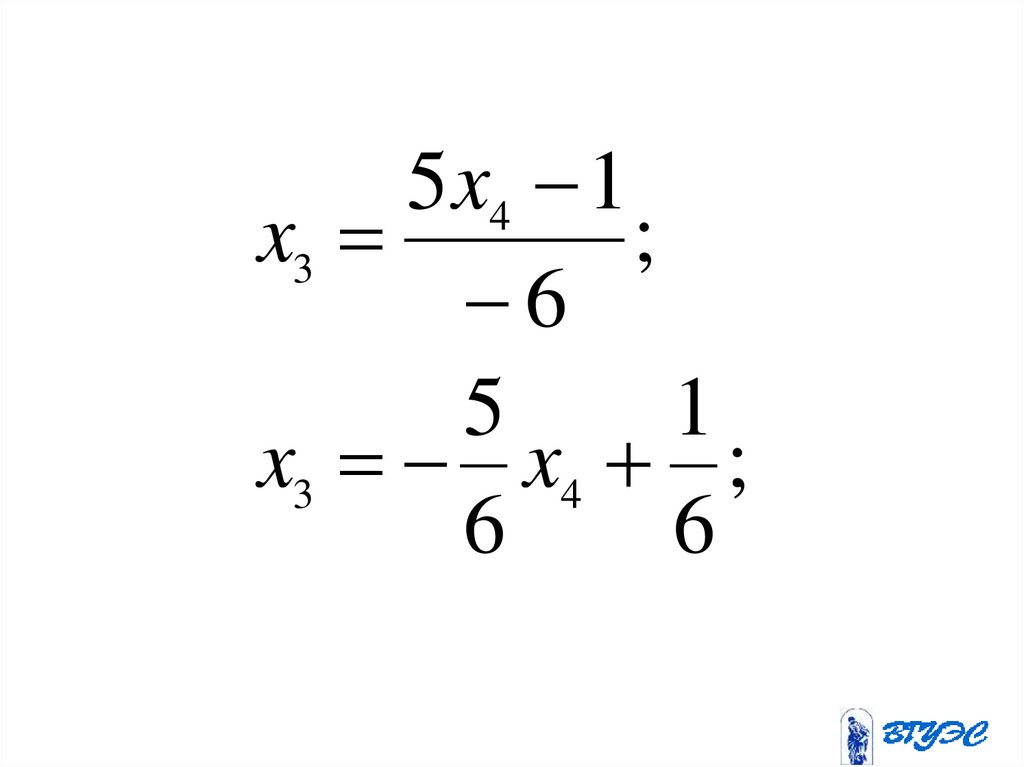
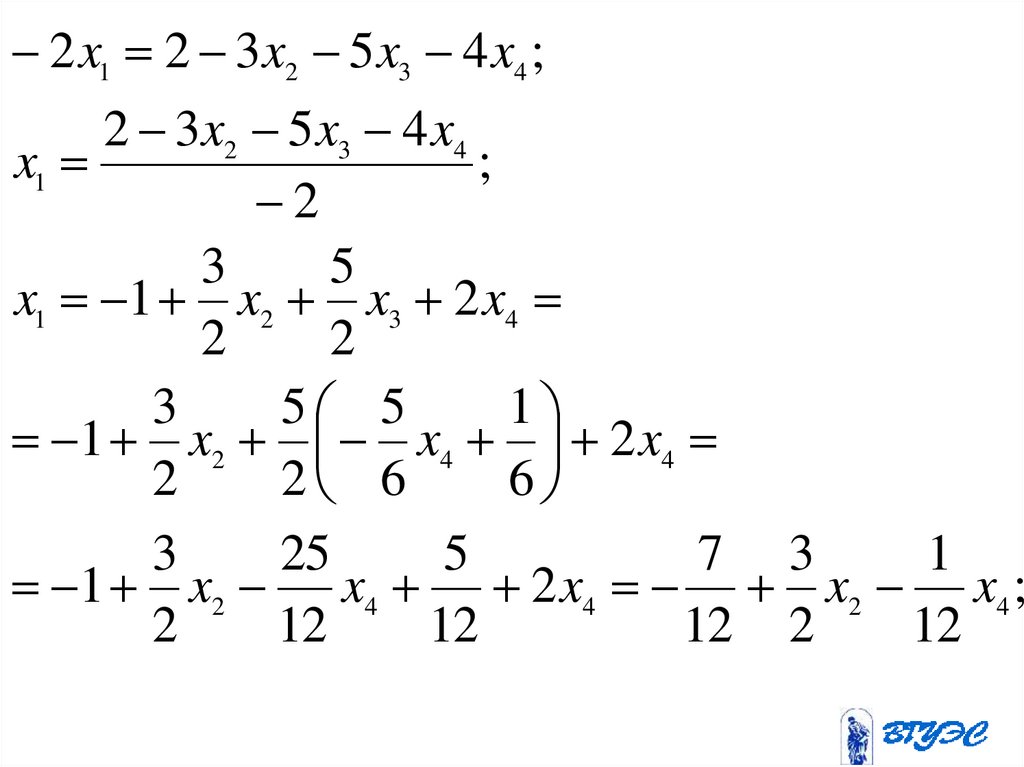
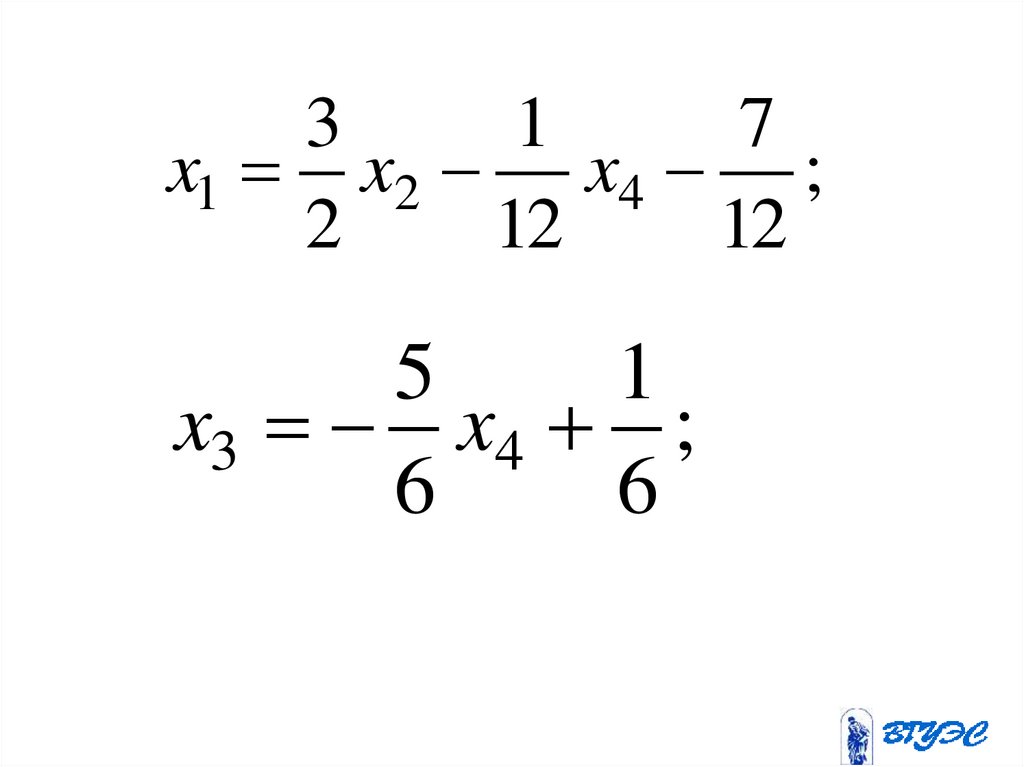
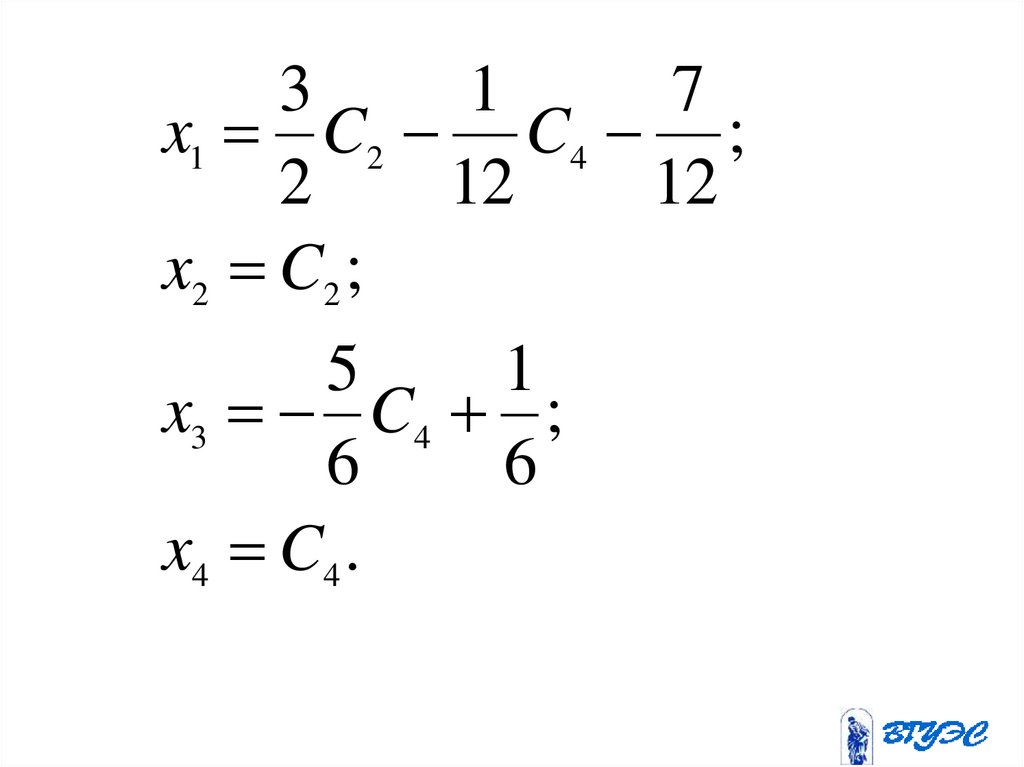


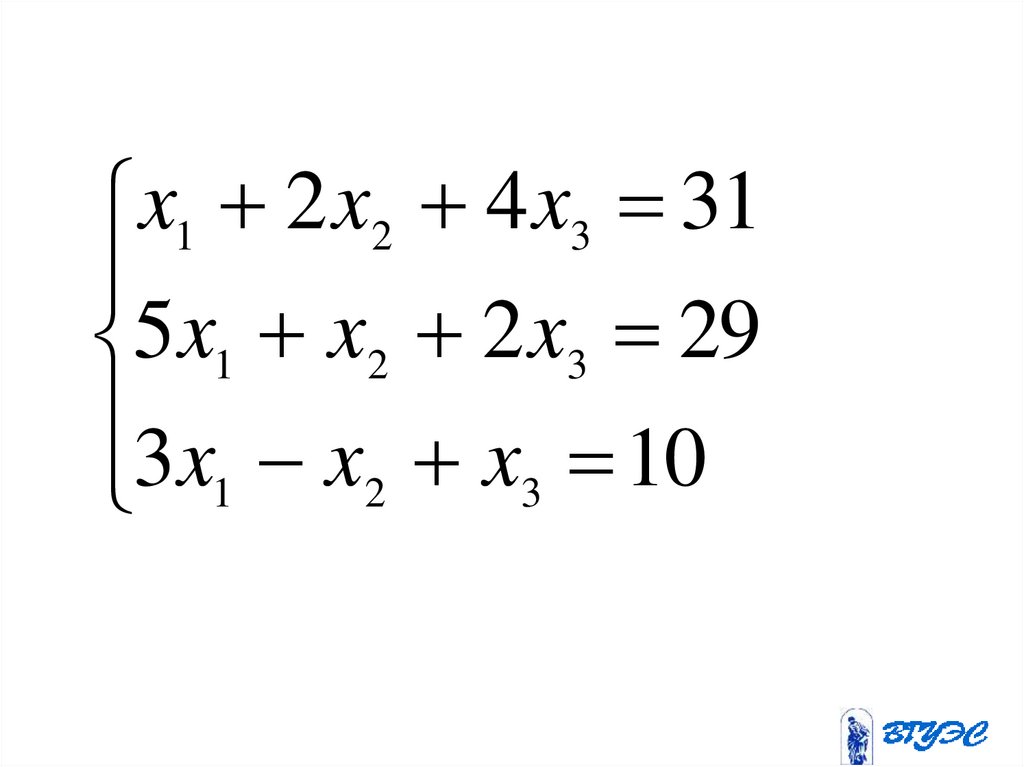










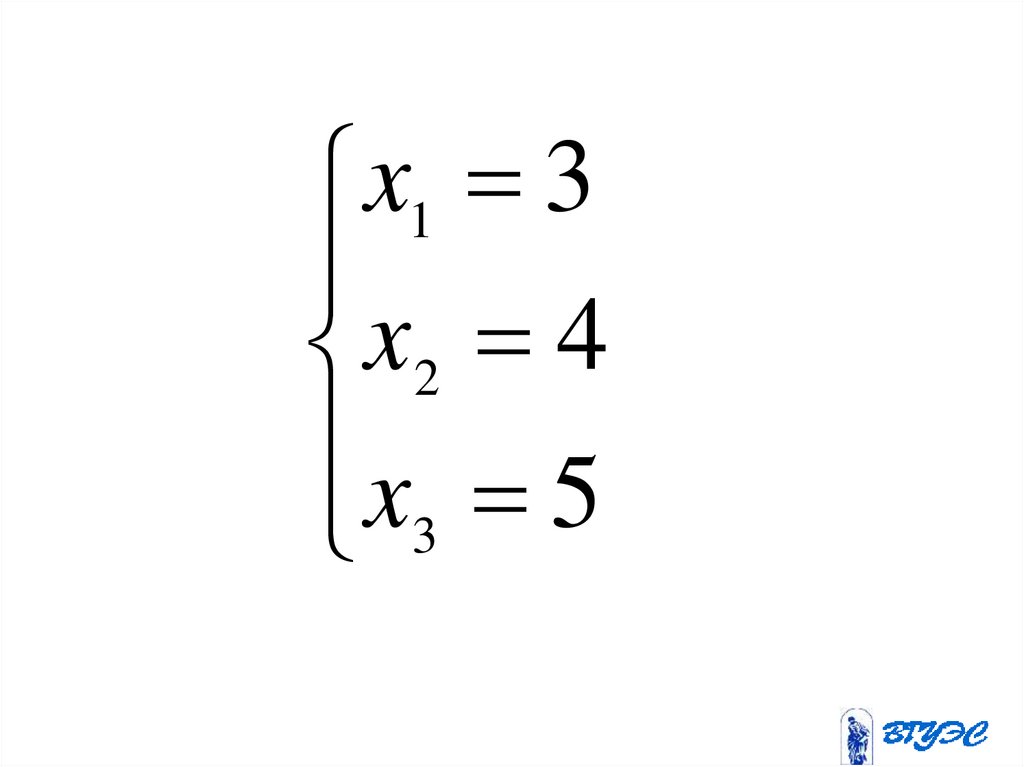
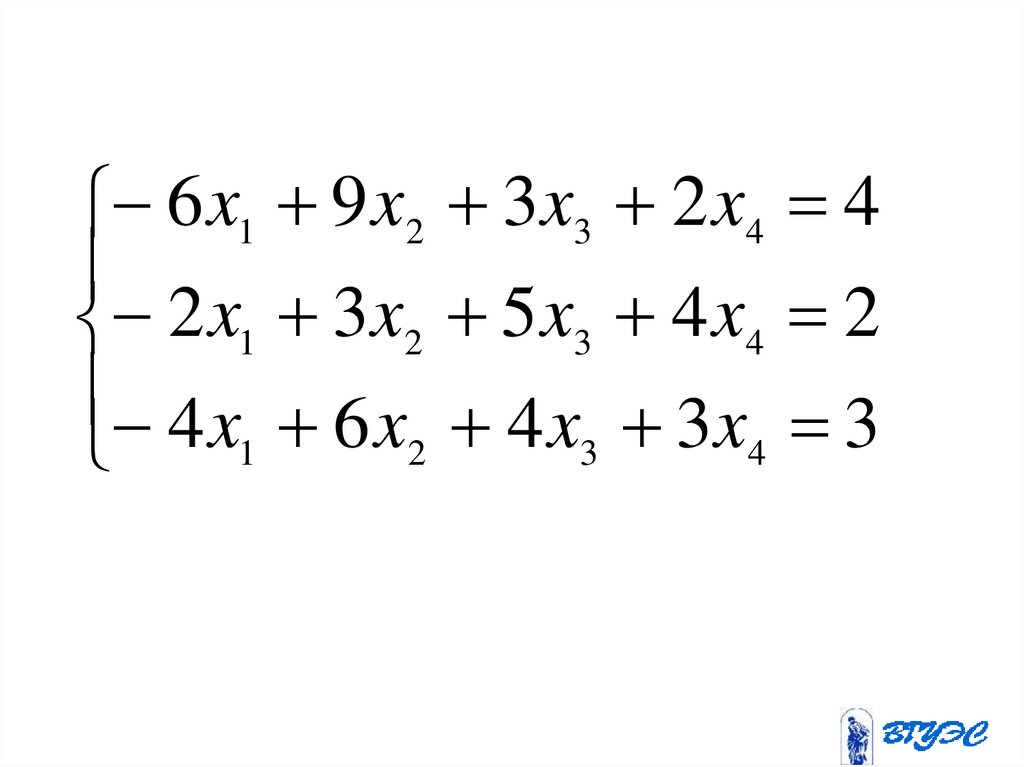


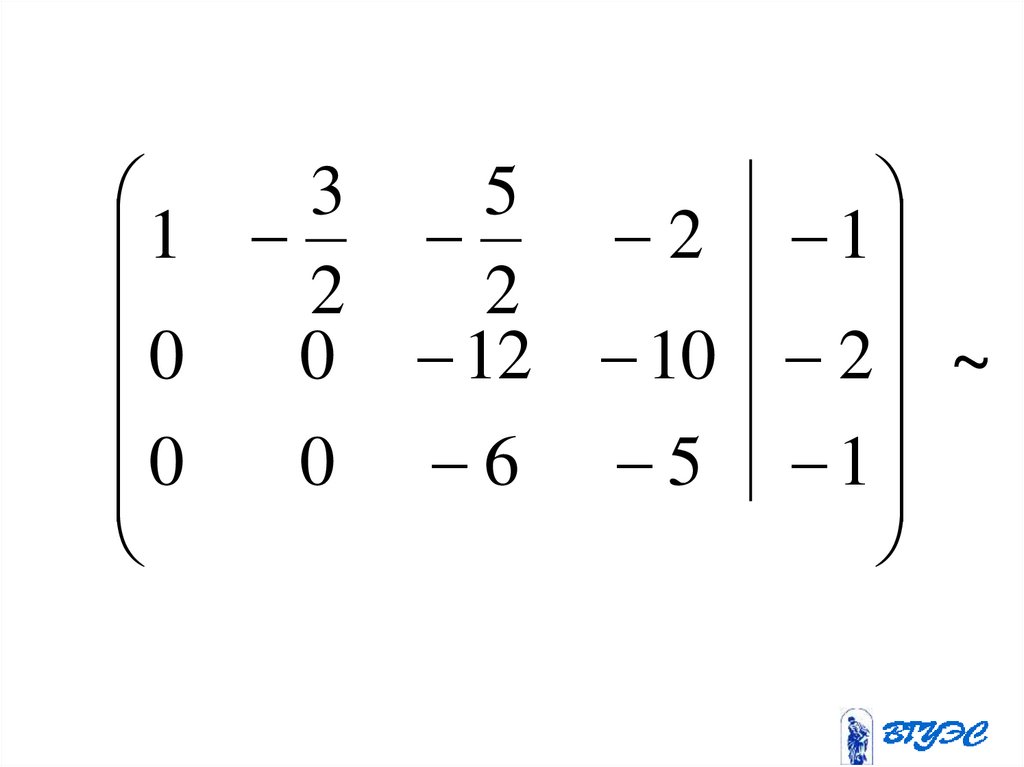
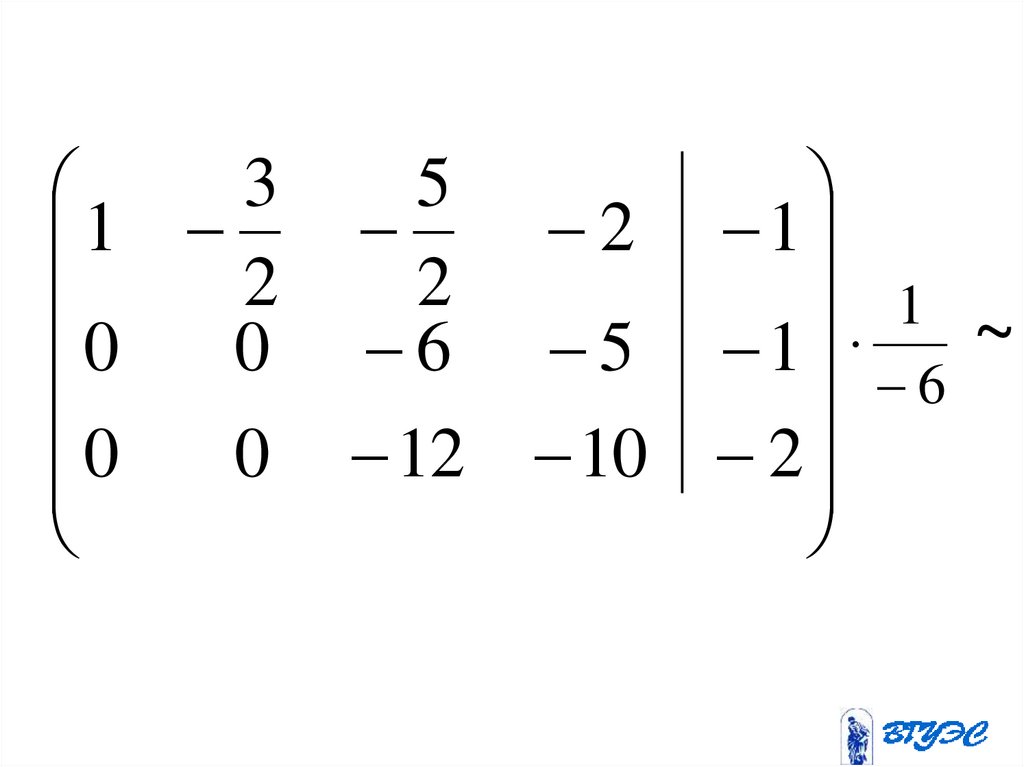


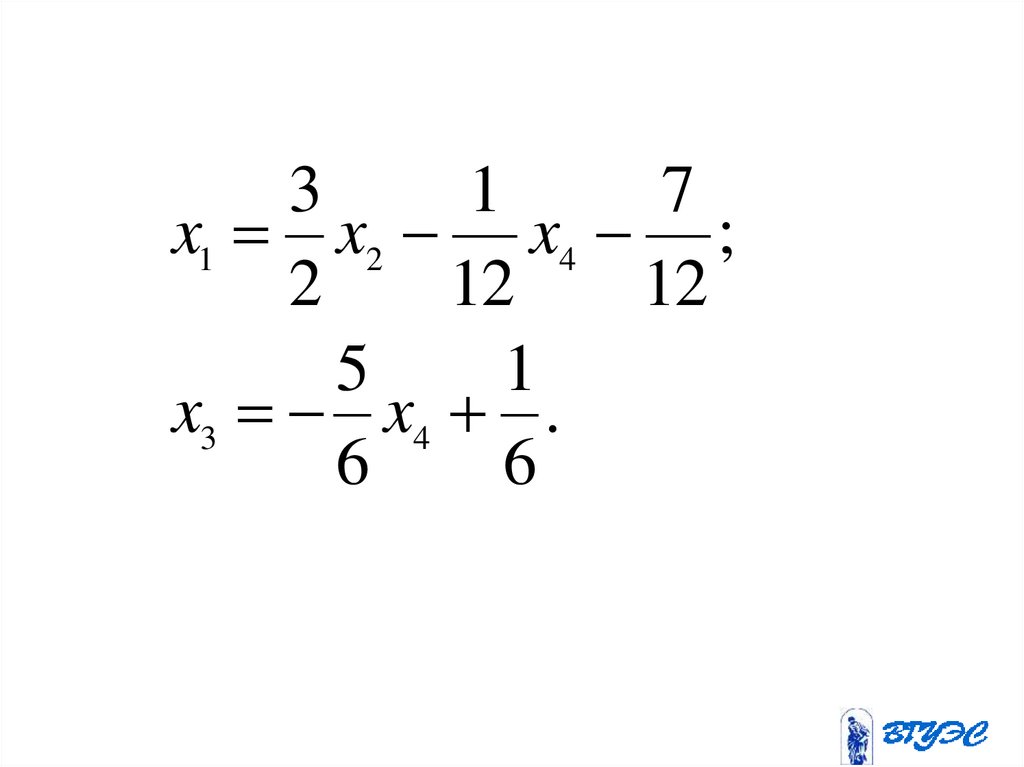
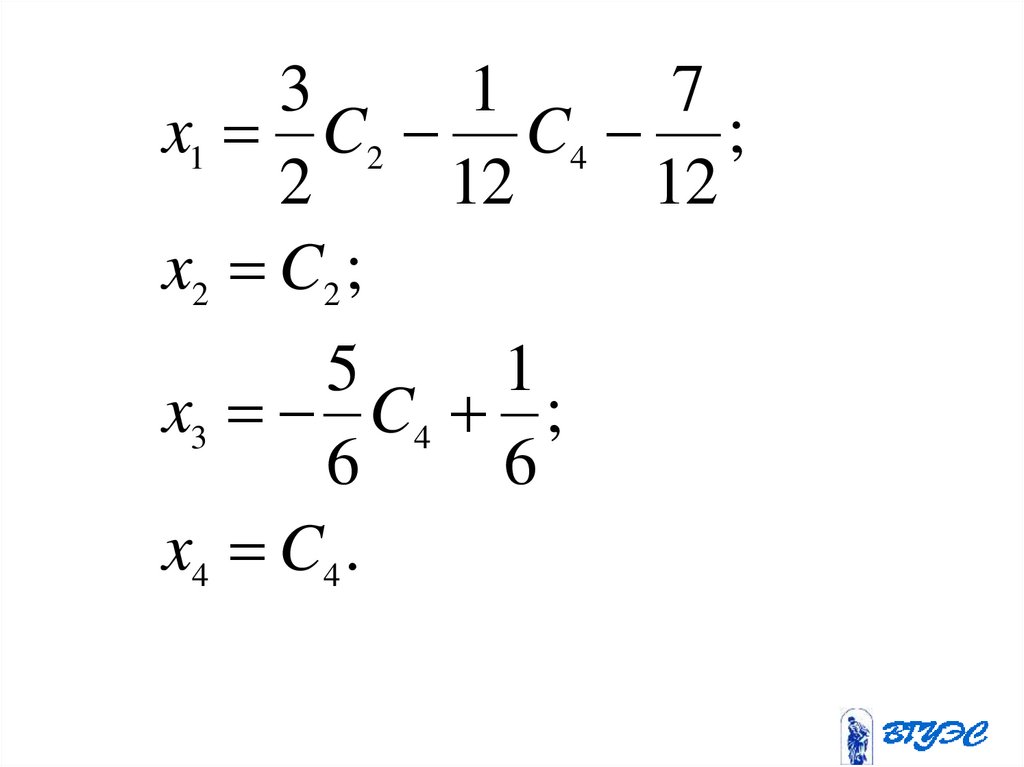


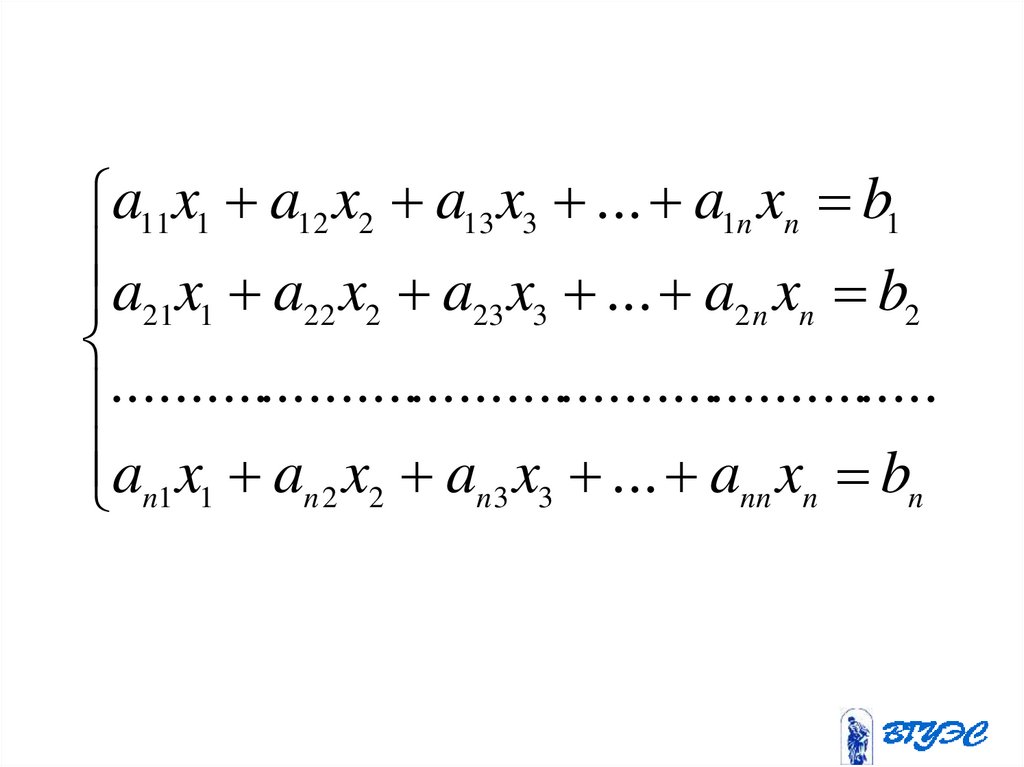

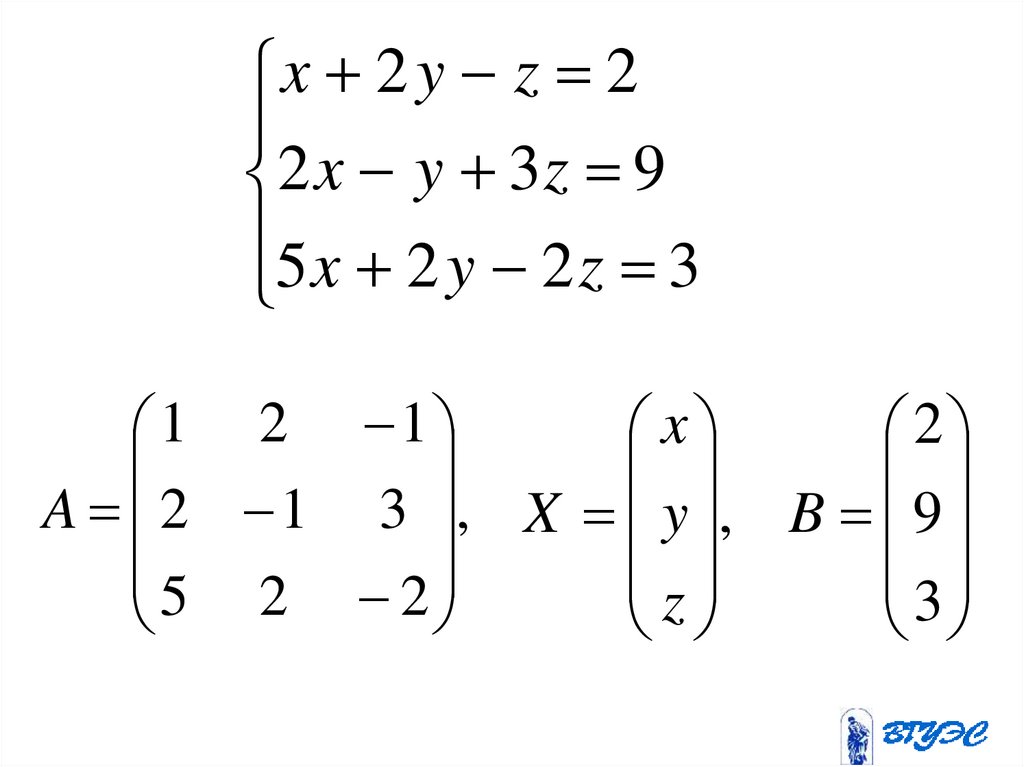
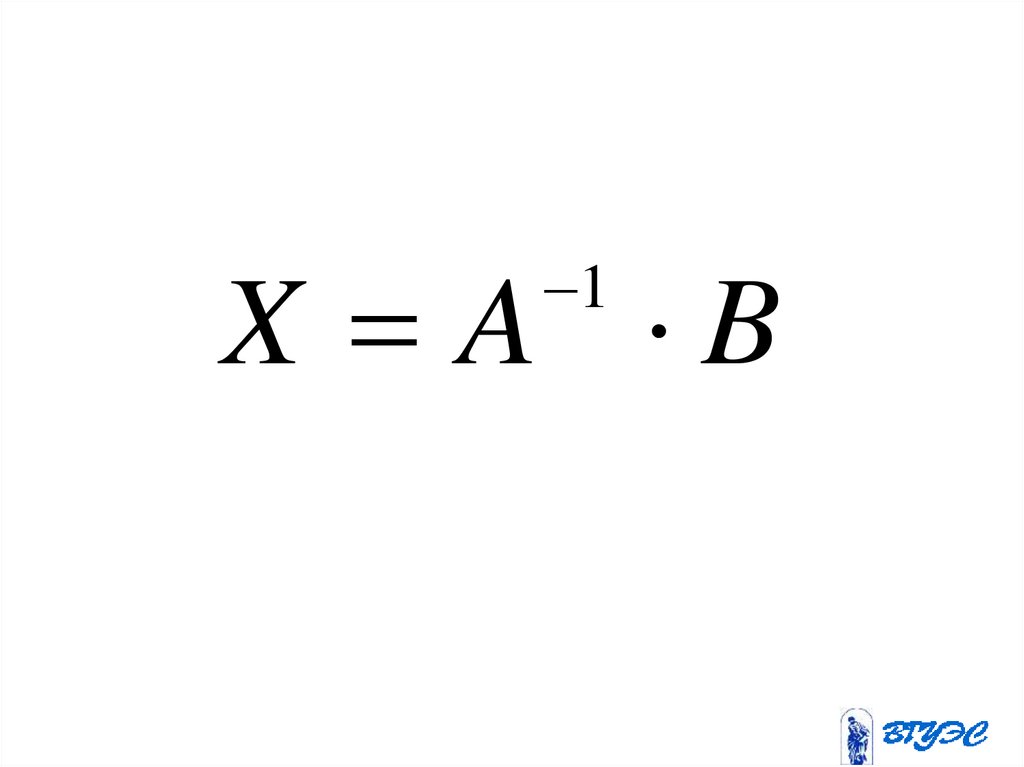
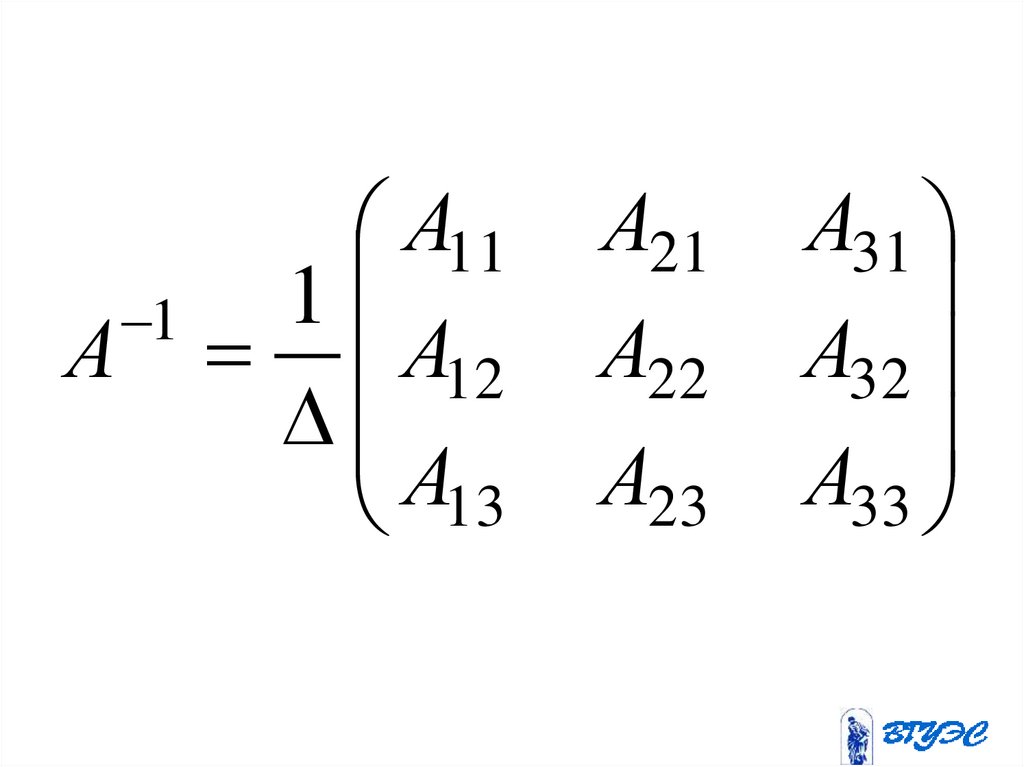
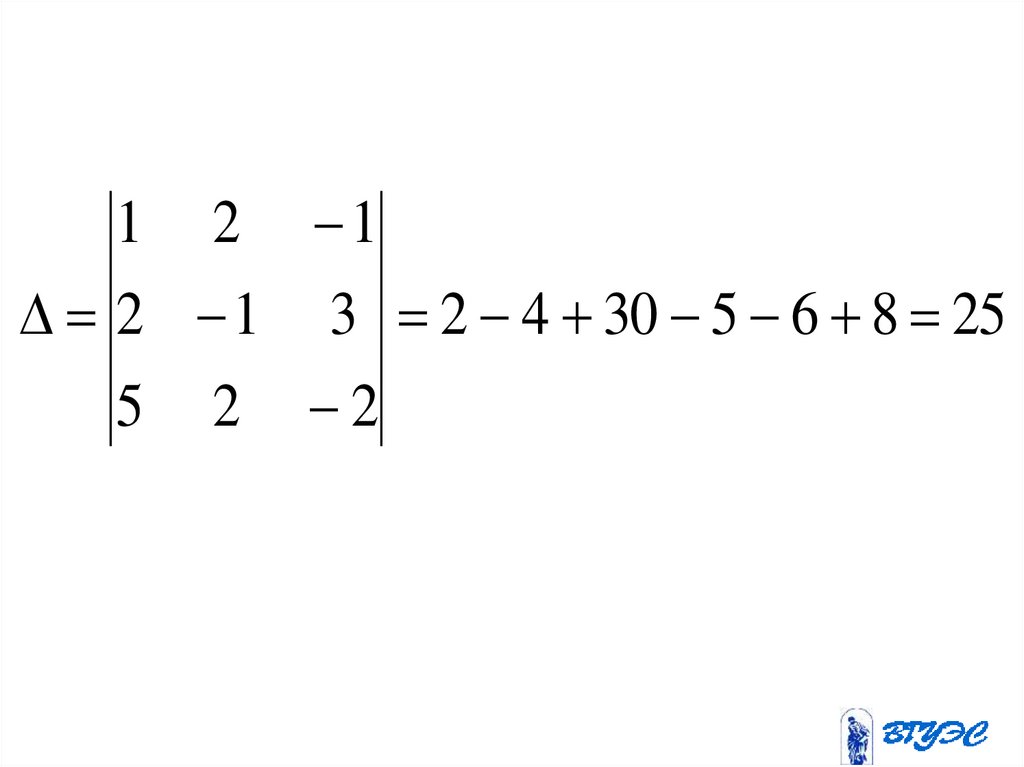

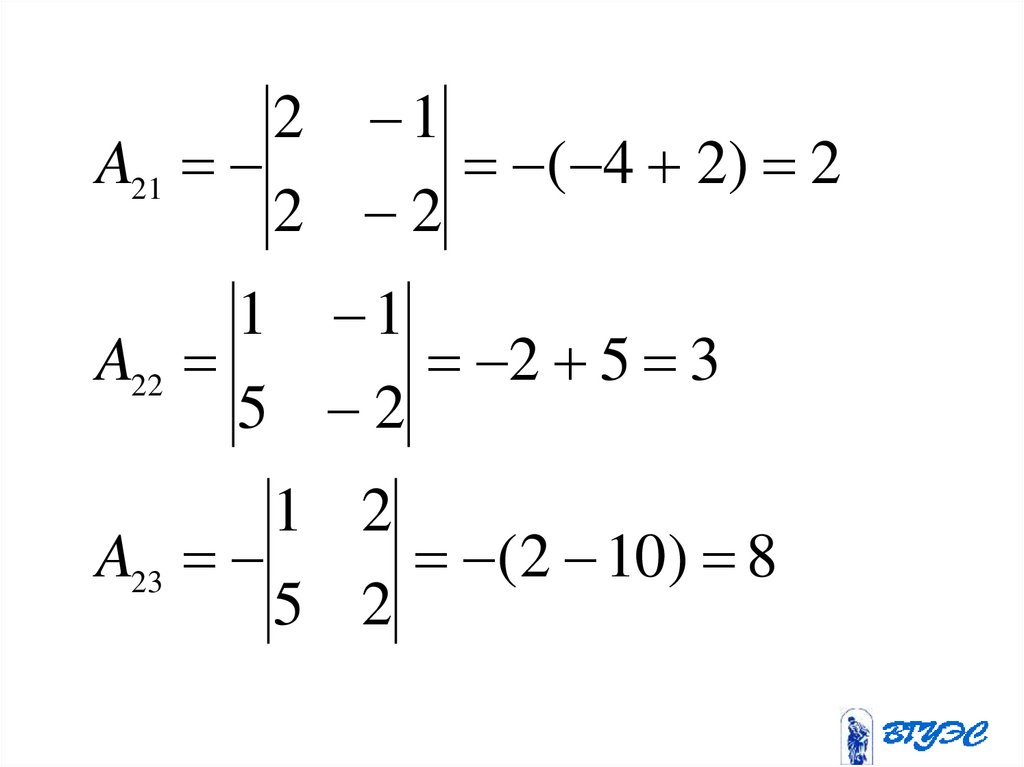
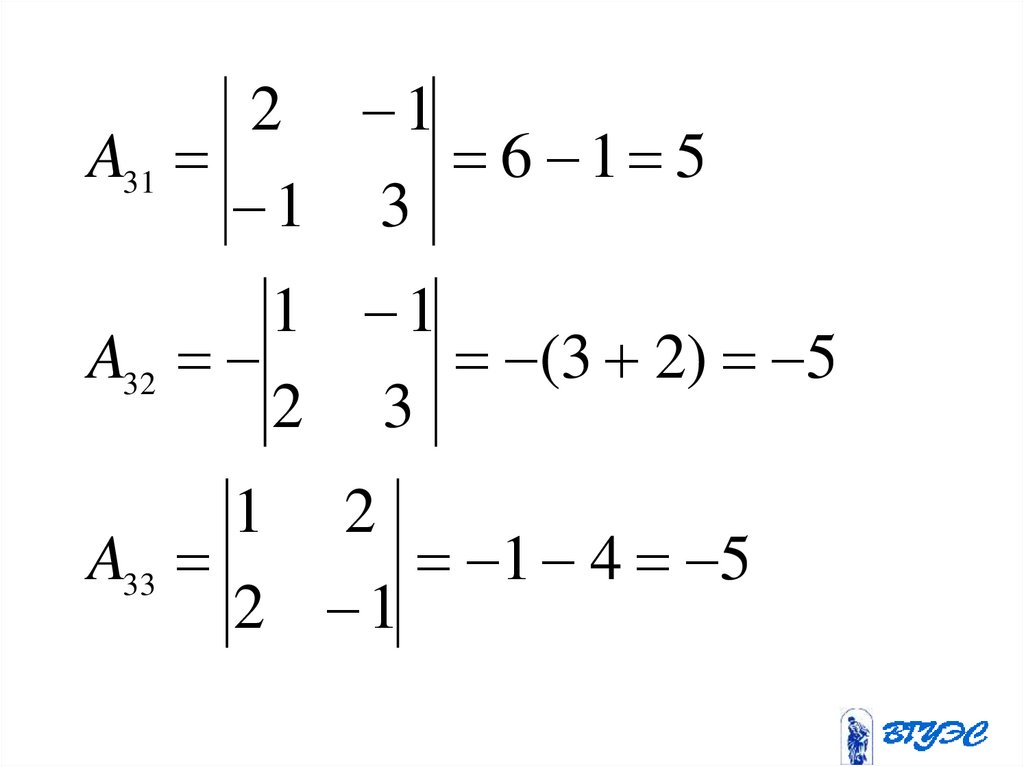
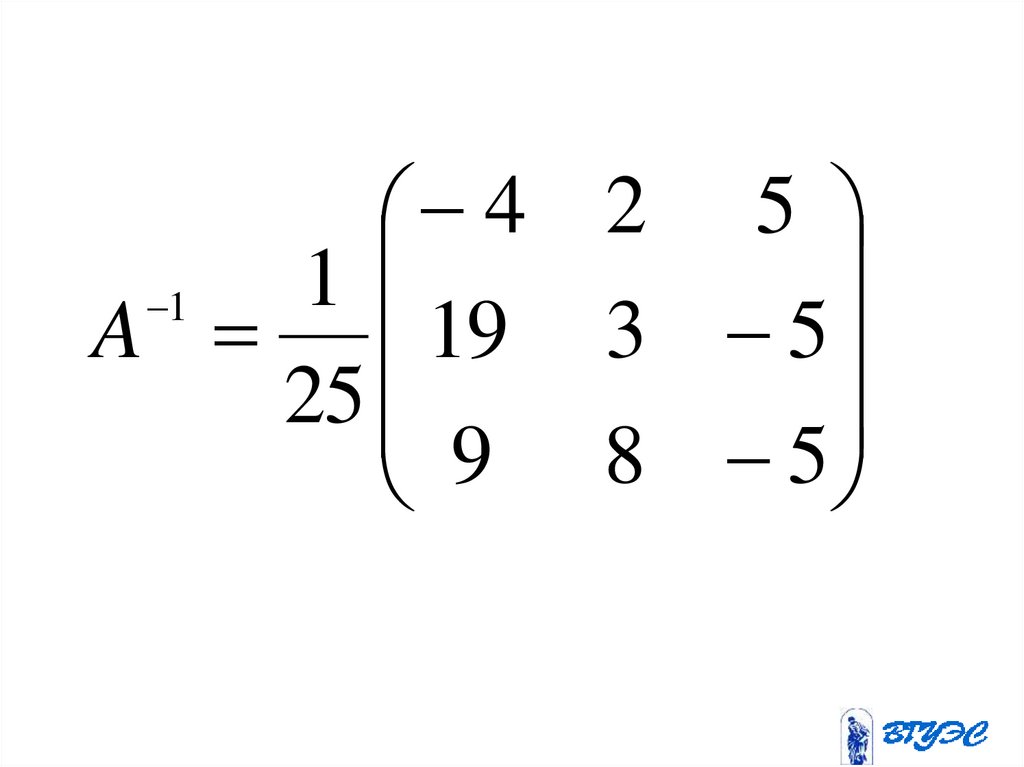

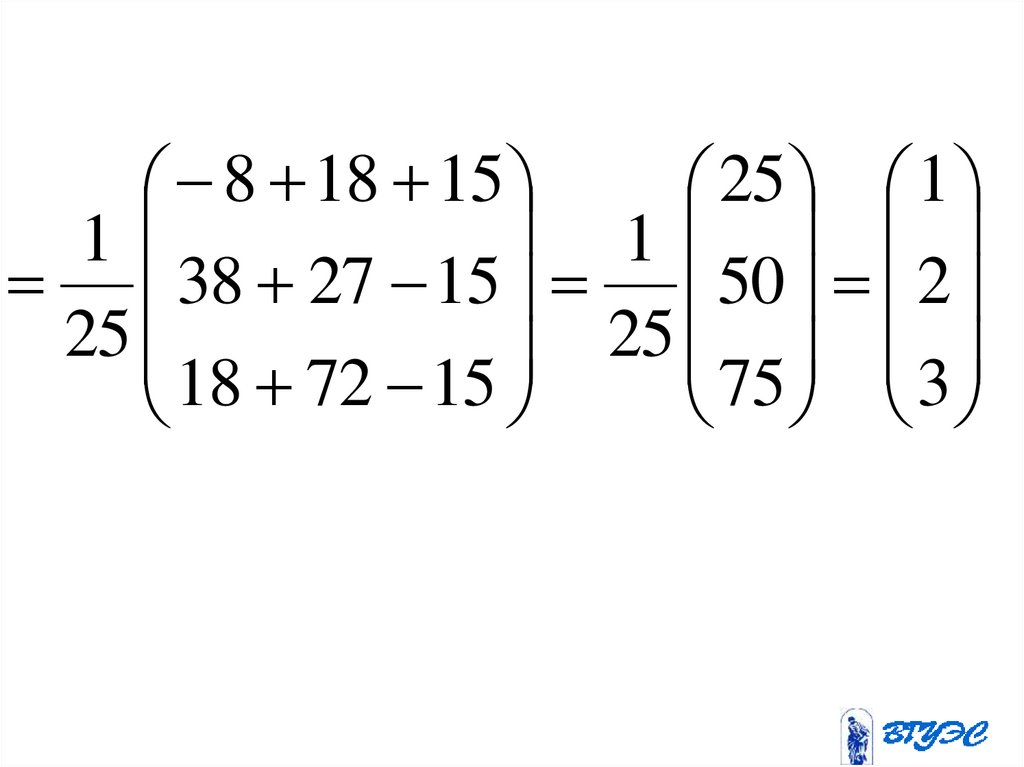
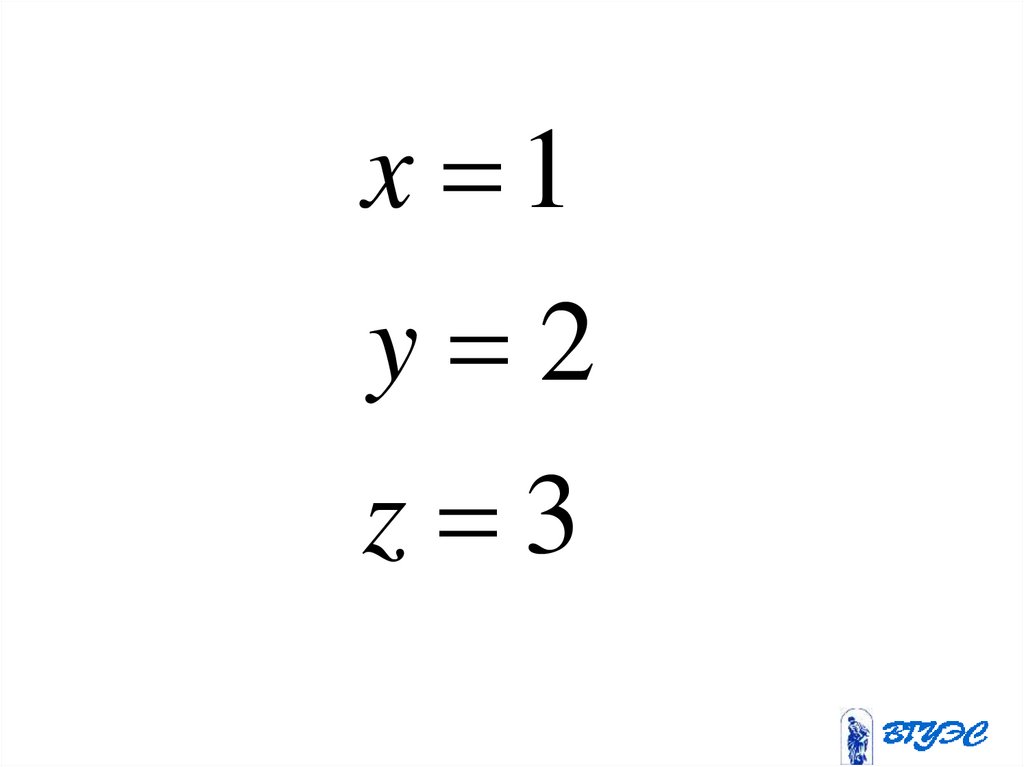


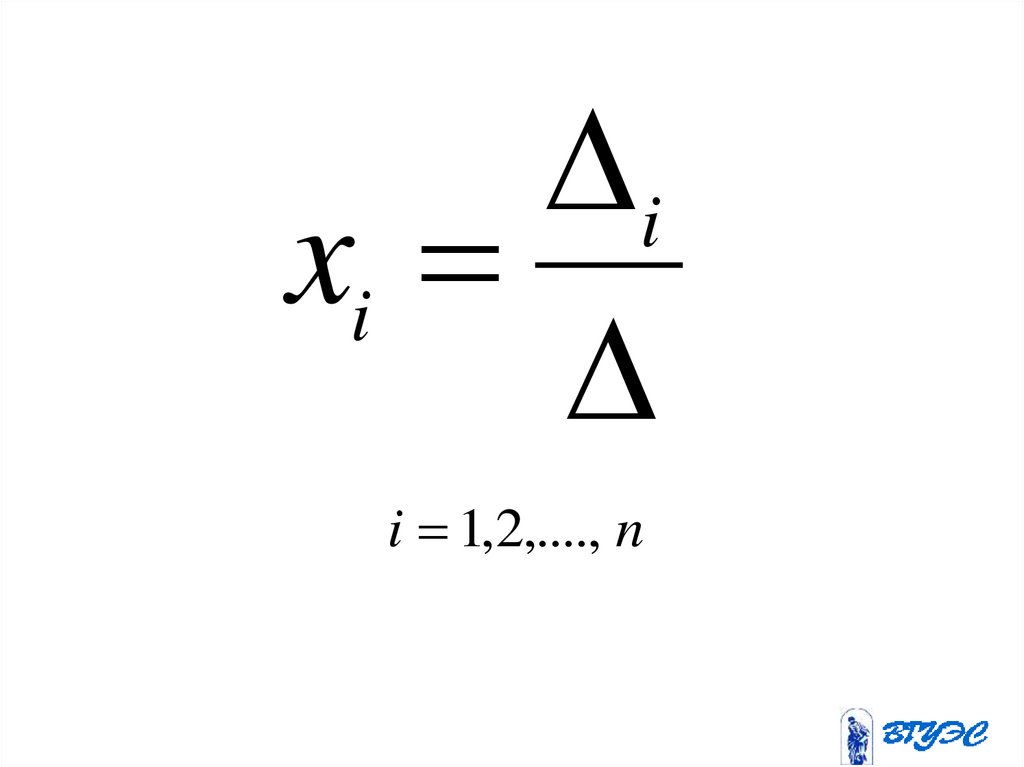



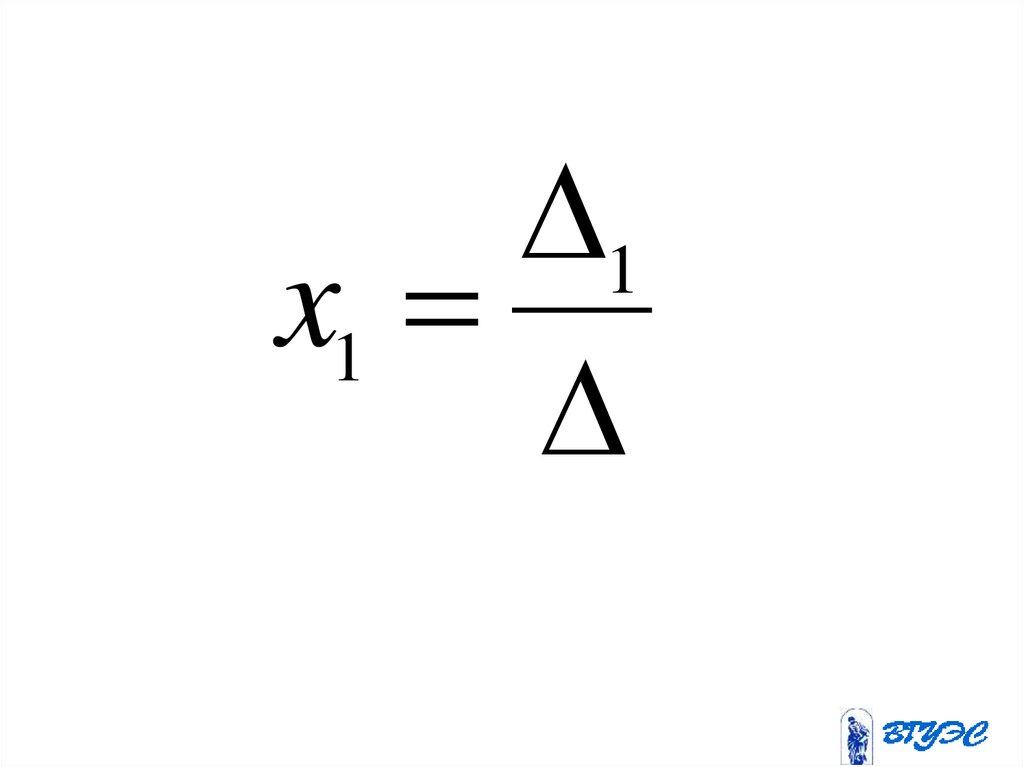
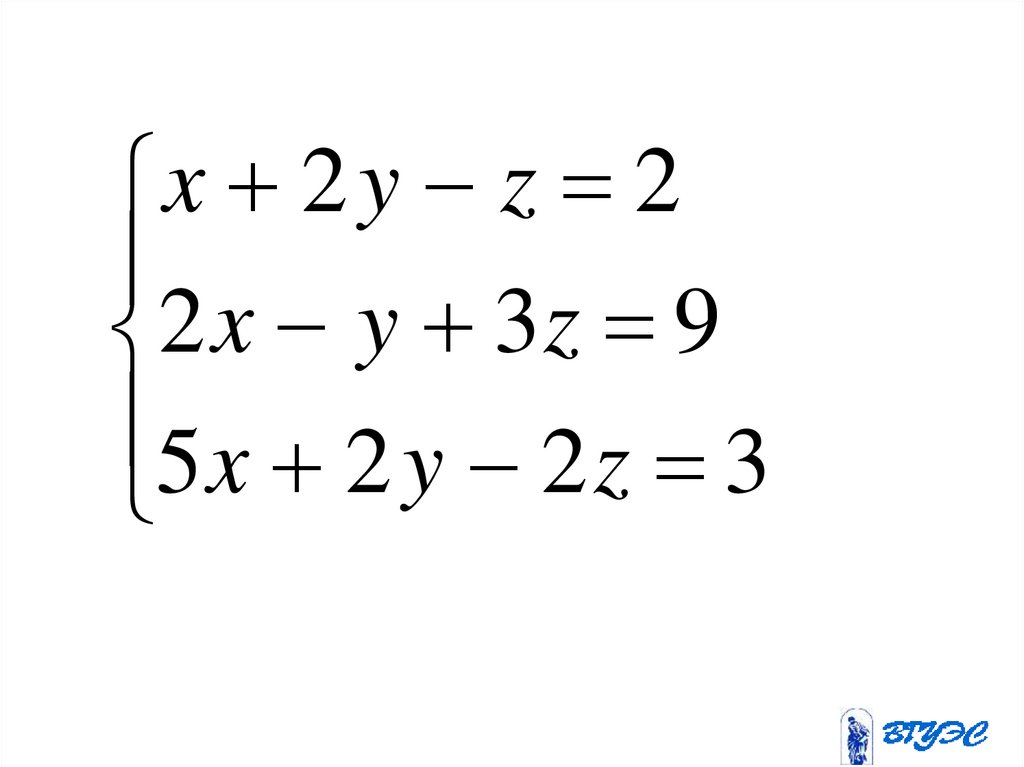

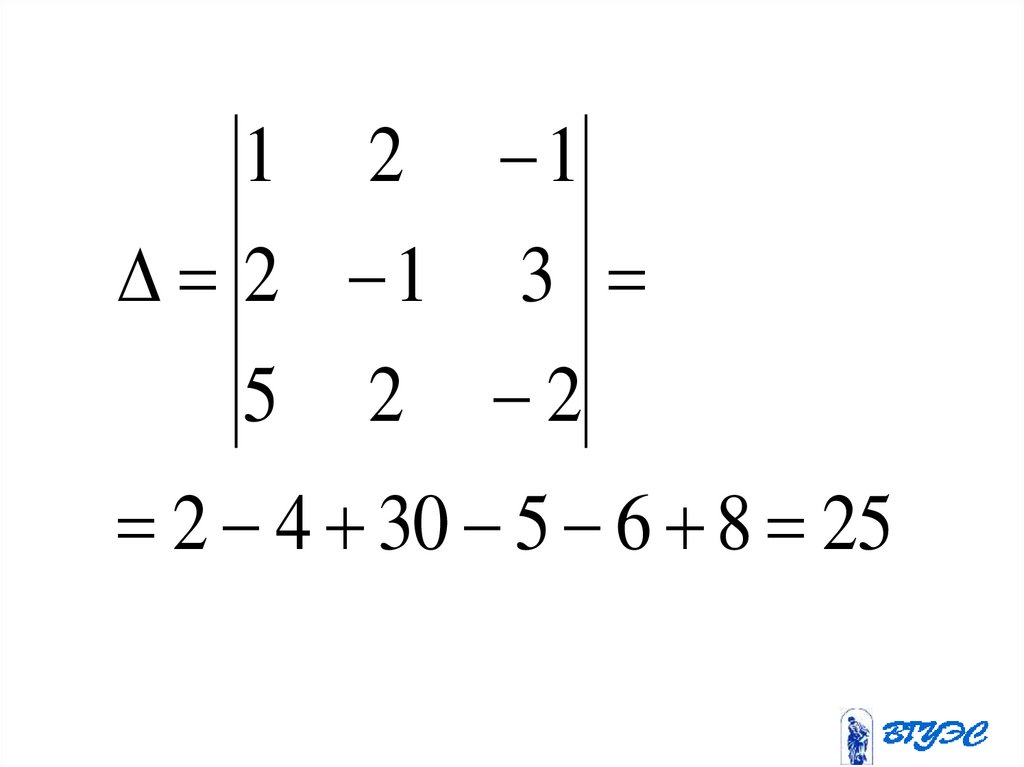
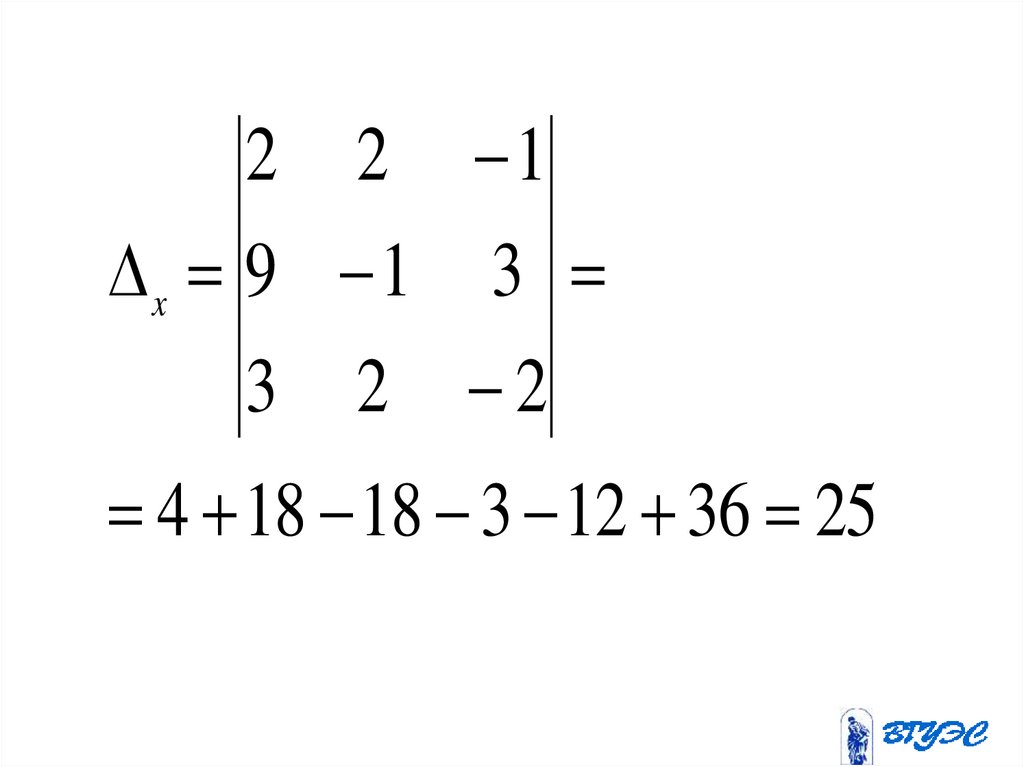
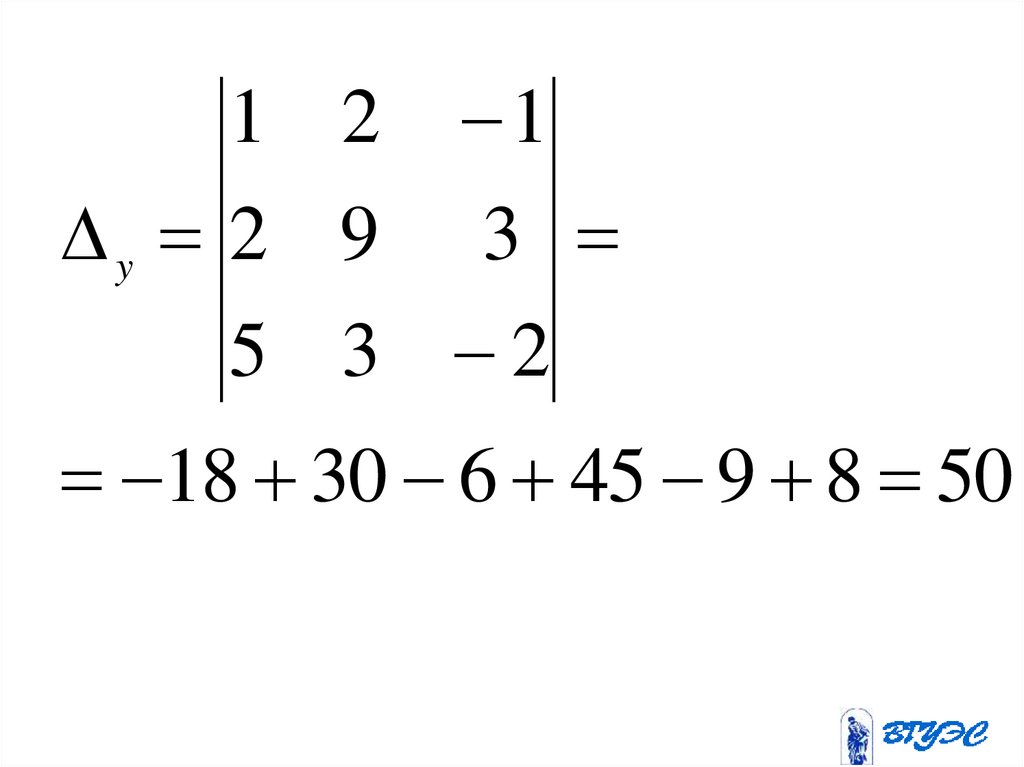
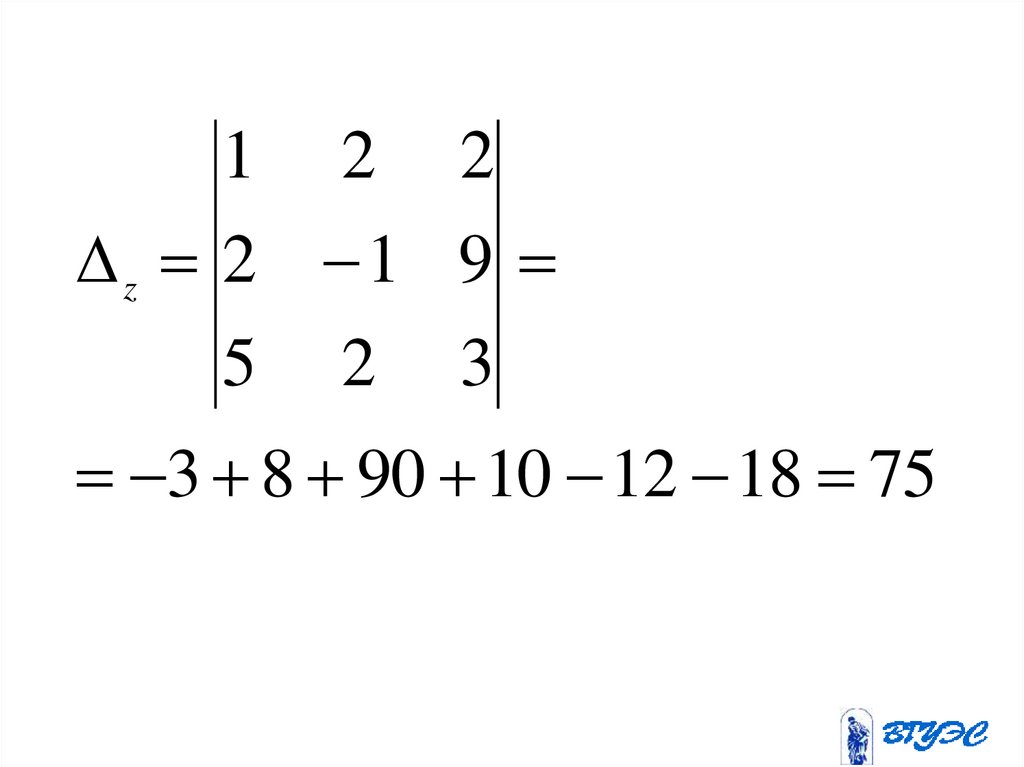
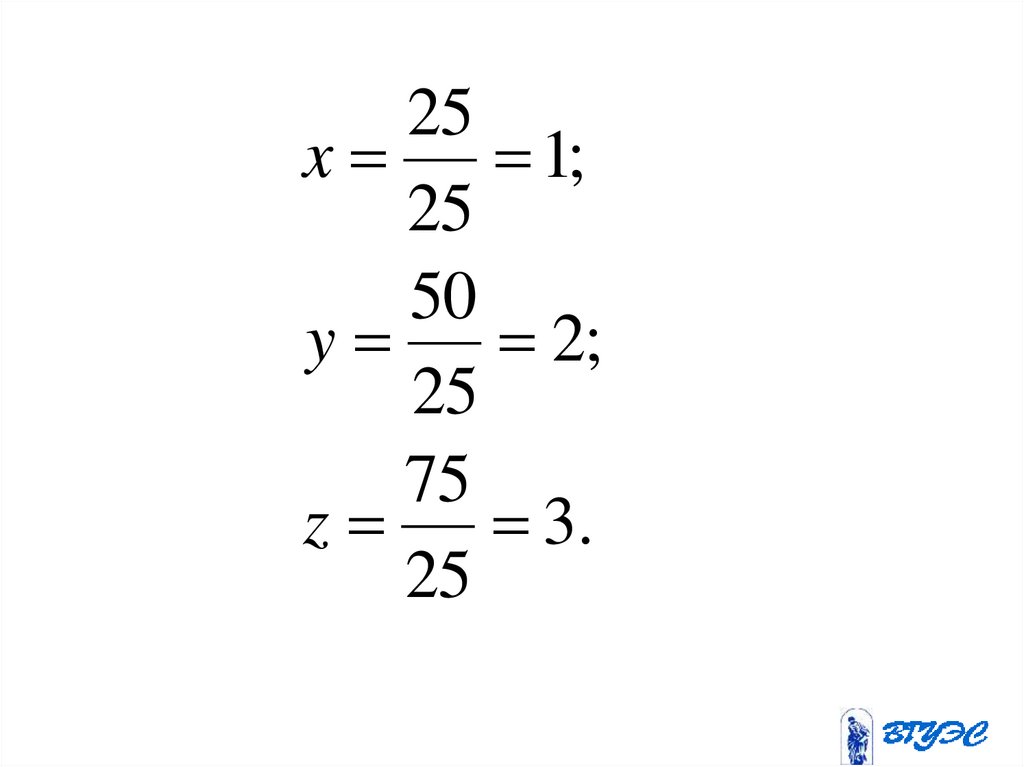

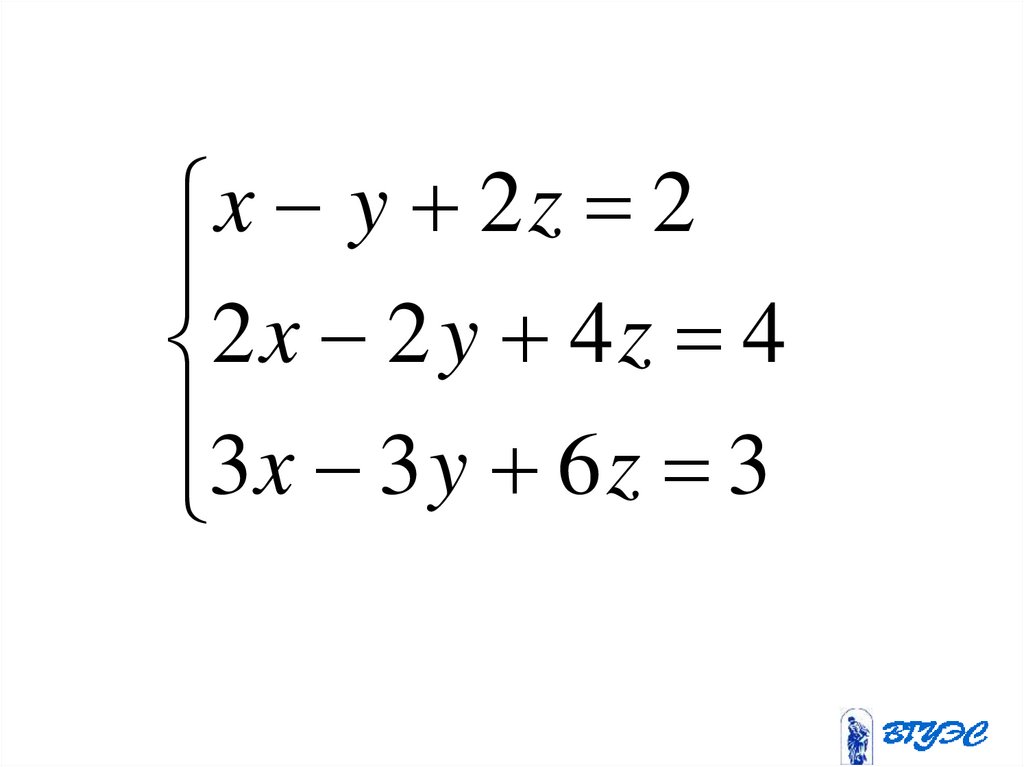







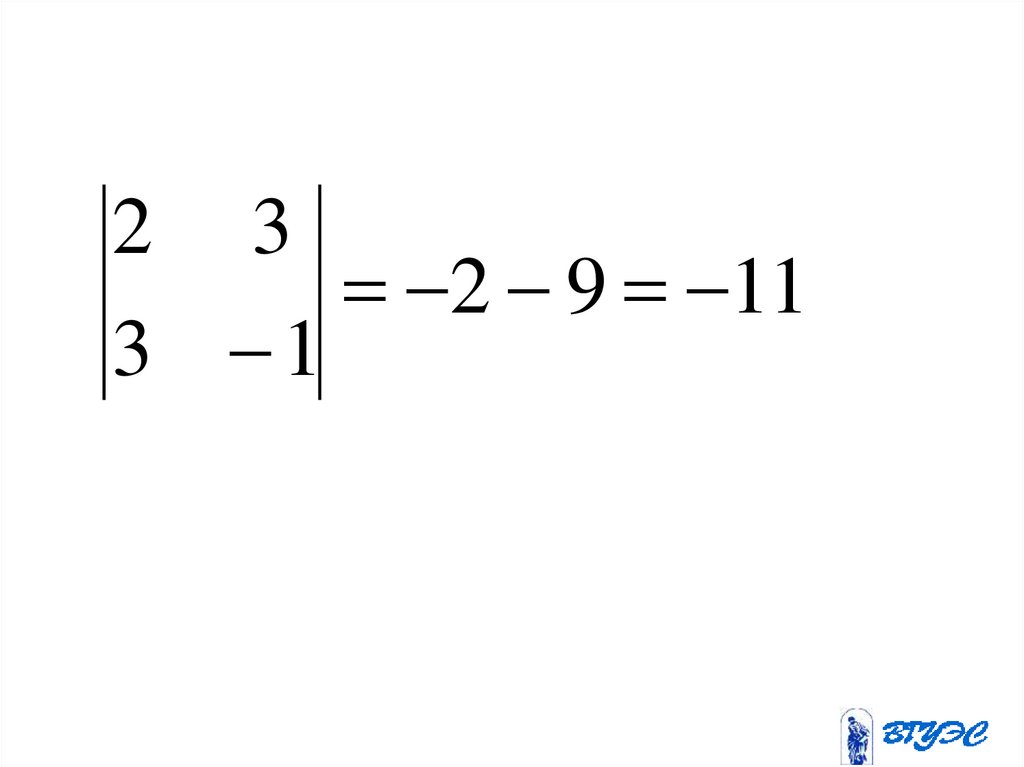

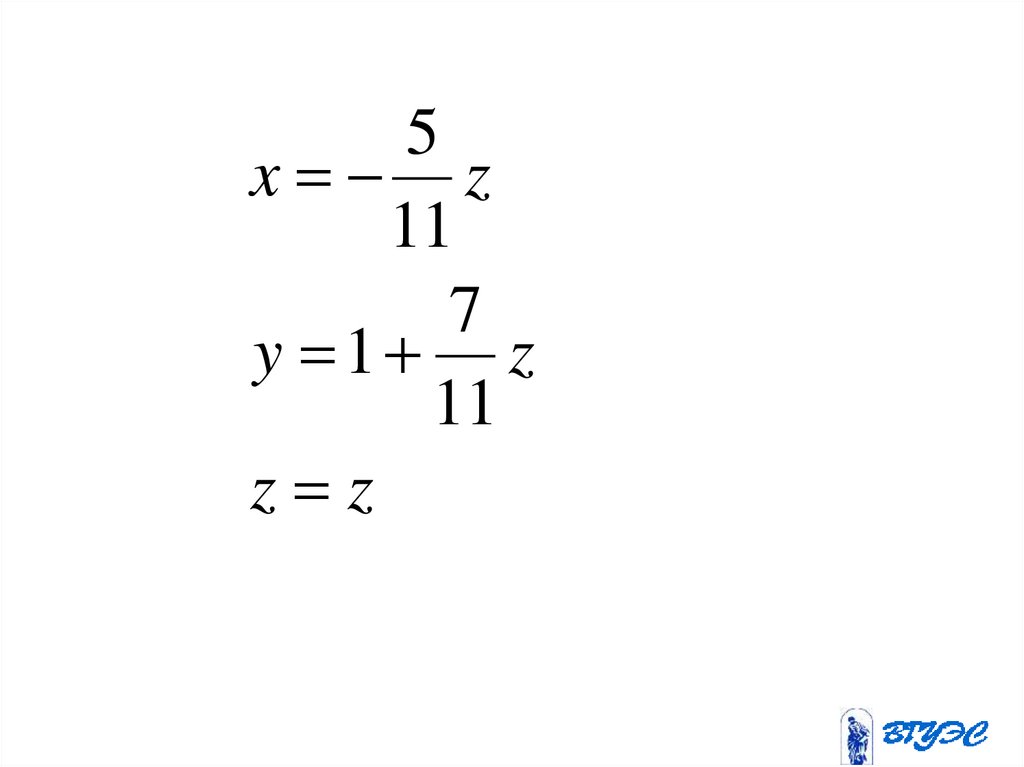



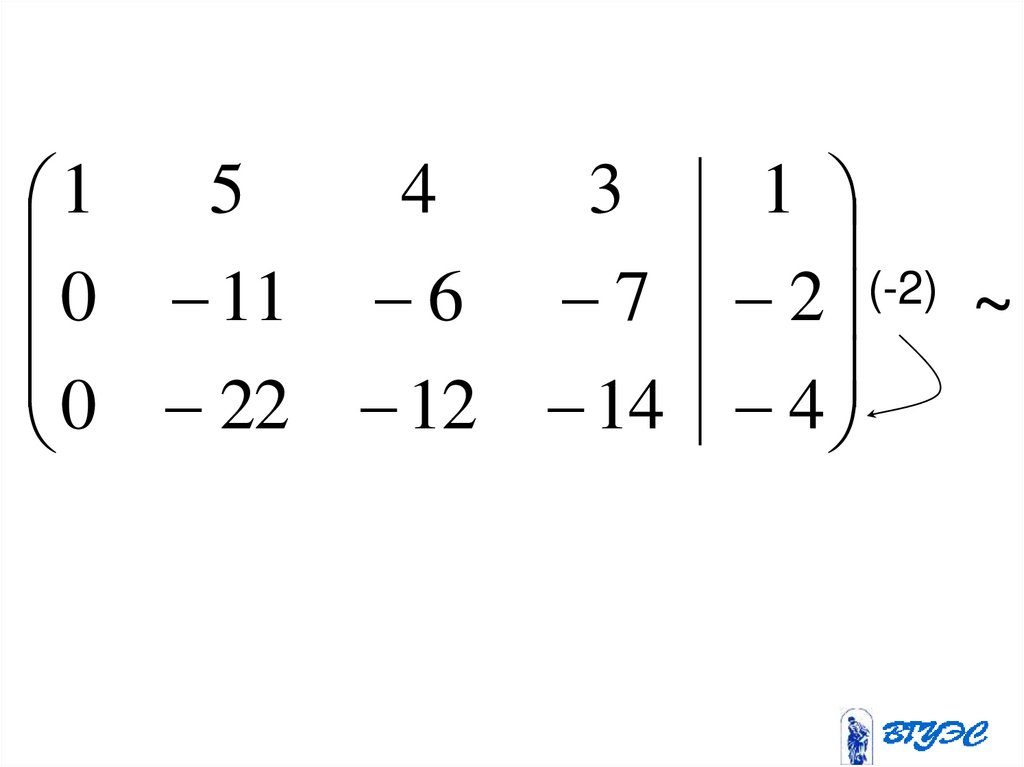




 mathematics
mathematics








