Similar presentations:
Алгебра: Матрицы. Действия с матрицами. Определитель. Его вычисление и основные свойства
1. Лекция №1
1Лекция №1
Алгебра:
Матрицы. Действия с матрицами.
Определитель. Его вычисление и основные
свойства. Система линейных
алгебраических уравнений (СЛАУ). Методы
решения СЛАУ.
2. Матрицы.
2Матрицы.
Определение: Матрица размерности mxn – это
таблица чисел расположенных в m строках и n
столбцах вида
a11 a12 a13
a21 a22 a23
a
a
a
33
31 32
Матрицы бывают квадратные:
a11 a12
Прямоугольные: a21 a22
a
a
31 32
a11 a12
a21 a22
a11 a12
или
a21 a22
a13
a23
3. Матрицы.
3Матрицы.
Главная диагональ
Побочная диагональ
0 0 0
O 0 0 0
0 0 0
Нулевая матрица
0 0 0
O 0 0 0
0 0 0
Матрица столбец
b1
b2
b
3
1 0 0
E 0 1 0
0 0 1
Единичная матрица
1 0 0
E 0 1 0
0 0 1
Матрица строка
a1
a2
a3
4. Действия над матрицами.
4Действия над матрицами.
Сложение матриц:
a11 a12
a21 a22
a13 b11 b12 b13 a11 b11 a12 b12
a23 b21 b22 b23 a21 b21 a22 b22
a13 b13
a23 b23
Вычитание матриц:
a11 a12 a13 b11 b12 b13 a11 b11 a12 b12 a13 b13
a21 a22 a23 b21 b22 b23 a21 b21 a22 b22 a23 b23
Умножение матрицы на число:
a11 a12
a21 a22
a13 a11 a12 a13
a23 a21 a22 a23
5. Действия над матрицами
5Действия над матрицами
Умножение матриц:
a11 a12
b11 b12 b13
a 21 a 22
b21 b22 b23
a
31 a32
a11 b11 a12 b21 a11 b12 a12 b22
a 21 b11 a 22 b21 a 21 b12 a 22 b22
a b a b
31 11 32 21 a31 b12 a32 b22
a11 b13 a12 b23
a 21 b13 a 22 b23
a31 b13 a32 b23
6. Пример умножения матриц.
6Пример умножения матриц.
1 0
1 2 0
2 1
1 1 0 1 1
1 1 0 0 1 2 0 ( 1) 1 0 0 1
2 1 1 0 2 2 1 ( 1) 2 0 1 1
1 1 1 0 1 2 1 ( 1) 1 0 1 1
2 0
1
2
3 1
1 3 1
7. Действия над матрицами.
7Действия над матрицами.
Операции сложения и умножения матриц обладают
следующими свойствами:
Сложения:
1. А+В=В+А (переместительный закон)
2. А+(В+С)=(А+В)+С (сочетательный закон)
3. А+0=А
4. (α·β)·А= α·(β·А)
5. (α+β)·А= α·А+β·А (распределительный
6. (А+В)·α=α·А+α·В
закон)
Умножения:
1. А·В≠В·А
2. А·(В·С)= (А·В)·С
3. А·(В+С)= А·В+А·С
(А+В)·С= А·С+В·С
4. А·Е= Е·А=А
8. Определитель матрицы.
8Определитель матрицы.
Каждой квадратной матрице ставится в
соответствие число, называемое
определителем матрицы.
Обозначается: det|A| или ||A|| или |A|
9. Вычисление определителя.
9Вычисление определителя.
Для матрицы размера 2х2, определитель
вычисляется по следующей формуле:
a11
a12
a21 a22
a11 a22 a12 a21
Для вычисления определителя матрицы размера
3х3 (nxn), введем понятие миноров и
алгебраических дополнений.
10. Вычисление определителя.
10Вычисление определителя.
Будем называть минором (Mkl) определитель
матрицы полученной из исходной после
вычеркивания из нее k-ой строки и l-го столбца.
a11 a12 a13
a21 a22 a23
a
a
a
33
31 32
M 11
a22
a23
a32
a33
M 23
a11
a12
M 32
a31 a32
a11
a13
a21 a23
a22 a33 a23 a32
a11 a32 a12 a31
a11 a23 a13 a21
11. Вычисление определителя.
11Вычисление определителя.
Алгебраическим дополнением элемента
матрицы с индексами k, l называется число ,
полученное умножением минора (Mkl) на (-1)
в степени (k+l).
Akl ( 1)
k l
M kl
12. Вычисление определителя.
12Вычисление определителя.
Определитель матрицы размера более чем 3х3,
вычисляется путем разложения этой матрицы
по строке или столбцу, следующим образом:
a11
a12
det A a21 a22
a31 a32
a13
a23 a11 A11 a12 A12 a13 A13
a33
a21 A21 a22 A22 a23 A23
a31 A31 a32 A32 a33 A33
a11 A11 a21 A21 a31 A31
a12 A12 a22 A22 a32 A32
a13 A13 a23 A23 a33 A33
13. Вычисление определителя.
13Вычисление определителя.
Для вычисления определителя матрицы 3х3
можно использовать следующую формулу:
a11 a12 a13
a21 a22 a23
a
31 a32 a33
a11 a12 a13 a11 a12
a21 a22 a23 a21 a22
a
a
a
a
a
33
31
32
31 32
a11 a22 a33 a12 a23 a31 a13 a21 a32
a13 a22 a31 a11 a23 a32 a12 a21 a33
14. Пример вычисление определителя.
14Пример вычисление
определителя.
1 2
1 3
1 3 2 1 3 2 1
15. Пример вычисление определителя.
15Пример вычисление
определителя.
1
0 1
1
2
1 1
3 1 2 0 0 3 ( 1) ( 1) 1 1
0
( 1) 2 ( 1) 1 3 1 0 1 0 0 0 1 2 3 0 6
1 0 1 1 0
1 2 3 1 2
1 1 0 1 1
16. Пример вычисление определителя.
16Пример вычисление
определителя.
1
0 1
1
2
1 1
3 1 ( 3) 0 ( 3) ( 1) 3 3 3 6
0
1 1
A11 ( 1)
1 2
A12 ( 1)
1 3
A13 ( 1)
M 11
2 3
1 0
M 12 1
M 13
1
2 0 3 1 0 3 3
1
3
1 0
2
1 1
1 (1 0 3 ( 1)) 1 (0 3) 3
1 1 2 ( 1) 1 2 3
17. Свойства определителей.
17Свойства определителей.
Свойство 1. При перестановке двух строк (или столбцов)
определитель меняет знак.
Свойство 2. Общий множитель какой-либо строки или
столбца можно выносить за знак определителя.
Свойство 3. Если в определителе две строки (или два
столбца) пропорциональны (в частности, равны), то
определитель равен нулю.
Свойство 4. При замене всех строк определителя на
столбцы с теми же номерами
величина
его не
изменится.
18. Свойства определителей.
18Свойства определителей.
Свойство 5. Если все элементы некоторой строки (столбца)
нули, то определитель равен нулю.
Свойство 6. Определитель не изменится, если к элементам
какой-либо строки (столбца) прибавить соответствующие
элементы другой строки (столбца), умноженные на одно и
тоже число.
Свойство 7. Сумма парных произведений элементов какойлибо
строки
(столбца)
на
соответствующие
алгебраические дополнения другой строки (столбца)
равна нулю.
19. Система линейных алгебраических уравнений (СЛАУ)
19Система линейных
алгебраических уравнений
(СЛАУ)
Система вида:
где
x
y
z
a11 a12
a21 a22
a
31 a32
a13
a23
a33
a11 x a12 y a13 z f1
a21 x a22 y a23 z f 2
a x a y a z f
32
33
3
31
матрица системы,
- вектор неизвестных,
f1
f2
f 3
- вектор правой
части
уравнения,
называется системой линейных алгебраических
уравнений (СЛАУ).
20. Система линейных алгебраических уравнений (СЛАУ)
20Если обозначим:
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
x
x y
z
f
f1
f2
f 3
То нашу систему можно записать в виде:
Тогда решение будет иметь вид:
где
A
1
A x f
x A 1 f
обратная матрица системы.
21. Система линейных алгебраических уравнений (СЛАУ)
21Система линейных
алгебраических уравнений
(СЛАУ)
Обратная матрица – это такая матрица при умножении на
которую самой матрицы получается единичная матрица.
A A
1
E
22. Система линейных алгебраических уравнений (СЛАУ)
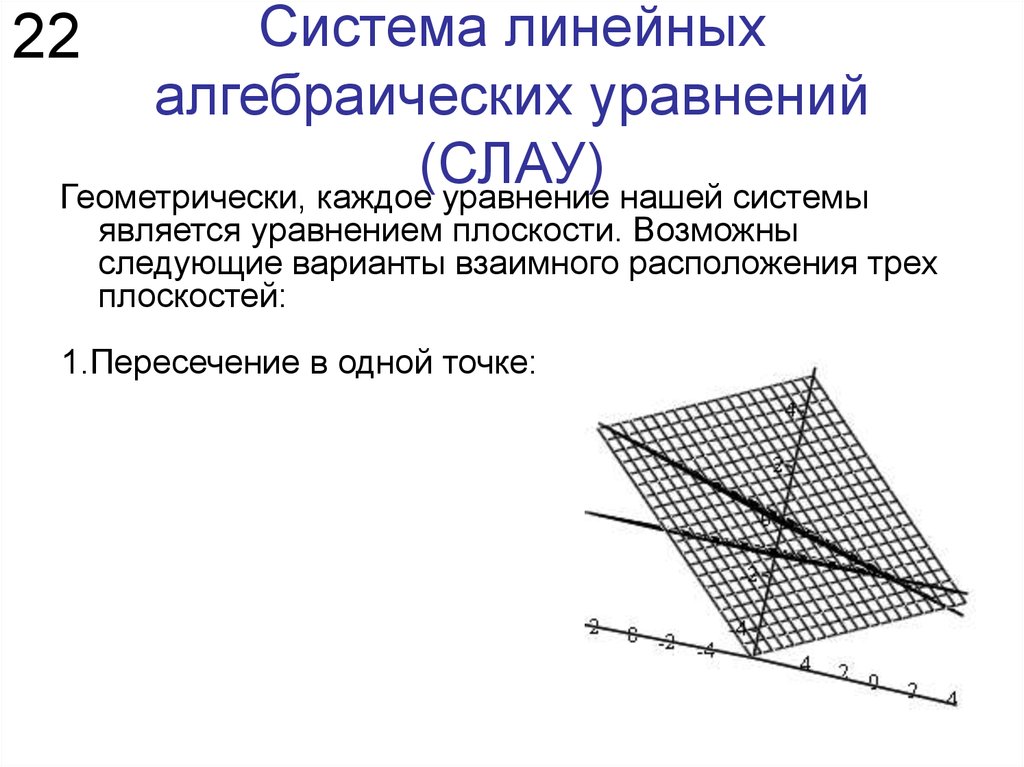
Геометрически, каждое уравнение нашей системы22
является уравнением плоскости. Возможны
следующие варианты взаимного расположения трех
плоскостей:
1.Пересечение в одной точке:
23. Система линейных алгебраических уравнений (СЛАУ)
23Система линейных
алгебраических уравнений
(СЛАУ)
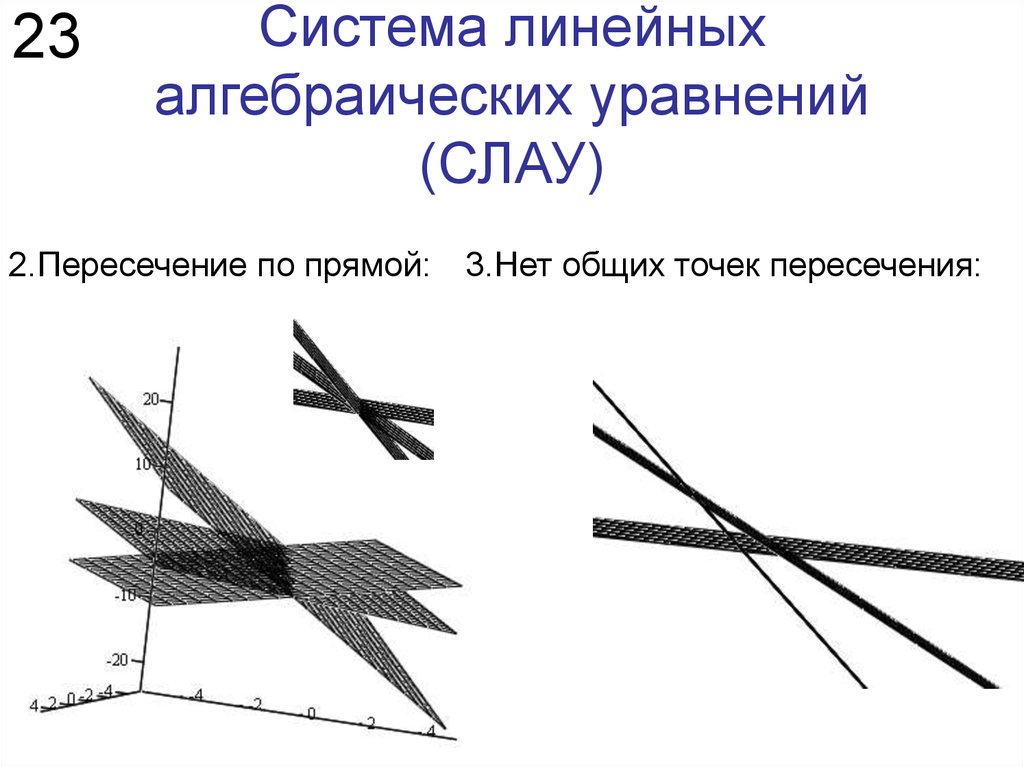
2.Пересечение по прямой: 3.Нет общих точек пересечения:
24. Система линейных алгебраических уравнений (СЛАУ)
24Система линейных
алгебраических уравнений
(СЛАУ)
В первом случае определитель нашей системы
НЕ равен нулю, а значит решение существует
и единственно.
Найти решение такой системы мы можем двумя
методами: 1. Методом Крамера, 2. Методом
обратной матрицы.
Во втором случае решений системы бесконечно
много, и решить эту системы мы можем при
помощи метода Гаусса.
В третьем случае система не имеет решения,
проверить это можно также методом Гаусса.
25. Метод Крамера.
25Метод Крамера.
Данный метод сводиться к нахождению четырех
определителей:
f1
a12
a13
a23
D1 f 2
a22
a23
a32
a33
f3
a32
a33
a11
f1
a13
D 2 a21
a11
a12
f1
f2
a23
D3 a21 a22
f2
a31
f3
a33
a31
f3
a11
a12
a13
D a21 a22
a31
a32
26. Метод Крамера.
26Метод Крамера.
В результате получим решение СЛАУ:
D1
x
D
D2
y
D
D3
z
D
27. Метод Крамера. Пример.
27Метод Крамера. Пример.
Решить систему уравнений:
x
x
0
y
y
y
1 1 0
A 0 1 2
1 1 1
2 z 4
z
2
0
f 4
2
28. Метод Крамера. Пример.
28Метод Крамера. Пример.
Вычислим определитель системы:
D A 1 A11 1 A12 0 A13
1 1 0
A 0 1 2
1 3 1 2 5
1 1 1
1 2
1 1
A11 ( 1)
1 2 3
1 1
1 2
A12 ( 1)
0 2
1 1
1 ( 0 2 ) 2
29. Метод Крамера. Пример.
29Метод Крамера. Пример.
1 1 0
A 0 1 2
1 1 1
0
f 4
2
0 1 0
D1 4 1 2 0 A11 1 A12 0 A13 1 0 0
2 1 1
1 2
A12 ( 1)
4 2
2 1
1 (4 4) 0
30. Метод Крамера. Пример.
30Метод Крамера. Пример.
0
f 4
2
1 1 0
A 0 1 2
1 1 1
1 0 0
D 2 0 4 2 1 A11 0 A12 0 A13 1 0 0
1 2 1
1 1
A11 ( 1)
4 2
2 1
4 4 0
31. Метод Крамера. Пример.
31Метод Крамера. Пример.
0
f 4
2
1 1 0
A 0 1 2
1 1 1
1 1 0
D3 0 1 4 1 A11 0 A21 1 A31 1 6 1 4 10
1 1 2
1 4
1 1
A11 ( 1)
2 4 6
1 2
A31 ( 1)
3 1
1 0
1 4
4 0 4
32. Метод Крамера. Пример.
32Метод Крамера. Пример.
В результате мы получили: D=5, D1=0,
D2=0, D3=10.
D1 0
x
0
D 5
D2 0
y
0
D 5
D3 10
z
2
D
5
33. Метод Крамера. Пример.
33Метод Крамера. Пример.
x
x
0
y
y
y
0 0
0
0 0
2 z 4
z
2
0
2 2 4
2
2
34. Решение СЛАУ методом обратной матрицы.
34Решение СЛАУ методом
обратной матрицы.
A x f
x A f
1
A11
1
1
A
A12
A
A13
A21
A22
A23
A31
A32
A33
35. Решение СЛАУ методом обратной матрицы.
35Решение СЛАУ методом
обратной матрицы.
x
x
0
y
y
2 z 4
y
1 1 0
A 0 1 2
1 1 1
z
2
0
f 4
2
36. Решение СЛАУ методом обратной матрицы.
36Решение СЛАУ методом
обратной матрицы.
1 1
A11 ( 1)
1 2
A12 ( 1)
1 3
A13 ( 1)
A31 ( 1)
1
1 1
0 2
1 1
0
3 2
1 2 3
1(0 2) 2
1
1 1
3 1
A32 ( 1)
2
1 0
1 0
1 2
0 2
0 1 1
A21 ( 1)
2 1
A22 ( 1)
2 2
A23 ( 1)
2 3
1
0
1(1 0) 1
1 1
1 0
1
1 1
1 1 0
A 0 1 2
1 1 1
(1 0) 1
1
1 1
1( 1 1) 2
2 0 2
1(2 0) 2,
A33 ( 1)
3 3
1 1
0 1
1 0 1
37. Решение СЛАУ методом обратной матрицы.
37Решение СЛАУ методом
обратной матрицы.
3 1 2
1
1
A 2 1 2
5
1
2
1
3 1 2 0
1
1
x A f 2 1 2 4
5
2
1
2
1
3 0 ( 1) 4 2 2
0 0
1
1
2 0 1 4 ( 2) 2 0 0
5
5
( 1) 0 2 4 1 2
10 2
38. Метод Гаусса
38Метод Гаусса
Расширенной матрицей системы
A x f
будем называть матрицу вида
a11 a12
A | f a21 a22
a
31 a32
a13
a23
a33
f1
f2
f 3
39. Метод Гаусса
39Метод Гаусса
Ранг матрицы – это размер наибольшего
ненулевого минора этой матрицы.
Ранг
матрицы
с
ненулевым
определителем равен размеру этой
матрицы.
40. Метод Гаусса
40Метод Гаусса
Для того, чтобы СЛАУ была совместна ранг матрицы
системы должен быть равен рангу расширенной
матрицы.
Заметим:
1. Если ранг матрицы системы равен размерности
самой матрицы, то система имеет единственное
решение.
2. Если ранг матрицы системы равен рангу
расширенной матрицы, но меньше размерности
самой матрицы системы, то система имеет
бесконечное множество решений.
3. Если ранг матрицы системы меньше ранга
расширенной матрицы, то система несовместна и
решений не существует.
41. Метод Гаусса
41Метод Гаусса
Сам метод Гаусса состоит в том, чтобы
преобразованием строк получить нули
под главной диагональю расширенной
матрицы системы.
42. Метод Гаусса
42Метод Гаусса
x
x
0
y
y
2 z 4
y
1 1 0
A 0 1 2
1 1 1
z
2
0
f 4
2
43. Метод Гаусса
43Метод Гаусса
1 1 0
(A | f ) 0 1 2
1 1 1
1 1 0
0 1 2
0 2 1
0
4
2
1 1 0 0
0 1 2 4
0 0 5 10
0
4
2
Вычитаем из 3 строки
первую строку
Добавим к 3 строке вторую
умноженную на 2
44. Метод Гаусса
44Метод Гаусса
1 1 0 0
0 1 2 4
0 0 5 10
Теперь из расширенной матрицы
запишем получившуюся систему:
0
x y
y 2z 4
5 z 10
45. Метод Гаусса
45Метод Гаусса
Осталось только решить нашу систему.
Из последнего уравнения получаем z=2,
подставляем это значение z во второе
уравнение и получаем y=0, теперь
подставляем значение y в первое
уравнение и получаем x=0.
46. Метод Гаусса
46Метод Гаусса
Исследовать СЛАУ на совместность:
x y z 1
x 4 y 3z 0
3 x 2 y z 2
Запишем расширенную матрицу системы:
1 1 1 1
1 4 3 0
3 2 1 2
47. Метод Гаусса
47Метод Гаусса
1 1 1 1
1 4 3 0
3 2 1 2
Вычитаем из 2 строки
первую
1 1 1
0 5 4
3 2 1
1
1
2
Вычитаем из 3 строки
первую умноженную на 3
1 1 1
0 5 4
0 5 4
1
1
1
1 1 1
0 5 4
0 0
0
1
1
0
Вычитаем из 3 строки
вторую
48. Метод Гаусса
48Метод Гаусса
1 1 1
0 5 4
0 0
0
1
1
0
Заметим, что наибольший ненулевой минор имеет
размерность 2, а количество неизвестных системы
равно 3, т.е. ранг системы совпадает с рангом
расширенной матрицы, но он меньше чем количество
неизвестных системы – это означает, что наша
система имеет бесконечное множество решений.
49. Метод Гаусса
49Метод Гаусса
Исследовать СЛАУ на совместность:
x y z 1
x 4 y 3z 1
3 x 2 y z 2
Запишем расширенную матрицу системы:
1 1 1 1
1 4 3 1
3 2 1 2
50. Метод Гаусса
50Метод Гаусса
1 1 1 1
1 4 3 1
3 2 1 2
Вычитаем из 2 строки
первую
1 1 1 1
0 5 4 0
3 2 1 2
Вычитаем из 3 строки
первую умноженную на 3
1 1 1
0 5 4
0 5 4
Вычитаем из 3 строки
вторую
1
0
1
1 1 1 1
0 5 4 0
0 0
0
1
51. Метод Гаусса
51Метод Гаусса
Заметим, что наибольший
ненулевой минор имеет
размерность 3.
Заметим, что ран матрицы
самой системы равен 2 –
это означает, что наша
система
не
имеет
решения,
т.к.
ранг
расширенной
матрицы
больше ранга матрицы
системы.
1 1 1 1
0 5 4 0
0 0
0 1
1 1 1
0 5 0
0 0 1

















































 mathematics
mathematics








