Similar presentations:
Решение систем линейных алгебраических уравнений (СЛАУ)
1. Решение систем линейных алгебраических уравнений (СЛАУ)
2. Определитель матрицы второго порядка
Определителем матрицы второго порядка называютчисло, которое вычисляется по формуле:
a11 a12 a11 a12
det
a11a22 a12a21
a21 a22 a21 a22
а11 и а22 образуют главную диагональ матрицы;
а12 и а21образуют побочную диагональ матрицы
3. Вычислите устно
Составьте и вычислите определительматрицы системы второго порядка
2 1
y 2x 2
2 ( 5) 3 1 7
3 5
3
x
5
y
5
4. Определитель матрицы третьего порядка
a11 a12 a13det a21 a22 a23
a31 a32 a33
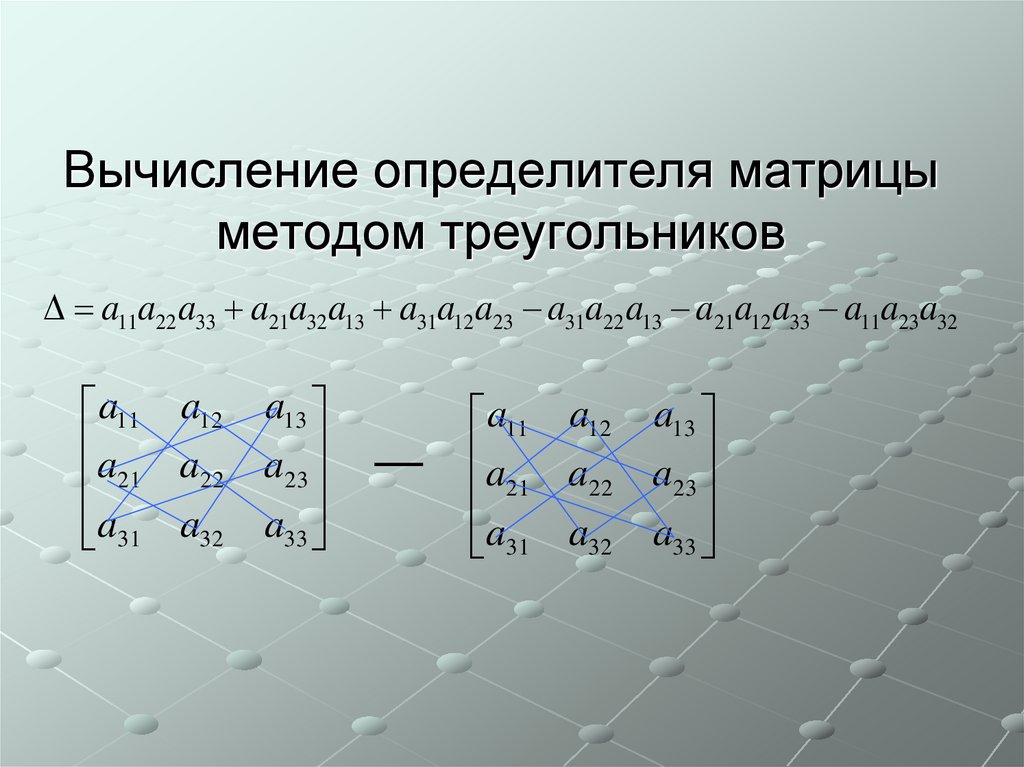
a11a22a33 a21a32a13 a31a12a23 a31a22a13 a21a12a33 a11a23a32
5. Вычисление определителя матрицы методом треугольников
a11a22 a33 a21a32 a13 a31a12 a23 a31a22 a13 a21a12 a33 a11a23a32a11 a12
a
a
21
22
a31 a32
a13
a23
a33
a11 a12
a
21 a22
a31 a32
a13
a23
a33
6. Вычислите определитель третьего порядка
2 1 32 2 1 2∙(-2)∙1 + (-1)∙1∙1+2∙1∙3-3∙(-2)∙1-2 ∙(-1)∙1-1∙1∙2=7
1 1 1
7. Система из m линейных уравнений с n неизвестными имеет вид:
a11 x1 + a12 x2 +... + a1n xn = b1,a21 x1 + a22 x2 +... + a2n xn = b2,
... ... ...
am1 x1 + am2 x2 +... + amn xn = bm.
...
где аij (i =1..m ; j =1..n ) – заданные
коэффициенты системы
bi – свободные члены системы
xj - неизвестные действительные числа
8. Решение СЛАУ
Решением системы линейныхалгебраических уравнений является
упорядоченный набор значений
переменных, который будучи
подставлен в каждое уравнение, даёт
верные равенства.
9. Способы решения СЛАУ
способ подстановкиспособ сложения
графический способ (две переменные)
методом Крамера
методом Гаусса
другие
10. Габриэль Крамер (Gabriel Cramer), швейцарский математик
Датарождения:31 июля 1704
Место
рождения:Женева,
Швейцария
Дата
смерти:4 января 1752
(47 лет)
Место смерти:Баньольсюр-Сез,Франция
11.
Крамер одним из первых математиковпришел к понятию определителя, вывел
формулы решения СЛАУ, доказав
соответствующую теорему в 1750 году
в своей работе «Введение в анализ
кривых линий».
12. Теорема Крамера
• Система линейных алгебраическихуравнений имеет единственное решение
тогда и только тогда, когда определитель
этой системы отличен от нуля.
13. Метод Крамера
Метод широко применяется (как и самопонятие определителя) не только в
высшей алгебре, но и в других разделах
высшей математики, в механике и
теоретической физике.
14. Метод Крамера для систем второго порядка
a11x a12 y b1a21x a22 y b2
a11 a12
a21 a22
b1
x
b2
a12
a22
a11 b1
y
a21 b2
Если определитель основной матрицы 0, система имеет
единственное решение, которое находится по формулам:
x
x
y
y
15.
• Если Δ=0 и хотя бы один из Δj≠0, то системанесовместна, то есть не имеет решения.
• Если Δ=0 и каждый из Δj=0, то система
имеет бесконечное множество решений.
16. Пример№1 Решите систему методом Крамера
2х+3у = 123х - 2у = 5
Матрица системы и
столбец свободных
членов
2 3 12
3 2 ; 5
2 3
13 Система имеет единственное решение
3 2
12 3
2 12
1
39 2
26
5 2
3 5
39
26
x
;y
13
13
Ответ: (3;2)
17. Пример№2 Решите систему методом Крамера
у–х=12х - 2у = -2
Матрица системы и 1
столбец свободных
2
членов
1 1
det
1 ( 2) 1 2 0
2 2
1 1
;
2 2
Система не может иметь
единственное решение
1
1
1 det
1 ( 2) 1 ( 2) 0
2 2
Система имеет
1 1
бесконечное множество
2 det
(
1
)
(
2
)
1
2
0
решений
2
2
18. Решите системы методом Крамера
y 2x 1y 2 x 1
6 y 4 x 24
2 x 8 y 10
5 x y 11
3 x 2 y 8
19. Системы трёх линейных уравнений с тремя неизвестными
a11x a12 y a13 z b1a21x a22 y a23 z b2
a x a y a z b
32
33
3
31
a11 a12 a13
a a a
21 22 23
a31 a32 a33
2 x y 3z 1
2 x 2 y z 1
x y z 0
2 1 3
2 2 1
1 1 1
20.
Пример:x1 x 2 x3 6
x1 x 2 2 x3 5
2 x x x 1
2
3
1
Уравнение в матричном виде
1 1 1 x1 6
1 1 2 x 5
2
2 1 1 x3 1
Определитель матрицы:
1 1 1
1 2
1 2
1 1
1 1 2 1*
1*
1*
1 5 3 7
1 1
2 1
2 1
2 1 1
Система имеет единственное решение.
21.
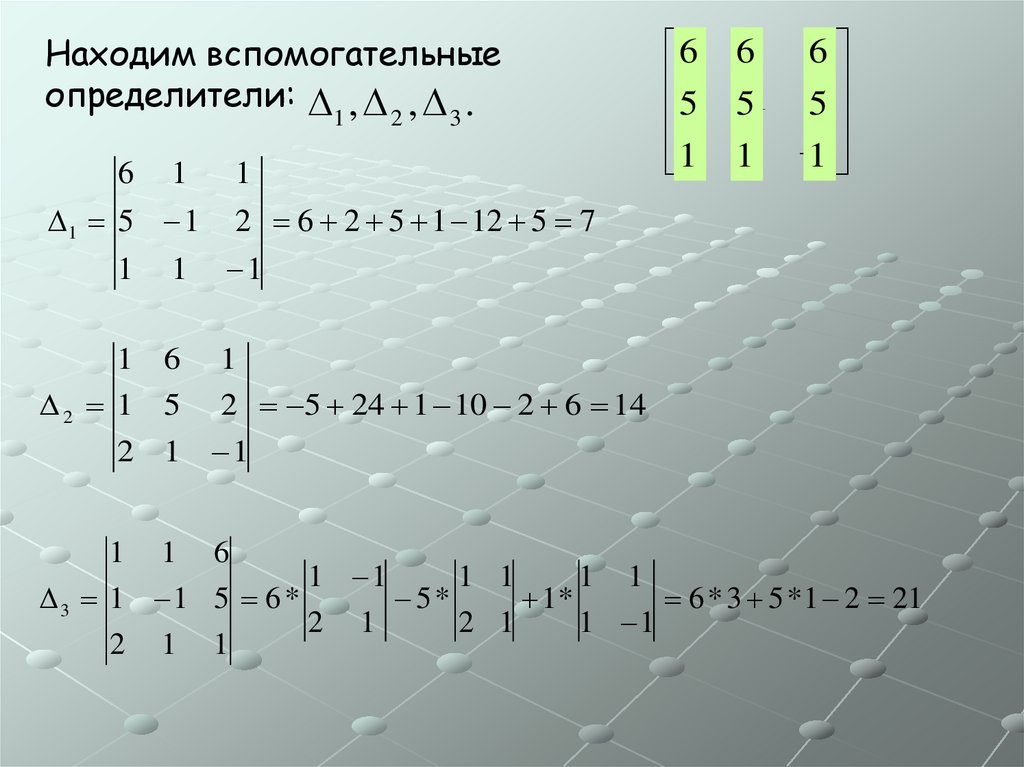
Находим вспомогательныеопределители: , , .
1
2
3
6 1 1
1 5 1 2 6 2 5 1 12 5 7
1 1 1
16 61 16
1 1 2
5
5 5
1
2 1 11
1 6 1
2 1 5 2 5 24 1 10 2 6 14
2 1 1
1 1 6
1 1
1 1
1 1
3 1 1 5 6 *
5*
1*
6 * 3 5 *1 2 21
2 1
2 1
1 1
2 1 1
22.
1 7x1
1
7
2 14
x2
2
7
3 21
x3
3
7
X=(1;2;3)
Проверка:
1+2+3=6 (6=6)
1-2+6=5 (5=5)
2+2-3=1 (1=1)
x1 x 2 x3 6
x1 x 2 2 x3 5
2 x x x 1
2
3
1
23.
Самостоятельная работа24.
25. Метод Гаусса
26. Цели и задачи:
Цель:Научиться решать системы линейных
алгебраических уравнений (СЛАУ).
Задачи:
Изучить решение СЛАУ методом Гаусса
Рассмотреть возможные варианты решений системы
27. Введение
Сначала немного систематизируем знания осистемах линейных уравнений. Система линейных
уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).
28. Метод Гаусса
Метод Гаусса – наиболее мощный и универсальныйинструмент для нахождения решения любой системы
линейных уравнений. Как мы помним, правило
Крамера непригодно в тех случаях, когда система
имеет бесконечно много решений или несовместна. А
метод последовательного исключения неизвестных в
любом случае приведет нас к ответу!
29.
30.
Метод Гаусса или метод исключения неизвестныхсостоит в последовательном исключении во втором
уравнении первой неизвестной, в третьем
уравнении первой и второй неизвестных и т. д. Пока
не получится система треугольного или
трапецеидального вида.
Метод удобнее применять на расширенной матрице
31. Элементарные преобразования:
1) Строки матрицы можно переставлять местами2) Если в матрице есть (или появились)
пропорциональные (как частный случай –
одинаковые) строки, то следует удалить из матрицы
все эти строки кроме одной.
3) Если в матрице в ходе преобразований появилась
нулевая строка, то ее также следует удалить.
4) Строку матрицы можно умножить (разделить) на
любое число, отличное от нуля
К строке матрицы можно прибавить другую строку,
умноженную на число, отличное от нуля.
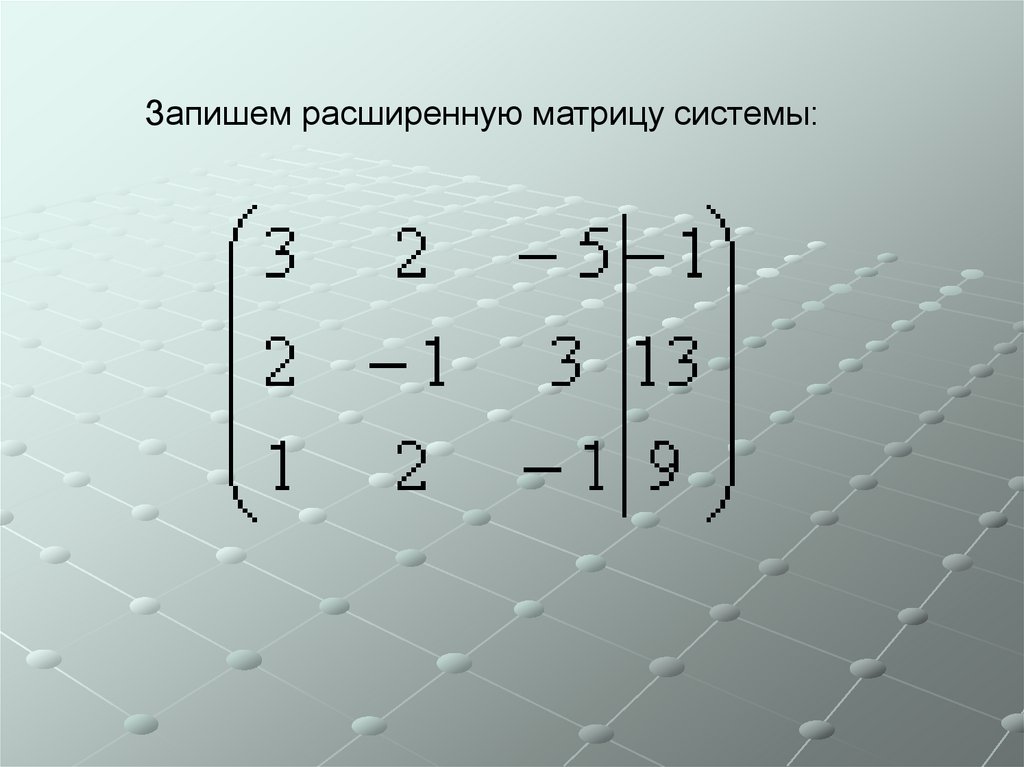
32. Пример 1 Решить методом Гаусса систему уравнений:
33.
Запишем расширенную матрицу системы:34.
Наша цель – с помощью элементарныхпреобразований привести матрицу к ступенчатому
виду. С чего начать действия?
35.
Сначала смотрим на левое верхнее число:Почти всегда здесь должна находиться единица.
Как организовать единицу? Смотрим на первый
столбец – готовая единица у нас есть!
Преобразование первое: меняем местами первую и
третью строки:
36.
Теперь нужно получить нули вот на этих местах:Нужно ко второй строке прибавить первую
строку, умноженную на –2. Умножаем первую
строку на –2: (–2, –4, 2, –18). И последовательно
проводим сложение, ко второй строке
прибавляем первую строку, уже умноженную на
–2:
37.
Аналогично разбираемся с третьей строкой (3, 2,–5, –1). Чтобы получить на первой позиции ноль,
нужно к третьей строке прибавить первую
строку, умноженную на –3.
38.
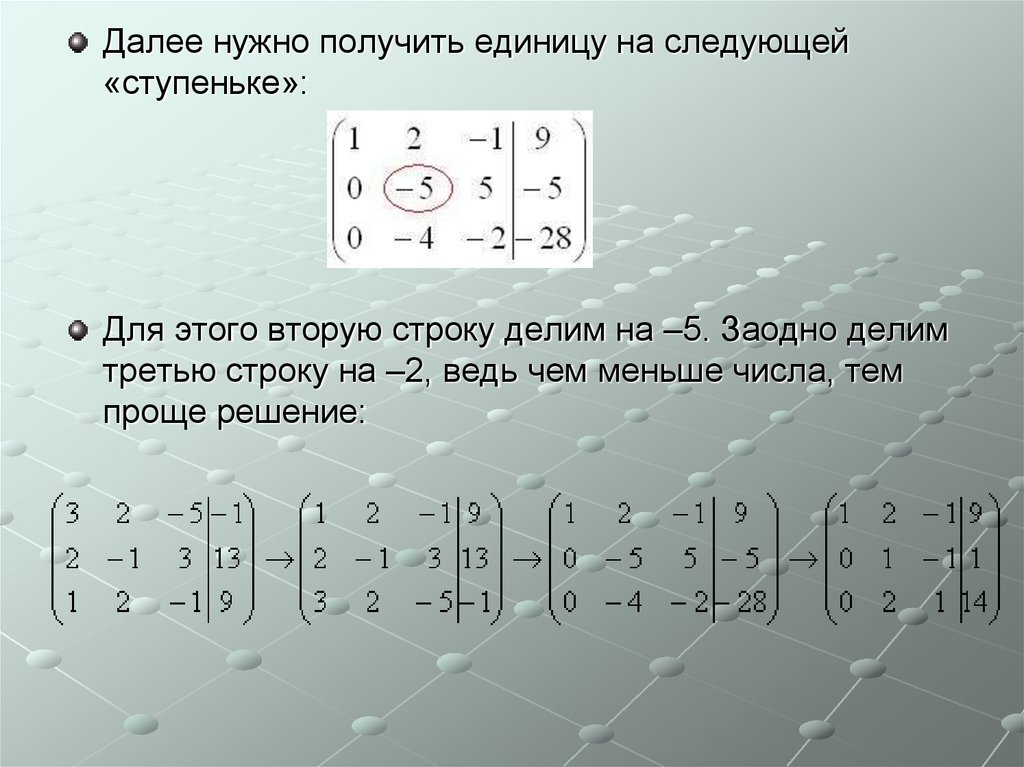
Далее нужно получить единицу на следующей«ступеньке»:
Для этого вторую строку делим на –5. Заодно делим
третью строку на –2, ведь чем меньше числа, тем
проще решение:
39. На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
40.
Для этого к третьей строке прибавляем вторуюстроку, умноженную на –2:
Последнее выполненное действие – делим третью
строку на 3.
41.
В результате элементарных преобразованийполучена эквивалентная исходной система
линейных уравнений:
42.
Теперь в действие вступает обратный ход методаГаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат: z=
4
Смотрим на второе уравнение: y-z=1.
y-4=1
y=5
И, наконец, первое уравнение: x+10- 4 =9
x=3
Ответ: (3;5;4)
Замечание: для любой системы уравнений можно и
нужно сделать проверку найденного решения!
43. Пример 2 Решить методом Гаусса систему уравнений:
44. Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Решение:Запишем расширенную матрицу системы и с помощью
элементарных преобразований приведем ее к
ступенчатому виду
.
45. Обратный ход:
Ответ:46. Выводы:
Метод Гаусса универсальный, позволяетрешать любую СЛАУ.
Слау может иметь единственное решение,
если расширенная матрица преобразуется в
треугольную, причем имеет уравнение вида
а*х=в.
Слау может иметь бесконечно много решений,
если, если матрица преобразуется в
трапецеидальный вид.
Слау не имеет решения, если расширенная
матрица преобразуется в треугольную, причем
имеет уравнение вида 0*х=а












































 mathematics
mathematics








