Определители и их свойства. Лекции 9,10

1. Определители и их свойства

a11
a12
a21
a22
Определители и
их свойства
Решение линейных уравнений с
помощью правила Крамера.
Обратные матрицы.
Решение систем уравнений с помощью
обратных матриц
a11
A a21
a
31
a12
a22
a32
a13
a23
a33
a11
a12
a13
a21
a22
a23
a31
a32
a33

2. Понятие определителя

Понятие определителя (или детерминанта )
квадратной матрицы A порядка n , которое
обозначается через det A
или A
, введем
индуктивным методом.
При n 1 A a11
n 2
a11
a12
a21
a22
а11а 22 а12 а 21
Перейдем к индуктивному шагу: предположим, что
нами уже введено понятие определителя порядка
n 1 , соответствующего произвольной квадратной
матрице n 1 го порядка.

3. Понятие минора элемента

Определение. Минором некоторого элемента a ij
матрицы A порядка n называется определитель
n 1 порядка, соответствующий матрице, которая
получается из исходной матрицы A в результате
вычеркивания той строки и того столбца, на
пересечении которых стоит элемент a ij , т.е. i
строки и j го столбца.
Минор элемента a ij обозначается M ij .

4. Определение определителя

n
Определение. Определителем
соответствующим матрице
а1n
а11 а12
a
a
a
22
2n
A 21
ann
an1 an 2
называется число, равное
a11M 11 a12 M 12 ... ( 1)
и обозначаемое
det A
n 1
n
-го порядка,
a1n M 1n 1
j 1
, либо
A
1 j
a1 j M 1 j

5.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
det A A
а11
а12
а1n
a21
a22
a2 n
n
1
j 1
an1 an 2
1 j
a1 j M 1 j .
ann
Эта формула называется разложением определителя
го порядка по первой строке.
n

6. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ

а11
а12
а1n
a21
a22
a2 n
an1 an 2
a22
a11
1 j
ann
a 21 a 2 j 1
a1 j
a n1 a n j 1
1
1 n
a21
a23
a2 n
a12
an 2
ann
1
a2 n
an1 an 3
ann
a 2 j 1 a 2 n
a n j 1 a nn
a 21 a 2 n 1
a1n
a n1 a n n 1
(3)

7.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
Теорема 1. Каков бы ни был номер строки
i
i 1, 2,...n для определителя матрицы
справедлива формула
A 1 ai1M i1 1
i 1
n
1
j 1
i j
i 2
ai 2 M i 2 ... ( 1) i n ain M in
aij M ij .
Эта формула называется разложением определителя
го порядка по i ой строке.
n

8.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
Теорема 2. Каков бы ни был номер столбца
j 1, 2,...n для определителя матрицы
j
справедлива формула
A 1
1 j
n
1
i 1
i j
a1 j M 1 j 1
2 j
a2 j M 2 j ... ( 1) n j anj M nj
aij M ij .
Эта формула называется разложением определителя
го порядка по j му столбцу.
n

9. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ

Определитель может быть вычислен
разложением по элементам его л ю б о й
строки или столбца.
Замечание. Для определителя используют
те же термины (элементы, строки, столбцы,
главная и побочная диагонали), что и для
соответствующей квадратной матрицы, чей
определитель вычисляется.

10. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ

В качестве примера рассмотрим определитель
третьего порядка
a11
a12
a13
a21 a22
a23 a11
a31 a32
a33
a22
a23
a32
a33
a12
a21 a23
a31 a33
a13
a21 a22
a31 a32
(2)

11. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Свойства определителя:

1. Определитель не меняется при замене в нем
всех строк соответствующими (по номеру)
столбцами;
2. Определитель равен нулю, если содержит
нулевую строку или нулевой столбец;
3. Определитель равен нулю, если содержит две
одинаковые строки или два одинаковых столбца;

12. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Свойства определителя:

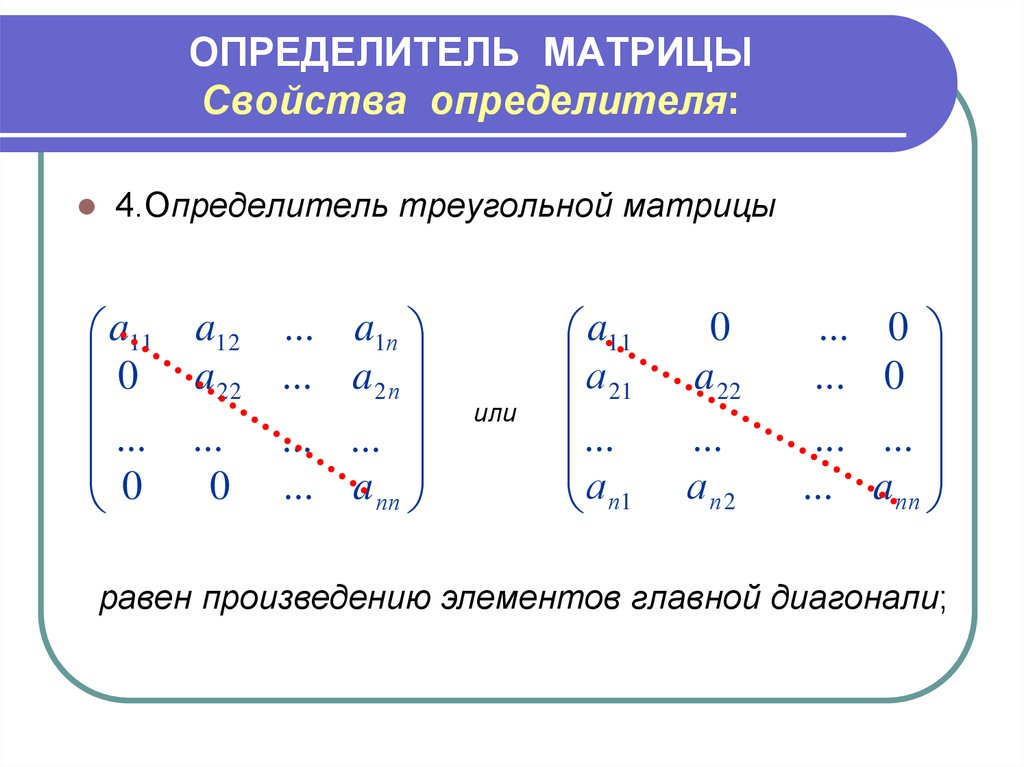
4.Определитель треугольной матрицы
a11 a12 ... a1п
0 a
...
a
2п
22
... ... ... ...
0
0
...
a
пп
или
a11
а
21
...
а
п1
0
a 22
...
ап 2
... 0
... 0
... ...
... a пп
равен произведению элементов главной диагонали;

13. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Свойства определителя:

5. Определитель изменит знак на противоположный,
если в нем поменять местами любые две строки или
столбца (то есть применено элементарное
преобразование первого типа);
6. Если строку (столбец) определителя умножить на
некоторое число (то есть применено элементарное
преобразование третьего типа), то определитель
умножится на это число.

14. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Свойства определителя:

7. Определитель не изменится, если в нем
заменить строку суммой этой строки и некоторой
другой,
умноженной
вспомогательной,
на
какое-либо
предварительно
число
(то
есть
применено элементарное преобразование второго
типа);

15. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Свойства определителя:

8. Определитель произведения квадратных матриц
равен произведению определителей сомножителей.
AB A B .
т.е.
Определение. Алгебраическим дополнением
элемента
a ij
матрицы
число, равное Aij 1
A
i j
порядка
n
называется
M ij , (i 1, 2,...n,
j 1, 2,...n).
Используя алгебраическое дополнение, имеем
n
A aij Aij .
j 1

16. Обратная матрица

Пусть
A квадратная матрица n го, E
единичная матрица того же порядка.
Определение. Матрица
B
называется обратной
для квадратной матрицы , если
AB BA E.
Замечание. Обратная матрица
такого же порядка,
что и матрица
A
B
.
1
A обозначается A .
AA 1 A 1 A E.
Обратная матрица для матрицы

17. Обратная матрица

Определение. Матрица называется невырожденной,
если определитель этой матрицы отличен от нуля:
A 0,
в противном случае матрица называется
вырожденной.
Теорема. Если матрица
A
имеет обратную, то эта
матрица является невырожденной:
1
A
A
1
A 0.

18. Обратная матрица

Теорема. Всякая невырожденная матрица имеет
обратную, причем
A11
1 A12
1
A
A
A1n
A21
A22
A2 n
An1
An 2
,
Ann
где Aij алгебраическое дополнения элемента
матрицы
A.
a ij

19. Обратная матрица

Обратную матрицу можно вычислить по
следующей формуле
где
A
,
A алгебраическое дополнения элемента a ij
T
ij
в определителе
A.
A 1
AijT
T
A , транспонированной к матрице

20. Примеры

Пример 1. Найти матрицу, обратную данной:
Решение. Найдем определитель матрицы.
3 1 0
A 2 1 1
2 1 4
3
A 2
2
1 0
1
0
1 1
1 4
1 0
1
1 1
1 1 4
1 2
( 1)
1
1
1 4
5

21. Примеры

3 2 2 Найдем алгебраические дополнения
AT 1 1 1
T
матрицы A .
0 1 4
1 1
1 2
A11 ( 1) (4 1) 5; A12 ( 1) ( 4 0) 4;
1 3
2 1
2 2
2 3
A13 ( 1) ( 1 0) 1; A21 ( 1) ( 8 2) 10;
A22 ( 1)
(12 0) 12; A23 ( 1)
(3 0) 3;
A31 ( 1)3 1 (2 2) 0; A32 ( 1)3 2 ( 3 2) 1;
A33 ( 1)3 3 (3 2) 1.

22. Примеры

Составляем обратную матрицу
A11 5; A12 4; A13 1; A21 10;
A22 12; A23 3;
A31 0;
A32 1;
A33 1.
5 4 1
1 4 / 5 1/ 5
1
1
A 10 12 3 ; A 1 2 12 / 5 3 / 5 .
5
0 1/ 5 1/ 5
0
1
1

23. Примеры

Проведем проверку, умножив
3 1 0
A 2 1 1
2 1 4
A на
A 1.
1 4 / 5 1/ 5
1
A 2 12 / 5 3 / 5 .
0 1/ 5 1/ 5
1 0 0
1
A A 0 1 0 E.
0 0 1

24. Решение матричных уравнений

Теорема. Если A 0 и A, B матрицы порядка, n
то решение матричных уравнений
A X B и
X A B,
где X квадратная матрица порядка n , находится
по соответствующей из формул:
X A 1 B и
X B A 1.

25. Решение матричных уравнений

С 0 ,где A, B, С
матрицы размерностью n n, n m, m m
Теорема. Если
A 0и
соответственно ,то решение матричного уравнения
A X С B,
где X матрица размерности n m, находится по
формуле:
X A 1 B С 1.

26. Примеры

Пример. Решить матричное уравнение
1 2
3 5
, B
.
A
3 4
5 9
A X B, где
Решение. Найдем A 1 .
1 3
,
A 4 6 2; A
2 4
T
1
X A B,
1 4 2
A
2 3 1
1
1
1 4 2 2
A
2 3 1 1,5 0,5
1
1 3 5 1 1
2
X
1,5 0,5 5 9 2 3

27. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 1. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ

О п р е д е л е н и е 1. Системой линейных
алгебраических уравнений, состоящей из
двух уравнений с двумя неизвестными x и y,
называется система вида:
a11 x a12 y b1
a21 x a22 y b2 ,
(1)

28. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 1. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ

где – аij , bi
i, j 1, 2
некоторые постоянные
действительные числа .
a11 a12
О п р е д е л е н и е 2. Матрица A
a 21 a 22
называется матрицей системы (1); вектор
b1 называется столбцом свободных
b
b2 членов системы (1),
вектор
х
х столбцом неизвестных.
у

29. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 1. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Теорема 1 (правило Крамера). Если определитель
матрицы системы (1) не равен нулю, то система (1)
имеет единственное решение, вычисляемое по
формулам:
1
x
,
где
2
y
A ; j j 1, 2
определители, полученные из
заменой его
j-го столбца столбцом свободных членов .

30. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 1. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Теорема 2. Если у системы (1)
из определителей
0,
но хотя бы один
1 или 2отличен от нуля, то
система (1) не имеет решения. Если у системы (1)
1 2 0
, то система (1) имеет бесконечное
множество решений.

31. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 2. СИСТЕМЫ ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Определение 3. Системой линейных алгебраических
уравнений, состоящей из трех уравнений с тремя
неизвестными x, y и z, называется система вида:
a11 x a12 y a13 z b1
a 21 x a 22 y a 23 z b2
a x a y a z b ,
32
33
3
31
где
(2)
a ij , b i i , j 1, 2 , 3
– некоторые постоянные действительные числа.

32. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 2. СИСТЕМЫ ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Определение 4. Матрицей системы (2), столбцом
свободных членов системы (2) и столбцом неизвестных
системы (2) называются, соответственно, матрица A,
вектор
b
и вектор
a11 a12
A a21 a22
a
31 a32
x
a13
b1
a23 ; b b2 ;
b
a33
3
x
x y
z

33. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 2. СИСТЕМЫ ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Теорема 3. (правило Крамера). Если определитель
матрицы системы (2) не равен нулю, то система (2)
имеет единственное решение,
вычисляемое по
,
1
2
формулам: x
; y ; z 3.
где A ;
j j 1, 2 ,3
определители, полученные из заменой его j-го
,
,
.
столбца столбцом свободных членов .
.

34. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 2. СИСТЕМЫ ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Теорема 4. Если у системы (2)
.
бы один из определителей
0
1 , 2 или
, но хотя
3
отличен от нуля, то система (2) не имеет решения.
Если выполнены условия
1 2 3 0
то система (2) или имеет бесконечное множество
решений.

35. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Примеры

Пример 1. Решить систему:
Решение. В данном примере имеем:
1 0 2
А 3 1 0 ,
4 1 3
1 ,
b 1
1
,
A 3 6 8 1 0.
Вычислим:
x 2z 1
3 x y 1
4 x y 3 z 1.
x
x y
z

36. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Примеры

1
0
2
1 1 2
1
0 1
1 1 1 0 3; 2 3 1 0 8; 3 1 1 1.
3
1 1 3
4 1 3
4 1 1
Отсюда находим:
1 3
2 8
1
x
3; y
8; z
1.
1
1
1