ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 1-го и 2-го ПОРЯДКОВ

РАЗЛОЖЕНИЕ ПО ЛЮБОЙ СТРОКЕ (ЛЮБОМУ СТОЛБЦУ)

МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИ-ТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКА

ПРИМЕР ИСПОЛЬЗОВАНИЯ МЕТОДА ТРЕУГОЛЬНИКОВ

ОПРЕДЕЛИТЕЛЬ ТРЕУГОЛЬНОЙ МАТРИЦЫ РАВЕН ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ ГЛАВНОЙ ДИАГОНАЛИ

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА

ОБЩИЙ ВИД СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ

МАТРИЧНЫЙ ВИД СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

ГЛАВНЫЙ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

ПРИМЕНЕНИЕ МЕТОДА КРАМЕРА НА ПРИМЕРЕ СИСТЕМЫ ИЗ 3-х УРАВНЕНИЙ

НЕОБХОДИМОЕ УСЛОВИЕ ПРИМЕНИМОСТИ ФОРМУЛ КРАМЕРА

ФОРМУЛЫ КРАМЕРА ДЛЯ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ

ПРИМЕР РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА

ВЫЧИСЛЕНИЕ ГЛАВНОГО И ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ

362.95K

Category: $mathematics$ mathematics

Определители и их применения

2. ПЛАН

1. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ
МАТРИЦЫ
2. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ
ДОПОЛНЕНИЯ
3. СПОСОБЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛИТЕЛЕЙ
4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
2

3. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ

4. ОБОЗНАЧЕНИЯ

КВАДРАТНАЯ МАТРИЦА n-го ПОРЯДКА
a11
A
a
n1
a1n
ann
ОБОЗНАЧЕНИЯ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
a11
a1n
an1
ann
A det A
4

5. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 1-го и 2-го ПОРЯДКОВ

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1-го ПОРЯДКА
a11 a11
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2-го ПОРЯДКА
a11
a12
a21
a 22
a11 a22 a21 a12
5

6. МНЕМОНИЧЕСКОЕ ПРАВИЛО

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
2-го ПОРЯДКА РАВЕН
ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ
ГЛАВНОЙ ДИАГОНАЛИ
МИНУС
ПРОИЗВЕДЕНИЕ ЭЛЕМЕНТОВ
ПОБОЧНОЙ ДИАГОНАЛИ
6

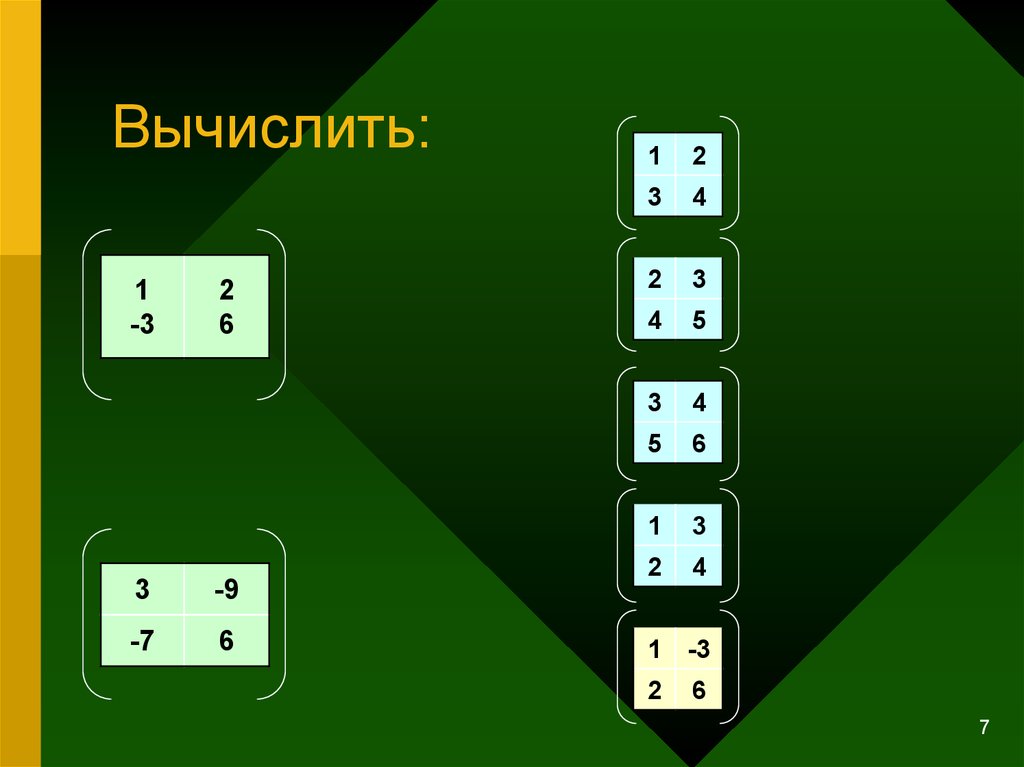
7. Вычислить:

1
-3
2
6
3
-9
-7
6
1
2
3
4
2
3
4
5
3
4
5
6
1
3
2
4
1
-3
2
6
7

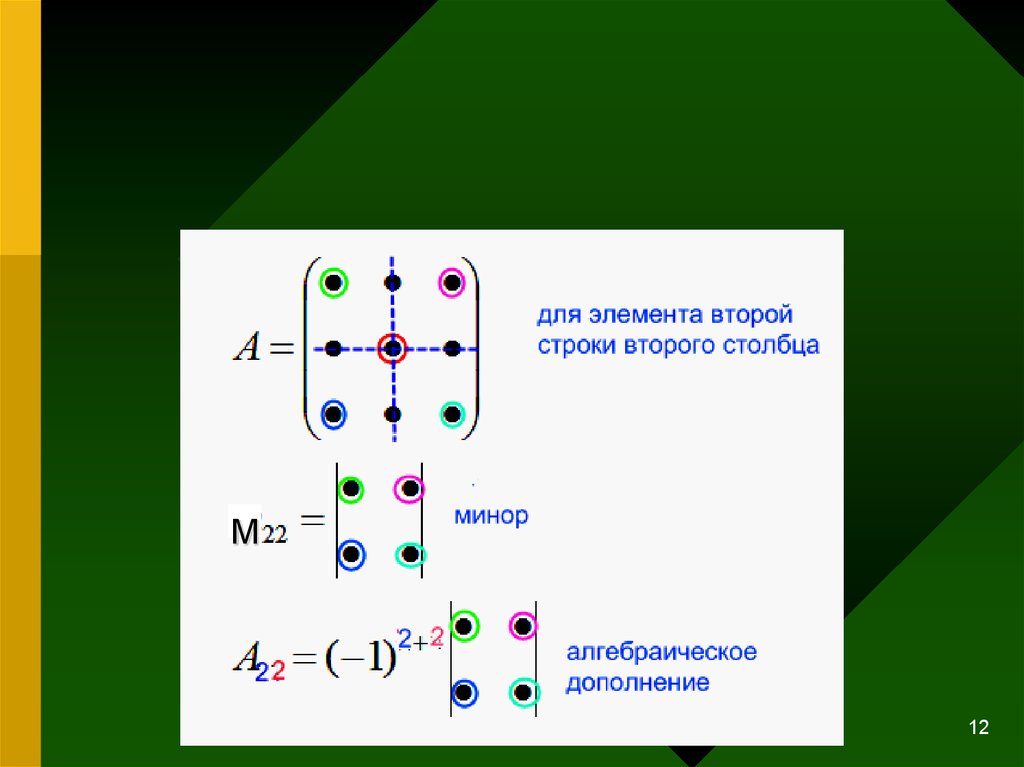
8. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ

9. МИНОР ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯ

МИНОРОМ ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯ
НАЗЫВАЕТСЯ ОПРЕДЕЛИТЕЛЬ,
ПОЛУЧЕННЫЙ ИЗ ИСХОДНОГО
ОПРЕДЕЛИТЕЛЯ ПРИ ПОМОЩИ
ВЫЧЕРКИВАНИЯ СТРОКИ И
СТОЛБЦА, В КОТОРЫХ
СТОИТ ЭТОТ ЭЛЕМЕНТ.
9

10. ПРИМЕР ВЫЧИСЛЕНИЯ МИНОРА

МИНОР M 21 ЭЛЕМЕНТА a21 ОПРЕДЕЛИТЕЛЯ
3
4
7
1 2
2
0
9 1
10

11. АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ

АЛГЕБРАИЧЕСКИМ ДОПОЛНЕНИЕМ Aij
ЭЛЕМЕНТА aij ОПРЕДЕЛИТЕЛЯ
НАЗЫВАЕТСЯ ЧИСЛО
Aij ( 1)
i j
M ij ,
ГДЕ M ij МИНОР ЭЛЕМЕНТА aij
11

13. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ

14. РАЗЛОЖЕНИЕ ПО ЛЮБОЙ СТРОКЕ (ЛЮБОМУ СТОЛБЦУ)

ОПРЕДЕЛИТЕЛЬ
РАВЕН СУММЕ ПРОИЗВЕДЕНИЙ
ЭЛЕМЕНТОВ ЛЮБОЙ СТРОКИ
(ЛЮБОГО СТОЛБЦА) НА ИХ
АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
14

15. ПРИМЕР ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЯ

РАЗЛОЖИМ ОПРЕДЕЛИТЕЛЬ ПО 2-й СТРОКЕ
3
1
4
2
7
9 1
2
4* 2 1
0 ( 1)
1
3
2
( 1) 2 2
0
9 1
1
2
2*
7
1 (3 14) 19 11 8
=4* ( 1) ( 1 18) 2∙
=4∙19-2∙11=
15

Определитель N-го порядка находится по формуле:
где
aij – элемент матрицы;
Мij – минор элемента aij. Минором элемента aij
матрицы А называется определитель матрицы,
которая была получена путем удаления из
матрицы А строк и столбцов, которые содержат
элемент aij
16

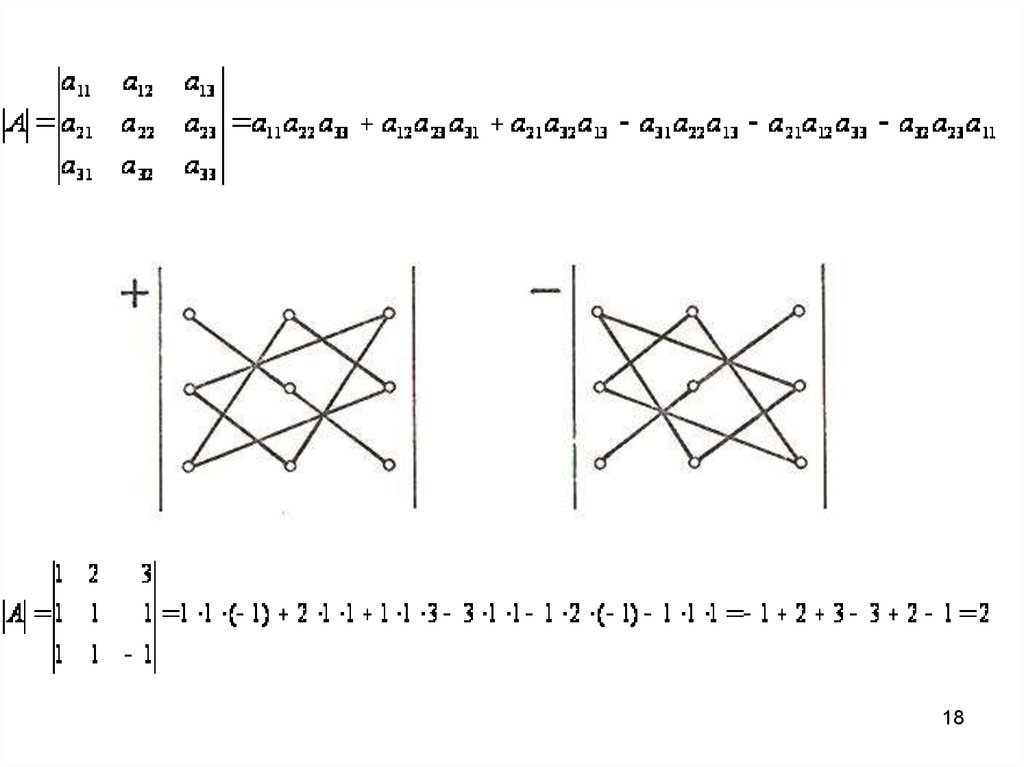
17. МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИ-ТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКА

МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯ
ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКА
a12
a33 a31
a22
a
31
a13
a21
a12
a11
a22
a23 a21
a11
a33
a32
a32
a13
a23
17

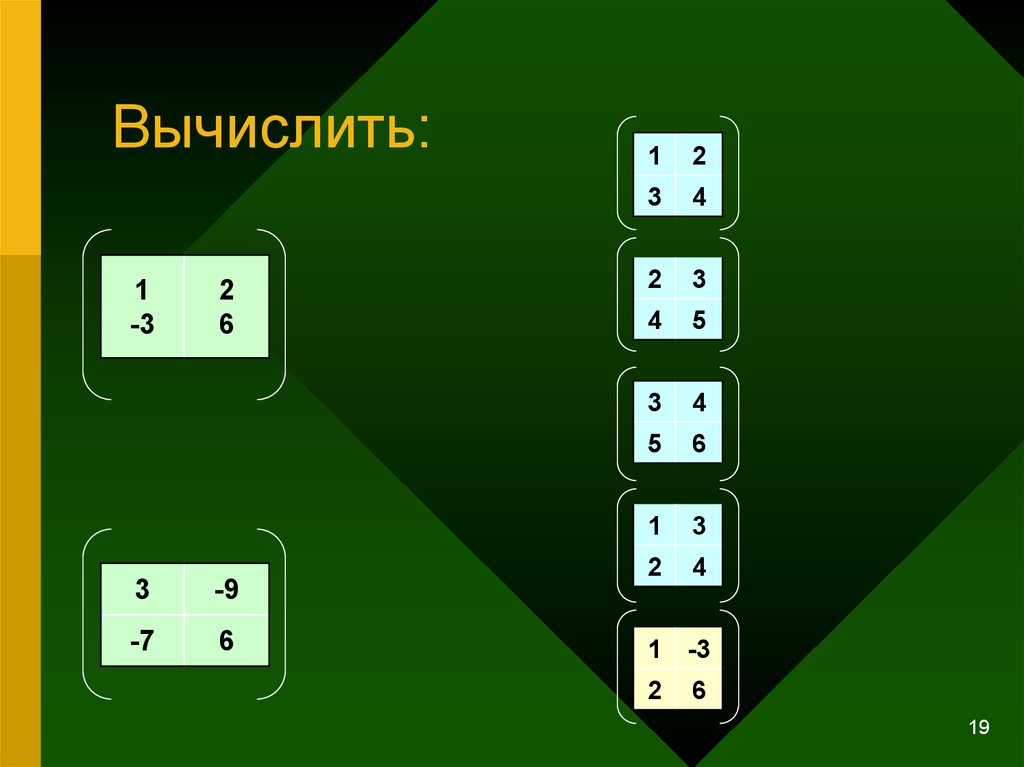
18. 19. Вычислить:

1
-3
2
6
3
-9
-7
6
1
2
3
4
2
3
4
5
3
4
5
6
1
3
2
4
1
-3
2
6
19

20. ПРИМЕР ИСПОЛЬЗОВАНИЯ МЕТОДА ТРЕУГОЛЬНИКОВ

2
3
5
1 3
3
2
4
1
2 1 1 3 ( 3) ( 3) 5 ( 2) 4
4 1 ( 3) 5 3 1 ( 2) ( 3) 2
2 27 40 12 15 12 26
20

21. ОПРЕДЕЛИТЕЛЬ ТРЕУГОЛЬНОЙ МАТРИЦЫ РАВЕН ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ ГЛАВНОЙ ДИАГОНАЛИ

3
0
0
1 2
2
0 3 2 1 6
0 1
21

22.

1
-3
2
2
6
-1
3
-7
3
1
2
3
2
2
1
3
1
3
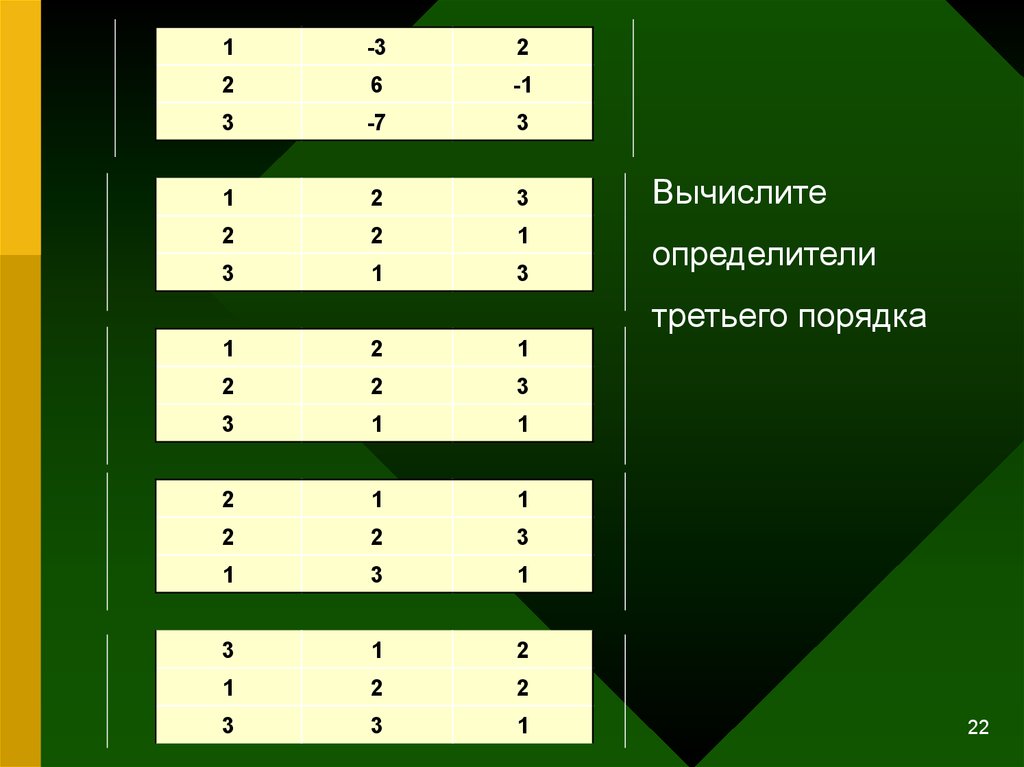
Вычислите
определители
третьего порядка
1
2
1
2
2
3
3
1
1
2
1
1
2
2
3
1
3
1
3
1
2
1
2
2
3
3
1
22

23. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА

24. ОБЩИЙ ВИД СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ

a11 x1 a12 x2
a x a x
21 1
22 2
an1 x1 aт 2 x2
a1n xn b1 ,
a2 n xn b2 ,
ann xn bn
24

25. МАТРИЧНЫЙ ВИД СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

a11
a
21
...
a
n1
a12
...
a22
...
...
...
an 2
...
a1n x1 b1
a2 n
x2
b2
... ... ...
ann xn bn
25

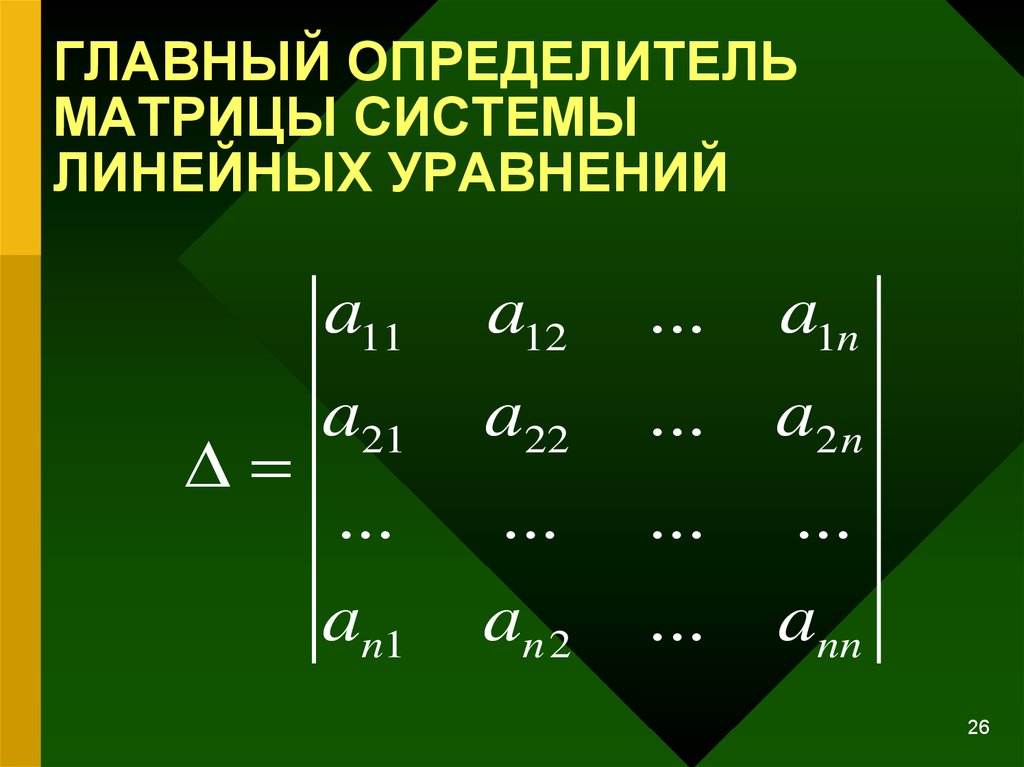
26. ГЛАВНЫЙ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

a11
a12
...
a1n
a21
a22
...
a2 n
...
...
...
...
an1
an 2
...
ann
26

27. ПРИМЕНЕНИЕ МЕТОДА КРАМЕРА НА ПРИМЕРЕ СИСТЕМЫ ИЗ 3-х УРАВНЕНИЙ

a11
a
21
a
31
a12
a22
a32
a13 x1 b1
a23 x2 b2
a33 x3 b3
27

28. НЕОБХОДИМОЕ УСЛОВИЕ ПРИМЕНИМОСТИ ФОРМУЛ КРАМЕРА

a11
a12
a13
a21
a22
a23 0
a31
a32
a33
28

29. ВЫЧИСЛЕНИЕ ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ

b1 a12 a13
a11
1 b2 a22 a23 ; 2 a21
b3 a32 a33
a31
a11
a12
b1
3 a21
a22
b2
a31
a32
b3
b1
a13
b2
a23
b3
a33
29

30. ФОРМУЛЫ КРАМЕРА ДЛЯ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ

1
x1
,
2
x2
,
3
x3
30

31. ПРИМЕР РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА

2 x y 3z 13,
4 x 3 y z 7,
x 2 y 5 z 15
31

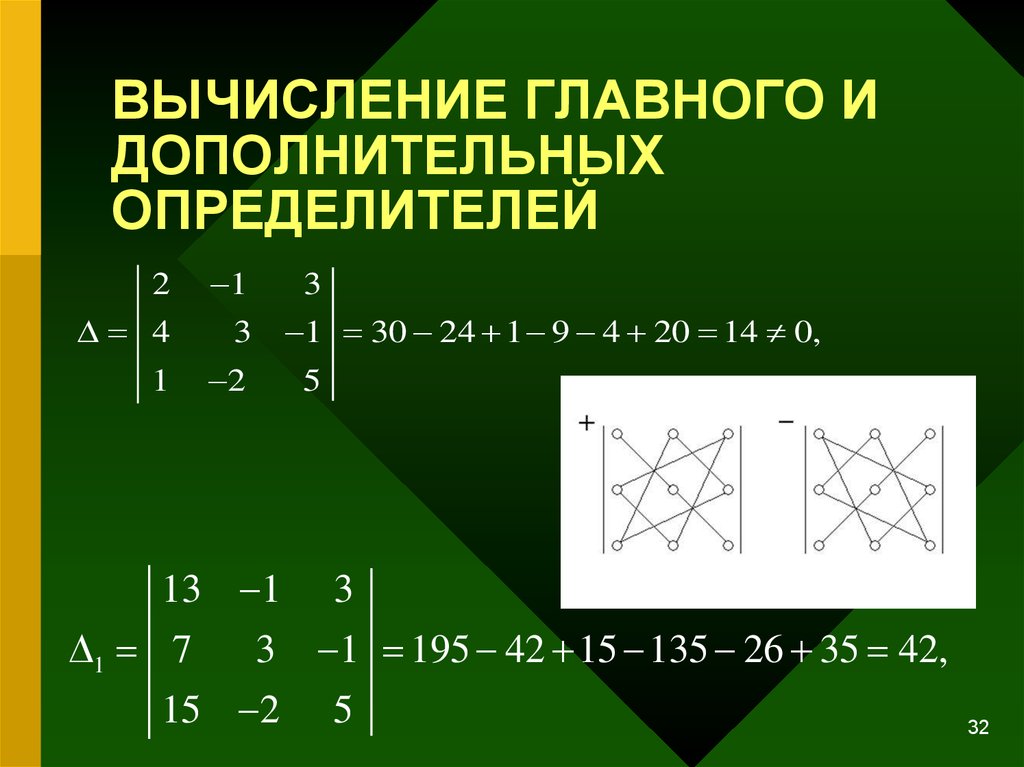
32. ВЫЧИСЛЕНИЕ ГЛАВНОГО И ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ

2
1
4
3
1
2
3
1 30 24 1 9 4 20 14 0,
5
13 1
1 7
3
15 2
3
1 195 42 15 135 26 35 42,
5
32

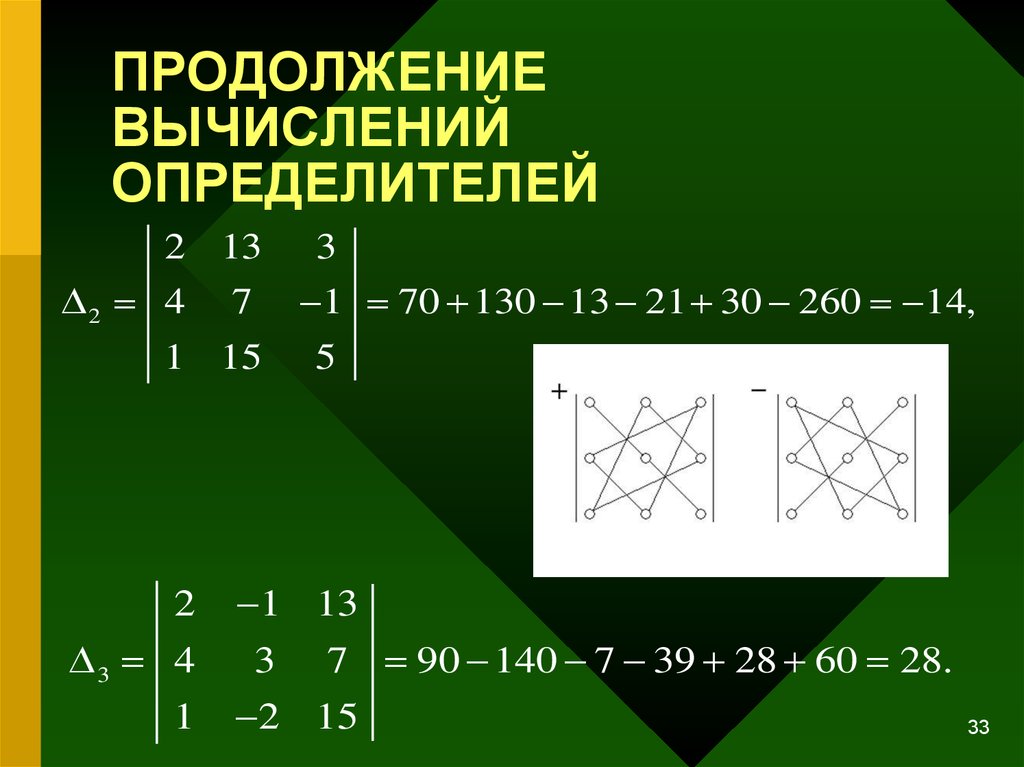
33. ПРОДОЛЖЕНИЕ ВЫЧИСЛЕНИЙ ОПРЕДЕЛИТЕЛЕЙ

2 13
2 4
1 70 130 13 21 30 260 14,
7
1 15
2
3 4
1
3
5
1 13
3
7 90 140 7 39 28 60 28.
2 15
33

34. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ

1 42
x
3,
14
2 14
y
1,
14
3 28
z
2.
14
34