Similar presentations:
Матрицы. Виды матриц. Операции над матрицами. Системы линейных алгебраических уравнений
1. Лекция 1.
МатрицыВиды матриц
Операции над матрицами
Системы линейных
алгебраических уравнений
2. Немного истории
• Ценность научного творчества безгранична.Для общего прогресса человечества
наиболее ценным является творчество,
устанавливающее новые пути, по которым
идут исследователи.
• К числу учёных новаторов принадлежит
гениальный немецкий математик Карл
Фридрих Гаусс. Основная черта научных
работ Гаусса – это их исключительная
разносторонность. Гаусс также считался
одним из создателей неэвклидовой
геометрии.
3.
Он занимался высшей алгеброй, теориейчисел, дифференциальной геометрией,
теорией вероятности, теорией электричества
и магнетизма, вопросами капиллярности,
геодезией и астрономией. Во всех этих
областях Гаусс сделал оригинальные
открытия.
Габриель Крамер – швейцарский математик.
Установив и опубликовав в 1705 году правило
решения систем линейных уравнений с
буквенными коэффициентами, он внёс
значительный вклад в развитие алгебры.
4.
• Матрицей размерностью m x nназывается прямоугольная таблица
чисел (элементов матрицы),
содержащая m строк и n столбцов.
Если m=n, матрицу называют
квадратной матрицей порядка n.
5.
Обозначения:a11
a 21
...
a
m1
a12
a 22
...
am2
... a1n
... a 2 n
... ...
... a mn
a11
a
21
...
a m1
a12
a 22
...
am2
... a1n
... a 2 n
... ...
... a mn
6. Виды матриц
Нулевая матрица0=
0
0
...
0
0
0
...
0
...
...
...
...
0
0
...
0
7.
Матрица, противоположная матрице А-А =
a11
a
21
...
a m1
a12
a 22
...
am2
... a1n
... a 2 n
...
...
... a mn
Трапециевидная
(ступенчатая)
матрица
a11
0
...
0
0
...
0
a12
... a1r
a 22
... a 2 r
...
0
... ...
... a rr
0
...
0
...
0
...
0
...
0
... a1n
... a 2 n
... ...
... a m
... 0
... ...
0 0
8.
Матрица-строка:a11
a12.......
a1n
Матрица-столбец:
Верхняя треугольная
матрица:
a11
0
...
0
a12
a 22
...
0
... a1n
... a 2 n
... ...
... a mn
a11
a
21
.
a m1
9.
Нижняя треугольнаяматрица
Диагональная матрица
a11
a
21
...
a m1
0
a 22
...
am2
a11
0
...
0
0
a 22
...
0
... 0
... 0
... ...
... a mn
... 0
... 0
... ...
... a mn
10.
10
Е = ...
0
Единичная матрица
0
1
...
0
...
...
...
...
0
0
...
1
Если все aij действительные, то матрица А
называется действительной; если хотя бы
одно из чисел aijкомплексное, то матрица
называется комплексной.
11. Операции над матрицами
Суммой матриц А = ( aij) и В = ( bij)одинаковых размеров называется
матрица С = ( cij) тех размеров, у
которой cij =aij + bij , для любых i, j.
aij
bij
C=A+B
bij
cij
12. Свойства сложения матриц:
A +B = B + A
(A +B) +C = A + (B + C)
A+0=A
A + (-A) = 0, для любых А, В, С
одинаковых размеров.
13.
Пример 1: Найти сумму матриц: С = А + ВА=
2 3
1
4 1 6
5 0 1
В =
0 1 2
3 1 3
2 1 0
С=
1 5
1
0 9
7
3 1 1
14. Чтобы вычесть из матрицы А матрицу В, нужно к матрице А прибавить матрицу, противоположную матрице В. А – В = А + (-В)
• Найти разность матриц А – В1
2
• А=
3 4
Решение: С = А – В
2 1
В=
2 3
15.
А= 12
3 4
3
1
С=
5 7
1
2 3
- В = 2
16. Произведением матрицы А = (aij) на число k называется матрица С = (cij) тех же размеров, у которой cij = k · aij для любых i,j.
C=k·A• Пример 3: Дана матрица
1 2 1
А = 2 3 0
2 4 2
• Тогда 2А = 4 6 0
6 4 10
3 2
5
17. Свойства умножения матрицы на число:
1)1 A A
2) ( A) ( ) A
3) ( A B) A B
4) ( ) A A A
для любых А,В одинаковых размеров, любых α, β R
18. Произведением матрицы А = ( ) размеров mхn на матрицу В = ( ) размеров nхp называется матрица С = (cij) размеров mхp, = a i1 b
Произведением матрицы А = ( aik ) размеровmхn на матрицу В = ( bkj) размеров nхp
называется матрица С = (cij) размеров mхp,
= a i1 b 1j + a i2 b 2 j + … + a in b n j .
C = AB
Свойства умножения матриц:
AE = EA = A
A0 = 0A = 0
(AB)D = A(BD)
(A + B)D = AD + BD
D(A + B) = DA + DB (при условии, что все указанные
операции имеют смысл). Для квадратных матриц
АВ≠ВА
( AB) ( A) B A( B)
19.
Даны матрицы:1
3 2
А =
5 2 1
и В=
1
2
0
С = АВ
3 4 0
С =
5 4 0
1
С =
9
20. Транспонирование матриц.
a11a
А= 21
...
a m1
T
A
a12
a 22
...
am2
... a1n
... a 2 n
... ...
... a mn
т =
А
a11
a
21
...
a1n
– транспонированная матрица.
a12
a 22
...
a2n
... a m1
... a m 2
... ...
... a mn
21. Свойства транспонирования
1. ( A ) AT T
2. ( A)
T
A
3. ( A B)
T
T
A B
T
4. ( AB) B A
T
T
T
T
22. Обратная матрица.
1• Матрица A
1
называется обратной для матрицы А, если
1
• A A = A A =E
A11... A21... An1
A ... A ... A
1 12
22
n2
1
A
...
...
det A ...
A1n ... A2 n ... Amn
23. Aij – алгебраические дополнения элементов aij матрицы А.
Свойства обратной матрицы:1 1
• 1. ( A ) A
• 2.
• 3.
( AB)
1
B A
1
1
det A
det A
1
1
24. Ранг матрицы
• Ранг матрицы – наивысшийпорядок отличных от нуля её
миноров.
• Обозначение: rang A, rgA
25.
Теорема.Ранг матрицы не изменяется
элементарных преобразованиях матрицы.
при
Элементарные преобразования матрицы:
1) Отбрасывание нулевой строки(столбца)
2) Умножение
всех
элементов
строки(столбца)
матрицы на число не равное нулю
3) Изменение порядка строк(столбцов) матрицы
4) Прибавление
к
каждому
элементу
одной
строки(столбца) соответствующих элементов другой
строки(столбца), умноженных на любое число
5) Транспонирование матрицы
26.
Определители квадратных матрицМиноры
Алгебраические дополнения
27. Определители
Обозначение: , det A(детерминант).
Они существуют у квадратных матриц.
Определение 1. Определителем
второго порядка
называется выражение
a1
b1
a2
b2
a1b2 a2b1 .
28. Определитель матрицы второго порядка
Определителем матрицы второго порядка , илиопределителем второго порядка, называется число,
равное разности произведения элементов главной и
побочной диагоналей.
a1
a2
b1
a1 b2 a2 b1
b2
1 3
7 9
29. Определитель матрицы
a1b1
a2 b2
1 3
7 9
a1 b2 a2 b1
1 9 7 3 9 21 12
3 3
3 8 6 3 24 18 6
6 8
30.
Свойства определителей:1. Если в определителе какие-либо две строки
(столбца) равны между собой, то такой
определитель равен 0.
2. Общий множитель всех элементов какой-либо
строки (или столбца) можно выносить за знак
определителя.
3. Если поменять в определителе местами какиелибо две строки (столбца), то определитель
меняет знак.
4. Если все элементы какой-либо строки (столбца)
определителя равны 0, то такой определитель
равен 0.
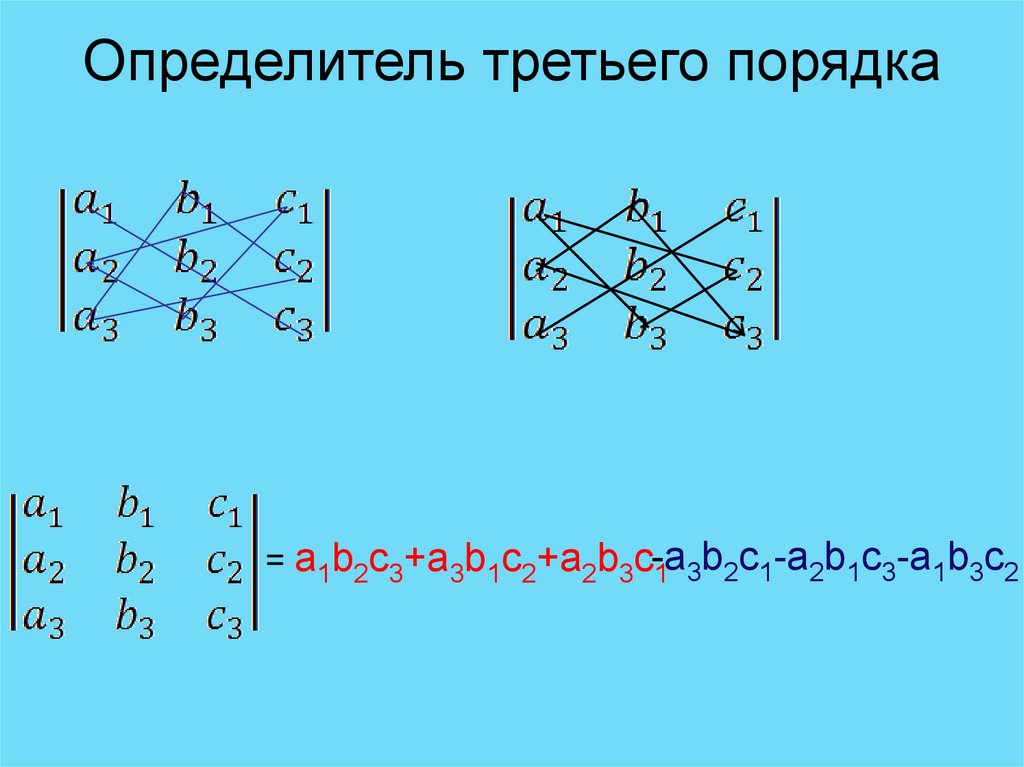
31. Определитель матрицы третьего порядка
Определителем матрицы третьегопорядка, или определителем третьего
порядка, называется число, которое
вычисляется по формуле:
= a1⋅b2⋅c3
⋅
+ a3⋅b1⋅c2 + a2⋅b3⋅c1 - a3⋅b2⋅c1 - a2⋅b1⋅c3- a1⋅b3⋅c2
32. Определитель третьего порядка
= a1b2c3+a3b1c2+a2b3c-a1 3b2c1-a2b1c3-a1b3c2
33.
Определитель третьего порядка= a1b2c3+a3b1c2+a2b3c1-a3b2c1-a2b1c3-a1b3c2
=6⋅1⋅2 +(-2) ⋅3⋅(-3) +4⋅(-3) ⋅0-(-2) ⋅1⋅0 -4⋅3⋅2-6⋅(-3) ⋅(-3) =-48
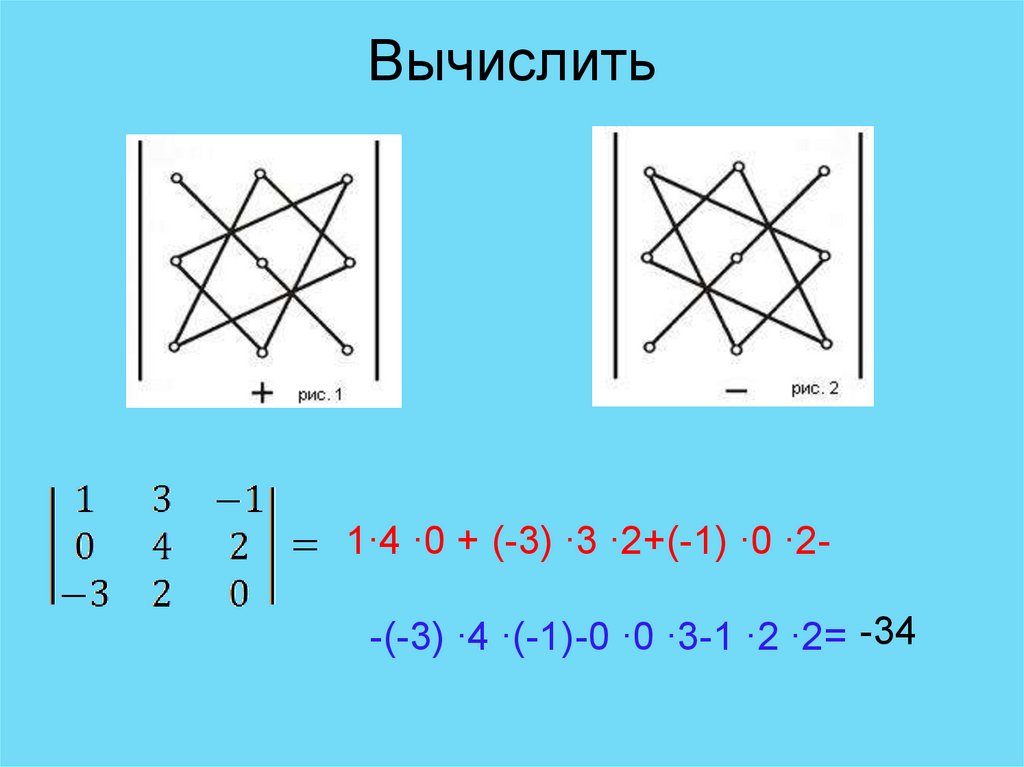
34. Вычислить
1∙4 ∙0 + (-3) ∙3 ∙2+(-1) ∙0 ∙2-(-3) ∙4 ∙(-1)-0 ∙0 ∙3-1 ∙2 ∙2= -3435. Вычислить
836. Способы вычисления определителя третьего порядка
a1 b1a2 b2
a3 b3
c1
c2
c3
=
a1
b2
c2
b3
c3
где a1 , b1 , c1 , a 2 , b2 , c2 , a3 , b3 , c3
b2
b3
c2 a2
,
c3 a 3
c2 a2
,
c3 a 3
b1
a2
c
a3
c3
c1
a2
b2
a3
b3
,
- элементы определителя,
b2
b3
- миноры элементов а1, b1, c1
37.
Минором Мij какого – либо элемента aijопределителя порядка n называется
определитель порядка n – 1,
полученный из вычерчиванием i– й
строки и j – го столбца. Это первый
способ.
a11
a 21
...
a12
a 22
...
... a1n
... a 2 n
... ...
a n1
an 2
... a nn
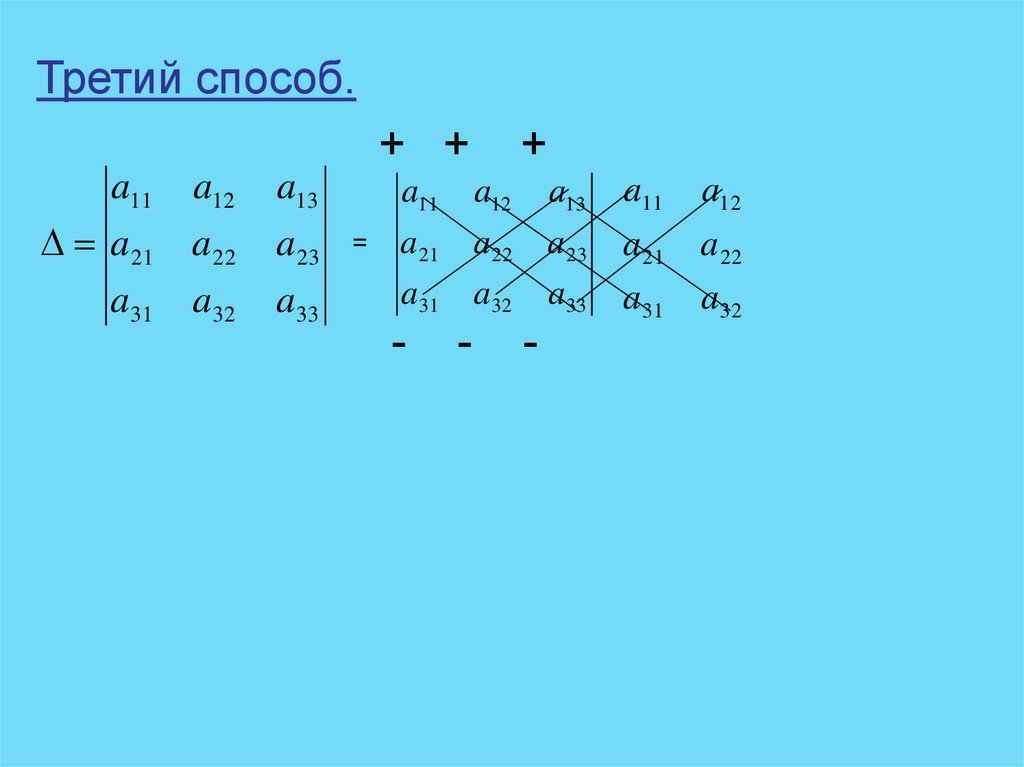
38.
Третий способ.+ +
a11
a 21
a31
a12
a 22
a32
a13
a 23
a33
=
a11
a 21
a31
-
+
a12
a 22
a32
-
a13
a 23
a33
-
a11
a12
a 21
a 22
a31
a32
39. Алгебраическое дополнение
• Алгебраическим дополнением элементааij определителя называется
определитель Ay ( 1) i j M y , где Мy
– минор элемента aij.
Для нахождения определителя III
порядка можно использовать две
теоремы.
40. Теорема 1.Определитель равен сумме произведений элементов какой – либо строки на их алгебраические дополнения
a1 A1 b1 B1 c1C1 (1)a 2 A2 b2 B2 c 2 C 2 (2)
a3 A3 b3 B3 c3C3 (3)
41. Теорема 2. Определитель равен сумме произведений элементов какого – либо столбца на их алгебраические допол-нения.
Теорема 2. Определитель равен суммепроизведений элементов какого – либо
столбца на их алгебраические дополнения.
a1 A1 a 2 A2 a3 A3 (4)
b1 B1 b2 B2 b3 B3 (5)
c1C1 c 2 C 2 c3C3 (6)
42. Пример 5: Найти определитель:
2 1 2Пример 5: Найти определитель: 0 3 1
1 1 3
2 2
52 1
3 ( 1)
1 ( 1)
3(6 2) ( 2 1) 3 4 3 15
1 3
1 1
4
43.
Определителем четвёртого порядкаa1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
d4
называется
выражение a1 A1 b1 B1 c1C1 d1 D1 , где
A1, B1, C1, D1 - алгебраические
дополнения элементов a1, b1, c1, d1.
44.
Решение систем линейных уравненийметодом Крамера
45.
Пусть дана система:a11 x1 a12 x 2 ... a1n x n b1 ,
a x a x ... a x b ,
21 1
22 2
2n n
2
...............................................
a m1 x1 a m 2 x 2 ... a mn x n bm
Составим матрицу А из коэффициентов при неизвестных
a11
a 21
A
...
a
m1
a12
a 22
...
am2
... a1n
... a 2 n
... ...
... a mn
46.
Найдём определительdet A=
a11
a 21
...
a m1
a12
a 22
...
am2
... a1n
... a 2 n
... ...
... a mn
Правило Крамера. Если m=n и det A≠0, то система
совместна и имеет единственное решение
det Ai
xi
,
det A
где det Ai – определитель, полученный из det A
заменой i-ого столбца столбцом свободных
членов.
47. Решение системы линейных уравнений :
Находим определитель системы .Вычисляем определители х1, x2, …
Возможны три случая:
Если ≠0, то система имеет
x2
x1
,...
x1
, x2
единственное решение:
Если =0, но хотя бы один из
определителей хi не равен нулю, то система
не имеет решений.
• Если =0, х1=0, х2=0, …, хn=0, то
система имеет бесконечное множество
решений.
48. Решение систем уравнений с двумя переменными
a1 x b1 y c1a2 x b2 y c2
x
c1
b1
c2
b2
x
x
y
a1
b1
a2
b2
a1
c1
a2
c2
y
y
49. Решение систем уравнений с двумя переменными
a1 x b1 y c1a2 x b2 y c2
5 x 3 y 7
2 x 3 y 7
5 3
5 3 2 3
2 3
21 0
a1
b1
a2
b2
7 3
7 3 7 3 21 21 42
x
7 3
50.
5 x 3 y 72 x 3 y 7
5 3
5 3 2 3 21 0
2 3
7 3
7 3 7 3 42
x
42
x
7 3
x
2
5 7
5 7 2 7 21
y
2 7
y
21
21
1
y
21
51.
x 7 y 152 x y 4
1 7
1 2 7 1 14 13 0
2 1
15 7 15 28 13
x
x
4 1
x
1
1 15
4 30 26
y
2 4
y
y
2
52.
Пример. Решить систему:Решение:
2 x 3 y 5,
x 3 y 2
2 3
6 3 3 x 5 3 15 6 9
1 3
2 3
2 5
y
4 5 1
1 2
9
x 3
3
1
y
3
53. Решение систем уравнений с тремя переменными
zy
x
a1 x b1 y c1 z d1
z
y
x
a2 x b2 y c2 z d 2
a x b y c z d
3
3
3
3
a1 b1 c1
a2 b2 c2
a3 b3 c3
d1
x d2
d3
b1
b2
b3
c1
c2
c3
a1
y a2
a3
d1
d2
d3
c1
c2
c3
a1
z a2
a3
b1
b2
b3
d1
d2
d3
54. Решение систем линейных уравнений с тремя переменными
zy
x
3 x 2 y 4 z 8
z
y
x
2 x 4 y 5 z 11
4 x 3 y 2 z 1
3 2 4
2 4 5 19
4 3 2
55. Решение систем уравнений с тремя переменными
zy
x
3x 2 y 4 z 8
z
y
x
2 x 4 y 5 z 11
4 x 3 y 2 z 1
3 2 4
2 4 5 19
4 3 2
8 2 4
x 11 4 5
1 3 2
56. Решение систем уравнений с тремя переменными
3 x 2 y 4 z 8z
y
x
z
y
x
2 x 4 y 5 z 11
4 x 3 y 2 z 1
19
8 2 4
x 11 4 5 38
1 3 2
x 38
x
2
19
57. Решение систем уравнений с тремя переменными
zy
3x 2 y 4 z 8
z
y
x 2
2 x 4 y 5 z 11
4 x 3 y 2 z 1
19
3 2 4
2 4 5 19
4 3 2
3 8 4
y 2 11 5
4 1 2
58. Решение систем уравнений с тремя переменными
3x 2 y 4 z 82 x 4 y 5 z 11
4 x 3 y 2 z 1
3 8 4
y 2 11 5 57
4 1 2
x 2
y 3
19
y
57
y
3
19
z
z
59. Решение систем уравнений с тремя переменными
3x 2 y 4 z 82 x 4 y 5 z 11
4 x 3 y 2 z 1
3 2 4
2 4 5 19
4 3 2
3 2 8
z 2 4 11
4 3 1
x 2
19
y 3
z
z
60. Решение систем уравнений с тремя переменными
3x 2 y 4 z 82 x 4 y 5 z 11
4 x 3 y 2 z 1
3 2 8
z 2 4 11 19
4 3 1
x 2
y 3
19
z 19
z
1
19
z 1
61. Решение систем уравнений с тремя переменными
3x 2 y 4 z 82 x 4 y 5 z 11
4 x 3 y 2 z 1
x 2
Проверка
3 2 2 3 4 1 6 6 4 8
2 2 4 3 5 1 4 12 5 11
4 2 3 3 2 1 8 9 2 1
y 3
z 1
62.
Пример 2. Решить систему: 2 x x x 2,1
2
3
x1 x2 5 x3 7,
2 x 3x 3x 14
2
3
1
Решение:
2 1 1
2 1 1 2 1
1 1 5 1 1 5 1 1 6 10 21 14 30 21 22
2 3 3 2 3 3 2 3
63.
Находим:х1,
х2,
х3.
2 1 1
2 1 1 2 1
x1 7 1 5 7 1 5 7 1 6 70 21 14 30 21 22
14 3 3 14 3 3 14 3
2 2
1
2 2
1 2 2
x 2 1 7 5 1 7 5 1 7 42 20 14 14 140 6 44
2 14 3 2 14 3 2 14
2 1 2
2 1 2 2 1
x3 1 1 7 1 1 7 1 1 28 14 6 4 42 14 44
2 3 14
2 3 14 2 3
64.
Применяем формулы Крамера:x1 22
x1
1
22
x2 44
x2
2
22
x3
44
x3
2
22
х1=1;
х2=2;
х3=-2
65.
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХУРАВНЕНИЙ С ПОМОЩЬЮ
ОБРАТНОЙ МАТРИЦЫ
66.
Дана система (1):a11
A a 21
a31
a12
a 22
a32
a11 x1 a12 x2 a13 x3 b1
a 21 x1 a 22 x2 a 23 x3 b2
a x a x a x b
32 2
33 3
3
31 1
a13
x1
b1
a 23 ; X x2 ; B b2
x3
b3
a33
Матричная запись системы линейных уравнений имеет
1
вид(2): АХ=В Отсюда: Х= A 1 B , где А
матрица,
обратная матрице А.
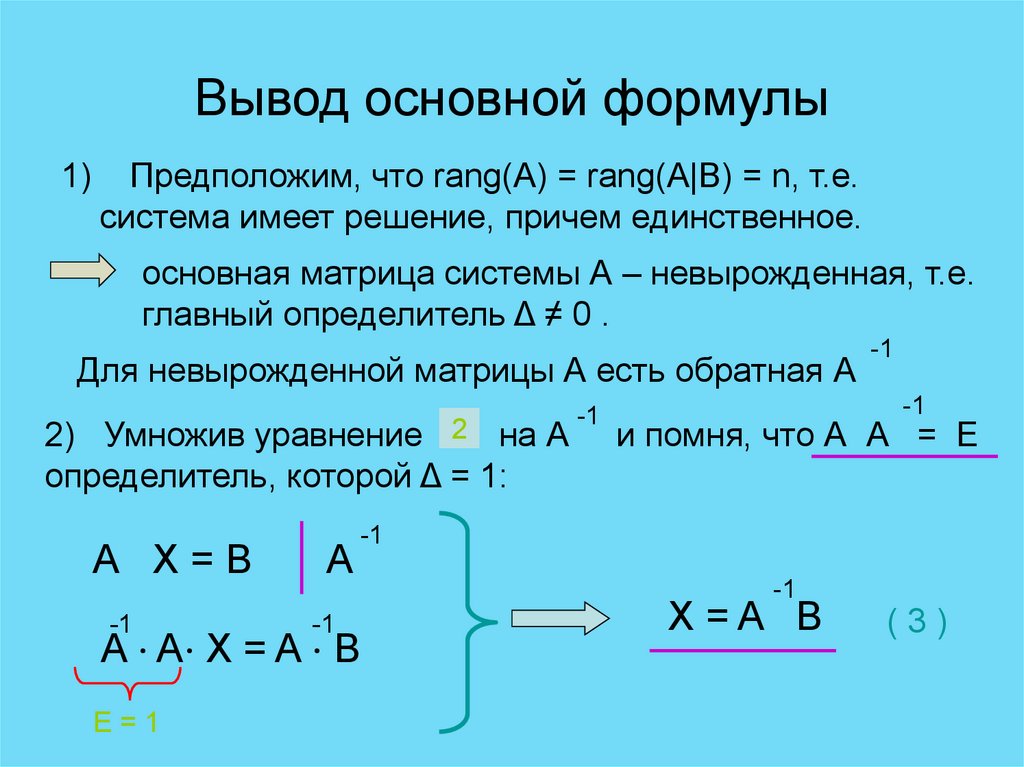
67. Вывод основной формулы
1)Предположим, что rang(A) = rang(A|B) = n, т.е.
система имеет решение, причем единственное.
основная матрица системы А – невырожденная, т.е.
главный определитель Δ ≠ 0 .
Для невырожденной матрицы А есть обратная А
2) Умножив уравнение 2 на А
определитель, которой Δ = 1:
А Х=В
Α
-1
-1
A ⋅ A⋅ X = A ⋅ B
Е=1
-1
-1
-1
и помня, что А А = Е
-1
-1
Χ=Α Β
(3)
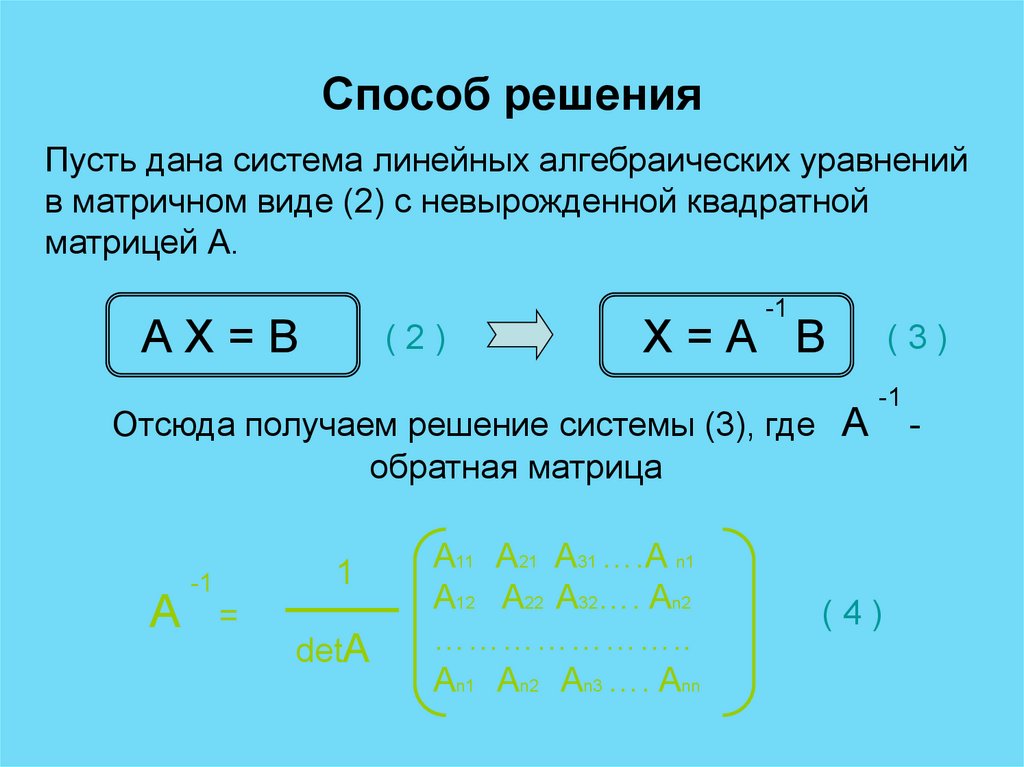
68. Способ решения
Пусть дана система линейных алгебраических уравненийв матричном виде (2) с невырожденной квадратной
матрицей А.
-1
АХ=В
(2)
Х=А В
Отсюда получаем решение системы (3), где А
обратная матрица
А
1
-1
=
detА
A11 A21 A31 ….A n1
A12 A22 A32…. An2
…………………..
An1 An2 An3 …. Ann
(3)
-1
(4)
-
69. Рассмотрим пример 1
Задание.Найти решение системы
с помощью обратной матрицы.
Х1 + Х2 = 3
Х1 – Х2 = 1
Решение.
1) Запишем систему в матричном виде
А=
1 1
1 -1
1 1
1 -1
Х1
Х2
Х=
Х1
Х2
=
3
1
В=
АХ=В
3
1
- матричный вид системы
70.
2) Получаем решение системы-1
где А - обратная матрица
-1
А =
1
Δ
A11 A21
A12 A22
-1
Х=А В
где Δ - главный определитель системы,
Аij – алгебраические дополнения
3) Вычислим обратную матрицу
Δ=
-1
А =
1 1
1 -1
1
-2
= -1-1 = -2 ≠ 0
-1 -1
-1 1
1
=
2
А – невырожденная матрица
1
1
1
-1
71.
-13) Найдём решение системы
Х=А В
1
1
-1
Х=А В =
2
1 1
1 -1
Ответ: Х1 = 2 ; Х2 = 1
3
1
=
2
4
2
=
2
1
72.
Пример 2. Решить с помощью обратной матрицысистему уравнений:
Решение:
Находим определитель
2 x1 x 2 x3 2
x1 x 2 5 x3 7
2 x1 3 x 2 3 x3 14
(det A)
2 1 1 2 1
1 1 5 1 1 6 10 3 2 30 3 22
2 3 3 2 3
Если
= 0, то система не имела бы решения.
73.
Вычислим алгебраические дополнения для элементовкаждой строки.
3 15 18
2 1
A22 ( 1)
6 2 8
2 3
1 5
A12 ( 1)
( 3 10) 13
2 3
2 1
A23 ( 1)
(6 2) 4
2 3
A11 ( 1)
2
1
5
3 3
3
A13 ( 1) 4
1 1
3 2 1
2 3
1 1
A21 ( 1)
( 3 3) 6
3 3
3
4
5
1 1
A31 ( 1)
5 1 4
1 5
4
2 1
A32 ( 1)
(10 1) 3
1 5
5
2 1
A33 ( 1)
2 1 1
1 1
6
74.
Составляем обратную матрицу:18 6 4
1
1
A
13
8
9
22
1
4
1
2
B 7
14
4 2
18 6
1
X 13 8 9 7
22
4 1 14
1
18 2 6( 7) 4 14
22 1
1
1
13 2 ( 8)( 7) ( 9)14 44 2
22
22
2
1
2
(
4
)(
7
)
1
14
44
Отсюда:
x1 1
x2 2
x 2
3
75. Рассмотрим пример 3
Задание.Найти решение системы
с помощью обратной матрицы.
Решение.
1) Запишем систему в матричном виде
1 2 -1
А = 2 -1 1
1 1 2
Х=
Х1
Х2
Х3
В=
2) Составим матричное уравнение
АХ=В
4
1
5
1 2 -1
2 -1 1
1 1 2
Х=
4
1
5
76.
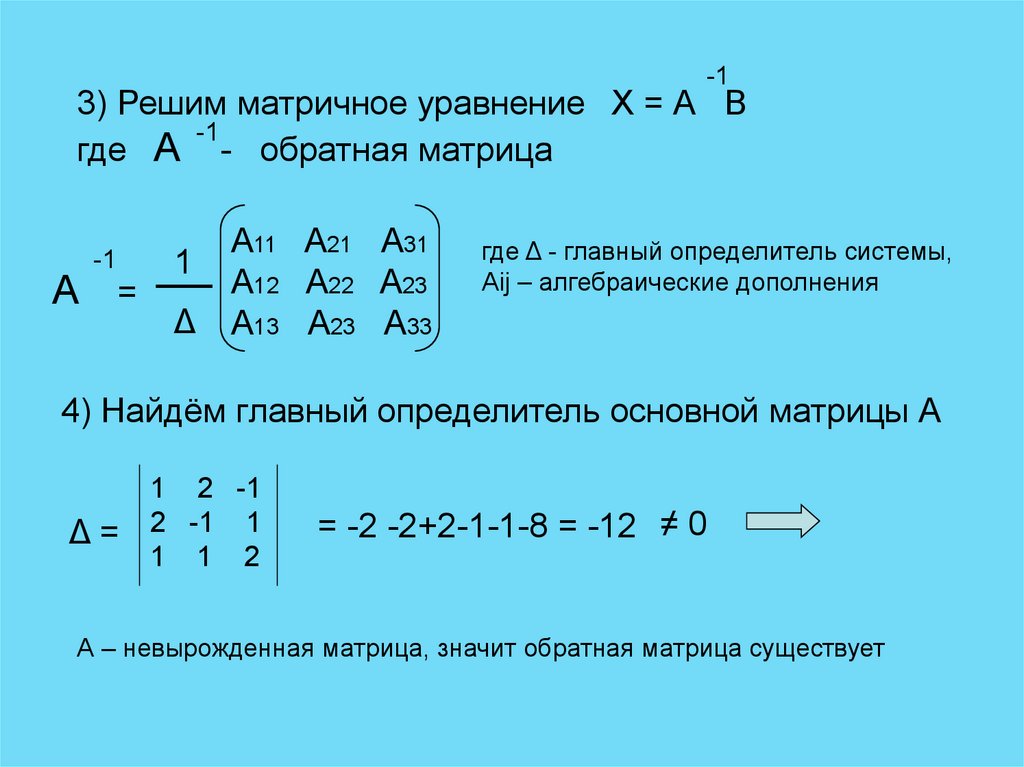
-13) Решим матричное уравнение Х = А В
-1
где А - обратная матрица
-1
А =
A11 A21 А31
1
A12 A22 А23
Δ А13 А23 А33
где Δ - главный определитель системы,
Аij – алгебраические дополнения
4) Найдём главный определитель основной матрицы А
Δ=
1 2 -1
2 -1 1
1 1 2
= -2 -2+2-1-1-8 = -12 ≠ 0
А – невырожденная матрица, значит обратная матрица существует
77.
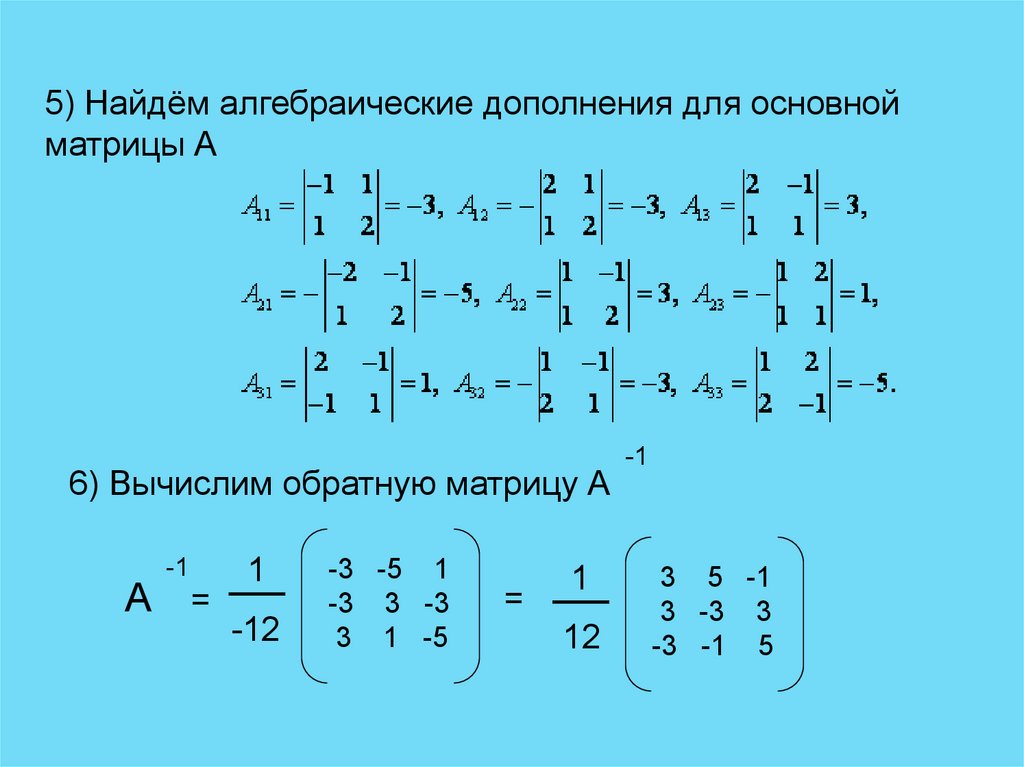
5) Найдём алгебраические дополнения для основнойматрицы А
6) Вычислим обратную матрицу А
-1
А =
1
-12
-3 -5 1
-3 3 -3
3 1 -5
=
1
12
-1
3 5 -1
3 -3 3
-3 -1 5
78.
7) Найдём неизвестную матрицу Х, которая являетсярешением данной системы
-1
Х=А В =
1
3 5 -1
3 -3 3
-3 -1 5
12
=
1
12
12
24
12
=
1
2
1
=
Х1
Х2
Х3
Ответ: Х1 = 1 ; Х2 = 2 ; Х3 = 1
4
1
5
=
1
12
12+5-5
12-3+15
-12-1+25
=
79. Рассмотрим пример 4
Задание.Найти решение системы
с помощью обратной матрицы.
Решение.
1) Запишем систему в матричном виде
1 -3
А = 1 -1
1 -2
4
7
1
Х=
Х1
Х2
Х3
В=
2) Составим матричное уравнение
АХ=В
6
7
2
1 -3
1 -1
1 -2
4
7
1
Х=
6
7
2
80.
-13) Решим матричное уравнение Х = А В
-1
где А - обратная матрица
-1
А =
A11 A21 А31
1
A12 A22 А23
Δ А13 А23 А33
где Δ - главный определитель системы,
Аij – алгебраические дополнения
4) Найдём главный определитель основной матрицы А
Δ=
1 -3
1 -1
1 -2
4
7
1
= 1∙13 + 1∙(-5) + 1∙(-17) = -9 ≠ 0
А – невырожденная матрица, значит обратная матрица существует
81.
5) Найдём алгебраические дополнения для основнойматрицы А
6) Вычислим обратную матрицу А
-1
А =
1
-9
13 -5 -17
6 -3 -3
-1 -1 2
=
1
9
-1
-13
-6
1
5
3
1
17
3
-2
82.
7) Найдём неизвестную матрицу Х, которая являетсярешением данной системы
-1
Х=А В =
1
9
=
1
9
-9
-9
9
=
-13
-6
1
-1
-1
1
5
3
1
17
3 ∙
-2
=
Х1
Х2
Х3
Ответ: Х1 = -1 ; Х2 = -1 ; Х3 = 1
6
7
2
=
1
9
-78+35+34
-36+21+6
6+7-4
=
83. Итак, для этого метода нужно:
Найти и посчитать матрицу, обратную дляосновной матрицы системы
(если она существует);
умножить полученную матрицу на матрицустолбец свободных членов
полученная в результате умножения тоже
матрица-столбец и есть решение системы.
84.
Теорема.Ранг матрицы не изменяется
элементарных преобразованиях матрицы.
при
Элементарные преобразования матрицы:
1) Отбрасывание нулевой строки(столбца)
2) Умножение
всех
элементов
строки(столбца)
матрицы на число не равное нулю
3) Изменение порядка строк(столбцов) матрицы
4) Прибавление
к
каждому
элементу
одной
строки(столбца) соответствующих элементов другой
строки(столбца), умноженных на любое число
5) Транспонирование матрицы
85. Вычисление ранга матрицы с помощью метода элементарных преобразований
Задание.Найти ранг матрицы
А=
0 4 10 1
4 8 18 4
10 18 40 17
1 7 17 3
Решение.
Шаг 1. Из третий строчки вычтем вторую, умножив
её на число два ( преобразование 3)
0 4 10 1
0
4
10
1
4 8 18 4
4
8
18
4
10 18 40 17 ⇔ 10-4 2 18-8 2 40-18 2 17-7 2 ⇔
1 7 17 3
1
7
17
3
ПРЕОБРАЗОВАНИЕ 3
0
4
2
1
4
8
2
7
10
18
4
17
1
4
3
3
86.
Шаг 2. От второй строки отнимаем четвертую,умноженную на число четыре ( преобразование 3)
0
4
2
1
4
8
2
7
10
18
4
17
1
4
3
3
⇔
0
4
10
1
0 4 10 1
4-1 4 8-7 4 18-17 4 4-3 3 ⇔ 0 -20 -50 -5
2
2
4
3
2
2
4 3
1
7
17
3
1
7 17 3
Шаг 3. От третий строки отнимаем четвертую,
умноженную на число два ( преобразование 3)
0 4 10 1
0 -20 -50 -5
2
2
4 3
1
7 17 3
0
4
0
-20
⇔ 2-1 2 2-7 2
1
7
10
1
-50
-5
4-17 2 3-3 2 ⇔
17
3
ПРЕОБРАЗОВАНИЕ 3
0 4 10 1
0 -20 -50 -5
0 -12 -30 -3
1 7 17 3
87.
Шаг 4. Ко второй строке прибавим первую, умноженнуюна число пять ( преобразование 3)
0 4 10 1
0
4
10
1
0 4 10 1
0 -20 -50 -5 ⇔ 0-0 5 -20+4 5 -50+10 5 -5+1 5
0 0 0 0
⇔
0 -12 -30 -3
0
-12
-30
-3
0 -12 -30 -3
1 7 17 3
1
7
17
3
1 7 17 3
Шаг 5. К третьей строке прибавим первую, умноженную
на число три ( преобразование 3)
0 4 10 1
0 0 0 0
0 -12 -30 -3
1 7 17 3
0
4
10
1
0
0
0
0
0
0
⇔ 0+0 3 -12+ 4 3 -30+10 3 -3+1 3 ⇔ 0
1
7
17
3
1
ПРЕОБРАЗОВАНИЕ 3
4 10
0 0
0 0
7 17
1
0
0
3
88.
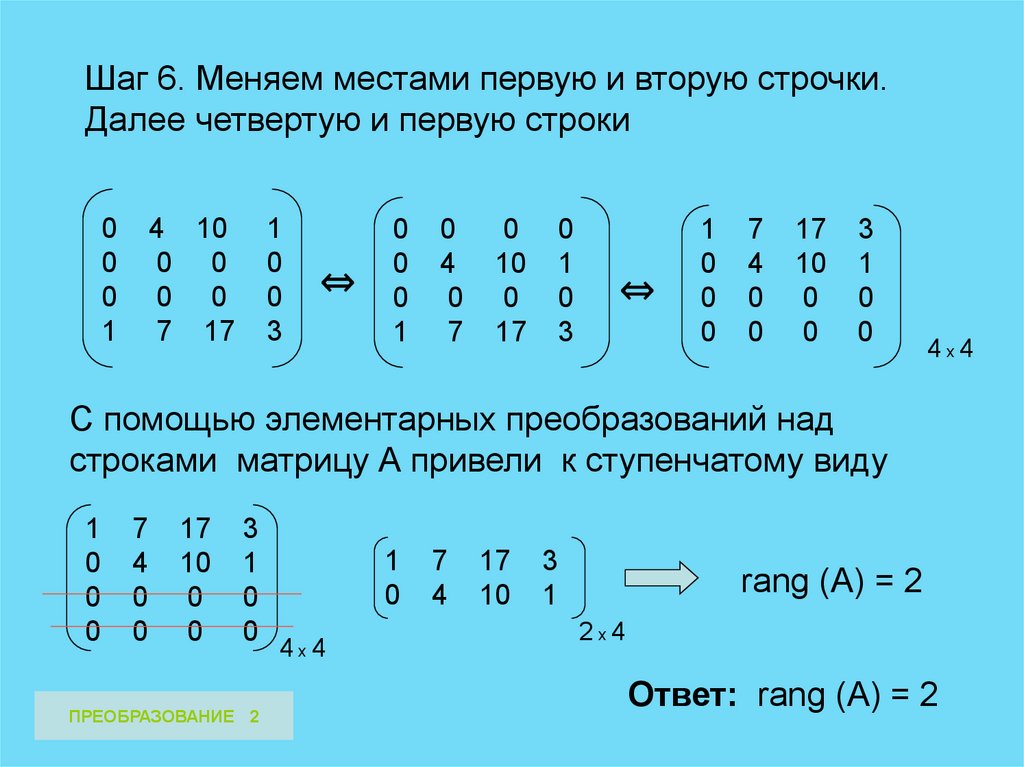
Шаг 6. Меняем местами первую и вторую строчки.Далее четвертую и первую строки
0
0
0
1
4 10
0 0
0 0
7 17
1
0
0
3
⇔
0
0
0
1
0
4
0
7
0
10
0
17
0
1
0
3
⇔
1
0
0
0
7
4
0
0
17
10
0
0
3
1
0
0
4х4
С помощью элементарных преобразований над
строками матрицу А привели к ступенчатому виду
1
0
0
0
7
4
0
0
17
10
0
0
3
1
0
0
ПРЕОБРАЗОВАНИЕ 2
1
0
4х4
7
4
17
10
3
1
rang (A) = 2
2х4
Ответ: rang (A) = 2
89.
90.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХУРАВНЕНИЙ МЕТОДОМ
ГАУССА.
91. Метод Гаусса – метод последовательного исключения переменных.
Пусть задана система:a11 x1 a12 x 2 ... a1n x n b1 ,
a x a x ... a x b ,
21 1
22 2
2n n
2
...............................................
a s1 x1 a s 2 x 2 ... a sn x n bs
92.
1. Составим расширенную матрицу.
2. С помощью элементарных преобразований строк
расширенную матрицу приведём к треугольному
(ступенчатому) виду.
3. Вернувшись к системе уравнений, находим
неизвестные.
Элементарными преобразованиями матрицы
называют:
Умножение какой-нибудь строки (столбца) на
отличное от нуля число.
Прибавление к какой-нибудь строке (столбцу)
другой её строки (столбца), умножение на любое
число, отличное от нуля.
Перестановку местами любых двух строк.
93. Пример 6. Решить систему уравнений методом Гаусса:
2 x1 x2 x3 2,x1 x2 5 x3 7,
2 x 3x 3x 14
2
3
1
94.
Составим расширенную матрицу иприведём её к треугольному виду с
помощью элементарных преобразований.
2 1 1 2 1 1 5 7
2 2
1 1 5 7 2 1 1 2
2 3 3 14 2 3 3 14
95.
Получаем:1 1
5 7 1 1
5 7 1 1
5 7
0 1 9 16 0 1 13 28 0 1 13 28
0 1 13 28 0 0 22 44 0 0 1 2
Вернёмся к системе уравнений
x1 x 2 5 x3 7,
x 2 13x3 28,
x 2
3
x1 1,
x 2 2,
x 2
3
x1 x 2 10 7,
x 2 26 28,
x 2
3
x1 2 3,
x2 2,
x 2
3
x1 x2 3,
x2 2,
x 2
3
Ответ: х1=1; х2=2; х3=-2
96.
Метод Гаусса применим к любой системелинейных уравнений. При этом система будет
несовместной, т.е. не иметь решения, если
после преобразований мы получим
уравнение, в котором коэффициенты при
всех неизвестных равны нулю, а свободный
член отличен от нуля.
Пример 7. Решить систему:
x1 5 x 2 8 x3 x 4 3,
3x x 3x 5 x 1,
1
2
3
4
x1 7 x3 2 x 4 5,
11x 2 20 x3 9 x 4 2
97.
Решение: Составим расширенную матрицу ипреобразуем её.
1 5 8 1 3
3 1
3 1 3 5 1
1 0 7 2 5
0 11 20 9 2
1 5 8 1 3
0 16 21 8 8
0 5
1
1 8
21 20
0 11 20 9 2
98.
Получаем:1 5 8
1 3 1 5
0 89 0 29 160 0 89
0
5
1
1 8
0
5
0 89 0 29 162 0
0
8
1 3
0 29 160
1
1 8
0
0 2
Мы видим, что последнее уравнение
будет 0 = 2. Значит, заданная система
будет несовместной, т.е. не иметь
решения. Совместная система будет
неопределённой, (то есть иметь решений
больше, чем одно), если после преобразований матрица приводится к трапециевидному виду.
99.
Пример 8. Решить систему:x1 x 2 x3 x 4 1,
x x 2 x x 0,
1
2
3
4
x1 x 2 4 x3 3x 4 2,
x1 x 2 7 x3 5 x 4 3
Решение: Составим расширенную матрицу и преобразуем её.
1
1
1
1
1 1
1 1
1 1 1
1 2 1 0
1 4
3 2
1 7
5 3
100.
Получаем:1
0
0
0
1 1
1 1 1
0 3 2 1 0
0 3
2 1
0
0 6
4 2 0
1
0
0
0
1
3
3
3
1 1 1
2 1 0
21
0
2 1 0
1
0
0
0
1
3
0
0
1 1
2 1
0 0
0 0
Вернёмся к системе уравнений.
x1 x 2 x3 x 4 1,
3x 2 x 1,
3
4
0 0,
0 0
x1 x 2 x3 x 4 1,
2
1
x3 x 4 ,
3
3
x 4 любое
2
1
x
x
x
x 4 1,
2
4
1
3
3
2
1
x
x
,
3
4
3
3
x 4 любое
101.
В итоге имеем:1
2
x
x
x
, x 2 любое
2
4
1
3
3
2
1
x3 x 4 ,
3
3
x 4 любое
1
2
x1 x 2 3 x 4 3 ,
2
1
x3 x 4 ,
3
3
x 2 , x 4 любое
102.
Рассмотрим случай, когда заданная системасостоит из линейных однородных уравнений, то есть
уравнений, свободные члены которых равны нулю.
Такая система всегда совместна, так как обладает
нулевым решением (0; 0; …; 0). Если в системе
линейных однородных уравнений число уравнений
меньше числа неизвестных, то эта система обладает,
помимо нулевого решения, также и ненулевыми
решениями. Таких решений будет бесконечно много.
Пример 9. решить систему:
4 x1 x2 3x3 x4 0,
2 x1 3x2 x3 5 x4 0,
x 2 x 2 x 3x 0
2
3
4
1
103.
Решение:Эта система однородных уравнений; причём число
уравнений меньше числа неизвестных (3<4), поэтому
данная система будет неопределённой.
• Составим матрицу из коэффициентов (так как
свободные члены равны нулю) и преобразуем её.
5 13 0 2
0 2
0 9
4 1 3 1
5 11 0 7
5 11
1 5 0 7
2 3
1 2 2 3
1 2 2 3 1 2 2 3
104.
Вернёмся к системе уравнений:2 x 2 2 x 4 0,
7 x 2 5 x3 11x 4 0,
x 2 x 2 x 3x 0
2
3
4
1
x2 x4 ,
4
x3 x 4 ,
5
3
x
1 5 x 4
Как мы видим, с помощью метода Гаусса можно
решить любую систему, содержащую любое
число линейных уравнений с любым числом
неизвестных. Это один из самых эффективных
методов решения систем линейных уравнений.














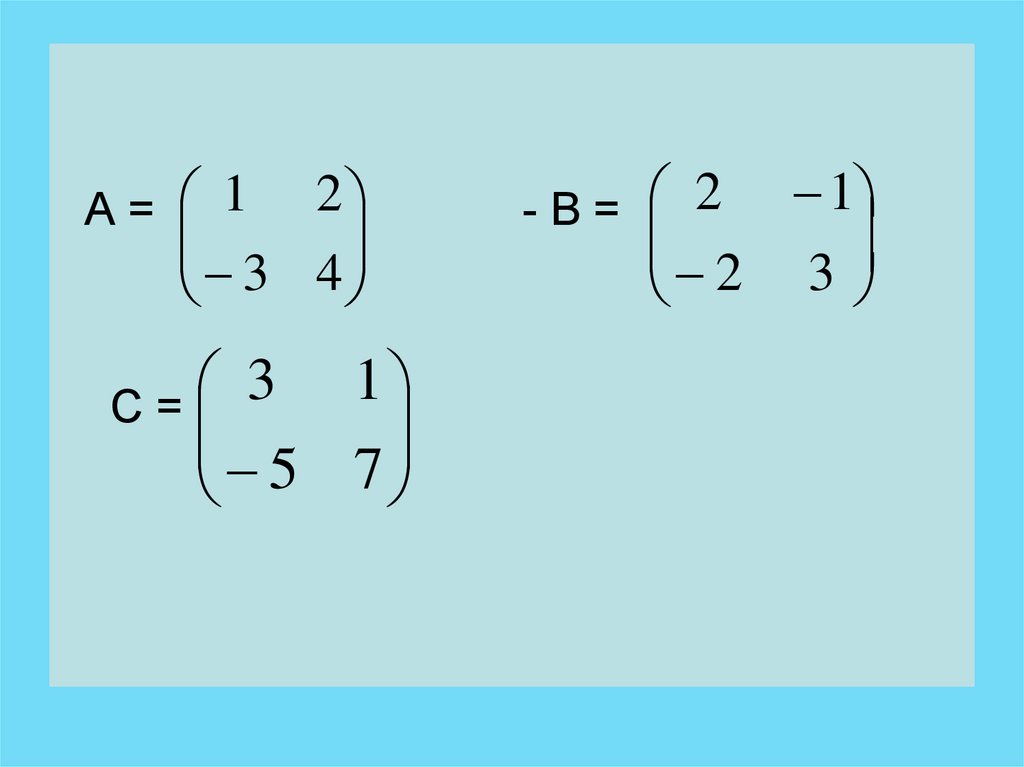































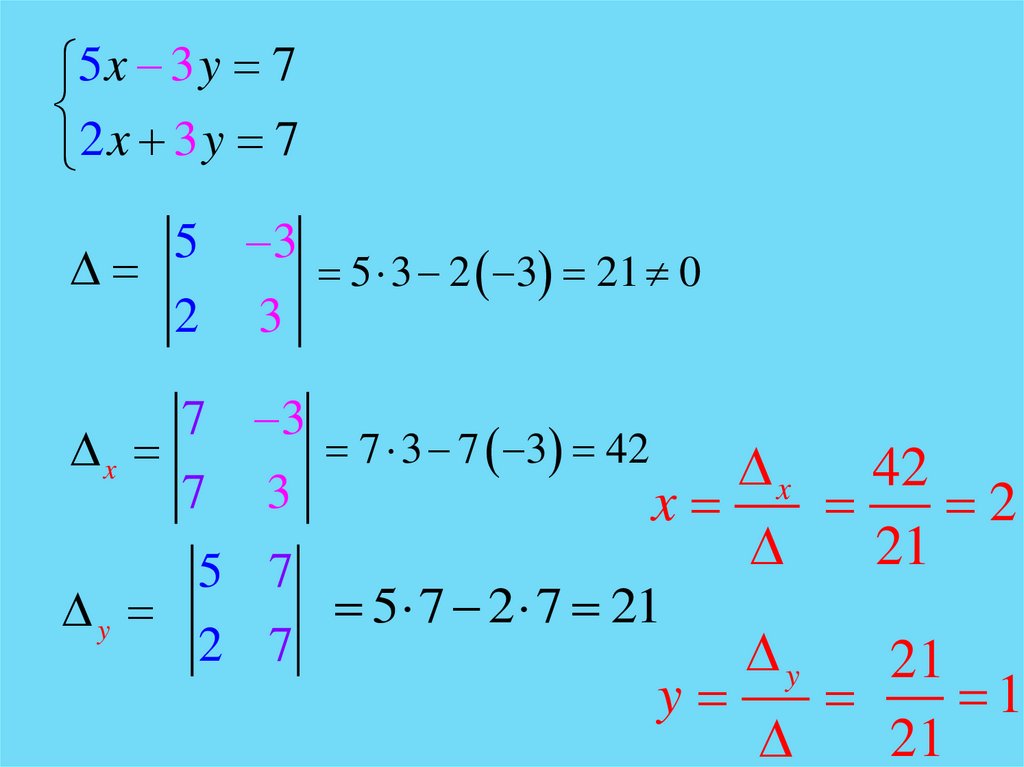

















































 mathematics
mathematics








