Similar presentations:
Линейная алгебра. Ранг матрицы. Метод Гаусса решения систем линейных уравнений. Лекция 5
1. Линейная алгебра
Ранг матрицыМетод Гаусса решения систем линейных
уравнений
Исследование систем линейных уравнений
2. Ранг матрицы
Рассмотрим прямоугольную матрицу размерностью (m x n).a11 a12
a 21 a 22
a
a 32
31
a m1 a m 2
a13
a 23
a 33
am 3
a1n
aa1111 a12 aa131n
a 2n
a1112 aa121n
22aa 3121 a3222 aa233n
M33M
a3n M
a2132 aa223n
aam311 aam322 a 33mn
amn
Выделим в этой матрице произвольное число k строк и k столбцов.
Элементы матрицы А, стоящие на пересечении выделенных строк
и столбцов, образуют определитель k - ого порядка.
порядок минора матрицы
3.
Таких миноров матрицы А размера (m x n) можносоставить
С C
k
m
k
n
n!
штук, где C
k !(n k )!
k
n
-
число сочетаний из n элементов по k .
Рангом матрицы называется наибольший порядок отличного от
нуля минора этой матрицы и обозначается r, r(A), rang A, rg A, Rg A.
Минор, порядок которого определяет ранг матрицы, называется
базисным. У матрицы может быть несколько базисных миноров.
Строки и столбцы, на пересечении которых стоят элементы
базисного минора, называются базисными.
4. Ранг матрицы
2 3 4 5A 0 2 3 1
0 2 2 4
2 3 4
0 2 3 20
Матрица А имеет 4 минора 3 - его порядка,
например:
18 миноров 2 - го порядка, например:
2
3
0 2
0
4
12 миноров 1 - го порядка – сами элементы.
Наибольший порядок отличного от нуля минора
этой матрицы равен 3, поэтому: r ( A ) 3
2
2
5. Свойства ранга матрицы
При транспонировании матрицы её ранг не меняется.Если вычеркнуть из матрицы нулевую строку(столбец), то ранг
матрицы не изменится
Ранг матрицы не изменится при элементарных преобразованиях и
равен количеству ненулевых строк в ступенчатой матрице.
Ранг канонической матрицы равен числу единиц на главной
диагонали.
1 3 2 II
A 0 5 4 ~
1 7 6
1 3 2
0 5 4 ( 2)
0 10 8
r( A ) 2
1 3 2
0 5 4
0 0 0
6. Методы вычисления ранга матрицы
1. Метод элементарных преобразований (методГаусса).
2. Метод окаймляющих миноров.
Минор M k 1 порядка (k+1), который в себе содержит
минор
M k порядка k называется окаймляющим
минором.
7.
Пример:Вычислить ранг матрицы:
1 2 1 3
0
1 1
2
1 2 2 4
7 6 1 7
Решение:
1. Выберем минор второго порядка, находящийся в
верхнем левом углу,
12
12
M
1 2
2
0
4
Вывод: минор второго порядка не равен нулю,
следовательно ранг не менее двух.
2. Составляем миноры третьего порядка, окаймляющие
отличный от нуля минор второго порядка. Для этого
добавим к M 12 третью строку и третий столбец.
12
8.
123M 123
1
2
2
0
1 3 2
1 0 0
1 2 2
124
M 123
1
2
5 3
1 1 ( 1)
( 6 6) 0
3 2
3 2 2
2 3
7 2 3
2
5 7
0 1 0 0 1 1 ( 1)
0
7 2
1 2 4
7 2 4
1
2
123
M 124
1 2 1 3 2 1
2
5 3
2 0
1 0 0
1 1 ( 1)
0
9 6
7 6 1 9 6 1
9.
1 2 37
124
M 124
2 0 1 0
7 6
7
2 3
2
5 7
0 1 1 ( 1)
0
21 6
21 6 7
Все миноры третьего порядка, окаймляющие минор второго
порядка, равны нулю. А это значит, что rang A=2.
10.
S1, S2, … , Sk – строки (столбцы) матрицы Аα1, α2, … , αk – некоторые числа
Выражение вида α1S1 + α2S2 + … + αkSk называется
линейной комбинацией
Строки (столбцы) S1, S2, … , Sk называют линейно
зависимыми, если существуют числа α1, α2, … , αk, не
все равные нулю одновременно, такие, что линейная
комбинация α1S1 + α2S2 + … + αkSk = 0 (нулевой матрице).
Если же
+ αkSk = 0 возможно
2S…
1 равенство
2 0 3 α1SS1 1 + α2S2 +
1 S2 S4 =
при условии
α1 = α2 = … = αk = 0, то строки
только
O
1 0 S11, 2S 2, S2… , Sk= (0называют
0 0 0) =линейно
(столбцы)
A
0 2 5 5 S3
независимыми.
S1, S2, S4 – линейно
1 4 1 8 S
зависимы
4
11.
Лемма (о линейной зависимости). Строки (столбцы)S1, S2, … , Sk линейно зависимы тогда и только тогда,
когда хотя бы одна из них является линейной
комбинацией других.
Теорема (о базисном миноре). 1. Базисные строки
(столбцы) матрицы линейно независимы.
2. Любая строка (столбец) матрицы является линейной
комбинацией базисных строк (столбцов).
Следствие (критерий равенства нулю определителя). Определитель матрицы A равен нулю тогда и
только тогда, когда его строки (столбцы) линейно
зависимы.
12.
Линейным уравнением называется выражение видаa1 x1 a 2 x 2 a n x n b
где
a1 , a 2 , , a n , b
– числа.
a1 , a 2 , , a n – коэффициенты уравнения
b – свободный член
Если b 0 , то уравнение называют однородным.
Если b 0 , то уравнение называют неоднородным.
13.
Системой m линейных уравнений с nнеизвестными,называется система вида
a11x1 a12 x2 a1n xn b1 ,
a x a x
a 2 n xn b 2 ,
21 1
22 2
am1 x1 am 2 x2 amn xn bm .
a11
a
A 21
am1
a12
a22
am 2
a11 a12
a
a22
21
A
am1 am 2
(*)
a1n
a2 n - основная матрица
b1
x1
b
x
amn
из свободных
2 столбец
X 2 Bстолбец
из неизвестных
a1n
a2 n
amn
xn
членов
bm
b1
b2
Тогда система
принимает вид:
-расширенная
матрица
AX = B
bm
14.
Т.е.система в матричном виде примет вид : A X Ba11 a12 a13 a1n x1 b1
a 21 a 22 a 23 a 2n x 2 b 2
a a a a x b
mn n
m
m1 m 2 m 3
b1
a11 a12 a13 a1n
a21 a22 a23 a2 n b2
B A B
a a a a b
m
mn
m1 m 2 m 3
Если закрепить раз и
навсегда нумерацию
неизвестных, то можно
опустить неизвестные в
записи системы и
записать ее в виде
матрицы, отделяя
столбец свободных
членов вертикальной
чертой.
Расширенная матрица
системы
15.
Упорядоченный набор чисел c1, c2, …, cn называетсярешением системы (*), если он обращает в тождество
каждое уравнение системы.
c1
c 2 – решение системы
C
c
n
Система уравнений называется совместной, если
она имеет хотя бы одно решение, и несовместной,
если она не имеет ни одного решения.
Система уравнений называется определенной, если
она имеет единственное решение, и неопределенной,
если она имеет более одного решения.
16.
Решить СЛАУ – значит решить две задачи:- выяснить, имеет ли СЛАУ решения;
- найти все решения, если они существуют.
Определить совместность и определенность.
x1 x2 3;
x1 x2 1.
x1 x2 3;
x1 x2 4.
совместная и определенная несовместная
x1 x2 3;
2 x1 2 x2 6.
совместная и неопределенная
Если столбец свободных членов равен нулевой матрице,
то система называется однородной, в противном случаи
она является неоднородной.
Системы называются равносильными (эквивалентными), если каждое решение одной системы
является решением другой, и наоборот.
17. Исследование систем линейных уравнений
Теорема Кронекера - Капелли.Для того, чтобы система линейных алгебраических уравнений
была совместна (имела решение ), необходимо и достаточно,
чтобы ранг расширенной матрицы
системы равнялся рангу
матрицы коэффициентов: r (B) r ( A )
Если r(B) r ( A ) n (числу неизвестных), то система
совместна и определенна (имеет единственное решение).
Если r(B) r ( A ) n ,то система совместна и неопределенна
(имеет бесконечное множество решений).
Если r (B) r ( A ) ,то система несовместна (не имеет решений).
При решении систем линейных алгебраических уравнений нет
необходимости заранее вычислять ранги основной и расширенной
матриц. Их определение производится автоматически при
выполнении метода исключения Гаусса.
18. Метод Гаусса решения систем линейных уравнений
Следующие действия над расширенной матрицей системыназываются элементарными преобразованиями.
Умножение элементов строк на одно и то же число, не равное
нулю
Перестановка местами двух строк
Прибавление к элементам строки элементов другой строки,
умноженных на произвольный множитель.
Конечной целью элементарных преобразований является
получение верхнетреугольной матрицы, у которой все элементы,
стоящие под главной диагональю равны нулю. Преобразования
стараются производить так, чтобы на главной диагонали
появлялись единицы.
a11 a12
a 21 a 22
a
31 a 32
a13
a 23
a33
b1
b2
b3
1 c12
0 1
0 0
c13
c 23
1
d1
d2
d3
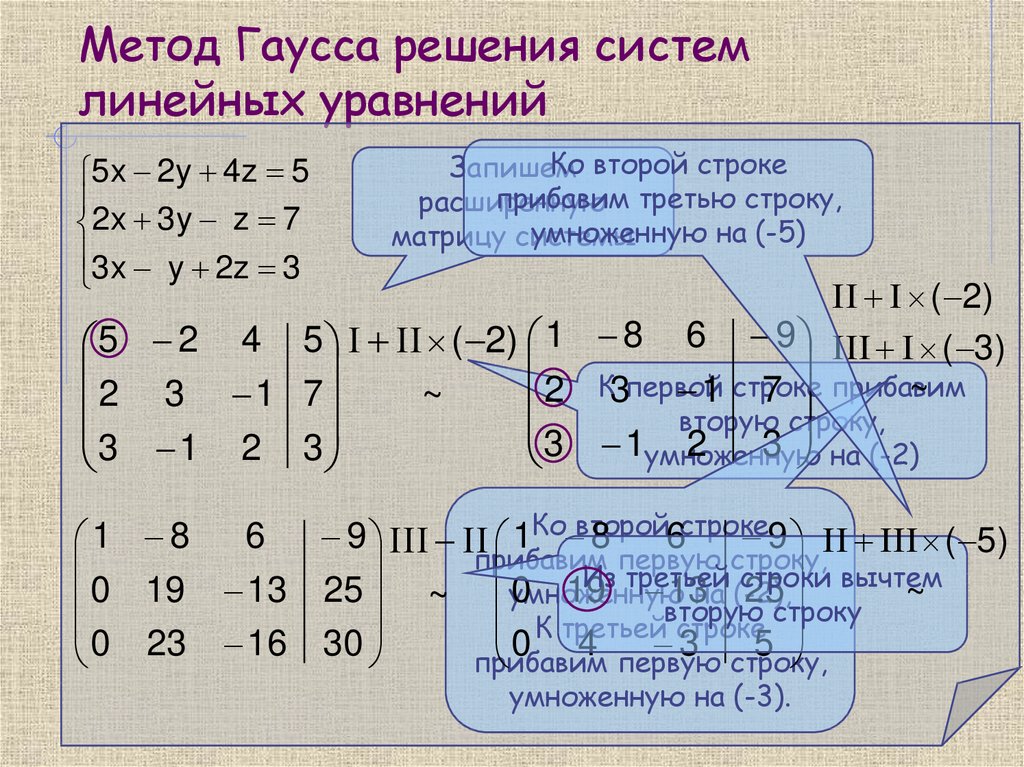
19. Метод Гаусса решения систем линейных уравнений
5x 2y 4z 52x 3y z 7
3x y 2z 3
Ко второй строке
Запишем
прибавим третью строку,
расширенную
умноженную на (-5)
матрицу системы
( 2)
5 2 4 5 ( 2) 1 8 6 9 ( 3)
~
1 строке
7 прибавим
2 К3первой
~
2 3 1 7
строку,
3 1 вторую
3 1 2 3
2
3
умноженную
на (-2)
6
9 1Ко второй
8
6строке
9 ( 5)
1 8
прибавим
первую
строку,
вычтем
Из третьей строки
0 19 13на (-2),
25
~
0 19 13 25 ~ умноженную
вторую строку
строке
0 23 16 30
0 К третьей
4 первую
3 строку,
5
прибавим
умноженную на (-3).
20. Метод Гаусса решения систем линейных уравнений
( 1)1 8 6 9 4 1 8 6 9
: 5
0
~
0 1 2
0 1 2 0
~
строке
0 4 3 5
0 К0третьей
прибавим
5
5
вторую строку,
умноженную на 4
1 8 6 9
Вторую строку умножим
на (-1), третью
строку
Восстановим
систему:
0 1 2 0
разделим на 5
0 0
1
1
x 8y 6z 9
y 2z 0
z 1
x 1 y 2
x 9 8y 6z
y 2z 2
z 1
z 1
x 9 16 6 1
y 2
z 1
21. Исследование систем линейных уравнений
2x1 2x 2 2x 3 4x1 x 2 x 3 0
3 x1 3 x 2 x 3 2
x1 x 2 3 x 3 2
2 2 2 4
:2
1 1 1 0
3 3 1 2 ~
1 1 3 2
1 1 1 2 ( 3)
1 1 1 0 V
~
3 3 1 2
1 1 3 2
: ( 2)
1
0
0
0
2
0 2 2
0 4 4
0 4
4
1
1
: ( 4)
V : 4
~
22. Исследование систем линейных уравнений
10
0
0
1 1 2
0 1 1 V
~
0 1 1
0 1 1
r(B) r( A ) 2
1
0
0
0
1 1 2
0 1 1
0 0 0
0 0 0
система совместна
n 3 - число неизвестных
r(B) n система неопределенна
n r 3 2 1 - число свободных переменных
Восстановим систему:
Пусть x 2 t.
x1 1 t
x1 2 t x 3 1 t
x1 t x 3 2
x2 t
x3 1
x3 1
x 1
3
23. Исследование систем линейных уравнений
x 2y 4z 12x y 5z 1
x y z 3
1 2 4 1
2 1 5 1
1 1 1 3
( 2)
~
1 2 4 1 1 2 4 1
~
0 3 3 3
0 3 3 3
0 3 3
0 0
2
0
5
r(B) 3
r( A ) 2
r(B) r( A ) система несовместна







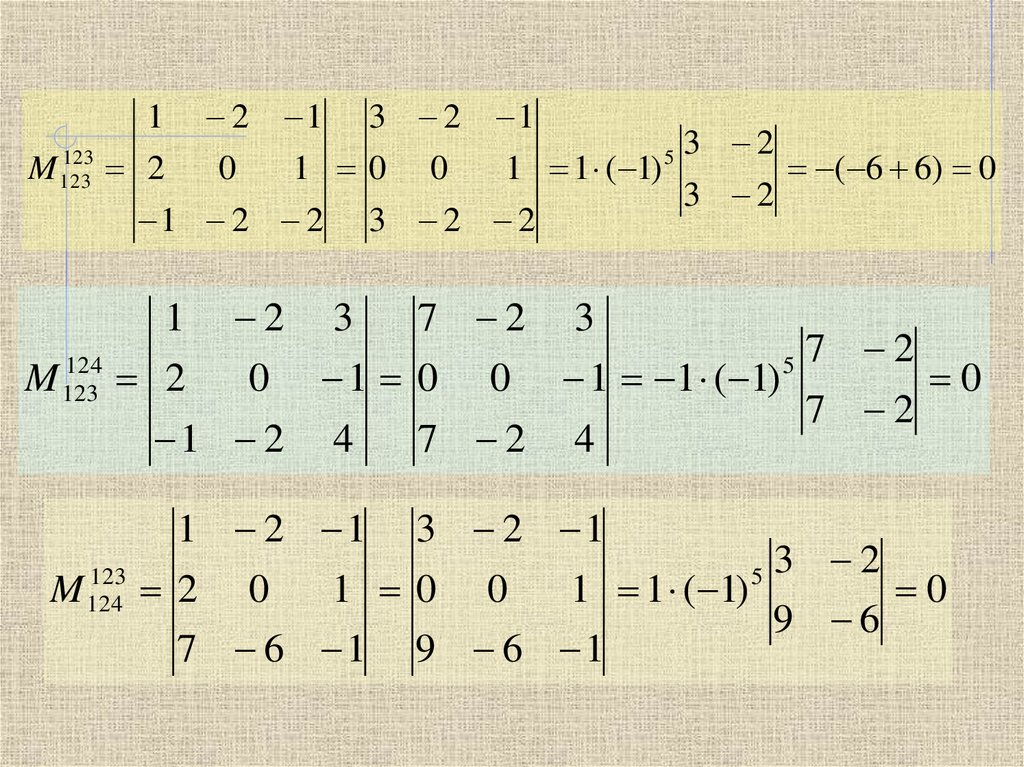














 mathematics
mathematics








