Линейная алгебра. Метод Гаусса решения систем линейных уравнений

1. Линейная алгебра

Метод Гаусса решения систем линейных
уравнений

2. Метод Гаусса решения систем линейных уравнений

Рассмотрим задачу решения системы линейных уравнений
размерностью (m x n). Запишем систему в матричном виде: A X B
Если закрепить раз и
a11 a12 a13 a1n x1 b1 навсегда нумерацию
a 21 a22 a23 a2n x 2 b2 неизвестных, то можно
неизвестные в
опустить
системы и
записи
a a a a x b записать ее в виде
mn n
m матрицы, отделяя
m1 m 2 m3
b1
a11 a12 a13 a1n
a21 a22 a23 a2 n b2
B A B
a a a a b
m
mn
m1 m 2 m 3
столбец свободных
членов вертикальной
чертой.
Расширенная матрица
системы

3. Метод Гаусса решения систем линейных уравнений

Следующие действия над расширенной матрицей системы
называются элементарными преобразованиями.
Умножение или деление элементов строк на одно и то же
число, не равное нулю
Перестановка местами двух строк
Прибавление к элементам строки элементов другой строки,
умноженных на произвольный множитель.
Конечной целью элементарных преобразований является
получение верхнетреугольной матрицы, у которой все элементы,
стоящие под главной диагональю равны нулю. Преобразования
стараются производить так, чтобы на главной диагонали
появлялись единицы.
a11 a12
a 21 a 22
a
31 a32
a13
a 23
a33
b1
1 c 12
b2 0 1
0 0
b3
c 13
c 23
1
d1
d2
d3

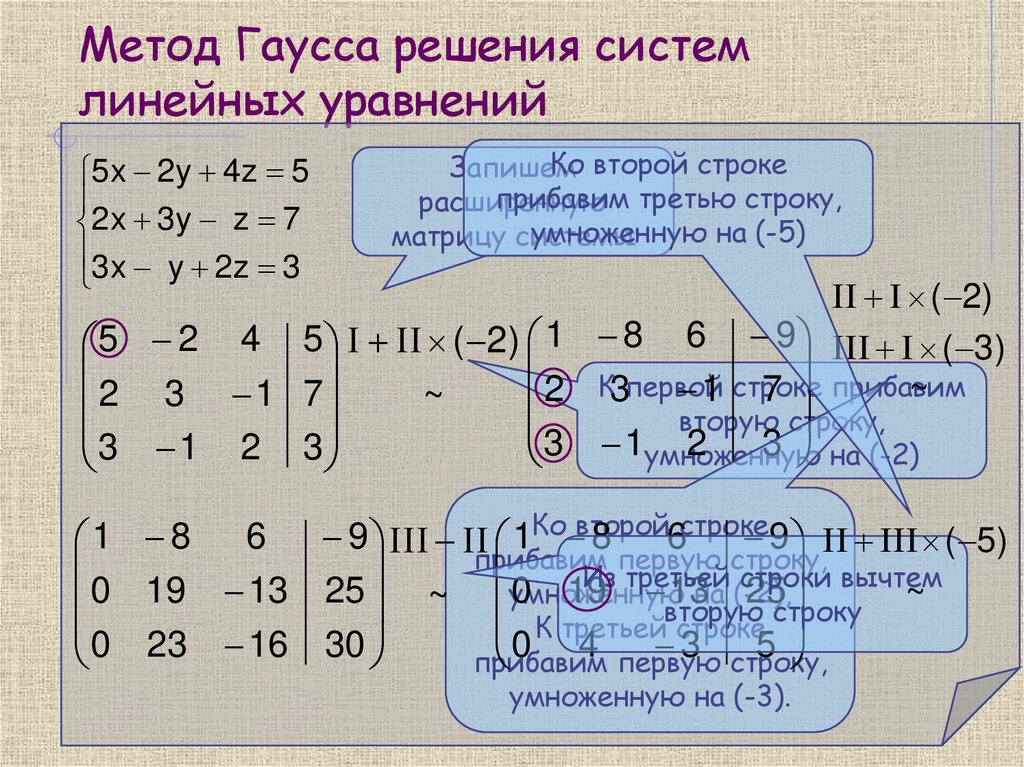
4. Метод Гаусса решения систем линейных уравнений

5x 2y 4z 5
2x 3y z 7
3x y 2z 3
Ко второй строке
Запишем
прибавим третью строку,
расширенную
умноженную на (-5)
матрицу системы
( 2)
5 2 4 5 ( 2) 1 8 6 9 ( 3)
~
1 строке
7 прибавим
2 К3первой
~
2 3 1 7
строку,
3 1 вторую
3 1 2 3
2
3
умноженную
на (-2)
6
9 1Ко второй
8
6строке
9 ( 5)
1 8
прибавим
первую
строку,
вычтем
Из третьей строки
0 19 13на (-2),
25
~
0 19 13 25 ~ умноженную
вторую строку
строке
0 23 16 30
0 К третьей
4 первую
3 строку,
5
прибавим
умноженную на (-3).

5. Метод Гаусса решения систем линейных уравнений

( 1)
: 5
~
1 8 6 9 4 1 8 6 9
0
~
0 1 2
0 1 2 0
строке
0 4 3 5
0 К0третьей
прибавим
5
5
вторую строку,
умноженную на 4
1 8 6 9
Вторую строку умножим
на (-1), третью
строку
Восстановим
систему:
0 1 2 0
разделим на 5
0 0
1
1
x 8y 6z 9
x 9 8y 6z
x 9 16 6 1
y
2
z
0
y 2
y 2z 2
z 1
z 1
z
1
x 1 y 2
z 1