Повторение: матрицы, определители, СЛУ. Тема 4

1.

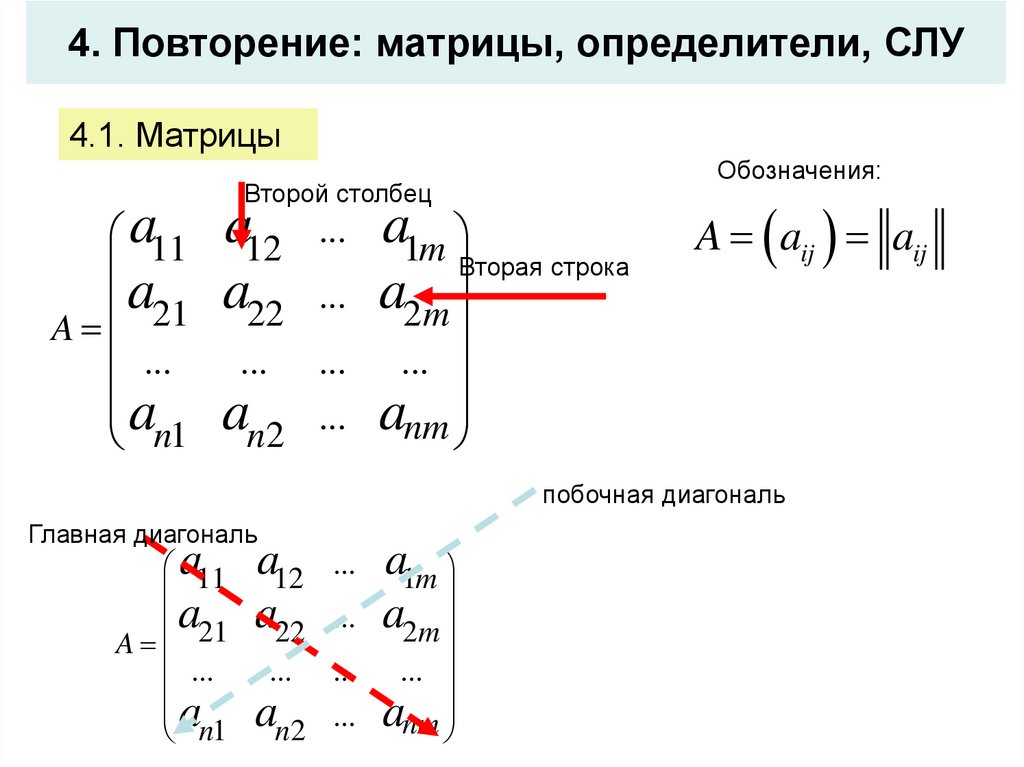
4. Повторение: матрицы, определители, СЛУ
4.1. Матрицы
a11
a21
A
...
a
n1
Второй столбец
Обозначения:
a12 ... a1m
Вторая строка
a22 ... a2m
...
...
an2 ...
A aij aij
...
anm
побочная диагональ
Главная диагональ
a11
a21
A
...
a
n1
a12 ... a1m
a22 ... a2m
...
...
an2 ...
...
anm

2.

4.2. Линейные операции над матрицами
a11
a21
A
...
a
n1
a12 ... a1m
a22 ... a2m
a
ij i 1,n
... ... ...
j 1,m
an2 ... anm
a) умножение матрицы на число :
б) сложение матриц :
Матрицы разного размера
складывать нельзя
Вычитание — это тоже сложение
A a
ij i 1,n
j 1,m
A a
, B b
ij i 1,n
ij i 1,n
j 1,m
j 1,m
C A B a b
ij i 1,n
ij
j 1,m

3.

в) умножение матриц :
i-я строка А
A a
, B b
ij i 1,n
ij i 1,m
j 1,m
j 1,k
j j-й столбец В
C AB a b
i
i 1,n
j 1,m
A n m
AB n k
B m k
C c
ij i 1,n
j 1,k
г) транспонир ование матриц :
A a
,
ij i 1,n
j 1,m
AT a
ji j 1,m
i 1,n

4.

4.3. Определители
Бывают только у квадратных матриц
Обозначение:
1 1:
det A A A
a a
a b
2 2 :
ad bc
c d
a11 a12 a13
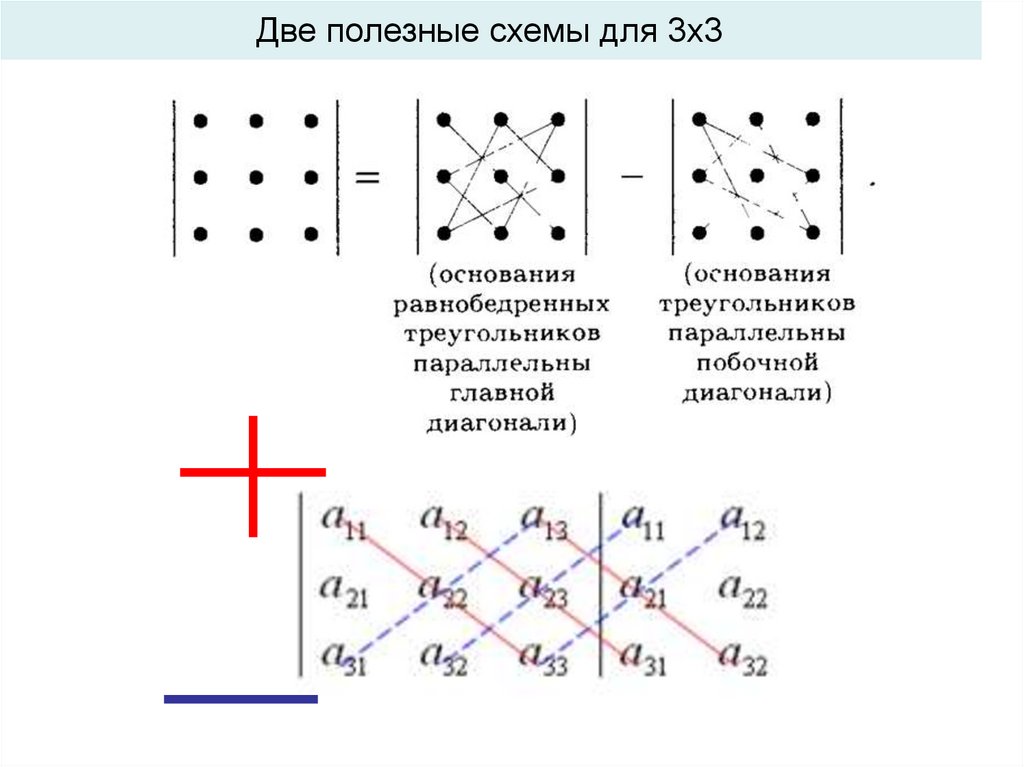
3 3: a21 a22 a23 a11a22 a33 a12 a23 a31 a13 a21a32
a a a
a13 a22 a31 a12 a21a32 a11a23 a33
31 32 33

5.

Две полезные схемы для 3х3

6.

4.4. Свойства определителей
1) det 0 0
2) det E 1
1
4) det A
det A
1
3) det A det A
T
5) det AB det A det B
6) При добавлении к любой строке (столбцу) линейной комбинации
других строк (столбцов) определитель не изменится:
ai j a j ,
где λj - некоторое число, ai , aj - строки матрицы
7) Если две строки (столбца) совпадают, то определитель равен нулю.
8) Если переставить две строки (столбца), то определитель меняет знак .
9) Если хотя бы один ряд нулевой, то определитель равен нулю.
10) Общий множитель элементов какого-либо ряда определителя можно
вынести за знак определителя.

7.

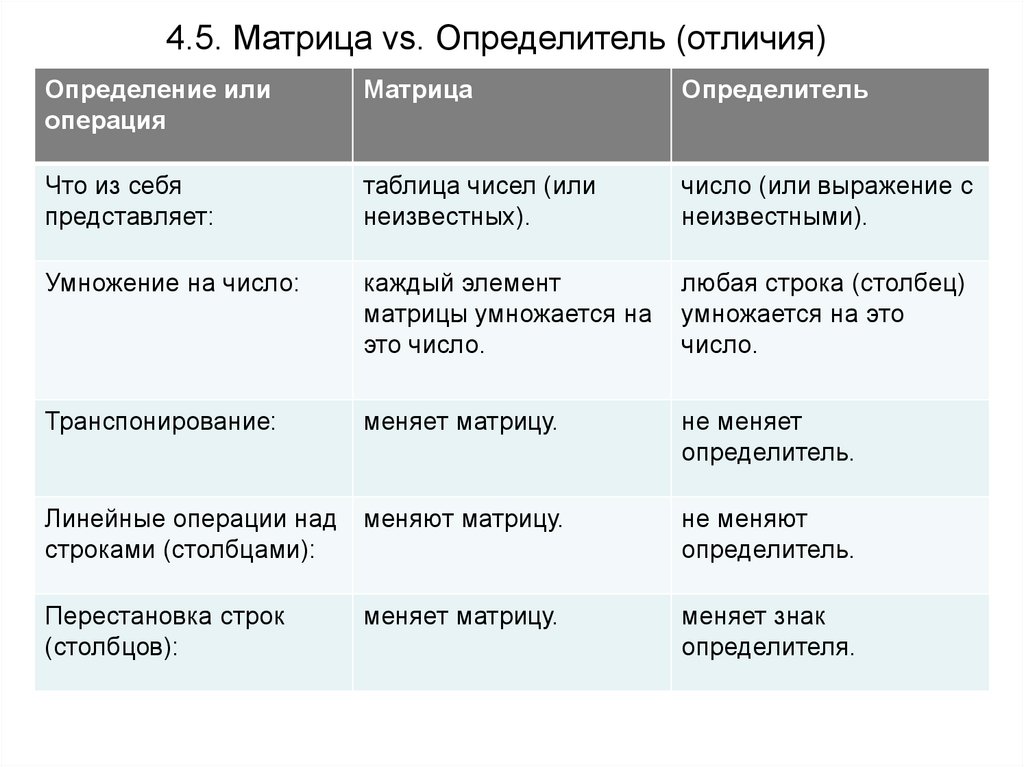
4.5. Матрица vs. Определитель (отличия)
Определение или
операция
Матрица
Определитель
Что из себя
представляет:
таблица чисел (или
неизвестных).
число (или выражение с
неизвестными).
Умножение на число:
каждый элемент
матрицы умножается на
это число.
любая строка (столбец)
умножается на это
число.
Транспонирование:
меняет матрицу.
не меняет
определитель.
Линейные операции над меняют матрицу.
строками (столбцами):
не меняют
определитель.
Перестановка строк
(столбцов):
меняет знак
определителя.
меняет матрицу.

8.

4.6. Вычисление обратной матрицы
Методом
присоединённой
матрицы:
1
A
A
det A ij
1
T
где
A
ij
i 1,n
j 1,n
AÏ
T
- присоединенная (союзная) матрица,
или транспонированная матрица
алгебраических дополнений
Методом элементарных преобразований.
1. Записать рядом две матрицы: A|E.
2. Получить нижний треугольник нулей матрицы А (выполнить прямой ход).
3. Получить верхний треугольник нулей матрицы А (выполнить обратный
ход).
4. Получить в главной диагонали преобразуемой матрицы единицы. Тогда на
месте исходной единичной матрицы Е будет находиться обратная
матрица А-1.

9.

4.7. Система линейных уравнений (СЛУ)
a11 x1 a12 x2
a x a x
21 1
22 2
..
...
an1 x1 an 2 x2
a11 a12
a a
A 21 22
... ..
an1 an 2
... a1m xm b1
... a2 m xm b2
AX B
...
...
... anm xm bn
... a1m
x1
x
... a2 m
, n m X 2 , m 1
... ...
...
... anm
xm
b1
b
B 2 , n 1
...
bn
Способы решения.
1. С помощью обратной матрицы.
2. Методом Крамера.
3. Методом Гаусса (с помощью элементарных преобразований).

10.

4.8. Определитель vs. СЛУ (отличия)
Определение или
операция
Определитель
СЛУ
Что из себя
представляет:
число
набор уравнений
Способы вычисления: (а) по схематическому
правилу;
(б) разложение по
строке (столбцу);
(в) с помощью нулей.
(а) с помощью обратной
матрицы;
(б) методом Крамера;
(в) методом Гаусса.
Преобразования:
(а) элементарные: кроме
линейных преобразований,
можно ещё умножать строки
на любое число, отличное
от нуля;
(б) перестановка строк не
меняет СЛУ.
(а) линейные: из строки
(столбца) можно
вычитать другие,
умноженные на
подходящие числа;
(б) перестановка строк
(столбцов) меняет знак

11.

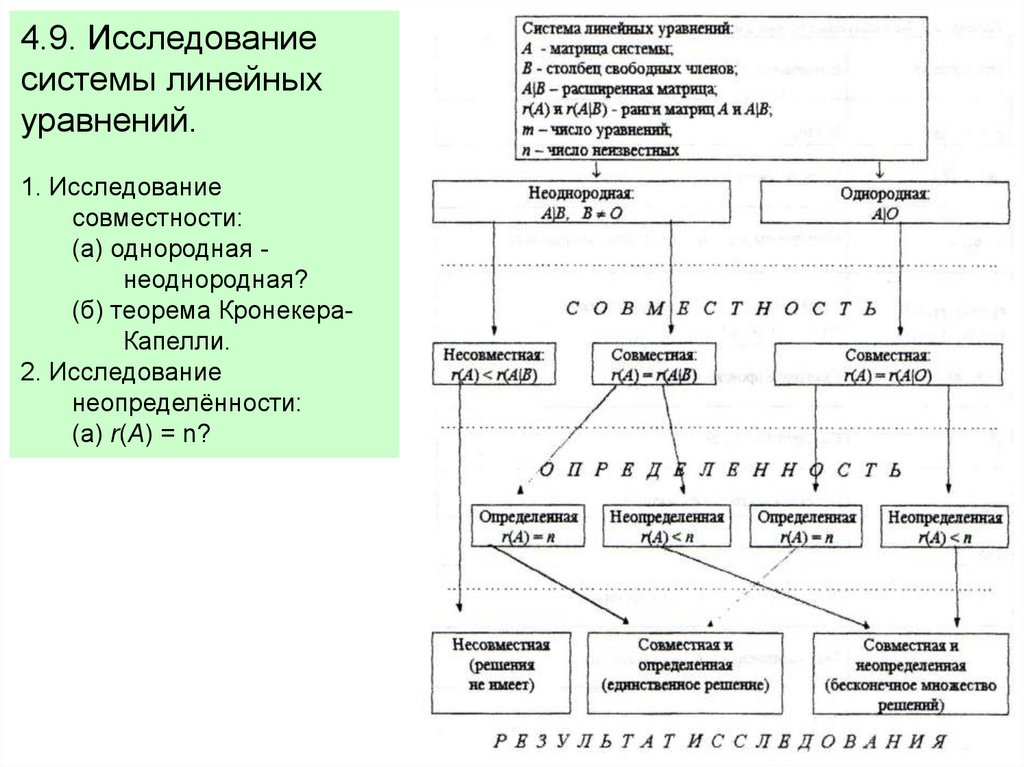
4.9. Исследование
системы линейных
уравнений.
1. Исследование
совместности:
(а) однородная неоднородная?
(б) теорема КронекераКапелли.
2. Исследование
неопределённости:
(а) r(A) = n?

12.

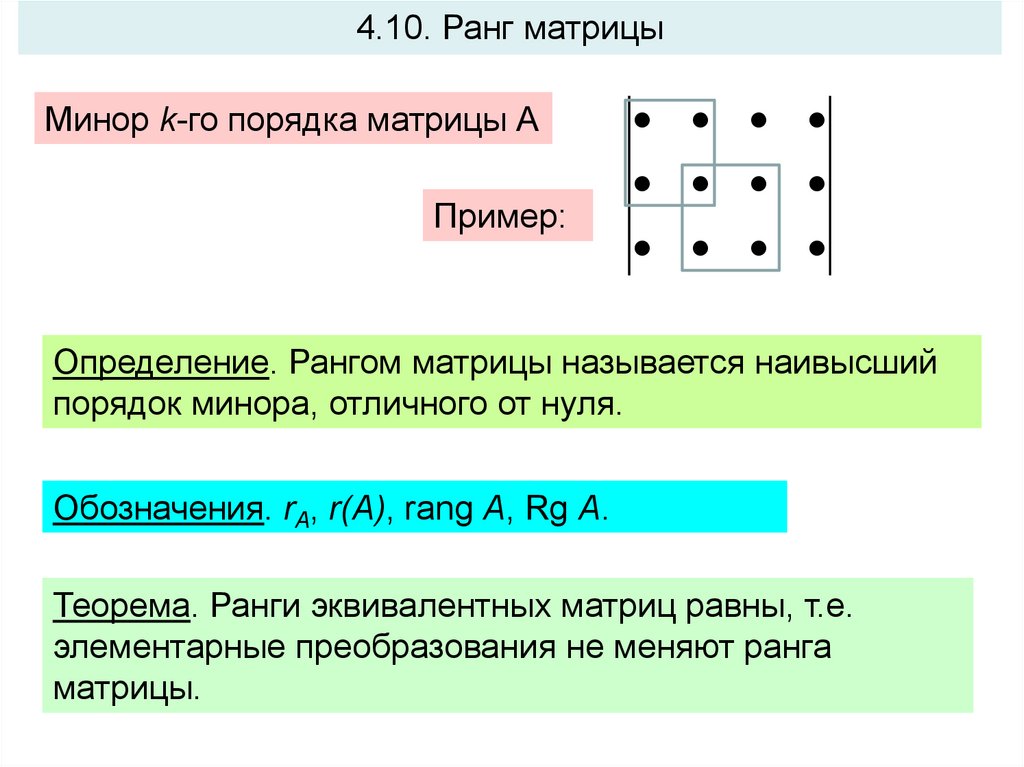
4.10. Ранг матрицы
Минор k-го порядка матрицы А
Пример:
Определение. Рангом матрицы называется наивысший
порядок минора, отличного от нуля.
Обозначения. rA, r(A), rang A, Rg A.
Теорема. Ранги эквивалентных матриц равны, т.е.
элементарные преобразования не меняют ранга
матрицы.

13.

Способы вычисления ранга матрицы.
1. Метод окаймляющих миноров (по определению).
2. Метод элементарных преобразований.
Метод элементарных преобразований.
1. С помощью элементарных преобразований получить в левом
верхней углу единичную (или треугольную) матрицу.
2. Нулевые строки переставлять вниз, а нулевые столбцы - вправо.
3. Ранг матрицы равен порядку полученной единичной или треугольной
матрицы.
Связь нахождения ранга с методом Гаусса.
1. Если в процессе нахождения ранга обнаружилось, что система совместна,
продолжаем элементарные преобразования, пока не получим единичную
матрицу слева вверху.

14.

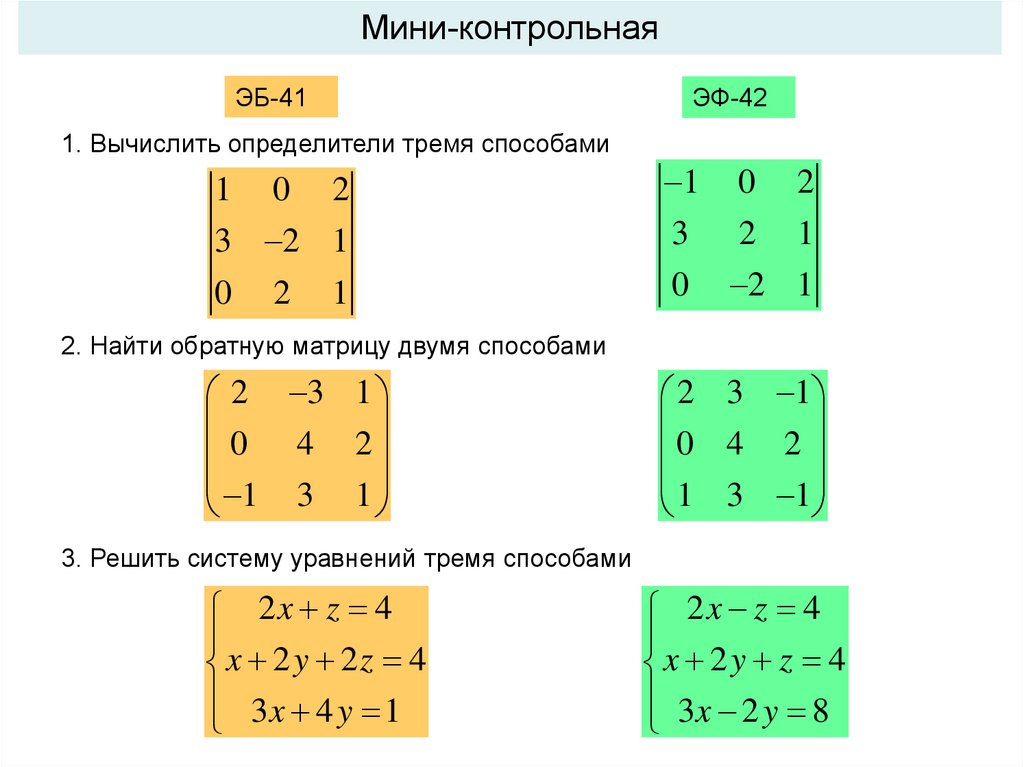
Мини-контрольная
ЭБ-41
ЭФ-42
1. Вычислить определители тремя способами
1 0 2
3 2 1
0 2 1
1 0 2
3 2 1
0 2 1
2. Найти обратную матрицу двумя способами
2 3 1
0 4 2
1 3 1
2 3 1
0 4 2
1 3 1
3. Решить систему уравнений тремя способами
2x z 4
x 2 y 2z 4
3x 4 y 1
2x z 4
x 2 y z 4
3x 2 y 8