Similar presentations:
Скалярное произведение векторов
1.
2. Цели урока:
Ввести понятия угла междувекторами и скалярного
произведения векторов.
Рассмотреть формулу
скалярного произведения в координатах.
Показать применение скалярного произведения
векторов при решении задач.
3. Повторение:
Какие векторы называются равными?а
a b, если a b ; а b
b
Как найти длину вектора по координатам его
начала и конца?
В
х
АВ
х А уВ у А
2
2
А
Какие векторы называются коллинеарными?
а b или а b
b
а
В
а b
x1 x2
y1 y 2
z z
2
1
4. Повторение:
(Векторы в пространстве)1) Дано: А 3; 2;4 В 4;3;2
30
Найти: АВ
2) Дано: А 2; 3;1 В 4; 5;0 С 5;0; 4 D 7; 2; 3
Равны ли векторы АВ и CD ?
АВ 2; 2; 1
CD 2; 2;1
Нет, т.к.равные векторы имеют равные
координаты.
3) Дано: Коллинеарны ли векторы
А 1; 3;4
В 5;1; 2
С 2;0;1 D 4; 2;2
АВ 8;4; 6
CD 2; 2;1
АВи CD ?
Нет
5. Угол между векторами.
bа
ОА а
ab
А
α
О
В
ОВ b
6. Примеры:
1. a2, b
2. a
5, b
3. a
7, b
4. a
1, b
a
,
7
b
5.
3,
1,
4,
a b
0
60
0 a b
30
0
45
a b
0
2 3 cos 60
0
5 1 cos 30
0
7 4 cos 45
3
5 3
2
14 2
1,
0
120 a b
0
1 1 cos 120
,
5
0
90 a b
0
7 5 cos 90
1
2
0
7.
Свойства скалярного произведенияa b a b cos
0
cos
90
0 a b 0
1. Если a b , то
0
cos
180
1 a b a b
2. Если a b , то
3. Если а b , то cos 0
0
1
a b a b
2
4. Если a b , то
a b a a a a a a
Скалярное произведение
a a
называется
скалярным квадратом вектора
2
8. Скаляр – лат. scale – шкала.
Ввёл в 1845 г.У. ГАМИЛЬТОН,
английский
математик.
9. Формула скалярного произведения векторов в пространстве.
а x1 ; y1 ; z1b x2 ; y2 ; z2
a b x1 x2 y1 y2 z1 z2
Скалярное произведение двух
векторов равно сумме
произведений соответствующих
координат этих векторов.
10. Вычислить скалярное произведение векторов
а = (4; –6; 3), b = (–5; 2; –5), c = (0; –3; –4).a•b =
a•c =
b•c =
11. Формула для вычисления угла между векторами, заданными своими координатами
а x1 ; y1 ; z1b x2 ; y2 ; z2
a b a b cos
12. Формула для вычисления угла между векторами, заданными своими координатами
cos α =cos
a•b
a•b
x1 x2 y1 y2 z1 z 2
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2
13. Решение задач
1. В треугольнике АВС найти величину угла В, еслиА (0; 5; 0), В (4; 3; -8), С (-1; -3; -6).
2. Определить угол между векторами АВ и СD, если
А (1; -3; -4), В (-1; 0; 2), С (2; -4; -6), D (1; 1; 1).
14.
Скалярное произведение координатных векторов1
i
и
j
равно нулю, т.к. угол между
векторами прямой
:
y
1
ПОДУМАЙ!
1
j
2
–1
3
0
ПОДУМАЙ!
ВЕРНО!
Проверка
О
x
i
1
15.
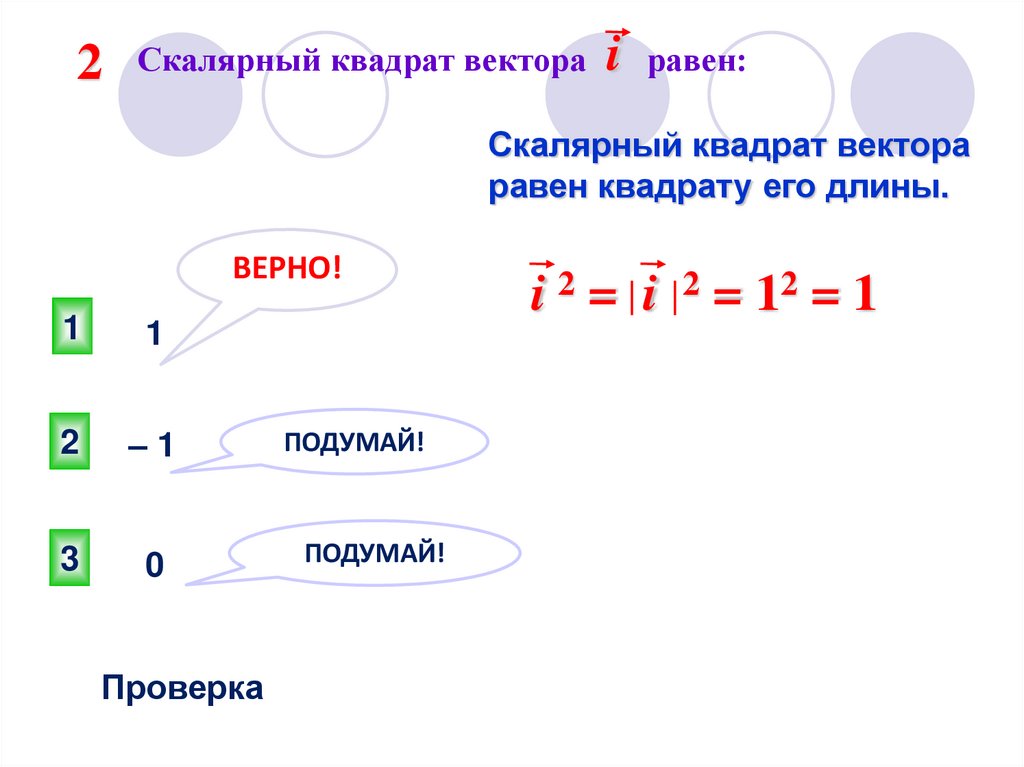
2Скалярный квадрат вектора
i
равен:
Скалярный квадрат вектора
равен квадрату его длины.
ВЕРНО!
1
1
2
–1
3
0
Проверка
ПОДУМАЙ!
ПОДУМАЙ!
i2= i
2
= 12 = 1
16.
123 Если a b = 12,
то векторы
a
и
b:
ВЕРНО!
a = 33,
b = 4,
4
a b = a b cos a b
12 = 3 4 cos a b
cos a b = 1
a b = 00
ПОДУМАЙ!
a b
1
сонаправлены;
2
перпендикулярны;
3
противоположно направлены.
Проверка
ПОДУМАЙ!
17.
x y = –20–20, x = 44,
y = 5,
5
4
то векторы x и y :
x y = x y cos x y
Если
–20 = 4 5 cos x y
ПОДУМАЙ!
1
сонаправлены;
ПОДУМАЙ!
2
перпендикулярны;
ВЕРНО!
3 противоположно направлены.
Проверка
cos x y = –1
x y = 1800
если
x
y
18.
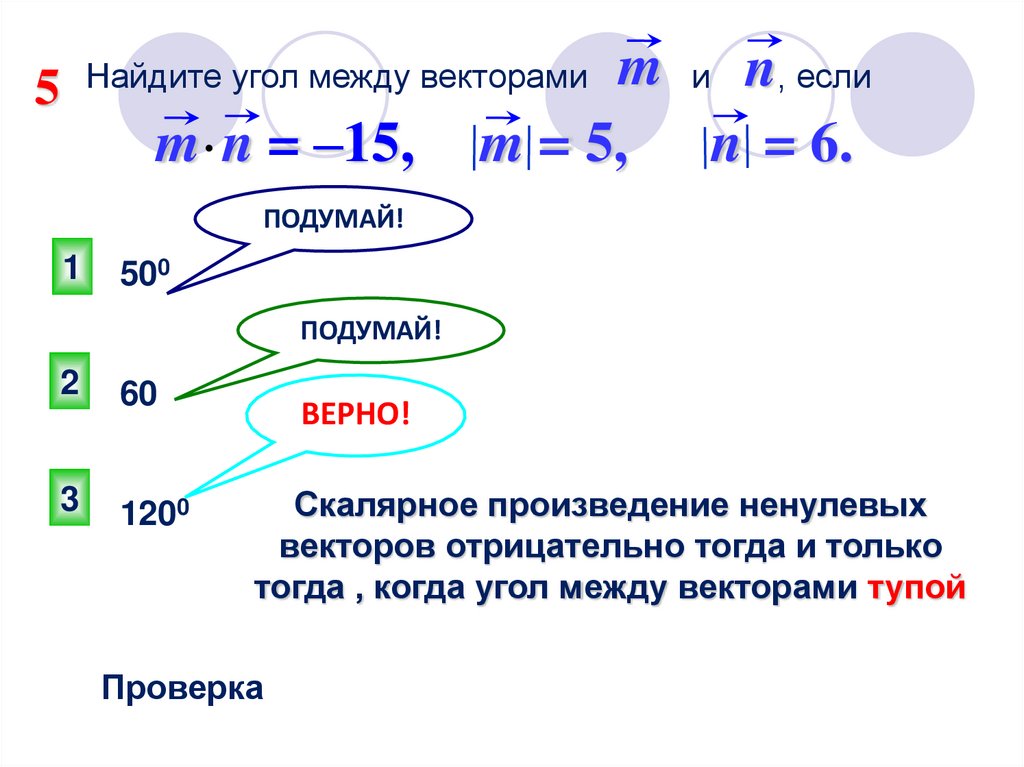
m и n, еслиm = 5, n = 6.
Найдите угол между векторами
5
m n = –15,
ПОДУМАЙ!
1
500
ПОДУМАЙ!
2
600
3
1200
ВЕРНО!
Скалярное произведение ненулевых
векторов отрицательно тогда и только
тогда , когда угол между векторами тупой
Проверка
















 mathematics
mathematics








