Similar presentations:
Угол между векторами. Скалярное произведение векторов. 11 класс
1.
11 класс.МОУ СОШ №256
г.Фокино.
2. Цели урока:
• Ввести понятия угла междувекторами и скалярного
произведения векторов.
• Рассмотреть формулу
скалярного произведения в координатах.
• Показать применение скалярного произведения
векторов при решении задач.
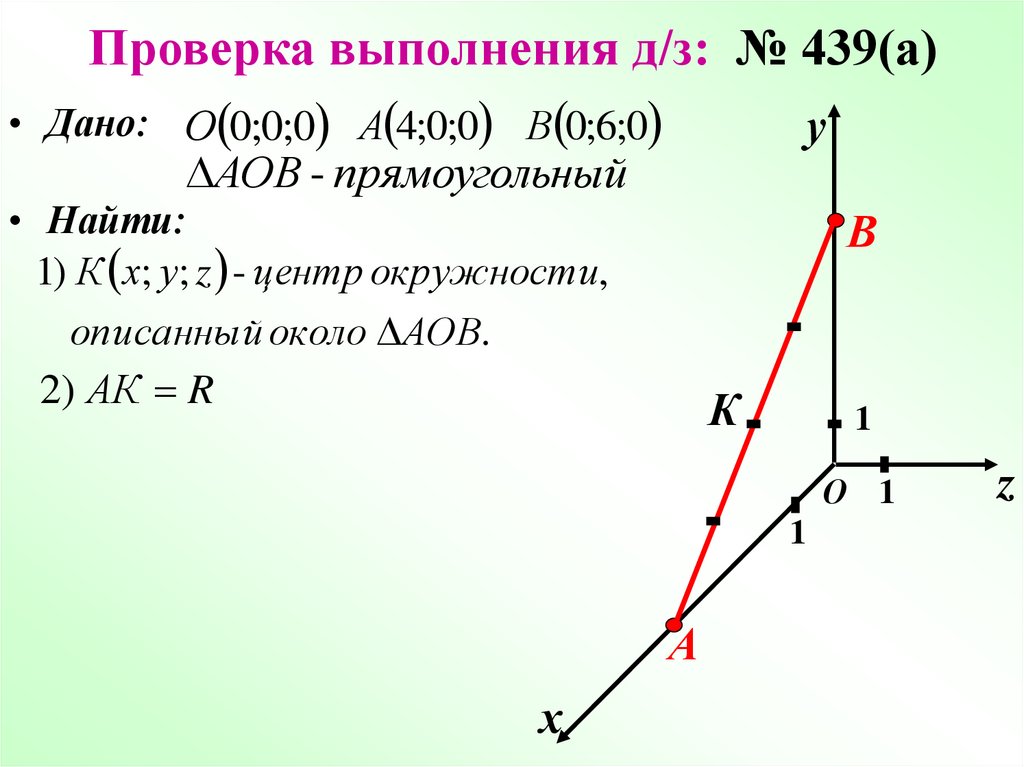
3. Проверка выполнения д/з: № 439(а)
• Дано: О 0;0;0 А 4;0;0 В 0;6;0у
АОВ - прямоугольный
• Найти:
1) К х; у; z - центр окружности,
В
описанный около АОВ.
2) АК R
К
1
О 1
1
А
х
z
4. Проверка выполнения д/з: № 439(а)
• Решение:Центр окружности К – середина
гипотенузы АВ. Найдем координаты К.
0 0
0 6
4 0
0
3 z
х
2 у
2
2
2
4 2 0 3 0 0 13
Ответ:
2
2;3;0 ;
В
К
К (2; 3; 0)
R АК
у
2
2
13
х
А
1
О 1
1
z
5. Повторение:
• Какие векторы называются равными?а
a b, если a b ; а b
b
• Как найти длину вектора по координатам его
начала и конца?
В
АВ
х х у у
2
2
А
• Какие векторы называются коллинеарными?
а b или а b
а
b
В
А
В
А
x1 x2
а b y1 y 2
z z
2
1
6. Повторение. (Устно)
Векторы в пространстве.А 3; 2;4 В 4;3;2
1) Дано:
Найти: АВ
30
2) Дано: А 2; 3;1 В 4; 5;0 С 5;0; 4 D 7; 2; 3
Равны ли векторы АВ и CD ?
Нет, т.к.равные векторы имеют равные
координаты.
АВ 2; 2; 1
CD 2; 2;1
3) Дано: ? Коллинеарны ли векторы АВ и CD ?
А 1; 3;4
В 5;1; 2
С 2;0;1
D 4; 2;2
АВ 8;4; 6 CD 2; 2;1
Нет
7. Угол между векторами.
bОА а ОВ b
ab
Если а b, то аb 0
а
0
0
0
А
α
О
В
Если а b то ab 180
Если а b то ab 90
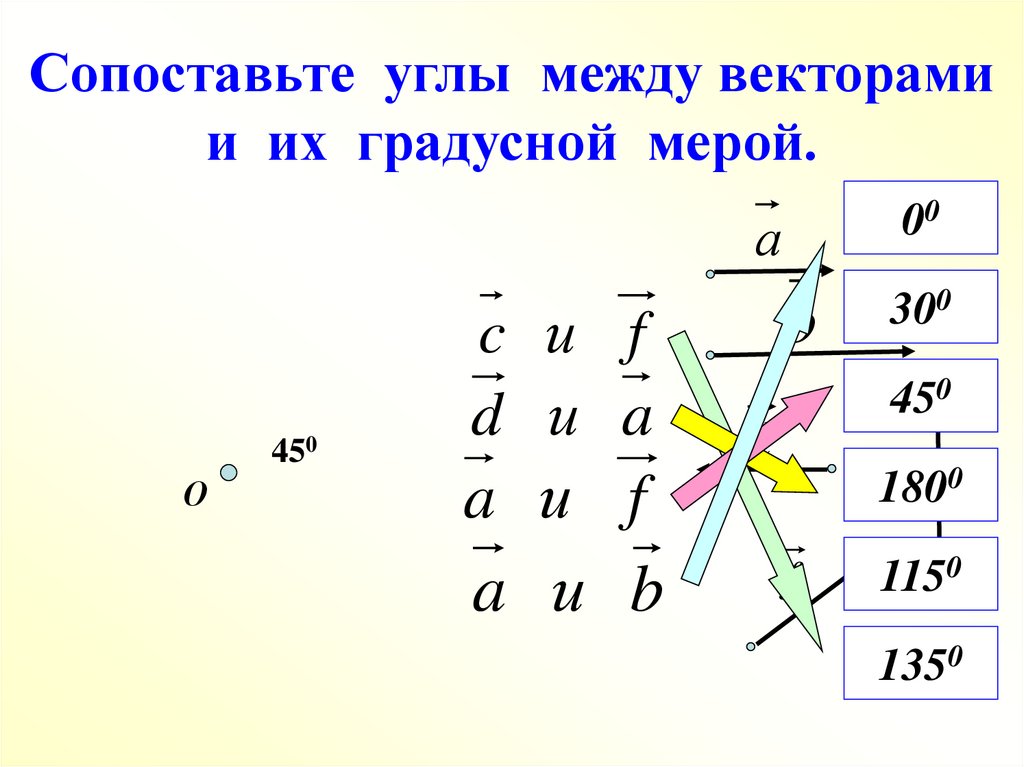
8. Сопоставьте углы между векторами и их градусной мерой.
00а
450
О
c и f
d и a
a и f
a и b
b
300
450
d
1800с
f
1150
1350
9. Скалярное произведение векторов.
Скалярным произведениемдвух векторов называется
произведение их длин
на косинус угла между
ними.
а
b
a b a b cos
10. Скаляр – лат. scale – шкала.
Ввел в 1845 г.У. ГАМИЛЬТОН,
английский
математик.
11.
Вспомним планиметрию…a b a b cos
Если a b , то
cos 90 0
0
a b 0
0
a
b
Если
, то cos 180 1 a b a b
Если а b , то
cos 0 1 a b a b
0
2
Если a b , то a b a a a a a a
Скалярное произведение a a называется
скалярным квадратом вектора
2
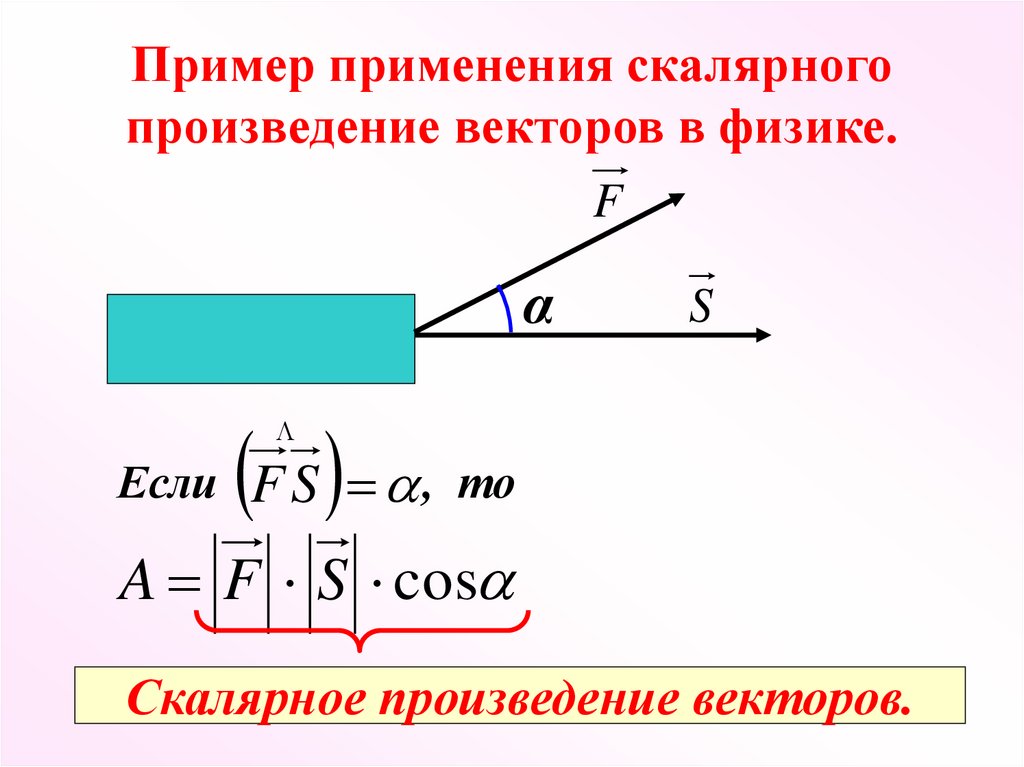
12. Пример применения скалярного произведение векторов в физике.
Fα
S
F S , то
Если
A F S cos
Скалярное произведение векторов.
13. Формула скалярного произведения векторов в пространстве.
а x1 ; y1 ; z1b x2 ; y2 ; z2
a b x1 x2 y1 y2 z1 z2
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
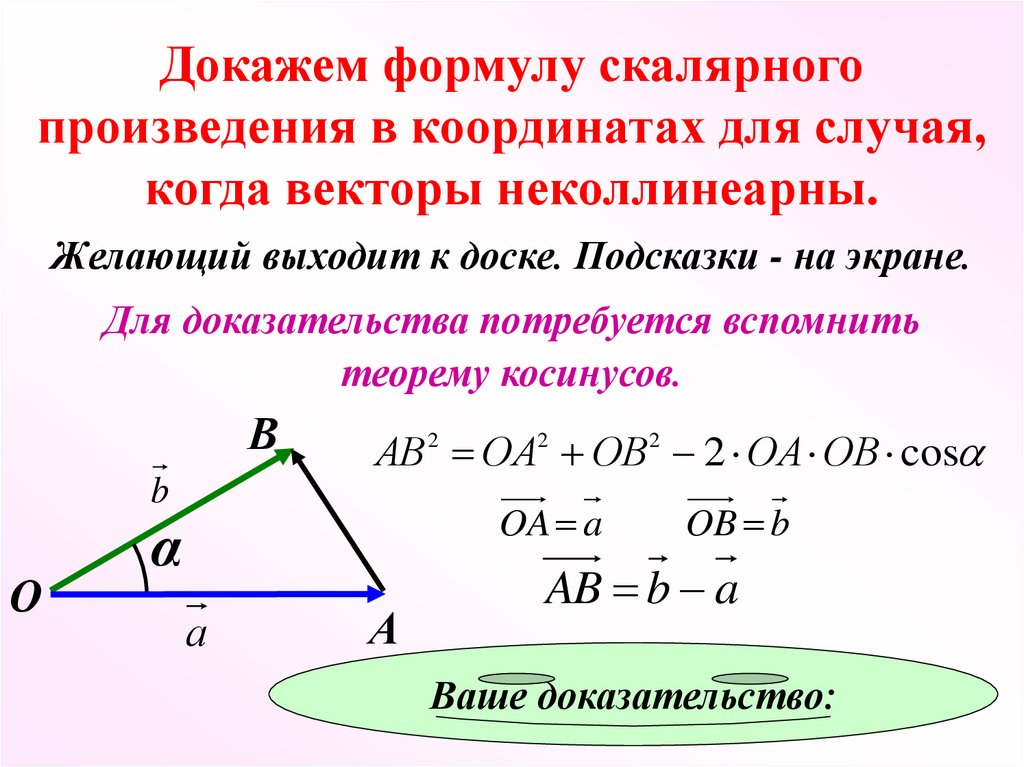
14. Докажем формулу скалярного произведения в координатах для случая, когда векторы неколлинеарны.
Желающий выходит к доске. Подсказки - на экране.Для доказательства потребуется вспомнить
теорему косинусов.
В
АВ 2 ОА2 ОВ2 2 ОА ОВ cos
b
О
OA a
α
а
А
OB b
AB b a
Ваше доказательство:
15. Дома, следуя рекомендациям в учебнике, вывести формулу cos α для двух ненулевых векторов в пространстве, зная их координаты.
cosx1 x2 y1 y2 z1 z 2
x y z x y z
2
1
2
1
2
1
2
2
2
2
«Геометрия 10-11», глава V, § 2, п.47.
+
№№ 141 (в – з); 443 (д; е)
2
2
16. Решение задач.
Дан куб АВСDA1B1C1D1.Найдите угол между векторами:
B1
В1 В и В1С
450
б) ВС и АС
450
а)
C
1
A1
D1
B
в) DA
и B1 D1
1350
A
C
D
17. № 443 (г)
Дано: куб АВСDA1B1C1D1;АВ = а; О1 – центр грани А1В1С1D1
Найти: ВА1 ВС1
1 способ:
ВА1С1 правильный
ВА1 ВС1 а 2
ВА ВС 60
C1
D1
A1
B1
1
0
1
ВА1 ВС1 а 2 а 2 cos60 а
0
Ответ: а2
D
2
A
C
B
18. № 443 (г)
Дано: куб АВСDA1B1C1D1;АВ = а; О1 – центр грани А1В1С1D1
Найти: ВА1 ВС1
2 способ:
ВА1 ВА АА1
A1
ВА1 ВС1 ?
ВС1 ВС СС1
C1
D1
B1
ВА1 ВС1 ВА АА1 ВС СС1
ВА ВС ВА СС1 АА1 ВС
D
АА1 СС1
0 0 0 а а cos0 a
0
2
A
C
B
Ответ: а2
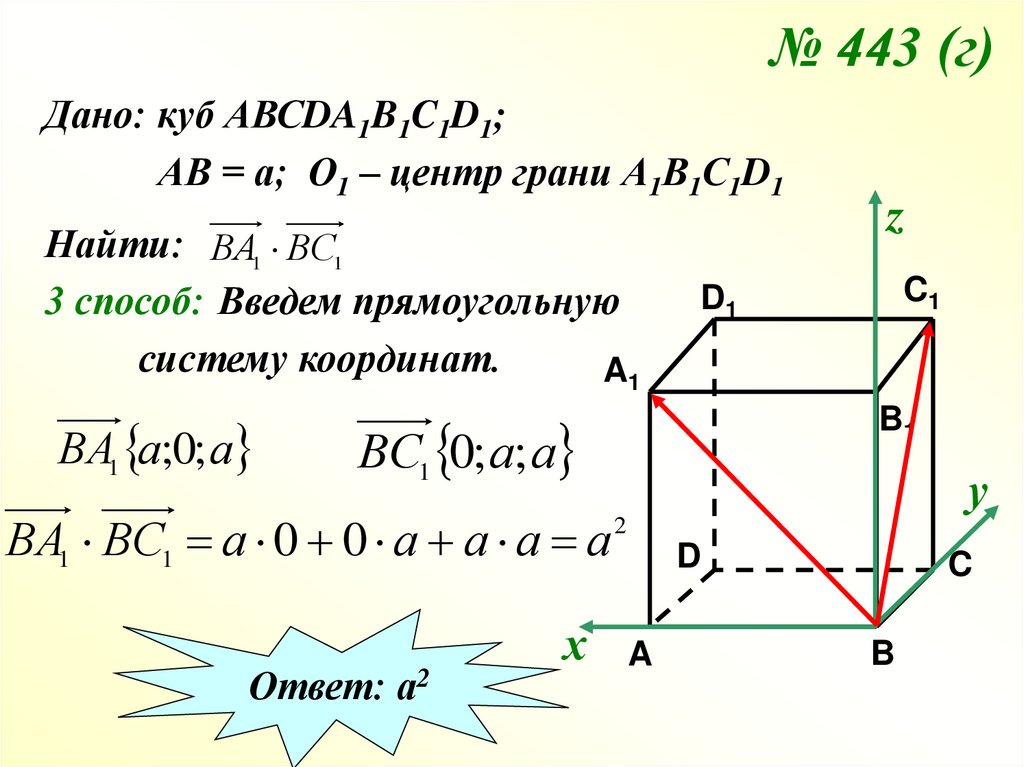
19. № 443 (г)
Дано: куб АВСDA1B1C1D1;АВ = а; О1 – центр грани А1В1С1D1
Найти: ВА1 ВС1
3 способ: Введем прямоугольную
систему координат.
A1
ВА1 а;0; а
Ответ: а2
х
C1
D1
ВС1 0; а; а
ВА1 ВС1 а 0 0 а а а а
z
B1
у
2
D
A
C
B
20. № 443
Решаем по группам:№ 443
1 – а)
а2
2 – б)
-2а2
3 – в)
0
Дополнительная задача:
Вычислите угол между вектором а и
координатным вектором i.
а 2;1;2
















 mathematics
mathematics








