Similar presentations:
Угол между векторами. Скалярное произведение векторов
1.
Угол между векторами.Скалярное произведение
векторов
2.
Повторение:• Какие векторы называются равными?
а
b
a
b
,если
a
b
;а
b
• Как найти длину вектора по координатам его
начала и конца?
В
АВ
х
х
у
у
В
А
В
А
2
2
А
• Какие векторы называются коллинеарными?
а b или а b
а
b
x1 x2
а b y1 y2
z z
2
1
3.
Повторение. (Устно)Векторы в пространстве.
; 2;4 В 4;3;2
1) Дано: А 3
30
Найти: АВ
; 5;0 С 5;0; 4 D 7; 2; 3
; 3;1 В 4
2) Дано: А 2
Равны ли векторы АВ и CD ?
Нет, т.к.равные векторы имеют равные
координаты.
2; 2; 1
АВ
2
CD
; 2;1
3) Дано: ? Коллинеарны ли векторы АВ и CD ?
А 1
; 3;4
В 9;1; 2
С 2;0;1
D 4
; 2;2
8;4; 6 CD
АВ
2
; 2;1
Нет
4.
Угол между векторами.b
ОА а ОВ b
ab
а
Если а b, то
0
Если а b то ab 180
А
0
α
О
аb 0
В
Если а b то ab 90
0
5.
Скалярное произведение векторов.Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.
а
b
a
b
a
b
cos
6.
Вспомним планиметрию…a
b a b cos
Если a b , то
cos90 0 a b 0
0
0
a
b
Если
, то cos
a b a b
180 1
Если а b , то
a b a b
cos0 1
0
2
2
b
a
a
a
a
a
a
Если a b , то a
Скалярное произведение a a называется
скалярным квадратом вектора
7.
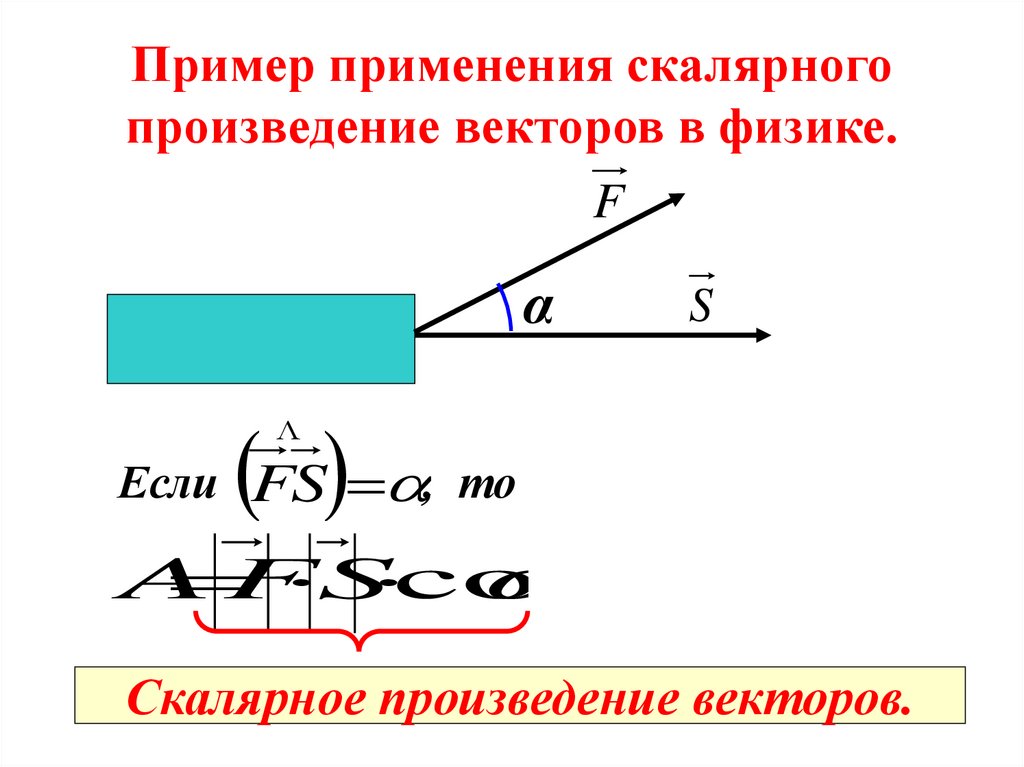
Пример применения скалярногопроизведение векторов в физике.
F
α
S
Если FS , то
A
F
S cos
Скалярное произведение векторов.
8.
Формула скалярного произведениявекторов в пространстве.
а x1;y1;z1
b x2;y2;z2
a
b
x
x
y
y
z
z
1
2
1
2
1
2
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
9.
Косинус угла между ненулевымивекторами
а x1;y1;z1
b x2;y2;z2
x
x
y
y
z
z
1
2
1
2
1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1
1
1
2
2
2
10.
Решение задач.Дан куб АВСDA1B1C1D1.
Найдите угол между векторами:
B1
В1 В и В1С
450
б) ВС и АС
450
а)
в) DA
и B1 D1
C1
A1
D1
B
1350
A
C
D
11.
№ 443 (г)Дано: куб АВСDA1B1C1D1;
АВ = а
Найти: ВА
1 ВС
1
1 способ:
C1
D1
ВА
С
правильный
A1
1
1
B1
ВА
ВС
а2
1
1
ВА
60
ВС
0
1
1
D
C
ВА
ВС
а
2
а
2
cos
60
а
1
1
0
Ответ: а2
2
A
B
12.
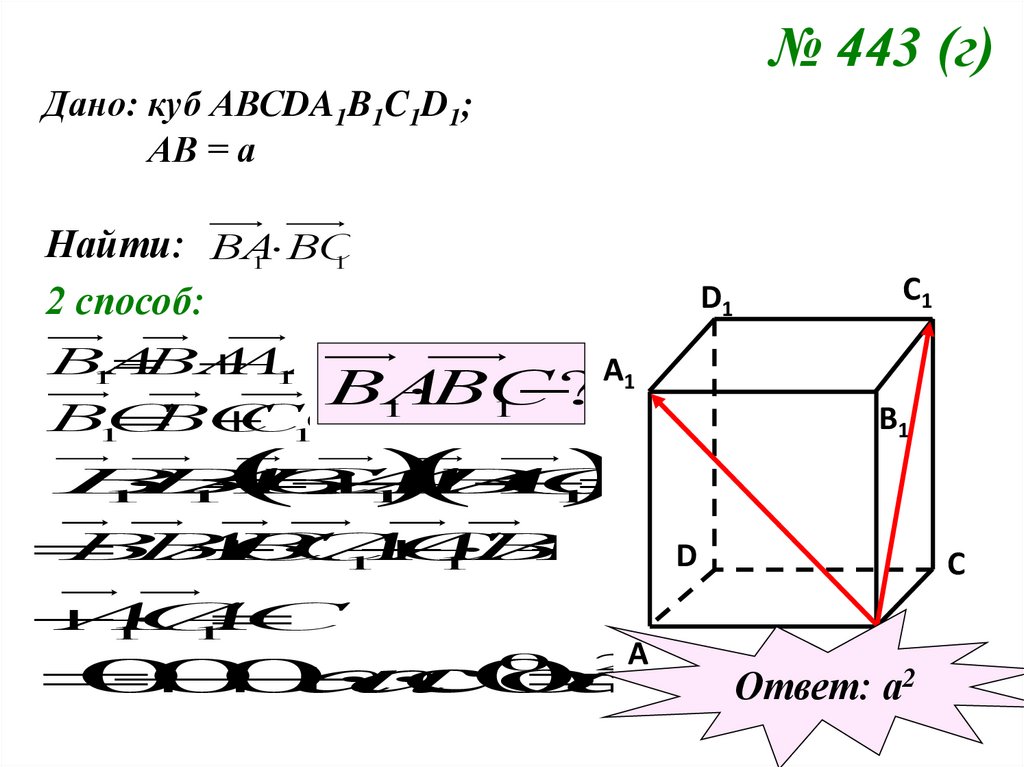
№ 443 (г)Дано: куб АВСDA1B1C1D1;
АВ = а
Найти: ВА
1 ВС
1
2 способ:
C1
D1
ВА
ВА
АА
A1
1
1
ВА
?
1 ВС
1
ВС
ВС
СС
1
1
B1
ВА
ВС
ВА
АА
ВС
СС
1
1
1
1
ВА
ВС
ВА
СС
АА
ВС
D
1
1
АА
СС
1
1
A
2
0
0
0
а
а
cos
0
a
0
C
B
Ответ: а2
13.
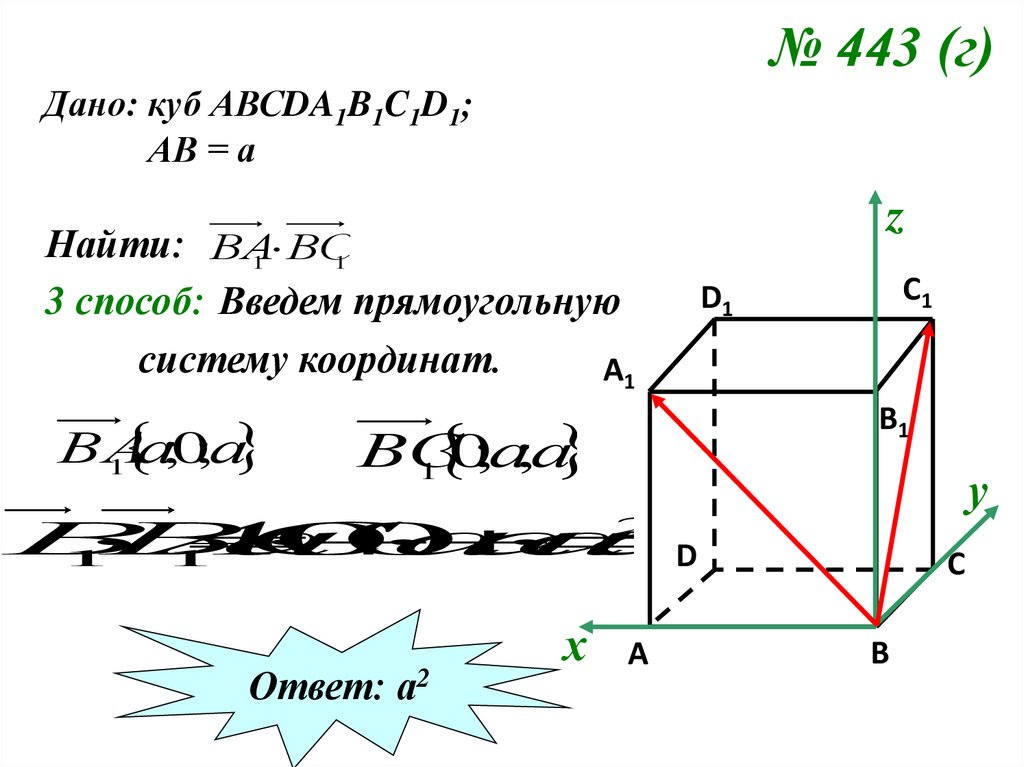
№ 443 (г)Дано: куб АВСDA1B1C1D1;
АВ = а
Найти: ВА
1 ВС
1
3 способ: Введем прямоугольную
систему координат.
A1
;0;а
ВА
1 а
z
C1
D1
B1
;а;а
ВС
1 0
у
ВА
ВС
а
0
0
а
а
а
а
D
1
1
2
Ответ: а2
х
A
C
B
14.
Скалярное произведение векторов.a
b
a
b
cos
а
b
а x1;y1;z1 b x2;y2;z2
a
b
x
x
y
y
z
z
1
2
1
2
1
2
x
x
y
y
z
z
1
2
1
2
1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1
1
1
2
2
2











 mathematics
mathematics








