Similar presentations:
Скалярное произведение векторов
1.
Скалярноепроизведение векторов
2. Устно:
1. cos 450 =2. tg 450 =
3. cos 600 =
4. sin 300 =
5. sin 600 =
6. sin 900 =
7. cos 900 =
8. tg 450 =
9. tg 900 =
10. sin2 x + cos2 y =
3. Диктант Даны точки A(2; -3), B(-1; 2), С(0; -4)
ABBC
1. Найдите координаты вектора AB
2. Найдите координаты вектора ВС
3. Найдите длину вектора AB
4. Найдите длину вектора BC
5. Произведение 5 · AB :
AB
BC
( 3 5)
( 1 6)
2
2
( 3) 5
2
1 ( 6)
5 AB
2
34
37
( 15 25)
4.
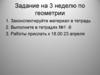
Угол между векторамиb
О
a
Угол между векторами
равен .
a b =
a
и
b
5.
Найдите угол между векторамиa b = 300
a
a c = 1200
d
300
c
b
f
b c = 900
d c = 1800
d f = 00
6.
ОпределениеСкалярным произведением двух
векторов называется произведение
их длин на косинус угла между ними.
a b = a b cos(a b )
Скалярное произведение векторов – число!
7.
Частный случай №1b
a
a b =
a b = 900
=0
a b cos 900 = 0
a b = 0
a b
8.
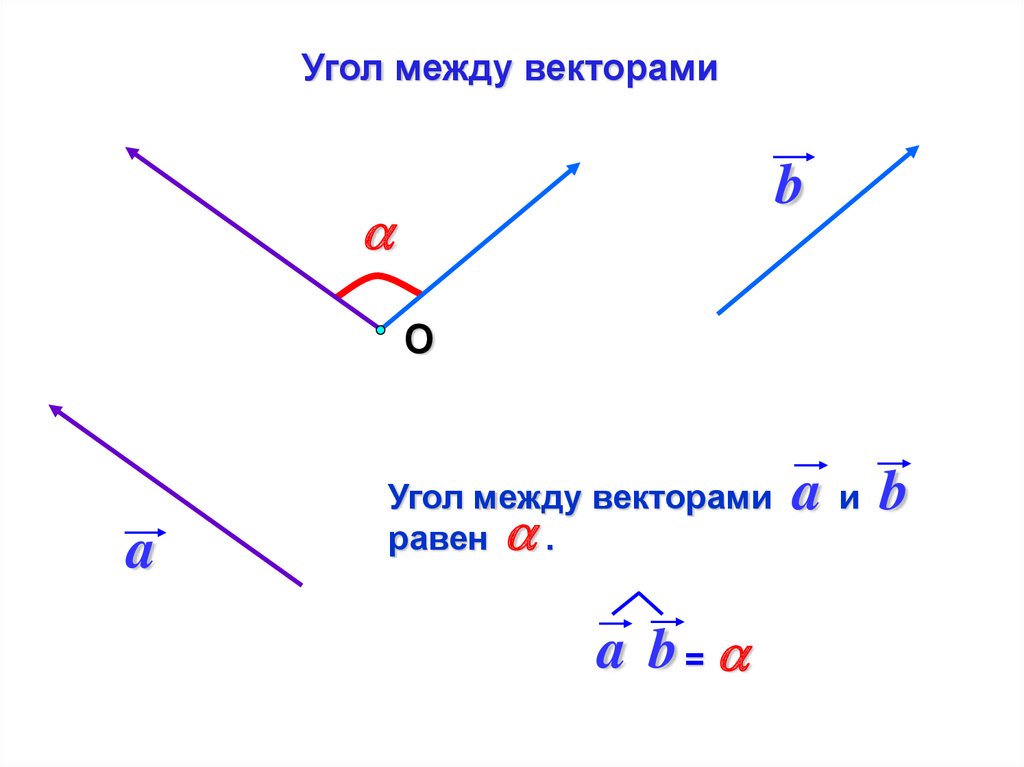
Частный случай №2a b < 900
b
a
a b =
>0
a b cos > 0
a b > 0 a b < 900
9.
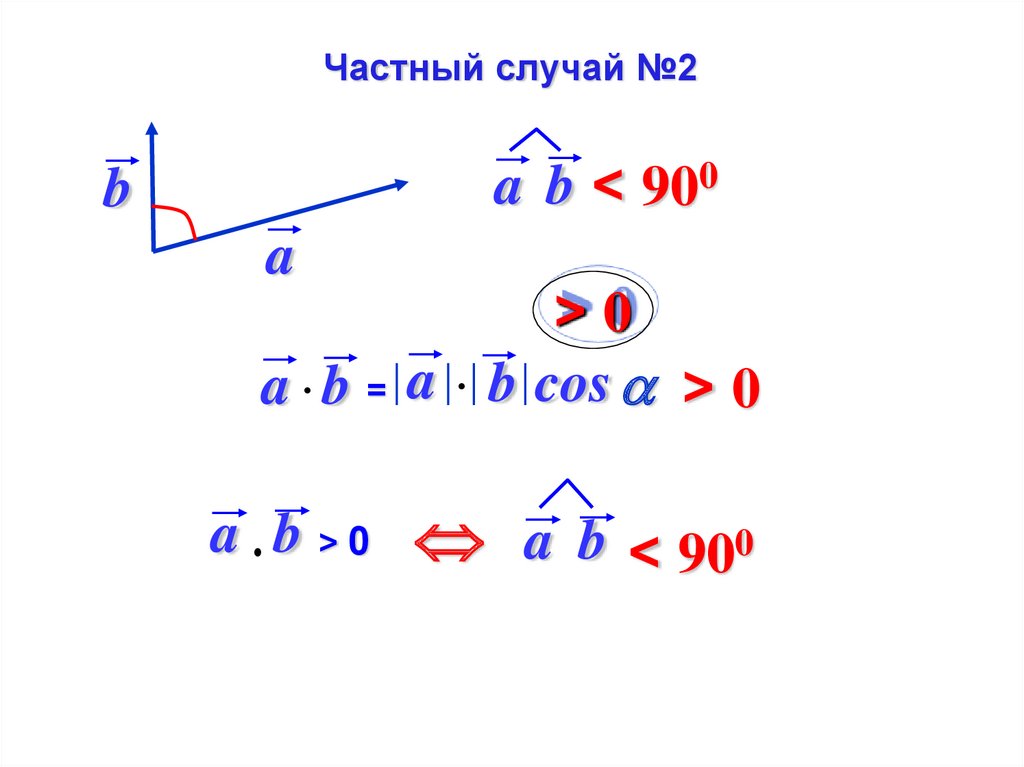
Частный случай №3b
a b > 900
a
a b =
<0
a b cos < 0
a b < 0 a b > 900
10.
Частный случай №4b
a b = 00
a
a b =
1
a b cos 00 = a b
b
a b = 1800
a
a b =
-1
a b cos1800 = – a b
11.
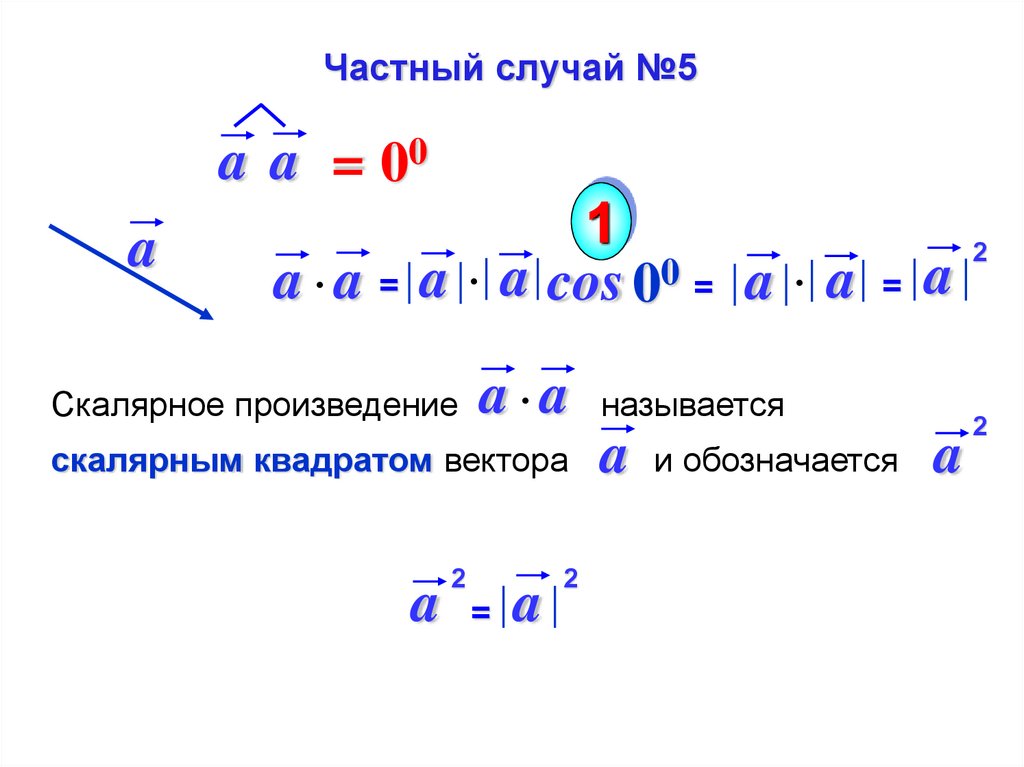
Частный случай №5a a = 00
a
a a =
1
a a cos 00 = a a
Скалярное произведение
a a
скалярным квадратом вектора
a
2
=
a
2
=
a
называется
a
и обозначается
a
2
2
12. Примеры:
1. a2 , b
2. a
5, b
3.
a
7, b
,
a
,
1
b
,
4.
5.
a
,
7 b
,3
,1
4
1
,
5
a b
0
60
0 a b
30
0
45
a b
0
120 a b
0
90 a b
0
2 3 cos 60
0
5 1 cos 30
0
7 4 cos 45
3
5 3
2
14 2
0
1 1 cos 120
0
7 5 cos 90
1
2
0
13.
тест1
ВС ВА =
ВС
ВА
ПОДУМАЙ!
1
2
9 3
9
cos ВС, ВА = 6 3 cos 600 = 18 12
В
600
6
ВЕРНО!
300
3
18
Проверка
ПОДУМАЙ!
С
А
14.
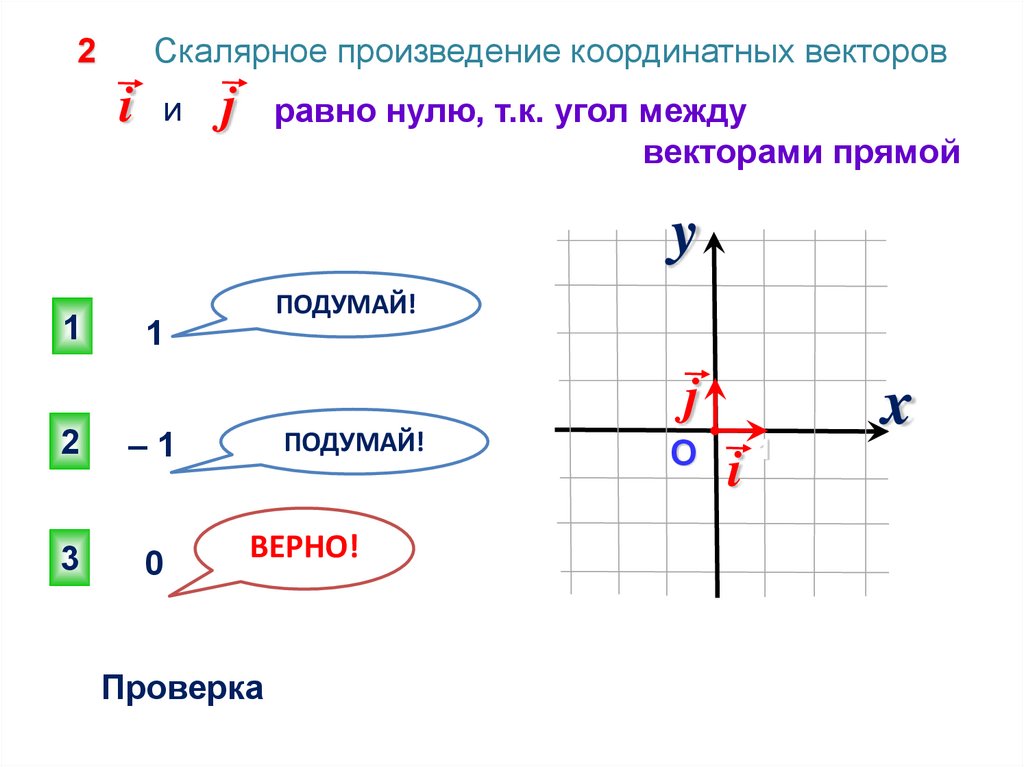
Скалярное произведение координатных векторов2
i
и
j
: равно нулю, т.к. угол между
векторами прямой
y
1
ПОДУМАЙ!
1
j
2
–1
3
0
ПОДУМАЙ!
ВЕРНО!
Проверка
О
x
i
1
15.
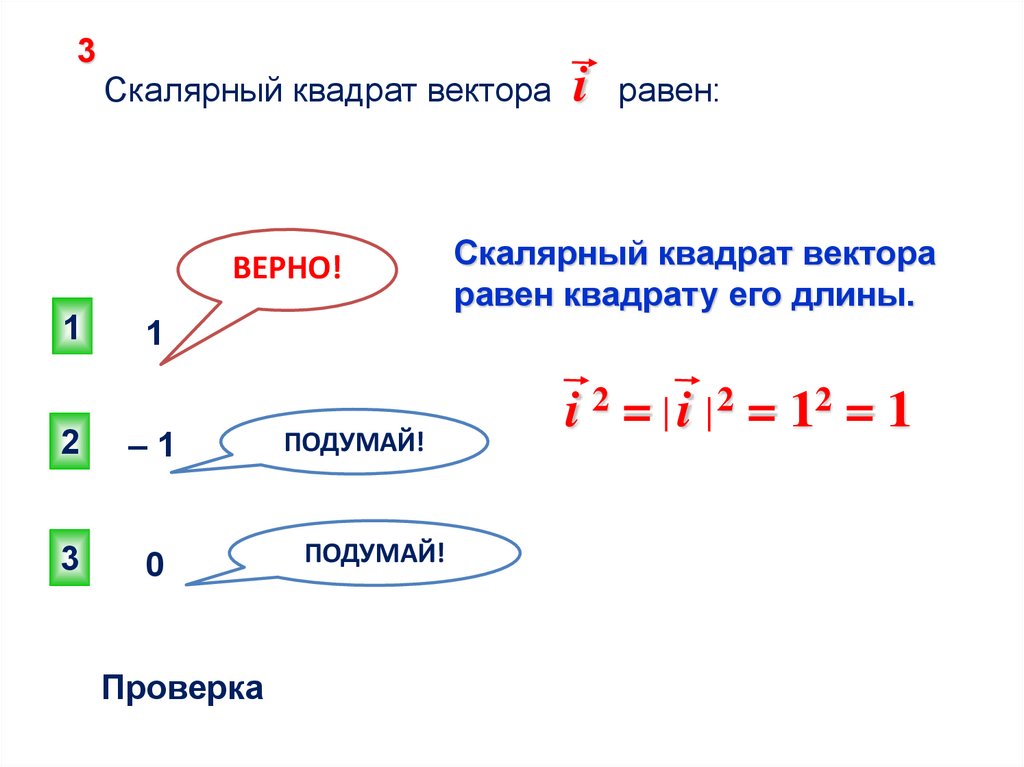
3Скалярный квадрат вектора
ВЕРНО!
1
i
равен:
Скалярный квадрат вектора
равен квадрату его длины.
1
2
–1
3
0
Проверка
ПОДУМАЙ!
ПОДУМАЙ!
i2= i
2
= 12 = 1
16.
a b = 12,12
a = 33,
b = 4,
4
то векторы a и b :
a b = a b cos a b
4 Если
ВЕРНО!
12 = 3 4 cos a b
cos a b = 1
a b = 00
ПОДУМАЙ!
если a
b
1
сонаправлены;
2
перпендикулярны;
3
противоположно направлены.
Проверка
ПОДУМАЙ!
17.
xy
=
–20
–20,
x
=
4
4,
5
то векторы x и y :
y = 5,
5
Если
x y = x y cos x y
ПОДУМАЙ!
1
–20 = 4 5 cos x y
сонаправлены;
ПОДУМАЙ!
2
3
перпендикулярны;
ВЕРНО!
противоположно направлены.
Проверка
cos x y = –1
x y = 1800
если
x
y
18.
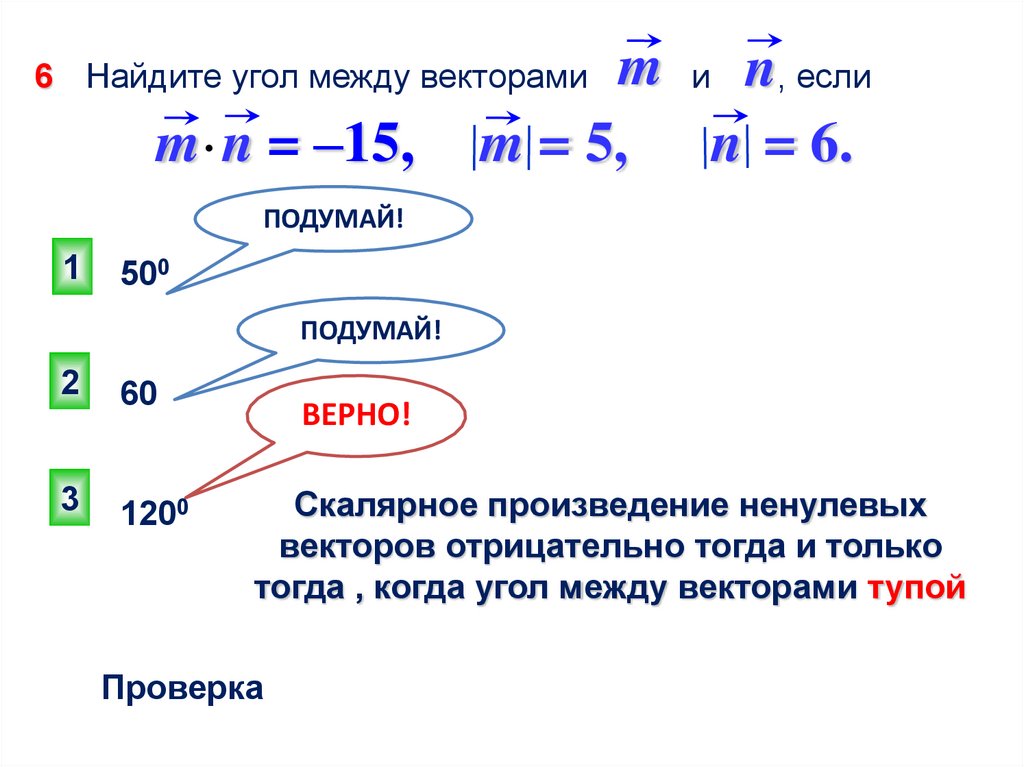
m и n, еслиm = 5, n = 6.
6 Найдите угол между векторами
m n = –15,
ПОДУМАЙ!
1
500
ПОДУМАЙ!
2
600
3
1200
ВЕРНО!
Скалярное произведение ненулевых
векторов отрицательно тогда и только
тогда , когда угол между векторами тупой
Проверка
19.
Формула для нахожденияскалярного произведения
через координаты векторов
a = x 1 i + y1 j
a b= ?
b = x2 i + y2 j
a b= (x1 i + y1 j) (x2 i + y2 j) =
= x1x2 + y1y2
a b = x1x2 + y1y2
20.
Пример №1Найти скалярное произведение векторов:
a {-6; 9}
b {-1; 0}
a b= x1x2 + y1y2
a b= -6 (-1) + 9 0 = 6
21.
Пример №2Найти скалярное произведение векторов:
a {0; 0}
b {22; 1}
a b= x1x2 + y1y2
a b= 0 22 + 0 1 = 0
22. Вычислите скалярное произведение векторов:
1.2.
a(1,1); b(1,2)
a b
a(-2,5); b(-9,-2)
a b
3.
a(-3,4); b(4,5)
4.
a(5,2); b(-9,4)
5.
a(-1,1); b(1,1)
a b
a b
a b
1 1 1 2
3
2 ( 9) 5 ( 2)
3 4 4 5
5 ( 9) 2 4
1 1 1 1
8
8
37
0
23.
a b = x1x2 + y1y2a b a b cos (a b)
a b
cos ( a b)
a b
x1 x2 y1 y 2
cos (a b)
a b
24. Дано:
a( 1 3) b( 5 2)1.
Вычислите скалярное произведение
векторов:
2.
Вычислите длину вектора a:
3.
Вычислите длину вектора b:
4.
Вычислите косинус угла между
a b
a
b
cos a b
векторами:
5.
Сделайте вывод: тупой, прямой или
острый угол мы получили
1 5 3 2
2
2
2
2
1 3
5 2
cos a b 0
11
10 29
11
10
29
11
290
угол острый















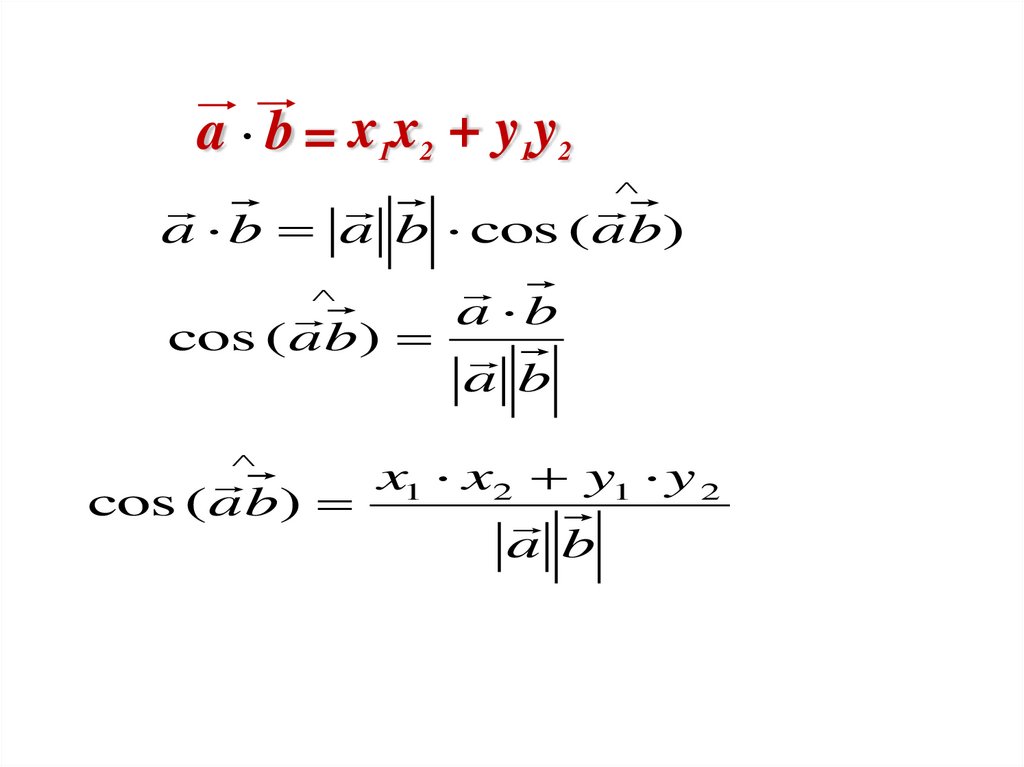

 mathematics
mathematics