1.12M

Category: $mathematics$ mathematics

Задача двух тел. Уравнения движения в задаче двух тел

1. Задача двух тел

2. Уравнения движения в задаче двух тел

Движение двух материальных точек
будем рассматривать в инерциальной
системе отсчета.
y
m2
m1
x
z
2

3.

m
F
k
r
x
c
o
s
r
m
F
m
x F
cos
krF
()
2
1
2
22
r
()
x
(
y
)
2
1
2
1
1
2
2
1
2
x2 3y
1z2
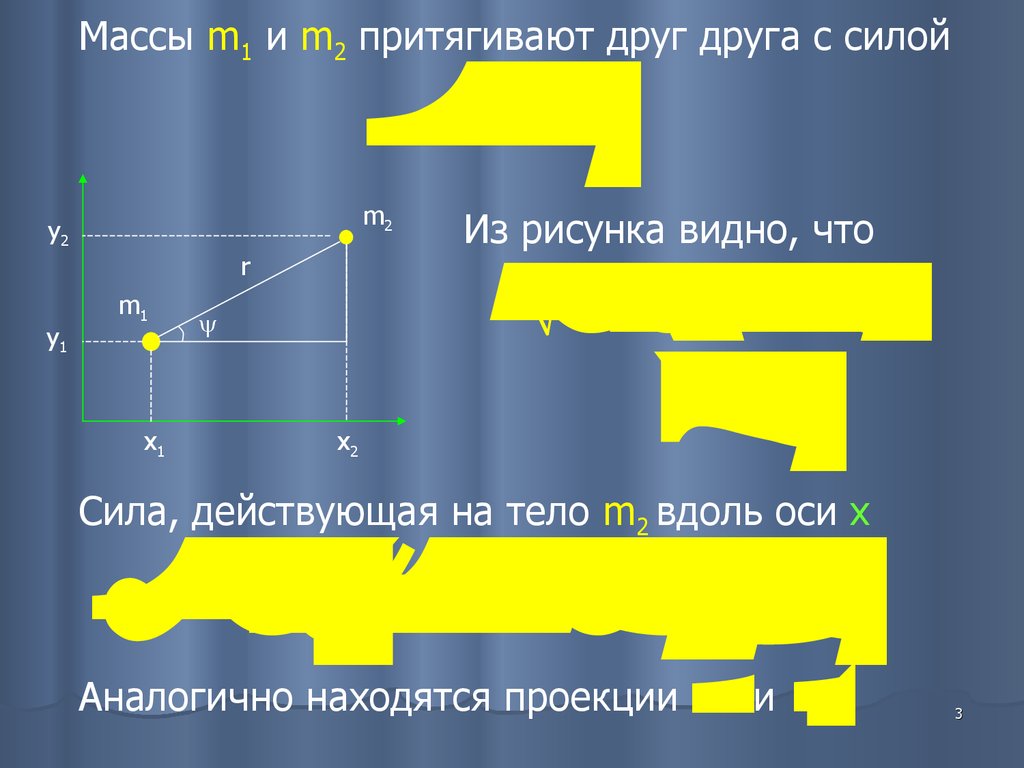
Массы m1 и m2 притягивают друг друга с силой
y2
m2
r
y1
m1
x1
Из рисунка видно, что
x2
Сила, действующая на тело m2 вдоль оси x
Аналогично находятся проекции
и
3

4.

2
k
m
1
xy
(z212
,krr2m
x
)
2
2
3
y31(z 2).
Уравнения движения тела m2, притягиваемого
телом m1 будут иметь вид
(1)
4

5.

2
k
m
xy
(z12
,krrm
x
)
12
1
3
2
y
z
.
1)
3(
Аналогично находим уравнения движения тела m1
под влиянием притяжения от тела m2
(2)
5

6.

2
k
()
m
1
2
xy
(
x
)
,
2
12
1
3
r
y
2
k
()
m
1
z2 12
r32(z 1).
Вычитая из (1) уравнения (2) находим
уравнения движения тела m2 относительно m1
6

7.

k
()
m
x x
,,
y
y
z
z
x
,
0
r
yr3z
0.
2
1
2
21321
Вводя обозначения
и
окончательно получим
(3)
7

8. Интегралы площадей

Умножаем первое уравнение системы (3) на –y,
второе – на x, и складываем их. Затем
складываем второе, умноженное на –z, с третьим,
умноженным на y и первое, умноженное на z с
третьим, умноженным на –x.
x
&
x& 3 0
r
y
&
y& 3 0
r
z
&
z& 3 0
r
y
x
z
z
y
x
8

9. Интегралы площадей

x
y a0123
,,,y
z 0a,zx
z 0.a
Интегралы площадей
В итоге получим:
Интегрируя эти соотношения, находим
(4)
9

10.

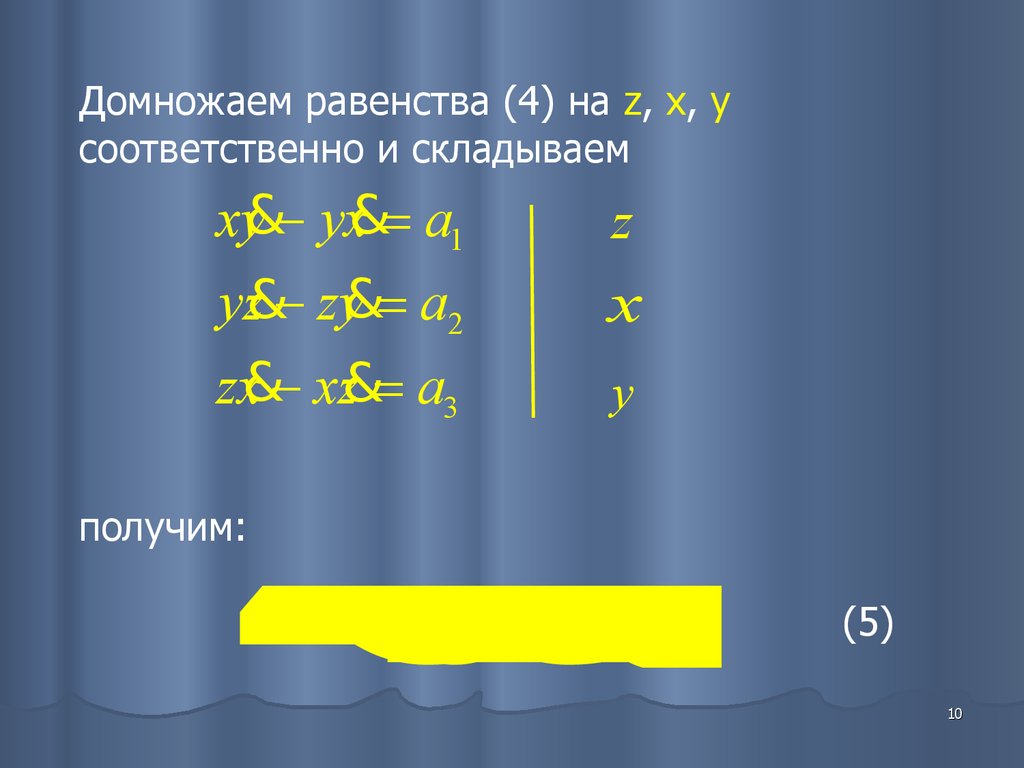
a1z 2xa3y 0
Домножаем равенства (4) на z, x, y
соответственно и складываем
xy& yx& a1
yz& zy& a2
x
zx& xz& a3
y
z
получим:
(5)
10

11.

Это уравнение плоскости, проходящей через
начало координат. В этой плоскости происходит
движение тела m2.
Постоянные а1, а2, а3 определяют положение
плоскости орбиты этого тела относительно осей
координат. Смысл этих постоянных можно
усмотреть из следующего рисунка.
11

12.

Q
y
R
r´
Δθ
θ
h
P
r
O
1
A
r
h
2
i
h
s
n
(
)
1
A
2r
Обозначим через ΔА –
площадь треугольника
OPQ, описанного радиусвектором за время Δt.
x
Поэтому
Из треугольника OPR
имеем
12

13.

A
1
s
i
n
(
)
r
tt
2
0
s
i
n
(
)
1
.
,dA
r
t 0122d t
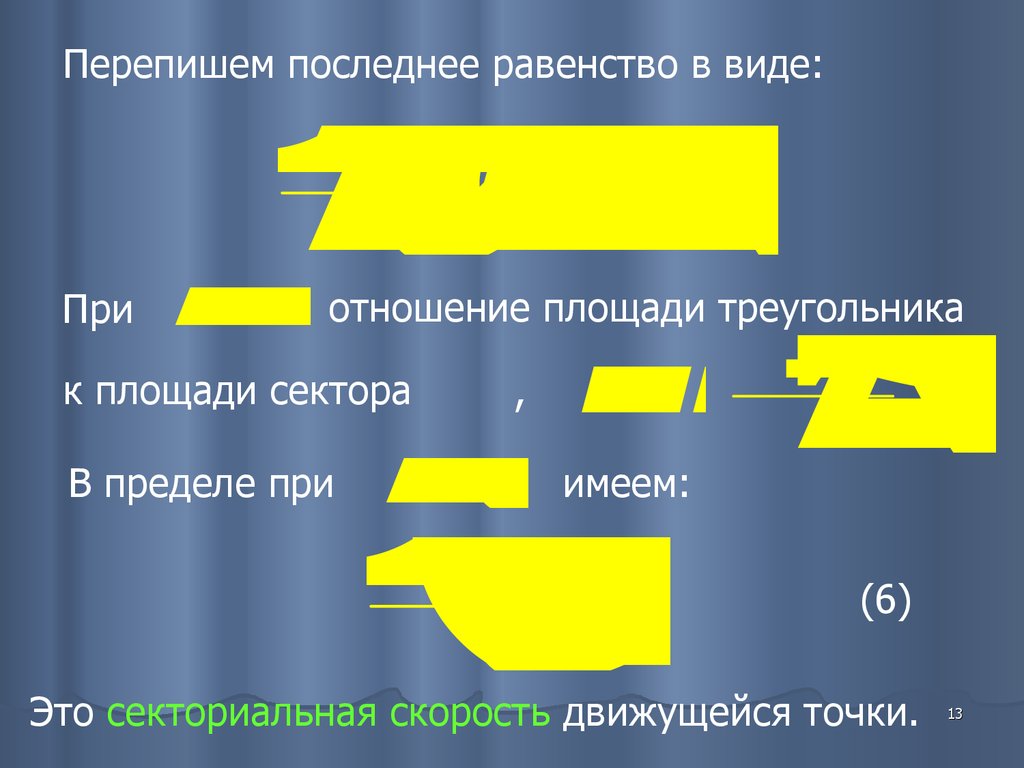
Перепишем последнее равенство в виде:
При
отношение площади треугольника
к площади сектора
В пределе при
,
имеем:
(6)
Это секториальная скорость движущейся точки.
13

14.

y
r axctg
yd A
,tx 12(ty
g
.x)x.
2
2
d
1
y
x
x
y
.
2
22
t r
Посмотрим теперь как будет выглядеть последнее
выражение в прямоугольных координатах:
Отсюда:
В итоге находим:
(!!!)
14

15.

c a a.
21232
Постоянные а1, а2, а3 – проекции удвоенной
секториальной скорости на плоскости xy, yz и zx!
Поэтому удвоенная секториальная скорость в
плоскости орбиты будет:
(7)
При решении астрономических задач положение в
пространстве плоскости орбиты принято
определять не коэффициентами ее уравнения, а
двумя углами Ω и i, имеющими смысл,
усматриваемый из следующего рисунка:
15

16.

z
Ω – долгота восходящего
y’
ζ
z’
S
Ωω
x’
x
Π
i
N
узла, отсчитывается от оси x в
сторону оси y (0°≤Ω≤360°);
i – наклон плоскости орбиты к
основной плоскости
(0°≤i≤90°).
Свяжем постоянные
y а1, а2, а3 с Ω и i.
Для этого перейдем
ξ
от системы
координат Sxyz к
системе Sx’y’z’ (в
ней орбита –
основная плоскость)
Сделаем два поворота: вокруг оси Sz на угол Ω и
вокруг оси Sx’ на угол i.
16

17.

xzy S B
C
x
c
o
s
y
s
i
n
,
.sin
y,
Поворот вокруг оси Sz на угол Ω
y
y´
x´
A
Ω
S
C
B
x
(8)
17

18.

xx
c
o
s
s
i
n
0
izz
yy
n0co01.
В матричной форме этот поворот можно записать
следующим образом:
(9)
18

19.

xx
x
,
yzii
y
c
o
s
i
z
s
i
n
,
z 1coi0nsiin
cco0isnozy.
Поворот вокруг оси Sx’ на угол i
z´
z″
y″
(10)
S
i
y´
В матричной форме:
(11)
19

20.

xxiix
c
o
s
s
i
n
0
1
0
0
x
izyiiy
yii
n
c
o
c
o
s
i
n
y
0
0
i
n
ii
c
o
s
z
c
o
s
c
o
s
i
n
s
iziiz
n0 incos
Таким образом, после двух поворотов, имеем:
Перемножив поворотные матрицы получим:
(12)
20

21.

aii
coin0s
ca123
oc
ssinin
sco
is ncos
0c
123
Так как компоненты удвоенной секториальной
скорости в системе координат Oxyz есть а1, а2, а3, а
в плоскости орбиты – 0, 0, с, то они связаны друг с
другом при помощи последнего соотношения:
Отсюда:
(13)
21

22.

xy
iz n.co
c
s
,s
Перепишем теперь интегралы площадей:
(14)
Осталось связать здесь с элементами орбиты
постоянную c. Для этого найдем сначала из
уравнений движения (3) интеграл живых сил
(интеграл энергии).
22

23.

,x
x
y
z
yz
r3(x
yz
)
Умножим первое, второе и третье уравнения
системы (3) на
x
&
x& 3 0
r
y
&
y& 3 0
r
z
&
z& 3 0
r
&
x
y&
z&
Сложив, получим:
23

24.

x
y
z
(
x
y
z
)
3
r
1
d
2
2
2
x
y
z
111
2
t
dd
d
r
d
2
2
22
x
y
z
r
22
rdtrdt t t r
3
32
Левую часть равенства
можно переписать в виде:
Правую – в виде:
24

25.

11
d
d
2
2
2
h2x t2 x y2 yz 2 z 2 r ht r
Таким образом, имеем:
Интегрирование последнего выражения дает
нам интеграл энергии:
(15)
Здесь
– постоянная интеграла энергии.
25

26.

r x2 y2
Так как движение происходит в плоскости, то
координата z″=0, а радиус-вектор
Интеграл площадей и интеграл живых сил в
плоскости орбиты будут иметь вид
x y& y x& c
x& y& 2 h
r
2
2
26

27.

x
x
r
c
o
s
u
,
y
r
s
i
n
u
rcosu r2u
2
i n2c,
r h .
r
c
o
s
u
Перейдем теперь от прямоугольных координат x
″, y″ к полярным координатам r, u
Интеграл площадей и интеграл живых сил в
полярных координатах будут иметь вид
(16)
(17)
27

28.

2
c
2
r
2
h
r
2
rdrt
d
c
2
h
tdutr r c2r du cr
Из равенств (16) и (17) имеем
c
u& 2
r
Таким образом
(18)
При помощи (16) можно найти
28

29.

d
c
c
2
h
u
r
r
r
c r
c
2
h
2
rc
r
c
q r,2
Q
hc.
2
2
22
2
2
Уравнение (18) можно переписать в виде:
Преобразуем подкоренное выражение:
Обозначим:
29

30.

Имеем:
Далее
d duqdQ
q
Q
q
Q
1
.
Q
u
.1q.
1
Q
, 1d
du.
Введем замену
Получим:
2
222
22
или
30

31.

r Q
u
a
c
o
s
cq o
s(2 h
cr
) cr22.h 2cos(u
),
Последнее выражение можно проинтегрировать
где ω – постоянная интегрирования.
Отсюда
Но
Поэтому
31

32.

1
1
2
h
c
o
s
(
u
)
.
rr
c
.
c
1
2
h
c
o
s
(
u
)
p
p
a
(
1
e
)
,1
ecosva
или
Отсюда
2
2222
2
Сравнивая теперь со стандартным уравнением
конического сечения
– параметр орбиты
где
– большая полуось
– эксцентриситет
32

33.

находим:
c p
,uh
v2
.a
u
,v
Здесь ω – аргумент перицентра (угловое
расстояние перицентра от узла).
– аргумент широты.
P
Ω
r
v
ω
Π
Т.о. мы определили
постоянные c и h через
общепринятые элементы
a, e, p.
33

34.

2
1
dV
.(1 arc(1oe
vrt a
a
s)ve,).
22
22
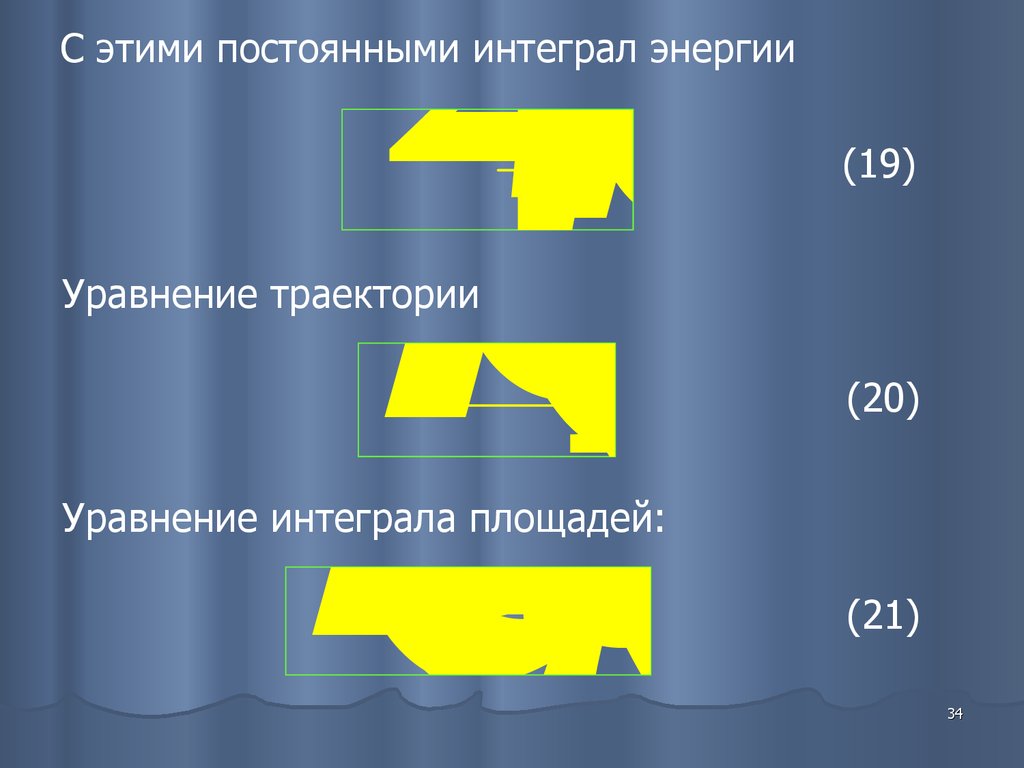
С этими постоянными интеграл энергии
(19)
Уравнение траектории
(20)
Уравнение интеграла площадей:
(21)
34

35.

C
S
N
S
a
e
,
a
c
o
s
E
,
N
r
v
.
a
e
r
c
o
s
rcosv(cosE
e).
Введем для случая эллиптического движения
некоторую вспомогательную переменную –
эксцентрическую аномалию E:
y
B
A
M‫׳‬
M
r
E
C
η
N
v
S
Из рис. видно, что
ξ
Π x
Поэтому:
Т.е.
(22)
35

36.

b
M
N
y
b 1
rsei2n,va
a
s(1c oes2E
a
in)E
,.M
N
rsinv.
Отношение малой и большой полуоси будет:
(см. след. слайд)
Здесь
Отсюда имеем:
(23)
Возводя (22) и (23) в квадрат и складывая,
получим:
(24)
36

37.

x2/a2+y2/b2=1 – уравнение эллипса
x'2/a2+y'2/a2=1 – уравнение окружности
x=x'
y=MN
y‘=M‘N
37

38.

2
1
e
s
i
n
E
scionv co.,
Подставляя (24) в (22) и (23), получим
соотношения, связывающие истинную и
эксцентрическую аномалии:
(25)
Можно найти также соотношения, связывающие
тангенсы половинных углов v и E:
38

39.

r1 1
c cvv
oossv2v
(in 22
a
)122
,vv
1
e
c
o
s
E
)
.
e
1
c
o
s
E
,tg2v 1
2
c
o
s
,
e tgE
.2
(25’)
Делим первое на второе:
Используя тригонометрические соотношения
окончательно находим:
(26)
39

40.

1
d
v
1
e
1
d
E
.
vE
tcosdE
t
22
c
o
s
22
E
2
st 2v1
c
o
edvt.
Найдем теперь уравнение, связывающее
переменную E со временем. Дифференцируя
соотношение (26) получим:
Отсюда
40

41.

E
11
v
cos2 (1 cosE
),cos2 (1 cosv),
22
Учитывая, что
Имеем
dE 1 CosE 1 e dv
dt 1 Cosv 1 e dt
Из интеграла площадей (21)
2
a
(1
e
)
dv
dt
r2
41

42.

d
E
1
,
3
t(1
a
e
c
o
s
E
ecos)3.
Используя также выражение для радиус-вектора
(24)
r a (1 e cos E ).
и второе из соотношений (25’)
r r cos v a(1 e)(1 cos E ).
находим:
Откуда имеем
42

43.

i nE
E
e
s
a3(t
).
Интегрируя, находим:
(27)
Здесь
– постоянная интегрирования (момент
прохождения через перигелий), а само
уравнение – знаменитое уравнение
Кеплера.
Чтобы связать движение в плоскости орбиты с
движением в пространстве, надо сделать еще
один поворот системы координат.
43

44.

xyz coin0s
x
c
o
s
s
i
n
,
y
izcsoi0n
n
c
o
.10
.
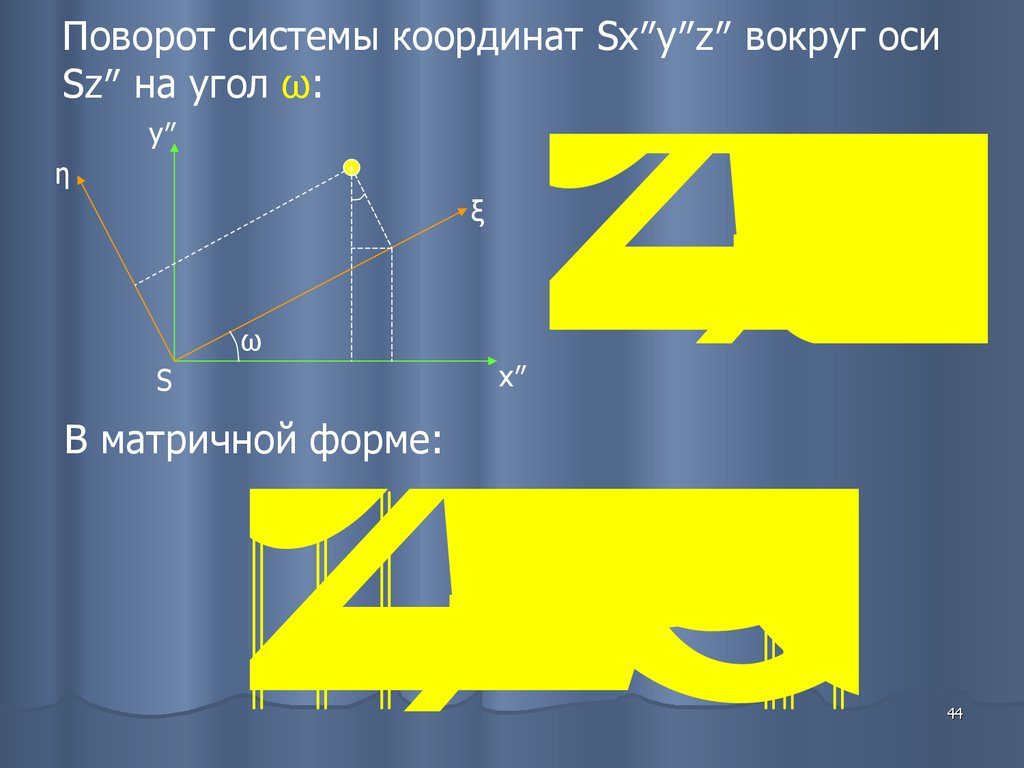
Поворот системы координат Sx″y″z″ вокруг оси
Sz″ на угол ω:
y″
η
ξ
ω
S
x″
В матричной форме:
44

45.

x
,X
{
y(i)
z} Z(
)X
iZ
(i
){
,
0}Z
(
)
xyz coin0s
scoi0n
01coi0nsii
0
c
o
s
s
i
n
0
icosn0co01
.
Таким образом, получить выражения для
координат x, y, z через элементы орбиты можно
при помощи трех поворотных матриц:
Сокращенно это можно записать так:
(28)
где
– матрица, соответствующая повороту
вокруг оси абсцисс на угол , а
и
матрицы поворота вокруг оси аппликат на угол
соответственно.
и угол
45

46.

rcionsv
a(c1osE
e2in),.
Так как движение в задаче двух тел происходит
в плоскости, то в прямоугольной орбитальной
системе координат {ξ, η, ζ} координата ζ=0, а
координаты ξ и η, как это следует из рисунка на
слайде 35 и соотношений (22) и (23)
(29)
46

47.

iM
E
e
s
n
E
M
,
n(nt )
./a3
Уравнение Кеплера, связывающее
эксцентрическую аномалию и время, обычно
записывают в виде:
где
средняя аномалия
Среднюю аномалию обычно представляют в виде
M n(t t 0 ) M 0 где M 0 n(t 0 )
Величина
есть среднее движение
по орбите.
47