Задача о положении механизмов параллельной структуры

1. Прямая задача о положении механизмов параллельной структуры

2. Постановка задачи

По заданному вектору обобщенных координат манипулятора
q=(q1, q2 , ..., qN )T
найти положение и ориентацию его схвата s = f (q) .
Кафедра мехатроники и робототехники М6-КФ
Постановка задачи

3. Платформа Гью-Стюарта 6-3 (Робот 6-3)

B2 B3
z
r
x
B1 B6
L L1 L2 ... L6
y
o
- обобщенные координаты
hmp
B4 B5
L5
X xo
L4
L6 L
1
L2
A5
A6
X
A1
A4
b
L3
A3
R
zo ,
- положение и ориентация платформы
Z
O
yo
Y
A2
hb
R , , p x0 , y0 , z0
T X
,
0
1
Кафедра мехатроники и робототехники М6-КФ
Платформа Гью-Стюарта 6-3 (Робот 6-3)

4. Решение с помощью вычисления аналитического уравнения плоскости

z (n)
c
Δbc
o
Δac
y
Δab
r
a
α
b
x
Z
L4
L5
L6
E
D
F
L1
L2
B
X
xc xa
y ya
yb ya
yc ya 0,
z za
zb za
zc z a
L3
Y
A
xb xa
( x xa )d1 ( y ya )d 2 ( z za )d3 0,
O
R
x xa
C
d1 ( yb ya )( zc za ) ( yc ya )( zb za ),
d 2 ( xb xa )( zc za ) ( xc xa )( zb za ),
d3 ( xb xa )( yc ya ) ( xc xa )( yb ya ).
Кафедра мехатроники и робототехники М6-КФ
Решение с помощью вычисления аналитического
уравнения плоскости

5. Координаты шарниров основания

2
2
4
4
R c b R c 3 b R c 3 b R c 3 b R c 3 b R c b
2
2
4
4
A R s b R s b R s b R s b R s b R s b ,
3
3
3
3
hb
hb
hb
hb
hb
hb
1
1
1
1
1
1
cos c
sin s
Кафедра мехатроники и робототехники М6-КФ
Координаты шарниров основания

6. Полученная система уравнений

2
2
2
2
x
x
y
y
z
z
a
b
a
b
ab ,
a b
2
2
2
2
x
x
y
y
z
z
a c
a
c
a
c
ac ,
2
2
2
2
x
x
y
y
z
z
b c b
c
b
c
bc ,
2
2
2
xa A1,1 ya A 2,1 za A 3,1 L21 ,
2
2
2
2
x
A
y
A
z
A
L
b 2,2 b 3,2 2 ,
b
1,2
2
2
2
xb A1,3 yb A 2,3 zb A 3,3 L23 ,
x A 2 y A 2 z A 2 L2 ,
1,4
c
2,4
c
3,4
4
c
2
2
2
2
x
A
y
A
z
A
L
1,5
c
2,5
c
3,5
5,
c
2
2
2
2
xa A1,6 ya A 2,6 za A 3,6 L 6 .
ab , ac , bc
– расстояние между шарнирами
подвижной платформы
Li , i 1..6
– элементы вектора обобщенных
координат манипулятора
Кафедра мехатроники и робототехники М6-КФ
Полученная система уравнений

7.

xa xb xc
xo
3
ya yb yc
yo
3
za zb zc
zo
3
Каноническое уравнение плоскости:
Ax By Cz D 0,
A d1
B d 2
C d3
D xa d1 ya d 2 za d3
Кафедра мехатроники и робототехники М6-КФ
Координаты вспомогательной точки:

8. Элементы матрицы поворота

Направляющие косинусы оси ОZ
cos oz
A
A B C
2
2
2
cos oz
,
B
A B C
2
2
Направляющие косинусы оси ОX
cos ox
cos ox
cos ox
xa
xa xb xc
3
2
2
2
2
2
2
2
xa xb xc
ya yb yc
za zb zc
x
y
z
a
a
a
3
3
3
ya
ya yb yc
3
2
xa xb xc
ya yb yc
za zb xc
x
y
z
a
a
a
3
3
3
za
2
za zb zc
3
xa xb xc
y yb yc
z z z
ya a
za a b c
xa
3
3
3
,
,
,
2
,
cos oz
C
A B C
2
2
2
,
Кафедра мехатроники и робототехники М6-КФ
Элементы матрицы поворота

9. Элементы матрицы поворота и вектора переноса

Направляющие косинусы оси ОY
cos oy cos oz cos ox cos oz cos ox ,
cos oy cos oz cos ox cos oz cos ox ,
cos oy cos oz cos ox cos oz cos ox .
Элементы вектора переноса
o xo
yo
xa xb xc
3
ya yb yc
zo
hmp n.
3
z
z
z
a b c
3
Кафедра мехатроники и робототехники М6-КФ
Элементы матрицы поворота и вектора переноса

10. Искомая матрица однородного преобразования

cos ox
cos o x
T X
cos ox
0
cos oy
cos oz
cos oy
cos oz
cos oy
cos oz
0
0
xo
yo
.
zo
1
Кафедра мехатроники и робототехники М6-КФ
Искомая матрица однородного преобразования

11. Платформа Гью-Стюарта 6-6 (Робот 6-6)

B5
B6
r
z
B4
o
x mp
hmp
B5
y
x
B2 B3
B1
B6
o
B1 mp
B4
y
r B2
hmp
B3
L2
L6
L1
L4
A4
b
A6
A3
O
R
A1
L4
L2
L3
L3
Z
A5
L5
L6
L5
X
z
L1
hb
Y
X
A2
A6
A1
Z
A5
b
A4
O
R
A3
Y
A2
hb
Кафедра мехатроники и робототехники М6-КФ
Платформа Гью-Стюарта 6-6 (Робот 6-6)

12. Введение виртуальных точек

V
B2
B3
y
WB5 B6U 2r sin mp
mp
r
B1
o
U
x
mp
3
B4
W
B5
B6
B5 B6 2r sin mp
3
Кафедра мехатроники и робототехники М6-КФ
Введение виртуальных точек

13. Координаты шарниров, выраженные через виртуальные точки

B2 xB
B3 xB
B4 xB
B5 xB
B6 xB
yB1
zB1 xU K xV xU yU K yV yU zU K zV zU ,
2
yB2
zB2 xV K xV xU yV K yV yU zV K zV zU ,
3
yB3
z3 xV K xW xV yV K yW yV zV K zW zV ,
4
yB4
5
yB5
6
yB6
B1 xB1
zB xW K xU xW
zB xU K xW xU
zB4 xW K xV xW yW K yV yW zW K zV zW ,
5
yW K yU yW zW K zU zW ,
6
yU K yW yU zU K zW zU ,
Коэффициент линейной пропорциональности K
r sin mp
2r sin mp r sin mp
3
Кафедра мехатроники и робототехники М6-КФ
Координаты шарниров, выраженные через
виртуальные точки

14.

xB1
yB1
C
z B1
1
xB2
xB3
xB4
xB5
yB2
yB3
yB4
yB5
z B2
z B3
z B4
z B5
1
1
1
1
xB6
yB6
.
z B6
1
Кафедра мехатроники и робототехники М6-КФ
2
2
2
2
x
x
y
y
z
z
U
V
U
V
UV ,
U V
2
2
2
2
x
x
y
y
z
z
U W
U
W
U
W
UW ,
2
2
2
2
x
x
y
y
z
z
VW
,
V
W
V
W
V
W
2
2
2
2
C
A
C
A
C
A
L
1,1
1,1
2,1
2,1
3,1
3,1
1,
2
2
2
2
C1,2 A1,2 C2,2 A 2,2 C3,2 A3,2 L 2 ,
2
2
2
C1,3 A1,3 C2,3 A 2,3 C3,3 A 3,3 L23 ,
C A 2 C A 2 C A 2 L2 ,
1,4
2,4
2,4
3,4
3,4
4
1,4
2
2
2
2
C
A
C
A
C
A
L
1,5
2,5
2,5
3,5
3,5
5,
1,5
2
2
2
2
C1,6 A1,6 C2,6 A 2,6 C3,6 A3,6 L 6 .

15. Элементы матрицы поворота

Направляющие косинусы оси ОZ
cos oz
A
A B C
2
2
2
cos oz
,
B
A B C
2
2
Направляющие косинусы оси ОX
cos ox
cos ox
cos ox
xU
xU xV xW
3
2
2
2
2
2
2
2
xU xV xW
yU yV yW
zU zV zW
x
y
z
U
U
U
3
3
3
yU
yU yV yW
3
2
xU xV xW
yU yV yW
zU zV zW
x
y
z
U
U
U
3
3
3
zU
2
zU zV zW
3
xU xV xW
y yV yW
z zV zW
yU U
zU U
xU
3
3
3
,
,
,
2
,
cos oz
C
A B C
2
2
2
,
Кафедра мехатроники и робототехники М6-КФ
Элементы матрицы поворота

16. Элементы матрицы поворота и вектора переноса

Направляющие косинусы оси ОY
cos oy cos oz cos ox cos oz cos ox ,
cos oy cos oz cos ox cos oz cos ox ,
cos oy cos oz cos ox cos oz cos ox .
Элементы вектора переноса
o xo
yo
xU xV xW
3
y yV yW
zo U
3
zU zV zW
3
h n.
mp
Кафедра мехатроники и робототехники М6-КФ
Элементы матрицы поворота и вектора переноса

17. Искомая матрица однородного преобразования

cos ox
cos o x
T X
cos ox
0
cos oy
cos oz
cos oy
cos oz
cos oy
cos oz
0
0
xo
yo
.
zo
1
Кафедра мехатроники и робототехники М6-КФ
Искомая матрица однородного преобразования

18. Моделирование движения механизма

Алгоритм:
1. Выбрать закон изменения обобщенных координат.
2. Если закон непрерывный – дискретизировать.
3. Для набора дискретных значений решить прямую
задачу.
4. Отобразить график движения.
Дискретный закон движения:
Li ,n 1 Li ,n
Li , f Li ,s
N
t , n 0..N , Li ,0 Li ,s ,
Кафедра мехатроники и робототехники М6-КФ
Моделирование движения механизма

19. Численный пример

r 50
20
0
1
0
1
2
3
4
t
5
6
7
-1
8
40
1
20
0
0
y
b mp
40
0
z
hb hmp 5
0
1
2
3
4
t
5
6
7
-1
8
200
1
150
0
100
x
R 100
0
1
2
3
4
t
5
6
7
8
-1
18
0
1
2
3
4
t
5
6
7
8
0
1
2
3
4
t
5
6
7
8
0
1
2
3
4
t
5
6
7
8
Кафедра мехатроники и робототехники М6-КФ
Численный пример

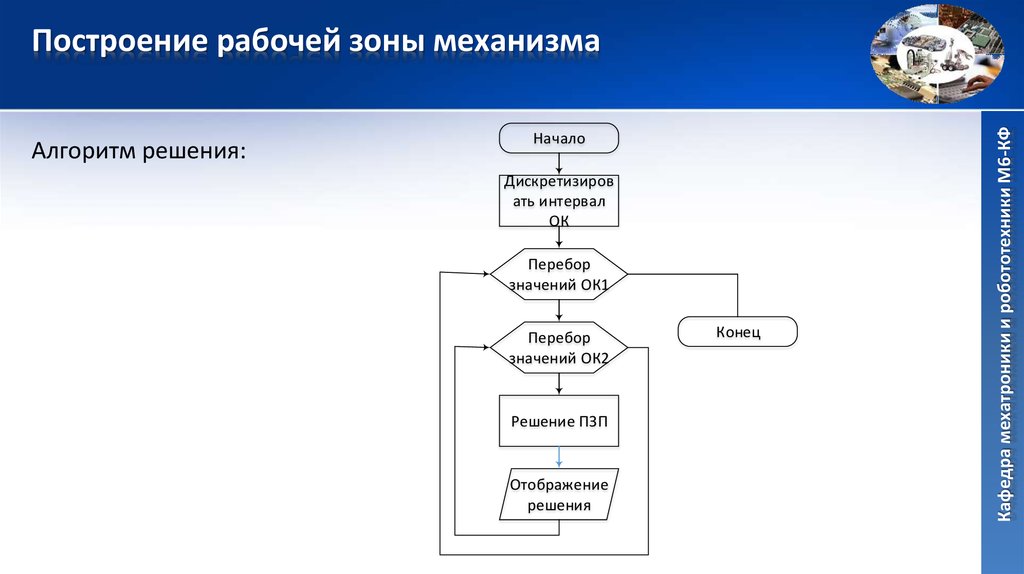
20. Построение рабочей зоны механизма

Алгоритм решения:
Начало
Дискретизиров
ать интервал
ОК
Перебор
значений ОК1
Перебор
значений ОК2
Решение ПЗП
Отображение
решения
Конец
Кафедра мехатроники и робототехники М6-КФ
Построение рабочей зоны механизма