Similar presentations:
Системы координат, применяемые в механике полета
1. ЛЕКЦИЯ 2 2.1. Системы координат, применяемые в механике полета
• инерциальные СК,• земные СК
• подвижные, т.е. движущимися вместе с ЛА.
Стандартизация различных СК - ГОСТ №20058-80
2.
Общий принцип построения СК:• выбирается основная координатная плоскость системы
• направление основной оси и расположение начала отсчета
(начала СК).
• оговаривают, соответствует их положение некоторому
фиксированному моменту времени или оно выбирается
средним за некоторый промежуток времени.
3.
Основные координатные плоскости:• плоскость эклиптики,
• плоскость экватора,
• плоскость движения (орбиты) ЛА,
• плоскость, касательная к поверхности Земли в точке
старта (плоскость местного горизонта),
• плоскость геометрической симметрии ЛА и др.
СК могут быть:
• прямоугольные,
• косоугольные,
• криволинейные
4.
Начало СК может быть:• расположено в центре Земли
• или на поверхности Земли (планеты),
• в центре масс
• в характерной точке ЛА (например, в центре объема).
5. Геоцентрическая экваториальная инерциальная СК (СК ОИXИYИZИ)
зZИ
Плоскость эклиптики
(Ecliptic plane)
YИ
XИ
Equinox point
Плоскость экватора
(Equatorial plane)
Рис.2.1
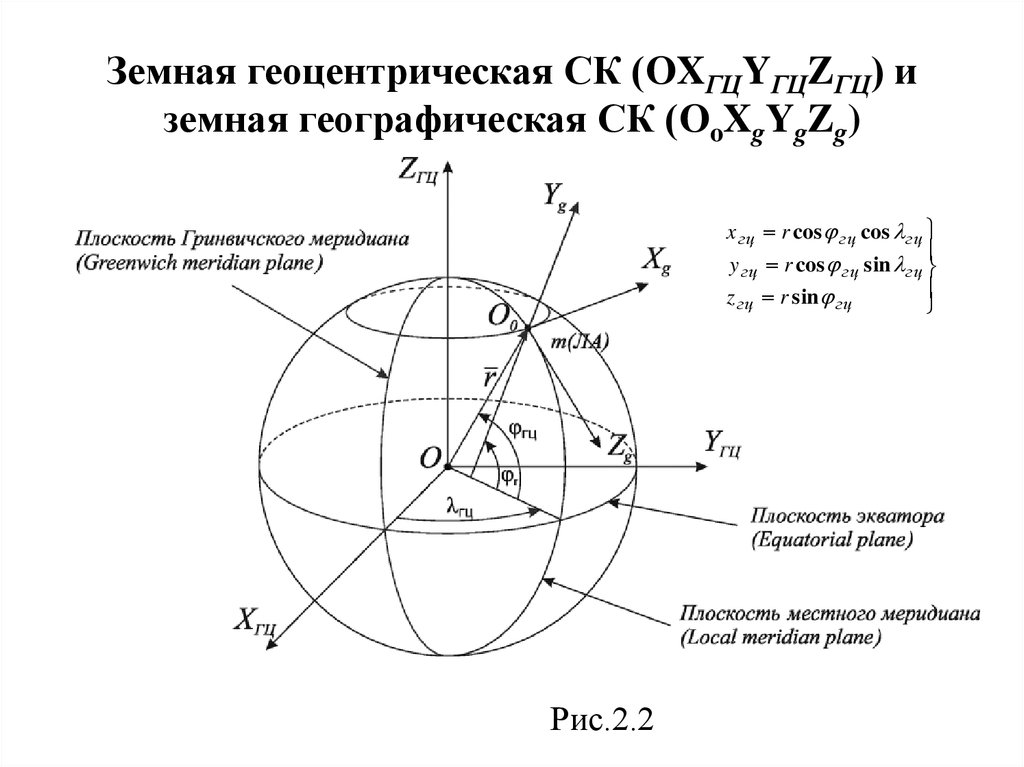
6. Земная геоцентрическая СК (OXГЦYГЦZГЦ) и земная географическая СК (OoXgYgZg)
x гц r cos гц cos гцy гц r cos гц sin гц
z гц r sin гц
Рис.2.2
7. Земная стартовая СК
YCNorth
Плоскость пуска
(стрельбы, бросания)
XC
o
Точка
старта
Цель
ZC
Рис.2.3
8. Земная нормальная СК , земная подвижная система координат и нормальная система координат
YgY0
Xg
O
Yg
X0
r
Z0
Zg
Xg
Oo
Zg
Местная горизонтальная
плоскость
Рис.2.4
9. Связанная система координат (OXYZ)
• 1 - Вертикальная плоскость симметрии ЛА (OXY),• 2- Горизонтальная плоскость симметрии ЛА (OXZ)
Y
1
Z
X
2
Рис.2.5
10. Скоростная СК (OXaYaZa)
YaY
плоскость
симметрии
X
Za
Xa , Va
Рис.2.6
11. 2.2. Углы, используемые для определения углового различных систем
• во-первых, взаимным положением начал разных СК, т.е.расстоянием между точками и и,
• во-вторых, взаимным угловым положением осей
различных СК.
1) взаимным положением начал разных СК, т.е. расстоянием
между точками и и,
2) взаимным угловым положением осей различных СК.
• три таких угла:
• угол прецессии ,
• угол собственного или чистого вращения
• и угол нутации .
12. Углы между осями связанной и нормальной СК (углы , и )
Исходное положение земной и связанной СКYg
Y
0
X
Z
Zg
0
0
Xg
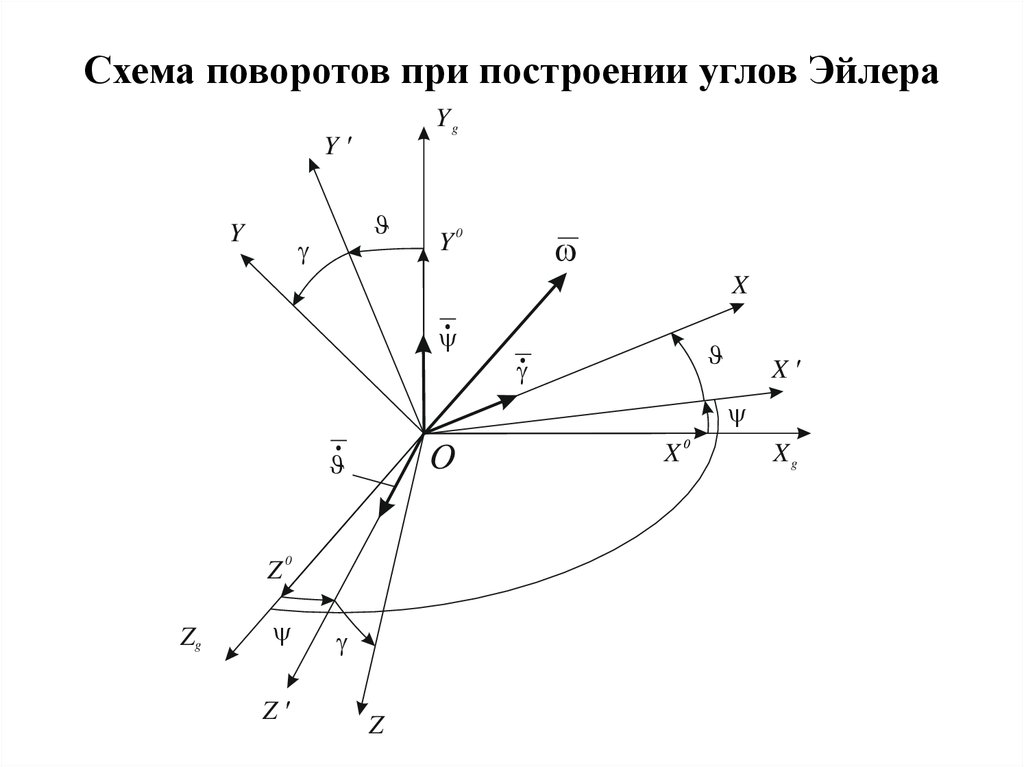
13. Схема поворотов при построении углов Эйлера
YgY
Y
Y
0
X
X
X
Z
Zg
0
Z
Z
0
Xg
14.
/ 0 // /
OX Y Z
OX Y Z
OXY Z OXYZ
0
0
исходное
положение
0
1 ый
поворот
вокруг
оси OY
2 ой
поворот
вокпуг
оси OZ /
3 ий
поворот
вокруг
оси OX
конечное
положение
• Угол рыскания (курса) - это угол между осью OX g и
проекцией продольной оси OX на местную горизонтальную
плоскостьOX g Z g ;
• Угол тангажа - это угол между продольной осью OX и
местной горизонтальной плоскостью OX g Z g ;
• Угол крена - это угол между поперечной осью OZ и
осью OZ g , смещенной в положение, соответствующее
нулевому углу рыскания.
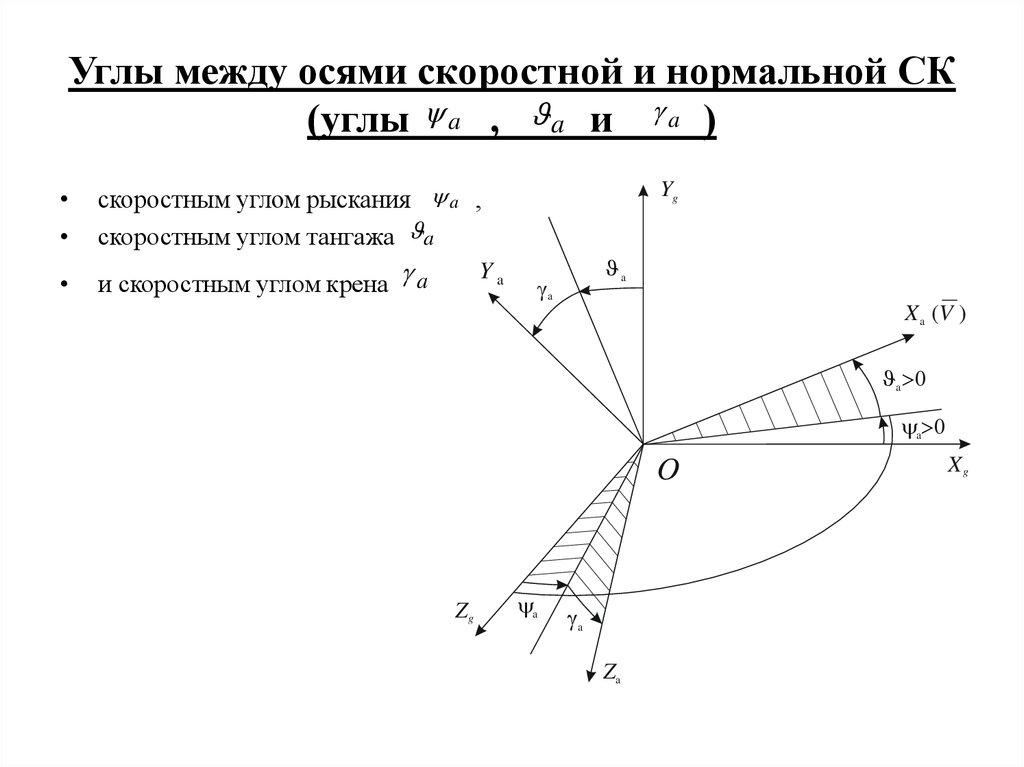
15. Углы между осями скоростной и нормальной СК (углы , и )
Углы между осями скоростной и нормальной СК(углы a , a и a )
скоростным углом рыскания a ,
скоростным углом тангажа a
и скоростным углом крена a
Ya
Yg
a
a
X a (V )
a
a
Xg
Zg
a
a
Za
16. Углы между осями траекторной и нормальной СК (углы и )
YKYg
XK (V K )
VП
Xg
Zg
ZK
17. Углы между осями траекторной и скоростной СК при
Wв 0• Траекторный угол совпадает со скоростным углом
рыскания, т.е. a ,
• а траекторный угол совпадает со скоростным
углом тангажа, т.е. a . Но в общем случае a 0
• и, следовательно, скоростные оси всегда развернуты
относительно траекторных на угол скоростного крена
a
18. Углы между осями связанной и скоростной СК (углы и )
Угол атакиУгол скольжения
Y
Y
X
a
Y
Xa (V)
X
Zа
Za
Z
Xa(V)
Z
19.
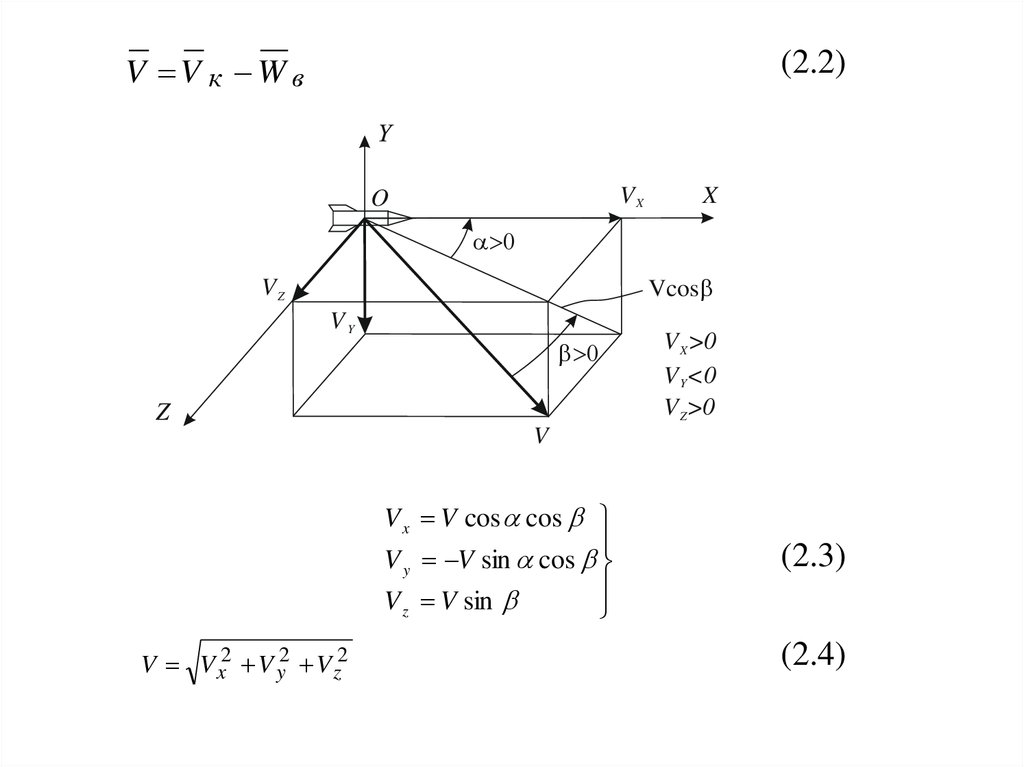
V V к W в(2.2)
VX
O
X
VZ
Vcos
VY
V X>0
V Y<0
V Z>0
V
V x V cos cos
V y V sin cos
V z V sin
V V x2 V y2 V z2
(2.3)
(2.4)
20.
arcsinarcsin
Vy
V x2 V y2
Vz
Vz
arcsin
V
V x2 V y2 V z2
(2.5)
(2.6)
21. 2.3. Матрицы перехода (таблицы направляющих косинусов)
rx1 c11 rx2 c12 ry2 c13 rz2ry1 c 21 rx2 c 22 ry2 c 23 rz2
rz1 c31 rx2 c32 ry2 c33 rz2
(2.7)
rx2 c11 rx1 c 21 ry1 c 31 rz1
ry2 c12 rx1 c 22 ry1 c 32 rz1
rz2 c13 rx1 c 23 ry1 c 33 rz1
(2.8)
c11 cos( X 1 , X 2 )
c 21 cos(Y1 , X 2 )
c31 cos(Z1 , X 2 )
c12 cos( X 1 ,Y2 )
c 22 cos(Y1 ,Y2 )
c32 cos(Z1 ,Y2 )
c13 cos( X 1 , Z 2 )
c 23 cos(Y1 , Z 2 )
c33 cos(Z1 , Z 2 )
22.
rx1rx2
ry1 A21 ry2
rz1
rz2
или
rx2
ry2 A12
rz2
rx1
ry1
rz1
c11
c12
c13
A21 c 21
c31
c11
c 21
c31
c 22
c 23
c 22
c32
c32
c33
A12 c12
c13
c 23
c33
T
A12 A21
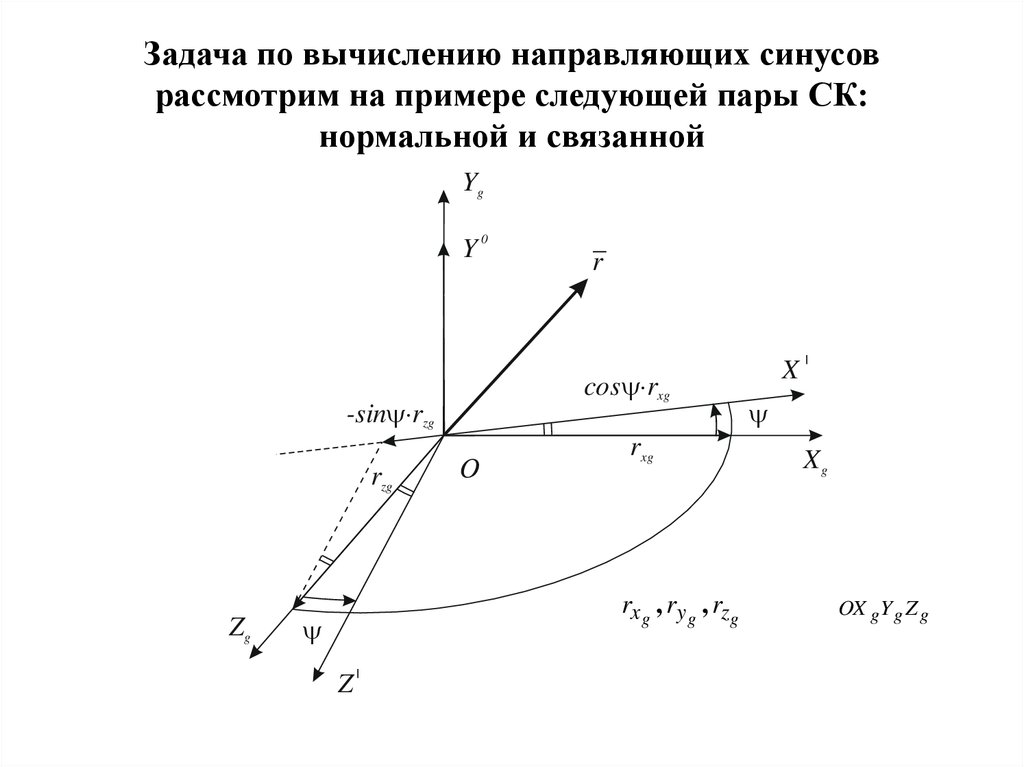
23. Задача по вычислению направляющих синусов рассмотрим на примере следующей пары СК: нормальной и связанной
YgY
-sin rzg
0
r
cos rxg
rxg
rzg
Zg
rx g , ry g , rz g
Z
|
X
|
Xg
OX g Y g Z g
24.
cosA 0
sin
0 sin
1
cos
0
A sin
0 cos
0
c11
c12
c13
A A A A c 21
c31
c 22
c 23
c32
c33
sin
0
1
cos
0
A 0 cos
0
1
0 sin
c11 cos cos ,
c12 sin ,
c13 sin cos ,
с21 cos sin cos sin sin ,
c22 cos cos ,
c23 cos sin sin sin cos ,
c31 cos sin sin sin cos ,
c32 cos sin ,
c33 cos cos sin sin sin .
0
rx
ry A
rz
rx g
ry g
rz g
rx g
rx
ry g AT
ry
rz g
rz
0
sin
cos
25. Таблица 2.1. Направляющие косинусы между осями нормальной и связанной СК
Связанные осиOX
OY
OZ
Нормальные оси
OX g
OY g
OZ g
c11
c12
c13
c21
c22
c23
c31
c32
c33




















 mathematics
mathematics








