Similar presentations:
Структура системы
1.
Структура системыx2
x1
w1
x3
w2 w3
x4
w4
x5
w5
xN
wN
Схема построения, использующая одну ЦАР.
Адаптивные коэффициенты рассчитываются с помощью
информации, полученной с каждого элемента ЦАР.
В качестве критерия – максимизация отношения
мощности сигнала к мощности помеха + шум (SINR), поэтому
расчет весовых коэффициентов производится следующим
образом:
w kRi 1n v s
где k – констанста, зависящая от задачи (MVDR – Minimum
Variance Distortionless Response; SMI – Sample Matrix Inversion):
kMVDR
y wH x
Рис. 1. Линейная антенная решетка, формирующая
адаптивную ЦАР (Adaptive Beamformer)
R i 1n E xx H
v s
1
; kSMI 1;
H
1
v s Ri n v s
- помеховая ковариационная матрица
пространственный
управляющий
вектор
антенной решетки в направлении на цель
1
2.
Структура системыЦАР с вспомогательными приемными
лучами, формируемыми из полной
приемной апертуры или ее частей.
В таком случае адаптивные коэффициенты:
1
w beam R beam
rmb
Всп. канал 1
Осн. канал
xbeam 1
Всп. канал N
xbeam N
w1
wN
1
R beam
помеховая
H
ковариационная матрица
E xbeam xbeam
вспомогательных каналов
ymain
ybeam w
H
beam
x
rmb
вектор
взаимной
корреляции
между
E y *main xbeam основным каналом и
вспомогательными
yout ymain ybeam
Рис. 2. Комбинированный метод
(Beamspace Adaptive Cancellation)
2
3.
Структура системыВспомогательные каналы
Основной канал
x2
x1
ymain
w1
H
yaux w aux
x
x3
w2 w3
yout ymain yaux
xN
wN
Аналоговая основная антенная решетка и
вспомогательная ЦАР. Критерий
минимизации среднеквадратической
ошибки. В таком случае адаптивные
коэффициенты:
1
w aux R aux
rma
помеховая
1
H
ковариационная матрица
R aux
E x aux x aux
вспомогательных каналов
rma
вектор
взаимной
корреляции
между
E y *main x aux основным каналом и
вспомогательными
Рис. 3. Комбинированный метод (Sidelobe Сanceller)
3
4.
Обращение матрицыВозможные варианты
1. Точные методы прямого вычисления:
Метод Гаусса-Жордана
Использование матрицы алгебраических дополнений
2. Итерационные методы:
Метод Шульца
Метод Якоби
Метод Гаусса - Зейделя
3. Точные методы использующие разложение матриц:
LU-разложение
Разложение Холецкого, LDLT разложение
Корневое разложение
QR-разложение
• Процесс Грама-Шмидта
• Отражения Хаусхолдера
• Повороты Гивенса
4
5.
Обращение матрицыQR разложение
A Q R
Q:Q Q
-1
a11 a12
a
a22
21
a
31 a32
a13 q11 q12
a23 q21 q22
a33 q31 q32
H
q13 r11 r12
q23 0 r22
q33 0 0
r13
r23
r33
5
6.
Обращение матрицыQR разложение с использованием поворотов Гивенса
Поворот Гивенса
Y
G(θ)*V
V
y
θ
x
cos
G V
sin
sin x
cos y
X
6
7.
Обращение матрицыQR разложение с использованием поворотов Гивенса
Y
c s
Gp
s c
x
с cos
2
2
x y
Gp G ( )
arctan x y
V
y
φ
Vp = Gp*V
x
X
s sin
y
x y
2
2
7
8.
Обращение матрицыПример QR разложения с использованием поворотов Гивенса
G 1 A = A G1
1 0 0 a11 a12
0 c s a
a
21 22
0 s c a
31 a32
a13 a11 a12
a22
a23 a21
a33 0 a32
a13
a23
a33
G 2 A G1 = A G 2
c s 0 a11 a12
s c 0 a a
21 22
0 0 1 0 a
32
a13 a11 a12
0 a22
a23
0 a32
a33
a13
a23
a33
G 3 AG2 = AG3
1 0 0 a11 a12
0 c s 0 a
22
0 s c 0 a
32
a13 a11 a12 a13
0 a22
a23
a23
0
a33
0 a33
A G G G R Q R
H
3
H
2
H
1
8
9.
00
1
I
a13
A a12
a11 *
in 1
B1
0
1
0
a23
a22 *
a21
0
in 2
1
0
0
a33 *
a32
a31
0
0
Обращение матрицы
Реализация в виде систолического массива
t8
t7
t6
t5
t4
t3
t2
t1
in 3
I1
I1
B1
I1
Массив GR
B1
Q
out 1
R
q13 q12 q11
r13
r13 r11 *
out 2
q23 q22 q21
r23 r22 *
0
0
out 3
in 1
B2
in 2
Массив IAM
I2
B2
I2
I2
in 3
q33 q32 q31 r33 *
0
0
0
0
t11
t7
t6
t5
t4
t10
t9
t8
out 1
C
0
0
0
c13
c12
c11
out 2
0
0
c23
c22
c21
B2
out 3
0
c33
c32
c31
t14
t13
t12
t11
t10
9
10.
Обращение матрицыМетод модифицированных квадратичных поворотов Гивенса (MSGR)
QR Decomposition-Based Matrix Inversion for High Performance Embedded MIMO Receivers. Lei Ma,
Member, IEEE, Kevin Dickson, Member, IEEE, John McAllister, Member, IEEE, and John McCanny, Fellow,
IEEE. IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 59, NO. 4, APRIL 2011.
Данный алгоритм позволяет:
Работать с комплексными числами
Избавиться от необходимости вычислять квадратные корни
В процессе работы не получить 0 на главной диагонали
Получить на главной диагонали треугольной матрицы
действительные числа
10
11.
Обращение матрицыОценка времени расчета и требуемых ресурсов
Количество необходимых
комплексных арифметических
устройств
N
N=4
N
N=4
N = 11
RT
5N - 1
19
54
LT
3N + 1
13
34
N = 11
С_SUM
3














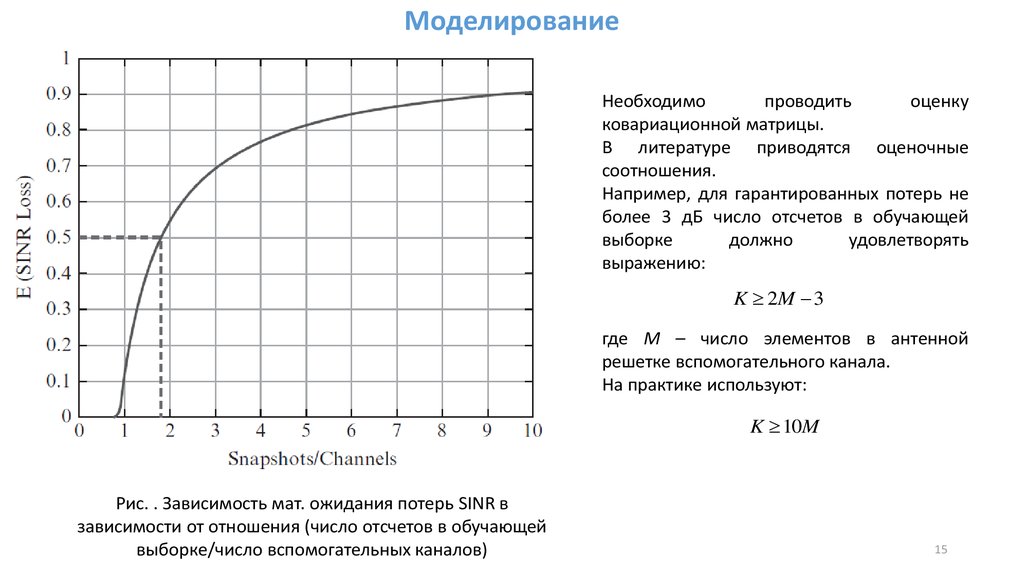

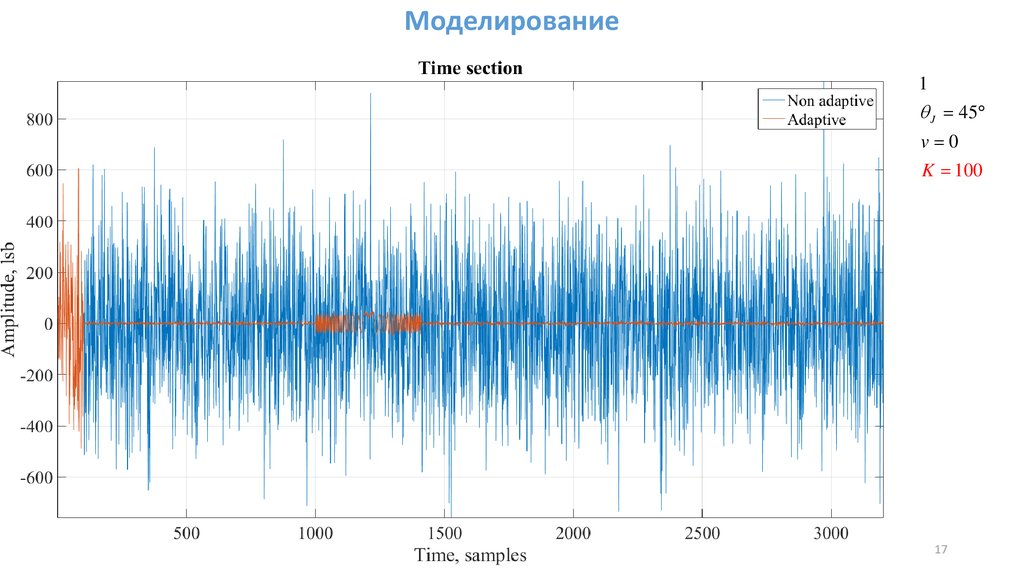

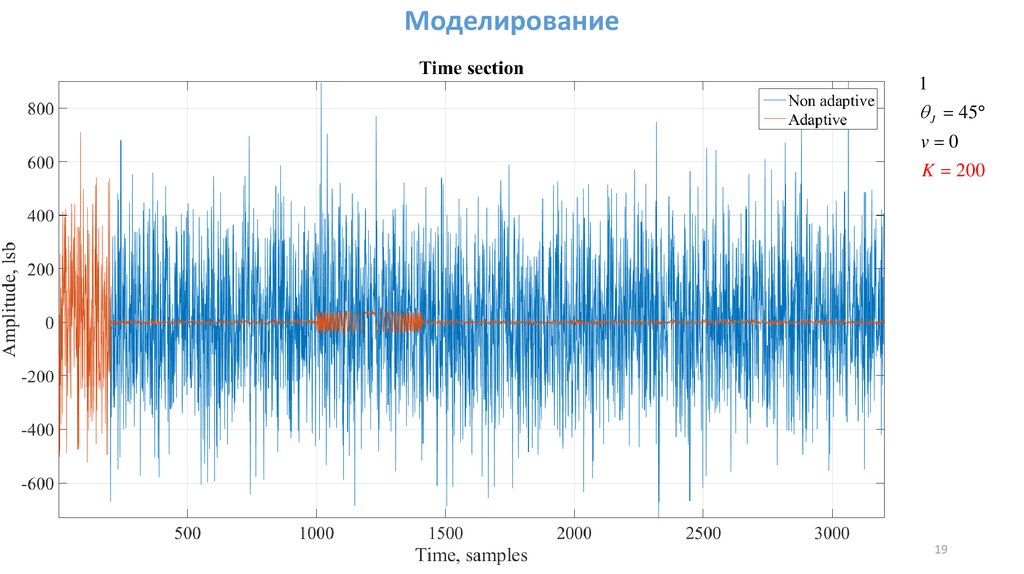




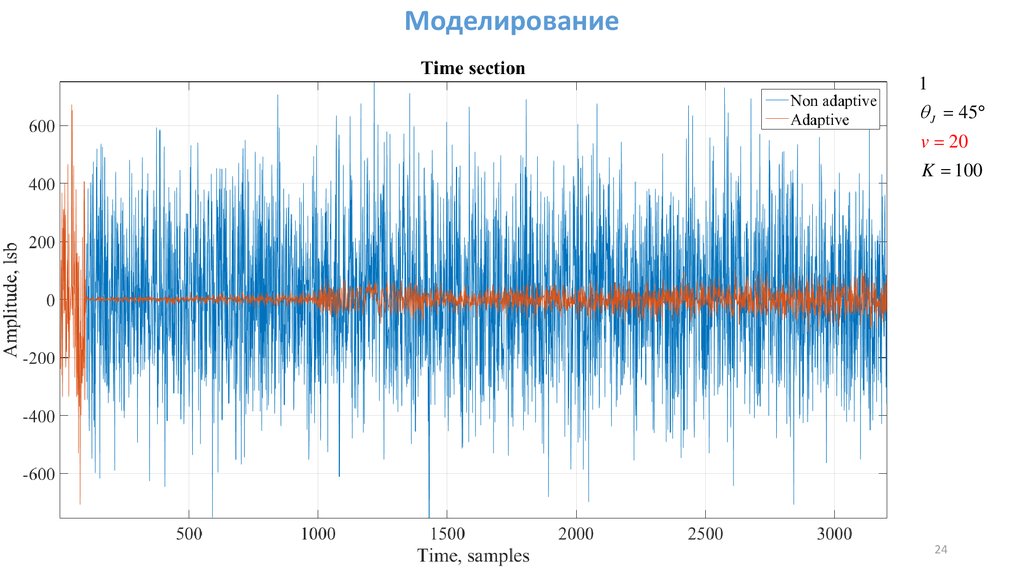







 mathematics
mathematics








