Системы линейных уравнений. Лекция 2

1.

МАТЕМАТИКА

2.

Лекцию читает
к.т.н., доцент
БОБРОВА
ЛЮДМИЛА ВЛАДИМИРОВНА

3.

Модуль 1.
ЛИНЕЙНАЯ АЛГЕБРА

4.

1.4. Системы
линейных
уравнений

5. 1.4.1. Основные понятия

Система двух линейных уравнений с двумя
неизвестными
a11x1 a12 x2 b1
a21x1 a22 x2 b2
x1 , x2 - переменные
a11, a12 , a21, a22 -коэффициенты системы
b1 , b2
-свободные члены

6.

Решением системы линейных уравнений
называется
совокупность
значений
неизвестных, которая при подстановке в
систему обращает все уравнения в тождества
Пример 1
Решением системы
3x1 x2 1
2 x1 2 x2 7
являются значения: х1 = 1; х2 = -2
3 1 ( 2) 1
2 1 2 _( 2) 7

7.

Система линейных уравнений называется
cовместной, если она имеет хотя бы одно
решение, и несовместной, если она не имеет
ни одного решения
Если решение одно –система определенная,
если больше чем одно- неопределенная

8.

1.4.2.Формулы Крамера
для системы двух линейных уравнений с
двумя неизвестными
D1
x1 D ,
D
x 2 .
2
D
D
a11
a12
a21 a22
a11x1 a12 x2 b1
a21x1 a22 x2 b2

9.

1.4.2.Формулы Крамера
для системы двух линейных уравнений с
двумя неизвестными
D1
x1 D ,
D
x 2 .
2
D
D
a11
D1
a12
a21 a22
b1
a12
b2
a22
a11x1 a12 x2 b1
a21x1 a22 x2 b2

10.

1.4.2.Формулы Крамера
для системы двух линейных уравнений с
двумя неизвестными
D1
x
,
1
D
x D2 .
2 D
D
a11
a12
a21 a22
D2
D1
a11
b1
a21 b2
b1
a12
b2
a22
a11x1 a12 x2 b1
a21x1 a22 x2 b2

11.

Пример 1.
Решить систему
уравнений:
Решение
D
D
a11
3 2
5
a12
a21 a22
1
3x1 2 x2 12
5 x1 x2 7
3 1 ( 2) 5 13
D1
x1 D ,
x D2 .
2 D

12.

3x1 2 x2 12
5 x1 x2 7
D1
D1
b1
a12
b2
a22
12 2
7
1
12 1 ( 2) 7 26
D=13
D1
x1 D ,
x D2 .
2 D

13.

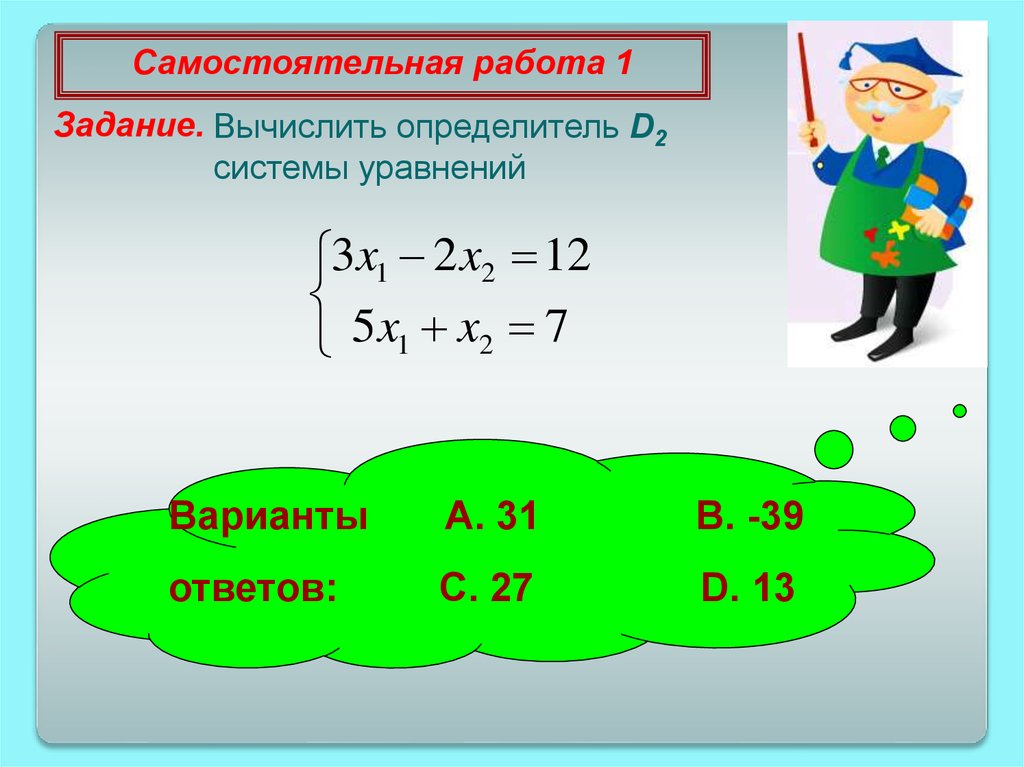
Самостоятельная работа 1
Задание. Вычислить определитель D2
системы уравнений
3x1 2 x2 12
5 x1 x2 7
Варианты
A. 31
B. -39
ответов:
C. 27
D. 13

14.

3x1 2 x2 12
5 x1 x2 7
D 2
D2
a11
Сверим ответы?
3 12
5
7
3 7 12 5 39
b1
a21 b2
D=13
D1=26
D1
x1 D ,
x D2 .
2 D

15.

3x1 2 x2 12
5 x1 x2 7
Находим значение переменной X1
D1 26
x1
2
D 13
D=13
D1=26
D2=-39
D1
x1 D ,
x D2 .
2 D

16.

Самостоятельная работа 2
Задание.
3x1 2 x2 12
5 x1 x2 7
Вычислить значение переменной X2
D=13
D1=26
D2=-39
D1
x1 D ,
x D2 .
2 D

17.

3x1 2 x2 12
5 x1 x2 7
Сверим ответы?
D2
39
x2
3
D
13
D1 26
x1
2
D 13
D=13
D1=26
D2=-39
D1
x1 D ,
x D2 .
2 D

18.

1.4.3.Теорема Крамера для системы n
уравнений c n неизвестными
1.Если определитель системы n линейных
уравнений с n неизвестными D 0 ,то система
совместна и имеет единственное решение:
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

19.

Теорема Крамера для системы n уравнений c
n неизвестными
2. Если D 0 и хотя бы один из определителей
D1 , D2 ,..., Dnотличен от нуля, то система
уравнений несовместна

20.

Теорема Крамера для системы n уравнений c
n неизвестными
3.Если все определители D, D1 , D2 ,..., Dn равны
нулю,
то
система
имеет
бесконечное
множество решений.

21.

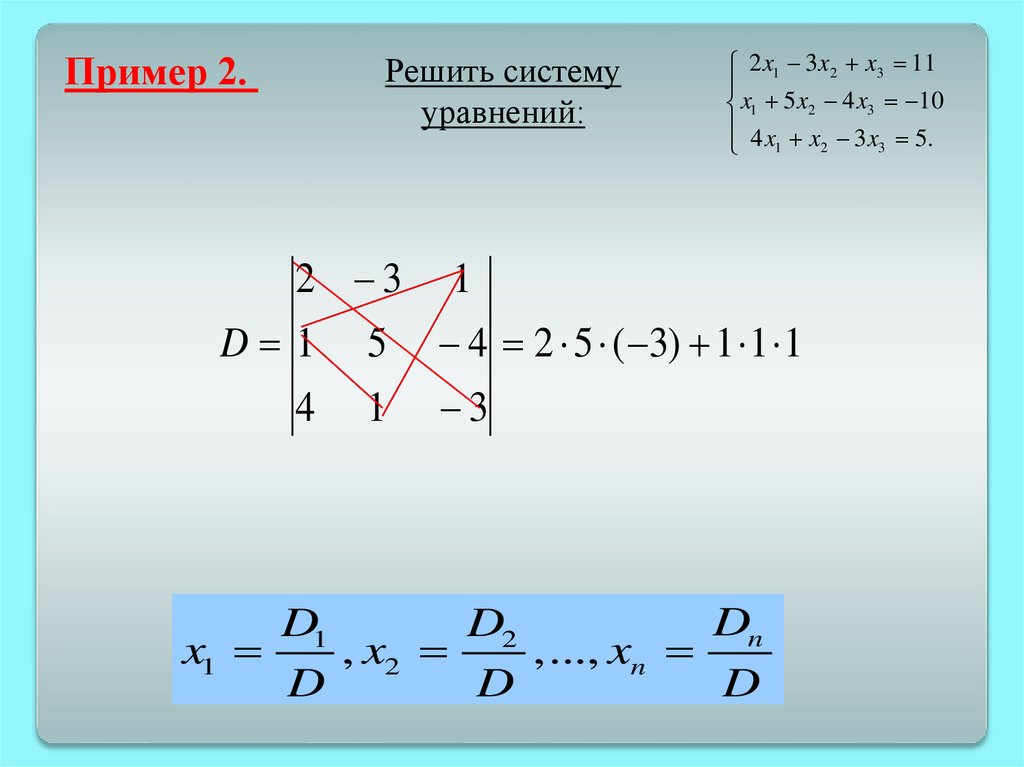
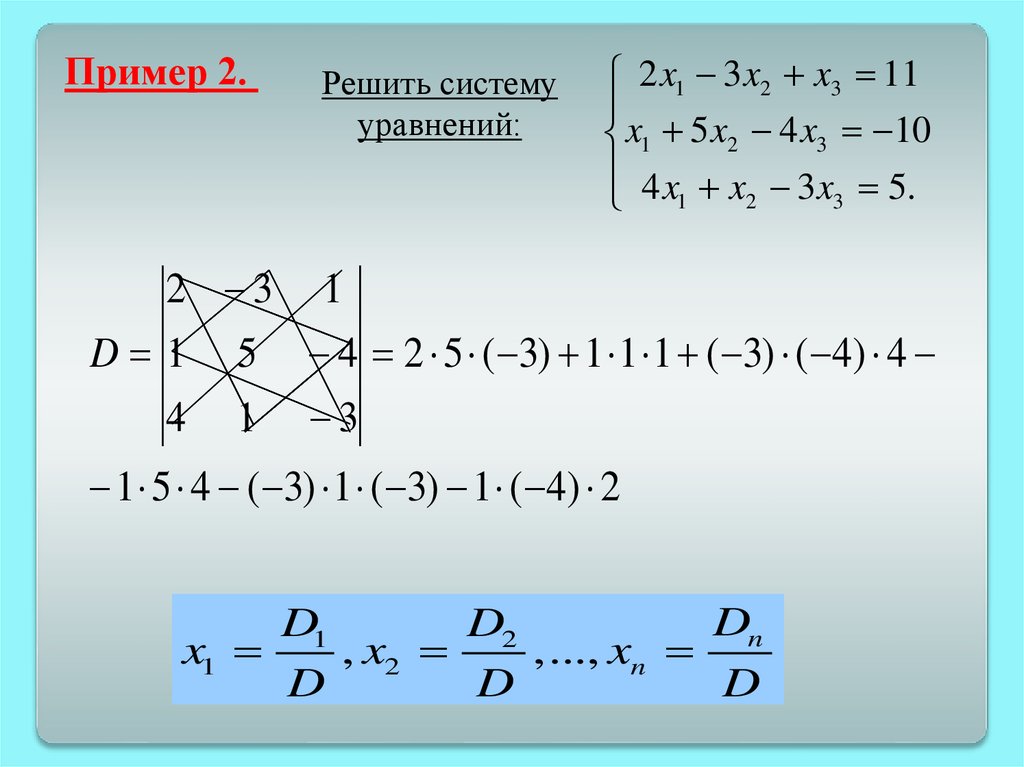
Пример 2.
Решить систему
уравнений:
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

22.

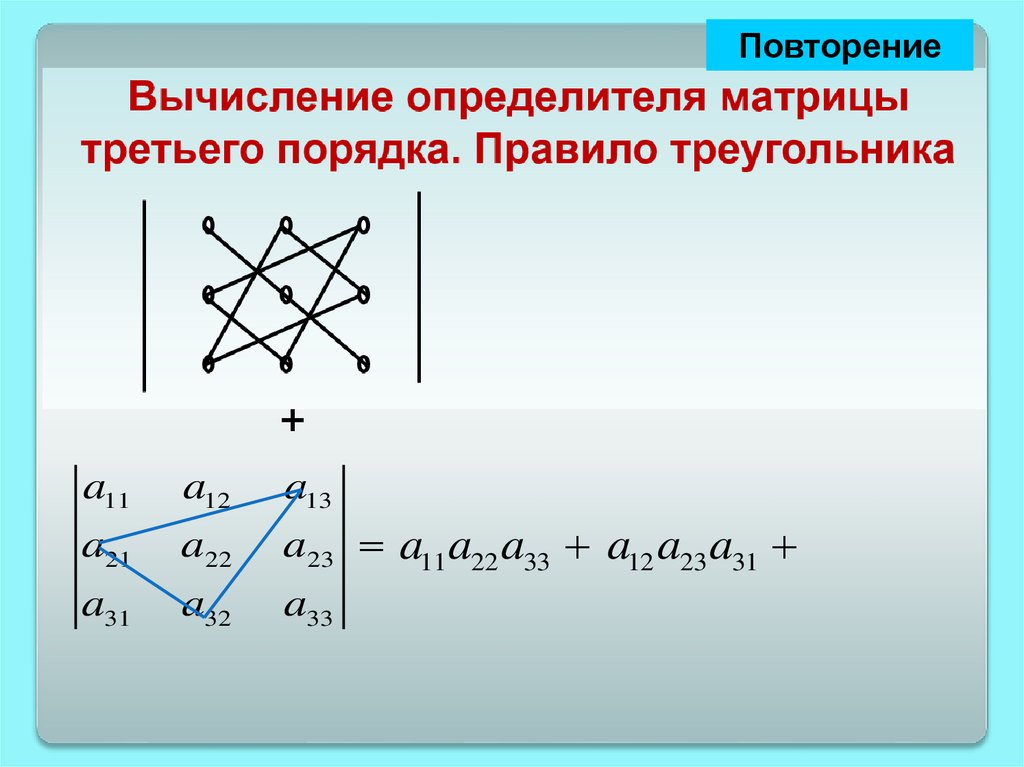
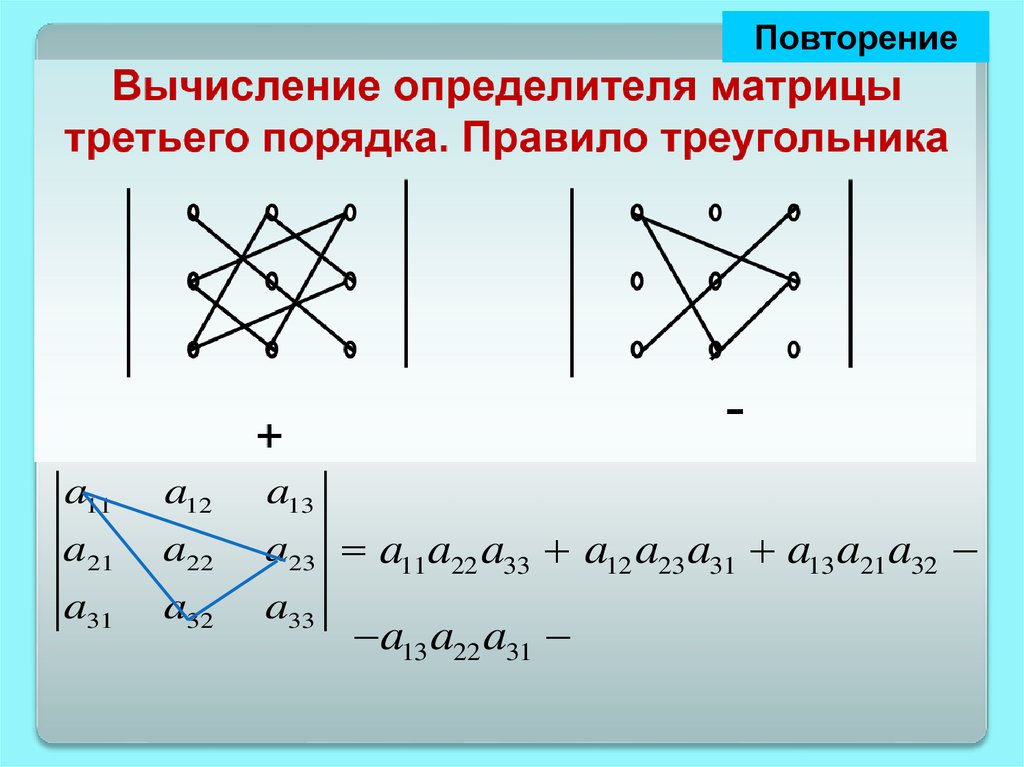
Повторение

23.

Повторение
+

24.

Повторение
+
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33
a33

25.

Повторение
+
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33
a33

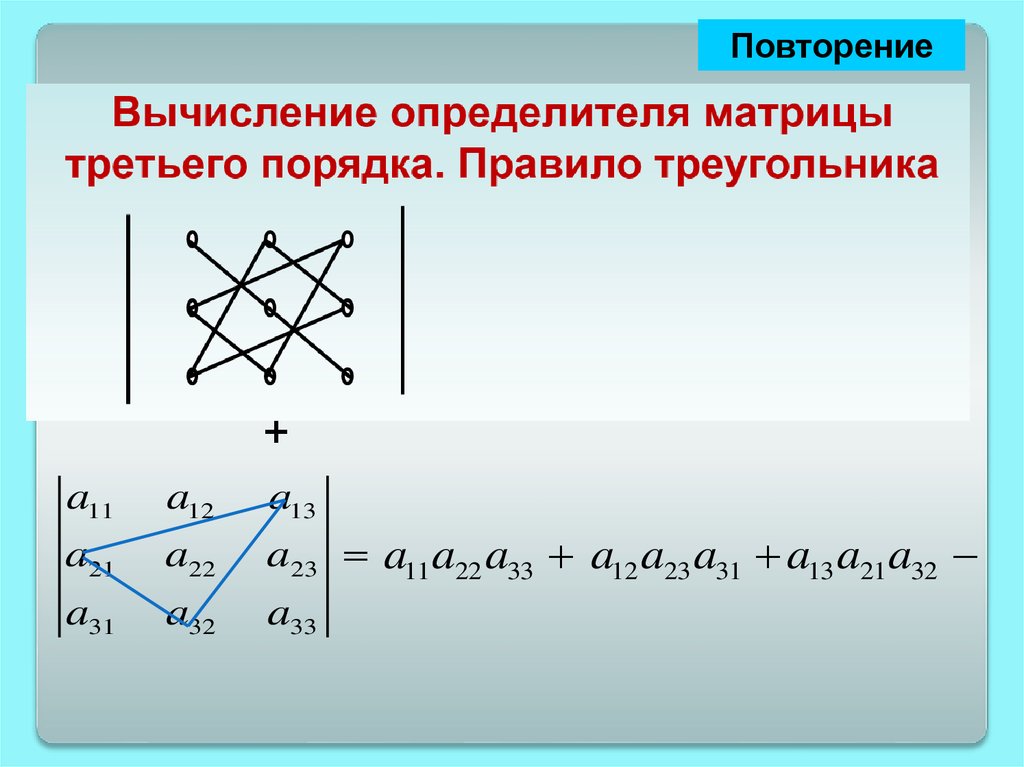
26.

Повторение
+
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33 a12 a23 a31
a33

27.

Повторение
+
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33 a12 a23 a31
a33

28.

Повторение
+
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a33

29.

Повторение
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a33

30.

Повторение
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a33
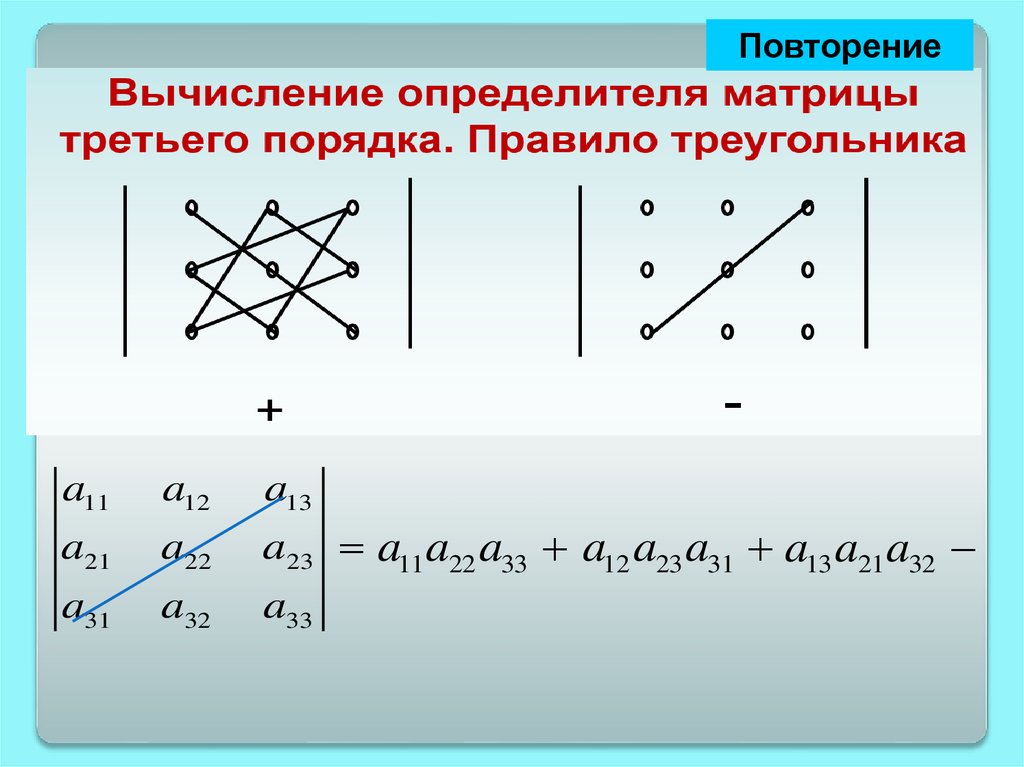
a13 a22 a31

31.

Повторение
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a33
a13 a22 a31

32.

Повторение
a11
a12
a13
a21
a22
a31
a32
a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a33
a13 a22 a31 a11a23 a32

33.

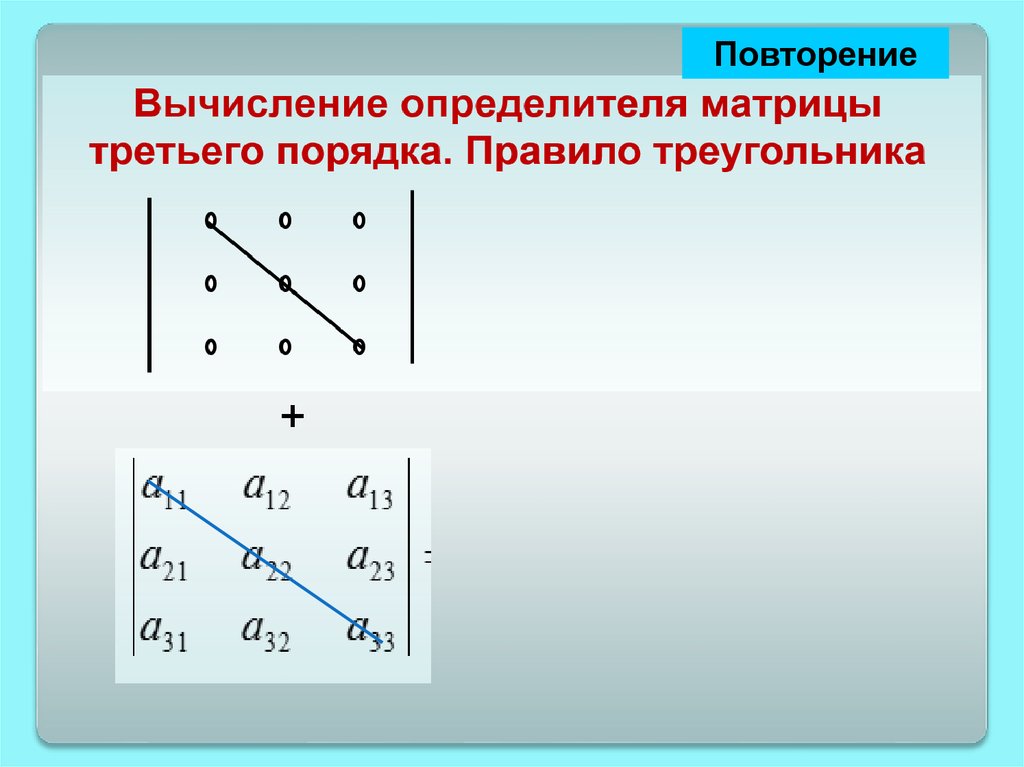
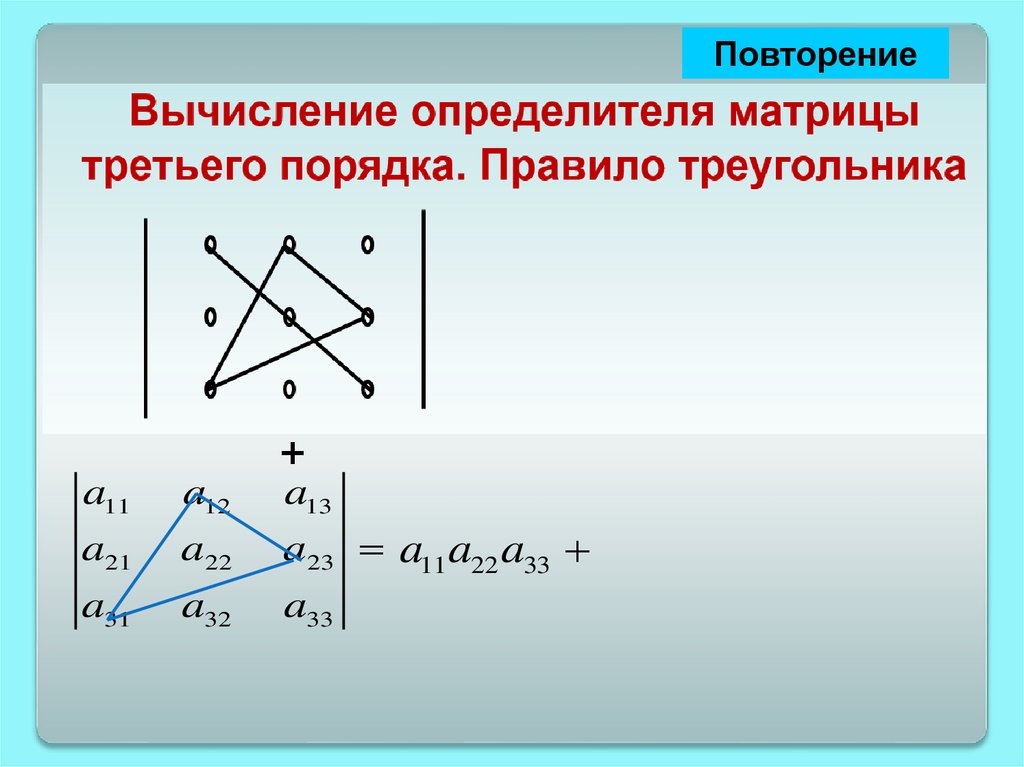
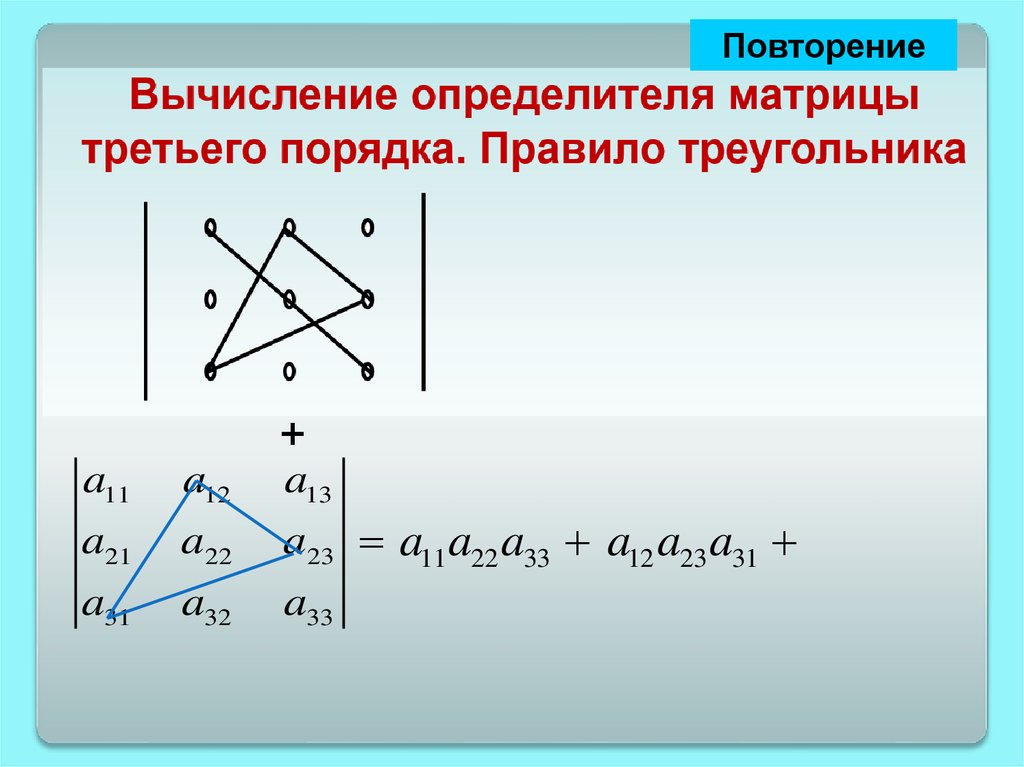
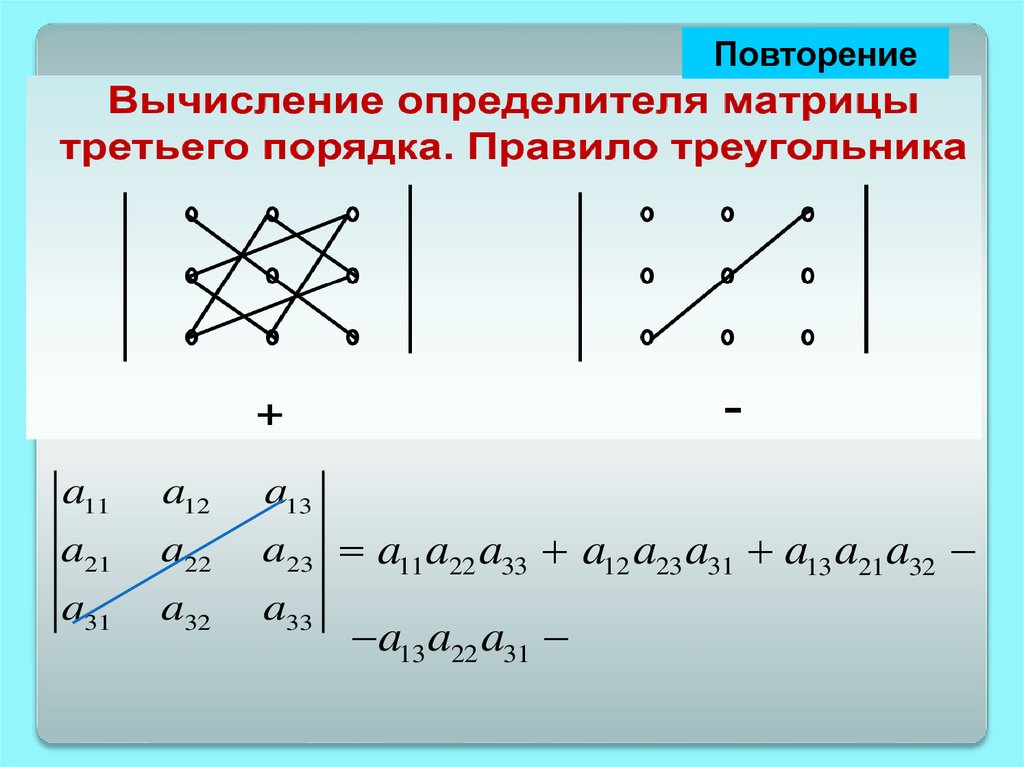
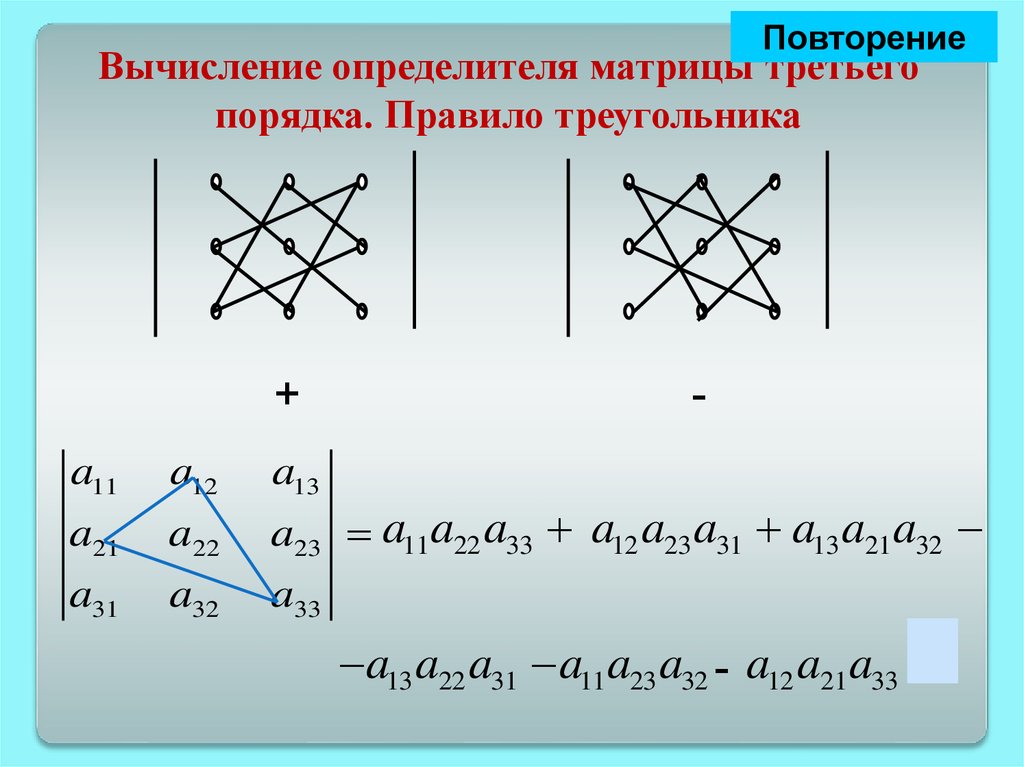
Повторение
Вычисление определителя матрицы третьего
порядка. Правило треугольника
+
-
a11
a12
a13
a21
a22
a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a31
a32
a33
a13 a22 a31 a11a23 a32 - a12 a21a33

34.

Решить систему
уравнений:
Пример 2.
2 3
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
1
D 1
5
4 2 5 ( 3)
4
1
3
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

35.

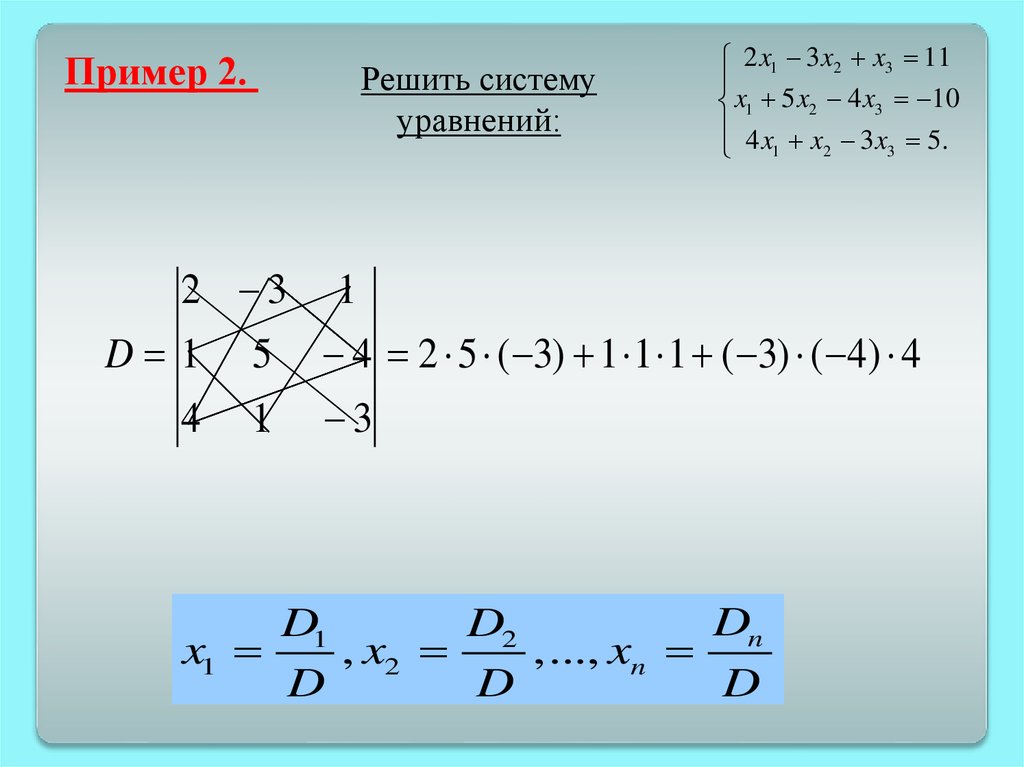
Пример 2.
Решить систему
уравнений:
2 3
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
1
D 1
5
4 2 5 ( 3) 1 1 1
4
1
3
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

36.

Пример 2.
Решить систему
уравнений:
2 3
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
1
D 1
5
4 2 5 ( 3) 1 1 1 ( 3) ( 4) 4
4
1
3
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

37.

Пример 2.
Решить систему
уравнений:
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
2 3 1
D 1 5 4 2 5 ( 3) 1 1 1 ( 3) ( 4) 4
4 1 3
1 5 4
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

38.

Пример 2.
Решить систему
уравнений:
2 3
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
1
D 1
5
4 2 5 ( 3) 1 1 1 ( 3) ( 4) 4
4
1
3
1 5 4 ( 3) 1 ( 3)
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

39.

Самостоятельная работа 4
Задание. Определите последнюю «тройку»
чисел
2 3
1
D 1
5
4 2 5 ( 3) 1 1 1 ( 3) ( 4) 4
4
1
3
1 5 4 ( 3) 1 ( 3)
Варианты
A. 1*1*1
B. 1*5*4
ответов:
C. 1*2*(-4)
D. 1*(-4)*1

40.

Пример 2.
2 3
Решить систему
уравнений:
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
1
D 1
5
4 2 5 ( 3) 1 1 1 ( 3) ( 4) 4
4
1
3
1 5 4 ( 3) 1 ( 3) 1 ( 4) 2
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

41.

Решить систему
уравнений:
Пример 2.
2 3
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
1
D 1
5
4 2 5 ( 3) 1 1 1 ( 3) ( 4) 4
4
1
3
1 5 4 ( 3) 1 ( 3) 1 ( 4) 2
30 1 48 20 9 8 2
Dn
D1
D2
x1
, x2
,..., xn
D
D
D

42.

Пример 2.
2 3
Решить систему
уравнений:
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
1
D 1
5
4 2 5 ( 3) 1 1 1 ( 3) ( 4) 4
4
1
3
1 5 4 ( 3) 1 ( 3) 1 ( 4) 2
30 1 48 20 9 8 2
Система определенная,
имеет решение

43.

2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
11
D1 10
5
3
1
5
4 11 5 ( 3) ( 3) ( 4) 5 ( 10) 1 1
1
3
1 5 5 ( 3) ( 10) ( 3) 1 ( 4) 11
165 60 10 25 90 44 6
D = -2

44.

2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
2
11
1
D2 1 10 4 2 ( 10) ( 3) 11 ( 4) 4 1 5 1
4
5
3
1 ( 10) 4 1 11 ( 3) 5 ( 4) 2
60 176 5 40 33 40 2
D = -2
D1 = -6

45.

Самостоятельная работа 5
4
Задание.
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
Найдите верно записанный определитель D3
2
a ).
11
D3 1 10 4
4
5
2 3
с ).
1
11
b).
3
5
4
4
1
3
1
5
4
1
3
D3 10
5
2 3
1
D3 1
3
d ).
11
D3 1
5
10
4
1
5

46.

2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1
2 3
D3 1
5
4
1
11
10 2 5 5 1 1 11 ( 3) ( 10) 4
5
11 5 4 1 5 ( 3) 1 ( 10) 2
50 11 120 220 15 20 4
D = -2
D1 = -6
D2 = 2

47.

D1 6
x1
3
D 2
D2
2
x2
1
D 2
D = -2
D2 = 2
D1 = -6
D3 = -4
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1

48.

Самостоятельная работа 6
Задание. Определите значение переменной х3
D = -2
D2 = 2
D1 = -6
D3 = -4
D1 6
x1
3
D 2
D2
2
x2
1
D 2

49.

D1 6
x1
3
D 2
D2
2
x2
1
D 2
D3 4
x3
2.
D 2
D = -2
D2 = 2
D1 = -6
D3 = -4
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1

50.

Проверка
2 x1 3x2 x3
x1 5 x2 4 x3
4 x x 3 x
2
3
1
X1 = 3
2 3 3 ( 1) 2 11
3 5 ( 1) 4 2 10
4 3 ( 1) 3 2 5
X2 = -1
X3 =2
2 x1 3 x2 x3 11
x1 5 x2 4 x3 10
4 x x 3 x 5.
2
3
1

51. 1.5. Матричный метод решения систем линейных уравнений (СЛУ)

Решаем систему уравнений:
a11 x1 a12 x2 a13 x3 b1
a21 x1 a22 x2 a23 x3 b2 (4)
a x a x a x b .
32 2
33 3
3
31 1

52. 1.5. Матричный метод решения систем линейных уравнений (СЛУ)

Решаем систему уравнений:
a11 x1 a12 x2 a13 x3 b1
a21 x1 a22 x2 a23 x3 b2 (4)
a x a x a x b .
32 2
33 3
3
31 1
Представим ее в виде:
a11 x1 a12 x2 a13 x3 b1
(5)
a21 x1 a22 x2 a23 x3 b2
a x a x a x b
32 2
33 3
31 1
3

53.

Введем обозначения матриц,
состоящих из коэффициентов и переменных:
a11
A a21
a
31
a12
a22
a32
x1
a13
a23 X x2
x
a33
3
b1
B b2 .
b
3

54.

Введем обозначения матриц,
состоящих из коэффициентов и переменных:
a11
A a21
a
31
a12
a22
a32
x1
a13
a23 X x2
x
a33
3
Тогда систему (5)
можно записать
в матричном виде:
AX B
b1
B b2 .
b
3
(6)
a11 x1 a12 x2 a13 x3 b1
a
x
a
x
a
x
22 2
23 3 b2
21 1
a x a x a x b
32 2
33 3
31 1
3
(5)

55.

Решаем систему (6):
AX B
Домножим обе части (6) на А-1:
1
1
A AX A B,
(6)

56.

AX B
Решаем систему (6):
(6)
Домножим обе части (6) на А-1:
1
1
A AX A B,
Но по определению обратной матрицы
1
A A E

57.

AX B
Решаем систему (6):
(6)
Домножим обе части (6) на А-1:
1
1
A AX A B,
Но по определению обратной матрицы
1
A A E
А при умножении матрицы на единичную
получаем основную матрицу: EX X ,

58.

AX B
Решаем систему (6):
(6)
Домножим обе части (6) на А-1:
1
1
A AX A B,
Но по определению обратной матрицы
1
A A E
А при умножении матрицы на единичную
получаем основную матрицу: EX X ,
Значит, матричное решение системы уравнений:
1
(7)
X A B.

59.

Пример 6. Решить систему
уравнений матричным
методом
Решение
AX B,
7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
1 2
3
X A 1B.
x1
7 2 3
A 9 3 4 ; X x2 ;
x
5 1 3
3
13
B 15 .
14

60.

7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
1 2
3
Пример 6. Решить систему
уравнений матричным
методом
Решение
X A 1B.
AX B,
A11
1
1
A A12
D
A13
A21
A22
A23
A31
A32
A33
Матрица
алгебраических
дополнений для
транспонированной
матрицы А

61.

7
2
3
D( A) 9
3
5
1
4 63 40 27 45 28 54 3
3
A11
1
1
A A12
D
A13
A21
A22
A23
A31
A32
A33
7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
3
1 2

62.

7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
3
1 2
Алгебраическое дополнение элемента aik:
Aik ( 1)
i k
M ik
Здесь Mik - минор элемента aik - определитель,
полученный из D(A) вычеркиванием строки I
и столбца k:
A11
1
1
A A12
D
A13
A21
A22
A23
A31
A32
A33
D 3

63.

Вычисляем алгебраические дополнения для первой строки
Первый столбец: i=1; k=1
7 2 3
1 1 3 4
A 9 3 4 ;
A11 ( 1)
9 4 5
1 3
5 1 3
D(A) = 3
7 2 3
A 9 3 4 ;
5 1 3
7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
3
1 2

64.

Вычисляем алгебраические дополнения для первой строки
Первый столбец: i=1; k=1
7 2 3
1 1 3 4
A 9 3 4 ;
A11 ( 1)
9 4 5
1 3
5 1 3
Второй столбец: i=1; k=2
1 2
A12 ( 1)
D(A) = 3
9 4
5 3
(27 20) 7
7 2 3
A 9 3 4 ;
5 1 3
7 2 3
A 9 3 4 ;
5 1 3
7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
3
1 2

65.

Вычисляем алгебраические дополнения для первой строки
Третий столбец: i=1; k=3
1 3
A13 ( 1)
D(A) = 3
9 3
5 1
7
A 9
5
2
3
1
3
4 ;
3
9 15 6
7 2 3
A 9 3 4 ;
5 1 3
A11 = 5
A12 = -7

66.

Вычисляем алгебраические дополнения для второй строки
Первый столбец: i=2; k=1
7 2 3
A 9 3 4 ;
2
3
A21 ( 1)2 1
(6 3) 3
5 1 3
1 3
D(A) = 3
7 2 3
A 9 3 4 ;
5 1 3
A11 = 5
A12 = -7
A13 = -6

67.

Вычисляем алгебраические дополнения для второй строки
Первый столбец: i=2; k=1
7 2 3
A 9 3 4 ;
2 1 2 3
A21 ( 1)
(6 3) 3
5 1 3
1 3
Второй столбец: i=2; k=2
A22 ( 1)
D(A) = 3
2 2
7 3
5 3
21 15 6
7 2 3
A 9 3 4 ;
5 1 3
7 2 3
A 9 3 4 ;
5 1 3
A11 = 5
A12 = -7
A13 = -6

68.

Вычисляем алгебраические дополнения для второй строки
Третий столбец: i=2; k=3
A23 ( 1)
D(A) = 3
2 3
7 2
5 1
7
A 9
5
2
3
1
3
4 ;
3
(7 10) 3
A11 = 5
A12 = -7
A21 = -3
A22 = 6
A13 = -6

69.

Вычисляем алгебраические дополнения для третьей строки
Первый столбец: i=3; k=1
2
2
3
A31 ( 1)
D(A) = 3
3 1
3
7
A 9
3
8 9 1
5
4
1
3
4 ;
3
A11 = 5
A12 = -7
A13 = -6
A21 = -3
A22 = 6
A23 = 3

70.

Вычисляем алгебраические дополнения для третьей строки
Первый столбец: i=3; k=1
A31 ( 1)
3 1
2
3
7
A 9
3
8 9 1
5
4
Второй столбец: i=3; k=2
A32 ( 1)
3 2
D(A) = 3
7 3
9 4
(28 27) 1
2
3
1
3
4 ;
3
7 2 3
A 9 3 4 ;
5 1 3
A11 = 5
A12 = -7
A13 = -6
A21 = -3
A22 = 6
A23 = 3

71.

Самостоятельная работа
Найдите алгебраическое
дополнение А33
D(A) = 3
7
A 9
5
2
3
1
3
4 ;
3
A11 = 5
A12 = -7
A13 = -6
A21 = -3
A22 = 6
A23 = 3
A31 = -1
A32 = -1

72.

Вычисляем алгебраические дополнения для третьей строки
Третий столбец: i=3; k=3
A33 ( 1)
D(A) = 3
3 3
7 2
9 3
7
A 9
5
2
3
1
3
4 ;
3
21 18 3
A11 = 5
A12 = -7
A13 = -6
A21 = -3
A22 = 6
A23 = 3
A31 = -1
A32 = -1

73.

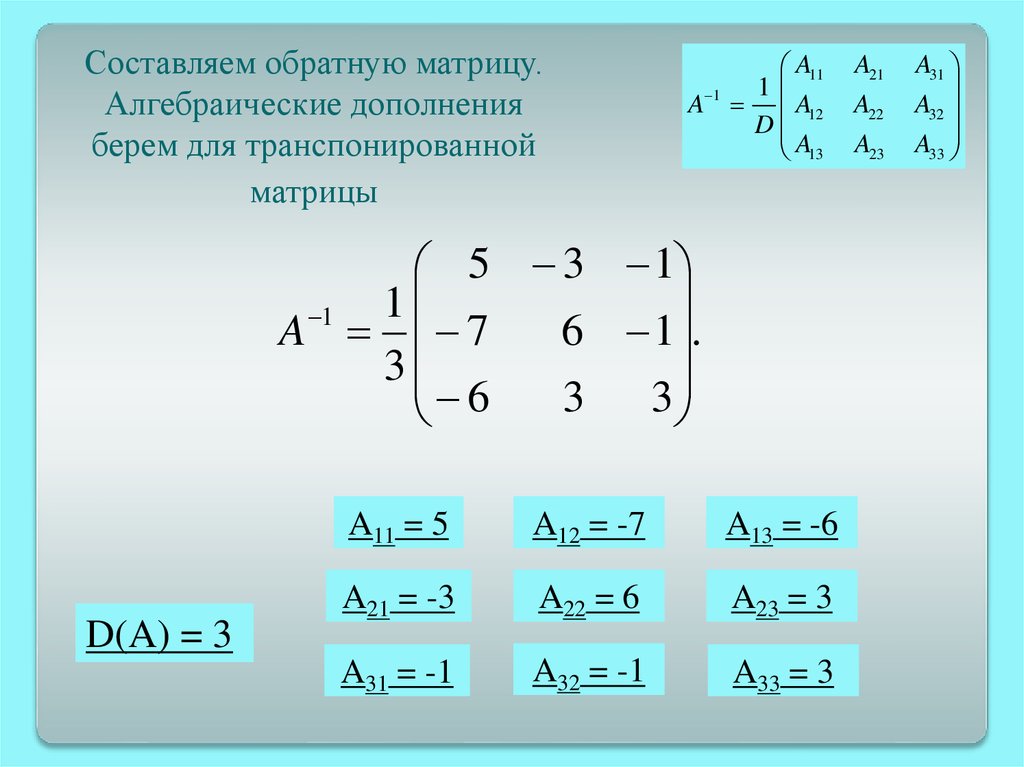
Составляем обратную матрицу.
Алгебраические дополнения
берем для транспонированной
матрицы
A11
1
A 1 A12
D
A13
5 3 1
1
1
A 7
6 1 .
3
6
3
3
D(A) = 3
A11 = 5
A12 = -7
A13 = -6
A21 = -3
A22 = 6
A23 = 3
A31 = -1
A32 = -1
A33 = 3
A21
A22
A23
A31
A32
A33

74.

Находим решение системы уравнений:
5 3 1 13
1
1
X A B 7 6 1 15
3
14
3
3
6
5 3 1
1
1
A 7
6 1 .
3
6
3
3
7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
3
1 2
13
B 15
14

75.

5 3 1 13
1
X 7 6 1 15
3
14
6
3
3
5 13 ( 3) 15 ( 1) 14
6 2
1
1
( 7) 13 6 15 ( 1) 14 15 5
3
3
3
(
6
)
13
3
15
3
14
9
Решение системы уравнений:
x1 2;
x2 5;
x3 3.

76.

Проверка
7 x1 2 x2 3 x3 7 2 2 ( 5) 3 3 13
9 x1 3x2 4 x3 9 2 3 ( 5) 4 3 15
5 x x 3 x 5 2 ( 5) 3 3 14
1
2
3
7 x1 2 x2 3x3 13
9 x1 3x2 4 x3 15
5 x x 3x 14
3
1 2
x1 2;
x2 5;
x3 3.